Mapping Design Principles to Instructional Realities in Early Grade Mathematics in South Africa: A Framework for Designing and Evaluating Learning and Teaching Support Materials

Abstract

The majority of children in mainstream (no fee, poorly resourced, African language dominant) public schools in South Africa fall significantly behind curricular norms in mathematics by Grade 3; the early learning gap grows across time. The provision of quality instructional materials is a well-recognised component of effective strategies to improve early grade mathematics in low- and middle-income contexts. However, there has been little explication of what constitutes quality instructional materials, nor long-term design work to contribute theory to this instructional design challenge. Across 15 years, the author has been working in an education design hub with teacher educators and teachers in the rural Eastern Cape, with the goal of improving early grade mathematics. The gains in mathematics performance have been among the most significant reported in research literature. This paper presents the design principles emerging from the work. Engaging the theoretical layers discussed by diSessa and Cobb, the paper contributes to design theory by emphasising the relationship between explicit instructional assumptions and design principles, integrating four ontological categories (motive, pedagogy, language use and mathematical meaning-making). Since 2011, the Department of Basic Education has provided learner workbooks to support teaching and learning in foundation phase mathematics at system scale. It is hoped that this paper will contribute to the ongoing development of this vital national resource. The paper makes explicit instructional assumptions and design principles (available for critique, adaptation, and refinement), and provides a more nuanced framework through which to assess and improve materials across time.

Keywords:

• Primary mathematics education
• design principles
• instructional design
• LTSM
• learner workbooks
• language in mathematics

1. Introduction

Research focusing on early primary school mathematics in mainstream schools in South Africa (no-fee, chronically under resourced and African language dominant) confirms the extreme inequality of the public system of education. Combining national datasets on learner performance in mathematics, Spaull and Kotze (2015) conclude that the learning deficit between the poorest 60% of children and the wealthiest 20% of children is approximately three grade levels by Grade 3 and increases as learners move through the system.

The provision of quality instructional materials is a well-recognised component of effective strategies to improve early grade mathematics in low- and middle-income contexts (Nag et al., 2014). While research has affirmed the importance of quality instructional materials (Nag, et. al., 2014; Spaull & Taylor, 2022), there has been little explication or theorisation of the instructional materials themselves. As such, we have little evidence about how to maximise ‘quality’ instructional materials, and few tested design principles through which to maximise their pedagogical impact.

Launched in 2010, the Magic Classroom Collective (MCC) is a longitudinal education design study, working with foundation phase teachers in isiXhosa-dominant rural primary school classrooms (Ramadiro & Porteus, 2017). The work responds to the historic neglect of educational research and development embedded within mainstream primary schooling. The goal is to develop a more nuanced understanding of instructional realities and to design tools capable of flourishing in these instructional contexts, deepening our understanding of ‘what works and why’.

Given the promising results emerging from the MCC in early grade mathematics (Porteus, 2022; Porteus et al., 2021), this paper extracts the design principles emerging from the long-term work, presenting a framework for designing and evaluating LTSM serving foundation phase mathematics in mainstream primary schools in South Africa. The goal of the paper is to present the design principles as an integrated whole and suggest how these principles come together to scaffold a unique set of teaching and learning materials. A more detailed discussion of any given principle is beyond the scope of the current paper.

2. Conceptual Framework

Educational design research is ‘the systematic study of designing, developing and evaluating educational interventions as solutions for complex problems in educational practice, which aims at advancing our knowledge about the characteristics of these interventions and the processes of designing and developing them’ (Plomp, 2007: 12). Researchers and practitioners (in this case rural foundation phase teachers) work together to ‘design and develop workable and effective interventions by carefully studying successive versions (or prototypes) of interventions in their target contexts’ (Plomp, 2007: 13).

As summarised by McKenney and Reeves (2012), research takes the form of iterative cycles in which ‘successive approximations of practical products’ (the intervention) go hand in hand with ‘successive approximations of theory’, often expressed through design principles. McKenney and Reeves (2012) point to the work of Bell, Hoadley and Lynn (2004) when they define design principles as:

an intermediate step between scientific findings, which must be generalised and replicable, and local experiences or examples that come up in practice … The principles are generated inductively from prior examples of success and are subject to refinement over time as others try to adapt them to their own experience. (p. 83)

diSessa and Cobb (2004) suggest that while a primary aim of design studies is to explicate theory, many struggle to capture theoretical contributions owing to the complexity of real-world settings. diSessa and Cobb (2004) remind us that the power of theory to ‘teach us how to see’:

bringing order to a vast array of seemingly disparate phenomena … They enable us to discriminate between relations that are necessary and those that are contingent. They delineate classes of phenomenon that are worthy of inquiry and specify how to look and what to see in order to understand them. (p. 79)

They highlight three levels of theorisation applicable to most design studies: orienting frameworks (meta-theories of learning), frameworks for action (emphasising the pedagogical) and domain-specific instructional theories (focused on significant disciplinary ideas and the objects of learning). While many design studies emphasise frameworks for action, diSessa and Cobb (2004) discuss the limitations of this level of theorisation. Given that instruction depends upon a range of factors (values, resources, cultures), too often design studies do not make explicit the instructional assumptions that underpin any pedagogical suggestion. They talk about ‘managing the gap’ to name the factors that underlie theory, especially those related to frameworks for action (diSessa & Cobb, 2004: 81–83).

Beyond these levels, they suggest that design studies can also contribute cross-cutting theoretical insights, what they call ‘ontological innovation’. Ontological innovations provide new lenses for making sense of what is happening in complex instructional settings. They can delineate new categories, suggest the reformulation of previously adopted categories, emphasise the relationship between categories that are frequently considered in isolation, or ask the designer to scrutinise previously implicit aspects of a design task (diSessa & Cobb, 2004: 84–85).

3. Intervention Design

The MCC education design collective brought together a senior design team, teacher educators and 55 foundation phase teachers (serving 2,100 children) from 13 primary schools in the deep rural Eastern Cape. An instructional toolkit was designed for each term. The spine of this toolkit was a mathematics learner workbook. The workbooks were field tested by teachers in classrooms, and reviewed and redesigned annually based on classroom observation, reflective discussions and teacher reflective questionnaires across more than 10 years.

During the earlier phase of the work (roughly 2010–2017), design principles focused on three primary goals: (1) legitimating and improving teachers’ use of isiXhosa as the language of teaching and learning in early grade mathematics; (2) establishing a daily instructional base-step (with mathematics taught as a daily ritual); and (3) supporting sensible sequencing, pacing and progression. By 2014, MCC classrooms had achieved stronger gains than any cohort presented in the intervention literature, improving between 29 percentage points (+1.7 SD) and 39 percentage points (+2.2 SD) on baseline results (Porteus, 2022).

Whereas previously these classrooms were homogenous (all children failing equally), they were now more complex; learner performance demonstrated a more bell-shaped curve. By 2017, the cohort took a small step back (Porteus, 2022). It became increasingly apparent that while teachers had improved their instructional pacing and progression, their relationship with mathematics and their ability to engage with more complex classrooms remained fragile. Further improvement in learner performance would require an expanded set of design principles whereby the design goals stretched beyond pacing and progression to transforming teachers’ relationship with mathematics, and teaching within more complex instructional settings (Porteus, 2022).

This paper presents the expanded set of design principles emerging from this next phase of work. The design principles emerged and transformed through a dialectical engagement between empirical engagement with instructional practice within the MCC, and ongoing engagements with the maths education literature. In order to capture this dialectic, we present design principles in relationship to empirical experience, supported by the literature which contributed to our thinking across this period.

4. Design Principles

4.1. Introduction

The design principles emerging in this phase of work are organised into four categories: instructional motive, pedagogy, mathematical meaning-making and language use. This section presents the design principles, linked to instructional assumptions. The following section will demonstrate how these principles come together to scaffold an unusual set of materials, accountable to the instructional realities of mainstream teachers.

4.2. Category: Instructional Motive

This category of design principles focuses on the instructional motive of teachers, framing how readily teachers pick up, engage with and ultimately experiment with any given instructional tool.

4.2.1. Instructional motive principle 1: tools must assume low instructional motive, have an ‘easy on-ramp’, and quickly reward effort by demonstrating impact

Ryan and Deci (2000: 70) link intrinsic motivation to experiences of competence, connectedness and autonomy. While a full discussion is beyond the scope of this paper, teachers in mainstream schools have not experienced feelings of competence, connectedness and autonomy over extended periods of time. The tools provided to teachers across time (not well-tested within mainstream classrooms), have yet to produce these conditions in mainstream classrooms.

Instructional designers must accept that most mainstream teachers will not readily pick up and experiment with new instructional tools. Tools must have an ‘easy on-ramp’, must be productive (in the most rudimentary way) even when teachers invest minimal energy into making them work, and quickly reward effort by demonstrating impact.

The choice of a structured ‘learner workbook’ as the carrier (spine) of an instructional strategy (instead of lesson plans or manuals for example) is rooted in both how workbooks improve practice and motive among teachers who use them in a limited form and how they further transform motive and practice for teachers ready to invest more pedagogical energy (see Ramadiro & Porteus, 2017: 71–75).¹

Accepting the role of ‘structured’ materials in the short term, the goal is not ‘compliance’, but the development of teachers’ sense of agency (competence, connectedness and autonomy) across time.

4.2.2. Instructional motive principle 2: instructional tools must work without the early requirement of a teacher manual

Across years of work, we have found that only strong teachers (who have developed a stronger motive for teaching) read for instructional purposes (Ramadiro & Porteus, 2017: 72). While we must continue to support (and push) teachers to develop their relationship with reading for professional development, tools that rely on teachers reading supplementary materials (teacher guides, lesson plans, etc.) will not flourish in the short term.

High-value instructional scaffolding and signalling for mathematical instruction must be located in the learner workbooks themselves.

4.3. Category: Pedagogical Practice

This category of design principles focuses attention on pedagogical opportunities and constraints in mainstream classrooms.

4.3.1. Pedagogical principle 1: pedagogical practice (and imagery) must be productive within the resource constraints of mainstream classrooms

Mainstream classrooms are chronically under-resourced, without the organisational and pedagogical systems required to systematically use resources commonly suggested in instructional materials. Materials and instructional strategies that rely on resources (including learning manipulatives) beyond the chalkboard (and related provisions) are unlikely to be quickly generative for most teachers. Establishing high-value concepts through specific manipulatives (Cuisenaire rods, even bottle top strips) is unlikely to land across large numbers of classrooms in the short term.

Providing teachers with mathematically meaningful manipulatives is not the problem. (The MCC toolkit, for example, uses multifix cubes in Grades 2 and 3.) However, the consolidation of high value concepts cannot rely on manipulatives. The resources represent pedagogical stretch rather than core instructional strategy.

4.3.2. Pedagogical principle 2: instructional tools must provide strong scaffolding to develop teachers’ instructional base-step

In the early phase of the design collective, the primary binding constraint was teachers’ lack of instructional structure or ‘base-step’. Teachers struggled to teach across the curriculum in regular lessons across a day, week and term. A primary goal of the workbooks is to assist teachers to develop a sensible rhythm for daily teaching by establishing daily, weekly and termly ‘bites’ of teaching (Ramadiro & Porteus, 2017).

The MCC materials make explicit the structure of teaching across a day, week, term and year. There are four term-based workbooks. The first three terms have eight structured weeks of work; the last term has six weeks. A 12-page imithamo (bite sized piece, or ‘lesson-set’) structures each week, focusing on one concept area. Each week begins with four 2-page spreads, each designed to structure a daily lesson.

The materials embed a four-step lesson plan:

• Lesson starters—mental maths, including a call and response game (Fizz Pop), strategic counting and a pair-oriented fluency game.

• Game of the week—illustrated and described each week, teachers play the game every day during the week. While seemingly simple, these games represent a stretch for most teachers.

• Daily maths lesson—teachers then present the lesson of the day. Each daily two-page spread suggests a strategy to represent and talk about the concept of the day, easily drawn on the board.

• Learners practice lesson—after delivering the lesson on the board, learners complete the two-page spread of the workbook on their own, tightly linked to the daily lesson.

Each week includes an additional page, modelling word problems. The fifth day consists of a mini- assessment, a timed fluency activity, a discussion of key words, a page of practice and a page of spatial skills and puzzles. In total, there are 360 pages, structured within 30 teaching weeks; two-thirds of the pages present new work (two-page spread lessons) and one-third of the pages provide practice, assessments and games.

4.3.3. Pedagogical principle 3: the instructional method embedded within a toolkit must be achievable within a whole-class oriented teacher-directed pedagogical culture

The dominant pedagogical culture in mainstream classrooms remains whole-class oriented and teacher directed (Hoadley, 2016; Ramadiro & Porteus, 2017). The educational literature from low- and middle-income national contexts suggests that despite a range of training strategies and investments to transform a whole-class teacher-directed pedagogical culture in low-income contexts, there is little evidence that interventions successfully disrupted the culture in sustainable ways (Nag et al., 2014).

If one of the key goals of any instructional tool is to re-build teachers’ motive for teaching, the tool must provide teachers with experiences of competence—where efforts translate into results (Ryan & Deci, 2000). As such, a toolkit must be designed, in the first place, so that when a teacher puts in a bit of effort (even within a whole-class teacher-directed pedagogical culture) s/he will reap results in the form of learner progress. Said another way, the first goal is to improve whole-class teacher-directed pedagogy.

4.3.4. Pedagogical principle 4: while workable within a whole-class, teacher-directed pedagogical culture, tools must scaffold opportunities for pedagogical growth, establishing a bridge to more interactive and differentiated praxis

While tools must be initially productive within current whole-class-oriented pedagogical practices, they cannot simply reinforce current instructional constraints. Accepting that whole-class pedagogical practice is unlikely to transform through training alone, tools must establish small achievable ‘stretches’ for teachers ready to invest more energy. In the long run, we hypothesise that the leap from whole-class to more interactive and differentiated teaching will be achieved through small steps along a bridge. To expect a teacher to cross this bridge over time, each step must be achievable. When a teacher takes the existential risk of extending her practice, the step must be fully workable in her classroom context.

Two examples of small achievable steps along this bridge woven into workbooks include:

• Learners benefit from a tight relationship between the lesson (what the teacher writes on the board and talks about) and the work they undertake to practice the lesson of the day. Teachers often ask the struggling learners to complete work from previous days to ‘catch up’), unlinked from the day’s instructional messages and ideas. For each two-page lesson, the first page presents core work, increasing in complexity on the second page. For the few learners who do not complete the second page, teachers are encouraged to allow them to skip the second page, thereby keeping up with the next day’s lesson, so that struggling learners benefit from alignment of the work they do with daily instruction.

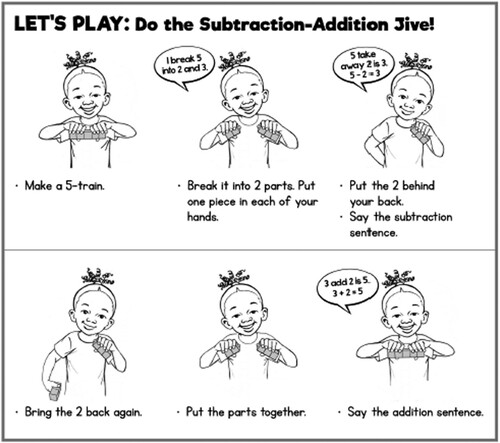
• In our work to develop the ‘small steps’ along the bridge to expanded praxis, we have found that teachers have more success moving from whole-class oriented practice to pair-based work (rather than other kinds of groups). In pairs, all learners engage the same activity at the same time. Workbooks illustrate and describe two games each week. The first game is more conceptual in nature. The second game focuses on fluency work. Games can be played at different pedagogical levels—from whole class, to pairs to differentiated pairs. See example in Figure 1.

Figure 1. Exemplar: ‘Game of the week’ (presented in English only for publication)

4.3.5. Pedagogical principle 5: a tool must provide sensible rhythms and tools for formative and summative assessment

Teachers struggle to develop assessment tools, and to make meaning of assessment for purposes of teaching. While a discussion is beyond the scope of this paper, a toolkit should offer sensible exemplars for formative and summative assessment. The MCC toolkit provides weekly mini-assessment tasks for teachers to consider whether the teaching goals of the week are achieved, as well as term-based assessment tasks, structured to the requirements of the national assessment management system. The formal assessment tasks focus on key conceptual markers per grade, and link with instructional strategies for learners who do not reach these goals.

4.4. Category: Mathematical Meaning-making

As emphasised in the work of Erath et al. (2021), it is difficult to separate ‘mathematical meaning-making’ from ‘language-use’ in the classroom. Nevertheless, we establish two interrelated categories. We present seven interrelated principles related to mathematical meaning-making, starting with the generative proposition that learner workbooks, in this context, must hold the burden of transforming teachers’ relationship with early grade mathematics. We discuss the interrelated category of language use below.

4.4.1. Mathematical meaning-making principle 1: the tool must embed a ‘teacher development programme’, building a claim to mathematical meaning-making among teachers

The early MCC learner workbooks presented CAPS-oriented mathematics with an emphasis on pacing and progression. By 2018, teachers had made significant gains in learner performance (through better pacing and progression), but continued to demonstrate a fragile relationship with mathematics itself (Porteus, 2022). When approaching the subtraction problem 92 − 58, 20% did not get the answer right, others relied on unit counting (Porteus & Mostert, 2022). The fragile relationship with mathematics among primary teachers is recognised in South African research literature (Taylor, 2019; Roberts, 2018; Venkat, 2013). Even so, the extent of alienation demonstrated in these artefacts suggest that the depth of the meaning-making crisis in the bones of the system has not been fully appreciated.

Most teachers have at best learned mathematics through an emphasis on memorisation; at worst mathematics’ memorisation has been ‘beaten in’. In a culture that is strongly faith based, the capacity for some children to ‘do some mathematics’ feels to many teachers to be God-given rather than ‘taught’. Over time this has translated into the reproduction of a system of memorisation, mathematical alienation and shame, with little claim on mathematical meaning-making among teachers handed down to learners.

This unusual design principle suggests that the learner workbook must carry the burden of transforming teachers’ relationship with early mathematics, establishing a claim to mathematical meaning-making among teachers, a pre-condition, we argue, for establishing a claim to meaning among learners.

4.4.2. Mathematical meaning-making principle 2: establish high-value mathematical goals for each grade, emphasising the structure of the number system and relationships between mathematical concepts

Without a deep relationship to mathematics as meaningful, teachers interpret curriculum goals as ‘lists’ needing to be covered, without seeing the structure and relationships through which mathematics builds across time. While the workbooks are guided by CAPS curriculum goals, they place emphasis on high value mathematical goals for each grade, with an emphasis on the structure of the number system and relationships between mathematical concepts.

The high value goals established for Grade 2, for example, include: (1) a deep understanding of place value (both additive and multiplicative); (2) consolidation of the structure of 2 (double, multiplying 2s, half, odd, even); (3) the relationship between addition and subtraction; and (4) an early recognition of the relationship between multiplication and division. When a learner does not understand place value, her mathematical future is difficult to heal (see also Morrison et al., 2021). When she is not able to multiply by 3, she is unlikely to continue to make meaning of maths in Grade 3.

4.4.3. Mathematical meaning-making principle 3: the tool must make explicit early grade learning trajectories, sharing theory (rather than only examples) with teachers

Given that many teachers have enjoyed such limited mathematical meaning-making, it goes without saying that few teachers understand the mental steps through which most children develop to understand any given mathematical concept. As such, when a child does not know how to do a specific mathematical task, teachers are unclear what constitutes a ‘step back’.

The work of Clements and Sarama (2021) has provided the most detailed and evidence-based map of learning trajectories, grounded in the experience of the US schooling system. They approach learning trajectories in three parts: (1) a specific mathematical goal; (2) a path along which children develop to reach that goal; and (3) a set of instructional activities aligned to developing children to progress along this path (Clements & Sarama, 2021: 3).

The work of Clements and Sarama (2021) provides starting points. However, their work assumes a different instructional context. Research informing learning trajectories in the context of mainstream classrooms in South Africa remains in its early stage. The learning trajectories presented in the MCC learner workbooks are informed by international research, developed and modified through empirical work within the MCC.

The design principle suggests that workbooks scaffold explicit learning trajectories, in order for teachers to deepen their own meaning-making, understand the ‘bite sized’ steps of meaning-making for children and know how and when to ‘step back’ when learners fall behind.

4.4.4. Mathematical meaning-making principle 4: select and build up a limited set of high impact mathematically meaningful representations, tightly aligned to strategy and procedure

As emphasised by Roberts (2019), CAPS does not make distinctions or selections between strategies (ways of thinking), representations (how thinking can be structured, leveraged and recorded) and procedure (a generalised step by step rule or method about how to create a particular representation to show a specific strategy). The lack of direction in regard to strategy and representation translates into learning material whereby multiple representations are used, but none are systematically developed to shed light on mathematical meaning across time and across concepts.

Given that the use of mathematical representations requires extensive practice over long periods of time (Askew, 2012), this design principle advocates for the careful selection of a limited set of strategies and mathematical representations to build up across time and a tight alignment between representations, strategy and procedure.

We selected the representational system based on: (1) the representation’s power to develop a mental framework through which to build mathematical meaning-making (its capacity to disrupt internalised imageries and scaffold more productive mental imageries); (2) the representation’s ability to grow (or travel) with learners and teachers into higher levels of mathematics; and (3) the extent to which the representational system is available for effective use (easily drawable by both teacher and learner) in mainstream classrooms.

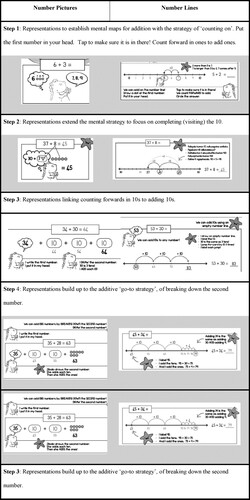
In the end, we chose a combination of number pictures (providing a counting pathway for number) and empty number lines (providing a measurement pathway for number); see Roberts and Porteus (2023).

4.4.5. Mathematical meaning-making principle 5: consolidate a meaningful ‘go-to’ method for new mathematical goals; focus on more flexible strategies where a ‘go-to’ strategy is already secure

In the context of a meaning-thirsty system, this design principle advocates for establishing a meaningful ‘go-to’ strategy for handling primary mathematical concepts, focusing on more flexible strategies once a go-to method is secure. In relationship to early additive relations, we suggest a go-to method must: (1) work every time; (2) expose teachers and children to a mental map of the number system, with an emphasis on place value (rather than conceptual short cuts); (3) require practice that consolidates an understanding of the number system; (4) lend itself to accurate instructional narratives; and (5) be easily externalised through chosen representations. The ‘go to’ strategy must be developed explicitly and illustrated through worked examples.

In additive relations, the MCC adopts the strategy of ‘breaking down the second number’ as the go-to strategy, building the strategy systematically through number pictures (numbers as discrete) (Porteus & Mostert, 2020) and through empty number lines (numbers as measurement/ordinal) (known as the ‘jump strategy’; Venkat & Graven, 2023); see Figure 2.

Figure 2. Representation, strategy and procedure: building a go-to strategy

4.4.6. Mathematical meaning-making principle 6: each daily lesson must constitute an ‘example space’, maximising the process of generalisation from specific examples

Children learn mathematics through engagement with examples rather than definitions or descriptions (Watson & Mason, 2006: 4). Watson and Mason approach an ‘example space’ as the active construction of a set of material (illustrations and examples) that allows for a process of generalisation from specific examples (Watson & Mason, 2006: 4), emphasising dimensions of possible variation (Watson & Mason, 2009).

In the workbooks, each ‘lesson’ (represented in a two-page spread) and each weekly set of work (umthamo, or bite sized piece) is designed with the goal of establishing an effective ‘example space’ for learning. Each example space focuses on a specific object of maths, presented, as much as possible, within a meaningful context, with a tight alignment between the object of learning, the context, the instructional narrative, strategy, representations, and worked examples. The example space introduces variation in ways that draw the eye to patterns of variation and invariance (Marton, 2014; Watson & Mason, 2006).

Responding to children’s fragile visual literacy, each page in end must feel ‘simple’. Small embellishments distract. While in constant tension with all of the other design principles, we continually re-learn the same lesson—when pages do not look and feel simple, they are poorly used in classrooms.

4.4.7. Mathematical meaning-making principle 7: the tool must provide ample opportunities for practice, build fluency and consolidate ‘known facts‘

Learners have few opportunities for practice and to build fluency. This reflects two distinct weaknesses. First, teachers feel compelled to move quickly from one lesson to the next, accountable to district ‘lesson trackers’ rather than the consolidation of learner maths knowledge. Second, most teachers teach at the same (slow) pace across the day, with little experience of speeding up maths for the purposes of building fluency.

The massive constraint to instructional design that may not be apparent in this discussion is the intense pressure on time/space. If we are going to cover curriculum goals, and at the same time build up concepts carefully, the space for presenting work is tight, even when strategies and procedures are narrowed. The pressure to ‘move quicker’ and do fewer examples in order to ‘keep up’ with curricular expectations are enormous. Ensuring well-paced conceptual progression, while maintaining adequate space for practice, is an ongoing balancing act.

The current workbooks scaffold opportunities to build fluency in three ways. Practice pages make up 20% of the workbook. Scaffolding for faster work to develop rapid recall is provided through the pair-based learner fluency games and a weekly rapid recall challenge.

4.5. Category: Language Use

Erath et al. (2021) undertook a review of four decades of research and development on language in mathematics classrooms, establishing a consensus among researchers that enhancing language is crucial for mathematical learning. Their work establishes six design principles for instruction, emphasising rich discursive practices and language routines, making connections between languages and representations, and scaffolding to combine language and mathematical learning opportunities.

The most important resource a child brings with her on the first day of schooling is her home language(s) (Ramadiro, 2018). Mathematics is not only dependent upon language but does not exist outside of language. As summarised by Barton (2012: 227): ‘we bring mathematics into existence by talking about it’ (Mostert, 2021: 46–47). The task of mathematical teaching is, at its core, an intentional and careful shift, building upon ‘everyday’ language to develop a ‘mathematical language’ with the capacity for greater abstraction (Clarkson, 2009; Mostert, 2021).

This category places the language of learning and teaching (LOLT) at the centre of workbook design. (The design principles relating to language-use in mathematics beyond a child’s home language are not included in this paper.) While policy supports the use of children’s home language in the foundation phase, the development of quality mathematical instruction in African languages has been undermined in several ways. Teachers do not develop an instructional register in African languages for maths through initial teacher education (Ramadiro, 2022); instructional materials are written in English, with little understanding of how African languages are best leveraged for learning; assessment policy/practice does not scaffold a reasonable language transition in primary mathematics; and there has been little investment in research and development through the normative lens of African languages. Taken together, these factors have led to mathematics being taught through a contracted (and often inaccurate) instructional style, where children’s languages are neither well used nor developed as resources for mathematical learning.

Accepting that we are far from the ‘rich discursive instructional practice’ described by Erath et al. (2021), this category of design principles combines language use and dialogic activity in mathematics classrooms to identify ways in which workbooks can scaffold achievable gains in this period.

4.5.1. Language use principle 1: assist teachers to leverage home language (LOLT) resources for primary mathematics instruction, developing and signalling high-value and learning friendly instructional narratives that bring a concept to life in the classroom

This principle emphasises the importance both normalising the use of African language instruction (LOLT) in mathematics and investing in the development of quality instructional narratives in African languages.

In the early work of the MCC, this principle was emphasised through basic workbook design and training. Materials were either developed through isiXhosa, or if designed in English, subject to a senior versioning exercise. Training was undertaken through the African language LOLT.

In the current phase, we build upon these foundations by developing and signalling quality instructional sentences that maximise learning within any given lesson, focusing on the alignment of language use, concept and mathematical representations. For any example space (and related representation, strategy and procedure), workbooks signal the priority instructional sentences or phrases that best bring the concept to life.

Even in more resourced (and monolingual) contexts, the shift from everyday language to developing a ‘mathematical language’ remains difficult for many children. Clarkson (2009) proposes that the difficulty has to do with teachers’ developing a strong enough ‘intermediary register’, what we call an ‘instructional register’—the language used by teachers to bring mathematical concepts to life in any language context.

With little investment in developing an instructional register in African languages, teachers’ maths instructional register remain underdeveloped and susceptible to English dominance. As an example, Mostert (2021) explores the language of number comparison. English-speaking educators use the words ‘more than’ and ‘less than’ for early number comparison. The isiXhosa word ‘ngaphezulu’ means both ‘more’ and ‘above’. Without understanding this nuance, South African designers continue to organise number charts from the top to the bottom, whereby larger numbers are below smaller numbers. To leverage isiXhosa for learning, a number chart should be presented bottom-up, whereby larger numbers are above smaller numbers.

We approach an instructional register as the development of phrases, sentences and stories to convey conceptual meaning, in any given language and classroom context. An instructional register is mathematically accurate, accessible, fluent (easy on the ear) and instructionally friendly (interesting and/or relatable to children). In the MCC workbooks, the interactions between two characters (Zibalo and Infinity) model teacher talk for a given concept. Just to re-iterate, while the characters talk in the learner workbooks, they are designed to whisper to teachers; the talk is beyond the reading capabilities of learners.

4.5.2. Language use principle 2: provide ways for children and teachers to externalise their thinking, as well as signal an instructional discourse that can expand productive classroom maths talk over time

Mathematics education research consistently emphasise the importance of rich discursive instructional environments in which children are encouraged to express their thinking, ask and answer questions, and talk about their strategies (Anghileri, 2006: 132; Erath et al., 2021).

A discussion of the complexity and constraints on classroom talk in mainstream classrooms lies beyond this paper. As a generalised starting point, the patterns of maths-oriented dialogic engagement between teachers and children are constrained. Verbal interactions between teachers and children are largely confined to call-and-response type interactions, or giving correct answers (Hoadley, 2016). The constraints are cultural and pedagogic, and reflect the low claim on mathematical meaning-making. We require more research and development of effective tools to assist teachers to expand classroom talk over time.

In the meantime, instructional toolkits must provide appropriate scaffolding to assist teachers develop their mathematical interactions with learners in modest and workable ways.

The MCC workbooks express this principle in two different ways. The chosen representations are easily drawable by learners. As such, learners externalise their thinking, providing insight into children’s mathematical thinking, even when classroom talk is constrained. Secondly, the workbooks signal simple yet high-value opportunities for teachers to engage in modest mathematical discussions. What do you see? What is the same? What is the different?

5. Translating Design Principles

As emphasised by the work of DiSessa and Cobb (2004), design principles do not provide ready-made solutions. Understanding the rules of thermodynamic does not translate easily into the shape of an airplane. The process of translating principles into workbook pages (learning days, weeks and terms) is complex, requiring ongoing interpretation and experimentation. This set of principles was largely consolidated in the 2017–2018 period; since then we have focused on applying them to Grade 2 (into Grade 3). While instructional design is often not seen as the work of senior research, we approach it as such.

Figure 3 demonstrates how key design principles translate into instructional pages. Exemplar A shows the first lesson (a two-page spread) of a week focusing on understanding place value, by drawing and interpreting number pictures. Exemplar B shows a lesson (two-page spread) focusing on ‘Zibalo’s love for 10’ working on a number line. Exemplar C shows a lesson focusing on the relationship between addition and subtraction. Several design principles discussed above are evident in these exemplars.

Figure 3. Exemplars: translating design principles into user friendly pages

6. Design Theory

Table 1 summarises the design principles in relationship to explicit instructional assumptions. diSessa and Cobb (2004) discuss the theoretical contribution of design studies. The design principles presented in this paper engage in this discussion in two ways.

Table 1. Framework and Design Principles

Mainstream instructional realities		Design principles
1. Instructional motive
1.1	Tools serving mainstream classrooms must assume low instructional motive.	Tools must have an ‘easy on-ramp’, and quickly reward effort by demonstrating impact.
1.2	Only the strongest teachers read for instructional planning and professional development.	Instructional tools must work without the early requirement of a teacher manual.
2. Pedagogical
2.1	Classrooms have severe resource constraints; instructional tools are often limited to a chalkboard.	Pedagogical practice (and imagery) must be productive within the resource constraints of mainstream classrooms.
2.2	Teachers struggle to establish an ‘instructional base step’.	Instructional tools must provide strong scaffolding to build learning momentum through consistent instructional days, weeks and terms.
2.3	Pedagogical culture is largely confined to whole-class oriented, teacher-directed praxis.	Instructional methods assumed within a toolkit must be achievable within a whole-class-oriented and teacher-directed pedagogical culture.
2.4	There are few known strategies to shift whole-class instructional praxis to more interactive and differentiated praxis in the context of low-income nations.	The tool must scaffold opportunities for pedagogical growth, establishing a bridge toward more interactive, autonomous and differentiated praxis.
2.5	Teachers struggle to develop assessment tools, and to make meaning of assessment for purposes of teaching.	The tool must provide sensible rhythms and tools for formative and summative assessment.
3. Mathematical meaning-making
3.1	Most teachers have little claim on mathematical meaning-making, having learned mathematics mainly through memorisation.	The tool must embed a ‘teacher development programme’, building a claim to mathematical meaning-making among teachers.
3.2	Teachers largely interpret curriculum goals as ‘lists’ needing to be covered, without seeing the structure and relationships through which mathematics builds across time.	Establish high-value mathematical goals for each grade, emphasising the structure of the number system and relationships between mathematical concepts.
3.3.	Most teachers do not understand how mathematical concepts develop for children. When a learner is not able to do a task at grade level, teachers are largely unable to assist.	Make explicit early grade learning trajectories, sharing theory (rather than only examples) with teachers.
3.4	Most teachers continue to understand maths education primarily as a task of memorisation, reproducing mathematical alienation at national scale.	Select and systematically build up a limited set of high impact mathematically meaningful representations, tightly aligned to strategy and procedure.
3.5	Teachers do not have systematic ‘go-to’ strategies that establish the basis to build flexibility into the future.	Consolidate a meaningful ‘go-to’ method for high-value mathematical goals, developing more flexible strategies when a ‘go-to’ strategy is secure.
3.6	Teachers are not yet able to select examples in ways to maximise mathematical structure and relationships.	Each daily lesson and weekly set of lessons must constitute an ‘example space’, maximising the process of generalisation from specific examples.
3.7	Children have little chance to practice and build mathematical fluencies.	Provide ample opportunities for practice, build fluency, and consolidate ‘known facts’.
4. Leveraging language and dialogic engagement: constraints and opportunities
4.1.	Teachers have not had an opportunity to develop an effective instructional narrative in African languages to teach primary mathematics. Most teachers’ way of talking about mathematical concepts is not fully accurate, coherent or friendly.	Assist teachers to leverage home language (LOLT) resources for primary mathematics instruction, signalling high-value and learning friendly instructional narratives that bring a concept to life in the classroom.
4.2	The culture of dialogic engagement between teachers and children is highly constrained.	Tools must expand maths dialogic engagement between children and teachers, by providing mechanisms for children to externalise their thinking, and signalling opportunities for maths talk.

First, diSessa and Cobb discuss levels of theorisation (orienting frameworks, frameworks for action and domain specific instructional theory). They discuss the complexity of theorisation, especially in relationship to frameworks for action, whereby theory is contingent upon complex instructional settings. They speak to ‘managing the gap’ to name the limitation behind many theoretical contributions of design studies, where the ‘gap’ represents the complex and often unstated instructional contexts in which design studies are undertaken.

In Table 1, we present each design principle in relationship with instructional assumptions. The presentation attempts to ‘manage the gap’, making transparent the function between instructional contexts and design principles. The validity of design principles relates to a time-bound instructional context—in this case, South African current mainstream early grade maths classrooms. By making instructional assumptions explicit, designers can critique and engage the assumptions themselves, as well as improve design principles capable of transforming them. This emphasises the need for renewing design principles as instructional contexts transform. It reminds us that quality materials can only be developed by designers with a deep understanding of any given instructional context, and how they can be transformed.

diSessa and Cobb (2004) also suggest that design studies can contribute cross-cutting theoretical insights, what they call ‘ontological innovation’, providing new lenses for making sense of what is happening in complex instructional settings. They can delineate new categories, suggest the reformulation of previous categories, emphasise the relationship between categories that are frequently considered in isolation, or ask the designer to scrutinise previously implicit aspects of a design task (diSessa and Cobb, 2004: 84–85). The longitudinal design work presented in this paper suggests an ontological innovation by focusing design attention on the four categories of instructional motive, pedagogy, mathematical meaning-making and language use for developing materials for early grade mathematics in mainstream instructional settings in South Africa.

7. Conclusion

The provision of quality instructional materials is a well-recognised component of strategies to improve early grade mathematics in low- and middle-income contexts (Nag et al., 2014). While South African intervention studies have started to explore the impact of quality instructional materials in both literacy and mathematics (Spaull & Taylor, 2022), there has been little theorisation of the instructional materials, nor explication of the instructional assumptions upon which they are designed. As such, we have few tested design principles through which to assess the quality of instructional materials or maximise their pedagogical impact. When materials do not work, the failure is too often shouldered by teachers. They lose faith in themselves, their children, developmental interventions and the learning–teaching nexus itself. Further, we risk the system itself losing interest in classroom-based instructional interventions. Rather than conceding we are still in the process of understanding and designing instructional materials and strategies that work in mainstream classrooms, Spaull and Taylor (2022), for example, suggest that “as a country we may be reaching a ”low ceiling“ beyond which it is not possible to extend” with investments focused on teacher training and instructional materials. While larger investments into the transformation of limiting superstructures of education may be equally decisive, this paper suggests that the “low” ceiling is likely to also reflect the limitations of the intervention tools themselves. It suggests that tools developed through detailed design research with teachers holds the potential to break through this “low ceiling” across time.

This paper presents design principles emerging across over 10 years of work within an education design hub (known as the Magic Classroom Collective) in rural South Africa. Engaging the theoretical discussion framed by diSessa and Cobb (2004), design principles are presented in relationship to explicit instructional assumptions, bringing together four ontological categories (motive, pedagogy, language use and mathematical meaning-making) to guide instructional design in support of teaching mathematics in mainstream early grade classrooms. The framework is especially important in highly unequal societies, whereby dominant (usually unstated) instructional ‘norms’ often reflect more resourced instructional settings.

Since 2011, the Department of Basic Education has provided learner workbooks to support teaching and learning in foundation phase mathematics at system scale. It is hoped that this paper will contribute to the ongoing development of this vital national resource, maximising its design to transform teaching of mathematics in mainstream classrooms.

For instructional designers, the paper makes explicit instructional assumptions, design categories and principles, available for critique, development, adaptation and refinement. For LTSM evaluators, the framework provides a more nuanced lens through which to assess and improve materials, especially in highly unequal educational settings.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Notes

1 Our experience is that motive expands when teachers experience children in their classrooms achieving more than they had come to expect. This begins a generative process whereby instructional efforts (and risks) translate into visible learning results; success begets success (Ramadiro & Porteus, 2017).