Treating design uncertainty in the application of Eco-indicator 99 with Monte Carlo simulation and fuzzy intervals

Abstract

In incremental eco-design improvements, design engineers attempt to modify an existing product via some eco-design measures to reduce the product’s environmental impacts (e.g. reduction of material usage and energy consumption). In this process, several design concepts can be proposed, and concept selection is required to allocate resources sensibly to promising design concepts only. In this context, the research purpose is to estimate the environmental impacts of each concept given the uncertainty of design information. In the proposed methodology, the fuzzy interval arithmetic is used to specify and propagate imprecise design information. Then, the centroid concept is applied to model different views of imprecision (i.e. pessimistic, balanced and optimistic) associated with fuzzy impact assessment. Accordingly, a decision scheme is developed to support concept selection and suggest the potential areas for further eco-design improvements. A coffee maker is used as an example to demonstrate the proposed methodology. Also, the Monte Carlo Simulation is applied for the same example to compare the numerical outcomes by the fuzzy interval approach.

Keywords:

• Eco-design concept selection
• Eco-indicator 99
• fuzzy interval arithmetic
• Monte Carlo simulation

1. Introduction

1.1. The application of Eco-indicator 99

In the process of eco-design, one important task is to estimate the environmental impacts (or eco-impacts) of the design choices in order to inform the subsequent actions and decisions. While life cycle assessment (LCA) has been commonly cited to estimate the eco-impacts of a product (Chang, Lee, and Chen 2014; Finnveden et al. 2009; Ramani et al. 2010), the application of full-scale LCA is often challenging in product design and development (Knight and Jenkins 2009; Millet et al. 2007). In our view, there are two practical challenges. Firstly, detailed design information is not always available for full-scale LCA at some decision points. Secondly, the use of full-scale LCA requires the expertise from environmental scientists and LCA specialists, who may not be part of the engineering design team.

In this context, Eco-indicator 99 is intended to assist design engineers with less dependence on LCA experts to assess eco-impacts in a design process (Goedkoop, Effting, and Collignon 2000). Its main utility is to provide a set of eco-indicators that can convert design properties (e.g. weights of chosen materials) into a single score of eco-impacts. This eco-impact score can be used to compare the eco-performance of various design ideas during the concept selection stage (Otto and Wood 2001). Then, design engineers only need to take responsibility of the design itself with less worry over the domain of environmental assessments (e.g. mapping from mid-point to end-point indicators (Bare and Gloria 2008)). Sample applications of Eco-indicator 99 include the comparison of building insulation materials (Audenaert, De Cleyn, and Buyle 2012) and lighting products (Casamayor and Su 2013).

Notably, the use of Eco-indicator 99 is convenient for designers because it was purposely developed as end-point indicators, where normalisation and weighting were pre-set to ‘simplify the interpretation’ of the LCA results (Goedkoop et al. 2016, 35). In contrast, other LCA methods (e.g. ReCiPe) mainly vary by how flexible they allow practitioners to enter values for normalisation and/or weighting, which in turn require knowledge from LCA experts. This also explains the choice of Eco-indicator 99 in this research.

The standard practice of Eco-indicator 99 only takes single-point estimates of design properties. Yet, when the design details have not been completed, design engineers may want to provide ‘range estimates’ rather than ‘point estimates’ for design properties. The research’s motivation of this paper is to generalise the application of Eco-indicator 99 by supporting range estimates (or numerical intervals) in the calculation of eco-impacts.

For example, by the designers’ experience, they may be able to estimate that the total weight of steel to be used in a new design is between X and Y kg. To apply Eco-indicator 99 in this situation, designers need to find a representative value between X and Y kg in the evaluation of eco-impacts. To relax the requirement of ‘crisp numbers’ to estimate eco-impacts, the proposed approach is to generalise the inputs of design properties as fuzzy intervals in the application of Eco-indicator 99. By this generalisation approach, designers can use both crisp and fuzzy quantities to specify design properties in Eco-indicator 99.

Concerning the issue of applicability in practice, as the proposed method works on the extension of Eco-indicator 99, it is still confined with the limitations of Eco-indicator 99 in a design context. Listed below are some situations where the proposed method is not applicable.

•	Design engineers are not confident to give quantitative estimations (no matter point or range estimates) for a design concept. This situation may take place if designers work on relatively new design and the design properties are highly uncertain.
•	The product is too complex in a sense that its eco-impacts cannot be fairly decomposed in the way prescribed in Eco-indicator 99. For example, designers choose a material that requires a new process not yet covered in Eco-indicator 99. In this situation, designers may need to work with LCA experts to analyse the product life cycle and aggregate eco-impacts.
•	The value weighting or other assumptions in Eco-indicator 99 are deemed not suitable for assessing the product. This situation may happen when the product incurs environmental concerns that are locally confined and not covered in Eco-indicator 99. In this situation, LCA experts are often required for more detailed analysis and assessment.

1.2. Literature review

In literature, Monte Carlo Simulation (MCS) is one common approach to analyse uncertainty in life cycle assessment (LCA) (Groen et al. 2014; Lloyd and Ries 2007). Hung and Ma (2009) have applied the MCS approach to compare the impact of uncertainty from various stages of LCA. According to the references of two LCA software tools, i.e. ecoinvent (Frischknecht et al. 2007) and SimaPro (Goedkoop et al. 2016), lognormal distribution is suggested to model the input variations. In this work, the MCS approach is discussed to convert design uncertainty to lognormal distribution for executing MCS in the context of Eco-indicator 99.

While the MCS approach is covered in this paper due to its popularity in LCA, the main focus of this paper is to apply fuzzy interval arithmetic (FIA) to handle design uncertainty in the context of eco-design concept selection. The motivation is twofold. Firstly, the calculations required in Eco-indicator 99 are similar to computing weighted sums, and doing simulations like in the case of MCS may not be necessary. Secondly, fuzzy interval is a general form of numerical intervals (Lawrence, Kacker, and Kessel 2015), and it is more natural for engineers to specify design uncertainty as interval (e.g. dimensional tolerance) than as statistical variance.

Regarding fuzzy set theory in LCA, it should be noted that the notions of fuzzy linguistics and fuzzy intervals are different. In fuzzy linguistics, fuzzy sets are used to model linguistic expressions, and triangular fuzzy numbers are often used to capture some evaluative notions (e.g. high, medium, low) (Pedrycz 1994). The relevant research works include the fuzzy inference rules for overall assessments (Afrinaldi and Zhang 2014; de Siqueira Campos Boclin and de Mello 2006; Gonzalez, Adenso-Diaz, and Gonzalez-Torre 2002). Also, fuzzy linguistic variables have been applied for quality function deployment (QFD) in LCA (Bovea and Wang 2003; Kuo, Wu, and Shieh 2009), the valuation process from empirical data to expert judgements (Guereca et al. 2007; Liu and Lai 2009) and the multi-criteria analysis in LCA (Agarski et al. 2016; Benetto, Dujet, and Rousseaux 2008; Kuo, Chang, and Huang 2006; Ng and Chuah 2015).

In contrast, fuzzy intervals do not convey linguistic expressions. Instead, they capture the numerical intervals of physical values (e.g. LCA inventory quantities) with indications of their degrees of likelihood. Weckenmann and Schwan (2001) used trapezoidal fuzzy numbers to model imprecise inventory data in LCA. Tan (2008) applied triangular fuzzy numbers to incorporate uncertainty in the matrix-based life cycle inventory (LCI) analysis. Reza, Sadiq, and Hewage (2013) used fuzzy numbers to quantify ‘Unit Emergy Values’ in environmental assessments. Clavreul et al. (2013) applied trapezoid distribution to capture ‘epistemic uncertainty’, which can be obtained by questioning experts on interval values (1395, 1396). This paper mainly follows similar questions to inquire the uncertainty intervals by designers.

In the LCA literature, possibility theory (Dubois and Prade 1988), in which fuzzy intervals were developed, has been discussed to address the uncertainty due to estimations by experts without experimental outcomes (Clavreul et al. 2013). In this paper’s work, design uncertainty is considered under this category of uncertainty because the estimations of design properties are mainly based on the experience of designers. In addition, Groen et al. (2014) have compared and indicated that FIA can take less time to analyse uncertainty propagation as compared to sampling-based approaches (e.g. Monte Carlo Simulation). Thus, this paper is intended to apply FIA to represent and propagate the interval estimates of design properties in the application of Eco-indicator 99.

1.3. Paper purposes and outline

In sum, this paper has two purposes. The first purpose is to develop the fuzzy interval approach to capture design uncertainty in the application of Eco-indicator 99 and support eco-design concept selection accordingly. The second purpose is to compare the results from the fuzzy interval and MCS approaches to verify the proposed methodology.

In the rest of this paper, Section 2 will frame the design decision problem in the context of Eco-indicator 99 and discuss how design uncertainty is processed in both MCS and fuzzy interval approaches. Section 3 will develop the decision-making method that interprets the uncertainty expressed as fuzzy intervals. Section 4 will discuss the coffee maker design application to demonstrate the proposed methodology, along with the comparison of the MCS approach. Section 5 will conclude this paper.

2. Uncertainty treatments with eco-indicators for design decision-making

2.1. The context of design decision making

Design engineers need to address different types of decisions in a design process, and the nature of a decision problem depends on the availability of design information at the decision point. To be precise, the application context of this paper is intended for incremental design changes for eco-design improvement. In view of information availability in this context, designers should know the information of existing products. By eco-design improvements, the driving force for a new design is the reduction of environmental impacts (e.g. reduction of material usage and energy consumption). When targeting for incremental changes, designers should be able to approximate the properties of a new design as numerical intervals. Alternately, Eco-Indicator 99, along with the proposed method, is not applicable if designers cannot approximate design uncertainty via numerical intervals.

Concerning incremental eco-design improvements, one typical consideration is the trade-off between (1) conventional ideas with marginal yet predictable improvement versus (2) innovative ideas with potentially good yet less predictable eco-performance. The proposed decision method is intended to evaluate this kind of trade-off using Eco-Indicator 99 and FIA to model and propagate design uncertainty. Notably, the traditional use of Eco-Indicator 99 only yields point estimates of eco-impacts, which cannot particularly address this kind of trade-off due to lack of uncertainty information. In addition, the proposed method is not intended to reduce uncertainty precisely. Instead, it is intended to perform unbiased propagation of uncertainty based on the input uncertainty (i.e. the designers’ estimations can have high or low uncertainty). Through this practice, design engineers can develop some insights on which uncertainty sources are more essential and which are less.

2.2. Formulation

To set a decision problem, it is assumed that design engineers have come up with a set of design concepts. Here, a design concept is referred to as ‘an approximate description of the technology, working principles, and form of the product’ (Ulrich and Eppinger 2008, 118). In the context of incremental improvements, it is assumed that design engineers can provide estimations of design properties, where the uncertainty levels can be set in terms of numerical intervals.

Let D be the given set of design concepts, symbolised as D = {d₁, d₂, …, d_i, …}. To assess the design concepts using eco-indicators, it is required to know some engineering quantities associated with each concept. Typical engineering quantities include the amounts of materials and disposals (in kg) and energy consumption (in kWh). Let Q be the set of engineering quantities for the use of eco-indicators, symbolised as Q = {q₁, q₂, …, q_j, …}. Then, the notation q_j(d_i) is used to denote the value of quantity q_j pertaining to concept d_i. For example, suppose that quantity q₁ is about the weight of steel to be used in a product. Then, q₁(d₁) = 12.0 kg means that concept d₁ will use 12.0 kg of steel.

In Eco-indicator 99, each eco-indicator represents an impact index (in a unit of million points, or mPt) associated with an engineering quantity. Let E be the set of eco-indicators, and it can be expressed as E = {e(q_j) | q_j ∈ Q}, where e(q_j) is the eco-indicator of quantity q_j. For example, the eco-indicator of steel (quantity q₁) is denoted as e(q₁), which is equal to 86 mPt/kg. Then, let T(d_i) be the overall environmental impact of concept d_i, and it can be formulated as follows.(1)

In the context of concept selection, the uncertainty comes from the engineering quantity (i.e. q_j(d_i)) since concept d_i has not been physically realised. Thus, the uncertainty treatments are intended to handle the variations of the term q_j(d_i). The next two sub-sections will discuss the application of fuzzy intervals and MCS to handle this uncertainty term q_j(d_i).

2.3. Fuzzy interval approach

In this approach, the trapezoidal fuzzy number (TrFN) is used to express the uncertainty of quantity q_j. Two reasons are provided and discussed below on the choice of TrFN.

•

Theoretical aspect: fuzzy sets under possibility theory are often used to capture the uncertainty due to belief or judgement (Dubois and Prade 1988). The uncertainty of design information belongs to this category, where designers’ estimations are taken as expert judgements over the ‘future design’ (Wood, Otto, and Antonsson 1992). Also, TrFN is a generalisation of triangular fuzzy numbers, numerical intervals and crisp numbers, and the quadruple expression (a1, a2, a3, a4) of TrFN can be used to define them. For example, we can set a1 = a2 and a3 = a4 to get a pure interval and a2 = a3 to get a triangular fuzzy number.

•

Practical aspect: numerical intervals are common for engineers to understand imprecise information (e.g. dimensional tolerances). Fuzzy numbers are treated as one kind of intervals, which values can be easily interpreted by design engineers.

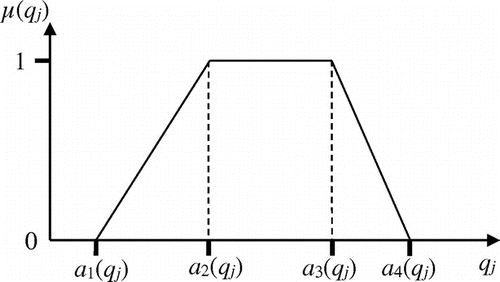
As the background, each TrFN (say, F_a) can be expressed as a quadruple, i.e. F_a = (a₁, a₂, a₃, a₄), in which a₁ represents the lower bound, a₂ to a₃ the range of typical values and a₄ the upper bound of the quantity. Then, let F(q_j) be the TrFN of q_j, and it is formulated as follows.

(2)

The membership function (denoted as μ(q_j)) of a TrFN reflects the likelihood of the actual value of the quantity q_j, and it is formulated in Equation (3(3) ). Figure 1 illustrates the plot of the membership function.(3)

Figure 1. Illustration of a trapezoidal fuzzy number.

To specify the TrFN in the design practice, expert judgements by designers are required to approximate the design properties if a design concept is adopted and developed. Such approximations include (1) the range of typical values and (2) the lower and upper bounds. While typical values represent the most possible values of design properties, the lower and upper bounds represent the optimistic and pessimistic estimations, respectively. In the formulation of TrFN, the lower and upper bounds are referred to a₁ and a₄, respectively, with the range of typical values from a₂ to a₃. For the design concept subject to higher uncertainty, designers can assign larger ranges of lower/upper bounds and typical values. As discussed before, the proposed method is not intended to reduce design uncertainty, which sources stem from the experience/skills of designers and their engineering analyses. Instead, after designers make interval approximations, the proposed method is used to propagate such information with the application of Eco-indicator 99.

To specify TrFN for a design concept, we have applied the following procedure in the design case of this research per incremental eco-design improvements.

•	Step 1: Identify the design data of the existing product.
•	Step 2: Specify the lower bound (i.e. a1) by considering the best design outcome (e.g. minimal material and energy usage) associated with the concept.
•	Step 3: Specify the upper bound (i.e. a4) by considering the worst design outcome (e.g. high material and energy usage) associated with the concept.
•	Step 4: Define the typical range (i.e. a2 and a3), which usually includes the middle of lower and upper bounds.

After defining the fuzzy engineering quantity F(q_j), it can be applied to Equation (1(1) ) by replacing q_j(d_i) with F((q_j(d_i)). To complete, let F(T(d_i)) be the fuzzy number of the overall environmental impact of concept d_i, and its formulation is given below.

(4)

Notably, FIA is applied here due to the arithmetic operations over the fuzzy numbers. As the background, suppose that there are two fuzzy numbers F_a = (a₁, a₂, a₃, a₄) and F_b = (b₁, b₂, b₃, b₄). Let w be a scalar, and ⊕ and ⊗ be fuzzy addition and multiplication, respectively. Equations (5(5) ) and (6) show the formulations for adding two TrFNs and multiplying a TrFN with a scalar. Notably, the eco-indicator calculations in Equation (4(4) ) only involve these two types of arithmetic operations, and fuzzy numbers after these operations still result in a fuzzy number (Lee 2006).(5) (6)

2.4. Monte Carlo simulation approach

Using MCS, the key notion is to treat engineering quantity q_j as a random variable. Taking the statistical distributions of q_j(d_i) as the inputs, MCS can be run using Equation (1(1) ) and yield the distribution of T(d_i) as the output. To apply MCS in this study, the lognormal distribution is applied to capture the input uncertainty (Frischknecht et al. 2007; Goedkoop et al. 2016). As the background, if a random variable W follows a normal distribution with the mean θ and the variance ω², the random variable X = exp(W) will have a lognormal distribution. It is common to use θ and ω² to specify X, which becomes the inputs to execute MCS.

When statistical variance is not available, expert judgements are required to estimate the variation associated with the lognormal distribution. Particularly, Frischknecht et al. (2007) suggested the use of the Pedigree matrix (Pedersen Weidema and Wesnæs 1996), which quantifies various types of uncertainty factors. Notably, the nature of this practice still relies on expert judgements to map the classified situations to indicator scores (ranging from 1.00 to 1.50).

To conduct the comparison study, the engineering quantities expressed as TrFN (i.e. F(q_j)) are treated as the original uncertainty inputs for both fuzzy number and MCS approaches. To apply MCS, these input TrFNs are first used to specify the corresponding lognormal distribution. Let F_a = (a₁, a₂, a₃, a₄) be the TrFN. The mean (i.e. E(⋅)) and variance (i.e. V(⋅)) of this TrFN can be calculated using the equations below, which are based on the work by Kacker and Lawrence (2007).(7) (8) (9)

Let W be a random variable following a normal distribution with the mean θ and the variance ω². Then, the random variable X = exp(W) follows lognormal distribution. To run the MCS based on lognormal distribution, we need to specify the values of θ and ω², which can be determined using the following equations (Johnson, Kotz, and Balakrishnan 1994).

(10) (11)

After lognormal distribution is specified for the engineering quantities (i.e. q_j), the MCS can be run using Equation (1(1) ) to yield the statistical distribution of the overall environmental impact, T(d_i) that is subject to the variations of q_j(d_i).

2.5. Methodological remarks

Functionally, both TrFN and MCS can handle the variation type of uncertainty with the use of eco-indicators. Here, the comparison of two approaches is based on two aspects: (1) the quantification of variation inputs and (2) the efficiency of propagating variations.

To quantify the variations of the inputs in TrFN, design engineers are required to estimate the upper and lower bounds (i.e. a₁ and a₄) and the range of typical values (i.e. a₂ and a₃). Arguably, such estimations are quite natural for engineers. Also, it is not required to set these four values to be different. In contrast, it is not quite direct for engineers to specify statistical variance that may be required in MCS. Notably, some execution of MCS may not require statistical variance. For example, SimaPro allows the inputs of ‘range’ and ‘triangular’ distributions to run MCS (Goedkoop et al. 2016). Even in this aspect, both TrFN and MCS are basically on par in view of specifying variations for numerical analysis.

In view of propagating variations, consider the traditional use of Eco-indicator 99 as one unit of calculations. Then, the proposed TrFN approach will take about four units of calculations due to the quadruple expression of TrFN. In contrast, MCS generally expects more than 100 units of calculations in order to yield good statistical distribution outcomes. Thus, the computational effort of the TrFN approach is considered less than that of the MCS approach.

3. Eco-design concept selection based on TrFN

3.1. Fuzzy number ranking and trade-off

By applying the fuzzy interval approach, the overall environmental impact (or eco-impact) of each design concept is expressed as F(T(d_i)), which is a TrFN. In the context of concept selection, it is desired to rank these TrFNs so that the concept with the lowest eco-impact can be identified. Yet, due to the presence of uncertainty, this ranking task becomes not trivial. One typical challenge is to choose between (1) a concept with a higher eco-impact but less uncertainty and (2) another concept with a lower eco-impact but more uncertainty. Given a TrFN as F_a = (a₁, a₂, a₃, a₄), higher eco-impact means higher values of a₂ and a₃, and higher uncertainty means a wider range between a₁ and a₄. This issue leads to the topic of fuzzy number ranking, which challenge is well recognised in the field (Abbasbandy and Hajjari 2009).

In our view, this basic challenge stems from the trade-off between two independent attributes: (1) mean value and (2) variation or uncertainty. Thus, simply reducing a TrFN into a single-value index for ranking may implicitly conceal the information related to such trade-off. More importantly, design engineers should try to understand the risk behind each option so that they can expect some possible consequences in their choices.

3.2. Three centroid indices of TrFN

To address the risk in the trade-off decision, the proposed method first applies the centroid index (Wang et al. 2006), which marks the geometric centre of a trapezoid. Let (x_c(F_a), y_c(F_a)) be the centroid point of a TrFN F_a = (a₁, a₂, a₃, a₄). Then, the centroid index is the distance (denoted as IN_c(F_a)) from the origin to the centroid point. The relevant formulations are provided below.(12) (13) (14)

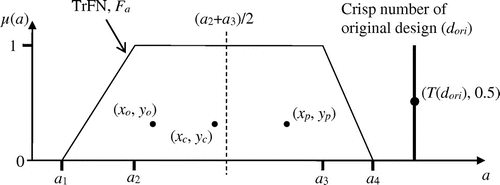
The above centroid index represents the ‘balanced’ view over the risk of uncertain results. By referencing the notions from Facchinetti, Ricci, and Muzzioli (1998), the pessimistic and optimistic centroid are proposed, and they focus on the aspects of poor and good results, respectively. Using eco-indicators, higher values mean poorer eco-performance. By taking (a₂ + a₃)/2 as the middle line, the pessimistic centroid focuses on the right-hand side of the trapezoid, which represents another TrFN with the quadruple as ((a₂ + a₃)/2, (a₂ + a₃)/2, a₃, a₄). Let (x_p(F_a), y_p(F_a)) be the pessimistic point of a TrFN, and IN_p(F_a) as the pessimistic centroid index. The relevant formulations are derived as follows. Figure 2 also illustrates the positions of different centroids of a TrFN.(15) (16) (17)

Figure 2. Illustration of centroid indices.

Similarly, the optimistic centroid focuses on the left-hand side of the trapezoid. Let (x_o(F_a), y_o(F_a)) be the optimistic point of a TrFN, and IN_o(F_a) as the optimistic centroid index. The relevant formulations are derived as follows.(18) (19) (20)

In sum, the design uncertainty expressed as TrFN is propagated through FIAand Eco-indicator 99, resulting in the eco-impact of a design also expressed as a TrFN. Given such a TrFN, the balanced centroid index (IN_c) represents the middle position of a trapezoid. In contrast, the pessimistic centroid index (IN_p) focuses on the prospect of high eco-impact (i.e. the right side of the trapezoid), while optimistic centroid index (IN_o) focuses on low eco-impact (i.e. the left side of the trapezoid). Then, designers can use IN_c, IN_p and IN_o to compare design concepts based on their tolerance of risk, which will be discussed in the next sub-section.

3.3. Concept selection based on three centroid indices

Based on three centroid indices, design engineers can use them to express their tolerance of risk in choosing design concepts. If they take the neutral prospect, the balanced centroid index (IN_c) is used to compare different concepts. Similarly, if they want lower risk (e.g. due to the lead time pressure and limited resources), they can use the pessimistic centroid index (IN_p) for concept comparison. Lastly, if they can take higher risk for potentially lower eco-impact (e.g. adequate resources available for developing competitive products), they can use the optimistic centroid index (IN_o).

Notably, eco-design concepts are often evolved and generated based on some earlier or original design. Using the three centroid indices, we can compare the eco-performance of each design concept with an original design. This can provide a benchmark to assess the improvement of eco-performance of new design concepts over the original one. Let d_ori be the original design, and T(d_ori) is its eco-impact according to Equation (1(1) ). Since the original design is physically existing (rather than conceptual), T(d_ori) is a crisp number (rather than a fuzzy number). Suppose that it has an imaginary centroid located at (T(d_ori), 0.5), as illustrated in Figure 2. Then, the corresponding index (denoted as IN_ori) of this imaginary centroid is formulated as follows.(21)

Accordingly, four scenarios are classified based on the comparison of IN_ori with respect to IN_c(d_i), IN_p(d_i), IN_o(d_i). It should be noted that IN_o(d_i) ≤ IN_c(d_i) ≤ IN_p(d_i).

Scenario 1: IN_p(d_i) ≤ IN_ori. Here, the pessimistic index of concept d_i is lower than the original design index. That is, the anticipated worst eco-impact of concept d_i can still bring better eco-performance than the original design. This is one best situation where d_i can reduce the eco-impact favourably compared with the original design. Design engineers should pursue the idea of concept d_i for further development and analysis.

Scenario 2: IN_c(d_i) ≤ IN_ori < IN_p(d_i). Here, the index of the original design falls between the balanced and pessimistic indices. That is, the anticipated worst case associated with concept d_i may effectively yield the eco-impact lower than the original design. Considerably, the design concept d_i is not bad. Yet, to reduce the risk from the pessimistic aspect, the design engineers should examine and improve the upper bounds of eco-impacts from the engineering quantities.

Scenario 3: IN_o(d_i) < IN_ori ≤ IN_c(d_i). Here, the index of the original design falls between the optimistic and balanced indices. That is, only the anticipated best case associated with concept d_i may effective yield the eco-impact than the original design. Considerably, the design concept d_i in this scenario is not promising, and design engineers should look for other design concepts. Alternately, they should consider more significant improvement over the typical values (i.e. a₂ and a₃) of eco-impact.

Scenario 4: IN_ori ≤ IN_o(d_i). Here, the design concept d_i cannot demonstrate the reduction of eco-impact even in the optimistic case. Generally, design engineers should not put more efforts in this design concept.

4. Application and comparison

4.1. Coffee maker and Eco-indicator 99

In this research, a coffee maker from the consumer market is selected to illustrate the proposed fuzzy number method. As the initial step, the coffee maker is analysed to assess its environmental impacts. In this context, the design manual of Eco-indicator 99 (Goedkoop, Effting, and Collignon 2000, 18–21) is applied, and four life cycle stages of assessment are set as follows.

•	Material production: examine the key construction materials of the coffee maker.
•	Processing: relate the construction materials to major manufacturing processes.
•	Use: check the resources required for coffee brewing such as electricity and filter papers.
•	Disposal: examine the material handling after the useful life of the coffee maker. This study assumes landfilling as the end-of-life option of the coffee maker.

In this assessment, the coffee maker is first disassembled, and its main construction materials are checked and weighted. For example, one main material is polystyrene (0.56 kg), which is used for making the housing structure and the carafe cover. Also, aluminium (0.082 kg) is used for the functioning of the heater tube. The material weights basically provide the information for the stages of material production, processing and disposal.

To examine the ‘use’ stage, this study assumes the useful life of a coffee maker to be three years, with two operations (total: 0.5 h) per day. It is checked that the electricity consumption of the coffee maker is 600 watts, leading to the overall consumption equal to 600 × 0.5 × 365 × 3 = 328.5 kWh in three years. Regarding filter papers, each weight is 0.89 g, and the total weight is equal to 0.89 × 2 × 365 × 3 = 1.95 kg in the three-year consumption.

Then, the eco-indicators for individual materials and resources at different life cycle stages are checked from the manual of Eco-indicator 99. Table 1 summarises the assessment results using the Eco-indicator 99.

Table 1. Assessment of environmental impacts based on Eco-indicator 99.

		Eco-indicator	Amount	Eco-impact score
Material production	Polystyrene (PS)	360 (mPt/kg)	0.56 kg	201.6 mPt
	Aluminium (Al)	780 (mPt/kg)	0.082 kg	63.96 mPt
	Steel	86 (mPt/kg)	0.075 kg	6.45 mPt
	Glass	58 (mPt/kg)	0.22 kg	12.76 mPt
Processing	Injection moulding (PS)	21 (mPt/kg)	0.56 kg	11.76 mPt
	Extrusion (Al)	72 (mPt/kg)	0.082 kg	5.904 mPt
	Sheet (steel)	30 (mPt/kg)	0.075 kg	2.25 mPt
Use	Electricity	37 (mPt/kWh)	328.5 kWh	12154.5 mPt
	Filter paper	96 (mPt/kg)	1.95 kg	187.2 mPt
Disposal (landfill)	Polystyrene (PS)	4.1 (mPt/kg)	0.56 kg	2.296 mPt
	Aluminium (Al)	1.4 (mPt/kg)	0.082 kg	0.1148 mPt
	Steel	1.4 (mPt/kg)	0.075 kg	0.105 mPt
	Glass	1.4 (mPt/kg)	0.22 kg	0.308 mPt
	Paper	4.3 (mPt/kg)	3.25 kg	13.975 mPt
			Total	12,663 mPt

4.2. Three design concepts for Eco-design improvement

To improve the eco-performance of the coffee maker, this study has referenced the design manual by Goedkoop, Effting, and Collignon (2000, 21) as well as some similar products in the market. In the context of incremental improvements, we have applied two eco-design guidelines: (1) reduction of disposal materials and (2) reduction of energy use. In view of material reduction, we have identified an opportunity to replace disposable paper filters. In view of energy reduction, we have identified two possible strategies to save the energy that is used to keep the coffee warm.

In this study, the morphological chart is used to generate three design concepts (Otto and Wood 2001; Ulrich and Eppinger 2008), and the result is presented in Table 2. In this morphological chart, the left column lists three relevant design functions, and the proposed design solutions for individual functions are highlighted with italicised texts. Further discussion of three design concepts is provided below.

•	Concept ‘x’: the design intent is to reduce the electricity consumption by decoupling the functions of boiling water and warming coffee. The original design has one aluminium tube to serve these two functions. The new design is to implement a regular heating element that focus on boiling water only. As warming coffee is less energy intensive, a smaller heating element is expected to serve this function. New control is needed to coordinate the use of electricity (e.g. only one heating element is turned on at most time). The new design may incur more use of metals (for the new heating system) in exchange for lower electricity consumption.
•	Concept ‘y’: the design intent is to eliminate disposable paper filters by a permanent filter. The trade-off is between the material usage between paper filters and a permanent filter along with washing water.
•	Concept ‘z’: the design intent is to reduce electricity that is used for warming coffee using an insulated jug. It is expected that the insulated jug generally uses more materials than the original carafe as the trade-off.

Among these three concepts, Concept ‘x’ is viewed as an innovative idea with higher level of uncertainty, while Concepts ‘y’ and ‘z’ are relatively conventional with lower uncertainty. This represents the trade-off situation discussed in Section 2.1. In the traditional use of Eco-indicator 99, designers need to develop more design details of these concepts (e.g. crisp quantities on material weights). Also, the uncertainty information cannot be conveyed by crisp values. At this point, the utility of the proposed fuzzy number approach is to allow engineers estimate the quantities in the application of Eco-indictor 99 without too much design development. Then, more engineering and design efforts can be devoted to the promising concept(s) later after the fuzzy assessments.

Table 2. Morphological chart to generate three design concepts.

	Concept ‘x’	Concept ‘y’	Concept ‘z’
	Guideline: reduction of energy use	Guideline: reduction of disposal material	Guideline: reduction of energy use
Function 1: Boil water	Regular heater for boiling water only	Aluminium tube	Aluminium tube
Function 2: Warm coffee	Smaller heater for warming only	Aluminium tube	Insulated jug
Function 3: Receive & filter coffee powder	Disposable filter paper	Permanent filter	Disposable filter paper

4.3. Application of trapezoidal fuzzy numbers (TrFN)

At this analysis point, designers already know the information in Table 1 as it represents the existing coffee maker. With Table 1 as the base reference, Table 3 provides the TrFNs as the estimation of quantities for the three design concepts. By applying Equation (4(4) ), the fuzzy environmental impact for each design concept is provided on the last row of Table 3. Listed below are the explanations concerning the estimated values of TrFNs.

•	Concept ‘x’: More materials of polystyrene, steel and aluminium are expected for a redesigned heating system. New design should reduce electricity consumption. However, since the design idea is comparatively new, electricity consumption is subject to a relatively large range of uncertainty. Further discussion of this point will be provided afterwards.
•	Concept ‘y’: More materials of polystyrene and steel are expected for the permanent filter with the elimination of filter papers. Regarding washing water, the lower and upper bounds of the daily use are 2 and 5 litres, respectively (leading to 2190 and 5475 kg of water in three years). Regarding electricity consumption, the difference between paper and permanent filters should be very small. Thus, we keep the typical value as 328.5 kWh (same as the original design), with marginal variations on lower and upper bounds.
•	Concept ‘z’: More materials of polystyrene and steel are expected for the insulated jug, in exchange for no use of glass and lower electricity consumption. Regarding electricity consumption, we expect the values lower than the baseline 328.5 kWh, leading to the overall range from 320 kWh to 327 kWh.

Table 3. Trapezoidal fuzzy numbers for each design concept.

	Concept ‘x’	Concept ‘y’	Concept ‘z’
Polystyrene (kg)	(0.56, 0.65, 0.71, 0.84)	(0.68, 0.75, 0.79, 0.85)	(0.82, 0.85, 0.89, 0.92)
Aluminium (kg)	(0.082, 0.16, 0.17, 0.19)	(0.082, 0.082, 0.082, 0.082)	(0.082, 0.082, 0.082, 0.082)
Steel (kg)	(0.075, 0.15, 0.16, 0.18)	(0.09, 0.095, 0.117, 0.12)	(0.27, 0.29, 0.31, 0.32)
Glass (kg)	(0.22, 0.22, 0.22, 0.22)	(0.22, 0.22, 0.22, 0.22)	(0, 0, 0, 0)
Filter paper (kg)	(1.95, 1.95, 1.95, 1.95)	(0, 0, 0, 0)	(1.95, 1.95, 1.95, 1.95)
Electricity (kWh)	(312, 321, 325, 330)	(328, 328.5, 328.5, 329)	(320, 322, 323, 327)
Washing water (kg) (Eco-indicator: 0.026 mPt/kg)	(0, 0, 0, 0)	(2190, 3285, 4380, 5475)	(0, 0, 0, 0)
Total eco-impact scores (mPt)	(12,052, 12,483, 12,664, 12,918)	(12,548, 12,623, 12,669, 12,739)	(12,458, 12,546, 12,601, 12,762)

To demonstrate the specification of TrFN (i.e. (a₁, a₂, a₃, a₄)) in this example, let us consider the electricity consumption of concept ‘x’. Per the discussion in Section 2.3, the reasoning of optimistic and pessimistic estimations, as well as the range of typical values, is provided as follows.

•	Optimistic estimation (a1): concerning the electricity use of the existing design (i.e. 328.5 kWh in Table 1), we estimate 90% energy is used for brewing coffee, and it stands for the minimum energy requirement. Then, the remaining 10% energy is used to warm coffee and cover energy loss. The optimistic view of concept ‘x’ is to save half of this 10% energy, giving the optimistic (lower bound) estimation as 328.5 × 0.95 ≈ 312 kWh.
•	Pessimistic estimation (a4): concerning a worst case scenario, the new concept ‘x’ may incur more energy loss than the existing design (e.g. less efficiency of the smaller heat). Yet, we do not anticipate a significant difference. Then, the pessimistic estimation (upper bound) is set as 330 kWh to represent the risk of no energy reduction in concept ‘x’.
•	Range of typical values (a2 and a3): based the lower and upper bounds as [312, 330] kWh, we take the middle point (i.e. 321 kWh) as one typical value. By taking the conservative view (i.e. concept ‘x’ has less ability to save energy), we take the middle point between 321 and 330 kWh as another typical value, leading to the range of typical values as [321, 325] kWh.

4.4. Decision analysis based on trapezoidal fuzzy numbers (TrFN)

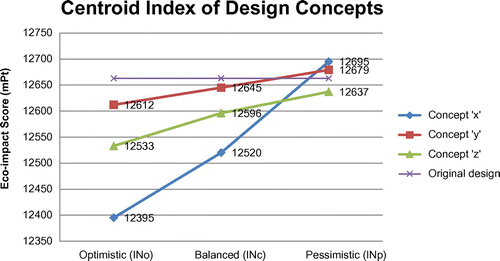
After obtaining the fuzzy environmental impacts, the centroid indices (discussed in Section 3.2) are applied for concept selection. The results of three centroid indices (i.e. IN_c, IN_p and IN_o) are plotted in Figure 3. By comparing the centroid indices among three concepts, three situations are classified with respect to the tolerance of risks.

•	Neutral tolerance of risk: the balanced centroid index (INc) is used, where concept ‘x’ has the best (lowest) eco-impact score.
•	Low tolerance of risk: it takes place when the company has limited resources with lead time pressure. The pessimistic centroid index (INp) is used, where concept ‘z’ has the best eco-impact score.
•	High tolerance of risk: it takes place when the company has enough resources for uncertain and potentially competitive concepts. The optimistic centroid index (INo) is used, where concept ‘x’ has the best eco-impact score.

Figure 3. Plot of centroid index of three design concepts.

By comparing the design concepts with the original design where IN_ori = 12663 mPt (based on Table 1), only concept ‘z’ belongs to the Scenario 1 (i.e. IN_p(d_i) ≤ IN_ori), where concepts ‘x’ and ‘y’ fall into the Scenario 2 (i.e. IN_c(d_i) ≤ IN_ori < IN_p(d_i). By summarising the decision analysis, the following recommendations for concept selection are suggested.

•	Concept ‘x’: while this concept is classified as a new yet uncertain idea, it has the best optimistic and balanced centroid indices. Yet, it has the worst pessimistic score. If the company has adequate resources to mitigate the risk from the pessimistic aspect (i.e. lowering the upper bound of the impact), this concept can have distinct eco-performance.
•	Concept ‘y’: this concept is not suggested because it cannot perform better concept ‘x’ in the optimistic and balanced cases. Its pessimistic case is even worse than the original design.
•	Concept ‘z’: this concept is considered a ‘safe’ choice if the company does not have adequate resources. Even in the pessimistic case, concept ‘z’ can bring in lower eco-impacts as compared to the original design (while other two concepts cannot do so).

Notably, while concepts ‘x’ and ‘z’ are recommended as the ‘risky’ and ‘safe’ choices, respectively, they both target for reducing electricity consumption. From the analysis of Eco-indicator 99 in Table 1, the electricity consumption actually takes about 95% of the total impact (i.e. 12154/12663). Comparatively, concept ‘y’ targets for less material usage, which has less margin for eco-design improvement. This partly explains why concept ‘y’ is not recommended.

As observed, while Eco-indicator 99 provides the quantitative ground for various trade-offs among design properties, the fuzzy numbers utilise the interval values to represent the corresponding risks. Then, the ‘risky’ or ‘safe’ choice can be interpreted with respect to the actual optimistic (best) or pessimistic (worse) eco-impact scores. Notably, in this decision-making, the tolerance of risk by designers is required in order to finalise the choice between concepts ‘x’ and ‘z’. Such arrangement in the methodology is needed as the tolerance of risk is quite situational per designers’ knowledge. Yet, the utility of the proposed method lies in the elimination of a less sensible choice (i.e. concept ‘y’), and it can inform designers the uncertainty nature behind each option.

4.5. Application of MCS and result comparison

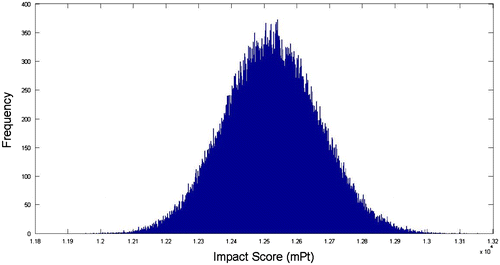
To perform MCS, we first determine the means and variances of TrFNs in Table 3 based on the equations in Section 2.4. Then, the lognormal distributions of input quantities (q_j) are specified for running MCS. In this study, MCS is run for 100,000 times to estimate the eco-impact score of each design concept. To illustrate, Figure 4 shows the probability density of concept ‘x’ after running MCS. As a general observation, the mean eco-impact score of concept ‘x’ is about 12,500 mPt, which is close to its fuzzy balanced centroid index (IN_c = 12520 mPt). This verifies that the centroid point approach can yield similar mean results that are based on MCS, given the same uncertainty inputs from Table 3.

Figure 4. Distribution of the eco-impact scores of concept ‘x’ using MCS.

Table 4 shows the numerical results of the fuzzy interval and MCS approaches. In this study, it is intended to check whether the results of both approaches are comparable in view of their means and variations. In particular, the variation aspect of MCS is checked via two statistical intervals: μ ± σ and μ ± 3σ, where μ and σ are the mean and standard deviation of the results from 100,000 runs of MCS, respectively. Then, the interval μ ± σ is compared with the typical range of TrFN (a₂ to a₃), and the interval μ ± 3σ is compared with the boundary range (a₁–a₄).

Table 4. Comparison of the fuzzy number and MCS approaches.

	Concept ‘x’	Concept ‘y’	Concept ‘z’
TrFN balanced eco-impact score (INc) (mPt)	12520	12645	12596
MCS mean eco-impact score (mPt)	12522	12645	12592
TrFN typical range: [a2, a3] (mPt)	[12483, 12664]	[12623, 12669]	[12546, 12601]
MCS interval: μ ± σ (mPt)	[12380, 12665]	[12621, 12669]	[12537, 12647]
TrFN boundary range: [a1, a4] (mPt)	[12052, 12918]	[12548, 12739]	[12458, 12762]
MCS interval: μ ± 3σ (mPt)	[12094, 12951]	[12573, 12717]	[12426, 12758]

In Table 4, the first two rows show that the mean eco-impact scores by MCS are close to the fuzzy balance eco-impact scores (IN_c), implying that both approaches yield no significant difference in view of mean values. By comparing the ‘typical ranges’ (i.e. the third and fourth rows), it is found that the TrFN intervals [a₂, a₃] are quite similar to the MCS interval of μ ± σ. The largest difference is found at the lower bound of concept ‘x’, where the percentage difference (from TrFN) is (12483–12380)/12483 = 0.825%. Alternately, the ‘boundary ranges’ (i.e. the last two rows) are similar in both approaches.

Based on these numerical comparisons, it is considered that both fuzzy interval and MCS approaches can yield similar results if they receive the same uncertainty inputs. From the aspect of computation, MCS requires some simulation and statistical set-ups (e.g. number of simulation runs and statistical distribution for random number generation). In contrast, the fuzzy interval approach does not require simulations, and this justifies its relative simplicity as the advantage in computation.

4.6. Remarks on uncertainty of Eco-indicator 99 in design concept comparison

The values of eco-indicators in Eco-indicator 99 are not entirely certain in reality, and they can also be subject to conventional types of uncertainty in LCA in general such as model and data uncertainty (Goedkoop, Effting, and Collignon 2000, 29–31). Model uncertainty is related to the use of analysis models in determining the environmental effects, which can range from short-term to long-term effects with diverse levels of scientific evidence (Lloyd and Ries 2007). As this kind of uncertainty is difficult to quantity, Goedkoop, Effting, and Collignon (2000) have developed three versions of eco-indicators, covering the perspectives of short-term, long-term and balance effects. This paper adopts the default option, which is the ‘Hierarchist’ (or balance) version of Eco-indicator 99.

Data uncertainty is related to the variations of numerical data used in the environmental analysis models (Huijbregts et al. 2001). In this aspect, Goedkoop, Effting, and Collignon (2000) suggested the distinction between absolute and relative uncertainty. Such distinction is generally intended to highlight different comparison contexts according to the similarity of options. In their discussion, relative uncertainty has ‘the tendency to compensate each other’ (30) and has less concern than absolute uncertainty. Since the design concepts based on incremental changes should not be too different from each other, the notion of relative uncertainty is applied in this paper.

In this study of coffee maker design, the variations of three design concepts mainly stem from the changes of materials and electricity consumption that are already found in the original design. By the notion of relative uncertainty, even though individual eco-indicators may carry their own uncertainty, their uncertainty levels should be similar among different design concepts. In particular, while electricity consumption takes a significant portion of eco-impacts, all design concepts should take electricity from the same source. Then, the uncertainty of the ‘electricity’ eco-indicator is similarly carried in assessing these design concepts. Aligned with the discussion in Goedkoop, Effting, and Collignon (2000), this supports the use of Eco-indicator 99 in the context of incremental eco-design improvements.

4.7. Remarks on using TrFN with Eco-indicator 99

When design concepts are proposed, the environmental impacts implied in these concepts are not usually clear. Thus, the common request from industry is the quantitative analysis that can generally estimate the eco-performance of the design concepts at hand. In this research, the quantitative analysis has two parts. Firstly, Eco-indicator 99 provides a set of eco-indicators for summing up environmental impacts from different sources. It can help to reveal some design trade-off for decision-making (e.g. more materials to compensate less electricity consumption in the coffee maker case). Secondly, engineering quantities as the properties of design concepts can be directly used for environmental assessments. It can help to advise eco-design improvement based on objective engineering and design properties.

To apply Eco-indicator 99, one effort is to provide the information of some engineering properties (e.g. weight of polystyrene), which may not be known precisely at the conceptual design stage. The proposal of using TrFN is to allow some flexibility for engineers to provide numerical intervals as their estimations in the application of Eco-indicator 99. Numerical intervals should be more natural than statistical variances to specify uncertainty information.

Also, when a concept is selected, the eco-impact results as numerical intervals can provide some directions for further design development. For example, the upper bound of eco-impacts of concept ‘x’ is caused by the uncertainty of electricity consumption. If concept ‘x’ is adopted, the engineers can focus on addressing this upper bound (instead of other design issues). Even if the revised concept can use more materials, it is understood that the saved electricity can compensate the eco-impacts from additional materials quite easily.

It is acknowledged that both FIA and MCS can propagate the uncertainty inputs and yield an overall eco-impact based on Eco-indicator 99. Since using Eco-indicator 99 mainly involves additions and multiplications, FIA is quite effective to obtain the interval results without running simulations. The coffee maker example has verified that both fuzzy arithmetic and MCS can yield comparable results given the same uncertainty inputs.

Currently, the proposed method supports only one TrFN for each engineering quantity. That is, it does not purposely address the case when multiple designers express different TrFNs as their expert judgements for one engineering quantity. While the detailed methodological development is deferred to future work, one conservative direction is to enlarge the uncertainty range by taking the extreme values at both ends expressed by multiple designers. For example, if two TrFNs are known as F_x = (1.0, 2.0, 3.0, 4.0) and F_y = (0.5, 2.5, 3.5, 3.8), the resulting TrFN will be (0.5, 2.0, 3.5, 4.0). That is, these TrFNs are aggregated by taking the lowest values of a₁ and a₂ and the highest value of a₃ and a₄.

5. Conclusions

In the application of Eco-indicator 99, this paper treats the uncertainty information pertaining to design concepts as numerical intervals, which are analysed via two approaches: Monte Carlo Simulation (MCS) and fuzzy intervals. While MCS is common in LCA, this paper proposes the fuzzy interval approach, in which fuzzy arithmetic is used to propagate uncertainty inputs and yield fuzzy eco-impact scores. To further support the concept selection process, three centroid indices based on fuzzy numbers are derived so that design engineers can evaluate the trade-off between (1) conventional ideas with marginal yet predictable improvement versus (2) innovative ideas with potentially good yet less predictable eco-performance. The coffee maker example is used to demonstrate the utility of the proposed fuzzy number approach and verify the comparable numerical outcomes between the fuzzy number and MCS approaches. Comparatively, the fuzzy interval approach has two advantages. Firstly, it does not require simulations and is simpler in view of computation. Secondly, the outcomes of fuzzy numbers can be used to analyse the risk level of various design concepts. Then, design engineers can select design concepts based on their tolerance towards the risk. In the future work, it is intended to implement the fuzzy interval approach with the computer-aided design software so that design engineers can analyse the eco-performance of a design concept with interval estimations.

Disclosure statement

No potential conflict of interest was reported by the authors.

Funding

This work was supported by the Libyan-North American Scholarship Program and NSERC Discovery Grant.

Notes on contributors

Abdulbaset Alemam is currently working as an assistant professor in University of Tripoli. The author’s research interests include design for the environment and manufacturing.

Xin Cheng is an MSc graduate in University of Calgary. The author’s research interests include fuzzy uncertainty, eco-design and building energy.

Simon Li is currently working as an assistant professor in University of Calgary. The author’s research interests include design and manufacturing.

Acknowledgement

The first author thankfully acknowledges the support of the Libyan-North American Scholarship Program. The second author received the financial support from the NSERC Discovery Grant.