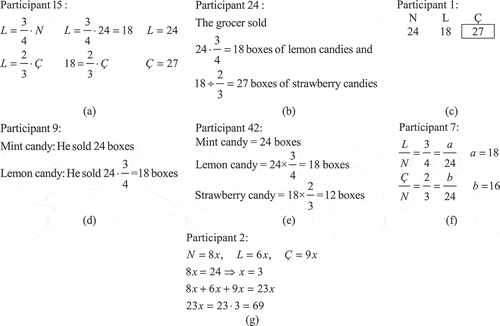Turkish Pre-service Middle Level Mathematics Teachers’ Knowledge for Teaching Fractions

Abstract

Fractions are a crucial mathematical topic, which is known as being challenging for both students, pre- and in-service teachers. The current study attempted to explore the extent of pre-service middle level mathematics teachers’ knowledge for teaching fractions. Fifty-one senior pre-service teachers took part in the study. The Knowledge for Teaching Fractions Test, which includes almost all characteristics of fractions, was employed to measure participants’ knowledge for teaching fractions. The Pre-service Teachers’ Mathematics Knowledge for Teaching Framework was used to conceptualize participants’ responses to the tasks in the Knowledge for Teaching Fractions Test. The findings showed that participants’ mathematical knowledge for teaching fractions was not satisfactory. Meanwhile, while they had sound common content knowledge for teaching fractions, their specialized content knowledge for teaching this topic was very poor. The implications for teaching fractions are discussed in the context of pre-service middle level teacher preparation.

Keywords:

• pre-service teachers
• fractions
• mathematical knowledge for teaching
• middle level education

Introduction

Research in many countries has consistently shown that students have great difficulty understanding fractions (Čadež & Kolar, 2018; Pantziara & Philippou, 2012; Steffe & Olive, 2010). In order for teachers to cope successfully with students’ difficulties, they must have robust mathematical knowledge for teaching fractions (Depaepe et al., 2015). However, the number of instruments that measure pre-service or in-service teachers’ mathematical knowledge for teaching is very limited because mathematics education researchers only started to design such instruments at the beginning of the 21st century (Krauss, Baumert, & Blum, 2008). More specifically, there is a dearth of studies that focus on designing comprehensive instruments to explore pre- and in-service mathematics teachers’ knowledge for teaching fractions in depth (Kazemi & Rafiepour, 2018). Accordingly, the purpose of the current study is twofold. First, it aims at designing a knowledge for teaching fractions test that addresses almost all characteristics of fractions. Second, the study intends to explore the extent of pre-service middle level mathematics teachers’ knowledge for teaching fractions via the test designed by the author.

Designing the Knowledge for Teaching Fractions Test

Measuring teacher knowledge is not simple due to its complex and multi-faceted nature (Gülmez-Dağ & Yıldırım, 2016; Shechtman, Haertel, Roschelle, Knudsen, & Singleton, 2013). It is internal and it cannot be entirely measured by observing teachers’ mathematical instruction or behaviors (Kazemi & Rafiepour, 2018). Therefore, researchers used a variety of methods such as written tests (e.g., Lin, Becker, Byun, Yang, & Huang, 2013; Utley & Reeder, 2012), interviews (e.g., Behr, Khoury, Harel, Post, & Lesh, 1997), classroom teaching experiments (e.g., Tobias, 2013), and a combination of two or more of the aforementioned methods (e.g., Lo & Luo, 2012) to measure pre-service teachers’ knowledge for teaching fractions.

The current study attempts to contribute to the body of literature on pre-service teachers’ knowledge for teaching fractions by proposing the Knowledge for Teaching Fractions Test that was designed based on the limitations of large- and small-scale studies conducted in the past. Large-scale studies such as the Mathematical Knowledge for Teaching in the United States (e.g., Ball, Thames, & Phelps, 2008; Hill, Rowan, & Ball, 2005), the Cognitive Activation in the Classroom Study in Germany (e.g., Baumert et al., 2010; Kunter et al., 2013), and Teacher Education and Development Study in Mathematics in seventeen countries (e.g., Senk et al., 2012) used single surveys with items covering many different topics to measure participants’ mathematical knowledge. However, such surveys may not help to uncover participants’ knowledge of mathematics in a deep and comprehensive way and consequently may not provide a holistic and rich picture about their knowledge (Kazemi & Rafiepour, 2018).

Moreover, there are relatively few small-scale studies that focus on pre-service teachers’ knowledge for teaching fractions in the Turkish context (e.g., Işık & Kar, 2012a; Işıksal & Çakıroğlu, 2011). On the other hand, there are many similar studies exploring pre-service teachers’ knowledge for teaching fractions in an international context (e.g., Li & Kulm, 2008; Lin et al., 2013; Lo & Luo, 2012; Newton, 2008; Son & Crespo, 2009; Tirosh, 2000; Tobias, 2013; Utley & Reeder, 2012; Yang, Reys, & Reys, 2009). However, these studies display a rather uneven distribution among components of knowledge for teaching fractions. More clearly, pre-service teachers’ common content knowledge and specialized content knowledge for teaching fractions received more attention from researchers, but teachers’ knowledge of content and students, knowledge of content and teaching, and knowledge of mathematics curriculum for teaching fractions has not been the focus of much of the research (Olanoff, Lo, & Tobias, 2014). Thus, the author of the current study paid particular attention to including several tasks for each component of teacher knowledge when designing the fractions test.

Measuring Pre-service Teachers’ Knowledge for Teaching Fractions

Fractions are widely used in mathematics education and have great importance in other disciplines as well (Ben-Chaim, Keret, & Ilany, 2012). For instance, fractions form the basis of introductory mathematics and other mathematical topics such as algebra and probability (Clarke & Roche, 2009). However, fractions are notorious for the difficulty encountered not only by students (e.g., Ni, 2001; Vamvakoussi & Vosniadou, 2010) but also by teachers (e.g., An, Kulm, & Wu, 2004; Izsak, 2008; Ma, 1999; Tirosh, 2000). As Lamon (2007) expressed, fractions “arguably hold the distinction of being the most protracted in terms of development, the most difficult to teach, the most mathematically complex, the most cognitively challenging, the most essential to success in higher mathematics and science, and one of the most compelling research sites” (p. 629).

The difficulty for teachers in teaching fractions to their students may stem in part from the conceptual richness of fractions (Li & Kulm, 2008) because teaching fractions conceptually requires teachers to make connections with other sources of mathematical knowledge and employ different representations and real-life contexts (Li, 2008). Moreover, teaching fractions in an inappropriate way or procedurally may lead to student misconceptions and consequently may inhibit their understanding of future concepts related to fractions (Kazemi & Rafiepour, 2018). Thus, mathematics teachers need to have a robust understanding of fractions in order to teach them to their students conceptually. Accordingly, the topic of fractions may provide a rich context for exploring the extent of pre-service teachers’ mathematical knowledge for teaching and this may, in turn, prove useful in shedding light on their strengths and weaknesses related to the teaching of fractions in a deep and comprehensive way.

Conceptual Framework

As argued by Li and Kulm (2008), Ball et al.’s (2008) Mathematical Knowledge for Teaching Framework may serve as a theoretical basis for measuring in-service teachers’ mathematical knowledge for teaching. However, pre-service teachers’ inexperience in teaching makes it debatable to directly use it for measuring pre-service teachers’ knowledge for teaching mathematics. Thus, in the current study, the Pre-service Teachers’ Mathematics Knowledge for Teaching Framework proposed by Li and Kulm (2008) was used to explore participants’ knowledge for teaching fractions. The specifications of each component of the framework are described in Table 1.

Table 1 The Components of the Pre-service Teachers’ Mathematics Knowledge for Teaching Framework (Li & Kulm, 2008, p. 836)

Components	Specifications
1. Common content knowledge	The type of mathematics content knowledge that is commonly required in school mathematics for all students. For this type of knowledge, pre-service teachers need to know no less than in-service teachers.
2. Specialized content knowledge	The type of mathematics content knowledge that is more specialized, and is at a higher and more abstract level than what school students need to learn. It also includes the expectations for pre-service teachers to know not only what and how, but also why for specific content topics. Because pre-service teachers are still in their college program studies, they are in a position to learn more about this type of mathematics content knowledge.
3. Knowledge of content and students	The knowledge about students’ learning difficulties and misconceptions related to specific mathematics content topics. Because of their limited teaching experience, pre-service teachers may have very limited exposure to this type of knowledge.
4. Knowledge of content and teaching	The type of knowledge that is used in the practice of teaching, such as the use of various representations for teaching specific mathematics content topics, the use of problem solving for teaching mathematics and in assessment. Given pre-service teachers’ inexperience in teaching, we will not expect pre-service teachers to be proficient in this type of knowledge.
5. Knowledge of mathematics curriculum	Part of Pedagogical Content Knowledge in Shulman’s categorization (Shulman, 1986), but not part of MKT. As curriculum knowledge is an important part of what pre-service teachers need to learn through their program of study, we include this component as well. It is the type of knowledge about state mathematics framework and the process of curriculum transformation from the intended to the implemented and to the achieved. However, we will restrict this type of knowledge requirement as not including the details about topic sequence and specific learning requirements.

Methodology

A survey design, which is one of the basic non-experimental research designs (Christensen, Johnson, & Turner, 2013), was used to explore the extent of pre-service middle level mathematics teachers’ knowledge for teaching fractions. The education system in Turkey, participants and context, data collection instrument, and data analysis procedures are explained in detail as follows.

Education System in Turkey

Turkey has a centralized education system and a national curriculum and The Ministry of National Education develops the national mathematics curriculum and supervises its implementation in all public or private schools. In the education year 2012–2013, the Ministry of National Education (2012) launched a new education system entitled 4 + 4 + 4. In the new education system, 4 years of primary level education (grade 1–4), 4 years of middle level education (grade 5–8), 4 years of secondary level education (grade 9–12), and altogether 12 years of education is compulsory for all students. The minimum compulsory age for schooling is 6 and the minimum permitted school-leaving age is 18.

In Turkey, the education year is approximately 36 weeks. Each week, the middle level students (grade 5–8) spend 5 lesson hours for compulsory mathematics courses and each lesson hour is 40 minutes. Thus, the instructional time spent on mathematics is 200 minutes per week for middle level students. Besides, an elective course entitled Applications of Mathematics is offered to them and 2 lesson hours (80 minutes) are allocated for this course per week (Ministry of National Education, 2018). However, not all middle graders take this course because it is elective.

In Turkey, fractions are taught at all levels of schooling. In primary grades, the students are expected to model a quarter and a half of a whole; identify unit fractions; label top and bottom numbers as numerators and denominators; and identify the three basic forms of fractions as proper fractions, improper fractions, and mixed numbers (Ministry of National Education, 2015). In the middle grades, more emphasis is given to the teaching of fractions. Grade 5 students are expected to compare and order unit fractions, locate them on the number line, convert between improper fractions and mixed numbers, simplify and expand fractions, and add and subtract fractions. Grade 6 students are expected to compare and order all forms of fractions, locate them on the number line, and perform multiplication and division operations with fractions. In grade 7, the students extend their understanding of fractions to rational numbers. Namely, they learn how to identify, compare, and order rational numbers; locate them on the number line; convert between repeating decimals and rational numbers; perform four operations with rational numbers; and solve real-world problems related to rational numbers (Ministry of National Education, 2013a). In secondary level, fractions are introduced to the students only in grade 9. In this grade, the students are expected to recall rational numbers and construct relationships among different number sets (Ministry of National Education, 2013b).

Participants and Context

The participants of the study were 51 pre-service senior middle level mathematics teachers (12 males and 39 females) who were enrolled in a teacher education program at a public university located in the inner region of Turkey. Their ages ranged between 22 and 24. The participants took all the courses offered by their teacher education program. By selecting senior pre-service teachers who were almost graduates, this study attempted to uncover, to some extent, the current status of middle level mathematics teacher education programs regarding the quality of pre-service teacher preparation and the corresponding inadequacies existing in them.

In Turkey, the courses that pre-service teachers must qualify in order to graduate from teacher education programs are specified by the Higher Education Council (HEC). According to the current program being implemented in middle level teacher education programs (Higher Education Council, 2006), pre-service teachers take three types of courses as mathematics (e.g., Geometry, Linear Algebra, and Differential Equations) mathematics education (e.g., Methods of Teaching Mathematics), and general education courses (e.g., Educational Psychology and Classroom Management). Pre-service teachers mainly take mathematics courses in their first and second years, mathematics education courses in their third and four years, and general education courses in all four years. The participants were representative of other middle level mathematics education majors in other universities in Turkey due to the fact that they took similar courses during their teacher education program.

The participating pre-service teachers had some exposure to the topic of fractions in the following courses offered by the mathematics teacher education program: Methods of Teaching Mathematics; Teaching Fractions, Ratios, and Proportions; and Teaching Practicum. The syllabus of the fractions course shows that fractions are covered comprehensively for about eight weeks and that specific time is allocated to the teaching of the following topics: definitions of fraction concepts and the relationships among fractions, decimals, percentages, ratios, and proportions; learning objectives regarding fractions in Turkish middle level mathematics curricula; students’ possible learning difficulties and misconceptions about fractions; fraction constructs; posing and solving fraction word problems; and fraction models. However, not all participants had taken the fractions course because it is elective. The distribution of participants with respect to gender, age, enrollment in the fractions course, cumulative grade point averages, and Methods of Teaching Mathematics course scores are presented in Table 2.

Table 2 The Distribution of Participants with respect to Their Background Characteristics

Pre-service middle level mathematics teachers’ background characteristics
Gender	f (%)	Cumulative grade point averages	f (%)
Male	12 (24)	Between 2.00 and 2.49	15 (29)
Female	39 (76)	Between 2.50 and 2.99	24 (47)
Enrollment in the fractions course		Between 3.00 and 3.49	9 (18)
Yes	13 (25)	Between 3.50 and 4.00	3 (6)
No	38 (75)	Methods of Teaching Mathematics course scores
Age		Between 50 and 59	2 (4)
Twenty-two	29 (57)	Between 60 and 69	25 (49)
Twenty-three	16 (31)	Between 70 and 79	14 (27)
Twenty-four	6 (12)	Between 80 and 89	9 (18)
		Between 90 and 100	1 (2)

Data Collection Instrument

The specifications given in Table 1 served as a guideline for selecting, adapting, or developing fraction tasks and for putting these tasks together as a test in measuring and interpreting pre-service middle level mathematics teachers’ knowledge for teaching fractions. The English version of the Knowledge for Teaching Fractions Test designed for this purpose is presented in the Appendix. Note that while some of the tasks included in the test were adapted from prior studies (e.g., Işık & Kar, 2012a, 2012b; Lamon, 2012; Li & Huang, 2008; Li & Kulm, 2008; LMT, 2008; Mack, 1990; Moseley, 2005), some other tasks were developed by the author.

As shown in the Appendix, the fractions test includes 17 main tasks and 11 of these tasks have several sub-tasks ranging between 2 and 5. Thus, there are altogether 48 tasks in the fractions test. Meanwhile, there are 12 open-ended tasks (Task 1, 2, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14), 3 matching tasks (Task 3, 4, and 17), and 2 true-false tasks (Task 15 and 16) in the test. Multiple choice tasks were not preferred due to the fact that they may be limited in terms of capturing the depth, breadth, and complexity of teacher knowledge (Beswick, Callingham, & Watson, 2012; Buchholtz et al., 2013; Schoenfeld, 2007).

If an instrument includes so many tasks to complete, it can be exhaustive for the participants and they may be reluctant to give exact answers to the tasks (Kazemi & Rafiepour, 2018). To avoid this possibility, the participants were asked to complete the fractions test in two sessions. The time elapsed between the two administrations was 2 weeks. In the first session, the participants completed the tasks regarding common content knowledge and specialized content knowledge for teaching fractions (Tasks 1 through 7). In the second session, they completed tasks regarding knowledge of content and students, knowledge of content and teaching, and knowledge of mathematics curriculum for teaching fractions (Tasks 8 through 17). For each session, the time allocated to the participants was 90 minutes. Thus, it took 180 minutes for the participants to complete the whole tasks included in the fractions test.

Validity of the Instrument

In the current study, the following three categories of test validation have been used to improve the quality of the Knowledge for Teaching Fractions Test: content validity, criterion validity, and construct validity. Content validity was established in two steps. First, a faculty member who is an expert in Turkish language and grammar checked the clarity and appropriateness of the language used in the instrument because some tasks were directly translated and adapted from English to Turkish and some others were developed by the researcher. Second, three mathematics educators with an expertise in knowledge and pedagogy for teaching fractions judged the instrument tasks based on the following questions: (a) Are there any tasks that do not measure fractional understanding? (b) Are tasks representative of all possible tasks that could be asked about fractions? Based on the feedback and comments of three mathematics educators, the fraction tasks were modified and refined.

To establish criterion-related validity, the participants’ performance on the fractions test was compared with their Methods of Teaching Mathematics course scores. A validity coefficient of 0.59 indicated that there was a strong positive correlation between the test scores and course courses (p < .05). This shows that the instrument designed in the current study does indeed measure pre-service teachers’ knowledge for teaching fractions because those who scored high on the fractions test also had high Methods of Teaching Mathematics course scores.

To address the issue of construct validity, first an extensive literature review on pre- and in-service teachers’ knowledge for teaching fractions was conducted and the majority of the tasks in the instrument were derived from the relevant literature. Besides, a table of specifications relating teacher knowledge components (see Table 1) to fraction tasks were prepared and the three mathematics educator experts were asked to examine this table and rate how well each task match with the corresponding knowledge component. After examining expert ratings, the fraction tasks were modified and refined to enhance the quality of the instrument.

Scoring and Data Analysis

Before scoring and data analysis, each participant’s answer sheet was labeled with a number between 1 and 51 to maintain confidentiality (i.e., Participant 1–51). When scoring pre-service teachers’ responses, the format of the tasks was considered. Namely, open-ended tasks were scored either as 0 (incorrect or blank answer), 0.5 (partially correct answer), or 1 (fully correct answer). In such tasks, to get full credit for a correct answer, the participants had to provide mathematically correct explanations as well. Pre-service teachers’ responses to matching and true-false tasks were scored either as 0 (incorrect or blank answer) or 1 (correct answer). In these tasks, participants were not required to make explanations.

Both quantitative and qualitative research techniques were used to analyze the data obtained in this study. As a quantitative technique, descriptive statistics including means (M), standard deviations (SD), frequencies (f), and percentages (%) were used. The mean is the average of all scores in a distribution. Thus, the means were determined by adding up all of the scores and then dividing this sum by the total number of scores for each task, component, and the whole test. The means range between 0 and 1. The closer the mean is to 1, the higher the level of achievement on a task, component, or test. Reporting only the means is not sufficient for describing the distribution of participant scores. Therefore, the means are reported along with standard deviations. The standard deviation tells us how spread out the scores are in a distribution. As with the means, the standard deviations range between 0 and 1; and the more spread out the scores are, the larger the standard deviations are.

As a qualitative technique, content analysis was performed to categorize pre-service teachers’ responses to open-ended tasks. Specific rubrics were prepared to code participants’ responses to each open-ended task. Prior to coding, first, all responses were read a few times so as to make sense of and better interpret the nature of different explanations provided by the participants. The coding criteria focused mainly on the correctness of participants’ responses and the methods used by them to solve each task. For instance, participants’ responses to Task 2 were classified into three broad categories in terms of correctness and several subcategories in terms of the solution methods used as follows: correct (i. solving by setting up equations, ii. solving in two separate steps without setting up an equation), partially correct (i. writing only the correct answer without any explanation, ii. incomplete solution), and incorrect (i. selection of wrong operations, ii. setting up wrong equations, iii. misunderstanding the problem).

The codings were carried out by considering pre-service teachers’ original responses in Turkish. The translations into English were made upon the completion of the coding process. Namely, the data were translated and presented in English after analyzing and summarizing participants’ responses to fraction tasks. The second coder is a mathematics education researcher with a doctoral degree in this field. She is fluent in both Turkish and English and she cross-checked the correctness of all codings and translations. The coding process was finalized when the conflicts between the two coders were resolved after discussing them in a number of meetings and reaching a common consensus.

Results

In this section, first, descriptive statistics results are reported to provide a more holistic picture of data and to better understand participants’ strengths and weaknesses related to the teaching of fractions. Next, participants’ responses to some of the specifically selected tasks (i.e., Task 2, Task 5a, Task 6c, Task 8, Task 14, and Task 17) are presented to provide a closer look at their knowledge for teaching fractions. Descriptive statistics results regarding participants’ knowledge for teaching fractions are presented by components and tasks in Table 3.

Table 3 Pre-service Teachers’ Knowledge for Teaching Fractions by Components and Tasks

Components and tasks	M	SD
Common content knowledge	0.82	0.24
Task 1	0.88	0.31
Task 2	0.66	0.45
Task 3	0.90	0.26
Specialized content knowledge	0.35	0.15
Task 4	0.31	0.28
Task 5	0.33	0.26
Task 6	0.23	0.24
Task 7	0.53	0.22
Knowledge of content and students	0.76	0.12
Task 8	0.46	0.14
Task 9	0.90	0.25
Task 10	0.92	0.16
Knowledge of content and teaching	0.50	0.15
Task 11	0.83	0.27
Task 12	0.59	0.28
Task 13	0.30	0.17
Task 14	0.26	0.43
Knowledge of mathematics curriculum	0.66	0.14
Task 15	0.91	0.15
Task 16	0.69	0.32
Task 17	0.40	0.24
Overall mean score	0.62	0.08

As depicted in Table 3, the participants’ overall mean score for the Knowledge for Teaching Fractions Test was found to be 0.62 (SD = 0.08). They displayed a higher achievement in common content knowledge (M = 0.82, SD = 0.24), knowledge of content and students (M = 0.76, SD = 0.12), and knowledge of mathematics curriculum components (M = 0.66, SD = 0.14), but they displayed a lower achievement in specialized content knowledge (M = 0.35, SD = 0.15), and knowledge of content and teaching components (M = 0.50, SD = 0.15) compared to their overall mean score.

Pre-service Teachers’ Common Content Knowledge for Teaching Fractions

As presented in Table 3, the pre-service teachers had sound common content knowledge for teaching fractions (M = 0.82, SD = 0.24). They especially did very well in single step fraction word problems (M = 0.90, SD = 0.26 for Task 3) and in comparing the quotients of two fraction division operations without actually computing them (M = 0.88, SD = 0.31 for Task 1). However, they displayed a lower performance and experienced some difficulties in solving multi-step fraction word problems (M = 0.66, SD = 0.45 for Task 2) compared to Task 1 and Task 3.

More specifically, 29 participants (57%) solved Task 2 correctly by setting up equations (see Participant 15’s answer in Figure 1a) or in two separate steps without setting up an equation (see Participant 24’s answer in Figure 1b). Seven participants (14%) provided partially correct answers due to writing only the correct answer without making any explanation (see Participant 1’s answer in Figure 1c) or due to not completing their solutions (see Participant 9’s answer in Figure 1d). For instance, Participant 9 provided an incomplete response by not calculating the number of strawberry candy boxes that the grocer had sold. Fifteen participants (29%) provided incorrect responses by either selecting wrong operations (see Participant 42’s answer in Figure 1e), setting up wrong equations (see Participant 7’s answer in Figure 1f), misunderstanding the problem (see Participant 2’s answer in Figure 1g), or leaving blank answers. To illustrate, Participant 42 provided an incorrect response by using multiplication instead of division to find the number of strawberry candy boxes sold. Participant 7 provided an incorrect response by setting up an equation that represents the ratio of the number of strawberry candy boxes to mint candy boxes sold rather than the ratio of the number of lemon candy boxes to strawberry candy boxes sold. Participant 2 misunderstood the problem and provided an incorrect response by finding the total number of candy boxes that were sold.

Figure 1. Sample participant responses to Task 2.

Pre-service Teachers’ Specialized Content Knowledge for Teaching Fractions

Table 3 shows that the pre-service teachers’ specialized content knowledge for teaching fractions was very weak (M = 0.35, SD = 0.15) compared to the other four components. More specifically, they had a very limited understanding of fraction constructs (M = 0.31, SD = 0.28 for Task 4), fraction representations (M = 0.33, SD = 0.26 for Task 5), and of posing fraction word problems (M = 0.23, SD = 0.24 for Task 6). Notwithstanding, pre-service teachers displayed a higher achievement in identifying whether the fraction multiplication procedure can be extended to other fraction operations or not (M = 0.53, SD = 0.22 for Task 7).

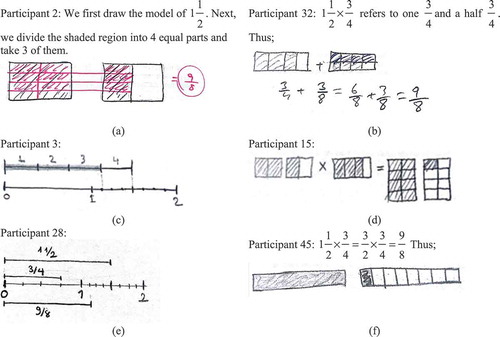
Task 5a and Task 6c were specifically selected to have a closer look at participants’ specialized content knowledge of fractions. The findings showed that 9 participants (18%) provided correct responses for Task 5a either by drawing a region (both operator and repeated addition interpretation of fractions were used) (see the answers of Participant 2 and Participant 32 in Figure 2a,b, respectively) or length model (only the operator interpretation of fractions was used) (see Participant 3’s answer in Figure 2c). Forty-two participants (82%) provided incorrect responses either by drawing region or length models of the multiplicand, multiplier, and product separately (see the answers of Participant 15 and Participant 28 in Figure 2d,e, respectively); finding the product by the multiplication algorithm and then drawing its region model (see Participant 45’s answer in Figure 2f); or leaving blank answers.

Figure 2. Sample participant responses to Task 5a.

Additionally, only 3 participants (6%) provided correct responses for Task 6c by using either measurement (e.g., Participant 4: If $\frac{1}{3}$ litre of milk is poured into an empty container with a volume of $1\frac{5}{7}$ litres, what fraction of the container will be filled?) or ratio interpretation of fractions (e.g., Participant 35: What is the ratio of $\frac{1}{3}$ loaf of bread to $1\frac{5}{7}$ loaves of bread?) Meanwhile, only one participant (2%) provided a partially correct response by posing a decontextualized fraction division task (i.e., Participant 41: Is the quotient a proper or an improper fraction when $\frac{1}{3}$ is divided by $1\frac{5}{7}$?). On the other hand, 47 pre-service teachers (92%) provided incorrect responses by using the following approaches in their solutions: combining two or more erroneous methods such as adding irrelevant information and posing a problem that requires inverting the divisor and multiplying it by the dividend (e.g., Participant 23: Esra has 27 crayons. She gave $\frac{1}{3}$ of $\frac{7}{12}$ of her crayons to her friend. How many crayons did Esra give to her friend?), posing a problem that requires multiplication of the dividend by the divisor (e.g., Participant 27: A farmer cultivated $\frac{1}{3}$ of his land and he planted wheat in $1\frac{5}{7}$ of the cultivated land. How much of his land did the farmer plant wheat?), selecting an irrelevant context for the given numbers (e.g., Participant 10: $\frac{1}{3}$ litre of milk is poured into bottles. Each bottle holds $1\frac{5}{7}$ litres. How many bottles are needed?), using a fraction greater than 1 to refer to a single whole (e.g., Participant 18: Emin first painted $\frac{1}{3}$ of a wall. Next, he drew a picture on $1\frac{5}{7}$ of the painted region. What fraction of the wall is covered with the picture?), posing a fraction addition problem (e.g., Participant 16: First, take $\frac{1}{3}$ of a number. Next, take $1\frac{5}{7}$ of the same number. What fraction of the number is taken altogether?), posing a problem that requires inverting the divisor and multiplying it by the dividend (e.g., Participant 19: $\frac{1}{3}$ of the whole bricks are yellow. $\frac{7}{12}$ of the yellow bricks are sold. How much of the whole bricks are sold?), not using appropriate units for the dividend or divisor (e.g., Participant 3: $\frac{1}{3}$ of a cake is cut into equal slices of $1\frac{5}{7}$. How much does each slice weigh?), and leaving blank answers.

Pre-service Teachers’ Knowledge of Content and Students for Teaching Fractions

As seen in Table 3, the pre-service teachers’ mean score for knowledge of content and students component was found to be 0.76 (SD = 0.12). Although they displayed a lower achievement in tasks related to the area model of fractions (M = 0.46, SD = 0.14 for Task 8), it appeared that they had a sound body of knowledge regarding fraction ordering strategies (M = 0.90, SD = 0.25 for Task 9) and fair sharing (M = 0.92, SD = 0.16 for Task 10).

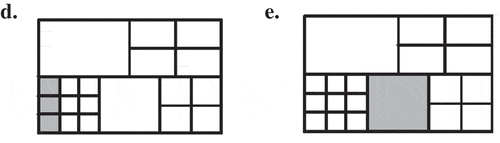
More specifically, none of the participants could provide a totally correct response for Task 8, but 45 of them (88%) could provide partially correct answers for it. In 37 of the partially correct answers, the participants had same shape-same size fractional parts conception and seemed to be unaware of the area model of fractions. For instance, Participant 29 explained her reasoning as follows: “Ayşe is mistaken. She must have divided the triangle into 3 equal parts. However, they are not equal to each other here. If I were Ayşe’s teacher, I would cut the 3 parts and have Ayşe examine whether they overlap with each other. By this way, she would see that the parts are not congruent and would notice her mistake”. In 7 of the partially correct answers, the participants used the S, 3S, 5S similarity rule in overlapping triangles and they indicated that the shaded region is 1/3 of the given triangle (see Participant 1’s answer in Figure 3a). Of all the partially correct answers, only one of them referred to a possible student overgeneralization and it was indicated that Ayşe might have the same length-same area misconception (Participant 32: Ayşe is mistaken. She is possibly overgeneralizing the length and area concepts. She may be thinking that if two sides of a triangle are trisected by two line segments, then the resulting parts must have the same area). Six participants (12%) provided incorrect responses for Task 8. Two of these participants erroneously conceived that fractional parts with the same area must also have the same length (see Participant 8’s answer in Figure 3b) and four of them left blank answers.

Figure 3. Sample participant responses to Task 8.

Pre-service Teachers’ Knowledge of Content and Teaching regarding Fractions

As shown in Table 3, the pre-service teachers’ mean score for the knowledge of content and teaching component was found to be 0.50 (SD = 0.15). Although they had solid knowledge of conceptual strategies for teaching how to order fractions (M = 0.83, SD = 0.27 for Task 11); they had lower knowledge about using pattern blocks, Cuisenaire rods, and geoboards as manipulatives for teaching fractions (M = 0.59, SD = 0.28 for Task 12); and much lower knowledge about which manipulatives, either concrete or virtual, to use in the teaching of fraction multiplication (M = 0.30, SD = 0.17 for Task 13). Likewise, when the participants were asked how they would explain to their students the rationale lying beneath the fraction division algorithm, most of them failed to provide a justification for this algorithm by using relevant representations or mathematical connections (M = 0.26, SD = 0.43 for Task 14).

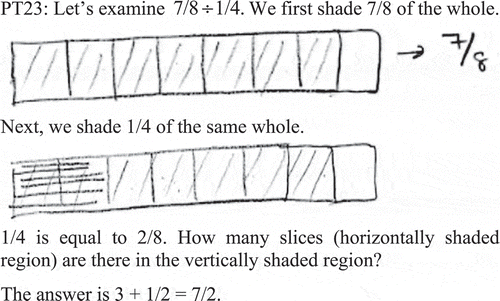
In more detail, 12 participants (23%) provided correct responses for Task 14. Seven of these participants made both numerical and pictorial explanations (see Participant 23’s answer in Figure 4), three of them provided only numerical explanations (e.g., Participant 9: Division means multiplying the first number by the multiplicative inverse of the second number. To give an example, $4÷2=4\times {\left(2\right)}^{-1}=4\times \frac{1}{2}$), and two of them provided only verbal explanations (e.g., Participant 15: When dividing a number by another number, we invert the “divisor” as “1/divisor” and then we perform the multiplication operation. If the divisor is a fractional number such as c/d, we first write it as 1/(c/d) = d/c, and then we multiply it by the dividend. Shortly, when dividing a fraction by another fraction, we find the multiplicative inverse of the divisor and multiply it by the dividend).

Figure 4. Participant 23’s response to Task 14.

On the other hand, 2 participants (4%) provided partially correct responses by making insufficient verbal explanations (e.g., Participant 13: Dividing a number by 2 and multiplying that number by 1/2 are the same things). Thirty-seven participants (73%) provided incorrect responses by either making irrelevant verbal explanations (e.g., Participant 44: I tell my students that I will explain it in the next lesson. I learn the rationale for flipping the divisor as soon as possible and tell it to my students in the next lesson); explaining that the rationales underlying the mathematical rules, procedures, or algorithms should not be questioned (e.g., Participant 19: I would tell my students that mathematics is composed of rules and that rules or algorithms must not be questioned); or leaving blank answers.

Pre-service Teachers’ Knowledge of Mathematics Curriculum for Teaching Fractions

As depicted in Table 3, the pre-service teachers’ mean score for the knowledge of mathematics curriculum component was found to be 0.66 (SD = 0.14). The majority of the participants could identify that ordering fractions, locating fractions on the number line, and multiplication and division with fractions are topics that are taught to students in grade 5 (M = 0.91, SD = 0.15 for Task 15). Participants’ mean curriculum knowledge decreased to some extent when they were asked to identify the correctness of given statements regarding the teaching of fraction topics at specific grade levels (M = 0.69, SD = 0.32 for Task 16). On the other hand, the participants displayed a lower performance in tasks that asked them to write down at which grade level the following fraction topics are first introduced: conversion between improper fractions and mixed numbers; comparing and ordering fractions and locating them on the number line; simplifying and expanding fractions; and four operations with fractions (M = 0.40, SD = 0.24 for Task 17).

More specifically, 16 participants (31%) could identify that comparing, ordering, and locating fractions on the number line are first taught in grade 6. Nineteen participants (37%) could determine that multiplication and division of fractions are first introduced to 6th graders. Twenty of them (39%) could determine that conversion between mixed numbers and improper fractions is first introduced to 5th graders. Twenty-two of them (43%) could identify that students learn to simplify and expand fractions initially in grade 5. Finally, 22 of them (43%) could determine that addition and subtraction of fractions are first introduced to 6th graders.

Discussion and Conclusions

This study explored the extent of pre-service middle level mathematics teachers’ knowledge for teaching fractions. Their level of common content knowledge, specialized content knowledge, knowledge of content and students, knowledge of content and teaching, and knowledge of mathematics curriculum for teaching fractions are discussed in more detail in the following paragraphs.

Pre-service Teachers’ Common Content Knowledge for Teaching Fractions

Participants’ common content knowledge for teaching fractions was measured through tasks that involved evaluation of the answers of the two fraction division operations and single- and multi-step fraction word problems. The findings showed that they had sound content knowledge for teaching fractions. The participating senior pre-service teachers are going to be practicing mathematics teachers in the very near future. Thus, with their mathematics preparation, it is not surprising that they had sound knowledge related to doing four operations with fractions and solving single- or multi-step fraction word problems. This finding is consistent with the findings of previous studies whose participants were either pre-service (e.g., Li & Kulm, 2008) or in-service mathematics teachers (e.g., Li & Huang, 2008; Ma, 1999).

Pre-service Teachers’ Specialized Content Knowledge for Teaching Fractions

In the current study, pre-service teachers’ specialized content knowledge for teaching fractions was measured via tasks that had to with fraction constructs, fraction representations, fraction word problem posing, and a nonstandard fraction division algorithm. The findings showed that, in contrast to common content knowledge, their specialized content knowledge for teaching fractions was very poor. More specifically, they had a very limited understanding of fraction word problem posing, fraction constructs, and fraction representations. Previous research has also reported that pre-service teachers’ specialized content knowledge for teaching fractions is very limited and that they have great difficulty posing fraction word problems, generating fraction representations (e.g., Ball, 1990; Li & Kulm, 2008; Simon, 1993; Toluk Uçar, 2009), and understanding fraction constructs (e.g., Pitta-Pantazi & Christou, 2011; Reeder & Utley, 2017; Vula & Kingji-Kastrati, 2018).

When participants were asked to pose a real-world problem for a division operation in which the dividend was smaller than the divisor (1/3 $÷$ 5/7), they used the following erroneous methods: posing a problem that represents a different numerical expression, using a fraction greater than 1 to refer to a single whole, adding irrelevant information, selecting an irrelevant context for the given numbers, posing a problem that represents a different operation, and not using appropriate units for the dividend or divisor, as found in the studies of Simon (1993), Kılıç (2015), and McAllister and Beaver (2012). The pre-service teachers’ limited understanding of fraction word problem posing might have stemmed from the fact that although problem posing was integrated into school mathematics instruction after the curriculum reform in 2005 (Ministry of National Education, 2009), such integration has not yet been put into practice for teacher education programs in Turkey. Accordingly, problem posing may still be regarded as a novel activity for Turkish pre-service teachers and as argued by Kılıç (2015) and Ellerton (2013), they must engage more in such activities to improve their understanding.

The pre-service teachers also used some erroneous methods when they were asked to translate from numerical to the pictorial representation of a multiplication operation ($11/2\times 3/4$). These erroneous methods were: drawing region or length models of the multiplicand, multiplier, and product separately; and finding the product by the multiplication algorithm and then drawing its region model. Luo, Lo, and Leu (2011) also found similar results in that the US and Taiwanese pre-service elementary teachers experienced difficulties in selecting the relevant pictorial representation for a given multiplication operation. The researchers conducted follow-up interviews with the pre-service teachers to diagnose possible sources of errors regarding translation among different fraction representations and they found out that the participants believed that the referent whole for the multiplicand and multiplier must be the same. Besides, it was revealed that the participants ignored the embedded operation and thought that the pictorial representation of a fraction addition operation must entirely look the same as that of fraction multiplication. It seems that the pre-service teachers who participated in the current study possibly hold the same erroneous beliefs or gaps in translating among different fraction representations.

Pre-service Teachers’ Knowledge of Content and Students for Teaching Fractions

In the current study, the tasks that were used to measure pre-service teachers’ knowledge of content and students focused on the following aspects: participants’ knowledge and awareness of students’ use of region or area models for shading a fractional part, awareness that gap thinking is one of the erroneous fraction comparison strategies used by the students, and knowledge of possible different strategies that may be used by the students for sharing a whole. The results showed that the level of pre-service teachers’ knowledge of content and students for teaching fractions was high. They displayed high performances in almost all tasks regarding knowledge of content and students. In other words, they had a sound body of knowledge of content and students regarding fraction ordering strategies and fair sharing and thus most of them were able to identify students’ possible conceptions and errors. This result is in line with the findings of Eroğlu (2012) who examined pre-service middle level mathematics teachers’ knowledge of student errors regarding fractions and are in contrast to the expectations of Li and Kulm (2008) who conjectured that pre-service teachers’ knowledge of content and students would be very limited in that they do not have adequate teaching experiences.

On the other hand, the participating pre-service teachers had relatively lower achievement regarding the use of region or area models for shading a fractional part (Task 8). This was due to the fact that they had the same size-same shape conception and seemed to be unaware of students’ likelihood of using an area model of fractions. This finding supports the claim that “a teacher’s decision about whether a certain student’s response is correct is based on that teacher’s content knowledge” (Even & Tirosh, 1995, p. 15). The participants might not have evaluated students’ possible mathematical thinking appropriately due to their limited understanding of equipartitioning.

Pre-service Teachers’ Knowledge of Content and Teaching regarding Fractions

In this study, the fraction tasks that were used to measure pre-service teachers’ knowledge of content and teaching focused on the following aspects: selection of specific strategies for ordering fractions, use of manipulatives for teaching fractions in general and fraction multiplication in particular, and selection of specific representations for explaining the underlying rationale of the fraction division algorithm. The findings showed that the level of their knowledge of content and teaching regarding fractions was not satisfactory. Besides, their knowledge of content and teaching regarding fractions tended to be incomplete and fragmentary because there were considerable discrepancies in their achievement across the four tasks administered. Namely, although they had a solid knowledge of strategies for ordering fractions; they had unsatisfactory knowledge about using pattern blocks, Cuisenaire rods, and geoboards as manipulatives for teaching fractions; and very poor knowledge about which manipulatives to use in the teaching of fraction multiplication and in justifying the fraction division algorithm by using relevant representations or mathematical connections.

The finding that the majority of the participating pre-service teachers could not explain the rationale lying beneath the fraction division algorithm runs counter to the results of Li and Huang (2008) in which all in-service Chinese elementary mathematics teachers were found to explain it in one way or other. As argued by Li and Kulm (2008), pre-service teachers’ fragmented knowledge of content and teaching may be attributed to their inexperience in teaching mathematics and consequently to their incompetency with this type of knowledge.

Pre-service Teachers’ Knowledge of Mathematics Curriculum for Teaching Fractions

In the current study, pre-service teachers’ knowledge of mathematics curriculum for teaching fractions was measured via tasks that had to do with identifying the grade placement of the basic fraction concepts based on the learning objectives included in the Turkish middle level mathematics curriculum. The findings showed that participants’ level of knowledge of mathematics curriculum for teaching fractions was satisfactory. This is in contrast with the findings of Li and Kulm (2008) and Li and Huang (2008) in which many of the US pre-service middle level mathematics teachers and Chinese elementary mathematics teachers were reported to have a limited understanding of the curriculum they taught. Li and Huang (2008) concluded that the teaching experience is unlikely to help in-service teachers improve their curricular knowledge given the fact that the pre-service and in-service teachers had similar and limited knowledge of the mathematics curriculum they taught.

The participating pre-service teachers’ higher performances in fraction tasks regarding knowledge of mathematics curriculum may in part be attributed to the impact of KPSS (Civil Servant Selection Examination), a high-stakes national examination taken by the senior pre-service teachers at the end of the spring semester in order to work at Turkish public schools. KPSS is a three-tier test that measures senior pre-service teachers’ knowledge in the following areas: general culture and skills, educational sciences, and mathematics. The participants might have previously worked on and thus had some experience about the curriculum objectives in order to be successful in the mathematics test administered to them as part of KPSS.

Implications

This study has some implications for curriculum developers, teacher educators, and researchers. First of all, given that the participants’ specialized content knowledge for teaching fractions was very limited, curriculum developers should enrich the existing mathematics teacher education program by designing and integrating new compulsory courses that specifically focus on improving pre-service teachers’ knowledge for teaching fractions in particular and mathematics in general. Curriculum developers may also consider the time allocated for covering mathematics teaching methods courses. Currently, pre-service middle level mathematics teacher education programs in Turkey offer only one compulsory mathematics teaching methods course and only four lesson hours are assigned weekly to this course. Accordingly, due to the scarcity of such courses and the limited number of lesson hours provided for these courses, Turkish teacher education programs pave the way for underprepared teachers with inadequate knowledge for teaching mathematics.

Mathematics teacher educators should design new elective courses that cover all aspects of fractions and that help pre-service middle level teachers provide students with robust fraction instruction when they start their teaching profession. Mathematics teacher educators can initially use the Knowledge for Teaching Fractions Test designed in the current study to identify pre-service teachers’ challenges and limitations related to fractions, then devise the content and sequencing of their elective courses accordingly. As Lamon (2012) stressed, learning fractions with depth requires understanding several interrelated concepts such as rates, ratios, and proportions. Thus, mathematics teacher educators may develop and implement specific teaching modules for such core mathematical concepts so as to maximize pre-service teachers’ knowledge for teaching mathematics.

The current study also has some general implications for middle level education. Teachers of other middle-grades subjects such as science and social studies are required to use their subject-specific knowledge in much of the school day and therefore they must be well-prepared for the content they teach (Kosnik & Beck, 2009). As students progress from elementary to middle grades, the content of the aforementioned subjects becomes increasingly more complex and abstract and naturally the knowledge needed by the teachers of these subjects becomes more demanding (Conklin & Daigle, 2012; Lee & Liu, 2010). Therefore, teacher education programs are responsible for preparing pre-service teachers to effectively teach all middle-grades subjects including science and social studies before they leave their programs. It is equally important that curriculum developers of and teacher educators in these middle-grades programs pay more attention to the content and structure of courses in order to help pre-service teachers gain a deeper and more complex knowledge that ensures high quality instruction.

Recommendations for Future Research

Findings from the current study may serve as springboards for future studies. Because almost all characteristics of fractions were considered extensively, the Knowledge for Teaching Fractions Test designed in this study may serve as a useful tool for mathematics education researchers to measure pre-service teachers’ knowledge for teaching fractions. The researchers may also use this test in combination with other data collection methods such as interviews and observations to explore pre-service teachers’ knowledge for teaching fractions in greater depth. Besides, it can be used as a guideline for constructing other instruments regarding fractions.

As argued by Olanoff et al. (2014), although many research studies have been conducted on pre-service teachers’ knowledge for teaching fractions, few of them focused on pre-service teachers’ knowledge of content and students, knowledge of content and teaching, and knowledge of mathematics curriculum. Thus, researchers should pay more attention to these components by using the relevant tasks included in the Knowledge for Teaching Fractions Test.

The focus in the current study was on pre-service teachers’ knowledge for teaching fractions because they form the backbone of many of the school mathematics and advanced mathematical topics. More research is needed from Turkey and other countries to explore pre-service teachers’ knowledge for teaching key mathematical concepts not only in the domain of numbers but also in other domains such as geometry, algebra, and statistics and probability.

In a broader sense, researchers in other middle-grades subject areas (such as science and social studies) may design tests and measure pre-service teachers’ knowledge for teaching the specific subject matter. As more and more studies are conducted on pre-service teachers’ knowledge for teaching the specific subject matter, there may appear a benchmark for developing content and pedagogy courses which warrant pre-service teachers a secure knowledge for teaching.

Notes

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Appendix:

The Knowledge for Teaching Fractions Test

A-Common Content Knowledge

1. Tell whether $\frac{9}{11}÷\frac{2}{3}$ is greater or less than $\frac{9}{11}÷\frac{3}{4}$without evaluating. Explain your reasoning (taken from Li & Kulm, 2008, p. 838).

2. Uncle Ahmet sells candies with mint, lemon, and strawberry flavors in his grocery store. One day, Uncle Ahmet sold 24 boxes of mint candies. The number of boxes of lemon candies he sold on that day was $\frac{3}{4}$ of the number of boxes of mint candies and was $\frac{2}{3}$ of the number of boxes of strawberry candies he sold. How many boxes of strawberry candies did Uncle Ahmet sell on that day in his grocery store (adapted from Li & Huang, 2008)?

3. Read the following problems and match them with their answers (adapted from Moseley, 2005).

a. My mother is planning to set up a fish tank for our goldfish. According to the manual, she needs 180 grams of gravel. However, we have only 90 grams of gravel at home. By how much should she reduce the amount of other materials to be put into the tank in order to prepare the tank with 90 grams of gravels?

b. There are 10 goldfish and an empty tank that has a capacity of 20 litres in our house. My mother will put 5 litres of water in this tank. How much fuller will the tank be after she puts the water into the tank?

c. Our fish tank is full of water and it has a capacity of 6 litres. My sister wants to divide this tank among 8 smaller tanks, each of which has a 1-litre capacity. How much water did she put in each smaller tank?

d. There are 10 goldfish in our house. These fish live in a 15-litre aquarium. The name of the biggest fish is Çöpçü. Çöpçü has his own 10 grams of food. If Çöpçü eats 6 grams of his food, what part of the food will he eat?

e. We have 9 fish in our tank. My father cleaned out this tank and then put 18 litres of water and 6 grams of gravel into it. What is the relationship between the amount of water and gravel put into the tank?

$\frac{1}{3}----\frac{1}{4}----\frac{1}{2}----0.75----\frac{3}{5}----$

B-Specialized Content Knowledge

4. Read Task 3 again and match the problems with the following fraction sub-constructs (adapted from Moseley, 2005).

a. Part-whole ____ b. Quotient ____ c. Ratio ____ d. Measure ____ e. Operator ____

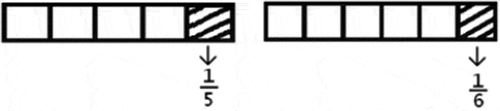
5. Draw a picture that models the following fraction operations: $\mathbf{a}.1\frac{1}{2}\times \frac{3}{4}\mathbf{b}.\frac{2}{3}+\frac{1}{2}\mathbf{c}.\frac{5}{7}÷\frac{1}{3}$ and write the following shaded areas as a product of fractions (adapted from Lamon, 2012):

6. Pose real-world problems for the following fraction operations (adapted from Işık & Kar, 2012a, 2012b):

$\mathbf{a}.\frac{6}{7}\times \frac{3}{4}\mathbf{b}.\frac{2}{3}-\frac{1}{2}\mathbf{c}.\frac{1}{3}÷1\frac{5}{7}\mathbf{d}.\frac{3}{4}÷\frac{1}{2}$

7. You are discussing fraction operations with one of your classmates. She explains her idea as follows: Doing multiplication operations with fractions is easy. What we have to do is just multiply the numerators and the denominators. I think we can do other fraction operations in the same way. That is,

a. Addition $\frac{a}{b}+\frac{c}{d}=\frac{(a+c)}{(b+d)}$b. Subtraction $\frac{a}{b}-\frac{c}{d}=\frac{(a-c)}{(b-d)}$ c. Division $\frac{a}{b}÷\frac{c}{d}=\frac{(a÷c)}{(b÷d)}$

How would you respond to your classmate’s ideas? Explain each operation separately (adapted from Li & Kulm, 2008).

C-Knowledge of Content and Students

Table

8. A teacher asked his/her students to shade one-third of a triangle. Ayşe shaded the triangle as given on the right. Is Ayşe’s answer wrong? If yes, what is her mistake? If you were Ayşe’s teacher, what would you do to have Ayşe notice her mistake (adapted from Johnson, 1998)?

9. A teacher asked Mert to explain whether $\frac{4}{5}$ is greater or less than $\frac{5}{6}$. After drawing the following two equal-length bars and shading $\frac{1}{5}$ and $\frac{1}{6}$ of them, respectively, he explained that $\frac{4}{5}$ is equal to $\frac{5}{6}$ because only one piece is missing from each bar.

Is Mert’s answer wrong? If yes, what is his mistake? If you were Mert’s teacher, what would you do to have Mert notice his mistake (adapted from Mack, 1990)?

10. Students A, B, C, and D were asked to solve the following task: “5 people share 2 pizzas equally. How much pizza does each person get?” The students explained their reasoning by drawing the following figures. Explain which students had a correct reasoning (adapted from Lamon, 2012)?

D-Knowledge of Content and Teaching

11. Suppose that you are mathematics teacher. You are going to teach your students how to compare and order fractions. Explain the strategies that you would use to demonstrate how to order the following fraction triples. Please, do not use common numerator and denominator algorithms (adapted from Clarke & Roche, 2009).

$\mathbf{a}.\frac{1996}{1997},\frac{1997}{1998},\frac{1998}{1999}\mathbf{b}.\frac{1}{7},\frac{4}{5},\frac{8}{19}$

12. Explain which of the following materials or tools can be used in the teaching of fractions (adapted from LMT, 2008)?

a. Pattern blocks   b. Cuisenaire rods   c. Geoboards

13. Explain the materials or tools that can be used in the teaching of multiplication of fractions.

14. During the lesson when you teach the algorithm for “division of fractions” (i.e., $\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}\times \frac{d}{c}$), students asked why you change from ‘division’ to ‘multiplication’ and flip the second fraction. How would you explain to students (taken from Li & Huang, 2008, p. 858)?

E-Knowledge of Mathematics Curriculum

15. Which of the following fraction topics should be taught to 5th grade students according to the Turkish middle level mathematics curriculum released in 2013?

Table

Fraction topics	Yes	No
a. Ordering fractions	()	()
b. Locating fractions on the number line	()	()
c. Multiplication and division with fractions	()	()

16. Which of the following statements are true according to the Turkish middle level mathematics curriculum released in 2013?

Table

Statements	True	False
a. Comparison of unit fractions is taught in grade 5.	()	()
b. The common denominator algorithm should be the first strategy to introduce when teaching addition and subtraction of fractions.	()	()
c. The 7th grade mathematics curriculum gives more weight to the teaching of rational number concepts when compared to the teaching of rational number operations.	()	()
d. The method for converting repeating decimals into rational numbers in the form of a/b is first taught in grade 7.	()	()

17. Some topics that are included in the Turkish middle level mathematics curriculum (Ministry of National Education, 2013a) are given below. Determine at which grade level these topics are first introduced to the middle level students (I: grade 5, II: grade 6; III: grade 7; IV: grade 8)?

a. Conversion between mixed numbers and improper fractions ()

b. Multiplication or division with fractions ()

c. Comparing, ordering, and locating fraction on the number line ()

d. Simplifying or expanding fractions ()

e. Addition or subtraction with fractions ()