Weighted Hazard Ratio Estimation for Delayed and Diminishing Treatment Effect

Abstract

Nonproportional hazards (NPH) have been observed in confirmatory clinical trials with time to event outcomes. Under NPH, the hazard ratio does not stay constant over time and the log rank test is no longer the most powerful test. The weighted log rank test (WLRT) has been introduced to deal with the presence of nonproportionality. We focus our attention on the WLRT and the complementary Cox model based on time varying treatment effect proposed by Lin and León. We investigate whether the proposed weighted hazard ratio (WHR) approach is unbiased in scenarios where the WLRT statistic is the most powerful test. In the diminishing treatment effect scenario where the WLRT statistic would be most optimal, the time varying treatment effect estimated by the Cox model estimates the treatment effect very close to the true one. However, when the true hazard ratio is large the proposed model overestimates the treatment effect and the treatment profile over time. In the delayed treatment scenario, the estimated treatment effect profile over time is typically close to the true profile. For both scenarios, we have demonstrated analytically that the hazard ratio functions are approximately equal under small treatment effects. When the assumed rate of how quickly the treatment effect profile is diminishing or delaying differs in the analysis from that in the true data generating mechanism, the estimated hazard ratio profile from the WHR approach is biased. Since in practice the true HR time profile may differ from that assumed in the WHR analysis, it may be preferable to use alternative approaches for effect estimation.

KEYWORDS:

• Nonproportional hazards
• Hazard ratio
• Weighted log rank test
• Clinical trials

1 Introduction

Randomised clinical trials (RCTs) are regarded as the gold standard for evaluating the effectiveness of a new treatment. In RCTs with time to event outcomes, the primary outcome is to measure the differences in the survival curves of the different arms and report the treatment effect to quantify treatment differences. The analysis of such trials are routinely accomplished by the log rank test and the Cox proportional hazard (PH) model. The hazard ratio is obtained from the Cox PH model to measure the effectiveness of the new treatment compared to the control group. The Cox PH model assumes that the hazard ratio between the treatment and control group stays constant from the start of study period until the end of the follow up period. Under PH, the log rank test is the most powerful test to detect differences in the survival curves (Fleming and Harrington 1991). However, nonproportional hazards (NPH) are commonly observed in RCTs and have been reported in many published trials for example, the IPASS trial in lung cancer (Mok et al. 2009) and the ICON7 trial in ovarian cancer (Kristensen et al. 2011). When the PH assumption does not hold, the log rank test is still valid but may suffer substantial power loss and the interpretation of the hazard ratio becomes difficult (Hernán 2010). There may be many reasons for non PH to exist in clinical trials, for instance due to delayed clinical effect in the case of immuno-oncology trials.

Various statistical methods have been proposed to analyze time to event outcomes in clinical trials under nonproportional hazards scenarios including restricted mean survival time (RMST) (Royston and Parmar 2013), weighted log rank tests (Fleming and Harrington 1981) and maximum combination test (MaxCombo) (Lin et al. 2020). The RMST measures the average survival time from time t = 0 to some pre-specified time horizon $t=\tau$ and it may be estimated as the area under the survival curve up to that time point. The weighted log rank test based on the Fleming-Harrington class of weights $G^{\rho ,\gamma }$ with weight $S{(t)}^{\rho } {(1-S(t))}^{\gamma }$ where S(t) is the survival function of the pooled patients from control and treatment group; the parameters ρ, γ allows one to down weight early, late or middle events. The MaxCombo test uses the Fleming-Harrington weight function to analyze time to event outcomes in the presence of non PH. The test avoids having to pre-specify the weight function and considers a procedure which selects the best test from the set of test statistics. The procedure consist of selecting the best combination of weighted log rank test statistics with different choices of ρ and γ. When the MaxCombo approach is used, Lin et al. (2020) suggest using the weighted hazard ratio for effect estimation. The estimated effect is obtained from a Cox model with a time-varying effect, where the weights are those associated with the weighted log rank test (Lin and León 2017).

This article focuses on the estimation of treatment effect under nonproportional hazards, particularly the weighted hazard ratio method proposed by Lin and León (2017). They propose fitting a particular Cox model with a time-varying covariate/effect for which the score test corresponds to a weighted log rank test. The model proposes an effect adjustment factor A(t) = $\frac{w(t)}{\max (w(t))}$ where w(t) is the weight function from the chosen weighted log rank test. This is incorporated in to the Cox PH model to provide time varying effect which can be viewed as the treatment coefficient β weighted by the adjustment factor A(t). The hazard ratio obtained from the model is expressed as $HR(t)=e^{\beta A(t)}$ = ${[H{R}^F]}^{A(t)}$ where HR^F represents the maximal effect at time t with A(t) = 1. In this article, we are interested in investigating whether the estimated treatment effect is unbiased under scenarios in which the associated weighted log rank test is the most powerful.

In Section 2, we describe the standard weighted log rank test and the proposed weighted hazard ratio estimation (Lin and León 2017) and its estimation of the time-varying HR. In Section 3, we compare the hazard ratio functions obtained from the proposed model with the true hazard ratio functions analytically. In Section 4, we assess, through simulations, the performance of the proposed model under the two non PH scenario with different choices of ρ and γ. Section 5 is a discussion.

2 Weighted Log Rank Tests and Effect Estimation

In this section, we will provide a brief overview of the log rank test and the weighted log rank test, as well as introduce weighted hazard ratio for effect estimation proposed by Lin and León (2017).

2.1 Weighted Log Rank Test

Let t₁,t₂,…,t_r be the ordered failure times across both treatment arms, $d_{1j}$ and $d_{2j}$ be the number of deaths at t_j in treatment and control arm, respectively with d_j= $d_{1j}$ +$d_{2j}$ and $n_{1j}$ and $n_{2j}$ be the number of individuals at risk before t_j with n_j = $n_{1j}$ + $n_{2j}$. Let $X_1,X_2,\dots ,X_r$ denote the treatment assignment where X_j=1 if the jth subject is assigned to treatment arm and X_j=0 if assigned to control arm. The log-rank test statistic is defined as, $$\begin{array}{c}Z=\frac{\sum _{j=1}^r(d_{1j}-e_{1j})}{{(\sum _{j=1}^r{V}_L)}^{1/2}}\hfill \end{array},$$where $e_{1j}$= $\frac{n_{1j}{d}_j}{n_j}$ is the expected number of failure at time $t_{(j)}$ under the null hypothesis of equal survival curves. V_L is the variance of the observed number of failures, V_L = ${\sum }_{j=1}^r\frac{n_{1j}{n}_{2j}{d}_j(n_j-d_j)}{n_j^2(n_j-1)}$. Under the null hypothesis of equal survival functions in the two treatment groups, asymptotically the test statistic has a Chi-squared distribution on one degree of freedom. Although the log rank test is still a valid test under nonproportional hazards it is not the most powerful test (Royston and Parmar 2013). Therefore, the weighted version of log rank test is sometimes used when the ratio of the two hazard functions are not constant over time (Fleming and Harrington 1981).

The weighted log rank test (WLRT) assigns a weight function to different time points depending on the expected type of nonproportional hazard scenario. For instance, in immuno-oncology trials there may be a delayed treatment effect and therefore the survival curve for the treatment group will only emerge to separate from the control survival curve after a certain period of time. In this case, higher weights can be allocated to later time points (Lin et al. 2020). Formally, the WLRT is defined as, (1) $$\begin{array}{c}{W}_K=\frac{\sum _{j=1}^{r}w(t_j)(d_{1j}-e_{1j})}{{(\sum _{j=1}^r{V}_L)}^{1/2}}\hfill \end{array},$$(1) with variance $$\begin{array}{c}{V}_K=\sum _{j=1}^{r}w{(t(j))}^2(\frac{n_{1j}{n}_{2j}{d}_j(n_j-d_j)}{n_j^2(n_j-1)})\hfill \end{array}$$ where $w(·)$ is the nonnegative weight function. We will consider the Fleming-Harrington family of weighted log rank test, commonly denoted as $G^{\rho ,\gamma }$ with weight, (2) $$w(t)=\widehat{S}{(t)}^{\rho }{(1-\widehat{S}(t))}^{\gamma }$$(2) where $\widehat{S}(t)$ is the Kaplan- Meier estimate of the survival function of the pooled patients from the treatment and control arm. The parameters ρ and γ control the shape of the weight function. $G^{0,0}$ represents the log-rank test with w(t) = 1 that has constant weight over time; delayed treatment effects can be tested using $G^{0,\gamma }$ with $w(t)={(1-\widehat{S}(t))}^{\gamma }$ that allocates higher weight at later time points to detect late survival difference, $G^{1,0}$ represents diminishing effect with $w(t)=\widehat{S}(t)$ that gives more weight the earlier time points to detect early separation; $G^{1,1}$ represents mid separation with $w(t)=\widehat{S}(t)(1-\widehat{S}(t))$ that puts more weight at the middle of the follow-up period than at the ends.

2.2 Weighted Hazard Ratios

Lin and León (2017) proposed fitting a Cox model to provide a time varying treatment effect estimate to complement the weighted log rank test. Lin and León propose fitting a Cox model with, $$\lambda (t;X)={\lambda }_0(t)e^{A(t)\beta X}$$where A(t) is defined by $$A(t)=\frac{w(t)}{\max (w(s))}$$ $\max (w(s))$ is evaluated over the values of t in the observed dataset and A(t) thus has a maximum value of 1. The time varying covariate $X^{*}(t)=A(t)X$ represents the treatment assignment weighted by the adjustment factor. Once $X^{*}(t)$ has been determined, the constant coefficient β can be estimated. It is shown in the paper that the score test of the null hypothesis that β = 0 in the proposed model above is equivalent to the weighted log rank test with the corresponding choice of weight function (Lin and León 2017). Lin and León used the fact that the score test from this Cox model corresponds to a particular weighted log rank to motivate estimating the time-varying treatment effect using this Cox model. The coefficient β can be interpreted as the maximal effect where the model assumes the patients experience the most benefit (A(t) = 1). To differentiate the time varying hazard ratio derived from the proposed method, we will denote this as HR_LL and it can be expressed as, (3) $$H{R}_{LL}(t)=\frac{{\lambda }_0(t)e^{A(t)\beta \times 1}}{{\lambda }_0(t)e^{A(t)\beta \times 0}}=e^{\beta A(t)}={\left[H{R}^F\right]}^{A(t)}$$(3) where HR^F=$e^{\beta }$ represents the maximal effect (i.e., at time t with A(t)=1). The time profile of the treatment effect can be observed as the treatment coefficient β weighted by the adjustment factor A(t). The estimate derived from the model provides a consistent time profile of the hazard ratio over time given that the true hazard ratio also varies over time as specified by A(t). If this does not hold then the treatment effect measure will in general no longer be unbiased for the true value of the hazard ratio at a given time.

3 Evaluation of Weighted Hazard Ratio Estimation Method

In this section we give expressions for the hazard ratio function for which the Fleming-Harrington (Fleming and Harrington 1991) $G^{\rho ,\gamma }$ test statistics are most efficient. We will also be exploring whether, for a given weight function, the Lin and León estimation method (Lin and León 2017) gives you the correct treatment effect profile if the true data generating mechanism is such that the corresponding weighted log rank test is the most powerful.

3.1 Diminishing Effect

Fleming and Harrington (1991) showed that the $G^{\rho }$ test statistic is the most powerful test statistic when the hazard ratio at time t is of the following form, (4) $$\frac{{\lambda }_2(t)}{{\lambda }_1(t)}=\frac{e^{\Delta }}{{\{S_1(t)\}}^{\rho }+e^{\Delta }[1-{\{S_1(t)\}}^{\rho }]}$$(4) where $S_1(t)=\hspace{0.17em}\exp \hspace{0.17em}(-{\int }_0^t{\lambda }_1(x)\text{dx})$ is the survival function for the control arm. The parameter $e^{\Delta }$ represents the hazard ratio at t = 0. The parameter ρ controls how quickly the effect diminishes. Note that the parameter γ is 0 in the (2) under the diminishing effect scenario. The above hazard ratio function (4) has its full treatment effect initially $e^{\beta }$ and decreases monotonically to 1. Later, we will demonstrate various examples with $\rho =0.5,1,2$ to further develop our understanding about the behavior of the weighted logrank test and the proposed model. We now calculate the weighted hazard ratio function proposed by Lin and León (2017) under the set up where the $G^{\rho }$ test statistic would be optimal. In order to calculate the proposed weighted hazard ratio function under the set up where WLRT is optimal, we will need to derive the true pooled survival function which is determined by finding the survival function of the two treatment arms. The hazard function for the treatment arm ${\lambda }_2(t)$ can be derived, assuming that the true data generating mechanism is such that that WLRT is optimal, by using (4) $$\begin{array}{c}{\lambda }_2(t)=\frac{{\lambda }_1(t)e^{\Delta }}{{\{S_1(t)\}}^{\rho }+e^{\Delta }[1-{\{S_1(t)\}}^{\rho }]}.\hfill \end{array}$$

Thus, the survival function for the treatment arm is, (5) $$\begin{array}{c}{S}_2(t)=\hspace{0.17em}\exp \hspace{0.17em}\left(-{\int }_0^t{\lambda }_2(x)dx\right)\hfill \\ =\hspace{0.17em}\exp \hspace{0.17em}\left(-{\int }_0^t\frac{{\lambda }_1(x)e^{\Delta }}{{\{S_1(x)\}}^{\rho }+e^{\Delta }[1-{\{S_1(x)\}}^{\rho }]}dx\right)\mathrm{}.\hfill \end{array}$$(5)

We can replace the adjustment factor A(t) with the weight function that the Lin and León method converges to (as n tends to $\infty$) (3), in this case S(t). For the Lin and León (2017) method, we estimate the pooled survival function S(t) by the Kaplan-Meier estimator for the pooled sample which is consistent for the true pooled survival function. Therefore, the Lin and León method consistently estimates, (6) $$\begin{array}{c}H{R}_{LL}(t)=e^{\beta A(t)}=e^{\beta {(0.5S_1(t)+0.5S_2(t))}^{\rho }}.\hfill \end{array}$$(6)

Substituting $S_2(t)$ in the hazard ratio function (6) for which this WLRT is optimal for gives, (7) $$\begin{array}{c}H{R}_{LL}(t)=\hspace{0.17em}\exp \hspace{0.17em}[\beta \left(\frac{1}{2}{S}_1(t)\right)\\ +\frac{1}{2}\exp \hspace{0.17em}\left(-{\int }_0^t\frac{{\lambda }_1(x)e^{\Delta }}{{\{S_1(x)\}}^{\rho }+e^{\Delta }[1-{\{S_1(x)\}}^{\rho }]}dx\right){)}^{\rho }]\mathrm{}.\end{array}$$(7)

When fitting the proposed model, the β is estimated from the Cox PH model once the adjustment factor A(t) is determined. Comparing the true hazard ratio function (4) with the proposed hazard ratio function (7), we see that the two expressions do not appear to be equal to each other. In Appendix B, we demonstrate that the two hazard ratio functions are approximately equal to each other when Δ is close to 0. We also demonstrate this equality graphically in the next section where we choose the value of $e^{\Delta }$ to compare the hazard ratio functions. We also compare the hazard ratio expressions analytically for some particular choices of ${\lambda }_1(t)$ and $e^{\Delta }$ to illustrate in Appendix A.

3.2 Delayed Treatment Effect

The paper by Garès et al. (2017) has provided an expression for the hazard function for which the Fleming-Harrington test $G^{\gamma }$ for detecting late effects is optimal. The parameter ρ is 0 in the weight function (2) under the delayed effect scenario. Assume the survival time in the control arm is exponentially distributed with some constant hazard λ₁. Then Garès et al. (2017) show that the $G^{\gamma }$ test is optimal for testing the hypothesis, (8) $$\begin{array}{c}{H}_0:{\lambda }_{CT}={\lambda }_{\mathit{TRT}}={\lambda }_1\hfill \\ H_1:{\lambda }_{\mathit{TRT}}(t)={\lambda }_{CT}\frac{L^{\gamma }({({\mathcal{L}}^{\gamma })}^{-1}({\mathcal{L}}^{\gamma }(e^{-{\lambda }_{1}t})+\phi ))}{L^{\gamma }(e^{-{\lambda }_{1}t})}\hfill \end{array}$$(8) where $L(x)={\int }_x^1\frac{(1-s)}{s}ds=1+\hspace{0.17em}\ln \hspace{0.17em}(x)-x$ and $\mathcal{L}(x)={\int }_{0.5}^x\frac{1}{s\hspace{0.17em}\log \hspace{0.17em}(s)+s-s^2}ds$. The expression for the hazard ratio has no closed form and needs numerical integration techniques to compute. Garès et al. (2017) has provided the definition for the parameter $\phi$ which is evaluated at some chosen time point τ and is of the following form, (9) $$\begin{array}{c}\phi ={\mathcal{L}}^{\gamma }(r(1-S_1(\tau ))+S_1(\tau ))-{\mathcal{L}}^{\gamma }(S_1(\tau ))\\ ={\mathcal{L}}^{\gamma }(S_2(\tau ))-{\mathcal{L}}^{\gamma }(S_1(\tau ))\end{array}$$(9) where r is the discrepancy rate, $r=\frac{S_2(\tau )-S_1(\tau )}{1-S_1(\tau )}$.

Similar to the diminishing effect scenario, we can check whether the true hazard ratio for which the $G^{\gamma }$ test is optimal, as given in (8), agrees with the hazard ratio estimation proposed by Lin and León (2017). The true hazard ratio under which the $G^{\gamma }$ test statistic is optimal is shown to be the second equation in (8). Now the weighted hazard ratio model proposed by Lin and León corresponds to, $$\begin{array}{c}H{R}_{LL}(t)=e^{\beta A(t)}=e^{\beta \frac{w(t)}{\max (w(s))}}\hfill \\ =e^{\beta \left(\frac{{\left(1-S(t)\right)}^{\gamma }}{\max (w(s))}\right)}=e^{\beta \left(\frac{{(1-0.5S_1(t)-0.5S_2(t))}^{\gamma }}{\max (w(s))}\right)}.\hfill \end{array}$$

From Garès et al. the survival in the treatment and control arm is defined as $$\begin{array}{c}{S}_2(t)={(\mathcal{L})}^{-1}(\mathcal{L}(e^{-{\lambda }_{1}t})+\mathcal{L}(S_2(\tau ))-\mathcal{L}(S_1(\tau )))\\ ={(\mathcal{L})}^{-1}(\mathcal{L}(e^{-{\lambda }_{1}t})+\phi )\end{array}$$and $S_1(t)=e^{-{\lambda }_1}t$ (Garès et al. 2017). We now substitute in for $S_1(t)$ and $S_2(t)$, (10) $$\begin{array}{c}H{R}_{LL}(t)=e^{\beta \left(\frac{{\left(1-0.5e^{-{\lambda }_{1}t}-0.5{\mathcal{L}}^{-1}(\mathcal{L}(e^{-{\lambda }_{1}t})+\phi )\right)}^{\gamma }}{{\left(1-0.5e^{-{\lambda }_1\tau }-0.5{\mathcal{L}}^{-1}(\mathcal{L}(e^{-{\lambda }_1\tau })+\phi )\right)}^{\gamma }}\right)}\mathrm{}.\hfill \end{array}$$(10)

As in Section 3.1, we show in Appendix C that if the Lin and León method estimates the correct hazard ratio at the time point when it is largest (at $t=\tau$), then it will estimate the HR at all other times correctly too under the condition that $\phi$ is small.

4 Simulation Studies

This section investigates the weighted hazard ratio method under diminishing and delayed effect using simulations Lin and León (2017). We will focus on investigating the method proposed by Lin and León and its properties when nonproportional hazards are present in the data. Specifically, we will empirically check the analytical results of Section 3 that showed that the Lin and León approach is approximately unbiased when the treatment effect is small, and how large the bias might be when the treatment effect is larger.

4.1 Scenario I: Diminishing Effect

We simulated the survival data where the treatment is assumed to have its maximal effect initially and decrease monotonically to 1. The survival function for the treatment arm is given in (5). Three different scenarios $\rho =0.5,1,2$ were considered to understand the behavior of the proposed model under various rates at which the effect diminishes. We also chose three different values of the maximum effect $e^{\Delta }=0.75,0.50,0.25$ to investigate whether substantial bias occurs when the treatment effect is larger. We fitted the Cox model proposed by Lin and León (2017) where the weight function $w(t)=\widehat{S}{(t)}^{\rho }$ for the non PH data we simulated is specified for three scenarios $\rho =0.5,1,2$. The study enrolls 200 patients, equally allocated in the two arms. The survival of the control arm follows an exponential distribution with hazard rate ${\lambda }_1(t)=0.5$. The survival in the treatment arm is as per equation (5)(5) $$\begin{array}{c}{S}_2(t)=\hspace{0.17em}\exp \hspace{0.17em}\left(-{\int }_0^t{\lambda }_2(x)dx\right)\hfill \\ =\hspace{0.17em}\exp \hspace{0.17em}\left(-{\int }_0^t\frac{{\lambda }_1(x)e^{\Delta }}{{\{S_1(x)\}}^{\rho }+e^{\Delta }[1-{\{S_1(x)\}}^{\rho }]}dx\right)\mathrm{}.\hfill \end{array}$$(5) . The follow up time is assumed to be 3 years; patients whose event time exceeds 3 years are censored. We conducted 5000 runs for each scenario.

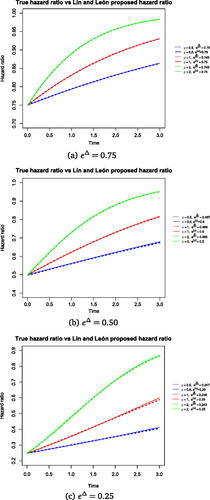
Figure 1 shows the true hazard ratio over time for which the $G^{\rho }$ statistic is optimal and the average hazard ratio profile over time estimated by the Lin and León method. The plot displays $e^{\overline{\widehat{\beta }}S{(t)}^{\rho }}$ where $\overline{\widehat{\beta }}$ is the average of the log hazard ratio at t = 0 estimated from the Lin and León method and S(t) is the true pooled survival function. The proposed model slightly overestimates the maximal effect when the true HR at t = 0, that is $e^{\Delta }$, is large, and continues to slightly overestimate during the follow up period. Note that when the treatment effect is small, the proposed model estimates the maximal effect very close to the true one, in line with our analytical results in Appendix B. We observe through our work that when the treatment effect is large, the proposed model is not able to estimate the maximal effect at t = 0 correctly which has an impact on the treatment effect profile over time, in that case the implied profile of treatment effect over time would not match the true one (as given by (4)).

Fig. 1 Hazard ratio over time targeted by weighted hazard ratio model and true hazard ratio over time under a data generating mechanism where the $G^{\rho }$ test is optimal. The solid lines show the true hazard ratio over time for $\rho =0.5,1,2$. The true hazard ratio for the three scenarios at t = 0 are $e^{\Delta }=0.75,0.50,0.25$ and the hazard rate in the control arm stays the same in all the scenarios ${\lambda }_1(t)=0.5$. The dotted lines show the proposed hazard ratio targeted by the weighted hazard ratio model. The hazard ratio for the dotted lines is the average of the hazard ratios estimated from fitting the Lin and León method and is as follows; the average of the log hazard ratio across 5000 simulations is $e^{\overline{\widehat{\beta }}}=0.75,0.497,0.247$, $e^{\overline{\widehat{\beta }}}=0.749,0.499,0.246$, $e^{\overline{\widehat{\beta }}}=0.748,0.495,0.243$ for $\rho =0.5,1,2$.

Next we investigated how the proposed method behaves when the value of ρ is misspecified that is the value used in the analysis differs from that used when simulating data. We set the true maximal HR at t = 0 as 0.75. We chose four different values of ρ for data generating purposes, namely, $\rho =0.5,1,1.5,2$. We fitted the Cox model proposed by Lin and León (2017) where the weight function $w(t)=\widehat{S}(t)$ was used, that is, analyzing in all four scenarios assuming ρ = 1. The survival distribution for the control and treatment arm remains the same as in the previous diminishing effect scenario. Figure 2 shows the hazard ratio profile targeted by the weighted hazard ratio approach proposed by Lin and León and the true hazard ratio over time. The solid lines represent the true hazard ratio profiles under the different ρ values, while the dashed lines represent the Lin and León estimated hazard ratio profiles estimated assuming ρ = 1. Note from the black lines that when the data generating value of ρ matches with the value of ρ used in the analysis, the hazard ratio profiles are approximately the same. However, when the value of ρ used in the analysis is incorrect, we can see that the estimated treatment effect differs from the true maximal effect of 0.75. When the data generating value of $\rho =0.5$ was used, the Lin and León HR profile overestimates until 6 months and then starts to underestimate until the end of the study. Similarly, when the data generating value of ρ is set to 1.5 and 2, the Lin and León method underestimates the maximal effect (0.783 and 0.806, respectively) and the HR profile at the start of the study but quickly starts to overestimate after about 6 months. The model misspecification differs depending on how quickly or slowly the treatment effect is diminishing over time. Figure 2 also shows that when the true treatment effect is diminishing slowly that is when $\rho =0.5$, then the method overestimates the initial effect, but then underestimates the effect at later times; however, when the true treatment effect is diminishing faster, then it underestimates the initial effect, but then overestimates the effect at later times.

Fig. 2 Hazard ratio over time targeted by weighted hazard ratio model and true hazard ratio over time under a data generating mechanism where the $G^{\rho }$ test is optimal. The solid lines show the true hazard ratio over time for $\rho =0.5,1,1.5,2$. The true hazard ratio for the four scenarios $\rho =0.5,1,1.5,2$ at t = 0 is $e^{\Delta }=0.75$ and the hazard rate in the control arm stays the same in all the scenarios ${\lambda }_1(t)=0.5$. The dotted lines show the proposed hazard ratio targeted by the weighted hazard ratio model estimated assuming that ρ = 1. The hazard ratio for the dotted lines is the average of the hazard ratios estimated from fitting the Lin and León method and is as follows: $e^{\overline{\widehat{\beta }}}=0.715,0.747,0.783,0.806$ for $\rho =0.5,1,1.5,2$.

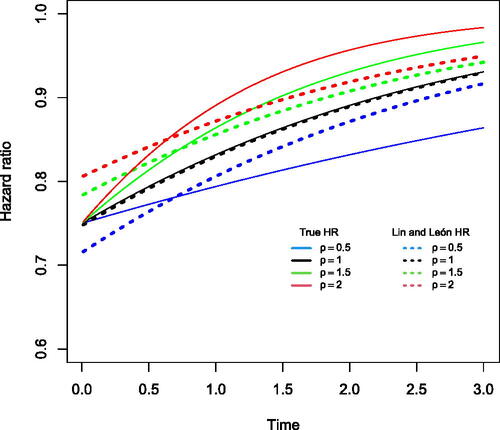
These results demonstrate that misspecification of ρ in the analysis can lead to quite biased estimates of the HR profile over time. We note that when ρ (and later γ) is misspecified, the HR profile over time which is estimated (on average) will depend on the censoring distribution.

4.2 Scenario II: Delayed Treatment Effect

In this scenario, the data were simulated based on the assumption that the treatment will have no effect at the start of the follow up and gradually increases to have its maximal effect at the final time point of follow up period. The study enrolls the same number of patients as in the diminishing effect scenario that is 200. The maximal treatment effect occurs at the final time point τ = 2. The survival times in the control arm are exponentially distributed with ${\lambda }_1(t)$=0.5. The survival times in the active arm can then be simulated using the expression for the hazard function given in (8). To simulate the survival times in the active arm, we calculated the value of $S_2(t)$ for t from 0 to τ in increments of 0.0005. We then simulated $U\sim U(0,1)$ and found the value of t such that $S_2(t)$ was closest to U. We consider two scenarios of $S_2(\tau )=0.6$ and 0.45 which provides the values of discrepancy rate r = 0.37 and 0.13 for $\gamma =0.5,1,2$ to verify our results obtained in Section 3. The mechanism behind simulating the nonproportional data in this way would ensure that the weight function ${(1-S(t))}^{\gamma }$ would provide the most powerful test statistic. Similar to the previous scenario, we applied the Lin and León Cox PH model to our simulated datasets and compared the estimated HR profile with the true HR profile over time. We again considered three scenarios of γ where it is varied to control the rate of how quickly the treatment effect reaches its maximum effect.

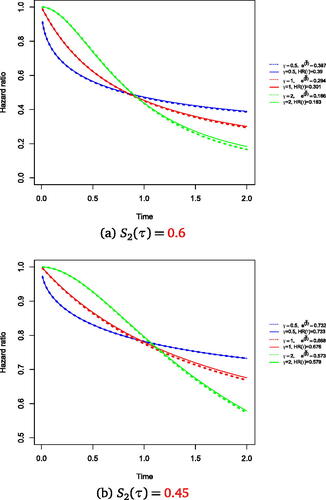
The true hazard ratio over time for which the $G^{\gamma }$ statistic is optimal and the average hazard ratio profile over time estimated by the Lin and León method is displayed in Figure 3. The plot displays the three HR profiles over time for $\gamma =0.5,1,2$ for two different values of $S_2(\tau )$. The solid lines represents the true HR profile and the dashed lines represents $e^{\overline{\widehat{\beta }}(1-S{(t)}^{\gamma }}$. Note that for both values of $S_2(\tau )$, the estimated average hazard ratio is overestimated for $\gamma =1,2$ and this deviation is reflected on the HR time profile. Though for other scenarios, we see that the Lin and León method estimates the treatment effect profile over time with minimal bias, in line with our analytical results in Appendix C. The proposed model closely estimates the maximal treatment effect for both scenarios where $\gamma =0.5$ and r is relatively small.

Fig. 3 Hazard ratio over time targeted by weighted hazard ratio model superimposed true hazard ratio over time under a data generating mechanism where the $G^{\gamma }$ test is optimal. The solid line shows the true hazard ratio over time for $\gamma =0.5,1,2$. The true HR for r = 0.37 at τ = 2 is $e^{\beta }=0.390,0.301,0.183$ and for r = 0.13 is $e^{\beta }=0.733,0.676,0.579$ for $\gamma =0.5,1,2$, respectively. The dashed lines show the proposed hazard ratio targeted by the weighted hazard ratio model. The hazard ratio for the dashed lines is the average of the hazard ratios across 5000 simulations estimated from fitting the Lin and León method and is as follows; $e^{\overline{\widehat{\beta }}}=0.387,0.294,0.166$, $e^{\overline{\widehat{\beta }}}=0.732,0.668,0.573$ for $r=0.37,0.13$ and $\gamma =0.5,1,2$, respectively

5 Discussion

In this article, we considered the Fleming-Harrington class of weights to simulate nonproportional hazard data for the which the same weight function would give the most optimal test. The Lin and León method consists of fitting a Cox model based on a time-varying treatment covariate. The score test from the proposed model gives a p-value which is equivalent to the weighted log rank test and the estimate derived from the model provides a time-profile of the treatment effect. We considered two nonproportional hazard scenarios to investigate its ability to correctly estimate the maximal treatment effect and the corresponding treatment effect profile over time when the data were simulated such that the corresponding weighted log rank test would be most powerful.

We showed analytically that the Lin and León method is approximately unbiased in both scenarios when the treatment effect is small and the assumed weight function is correctly specified. Our simulation results for the diminishing treatment effect scenario showed that the Lin and León method slightly overestimates the maximal treatment effect when the true treatment effect at t = 0 is large as well as when ρ is large. For scenarios where the treatment effect is small, the proposed model estimates the maximal effect very close to the true one. For the delayed treatment effect scenario, the Lin and León method slightly overestimates the maximal effect for $\gamma =1,2$ but in our simulations not by very much. The Lin and León method gave essentially unbiased estimates of the full effect and treatment effect profile over time for $\gamma =0.5$.

We have shown through simulations that under the delayed treatment effect scenarios, the proposed model is giving close to the correct profile over time when the treatment effect is small and the γ parameter is correctly chosen. However, this does not guarantee that the proposed model would provide unbiased results had the data generating mechanism been different, for example if the hazard in the control arm was not constant and changes over time.

Use of the weighted hazard ratio approach requires specification of ρ and γ. Although, the Type I error is controlled under an incorrect choice of ρ and γ, the power of the test will be to some extent adversely affected. For estimation of the treatment effect profile over time, the use of incorrect values would lead to biased estimates, as we have demonstrated in the results shown in Figure 2, while if the values of ρ and γ are close to the true values then the bias is expected to be minimal. Given the difficulty of specifying the value of ρ and γ, it may be preferable to use methods such as restricted mean survival time and milestone survival probabilities, which do not rely on correctly specifying how quickly or slowly the treatment effect changes over time, and for which the interpretation of the treatment effect is clinically meaningful to the clinicians and patients (Royston and Parmar 2013).

Supplementary Materials

The R files containing all code to replicate the simulation studies for delayed and diminishing treatment effect scenario.

Disclosure Statement

Jonathan Bartlett’s current/past institutions have received consultancy fees for the author’s advice on statistical methodology from AstraZeneca, Bayer, Novartis, Roche. J.B. has received consultancy fees from Bayer and Roche, and fees for provision of online courses from Roche.

Additional information

Funding

Bharati Kumar’s research was funded by a UK EPSRC studentship (2281147). Jonathan Bartlett was supported by the UK MRC (grant MR/T023953/1).

Appendix A:

Computation of the True Hazard Ratio Function and Proposed Hazard Ratio Function for the Diminishing Effect Scenario for General Value of ρ

We let ${\lambda }_1(t)={\lambda }_1$ and calculate the true hazard ratio function (4) and the proposed hazard ratio (7). The survival function for the control arm, $$S_1(t)=\hspace{0.17em}\exp \hspace{0.17em}\left(-{\int }_0^t{\lambda }_1(x)\right)\text{dx}=\hspace{0.17em}\exp \hspace{0.17em}(-{\lambda }_{1}t)$$

The hazard function for the treatment arm ${\lambda }_2(t)$ can be derived by the relationship in (4) $$\begin{array}{c}{\lambda }_2(t)={\lambda }_1\times e^{\Delta }{\left[\exp \hspace{0.17em}{(-{\lambda }_{1}t)}^{\rho }+[1-{\{\hspace{0.17em}\exp \hspace{0.17em}(-{\lambda }_{1}t)\}}^{\rho }]\times e^{\Delta }\right]}^{-1}\hfill \\ ={\lambda }_1\times e^{\Delta }{\left[e^{\Delta }+\hspace{0.17em}\exp \hspace{0.17em}{(-{\lambda }_{1}t)}^{\rho }\left\{1-e^{\Delta }\right\}\right]}^{-1}\hfill \end{array}$$

Thus, the survival function for the treatment arm is, $$\begin{array}{c}{S}_2(t)=\hspace{0.17em}\exp \hspace{0.17em}\left(-{\int }_0^t{\lambda }_2(x)\text{dx}\right)\hfill \\ {\int }_0^t{\lambda }_2(x)\text{dx}={\int }_0^t{\lambda }_1\times e^{\Delta }{\left[e^{\Delta }+\hspace{0.17em}\exp \hspace{0.17em}{(-{\lambda }_{1}x)}^{\rho }\left\{1-e^{\Delta }\right\}\right]}^{-1}\text{dx}\hfill \\ ={\left[\frac{1}{\rho }\log \hspace{0.17em}\left(1-e^{\Delta }+e^{\Delta }{\{\hspace{0.17em}\exp \hspace{0.17em}(-{\lambda }_{1}x)\}}^{\rho }\right)\right]}_0^t\hfill \\ S_2(t)=\hspace{0.17em}\exp \hspace{0.17em}\left(-\frac{1}{\rho }\log \hspace{0.17em}\left(1-e^{\Delta }+e^{\Delta }{\{\hspace{0.17em}\exp \hspace{0.17em}(-{\lambda }_{1}t)\}}^{\rho }\right)\right)\hfill \\ =\frac{1}{{\left[1-e^{\Delta }+e^{\Delta }{\{\hspace{0.17em}\exp \hspace{0.17em}({\lambda }_{1}t)\}}^{\rho }\right]}^{1/\rho }}\hfill \end{array}$$

Recall, the model proposed by Lin and León (2017) states that the hazard ratio between the two arms can be expressed as, $$\begin{array}{c}H{R}_{LL}(t)=\frac{{\lambda }_0{e}^{A(t)\beta \times 1}}{{\lambda }_0{e}^{A(t)\beta \times 0}}=e^{\beta A(t)}\hfill \end{array}$$

Let us substitute the pooled survival function, instead of A(t), (A1) $$\begin{array}{c}H{R}_{LL}(t)=e^{\beta A(t)}=e^{\beta {\left(0.5S_1(t)+0.5S_2(t)\right)}^{\rho }}\hfill \end{array}$$(A1)

For our example, the true hazard ratio under our data generating mechanism is expressed as, $$\begin{array}{c}HR(t)=\frac{e^{\Delta }}{e^{\Delta }+e^{\Delta }\left(1-{\{\hspace{0.17em}\exp \hspace{0.17em}(-{\lambda }_{1}t)\}}^{\rho }\right)}\hfill \end{array}$$

Now the hazard ratio described in (A1) is expressed as, $$\begin{array}{c}\frac{1}{2}{S}_1(t)+\frac{1}{2}{S}_2(t)=\frac{1}{2}\exp \hspace{0.17em}(-{\lambda }_{1}t)+\frac{1}{2}\frac{1}{{\left[1-e^{\Delta }+e^{\Delta }{\{\hspace{0.17em}\exp \hspace{0.17em}({\lambda }_{1}t)\}}^{\rho }\right]}^{1/\rho }}\hfill \\ H{R}_{LL}(t)=\hspace{0.17em}\exp \hspace{0.17em}[\beta ·(\frac{1}{2}\exp \hspace{0.17em}(-{\lambda }_{1}t)\hfill \\ {+\frac{1}{2}\frac{1}{{\left[1-e^{\Delta }+e^{\Delta }{\{\hspace{0.17em}\exp \hspace{0.17em}({\lambda }_{1}t)\}}^{\rho }\right]}^{1/\rho }})}^{\rho }]\hfill \end{array}$$

Appendix B:

Taylor Series Expansion of the True Hazard Ratio Function and the Proposed Hazard Ratio Function for the Diminishing Effect

In this section, we demonstrate that the true hazard ratio function and the proposed hazard ratio functions are approximately equal when $e^{\Delta }$ is close to 1 that is, when Δ is small. The evaluation of these results are executed generally for ρ. Recall the true hazard ratio function and the proposed hazard ratio function are of the following form, $$\begin{array}{c}HR(t,\Delta )=\frac{e^{\Delta }}{S_1{(t)}^{\rho }+e^{\Delta }\left(1-S_1{(t)}^{\rho }\right)}\hfill \\ H{R}_{LL}(t,\Delta )=\hspace{0.17em}\exp \hspace{0.17em}\left[\beta ·{\left(\frac{1}{2}{S}_1(t)+\frac{1}{2}{S}_2(t)\right)}^{\rho }\right]\hfill \end{array}$$

We first assume $\beta =\Delta$ in order to check whether the Lin and León model estimates the treatment effect over time correctly if it estimates the initial effect correctly.

Suppose we let $f(\Delta )=\frac{HR(t,\Delta )}{H{R}_{LL}(t,\Delta )}$. We now proceed with a Taylor series expansion for $f(\Delta )$, $$f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}{(x-a)}^n=f(a)+f\prime (a)(x-a)+f″(a)\frac{{(x-a)}^2}{2!}+···$$

We shall expand the first two terms of the series about Δ = 0, $$f(\Delta )\approx f(0)+f\prime (0)(\Delta -0)$$

When a = 0, f(0)=$\frac{HR(t,0)}{H{R}_{LL}(t,0)}$=1. We now find the first order derivative of $f(\Delta )$ with respect to Δ using the quotient rule, so we have $$\frac{H{R}_{LL}(t,0)\frac{\partial HR(t,0)}{\partial \Delta }-HR(t,0)\frac{\partial H{R}_{LL}(t,0)}{\partial \Delta }}{{(H{R}_{LL}(t,0))}^2}=\frac{\partial HR(t,0)}{\partial \Delta }-\frac{\partial H{R}_{LL}(t,0)}{\partial \Delta }$$

We derive the following derivatives for the true hazard ratio function using the product and chain rule, $$\begin{array}{c}\frac{\partial HR(t,\Delta )}{\partial \Delta }=\frac{e^{\Delta }}{S_1{(t)}^{\rho }+e^{\Delta }\left(1-S_1{(t)}^{\rho }\right)}-\frac{e^{\Delta }\left(e^{\Delta }\left(1-S_1{(t)}^{\rho }\right)\right)}{{\left(S_1{(t)}^{\rho }+e^{\Delta }\left(1-S_1{(t)}^{\rho }\right)\right)}^2}\hfill \\ \frac{\partial HR(t,0)}{\partial \Delta }=\frac{1}{S_1{(t)}^{\rho }+1-S_1{(t)}^{\rho }}-\frac{1-S_1{(t)}^{\rho }}{{\left(S_1{(t)}^{\rho }+1-S_1{(t)}^{\rho }\right)}^2}=S_1{(t)}^{\rho }\hfill \end{array}$$

Now, we find the derivative for the proposed hazard ratio function, $$\begin{array}{c}H{R}_{LL}(t,\Delta )=\hspace{0.17em}\exp \hspace{0.17em}\left[\Delta ·{\left(\frac{1}{2}{S}_1(t)+\frac{1}{2}{S}_2(t,\Delta )\right)}^{\rho }\right],\hfill \end{array}$$where we now emphasize the dependence of $S_2(t,\Delta )$ on Δ. $$\begin{array}{c}\frac{\partial H{R}_{LL}(t,0)}{\partial \Delta }=\{{\left(\frac{1}{2}{S}_1(t)+\frac{1}{2}{S}_2(t,\Delta )\right)}^{\rho }\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\hspace{1em}+\Delta \rho \left[{\left(\frac{1}{2}{S}_1(t)+\frac{1}{2}{S}_2(t,\Delta )\right)}^{\rho -1}\left(\frac{1}{2}\frac{\partial S_2(t,\Delta )}{\partial \Delta }\right)\right]\}\hfill \\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\times \hspace{0.17em}\exp \hspace{0.17em}\left[\Delta ·{\left(\frac{1}{2}{S}_1(t)+\frac{1}{2}{S}_2(t,\Delta )\right)}^{\rho }\right]\hfill \end{array}$$

We now evaluate the derivative of the proposed hazard ratio function at Δ = 0, $$\begin{array}{c}\frac{\partial H{R}_{LL}(t,0)}{\partial \Delta }={\left(\frac{1}{2}{S}_1(t)+\frac{1}{2}{S}_2(t,0)\right)}^{\rho }=S_1{(t)}^{\rho },\hfill \end{array}$$using the fact that $S_2(t,0)=S_1(t)$. We can substitute the results in the Taylor series expansion, $$\begin{array}{c}f(\Delta )\approx 1+\Delta (S_1{(t)}^{\rho }-S_1{(t)}^{\rho })=1\hfill \end{array}$$

The results confirms that the hazard ratio functions are approximately equal to each other when the treatment effect $e^{\Delta }$ is small.

Appendix C:

Taylor Series Expansion of the True Hazard Ratio Function and the Proposed Hazard Ratio Function for the Delayed Effect

We demonstrate the approximate equality of the two hazard ratio functions for the delayed effect when $\phi$ is small. We show the results for a general γ. Recall, the true hazard ratio and the proposed hazard ratio are of the following form, $$\begin{array}{c}HR(t,\phi )=\frac{L^{\gamma }({({\mathcal{L}}^{\gamma })}^{-1}({\mathcal{L}}^{\gamma }(e^{-{\lambda }_{1}t})+\phi ))}{L^{\gamma }(e^{-{\lambda }_{1}t})}\hfill \\ H{R}_{LL}(t,\phi )=e^{\beta \left(\frac{{\left(1-0.5e^{-{\lambda }_{1}t}-0.5{\mathcal{L}}^{-1}(\mathcal{L}(e^{-{\lambda }_{1}t})+\phi )\right)}^{\gamma }}{{\left(1-0.5e^{-{\lambda }_1\tau }-0.5{\mathcal{L}}^{-1}(\mathcal{L}(e^{-{\lambda }_1\tau })+\phi )\right)}^{\gamma }}\right)}\hfill \end{array}$$where $L^{\gamma }(x)={\int }_x^1\frac{{(1-s)}^{\gamma }}{s}ds$ and ${\mathcal{L}}^{\gamma }(x)={\int }_{0.5}^x\frac{1}{s{L}^{\gamma }(s)}ds$. Recall $S_2(t)={(\mathcal{L})}^{-1}(\mathcal{L}(e^{-{\lambda }_{1}t})+\phi )$ and $S_1(t)=e^{-{\lambda }_1}t$. We again assume that the Lin and León model estimates the maximal treatment effect β correctly. For simplicity we write β as some function of $\phi$ and note that the maximal treatment effect occurs at $t=\tau$, so we have $g(\phi )=\hspace{0.17em}\log \hspace{0.17em}(\frac{L^{\gamma }(S_2(\tau ,\phi ))}{L^{\gamma }(S_1(\tau ))})$, $$\begin{array}{c}H{R}_{LL}(t,\phi )=e^{g(\phi )\left(\frac{{\left(1-0.5S_1(t)-0.5S_2(t)\right)}^{\gamma }}{{\left(1-0.5S_1(t)-0.5S_2(t)\right)}^{\gamma }}\right)}\hfill \end{array}$$

We let $f(\phi )=\frac{HR(t,\phi )}{H{R}_{LL}(t,\phi )}$ and proceed with the first order Taylor series expansion for the ratio of the hazard ratio functions, that is $f(\phi )\approx f(0)+f\prime (0)(\phi -0)$ for small $\phi$. We check for $\phi =0,HR(t,0)=\frac{L^{\gamma }(S_2(t,0))}{L^{\gamma }(S_1(t))}=1$ and $H{R}_{LL}(t,0)=1$, hence $f(0)=\frac{1}{1}=1$. We now find the first order derivative of $f(\phi )$ with respect to $\phi$ and we get the same expression as for the diminishing effect, that is $$\begin{array}{c}f\prime (0)=\frac{\partial HR(t,0)}{\partial \phi }-\frac{\partial H{R}_{LL}(t,0)}{\partial \phi }\hfill \end{array}$$

The steps to determine the first order derivative using the quotient rule for the true hazard ratio functions are as follows, $$\begin{array}{c}HR(t,\phi )=\frac{L^{\gamma }(S_2(t,\phi ))}{L^{\gamma }(S_1(t))}\hfill \\ \frac{\partial HR(t,\phi )}{\partial \phi }=\frac{L^{\prime \gamma }(S_2(t,\phi ))\frac{\partial S_2(t,\phi )}{\partial \phi }{L}^{\gamma }(S_1(t))-0}{{\left(L^{\gamma }(S_1(t))\right)}^2},\hfill \end{array}$$

Using the inverse function theorem, we have $\frac{\partial S_2(t,\phi )}{\partial \phi }$=$\frac{1}{{\mathcal{L}}^{\prime \gamma }({({\mathcal{L}}^{\gamma })}^{-1}({\mathcal{L}}^{\gamma }(S_1(t))+\phi ))}$. Note that ${\mathcal{L}}^{\prime \gamma }(x)=\frac{1}{x{L}^{\gamma }(x)}$, so we have $$\begin{array}{c}\frac{\partial S_2(t,\phi )}{\partial \phi }={({\mathcal{L}}^{\gamma })}^{-1}\left({\mathcal{L}}^{\gamma }(S_1(t))+\phi \right)L^{\gamma }\left({({\mathcal{L}}^{\gamma })}^{-1}({\mathcal{L}}^{\gamma }(S_1(t))+\phi )\right)\hfill \end{array}$$

We now evaluate $\frac{\partial HR(t,\phi )}{\partial \phi }$ at $\phi =0$, $$\begin{array}{c}\frac{\partial HR(t,0)}{\partial \phi }=\frac{L^{\prime \gamma }(S_2(t,0))S_1(t)L^{\gamma }(S_1(t))L^{\gamma }(S_1(t))}{{(L^{\gamma }(S_1(t)))}^2}\hfill \\ =L^{\prime \gamma }(S_1(t))S_1(t)\hfill \end{array}$$

Note that $L^{\prime \gamma }(x)=\frac{{(1-x)}^{\gamma }}{x}$. We then have, $$\begin{array}{c}\frac{\partial HR(t,0)}{\partial \phi }=\frac{{(1-S_1(t))}^{\gamma }}{S_1(t)}{S}_1(t)={(1-S_1(t))}^{\gamma }\hfill \end{array}$$

Now we determine the first order derivative for the proposed hazard ratio function using the product and chain rule, $$\begin{array}{c}H{R}_{LL}(t,\phi )=e^{g(\phi )\left(\frac{{\left(1-0.5S_1(t)-0.5S_2(t,\phi )\right)}^{\gamma }}{{\left(1-0.5S_1(\tau )-0.5S_2(\tau ,\phi )\right)}^{\gamma }}\right)}\hfill \\ \frac{\partial H{R}_{LL}(t,\phi )}{\partial \phi }=H{R}_{LL}(t,\phi )\times \{g\prime (\phi )\frac{{\left(1-0.5S_1(t)-0.5S_2(t,\phi )\right)}^{\gamma }}{{\left(1-0.5S_1(\tau )-0.5S_2(\tau ,\phi )\right)}^{\gamma }}+\hfill \\ g(\phi )\left(\frac{{\left(1-0.5S_1(t)-0.5S_2(t,\phi )\right)}^{\gamma }}{{\left(1-0.5S_1(\tau )-0.5S_2(\tau ,\phi )\right)}^{\gamma }}\right)\prime \}\hfill \\ \frac{\partial H{R}_{LL}(t,0)}{\partial \phi }=H{R}_{LL}(t,0)\times \{g\prime (0)\frac{{\left(1-S_1(t)\right)}^{\gamma }}{{\left(1-S_1(\tau )\right)}^{\gamma }}+\hfill \\ g(0)\left(\frac{{\left(1-0.5S_1(t)-0.5S_2(t,\phi )\right)}^{\gamma }}{{\left(1-0.5S_1(\tau )-0.5S_2(\tau ,\phi )\right)}^{\gamma }}\right)\prime \}\hfill \end{array}$$

Note that $g(0)=\hspace{0.17em}\log \hspace{0.17em}(\frac{L^{\gamma }(S_2(\tau ,0))}{L^{\gamma }(S_1(\tau ))})=\hspace{0.17em}\log \hspace{0.17em}(1)=0$. We now determine $g\prime (0)$, $$\begin{array}{c}g(\phi )=\hspace{0.17em}\log \hspace{0.17em}\left(L^{\gamma }(S_2(\tau ,\phi ))\right)-\hspace{0.17em}\log \hspace{0.17em}\left(L^{\gamma }(S_1(\tau ))\right)\hfill \\ g\prime (\phi )=\frac{1}{L^{\gamma }(S_2(\tau ,\phi ))}\times L^{\prime \gamma }(S_2(\tau ,\phi ))\hfill \\ \hspace{1em}\times {({\mathcal{L}}^{\gamma })}^{-1}\left({\mathcal{L}}^{\gamma }(S_1(\tau ))+\phi \right)L^{\gamma }\left({({\mathcal{L}}^{\gamma })}^{-1}({\mathcal{L}}^{\gamma }(S_1(\tau ))+\phi )\right)\hfill \\ g\prime (0)=\frac{1}{L^{\gamma }(S_1(\tau ))}\times L^{\prime \gamma }(S_2(\tau ,0))\times S_1(\tau )L^{\gamma }(S_1(\tau ))\hfill \\ =\frac{{\left(1-S_1(\tau )\right)}^{\gamma }}{S_1(\tau )}{S}_1(\tau )={\left(1-S_1(\tau )\right)}^{\gamma }\hfill \end{array}$$

Substituting the results in $\frac{\partial H{R}_{LL}(t,0)}{\partial \phi }$ gives, $$\begin{array}{c}\frac{\partial H{R}_{LL}(t,0)}{\partial \phi }=e^0\times \left\{{\left(1-S_1(\tau )\right)}^{\gamma }\frac{{\left(1-S_1(t)\right)}^{\gamma }}{{\left(1-S_1(\tau )\right)}^{\gamma }}+0\right\}\hfill \\ ={\left(1-S_1(t)\right)}^{\gamma }\hfill \end{array}$$

We can substitute the results in the Taylor series expansion, $$\begin{array}{c}f(\phi )\approx 1+\phi \left\{{\left(1-S_1(t)\right)}^{\gamma }-{\left(1-S_1(t)\right)}^{\gamma }\right\}=1\hfill \end{array}$$

This result confirms that the hazard ratio functions are approximately equal to each other when the treatment effect is small in the case of delayed effect.