Micromorphic theory: a gateway to nano world

Abstract

Micromorphic theory (MMT) envisions a material body as a continuous collection of deformable particles; each possesses finite size and inner structure. It is considered as the most successful top-down formulation of a two-level continuum model, in which the deformation is expressed as a sum of macroscopic continuous deformation and internal microscopic deformation of the inner structure. In this work, the kinematics including the objective Eringen tensors is introduced. Balance laws are derived by requiring the energy equation to be form-invariant under the generalized Galilean transformation. The concept of material force and the balance law of pseudomomentum are generalized for MMT. An axiomatic approach is demonstrated in the formulation of constitutive equations for a generalized micromorphic thermoviscoelastic solid, generalized micromorphic fluid, micromorphic plasticity, and micromorphic electromagnetic–thermoelastic solid. Applications of MMT in micro/nanoscale are discussed.

Keywords:

• micromorphic theory
• Eringen tensors
• constitutive theory
• generalized micromorphic solid/fluid
• electromagnetic–thermoelastic coupling
• micro/nanomechanics

1. Introduction

Continuum approaches have dominated material modeling research over the past few decades. This approach to predict material deformation and failure, by implicitly averaging atomic scale dynamics and defect evolution over time and space, is valid only for large systems [1–3 3]. Therefore, lots of experimental observations of material behavior, especially at micro/nanoscale, cannot be explained within the continuum mechanics framework. On the other hand, molecular dynamics (MD) simulations [4] have become a powerful tool for elucidating complex mechanics phenomena. But the length and time scales that can be probed in MD are still fairly limited. The pros and cons of both continuum and atomistic models have motivated the development of various methods of microscale modeling and simulation. Microcontinuum field theories, or generalized continuum theories, including Cosserat theory [5], couple stress theory [6], micromorphic theory [7], microstructure theory [8], micropolar theory [9] are extensions of the classical field theory to microscopic space and time scales. Here let us briefly mention the relation of micromorphic theory to several others microscale theories. As a pioneer of the rational theories of polar continua, Cosserat obtained balance equations of momenta in the dynamic case. However, Cosserat theory is a special case of micropolar theory, where the balance law of microinertia is missing. Couple stress theory, by including high order stresses, provided a model that can support body and surface couples. However, it can be obtained from micropolar theory as a special case when the motion is constrained so that the macrorotations and microrotations coincide. Upon the assumptions of small deformation, slow motion, constant microinertia, spin isotropy and linear isotropic elasticity, micromorphic theory can be reduced to microstructure theory. However, those assumptions lead to a limitation in applications related to atomic motions, such as the thermal mechanical coupling, phase transition, anisotropic and large deformation problems. In addition, the local balance equations of energy, entropy, and microinertia are not given in microstructure theory. The above-mentioned discussion lends the credible support to claim that micromorphic theory is the most successful formulation of a microcontinuum model.

Micromorphic theory has been developed since 1964 by Eringen. It is considered to be the most successful top-down microscale model. The development of micromorphic theory was motivated by the query, “Is it possible to construct continuum theories that can predict physical phenomena on the atomic, molecular, or nano scales?” These would require supplying additional degrees of freedom to a material point, which has three degrees of freedom in classical field theory. After all, the molecules that constitute the internal structure of the material points undergo deformations and rotations arising from the displacements and rotations of their constituent atoms. Micromorphic theory envisions a material body as a continuous collection of deformable particles; each possesses finite size and inner structure. On the other hand, classical continuum mechanics considers a material body as a continuous collection of material points, each with infinitesimal size and no inner structure. The purpose of going beyond classical continuum mechanics is to take into account the microstructure of the material body in question while still keeping the advantages of continuum theory intact. A question arises: how can we reconcile the concept of the deformable particle with the continuum hypothesis? Eringen settled this question by replacing the deformable particle with a geometric point and some vectors attached to that point, which denote the orientations and intrinsic deformations of all the material points in the deformable particle [7,10–18 18]. This is compatible with the classical picture where a material point in a continuum is endowed with physical properties such as mass density, displacement vector, electric field, stress tensor, etc. Therefore micromorphic theory can be expected to unveil many new classes of physical phenomena that fall beyond classical field theories.

The organization of the remainder of this paper is as follows. In Section 2, we briefly present the kinematics of micromorphic theory. Balance laws and material force are derived in Section 3. Section 4 presents the axiomatic approach to formulate constitutive equations of generalized Micromorphic solid/fluid. In Sections 5 and 6, we derive the constitutive theories for micromorphic plasticity and micromorphic thermomechanics–electromagnetics, respectively. Finally, we conclude this paper with discussions in Section 7.

2. Kinematics

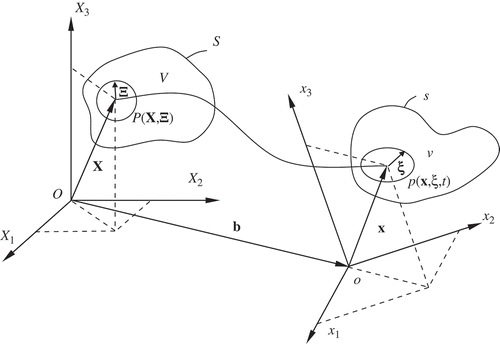
Micromorphic theory, developed by Eringen and Suhubi [10,11] and Eringen [12,13], constitutes extensions of the classical field theories concerned with the deformations, motions, and electromagnetic interactions of material media, as continua, in microscopic time and space scales. In micromorphic theory, a material body is considered as a continuous collection of deformable particles, each with finite size and inner structure. Geometrically, a deformable particle P is characterized by its centroid C located at X and vector Ξ relative to X of a generic point within the particle. As shown in Figure 1, a generic point in the particle is represented by the vector sum of X and Ξ in the reference state at time t = 0. The material is called a micromorphic continuum if the deformation carrying P(X,Ξ,t) to p(x,ξ,t) in the deformed state at time t can be expressed as

Figure 1. Macro- and micromotions of a material particle.

(1)

(2)

where χ _kK is called the microdeformation tensor. It can be seen that the macromotion, Equation (1)(1), accounts for the motion of the centroid of the particle whereas the micromotion, Equation (2)(2), specifies the deformation of the inner structure of the particle. Thus, the particle has nine independent degrees of freedom for both stretches and rotations in addition to the three classical translational degrees of freedom of the centroid. The micromotion stipulated by Equation (2)(2) can be called an affine motion, which deforms a sphere into an ellipsoid, as shown in Figure 1. To secure the axiom of continuity, which requires that the matter is indestructible and impenetrable, the Jacobians of the macromotion and the micromotion must be strictly positive, i.e.

(3)

Then there exist unique inverse motions

(4)

(5)

with

(6)

If the microgyration tensor is defined as

(7)

then it is straightforward to prove that

(8)

(9)

Let and ΔV(Δv) denote the mass density and the volume of the deformable particle in the Lagrangian (Eulerian) state and let primed quantities refer to those of the point in the particle. This leads to

(10)

where I_KL and i_kl are the microinertia of the deformable particle in the Lagrangian state and Eulerian state, respectively.

2.1. Objectivity

It is intuitively clear that the material properties do not depend on the coordinate frame selected. The measurements made by an observer, whether they are in motion or not, should be the same. If this viewpoint is accepted, then the measurements made in one frame of reference are sufficient to determine the material properties in all other frames, which are in rigid motion with respect to one another. In the formulation of the response functions, it is desirable to employ quantities that are not dependent on the motions of the observer. Such quantities are called objective or material frame-indifferent.

2.1.1.  Definition 1

Two motions and are called objectively equivalent if and only if

(11)

where a is a constant time shift, b_k (t) is a time-dependent translation, and Q_kl (t) are time-dependent full orthogonal transformations, i.e.

(12)

2.1.2.  Definition 2

Any tensorial quantity is said to be objective if in any two objectively equivalent motions it obeys the following tensor transformation law for all times:

(13)

Since Equation (11)(11) in general holds for arbitrary X and Ξ, it can be replaced by

(14)

If the micromotion is affine motion, then the second part of Equation (14)(14) can be rewritten as

(15)

It is worthwhile mentioning and can be easily verified that: (1) the position vector of the centroid of a particle x and its material time derivatives of various order including velocity v and acceleration , time t, velocity gradient ▿v and microgyration tensor ω are not objective; (2) the relative position vector ξ, micromotion χ _kK , and deformation gradient x_{k ,K} are objective.

The generalized Lagrangian strain tensors of micromorphic theory are defined as [12]

(16)

One may verify that the strain rates can be obtained as

(17)

and are objective.

2.2.  Eringen tensors

There are three kinds of Eringen tensors; the first order Eringen tensors are , , and . Eringen tensors of order n + 1 are defined as

(18)

After lengthy but straightforward derivation one may prove that Eringen tensors of any order are objective. One may also verify that

(19)

are objective. It is noticed that Eringen tensors play central roles in the formulation of constitutive equations of micromorphic fluids.

3. Balance laws

Eringen and Suhubi [10,11] and Eringen [7] derived the laws of conservation of mass, conservation of microinertia, balance of linear momentum, balance of momentum moments, and conservation of energy for micromorphic theory by means of a “microscopic space-averaging” process. Later Eringen [12] derived the balance laws in a more elegant way by starting with the following expression for the kinetic energy per unit mass, k, of a particle:

(20)

and, after the energy balance law is obtained, by requiring it to be form-invariant under the generalized Galilean transformation to yield the balance laws of linear momentum and moment of momentum. The balance laws of micromorphic theory, including the Clausius–Duhem inequality, can be expressed as [12]

(21)

(22)

(23)

(24)

(25)

(26)

where v is the velocity vector, t is the Cauchy stress, s = s ^T is the microstress, e is the internal energy density, q is the heat flux, h is the heat source per unit mass, η is the entropy density, θ is the absolute temperature, is the Helmholtz's free energy density, and the spin inertia is defined as

(27)

The body force and the body moment are defined as

(28)

The moment stress, a third order tensor, is defined as

(29)

with being the differential surface area with outward normal n_k . It is noticed that in micromorphic theory the Cauchy stress is not symmetric, i.e. . If the size of the particle is reduced to zero, i.e. , then it leads to . This means Equations (21)(21)* and (23) remain unchanged, Equation (22)(22)* becomes a trivial statement, i.e. 0 = 0, and Equations (24)(24)* (25)*– (26)(26)* are reduced to

(30)

(31)

(32)

Of course, under this limiting situation (size of the particle is vanishing or, say, a particle is regarded as a mathematical point), micromorphic theory is identical to classical continuum theory.

The balance laws expressed in Equations (21)(21)* (22)* (23)* (24)* (25)*– (26)(26)* are in the Eulerian description. In Lagrangian description, the balance laws can be written as [19]

(21)*

(22)*

(23)*

(24)*

(25)*

(26)*

where the stresses and heat flux in Eulerian and Lagrangian descriptions are related as

(33)

(34)

(35)

(36)

3.1.  Material forces

The concept of material forces was first introduced by Eshelby [20], elaborated and further developed by Maugin [21,22]. Material forces are generated by displacement, not in physical space, but on material manifold. For example, they can be generated by (i) an infinitesimal rigid displacement of a finite region surrounding a point of singularity in an elastic body [20], (ii) an infinitesimal displacement of a dislocation line [23], (iii) an infinitesimal increase in the length of a crack [24–26 26]. Material forces drive the motion of defects of various dimensions in condensed matter physics, e.g. phase-transition fronts in elasticity, Bloch and Neel walls in ferromagnetism, and elastic solitons [21,26]. This characteristic property of material forces also leads to their christening as inhomogeneity forces. Material inhomogeneity is defined as the dependence of properties (not the solution), such as density, elastic coefficients, viscosity, plasticity threshold, on the material point. These inhomogeneities may be more or less continuous such as in metallurgically superficially treated specimens or in a polycrystal observed at a mesoscopic scale, or it may change abruptly such as in laminated composite or in a body with foreign inclusions or cavities.

Eshelbian mechanics was extended to micromorphic theory. The formulation can be easily done by adding (a) Equation (23)(23)* multiplied by x_{l ,p} and (b) Equation (24)(24)* multiplied by . It leads to the balance law of pseudo-momentum,

(37)

where F ¹ is the material force due to body force f and body moment l,

(38)

F ² is the material force due to the inhomogeneity of and ,

(39)

K is the kinetic energy density (per unit volume in Lagrangian coordinates)

(40)

P is named as pseudo-momentum:

(41)

The detailed expressions of Eshelby stress tensor, pseudo-momentum, and material forces were derived for thermoelastic micromorphic solid. It was found that the material forces are due to (1) body force and body moment, (2) temperature gradient and (3) material inhomogeneities in density, microinertia, and elastic coefficients. The general expression of material forces due to the presence of dynamically propagating crack front was also derived. It was found that, at the crack front, material force is reduced to the J-integral in a very special and restrictive case [27].

4. Constitutive equations

The fundamental laws of micromorphic continua consist of a system of 20 partial differential equations, and one inequality. Given the external loads and h, there are 67 unknowns and θ. Clearly then, the system is highly indeterminate. Forty-seven independent additional equations are needed for the determination of motions and temperatures of a micromorphic body. This is also clear from the fact that the balance equations are valid for all micromorphic bodies irrespective of their physical constitutions. For bodies of different constitutions, the response of the body to external stimuli is very different. Thus, we must bring the constitutional nature of bodies into our formulation. For a constitutive theory to represent a material adequately, certain physical and mathematical requirements must be satisfied. The axiomatic approach to the formulation of constitutive equations was evolved in the course of the development of continuum mechanics. Axioms of causality, determinism, equipresence, objectivity, material invariance, neighborhood, memory, and admissibility are accepted as guiding principles not only in classical continuum mechanics [28] but also in micromorphic theory [12].

For the sake of discussion, in the following we are going to show the formulation of constitutive equations for micromorphic thermoviscoelastic solid and micromorphic fluid.

4.1.  Micromorphic thermoviscoelastic solid

For a micromorphic thermoviscoelastic solid, to begin with, the independent and dependent constitutive variables are set to be

(42)

(43)

where ; is the p-th order material time derivative of α, and similarly for . Following the axiom of equipresence, at the outset the constitutive relations are written as

(44)

It is noticed that the constitutive equation, Equation (44)(44), automatically satisfies the axiom of objectivity because it is expressed in Lagrangian forms. Substituting Equation (44)(44) into the Clausius–Duhem (CD) inequality, Equation (26)(26)**, this leads to

Since the CD inequality must be satisfied for all independent thermomechanical processes and Equation (45) is linear in , it leads to

(46)

Equation (46)(46) implies

(48)

One may decompose into elastic parts and dissipative parts as

(49)

Then the CD inequality becomes

(50)

Equation (49)(49)** and the CD inequality, Equation (50)(50)**, are the constitutive equations for p-th order micromorphic thermoviscoelastic solid. In the limiting case, i.e. p = 1, one has the following constitutive equations for simple micromorphic thermoviscoelastic solid:

(48)*

(49)*

(50)*

Clearly it can be seen that {} and {} are the thermodynamic forces and the corresponding thermodynamic fluxes. If p is zero and is eliminated from the list of independent constitutive variables, then we end up with the following constitutive equations for a heat-conducting micromorphic elastic solid:

(48)**

(49)**

(50)**

where Equations (49)(49)**** are the generalized Gibbs equations and Equation (50)(50)**** says heat flows from high temperature area to low temperature area.

4.2.  Micromorphic fluid

4.2.1.  Definition 3

A body is called a micromorphic fluid if every configuration of the body leaving the density and microinertia unchanged can be taken as the reference configuration.

If every configuration is to be taken as a reference configuration, then one can write X = x and Ξ = ξ with ρ and i unchanged. With this, we have

(51)

where δ _kK is the shifter between the Lagrangian coordinate and the Eulerian coordinate.

Therefore for micromorphic fluid, to begin with, the independent and dependent constitutive variables can be expressed as

(52)

(53)

where and are the p-th order Eringen tensors. Following the axiom of equipresence, at the outset the constitutive relations are written as

(54)

It should be noticed that, in the case of a solid, the dependency on the Lagrangian coordinate X indicating material inhomogeneity and, in the case of fluid, X → x according to the definition, but the Eulerian coordinate x is not objective – that is why x is not in the list of independent variables. It is also noticed that the p-th order strain rates become p-th order Eringen tensors when the micromorphic solid is “melted” into micromorphic fluid.

The constitutive equation, Equation (44)(44), because it is expressed in Lagrangian forms, automatically satisfies the axiom of objectivity. Now the constitutive equation, Equation (54)(54), is expressed in Eulerian forms, axiom of objectivity requires that [13]

(55)

For example,

(56)

(57)

Substituting Equation (54)(54) into the Clausius–Duhem (CD) inequality, Equation (26)(26)*, leads to

(58)

Since the CD inequality must be satisfied for all independent thermomechanical processes and Equation (58)(58) is linear in , it results in

(59)

(60)

(61)

where

(62)

If p = 1, the simple micromorphic fluid has the following constitutive equations:

(63)

(64)

(65)

These constitutive equations for a simple micromorphic fluid, Equations (63)(63) (64)– (65)(65), were obtained by Eringen [13].

5. Micromorphic plasticity

The formulation of constitutive theory for plasticity is unique in the sense that one needs to add a set of internal variables to the list of dependent constitutive variables and, of course, one needs to supply a set of governing equations for the newly added internal variables.

For micromorphic thermo-visco-elastic-plastic (TVEP) continuum, a set of internal variables is introduced as [19]

(66)

where are the plastic strains corresponding to the generalized Lagrangian strains α, β, γ, respectively; R, named as the hardening parameters, is a generalized vector of internal variables.

To separate the material behavior into two distinct parts: thermo-visco-elastic (TVE) part and thermo-visco-elastic-plastic (TVEP) part, a scalar-valued yield function is introduced as

(67)

where

(68)

For a set of fixed values of W, a hyper surface, named yield surface, is determined in the eighty-nine-dimensional space of U and V by

(69)

We also define the loading rate λ as the scalar product between the outward normal to the yield surface and the tangent vector to the trajectory in the {U, V} space, i.e.

(70)

Three distinct cases, unloading, neutral loading, and loading, can be defined by (a) f < 0, (b) f = λ = 0, and (c) f = 0 and λ > 0, respectively. The internal variables of plasticity, W, will remain unchanged in the cases of unloading and neutral loading.

Following the axiom of equipresence, the constitutive relations of a micromorphic TVEP material are initiated as

(71)

(72)

where

(73)

The Kuhn–Tucker conditions for general plasticity of a micromorphic continuum can now be expressed as

(74)

The CD inequality, Equation (26)(26)**, now reads

(75)

which leads to

(76)

(77)

(78)

where

(79)

Since the inequality, Equation (78)(78), must be satisfied for any value of the loading rate λ, it implies

(80)

Also, it is emphasized that a TVEP state should lead to another TVEP state; in other words, the consistency condition of plasticity requires that f = 0 and λ > 0 lead to another state with f = 0, which implies

(81)

This gives another constitutive constraint to the plasticity

(82)

6. Micromorphic electromagnetic–thermoelastic solid

Eringen [15] and Lee et al. [29] formulated the constitutive equations for a micromorphic electromagnetic–thermoelastic solid. Lee and Chen [30] studied the coupling problem of wave propagation in a micromorphic electromagnetic elastic solid. Here, in this work, we briefly go through the formulation of the constitutive theory of micromorphic electromagnetic–thermoelastic solid.

The balance laws in electromagnatics (EM) are the well-known Maxwell's equations, which can be expressed as

(83)

(84)

(85)

(86)

where D is the dielectric displacement vector, B the magnetic flux vector, E the electric field vector, H the magnetic field vector, J the current vector, q^e the free charge density, and c is the speed of light. The divergence of Equation (86)(86) with the use of Equation (83)(83) leads to

(87)

which is the law of conservation of charge.

The polarization vector, P_k , and the magnetization vector, M_k , are defined as

(88)

These EM vectors mentioned above are all referred to a fixed laboratory frame R_C . The Galilean transformations of inertial frames form a group that consists of time-independent spatial rotations and pure Galilean transforms, i.e.

(89)

where

(90)

The requirement of the form-invariance of the Maxwell's equations under the Galilean transformations leads to the following transformations [31]:

(91)

(92)

(93)

(94)

(95)

(96)

(97)

(98)

where the quantities, , are referred to a co-moving frame R_G with material particles of the body having velocities, v. A typical non-relativistic feature of these transformations, Equations (91)(91) (92) (93) (94) (95) (96) (97)– (98)(98), is the asymmetry between Equation (93)(93) and Equation (94)(94), which says, according to Galilean relativity, a polarized moving body will appear to be magnetized, whereas a magnetized moving body will not appear to be polarized. Although it is this lack of symmetry that stimulated the study of relativistic electrodynamics in the early 20th century, few observable conclusions can be made due to the difficulty of obtaining sufficiently high velocities for material media. The fully symmetric relativistic laws replacing Equations (93)(93)– (94)(94) may be found in Jackson [32].

The balance laws of linear momentum, moment of momentum, and energy of micromorphic continuum with EM interactions can be expressed as

(99)

(100)

(101)

where F, L, Π are the body force, body moment and energy source per unit volume of the EM origin, respectively. The detailed expressions are given as [12,31,33]

(102)

(103)

(104)

The second law of thermodynamics, also referred to as the Clausius–Duhem inequality, is expressed as

(105)

The Helmholtz's free energy density ψ with EM interaction is now introduced as

(106)

Then the Clausius–Duhem inequality can be becomes

(107)

Since the generalized Lagrangian strains [cf. Equations (16)(16)] and their material time derivatives of any order [cf. Equations (19)(19)] are objective, and hence they are suitable for being employed as independent constitutive variables in the development of a constitutive theory. In the same spirit, define the Lagrangian forms of the electric field vector and the magnetic flux vector as

(108)

and their material time derivatives are obtained:

(109)

We also define

(110)

(111)

(112)

where the superscript ‘m’ refers to the mechanical parts, i.e. if there is no EM interaction, then , . Note that the mechanical part of the microstress, , are also symmetric.

Now, the Clausius–Duhem inequality, Equation (107)(107), can be rewritten as

(113)

Let the independent and dependent constitutive variables be

(114)

(115)

and let the constitutive equations be written as Z =Z(Y). It is noticed that the axiom of objectivity is automatically satisfied. Now the CD inequality, Equation (113)(113), becomes

(116)

Since the inequality is linear in , , , , , , , it holds if, and only if,

(117)

(118)

(119)

(120)

Equations (117)(117) (118)– (119)(119) are the generalized Gibbs equations for a micromorphic electromagnetic–thermoelastic solid. These constitutive relations are further subjected to the axioms of material invariance and time reversal. It may be stated that the constitutive response functionals must be form-invariant with respect to a group of transformations of the material frame of reference and microscopic time reversal representing the material symmetry conditions, and these transformations must leave the density and charge at (X, t) unchanged [31]. The magnetic symmetry properties of solids cannot be discussed rationally by means of three-dimensional point groups only since magnetism is the result of the spin magnetic moment of electrons, which changes sign upon the time reversal. In other words, diamagnetic and paramagnetic crystals do not exhibit any orderly distribution of their spin magnetic moments, and are therefore ‘time symmetric’. The crystallographic point group is enough for the discussion of their material symmetries; on the other hand, for ferromagnetic, ferromagnetic and anti-ferromagnetic materials, which are characterized by an orderly distribution of spin magnetic moment, an additional symmetry operator is needed to take care of the time reversal. For a complete account of this subject, interested readers are referred to Shubnikov and Belov [34] and Kiral and Eringen [35].

7. Discussion

There is one concern in applying micromorphic theory to practical problem: it involves many material constants. How do we measure those material constants? Chen and Lee [36] proposed an algorithm to determine the material constants for micromorphic elastic solids, such as single crystals, through the phonon dispersion relations obtained by atomistic calculations or experimental measurements. Later Zeng et al. [37] extended the algorithm to determine material constants in non-local micromorphic theory. The phonon dispersion relations from atomistic calculations and/or experimental measurements provide the means to determine the material constants in micromorphic theory, which offers a great promise in the applications of semiconductor physics, MEMS, and other microsystems. Beyond what has been mentioned above, micromorphic theory, including its special cases microstretch theory and micropolar theory, has been applied to liquid crystals, theory of turbulence, blood, anisotropic fluids, suspensions, etc.

However, in micromorphic theory, there is an assumption that the micromotion is an affine motion [cf. Equation (2)(2)]. This assumption makes it difficult to describe the atomic motion of complex crystalline materials. To enlarge the domain of applicability of micromorphic theory, Chen and Lee [38] abandoned the assumption of affine motion, let the micromotions have the generality as , and formulated a generalized continuum field theory named atomistic field theory (AFT). Since AFT is a concurrent atomistic/continuum field theory in its own right, it has the advantage in dealing with some critical phenomena, especially those related to defect nucleation and evolution in solids such as dynamic crack propagation [39].