Temperature distribution effects on buckling behavior of smart heterogeneous nanosize plates based on nonlocal four-variable refined plate theory

ABSTRACT

This work presents a theoretical study for thermo-mechanical buckling of size-dependent magneto-electro-thermo-elastic functionally graded (METE-FG) nanoplates in thermal environments based on a refined trigonometric plate theory. Temperature field has uniform, linear, and nonlinear distributions across the thickness. Nonlinear thermal loadings are considered as heat conduction (HC) and sinusoidal temperature rise (STR). A power law function is applied to govern the gradation of material properties through the nanoplate thickness. Considering coupling impacts between magneto, electro, thermo-mechanical loadings, the equations of motion, and distribution of magneto-electrical field across the thickness direction of the METE-FG nanoplate are derived. The exact solutions for critical buckling temperatures of METE-FG nanoplates are introduced implementing Navier’s method. Moreover, the accuracy of the present formulation is examined by comparing the obtained results with published ones. Furthermore, the effects played by the magneto-electrical field, various temperature rises, nonlocality, power law index, side-to-thickness ratio, and aspect ratio on the critical buckling temperature response are all investigated and reported.

KEYWORDS:

• METE-FG nanoplate
• thermal buckling
• four-variable refined plate theory
• nonlocal elasticity

1. Introduction

Due to having intrinsic coupling effects and adaptive properties, smart structural elements such as beams and plates constructed from the intelligent materials play a major role in different fields of science. The magneto-electro-thermo-elastic (METE) materials are a class of new smart materials which have attracted intense attention of investigators in recent years. Since the METE materials are generated from both piezoelectric and piezomagnetic phases, their mechanical properties can be influenced by exerting magnetic and electric potentials. In other words, they can exhibit coupling effects between magnetic, electric, and thermo-mechanical fields. Recently, the concept of functionally graded materials (FGMs) is introduced to MEE nanomaterials which allow a gradual variation in their properties through the thickness direction. Therefore, considerable amount of researches are carried out for analysis of magneto-electro-thermo-elastic functionally graded (METE-FG) materials based on classical continuum mechanics [1–3].

In recent years, magneto-electro-elastic (MEE) materials have been broadly applied in nanoscale structures for many engineering applications such as micro/nano-electro-mechanical systems, thin films, and atomic force microscopes to achieve desired performances. Further, it is reported that neglecting small-scale effects lead to incorrect solutions and hence wrong designs. For studying the behavior of MEE nanodevices, the classical continuum mechanic is no longer reliable because it does not include any length scale parameter. Therefore, the nonlocal continuum theory proposed by Eringen [4,5] is extensively used in the literature for accurate analysis of MEE nanoscale structures. Vibration characteristics of nonlocal MEE beams based on classical beam theory is investigated by Ke and Wang [6]. Also, Ke et al. [7], employed nonlocal elasticity theory for frequency analysis of size-dependent MEE nanoplates. They reported than mechanical behavior of MEE nanoplates is significantly influenced by magnetic and electric fields. Li et al. [8] developed a nonlocal classical plate model for buckling and vibration of MEE nanoplates supported by elastic foundation. Li et al. [9] examined bending, buckling and free vibration of MEE nanobeams employing nonlocal theory. They showed the effects of the small-scale parameter and the electric and magnetic field intensities on the transverse displacement, rotation, buckling load, and natural frequency. Also, Ansari et al. [32] studied the effect of temperature field on forced vibration of MEE nanobeams based on the nonlocal third-order beam theory. Farajpour et al. [10] presented large-amplitude vibration analysis of MEE nanoplates based on nonlocal plate model.

Many researchers have paid their attention to the mechanical problems associated with nanoplates made of FGM. Natarajan et al. [11] examined vibration response of FG nanoplates via finite element method. Ansari et al. [33] examined three-dimensional bending and vibration behavior of FG nanoplates employing differential quadrature method. Recently, analysis of structures based on unified formulations has been presented by various researchers [12–18]. In this context, the classical plate theory model (CPL) or Kirchhoff theory, which ignores the shear deformation effect, only give acceptable results for thin plates. Then the first-order shear deformation based in Reissner and Mindlin was utilized but this theory needs a shear correction factor, which is difficult to calculate. Therefore higher order shear deformation theories (HSDTs) were introduced to avoid the shear correction factors. Further, The HSDTs can be developed using polynomial or non-polynomial thickness functions. In the case of FG nanoplates, Belkorissat et al. [19] presented vibration properties of FG nanoscale plates developing a nonlocal refined four-variable model. They stated that classical plate theory cannot capture shear deformation effect and suggested a new plate model containing four field variables and a shear strain function. Ansari et al. [20] employed nonlocal 3-D theory of elasticity for free vibration of FG nanoplates on supported by elastic foundation. Also, Barati et al. [21] employed an inverse cotangential refined theory to study thermal buckling behavior of nonlocal FG plates on elastic foundation. They mentioned that critical buckling temperature of FG nanoplates are related to the nonlocal parameter, material composition, and plate geometrical parameters.

Investigations on nonlocal intelligent FG nanostructures are very rare in the literature. Ebrahimi and Salari [22] examined buckling of FG piezoelectric nanobeams in electric field based on nonlocal elasticity. Narendar et al. [23] investigated wave propagation of MEE-FG nonlocal rods. Also, Ebrahimi and Barati [24–27] examined free vibration and stability of METE-FG nanobeams based on third-order beam model.

According to the above discussion, to the authors’ best knowledge, up to now, no study has been carried out on the continuum formulation of buckling behavior of METE-FG nanoplates under external electric and magnetic potentials as well as various thermal environments. Structural components are often exposed to vigorous thermo-mechanical loadings during manufacturing and working, and thus the temperature effects become a significant design factor in specific cases [28]. It is reported that the temperature increment leads to the reduction in the stiffness of the nanoplates due to the development of thermal stresses associated to the thermal expansion. Consequently, thermal effects become prominent when a METE-FG nanodevice operates in either extremely hot or cold temperature fields. Hence, there is strong scientific need to understand the thermo-mechanical buckling response of METE-FG nanoplates under magneto-electrical field considering various thermal loadings.

The motivation of the present work is to develop a size-dependent four-variable refined plate model characterizing the magneto-electro-thermo-mechanical buckling responses of METE-FG nanoplates. Four types of thermal loadings called uniform, linear, and sinusoidal temperature distributions and also HC are considered. According to a power-law distribution in terms of the volume fractions of the material phases, the material properties of the METE-FG nanoplate are varied from one interface to another. The coupled governing equations are obtained employing the principle of minimum potential energy. Navier’s method is selected in order to analyze the nonlocal METE-FG plates with simply supported boundary condition to obtain the critical buckling temperatures. To check the validity of the present plate model, the obtained results are compared with the previous results. Finally, the effects played by the magneto-electrical field, type of thermal loading, temperature changes, nonlocality, power-law index, side-to-thickness ratio, and aspect ratio on the critical buckling temperature response are reported.

2. Theoretical formulations

2.1. The material properties of METE-FG nanoplates

A METE-FG nanoplate with length a, width , and thickness is considered as indicated in Figure 1. The METE-FG nanoplate is subjected to a magnetic potential , an electric potential , and various thermal loadings. The effective material properties of METE-FG nanoplate can be expressed by

(1)

Figure 1. Geometry of FG nanoplate under magneto-electrical field.

and are the material properties of top and bottom sides, and are the volume fraction of top and bottom surfaces, respectively, and are related by

(2a)

where the volume fraction index p dictates the material variation profile through the nanoplate thickness and can be changed to capture the optimum distribution of component materials. Therefore, the material properties of METE-FG nanoplate are described using the following relation:

(2b)

It must be noted that, the top surface at of METE-FG nanoplate is fully , whereas the bottom surface is fully with the properties presented in Table 1. The position of the neutral axis of the MEE-FG plate is determined to satisfy the first moment with respect to elastic stiffness being zero as follows:

(3a)

Table 1. Magneto-electro-thermo-elastic coefficients of material properties (Ramirez et al. [3]).

Properties
	166	286
	77	173
	44.5	56.5
	−4.4	0
	11.6	0
	0	580.3
	0	550
	11.2	0.08
	12.6	0.093
	5	−590
	10	157
	0	0
	10	15.7
	3.2	2.5

Consequently, the position of neutral surface can be obtained as

(3b)

where z_ms and z_ns are distance from middle and neutral surfaces, respectively.

2.2. Kinematic relations

The displacement field at any point of the plate according to four-unknown refined shear deformation plate model can be expressed by

(4)

(5)

(6)

in which and are displacement of mid-plane along x, y-axis and are the bending and shear components of transverse displacement of a point on the mid-plane of the plate and is the time. denotes a shape function estimating the distribution of shear stress across the plate thickness. So it is not required to use any shear correction factor. The present theory has a function in the form [29]:

(7)

The electric potential and magnetic potential distributions across the thickness are approximated via a combination of a cosine and linear variation to satisfy Maxwell’s equation in the quasi-static approximation as follows [6]:

(8)

(9)

where . Also, and are the external electric voltage and magnetic potential applied to the MEE-FG plate. Nonzero strains of the four-variable plate model are expressed by

(10)

where

(11)

According to Equation (8), the relation between electric field and electric potential , can be obtained as

(12)

(13)

(14)

Also, the relation between magnetic field and magnetic potential can be expressed from Equation (9) as

(15)

(16)

(17)

Through extended Hamilton’s principle, the equation of motion can be derived by

(18)

Here, is strain energy, is work done by external forces. The virtual variation of strain energy can be written as

(19)

Substituting Equations (10) and (11) into Equation (19) yields

(20)

in which the variables at the last expression are expressed by

(21)

(22)

The first variation of work done by applied forces can be written in the form

(23)

where are in-plane applied loads. In this study, it is assumed that the METE-FG nanoplate is under external electric voltage, magnetic potential and the shear loading is ignored. So and are the normal forces induced by external electric voltage and external magnetic potential , respectively, and are defined as [30]

(24)

(25)

The following equations are obtained by inserting Equations (20) and (23) in Equation (18) when the coefficients of and are equal to zero:

(26)

(27)

(28)

(29)

(30)

(31)

2.3. Nonlocal elasticity theory for the METE materials

Unlike the local theory of elasticity, the nonlocal theory is naturally size-dependent and is adequate for the nanostructures such as piezoelectric nanoplates and MEE nanoplates. In this theory, the stress, electric displacement, and magnetic induction at a reference point of METE nanoscale structure are a function of the components of strain, electric and magnetic fields at that point and also all other points of the structure. Therefore, the basic relations for nonlocal METE structures can be written as

(32a)

(32b)

(32c)

where denotes the components of stress, electric displacement, and magnetic induction, are the components of linear strain, electric field, and magnetic field. Additionally, , , and are the components of elastic stiffness, dielectric permittivity, and magnetic permittivity coefficients. Finally, , , , , and are the piezoelectric, piezo-magnetic, MEE, pyroelectric, and pyromagnetic coefficients, respectively. is the nonlocal kernel function and is the Euclidean distance. is defined as scale coefficient, where is a material constant which is determined experimentally or approximated by matching the dispersion curves of plane waves with those of atomic lattice dynamics; and a and l are the internal and external characteristic length of the nanostructures, respectively. Finally, it is possible to represent the integral constitutive relations given by Equation (32) in an equivalent differential form as [7]

(33a)

(33b)

(33c)

where is the Laplacian operator. The stress–strain relations can be expressed by

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

By integrating Equations (34)–(44) over the area of plate cross section, the following relations for the force–strain and the moment–strain and other necessary relation of the refined FG plate can be obtained:

(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

in which the cross-sectional rigidities are defined as follows:

(56)

(57)

(58)

(59)

(60)

(61)

(62)

(63)

(64)

Also, normal forces and moments due to magneto-electrical field in Equations (45)–(47) can be defined by

(65)

(66)

(67)

The governing equations of refined four-variable shear deformation MEE-FG nanoplate in terms of the displacement can be derived by substituting Equations (45)–(52) into Equations (26)–(31) as follows:

(68)

(69)

(70)

(71)

(72)

(73)

3. Solution procedure

In this section, Navier’s method is implemented to solve the coupled governing equations for critical buckling temperature. Therefore, the following expansions of displacements are adopted to satisfy the simply supported boundary conditions of the METE-FG nanoplate:

(74)

(75)

(76)

(77)

(78)

(79)

where (, , , , , ) are the unknown coefficients. Inserting Equations (74)–(79) into Equations (68)–(73), respectively, leads to

(80)

(81)

(82)

(83)

(84)

(85)

By finding determinant of the coefficient matrix of the above equations and setting this multinomial to zero, we can find critical buckling temperatures:

(86)

4. Different types of thermal loading

4.1. Uniform temperature rise

For an FG nanoplate at reference temperature , the temperature rises uniformly to the final temperature which .

4.2. Linear temperature rise

When the nanoplate thickness is thin enough, the temperature rises linearly through the thickness as follows:

(87)

where in which and are the temperature of the top surface and the bottom surface, respectively.

4.3. Heat conduction

The one-dimensional temperature distribution through-the-thickness can be obtained by solving the heat conduction equation with the boundary conditions on lower and upper interfaces of the plate across the thickness:

(88)

The solution of above equation is

(89)

4.4 STR

The temperature field when METE-FG nanoplate is under sinusoidal temperature change across the thickness can be expressed by [27]

(90)

5. Numerical results and discussions

In this section, first of all, the accuracy of the present formulation is examined through example of isotropic FG nanoplates. The METE-FG nanoplate is modeled via a refined nonlocal four-variable theory with a trigonometric shear strain function. Moreover, it does not need a shear correction factor. This model is justified by an excellent agreement between the buckling results given by present study and available data in the literature [31] for the case of the FG nanoplate as presented in Table 2. In this case, we take a = 10 nm, E_c = 380 GPa, E_m = 70 GPa, and v_c = v_m = 0.3. Then, a parametric study is carried out to indicate the influences of the temperature environments (uniform temperature rise [UTR], linear temperature rise [LTR], STR, and HC) in conjunction with the magneto-electrical field, nonlocal, geometrical, and material parameters on the thermal buckling characteristics of the METE-FG nanoplates.

Table 2. Comparison of dimensionless buckling load () of simply supported square FG nanoplates (a/h = 10).

	µ = 0 nm^2		µ = 2 nm^2
Gradient index, p	HSDT [31]	Present	HSDT [31]	Present
0	18.6876	18.6877	10.4425	10.4426
0.5	10.0638	10.0638	5.6235	5.62359
2.5	6.2593	6.25935	3.4976	3.49769
5.5	5.5200	5.52002	3.0845	3.08455
10.5	4.9677	4.96776	2.7759	2.77596

HSDT: higher order shear deformation theory; FG: functionally graded.

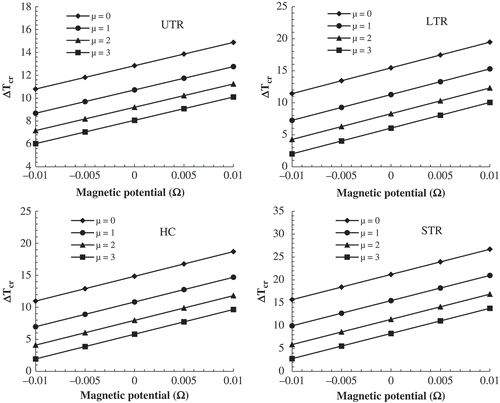
Numerical data for critical buckling temperature (ΔT_cr) of a SSSS METE-FG nanoplate under uniform, linear and STR and also heat conduction for various small scale parameter (µ), electric voltage (V), magnetic potential (Ω) are presented in Tables 3 and 4 when a = b = 100 h and p = 1. The numerical results show that the critical buckling temperature (ΔT_cr) is proportional to the magnetic field while it is inversely proportional to the electric voltage and nonlocal parameter. However, the bending rigidity of the METE-FG nanoplate diminishes by increasing the nonlocal parameter, leading to reduction in critical buckling temperature. For all types of thermal loading, increasing magnetic field intensity gives larger ΔT_cr, while increasing electric voltage gives smaller ΔT_cr. This is due to the fact that the piezoelectric constant e₃₁ is negative, while the piezomagnetic constant q₃₁ is positive. At a constant magnetic and electric potentials, STR and UTR, respectively, give largest and smallest buckling temperatures.

Table 3. Variation of critical buckling temperature of FG nanoplate for various electric voltages and nonlocal parameters (a = b = 100 h, p = 1).

			UTR					LTR
µ	V = −1	V = −0.5	V = 0	V = + 0.5	V = + 1	V = −1	V = −0.5	V = 0	V = +0.5	V = +1
0	14.3826	13.6099	12.8371	12.0644	11.2917	18.4904	16.9676	15.4448	13.922	12.3992
1	12.2664	11.4936	10.7209	9.9482	9.17549	14.3199	12.7971	11.2743	9.75153	8.22872
2	10.7491	9.97639	9.20368	8.43096	7.65825	11.3299	9.80708	8.28427	6.76147	5.23866
3	9.60807	8.83536	8.06264	7.28992	6.51721	9.08122	7.55841	6.03561	4.5128	2.98999
			HC					STR
0	17.7657	16.3026	14.8395	13.3763	11.9132	25.357	23.2687	21.1804	19.092	17.0037
1	13.7587	12.2956	10.8324	9.36932	7.9062	19.6377	17.5494	15.4611	13.3728	11.2845
2	10.8858	9.42269	7.95957	6.49645	5.03333	15.5373	13.449	11.3607	9.27238	7.18407
3	8.72529	7.26216	5.79904	4.33592	2.8728	12.4536	10.3653	8.27697	6.18866	4.10034

UTR: uniform temperature rise; LTR: linear temperature rise; FG: functionally graded.

Table 4. Variation of critical buckling temperature of FG nanoplate for various magnetic potentials and nonlocal parameters (a = b = 100 h, p = 1).

			UTR					LTR
µ	Ω = −0.01	Ω = −0.005	Ω = 0	Ω = +0.005	Ω = +0.01	Ω = −0.01	Ω = −0.005	Ω = 0	Ω = +0.005	Ω = +0.01
0	10.7989	11.818	12.8371	13.8563	14.8754	11.4281	13.4364	15.4448	17.4532	19.4616
1	8.6827	9.70181	10.7209	11.74	12.7591	7.25758	9.26596	11.2743	13.2827	15.2911
2	7.16546	8.18457	9.20368	10.2228	11.2419	4.26752	6.2759	8.28427	10.2926	12.301
3	6.02443	7.04353	8.06264	9.08175	10.1009	2.01886	4.02723	6.03561	8.04398	10.0524
			HC					STR
0	10.9801	12.9098	14.8395	16.7691	18.6988	15.672	18.4262	21.1804	23.9345	26.6887
1	6.97312	8.90278	10.8324	12.7621	14.6918	9.95273	12.7069	15.4611	18.2153	20.9695
2	4.10026	6.02992	7.95957	9.88923	11.8189	5.85229	8.60649	11.3607	14.1149	16.8691
3	1.93973	3.86939	5.79904	7.7287	9.65836	2.76857	5.52277	8.27697	11.0312	13.7854

UTR: uniform temperature rise; LTR: linear temperature rise; FG: functionally graded.

Critical buckling temperature (ΔT_cr) of METE-FG nanobeam as a function of volume fraction index (p) is presented in Figures 2 and 3 for various temperature fields (UTR, LTR, STR, and HC), electric potentials (V = −1, −0.5, 0, +0.5, +1) and magnetic potentials (Ω = −0.01, −0.005, 0, +0.005, +0.01) at a/h = 100 and µ = 1 nm². According to these figures, stiffness of the METE-FG nanoplate degrades by increasing the volume fraction index, leading to reduction in critical buckling temperature for all thermal environments, magnetic and electric potentials. The reduction in buckling temperatures with respect to volume fraction index is more announced for positive magnetic and electric potentials. Also, it should be stated that magnetic field has less important influence on critical buckling temperatures at higher volume fraction indices, while effect of elect field on ΔT_cr is more announced at lower volume fraction indices, because the upper surface of nanoplate has zero piezoelectric coefficient and the lower surface has zero piezomagnetic coefficient. Hence, graded nanoplates exhibit specific behaviors when they are subjected to the magneto-electrical field.

Figure 2. Variation of critical buckling temperature of METE-FG nanoplate versus gradient index for various electric voltages and thermal loadings (a/h = 100, µ = 1 nm², Ω = 0*10^-4).

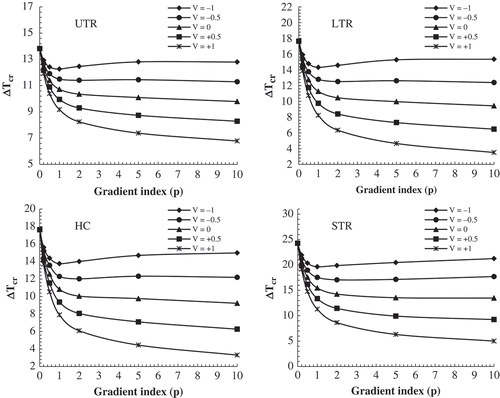
Figure 3. Variation of critical buckling temperature of METE-FG nanoplate versus gradient index for various magnetic potentials and thermal loadings (a/h = 100, µ = 1 nm², V = 0*10^-4).

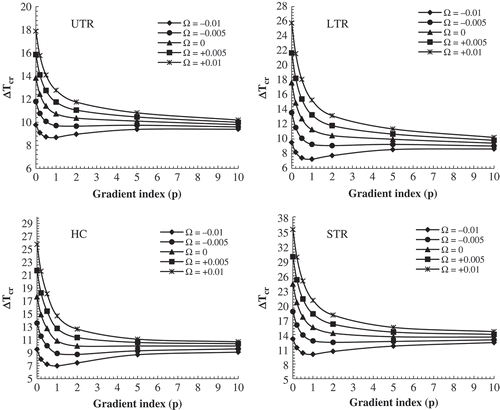
Figures 4 and 5 elucidate the variation of critical buckling temperature of METE-FG nanoplates versus electric and magnetic potentials, respectively, for various nonlocal parameters and thermal loadings at a/h = 100 and p = 1. It is noticed that for all kinds of thermal loadings application of local plate model overpredicts the critical buckling temperatures. Therefore, critical buckling temperatures decrease with increase in scale coefficient. Thus, nonlocal theory should be employed for accurate predictions of buckling temperatures. Also, for any kind of thermal loading, critical buckling temperature (ΔT_cr) increases and reduces linearly by increasing magnetic and electric field intensities. Also, at a constant nonlocal parameter, STR and UTR, respectively, lead to largest and smallest buckling temperatures.

Figure 4. Variation of critical buckling temperature of METE-FG nanoplate versus electric voltage for various nonlocal parameters and thermal loadings (a/h = 100, p = 1, Ω = 0*10^-4).

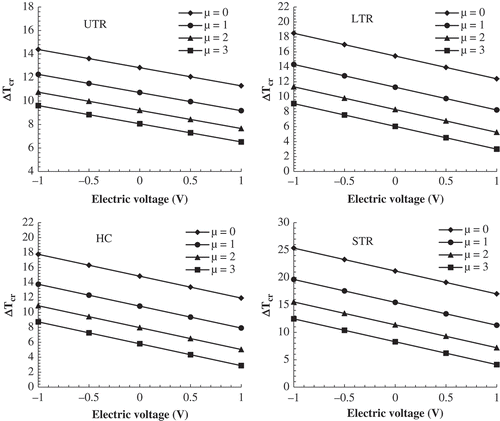
Figure 5. Variation of critical buckling temperature of METE-FG nanoplate versus magnetic potential for various nonlocal parameters and thermal loadings (a/h = 100, p = 1, V = 0*10^-4).

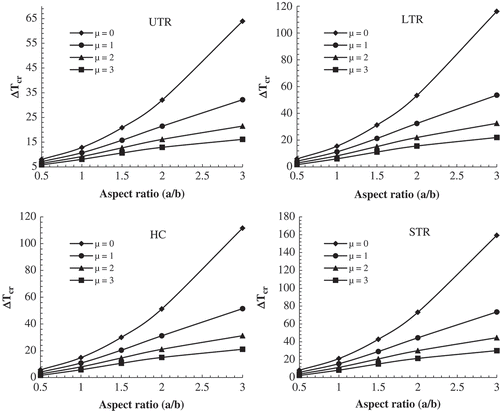
Variation of critical buckling temperature of METE-FG nanoplates versus aspect ratio (a/b) for various nonlocal parameters and thermal loadings is plotted in Figure 6 at a/h = 100, p = 1 and V = Ω = 0*10^-4. Irrespective of thermal loading type, increasing a/b gives larger critical buckling temperatures. Also, effect of nonlocality on ΔT_cr becomes more significant at higher aspect ratios for all kinds of temperature fields. Therefore, increase of critical buckling temperature with the rise of plate aspect ratio for a local plate model is more significant than nonlocal plate model.

Figure 6. Variation of critical buckling temperature of METE-FG nanoplate versus aspect ratio for various nonlocal parameters and thermal loadings (a/h = 100, p = 1, V = Ω = 0*10^-4).

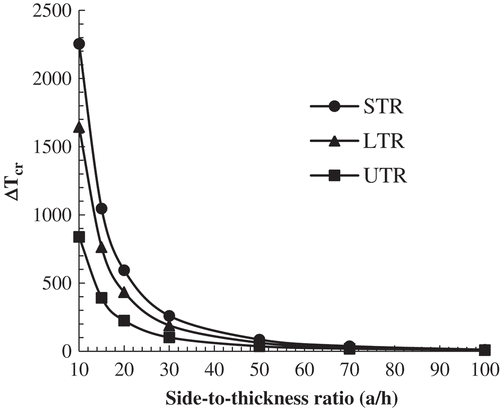
Figure 7 shows the critical buckling temperature of METE-FG nanoplate with respect to side-to-thickness ratio for uniform, linear, and sinusoidal temperature rises at a/b = 1, p = 1, µ = 2 nm², and V = Ω = 0. It is found that type of thermal loading has a major role on buckling temperatures of METE-FG nanoplates especially at lower side-to-thickness ratios at a fixed nonlocal parameter and material volume fraction index. STR gives higher buckling temperatures than LTR and the later gives higher buckling temperatures than UTR. Also, it is seen that with the increase of side-to-thickness ratio, critical buckling temperature reduces for all kinds of thermal environments.

Figure 7. Variation of critical buckling temperature of MEE-FG nanoplate versus side-to-thickness ratio for various thermal loadings (a/b = 1, p = 1, µ = 2 nm², V = Ω = 0*10^-4).

6. Conclusions

The motivation of this paper is to extend a size-dependent four-variable refined plate model characterizing the magneto-electro-thermo-mechanical buckling behavior of METE-FG nanoplates. Four types of thermal loadings called uniform, linear, and sinusoidal temperature distributions and also heat conduction are considered. According to a power-law distribution in terms of the volume fractions of the material phases, the material properties of the METE-FG nanoplate are varied from one interface to another. The coupled governing equations are obtained employing the principle of minimum potential energy. Navier’s method is implemented to explore the buckling temperatures of nonlocal METE-FG plates with simply supported boundary condition subjected to magneto-electro-thermal loadings. In order to validate the present model, the obtained results are compared with the previous results. It is observed that the bending rigidity of METE-FG nanoplate diminishes by increasing the nonlocal parameter, leading to reduction in critical buckling temperature. For all types of thermal loading, increasing magnetic field intensity gives larger buckling temperatures, while increasing electric voltage gives smaller ΔT_cr. Also, increasing the volume fraction index leads to reduction in critical buckling temperature for all thermal environments, especially for positive magnetic and electric potentials. Also, between considered thermal loadings, STR and UTR, respectively, lead to largest and smallest buckling temperatures.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Notes on contributors

Farzad Ebrahimi

Farzad Ebrahimi received his BS, MS and PhD degrees in Mechanical Engineering from the University of Tehran, Iran. Dr Ebrahimi is now an assistant professor in the Department of Mechanical Engineering at the International University of Imam Khomeini.

Mohammad Reza Barati

Mohammad Reza Barati received his BS degree from Imam Khomeini International University in Qazvin, Iran, in 2015. He is currently an MS student at Amirkabir University of Technology in Tehran, Iran. His research interests are vibration, nanomechanics and piezoelectric materials.