Size-dependent vibrations and waves in piezoelectric nanostructures: a literature review

ABSTRACT

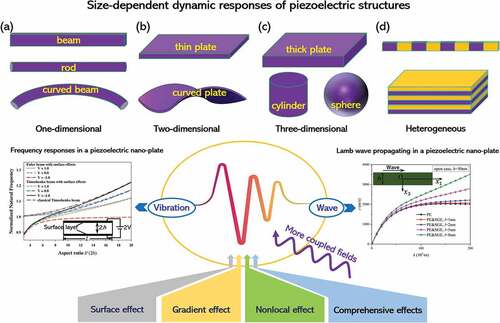
With the development and applications of nano-electro-mechanical systems, academic interest in the mechanical behavior of piezoelectric structures at nanoscale is increasing. Interesting unconventional phenomena have been observed either experimentally or through molecular dynamics simulation. The most common and also important one is the size-dependent characteristics. Classical continuum mechanics with necessary modifications has been proven to be very powerful in explaining these particular characteristics in a relatively simple theoretical framework. This article reviews the recent advances in understanding the size-dependent dynamic responses of piezoelectric nanostructures from the viewpoint of modified continuum mechanics. Particular attentions are paid to three advanced theories of piezoelectricity (e.g. gradient piezoelectricity, surface piezoelectricity, and nonlocal piezoelectricity) and their abilities to predict unconventional vibration and wave characteristics in piezoelectric structures and devices at the nanoscale. The article could serve as a useful reference for the future research on or design of nanostructures with multifield couplings.

Graphical Abstract

KEYWORDS:

• Size effect
• vibration
• wave
• piezoelectric structure
• continuum mechanics

Introduction

Miniaturization of structures is an irreversible technological trend for modern electromechanical devices and systems since it is obvious that more functional components are integrated into a chip, more powerful and more valuable is the chip. iPhone is such a representative system with many miniaturized structural components. These so-called micro-electro-mechanical systems (MEMS) and nano-electro-mechanical systems (NEMS) have been widely applied in daily life, medicine, industry, and engineering fields [1,2]. A nano- or even micro-sized structure may exhibit unusual, size-dependent behavior that is not encountered in the macro-structure with the same configuration [3,4]. These unconventional phenomena appear due to certain effects (e.g. surface effect [5,6], strain gradient effect [7–10], flexoelectric effect [11,12], and nonlocal effect [13–17]), which however are trivial and could be neglected in a general macro-sized structure.

Mathematical models based on the classical continuum mechanics without the inclusion of the effects like those mentioned above are not able to predict the size-dependent phenomena. Thus, the classical continuum field theories have to be modified such that these effects are properly incorporated. As a consequence, we have now different types of advanced continuum field theories of, for instance, elasticity, including surface elasticity, strain gradient elasticity, nonlocal elasticity, and modified couple stress theories. For more details about the modified continuum theories of elasticity, the interested readers are referred to the commendable review papers [18–20]. Compared with the experimental measurement or atomistic simulation, the models based on the modified continuum mechanics have several advantages, such as physically meaningful, analytically expressible, computationally economic, etc. Therefore, they have been widely employed to investigate the bending [21], vibration [22–26], wave propagation [27,28] and buckling [26,29–31] of small-scaled elastic structures, to interpret the experimentally or numerically observed size-dependent characteristics, and to guide the designs of MEMS or NEMS.

Piezoelectric materials have been widely applied in MEMS and NEMS, acting as a sensing material or an actuating material or both and relying on their capability to convert mechanical energy into electric energy and vice versa. Compared to the elastic materials, there is an additional electric field associated with the deformation of a piezoelectric material. So we need to consider both the mechanical equilibrium and the electric one to set up the governing equations, while the coupling between the electric and elastic fields, namely the piezoelectric effect, is embodied in the constitutive relations. Just as the elastic materials, we could also modify the classical piezoelectricity to get surface piezoelectricity, strain gradient piezoelectricity, or nonlocal piezoelectricity by including the appropriate small-scale effect(s). It is worth mentioning that the piezoelectric effect does not exist in materials with certain particular symmetries, while the flexoelectric effect induced by strain gradients exists in all materials and will manifest itself at the nanoscale [12,32].

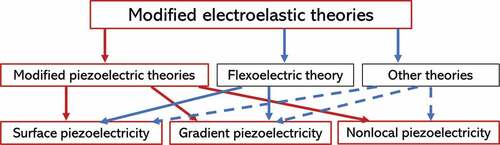
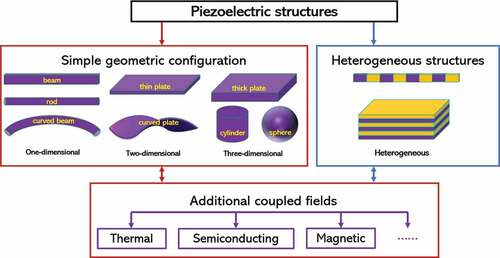
An excellent review has been made by Yan and Jiang [33] in 2017 on the modified continuum mechanics modeling of piezoelectric nanomaterials, with an emphasis on three typical advanced theories of electroelasticity, i.e. surface piezoelectricity, flexoelectricity, and nonlocal piezoelectricity. The purpose of our current survey is twofold: to pay attention only to the size-dependent dynamic responses of piezoelectric structures, and to reflect the most recent advances on the subject of interest. Also, the flexoelectric effect is not solely considered here since it is an entirely new effect (but could be regarded as one type of gradient effect) that is different from and independent of the piezoelectric effect, see Figure 1. Furthermore, only linear vibrations and waves are considered in the present survey, unless otherwise stated. Thus, we mainly focus on the modified linear theories of piezoelectricity, including gradient piezoelectricity, surface piezoelectricity, and nonlocal piezoelectricity. We also pay our attention to the piezoelectric structures of simple geometric configuration possibly with additional coupled fields (e.g. thermal, semiconducting, magnetic). The corresponding composite structures based on piezoelectric materials are also considered. The scope of this survey is illustrated in Figure 2. We hope the survey could be helpful to the researchers who are interested in the size-dependent dynamic performance of piezoelectric nanostructures.

Figure 1. Modified theories of electroelasticity featuring the coupling between the elastic and electric fields.

Figure 2. The scope of this review.

The classical and advanced theories of piezoelectricity

The classical linear theory of piezoelectricity [34] involves both the elastic and electric fields, for which the equilibrium equations without sources in Cartesian coordinates are respectively

(1) ${\sigma }_{ji,j}=\rho {\ddot{u}}_i,$(1)

(2) $D_{i,i}=0,$(2)

where ${\sigma }_{ij}$, $u_i$ and $D_i$ are the stress, mechanical displacement, and electric displacement, respectively; $\rho$ is the mass density; the subscript comma indicates derivative with respect to the coordinate that follows, and the dot over a quantity denotes its time derivative. The Einstein summation convention is adopted throughout the paper. The coupling between the two fields presents in the constitutive relations, through the piezoelectric constants $e_{ijk}$, as

(3) ${\sigma }_{ij}=c_{ijkl}^E{\gamma }_{kl}-e_{kij}{E}_k,D_i=e_{ikl}{\gamma }_{kl}+{\epsilon }_{ik}^{\gamma }{E}_k,$(3)

where ${\gamma }_{ij}$ and $E_i$ are the strain and the electric field intensity, respectively; $c_{ijkl}^E$ and ${\epsilon }_{ij}^{\gamma }$ are the elastic stiffness constants (the superscript E indicates a fixed electric field intensity when it is measured) and the dielectric constants (the superscript $\gamma$ indicates a fixed strain when it is measured), respectively. For simplicity, the superscripts E and $\gamma$ will be dropped in the following.

It should be noted that the electric field intensity vector $E_k$ is irrotational, which can be ensured by the introduction of the electric potential $\varphi$ such that

(4) $E_i=-{\varphi }_{,i}.$(4)

Further, the strain tensor ${\gamma }_{ij}$ can be expressed in terms of the mechanical displacement $u_i$ such as

(5) ${\gamma }_{ij}=\left(u_{i,j}+u_{j,i}\right)/2.$(5)

The combination of Equation 4(4) $E_i=-{\varphi }_{,i}.$(4) and Equation 5(5) ${\gamma }_{ij}=\left(u_{i,j}+u_{j,i}\right)/2.$(5) gives the generalized or extended geometric relations.

The classical linear theory of piezoelectricity described above is the long-wave and low-frequency limit of the equations of lattice dynamics [35], and usually applies to a general three-dimensional macroscopic piezoelectric body. Thus, the theory should be modified to account for the effects which manifest themselves in a microscopic piezoelectric body. There are many ways to make the modifications. In the following, we will show the modifications in three advanced theories of piezoelectricity, i.e. the gradient piezoelectricity, surface piezoelectricity, and nonlocal piezoelectricity.

Gradient piezoelectricity

Mindlin seems to be the first person who introduced the polarization gradient effect into the classical theory of piezoelectricity [36]. The polarization vector can be calculated as

(6) $P_i=D_i-{\epsilon }_0{E}_i,$(6)

where ${\epsilon }_0$ is the permittivity of free space. With Equation 6(6) $P_i=D_i-{\epsilon }_0{E}_i,$(6) , the constitutive relations in Equation 3 may be rewritten as

(7) ${\sigma }_{ij}=c_{ikjl}{\gamma }_{kl}+f_{ijk}{P}_k,E_i=f_{kli}{\gamma }_{kl}+a_{ik}{P}_k,$(7)

where the constants $f_{ijk}$ and $a_{ik}$ could be readily expressed in terms of the coefficients in Equation 3(3) ${\sigma }_{ij}=c_{ijkl}^E{\gamma }_{kl}-e_{kij}{E}_k,D_i=e_{ikl}{\gamma }_{kl}+{\epsilon }_{ik}^{\gamma }{E}_k,$(3) and Equation 6(6) $P_i=D_i-{\epsilon }_0{E}_i,$(6) . Mindlin suggested to treat the polarization gradient as an independent variable and the corresponding constitutive relations become

(8) $\begin{array}{cc}\hspace{0.17em}& {\sigma }_{ij}=c_{ikjl}{\gamma }_{kl}+f_{ijk}{P}_k+d_{klij}{P}_{l,k},E_i=f_{kli}{\gamma }_{kl}+a_{ik}{P}_k+g_{ikl}{P}_{l,k},\\ \hspace{0.17em}& E_{ij}=d_{ijkl}{\gamma }_{kl}+g_{kij}{P}_k+b_{ijkl}{P}_{l,k},\end{array}$(8)

where $d_{ijkl}$, $b_{ijkl}$ and $g_{ikl}$ are the newly introduced constants which are all related to the polarization gradient. $E_{ij}$ is the work-conjugate variable of the polarization gradient $P_{j,i}$. Accordingly, Equation 4(4) $E_i=-{\varphi }_{,i}.$(4) becomes

(9) $E_i-E_{ji,j}+{\varphi }_{,i}=0,$(9)

which indicates that the electric field intensity vector is no longer irrotational in this kind of gradient piezoelectricity.

It is interesting to note that for materials with centrosymmetry, the piezoelectric constants $e_{ijk}$ or $f_{ijk}$ vanish, but the electromechanical interaction still exists through constants $d_{ijkl}$ in these bodies with the polarization gradient effect. Equation 8(8) $\begin{array}{cc}\hspace{0.17em}& {\sigma }_{ij}=c_{ikjl}{\gamma }_{kl}+f_{ijk}{P}_k+d_{klij}{P}_{l,k},E_i=f_{kli}{\gamma }_{kl}+a_{ik}{P}_k+g_{ikl}{P}_{l,k},\\ \hspace{0.17em}& E_{ij}=d_{ijkl}{\gamma }_{kl}+g_{kij}{P}_k+b_{ijkl}{P}_{l,k},\end{array}$(8) actually is the primary version of the more comprehensive theory of gradient piezoelectricity with the flexoelectric effect which was put forward by Shen and Hu [37] as follows:

(10) $\begin{array}{rl}& {\sigma }_{ij}=c_{ikjl}{\gamma }_{kl}+f_{ijk}{P}_k+d_{klij}{P}_{l,k}+r_{ijklm}{\gamma }_{kl,m},E_i=f_{kli}{\gamma }_{kl}+a_{ik}{P}_k+g_{ikl}{P}_{l,k}+h_{jkli}{\gamma }_{jk,l},\\ & E_{ij}=d_{ijkl}{\gamma }_{kl}+g_{kij}{P}_k+b_{ijkl}{P}_{l,k}+{\eta }_{ijklm}{\gamma }_{kl,m},{\tau }_{ijm}=r_{klijm}{\gamma }_{kl}+h_{ijmk}{P}_k+{\eta }_{klijm}{P}_{k,l}+s_{ijmknl}{\gamma }_{kn,l}.\end{array}$(10)

As a result, the new material constants $r_{ijklm}$, $h_{jkli}$, ${\eta }_{ijklm}$, and $s_{ijmknl}$ appear due to the further inclusion of the strain gradient tensor ${\gamma }_{ij,m}$, the work-conjugate variable of which is the third-order stress tensor ${\tau }_{ijm}$. If we discard the polarization gradient in Equation 10(10) $\begin{array}{rl}& {\sigma }_{ij}=c_{ikjl}{\gamma }_{kl}+f_{ijk}{P}_k+d_{klij}{P}_{l,k}+r_{ijklm}{\gamma }_{kl,m},E_i=f_{kli}{\gamma }_{kl}+a_{ik}{P}_k+g_{ikl}{P}_{l,k}+h_{jkli}{\gamma }_{jk,l},\\ & E_{ij}=d_{ijkl}{\gamma }_{kl}+g_{kij}{P}_k+b_{ijkl}{P}_{l,k}+{\eta }_{ijklm}{\gamma }_{kl,m},{\tau }_{ijm}=r_{klijm}{\gamma }_{kl}+h_{ijmk}{P}_k+{\eta }_{klijm}{P}_{k,l}+s_{ijmknl}{\gamma }_{kn,l}.\end{array}$(10) , we will obtain the modified piezoelectric theory with the strain gradient effect, i.e. the classical theory of flexoelectricity.

There are still other possibilities of modifying the classical theory of piezoelectricity to include the gradient effects. For example, Yang et al. [38] established a modified piezoelectric theory with the electric field gradient effect taken into account, which has been applied to anti-plane problems of piezoelectric materials so as to characterize the small-scale effect [39–41].

Surface piezoelectricity

Just like the gradient piezoelectricity, the theory of surface piezoelectricity can be introduced in different ways. A straightforward way is to directly generalize the surface elasticity established by Gurtin and Murdoch (hereafter referred to as the GM theory) [42]. This was done by Huang and Yu [43] by adding the electric field terms into the surface constitutive relations as

(11) ${\sigma }_{\alpha \beta }^s={\sigma }_{\alpha \beta }^0+c_{\alpha \beta \xi \eta }^s{\gamma }_{\xi \eta }-e_{k\alpha \beta }^s{E}_k,D_i^s=D_i^0+e_{i\alpha \beta }^s{\gamma }_{\alpha \beta }+{\epsilon }_{ij}^s{E}_j,$(11)

where the superscript s denotes the surface material property, and ${\sigma }_{\alpha \beta }^0$, $D_i^0$ are the residual surface stress and residual surface electric displacement, respectively. The Greek index in Equation 11(11) ${\sigma }_{\alpha \beta }^s={\sigma }_{\alpha \beta }^0+c_{\alpha \beta \xi \eta }^s{\gamma }_{\xi \eta }-e_{k\alpha \beta }^s{E}_k,D_i^s=D_i^0+e_{i\alpha \beta }^s{\gamma }_{\alpha \beta }+{\epsilon }_{ij}^s{E}_j,$(11) takes the value of 1 or 2, representing one of the two tangential directions at a point on the surface, while the Roman index ranges over 1, 2 and 3 as before.

One can also treat the surface of a material body as a material layer with a very small thickness. This is the treatment proposed by Mindlin [44] and Tiersten [45] on another topic, but found to give the same results as the GM theory. Based on this idea, Chen [46,47] employed the state-space formalism to derive the governing equations of a piezoelectric plane surface, which shows a great superiority in the mathematical derivation. This approach can be readily applied to more sophisticated cases [48].

Nonlocal piezoelectricity

The typical nonlocal constitutive relations for a piezoelectric body (with volume V) read as

(12) $\begin{array}{cc}\hspace{0.17em}& {\sigma }_{ij}\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[c_{ijkl}^{\hspace{0.17em}}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })-e_{kij}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\\ \hspace{0.17em}& D_i\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[e_{ikl}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })+{\epsilon }_{ik}^{\hspace{0.17em}}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\end{array}$(12)

where $\alpha \left(\left|\mathbf{x}{ }^{\mathrm{\prime }}-\mathbf{x}\right|,\tau \right)$ is the nonlocal attenuation function incorporating into the constitutive equations the influence at the reference point $\mathbf{x}$ produced by the local strain/electric field intensity at the source point $\mathbf{x}{ }^{\mathrm{\prime }}$, and $\left|\mathbf{x}{ }^{\mathrm{\prime }}-\mathbf{x}\right|$ represents the Euclidean distance. $\tau =e_{0}a/l$ is the scale coefficient that incorporates the small-scale factor, in which the material constant $e_0$ is usually determined experimentally. The variables and l stand for the internal and external characteristic lengths of the nanostructure, respectively. Equation 12(12) $\begin{array}{cc}\hspace{0.17em}& {\sigma }_{ij}\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[c_{ijkl}^{\hspace{0.17em}}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })-e_{kij}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\\ \hspace{0.17em}& D_i\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[e_{ikl}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })+{\epsilon }_{ik}^{\hspace{0.17em}}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\end{array}$(12) indicates that the stress (electric displacement) at a point depends on the strain and electric field intensity at all points within the body. This is the nonlocality of the material response.

The classical theory of piezoelectricity is a degenerated case for which all the nonlocal material moduli in Equation 12(12) $\begin{array}{cc}\hspace{0.17em}& {\sigma }_{ij}\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[c_{ijkl}^{\hspace{0.17em}}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })-e_{kij}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\\ \hspace{0.17em}& D_i\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[e_{ikl}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })+{\epsilon }_{ik}^{\hspace{0.17em}}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\end{array}$(12) are Dirac delta functions. Further, it can be shown through Taylor’s expansion, that the gradient piezoelectricity can be seen as a weak nonlocal theory [35].

Following Eringen [49], the integral form of Equation 12(12) $\begin{array}{cc}\hspace{0.17em}& {\sigma }_{ij}\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[c_{ijkl}^{\hspace{0.17em}}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })-e_{kij}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\\ \hspace{0.17em}& D_i\left(\mathbf{x}\right)=\underset{V}{\int }\alpha \left(\left|\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }-\mathbf{x}\right|,\tau \right)\left[e_{ikl}{\gamma }_{kl}(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })+{\epsilon }_{ik}^{\hspace{0.17em}}{E}_k(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime })\right]\mathrm{d}V(\mathbf{x}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }),\end{array}$(12) can be transformed into a differential form, i.e.

(13) $\begin{array}{rl}& {\sigma }_{ij}-{\left(e_{0}a\right)}^2{\mathrm{\nabla }}^2{\sigma }_{ij}=c_{ijkl}^{\hspace{0.17em}}{\gamma }_{kl}-e_{kij}{E}_k,\\ & D_i-{\left(e_{0}a\right)}^2{\mathrm{\nabla }}^2{D}_i=e_{ikl}{\gamma }_{kl}+{\epsilon }_{ik}^{\hspace{0.17em}}{E}_k,\end{array}$(13)

which has been widely employed for its convenience in solving the boundary value problems [50].

It can be noted from Equation 10(10) $\begin{array}{rl}& {\sigma }_{ij}=c_{ikjl}{\gamma }_{kl}+f_{ijk}{P}_k+d_{klij}{P}_{l,k}+r_{ijklm}{\gamma }_{kl,m},E_i=f_{kli}{\gamma }_{kl}+a_{ik}{P}_k+g_{ikl}{P}_{l,k}+h_{jkli}{\gamma }_{jk,l},\\ & E_{ij}=d_{ijkl}{\gamma }_{kl}+g_{kij}{P}_k+b_{ijkl}{P}_{l,k}+{\eta }_{ijklm}{\gamma }_{kl,m},{\tau }_{ijm}=r_{klijm}{\gamma }_{kl}+h_{ijmk}{P}_k+{\eta }_{klijm}{P}_{k,l}+s_{ijmknl}{\gamma }_{kn,l}.\end{array}$(10) , Equation 11(11) ${\sigma }_{\alpha \beta }^s={\sigma }_{\alpha \beta }^0+c_{\alpha \beta \xi \eta }^s{\gamma }_{\xi \eta }-e_{k\alpha \beta }^s{E}_k,D_i^s=D_i^0+e_{i\alpha \beta }^s{\gamma }_{\alpha \beta }+{\epsilon }_{ij}^s{E}_j,$(11) , and Equation 13(13) $\begin{array}{rl}& {\sigma }_{ij}-{\left(e_{0}a\right)}^2{\mathrm{\nabla }}^2{\sigma }_{ij}=c_{ijkl}^{\hspace{0.17em}}{\gamma }_{kl}-e_{kij}{E}_k,\\ & D_i-{\left(e_{0}a\right)}^2{\mathrm{\nabla }}^2{D}_i=e_{ikl}{\gamma }_{kl}+{\epsilon }_{ik}^{\hspace{0.17em}}{E}_k,\end{array}$(13) that the three advanced theories of piezoelectricity mentioned above have different characteristic parameters, e.g. material constants associated with different gradient fields, surface parameters (residual surface stress, surface electric displacement, and surface electroelastic moduli), and nonlocal parameters. There is still no evidence that one theory is better than another, but in some cases one effect may prevail another [33,51]. It is also noted that, when more fields are present in piezoelectric materials, the above modified continuum theories of piezoelectricity should be further generalized by adding the corresponding physical field variables into the constitutive equations along with the additional field equations [52–54].

Vibrations of piezoelectric nanostructures

Vibration characteristics are crucial to the proper functioning of various devices, including those at the nanoscale, causing a surge of research interest in piezoelectric nanostructures as well from both academia and engineering. In this section, we will summarize the recent advances in size-dependent vibrations of piezoelectric nanostructures.

Size-dependent vibrations due to the gradient effect

The modified continuum theory of piezoelectricity with the gradient effect has been widely used to study the size-dependent vibration behaviors of piezoelectric nanostructures. The typical nano-sized structures include piezoelectric nanobeams (PNBs), nanorods (PNRs), nanoplates (PNPs), nanofilms (PNFs), etc. We summarize the recent studies which explore the gradient effect on vibrations of piezoelectric nanostructures in Table 1 for easy reference; these studies will be reviewed in the following.

Table 1. Summary of size-dependent vibrations of piezoelectric nanostructures due to the gradient effect with different gradient fields taken into account. Acronyms: PNB (piezoelectric nanobeam), PMR (piezoelectric microrod), PNS (piezoelectric nanoshell), PNP (piezoelectric nanoplate), PNF (piezoelectric nanofilm), PSC NW (piezoelectric semiconductor nanowire), PMP (piezoelectric microplate), FG (functionally graded), TB (Timoshenko beam), EB (Euler-Bernoulli beam), LR (Love rod), FB (first-order beam), KP (Kirchhoff plate), SDS (shear deformation shell), HSD (higher-order shear deformation).

Structures	Theoretical models	Gradient Fields	References
PNB	TB & EB	Strain gradient	[55,58,60]
PMR	LR	Strain gradient	[62]
PSC NW	FB	Strain gradient	[59]
PNS	SDS	Strain gradient	[64]
PNP	KP	Strain gradient; Polarization gradient	[56]
PNP	KP	Strain gradient	[61]
PNF	KP	Strain gradient; Electric field gradient	[57]
FG PNB	TB & EB	Strain gradient	[63,65,67,68]
FG PNB	EB	Strain gradient; Polarization gradient	[66,69,70]
FG PMP	HSD	Strain gradient	[71]

Flexoelectricity, referring to the coupling between electric polarization and strain gradient, is a type of the modified piezoelectricity with gradient effects. The flexoelectric effect on size-dependent vibrations has received considerable attention from researchers. Based on the Timoshenko beam model, the effects of flexoelectricity, rotary inertia, and shear deformation on free vibration of a simply-supported (SS) PNB shown in Figure 3(a) were investigated by Yan and Jiang using the extended linear theory of piezoelectricity [55]. Later, based upon the Kirchhoff plate model, the same research group studied the size-dependent vibration of a clamped PNP, as shown in Figure 3(c), by utilizing the strain gradient theory, in which both the strain gradient and polarization gradient were considered [56]. Numerical results shown in Figure 3(b and d) indicated that the flexoelectricity tends to lower the resonance frequencies of the PNB and PNP, and the decrease in the resonance frequency becomes more remarkable for the PNB and PNP with smaller thickness. Moreover, frequency-tuning of the PNB- and PNP-based nanodevices can be achieved by adjusting the applied electric load. Furthermore, Liang et al. [57] investigated the flexoelectric effect on the free vibration of an SS PNF by employing the Kirchhoff plate model and the strain gradient theory; therefore both the strain gradient and electric field gradient were taken into consideration. It was found that the flexoelectricity dominantly affects the natural frequencies of the PNF with nanoscale thickness. By using a strain gradient theory, Baroudi et al. took a look at the size-dependent vibration of an Euler-Bernoulli PNB with flexoelectricity under different boundary conditions and electric loads [58]. Their numerical results revealed that the flexoelectric effect and the higher-order stress induced by the strain gradient both have a prominent influence on the natural frequencies of the SS or cantilever PNBs at the nanoscale. Recently, based on the Mindlin’s strain gradient elasticity theory, Zhao et al. [59] studied the bending vibration of a cantilever piezoelectric semiconductor (PSC) nanowire with flexoelectricity and higher-order stress caused by the strain gradient. Their results showed that the effect of higher-order stress on the natural frequency of the PSC nanowire is greater than that of flexoelectricity. There also exist a few works on vibration characteristics of piezoelectric nanostructures when both the static and dynamic flexoelectric effects are taken into consideration. Based on the Timoshenko and Euler-Bernoulli beam models, Nguyen et al. investigated the dynamic flexoelectric effect on the free vibration of an SS PNB via a strain gradient theory [60]. Wang and Li employed the Kirchhoff plate model to study the free vibration of a PNP with the static and dynamic flexoelectricity [61]. Both the two studies indicated that, similar to the static flexoelectricity, the dynamic flexoelectric effect on the natural frequencies becomes prominent for the PNB- and PNP-based nanostructures with nanoscale thickness.

Figure 3. Size-dependent vibrations of piezoelectric nanostructures due to the gradient effect [55,56]. The italic V is the applied voltage and the Roman V is the unit of voltage, namely volt. $\omega$ and ${\omega }_0$ represent the resonance frequencies of piezoelectric nanostructures with and without flexoelectricity, respectively. (a) schematic of a simply-supported PNB under electric and mechanical loads; (b) variation of the normalized resonance frequency of the PNB versus beam thickness for different external electric loads; (c) schematic of a clamped PNP under electric and mechanical loads; (d) variation of the normalized resonance frequency of the PNP versus plate thickness for different external electric loads. Decreasing the thicknesses of PNB and PNP dramatically lowers the resonance frequencies of piezoelectric nanostructures no matter how large the applied voltage is and what the structural models are employed. (Reproduced with permission from Yan and Jiang [55]. Copyright 2013 by IOP Publishing, and reproduced with permission from Zhang et al. [56]. Copyright 2014 by American Institute of Physics AIP).

In addition, the influence of higher-order stress, namely the strain gradient elasticity, on the size-dependent vibrations in piezoelectric nanostructures has been reported. Arefi and Zenkour [62] studied the free vibration of a sandwiched microrod resting on a Pasternak foundation through a strain gradient theory, in which the couple stress and higher-order stress associated with the strain gradient were considered. They found that the larger the length scale parameter related to the deviatoric stretch gradients and the parameter of foundation, the higher the resonance frequencies of the piezoelectric microrod. Subsequently, they further employed the strain gradient theory to investigate free vibration of the sandwiched microbeam integrated with piezoelectric face-sheets and piezomagnetic face-sheets resting on Pasternak foundation based on the Euler-Bernoulli beam model [63,64]. The numerical results also reveal that the variations of three length-scale parameters associated with the dilatation gradient, deviatoric stretch gradient, and symmetric rotation gradient, respectively, lead to significant changes in the frequencies of the first three modes of piezoelectric microbeams.

While most studies as mentioned above focus on the traditional homogeneous materials, the emerging functionally graded piezoelectric materials (FGPMs) have also attracted much attention in recent years. As a consequence, various novel FGPM nanostructures have been fabricated and widely applied in MEMS and NEMS because of the outstanding material properties of FGPMs. Therefore, it is of vital importance to investigate the size-dependent vibrations of these FGPM nanostructures due to the gradient effect. Based on the Timoshenko beam model, Li et al. [65] studied the free vibration of an SS and FG PNB by using a modified strain gradient theory, where the couple stress and higher-order stress related to the strain gradient were considered. The numerical results indicated that the material length scale parameters and the material gradient index significantly affect the natural frequencies of the FG PNB. Based upon the Euler-Bernoulli beam model, Chu et al. [66] investigated the flexoelectric effect on the vibration responses of an FG PNB by using the extended Toupin’s piezoelectricity theory, in which the strain gradient and polarization gradient were considered. The simulation results revealed that the flexoelectric effect on the natural frequency of the FG PNB depends on the material volume ratio coefficient and gradient index, especially for the nano-sized PNB. In addition, the static and dynamic flexoelectric effects on the frequency of an SS and FG PNB (see Figure 4(a)) were studied by Yu et al. utilizing the extended linear theory of piezoelectricity and the Euler-Bernoulli beam model [67]. The numerical results shown in Figure 4(b and c) indicated that the static flexoelectricity significantly changes the resonance frequencies of the FG PNB for all vibration modes, while the dynamic flexoelectricity mainly affects the resonance frequencies of the higher-order vibration modes. Moreover, the natural frequencies of the FG PNB are prominently influenced by the material gradient index (see Figure 4(d)). Recently, the size-dependent vibrations of the FG PNBs with porosity and flexoelectricity were investigated by employing the strain gradient theory and different beam models [68–70]. These researchers found that the flexoelectric effect on the free vibration behaviors of the FG PNBs is considerably affected by the porosity coefficient and distribution. Also, Nguyen et al. [71] studied the size-dependent vibrations of an FGPM microplate with porosity by using the modified strain gradient theory, in which the couple stress and higher-order stress related to the strain gradient were considered. They found that the three length scale parameters, the material gradient index, and the porosity distribution all have remarkable influence on the natural frequencies of the FGPM microplate.

Figure 4. Size-dependent vibrations of a simply-supported FG PNB due to the gradient effect [67]: (a) variation of the effective flexoelectric coefficient versus thickness for different material gradient indexes m; (b) flexoelectric effect on the natural frequency of the first mode versus beam thickness for different dynamic flexoelectric coefficients M₃₃; (c) flexoelectric effect on the natural frequency of the third mode versus beam thickness for different dynamic flexoelectric coefficients M₃₃; (d) variation of the normalized frequency versus beam thickness for different material gradient index m. (Reproduced with permission from Yu et al. [67]. Copyright 2021 by Elsevier).

Size-dependent vibrations due to the surface effect

Due to the large ratio of surface area to volume at the nanoscale, surface effect becomes one of the reasonable and also successful explanations of the size-dependent mechanical properties of materials/structures at small scale. In recent years, the considerable advances in the modified continuum mechanics models incorporating the surface piezoelectricity and size-dependent vibrations of piezoelectric nanostructures due to the surface effect have been achieved. In this subsection, the research works related to the surface effect are reviewed and then summarized in Table 2 for easy reference.

Table 2. Summary of size-dependent vibrations of piezoelectric nanostructures due to the surface effect. Acronyms: PNW (piezoelectric nanowire), PNB (piezoelectric nanobeam), PNP (piezoelectric nanoplate), PNF (piezoelectric nanofilm), PNS (piezoelectric nanoshell), PNSP (piezoelectric nanosphere), PSC NB (piezoelectric semiconductor nanobeam), TB (Timoshenko beam), EB (Euler-Bernoulli beam), KP (Kirchhoff plate), TS (thin shell), GNS (Goldenveizer-Novozhilov shell).

Structures	Theoretical models	Surface parameters	References
PNW & PNB	EB & TB	Surface elasticity	[72,79,80,85]
PNB	EB & TB	Surface piezoelectricity	[73,76,78]
PNP & PNF	KP	Surface piezoelectricity	[74,75,77]
PNP	2D Equations	Surface piezoelectricity	[81,82]
PNS	2D Equations	Surface piezoelectricity	[83]
PNSP	TS	Surface piezoelectricity	[84]
PSC NB	1D PSC	Surface elasticity	[86]
PNS	GNS	Surface piezoelectricity	[87]

As a preliminary exploration, Wang and Feng investigated the effect of surface stress on the size-dependent vibration of PNWs by using the Euler-Bernoulli beam model and the GM theory [72], which took account of the residual surface stress and surface elasticity, but ignored surface piezoelectricity. The results indicated that the influence of surface stress on the natural frequencies becomes significant for the PNW with a nanoscale height. Subsequently, based on the Euler-Bernoulli beam model and the surface piezoelectricity model [43], the surface effect, including the residual surface stress, surface elasticity, and surface piezoelectricity, on the vibration properties of the PNB shown in Figure 5(a) was studied by Yan and Jiang [73]. It was found that the influences of residual surface stress and surface piezoelectricity on the resonance frequencies are more prominent than surface elasticity (see Figure 5(b)), which demonstrated the importance of surface piezoelectricity. The same authors further investigated the surface effect on the vibration behaviors of a clamped PNP by using the Kirchhoff plate model with surface piezoelectricity [74]. They demonstrated that the surface effect on the resonance frequencies, mainly due to the residual surface stress and surface piezoelectricity, becomes more prominent for the PNP with smaller thickness and larger plate aspect ratio. They also developed a modified Kirchhoff plate model to investigate the effect of surface parameters and surface-induced in-plane constraints on the vibration responses of PNPs [75]. The simulation results showed that the surface effect on the vibration behaviors significantly depends on the surface-induced in-plane constraints. A similar work, which studies the influence of surface effect and surface-induced initial field on the size-dependent vibration of PNBs under different boundary conditions, was conducted by Yue et al. using the Euler-Bernoulli beam model [76]. The numerical results indicated that, owing to the surface-induced initial stress, the surface effect on the resonance frequency of PNBs may be notably affected by the boundary conditions. Furthermore, built upon the Kirchhoff plate model, the surface effect on the vibration behavior of PNFs was studied by Zhang and Wang [50] using the surface piezoelectricity model, and similar conclusions to those in the paper of Yan and Jiang [77] were drawn. In addition, the surface effect on the free vibrations of piezoelectric nanostructures with shear deformation has been studied. For example, Xu et al. presented the analytical solutions for the free vibration of thick Timoshenko PNBs (see Figure 5(c)) based on the surface piezoelectricity model [78]. They found that the shear deformation and rotary inertia also have a significant influence on the resonance frequencies for the higher-order modes and the PNB with small length-to-thickness aspect ratio (see Figure 5(d)). Samaei et al. similarly investigated the surface effect on the vibration response of PNWs by using the modified Timoshenko beam model and the GM theory [79]. Recently, Liu and Keivan employed the Rayleigh and Timoshenko beam models to study the surface effect on the flexural vibration of axially moving piezoelectric nanowires based on the GM theory [80]. It was found that the effects of shear deformation, surface stress, and applied voltage on the natural frequencies are significantly dependent on the axial velocity.

Figure 5. Surface effect on the resonance frequencies of PNBs with surface piezoelectricity [73,78]: (a) schematic of a PNB with surface effect; (b) variation of the normalized resonance frequency versus beam thickness for different surface parameters; (c) schematic of a Timoshenko PNB with surface effect; (d) normalized frequency ratio $b_{\mathrm{T}\mathrm{B}}/b_{\mathrm{E}\mathrm{B}}$ versus length-thickness ratio $L/h$ for the first three modes. The subscript TB and EB represent the Timoshenko beam and Euler-Bernoulli beam, respectively. (Reproduced with permission from Yan and Jiang [73]. Copyright 2011 by IOP Publishing, and reproduced with permission from Xu et al. [78]. Copyright 2013 by IOP Publishing).

In addition, some interesting studies were reported, which establish novel theoretical models with surface effect and consider special curved nanostructures. For example, Zhang and his coauthors established the two-dimensional (2D) equations of piezoelectric nanostructures based on the surface piezoelectricity model, and they further employed the 2D equations to investigate the surface effect on the free vibrations of PNPs [81] (see Figure 6(a)), bimorph nano-actuators [82], and cylindrical PNSs [83]. In their works, the Miller-Shenoy coefficient and natural frequencies were obtained, and the results indicated that the surface effect has more remarkable influence on the resonance frequencies as the plate thickness decreases (see Figure 6(b)). Moreover, the energy conversion of PNP-based harvester (see Figure 6(c)) and the displacement actuation of the bimorph nano-actuator (see Figure 6(d)) are both enhanced by the surface effect. By using a thin shell layer model and the state-space formalism, Wu et al. established a theory of surface piezoelectricity for a spherical material boundary of a piezoelectric nanosphere, and they further studied comprehensively the surface effect on the free vibration of spherically isotropic piezoelectric nanospheres [84]. The numerical results showed that the surface effects, including the electroelastic effect, inertia effect, and transverse stress effect, have a particularly significant influence on the natural frequencies of the piezoelectric nanosphere. Recently, Wang and Han developed a nonclassical Euler-Bernoulli beam model of PNWs based on the Chen-Yao surface elasticity model, and they employed this model to investigate the surface effect on the free vibration of the PNW [85]. It was found that the surface effect becomes extremely remarkable for the PNW with nanoscale thickness. Based on the GM theory, Zhang et al. [86] established a one-dimensional (1D) multi-field coupling model, and then analyzed the size-dependent vibration of piezoelectric semiconductor (PSC) nanobeams due to the surface effect. They revealed that the surface effect tends to increase the natural frequencies and the damping effect caused by the motions of carriers. Fang et al. investigated the size-dependent vibration of small-scaled piezoelectric double-shells by combining the Goldenveizer-Novozhilov shell theory, thin plate theory, and electro-elastic surface theory [87]. The results revealed that surface piezoelectricity has a greater influence on the natural frequencies than surface elasticity and residual surface stress.

Figure 6. Surface effect on the vibration responses of piezoelectric nanostructures [81,82]: (a) schematic of a PNP-based harvester with surface effect under the mechanical load; (b) normalized natural frequency of the PNP with surface effect; (c) Output voltage of the PNP-based harvester for different plate thicknesses; (d) Deflections of a PNP-based actuator with and without surface effect. $\omega$ and ${\omega }_0$ represent natural frequencies of the PNP with and without surface effect, respectively. (Reproduced with permission from Zhang CL, Chen WQ, Zhang C [81]. Two-dimensional theory of piezoelectric plates considering surface effect. European Journal of Mechanics A/Solids, 2013, 41: 50–57. Copyright 2013 by Elsevier Masson SAS. All rights reserved) (Reproduced with permission from Zhang et al. [82]. Copyright 2013 by American Society of Mechanical Engineers ASME).

Size-dependent vibrations due to the nonlocal effect

Promoted by Eringen’s pioneering work, the nonlocal elasticity theory that can reasonably explain some phenomena related to the atomic and molecular scales was extended to piezoelectric materials by Zhou and Wang [50]. Recently, the nonlocal piezoelectricity theory has been widely employed to study the size-dependent vibrations of piezoelectric nanostructures with nonlocal effect. In this subsection, the research advances focusing on the nonlocal effect are reviewed and then summarized in Table 3 for easy reference.

Table 3. Summary of size-dependent vibrations of piezoelectric nanostructures due to the nonlocal effect. Acronyms: PNB (piezoelectric nanobeam), PNP (piezoelectric nanoplate), PNS (piezoelectric nanoshell), FG (functionally graded), TB (Timoshenko beam), EB (Euler-Bernoulli beam), KP (Kirchhoff plate), MP (Mindlin plate), LS (Love shell), SDP (shear deformation plate).

Structures	Nonlocal theories	References
PNB	Nonlocal TB & EB theory	[88,91,93]
PNB	Nonlocal higher-order SDP theory	[102]
PNP	Nonlocal KP & MP theory	[89,90,92,94,96,103,104]
PNP	Nonlocal thermoelastic theory	[99,100]
FG PNB	Nonlocal TB theory	[98,101]
FG PNS	Nonlocal LS theory	[97]
FG PNP	Nonlocal KP theory	[95]
FG PNP	Nonlocal 1st SDP theory	[105]

Ke and Wang first investigated the thermo-electro-mechanical vibration of PNBs under different boundary conditions based on the nonlocal piezoelectricity theory and Timoshenko beam model [88]. Subsequently, Ke and his coauthors employed the nonlocal Kirchhoff and Mindlin plate theories to study the thermo-electro-mechanical vibration of PNPs under different boundary conditions [89,90]. The numerical results indicated that the natural frequencies of the PNB and PNP tend to decrease as the nonlocal parameter increases, and the natural frequencies can be notably affected by the electro-mechanical loads and boundary conditions. Based upon the nonlocal piezoelectricity theory and Euler-Bernoulli beam model, Jandaghian and Rahmani investigated the free vibration of PNBs under different boundary conditions [91]. They also found that increasing the nonlocal parameter may lead to the decrease in the fundamental frequency for most boundary conditions, and the nonlocal effect on the natural frequency exhibits obviously size-dependent. In addition, Li et al. employed the Euler-Bernoulli beam model and Kirchhoff plate model to solve the problems of thermo-electro-mechanical vibrations of axially moving PNBs [92] and PNPs [93] based on the nonlocal piezoelectricity theory, respectively. The simulation results showed that the nonlocal parameter and axial average speed result in the decrease of natural frequencies, and the natural frequencies are also dependent on the material viscosity, temperature change and electric load. Using the Kirchhoff plate model, Zhu et al. analyzed the influence of material uncertainties on the thermo-electro-mechanical vibrations of the PNPs under different boundary conditions via the nonlocal piezoelectricity theory [94]. It was found that the uncertainty degree of material properties may significantly contribute to the influence of nonlocal parameter on the natural frequencies of the PNP.

The study on the size-dependent vibrations due to the nonlocal effect was further extended to the novel FGPM and piezoelectric layered nanostructures. Jandaghian and Rahmani investigated the size-dependent vibration of an SS and FG PNP through the nonlocal piezoelectricity theory and Kirchhoff plate model [95,96]. It was found that the natural frequencies are greatly influenced by the nonlocality, material volume fraction index, length-width aspect ratio, and electro-mechanical loads. Wang et al. presented the analytical solutions for free vibration of multilayered FG PNSs by utilizing the nonlocal piezoelectricity theory and Love’s thin shell model [97]. The results revealed that the natural frequencies of the sandwiched FG PNS are sensitive to the nonlocality, material gradient index, length-to-thickness ratio, and radius-to-thickness ratio. Based on the nonlocal Timoshenko beam theory, the free vibration of a rotating FG PNB with different boundary conditions was considered by Li et al. [98]. It was found that besides the nonlocal parameter, the change of rotating angular velocity also has a great influence on the natural frequencies. Moreover, the influences of these factors on natural frequencies and vibrational mode shapes depend on the boundary conditions. In addition, Li et al. explored the problem of size-dependent thermo-electro-mechanical vibration of multi-layered PNPs under thermal loads by using the nonlocal thermoelastic theory [99]. The numerical results indicated that although the thermal nonlocal parameter greatly increases the electric potential in the layered PNP (see Figure 7(a)), it also enhances the temperature in the volume (see Figure 7(b)) and thermal stress at the interface (see Figure 7(c)), such that the ability of heat isolation of surface coating will be greatly weakened and the large harmful thermal stress at the interface appears. However, the elastic nonlocal parameter can greatly improve the electric potential (see Figure 7(d)) without increasing the temperature in the volume (see Figure 7(e)) and the thermal stress at the interface (see Figure 7(f)), which is beneficial to harvesting more electrical energy. Subsequently, based on the nonlocal thermoelastic theory, Li et al. [100] further investigated the dynamic thermo-electro-mechanical response of laminated sandwich PNPs considering different ratios of piezoelectric material constants such as thermal modulus, pyroelectric constants, and thermal conductivity. The results demonstrated once again that the proper selections of thermal/elastic nonlocal parameters or material constant ratios could effectively improve electrical energy harvesting and heat isolation.

Figure 7. Size-dependent thermo-electro-mechanical responses of layered PNPs due to nonlocal effect [99]: distributions of electric potential in (a), temperature in (b), thermal stress in (c) for different thermal nonlocal parameters ${\chi }^{\left(i\right)}$; distributions of electric potential in (d), temperature in (e), thermal stress in (f) for different elastic nonlocal parameters $e{a}^{\left(i\right)}$. (Reproduced with permission from Li et al. [99]. Copyright 2019 by Elsevier).

It is worth noting that there also exist a few works on modeling the size-dependent vibrations of piezoelectric nanostructures with special configurations due to the nonlocal effect. For example, Ebrahimi and Daman [101] investigated the thermo-electro-mechanical vibration of a curved and simply-supported FG PNP shown in Figure 8(a) by utilizing the nonlocal Timoshenko beam theory. In this work, the increase of the nonlocal parameter (see Figure 8(b)) and curvature angle (see Figure 8(c)) results in the decrease of natural frequencies, while increasing the length-thickness ratio enlarges the natural frequencies (see Figure 8(d)). Arefi et al. [102] employed the nonlocal higher-order shear deformation beam theory to analyze the free vibration of a curved and sandwiched PNB reinforced with functionally graded carbon nano-tubes (FGCNT). The results proved once again that the natural frequencies have a negative correlation with the nonlocal parameter, curvature radius, and curvature angle. In addition, Zenkour and Arefi investigated the thermo-electro-mechanical vibration of an FGPM nanosheet resting on a visco-Pasternak foundation through the nonlocal Kirchhoff plate theory [103]. Using the same nonlocal theory, Bastami and Behjat studied the size-dependent vibration of an SS PNP deposited on the elastic medium [104]. Furthermore, Mao et al. [105] explored the free vibration of graphene nanoplatelet reinforced FGPM composite microplate resting on the Winkler foundation via the nonlocal piezoelectricity theory and first-order shear deformation plate model. The simulation results all showed that the natural frequencies of piezoelectric nanostructures decrease as the nonlocal parameter and material nonhomogeneous index increase, while the natural frequencies enhance as the stiffness of the foundation increases.

Figure 8. Size-dependent vibration of a curved and FG Timoshenko PNB due to nonlocal effect [101]: (a) schematic of curved FG PNB; (b) variation of the natural frequency versus power-law exponent for different nonlocal parameters $\mu$; (c) variation of the natural frequency versus power-law exponent for different curvatures $\alpha$; (d) variation of the natural frequency versus power-law exponent for different length-thickness aspect ratios L/h. (Reproduced with permission from Ebrahimi and Daman [101]. Copyright 2017 by Techno Press).

Size-dependent vibrations due to the comprehensive effect

In addition to the size-dependent vibrations due to each individual effect mentioned above, considerable interest has been also devoted toward the comprehensive effect by incorporating some or all of the effects (gradient, surface, and nonlocal) into one theoretical framework. In this subsection, the works related to the comprehensive small-scale effect on size-dependent vibrations in piezoelectric nanostructures are reviewed and then summarized in Table 4 for easy reference.

Table 4. Summary of size-dependent vibrations of piezoelectric nanostructures due to the comprehensive effect. Acronyms: PNW (piezoelectric nanowire), PNB (piezoelectric nanobeam), PNP (piezoelectric nanoplate), PNS (piezoelectric nanoshell), PNT (piezoelectric nanotube), TB (Timoshenko beam), EB (Euler-Bernoulli beam), KP (Kirchhoff plate), MSDP (modified shear deformation plate), SDS (shear deformation shell), FG (functional graded), GPT (gradient piezoelectricity theory), SPT (surface piezoelectricity theory), NPT (nonlocal piezoelectricity theory).

Theories	Structures	Theoretical models	References
SPT & NPT	PNW & PNB	EB	[106–108,110]
SPT & NPT	FG PNB	EB	[109]
SPT & NPT	PNP	KP & MSDP	[111,112]
GPT & SPT	PNW & PNB	EB & TB	[113–115]
GPT & SPT	PNP	KP	[116]
GPT & NPT	PNB	EB	[117,118]
GPT & NPT	FG PNS	1st SDS	[119]
GPT & NPT	PNP	KP	[120]
GPT & NPT	FG PNP	KP	[121]
GPT & SPT & NPT	PNB & PNT	EB	[122,124]
GPT & SPT & NPT	PNP	KP	[123]

Some efforts have been made to examine the surface and nonlocal effects on the size-dependent vibrations of piezoelectric nanostructures. For instance, based on the Euler-Bernoulli beam model, Gheshlaghi and Hasheminejad developed an analytical model to predict the surface and nonlocal effects on the free transverse vibrations of PNWs by utilizing the GM theory and the nonlocal theory [106]. Using the same modified continuum theory, Haghpanahi et al. [107] developed a finite element model for the size-dependent vibration analysis of PNWs. Also, the same theoretical framework was employed by Ebrahimi-Nejad and Boreiry to comprehensively analyze the free vibration of PNBs with surface and nonlocal effects under magneto-electro-mechanical loads [108]. Hashemi et al. investigated the surface effect on the free vibrations of an FG PNB by using the nonlocal Euler-Bernoulli beam theory and GM theory [109]. Furthermore, some researchers have also developed comprehensive continuum mechanics models by incorporating the surface piezoelectricity model into the nonlocal theory. Eltaher et al. studied the size-dependent vibration of PNBs through the surface piezoelectricity model and the nonlocal Euler-Bernoulli beam theory [110]. Adopting the nonlocal Kirchhoff plate theory with the incorporation of surface piezoelectricity, Karimi et al. carried out the vibration analysis of a bi-layer PNP under thermo-electro-mechanical loads [111]. Khorshidi et al. developed a comprehensive nonlocal surface-piezoelectricity model for the free vibration of PNPs based on the modified shear deformation theory [112]. The numerical results highlighted the significant and comprehensive influences of the surface and nonlocal parameters on the natural frequencies and mode shapes of piezoelectric nanostructures.

There are a few works on the size-dependent vibrations of piezoelectric nanostructures due to the gradient and surface effects. Based on the Euler-Bernoulli beam model, Liang et al. investigated the free vibration of PNWs with surface piezoelectricity and flexoelectricity taken into account simultaneously [113]. With the same beam model, the size-dependent vibration of a sandwiched piezoelectric composite microbeam was studied by Khabaz et al. using a higher-order strain gradient theory and surface piezoelectricity model [114]. Based on the Timoshenko beam model, Mohammadimehr et al. analyzed the free vibration of double-bonded piezoelectric microbeam through the strain gradient theory and GM theory [115]. Moreover, Yan employed the modified Kirchhoff plate model to investigate the flexoelectric and surface effects on the size-dependent vibration of a clamped circular PNP [116].

Some efforts have been devoted to the study of size-dependent vibrations of piezoelectric nanostructures due to the gradient and nonlocal effects. For example, Zhang et al. investigated the flexoelectric effect on the vibration characteristics of PNBs embedded in a viscoelastic medium based on the nonlocal Euler-Bernoulli beam theory [117]. Similarly, Zeng et al. studied the size-dependent vibration of a sandwiched PNB with flexoelectricity by using the nonlocal strain gradient theory and Euler-Bernoulli beam model [118]. In addition to the beam-based structures, vibration of size-dependent bimorph FGPM cylindrical shell was analyzed by Mehralian and Beni via the nonlocal strain gradient theory and first-order shear deformation shell theory [119]. Damping vibration of smart piezoelectric polymeric nanoplates resting on a viscoelastic substrate was studied by using the nonlocal strain gradient theory and Kirchhoff plate model [120]. Based on the same theoretical framework, Sharifi et al. investigated the free vibration of size-dependent FG PNPs due to the gradient and nonlocal effects [121].

Recently, some attention from researchers has been paid to the comprehensive influences of the gradient, surface, and nonlocal piezoelectricity on the size-dependent vibrations of piezoelectric nanostructures. Ebrahimi and Barati studied vibration characteristics of a PNB resting on a Winkler-Pasternak foundation by incorporating surface piezoelectricity and flexoelectricity into the nonlocal Euler-Bernoulli theory [122]. Utilizing the surface piezoelectricity model and nonlocal piezoelectricity theory, the same authors further performed the size-dependent vibration analysis of flexoelectric PNPs described by a Kirchhoff plate model [123]. In addition, Amiri et al. used the nonlocal Euler-Bernoulli beam theory to study the flexoelectric and surface effects on the free vibration of fluid-conveying piezoelectric nanotubes [124].

In summary, the comprehensive theoretical frameworks provide more accurate and all-sided predictions of the size-dependent vibrations of piezoelectric nanostructures than those obtained from the modified continuum mechanics models with an individual effect only.

Waves in piezoelectric nanostructures

Waves can do something different from vibrations. There are a lot of functional devices that work by virtue of their wave propagation characteristics, like surface acoustic wave (SAW) and bulk acoustic wave (BAW) devices. Consequently, wave propagation in piezoelectric nanostructures has been a hot topic in recent years. In this section, we will summarize the recent research advances in size-dependent wave propagations in piezoelectric nanostructures, and a summary of the related works is given in Table 5.

Table 5. Summary of size-dependent waves propagating in piezoelectric nanostructures. Acronyms: BG (Bleustein-Gulyaev), SH (shear horizontal), SV (shear vertical), GPT (gradient piezoelectricity theory), SPT (surface piezoelectricity theory), NPT (nonlocal piezoelectricity theory).

Theories	Waves	References
GPT	BG	[125]
GPT	BG & Love	[126]
GPT	Love	[130–132]
GPT	SH	[38]
GPT	Plane	[127–129,133]
GPT	Bulk	[62]
SPT	BG	[46]
SPT	Love	[136]
SPT	Rayleigh & BG	[137,138]
SPT	SH	[139–141]
SPT	Lamb & Flexure	[142–144]
SPT	Bulk	[145–147]
NPT	Rayleigh & BG	[148,149]
NPT	SH	[158,159]
NPT	Flexure	[151,163]
NPT	Longitudinal	[166]
NPT	SV	[150]
NPT	Bulk	[152–157,160–162,164]
SPT & NPT	Bulk	[165]
SPT & NPT	Bulk	[167]
GPT & NPT	Plane	[169,170]
GPT & NPT	Bulk	[168,171–173]
GPT & SPT & NPT	Longitudinal	[175]
GPT & SPT & NPT	Bulk	[174,176]

Size-dependent waves due to the gradient effect

The establishment of the advanced theory of gradient piezoelectricity enables one to predict the size-dependent wave motions in piezoelectric nanostructures due to the gradient effect. Yang et al. summarized the equations of gradient piezoelectricity theory considering the electric field gradient and then studied the size-dependence of anti-plane waves propagating in a circular cylindrical piezoelectric shell [38]. Subsequently, based on the same theory, Li et al. explored the effect of electric field gradient on the anti-plane surface wave (i.e. Bleustein-Gulyaev, BG) propagating over a piezoelectric half-space [125]. They found that the electric field gradient makes the anti-plane bulk wave and BG wave dispersive and the dispersion of waves is more pronounced when the wavelength approaches the microscopic characteristic length. Recently, based on the Love rod model, Arefi and Zenkour investigated the bulk wave propagation in a sandwich piezoelectric microrod by using a strain gradient theory [62], in which the couple stress and higher-order stress related to the strain gradient were considered. The results indicated that the phase velocity of bulk waves could be enhanced by the increase in the characteristic length scale parameters associated with the deviatoric stretch gradient and symmetric rotation gradient. Furthermore, Solyaev and Lurie presented the analytical solutions of the BG wave propagating over a piezoelectric half-space shown in Figure 9(a) and Love waves propagating in a surface elastic layer deposited on a piezoelectric half-space shown in Figure 9(c) [126]. The second gradient electroelasticity theory with the electric field gradient, strain gradient, and inertia gradient was used in their analysis. It was found that the natural frequencies of mode branches in the dispersion curves decrease as the length scale parameters rise. Moreover, the neglect of the inertia gradient causes the abnormal spatial dispersion of the BG and Love waves. Specifically, the phase velocity of the BG wave rises as the wavenumber increases (see Figure 9(b)), and the phase velocity of the Love wave exceeds the bulk shear wave velocity in the substrate (see Figure 9(d)).

Figure 9. Effect of gradient piezoelectricity on the anti-plane wave propagation in piezoelectric nanostructures [126]: (a) schematic of Bleustein-Gulyaev (BG) wave propagation problem; (b) variation of the nondimensional phase velocity versus nondimensional wavenumber for BG wave; (c) schematic of Love wave propagation problem; (d) variation of the nondimensional phase velocity versus nondimensional wavenumber for Love wave. (Reproduced with permission from Solyaev and Lurie [126]. Copyright 2021 by Elsevier).

Many research works have paid attention to the flexoelectric effect on wave propagation in piezoelectric nanostructures. For example, Jiao et al. [127] investigated the plane wave propagation and reflection in an infinite piezoelectric medium with flexoelectricity and higher-order stress related to the strain gradient. The results indicated that when the wavelength of the incident wave is close to the characteristic length, the small-scale effect on wave propagation becomes prominent whether the bulk material is at micro- or nano-scale or not. Subsequently, based on the same modified continuum theory, Jiao et al. [128] further investigated the reflection and transmission of plane waves propagating in a piezoelectric slab sandwiched by two piezoelectric half-spaces. They found that the small-scale effects could create new dispersive modes, and all types of reflection and transmission waves are significantly influenced by the flexoelectric effect. Yang et al. analyzed the influences of flexoelectricity and strain gradient elasticity on Lamb wave propagating in an infinite PNP [129]. Numerical results showed that, compared with the phase velocity of the classical piezoelectric Lamb wave, flexoelectricity causes a smaller phase velocity (see Figure 10(a)), while strain gradient elasticity causes a larger one (see Figure 10(b)). In addition to the plane waves, the flexoelectric effect on anti-plane waves in piezoelectric layered structures has also been studied. The behaviors of Love wave propagating in a piezoelectric guided layer deposited on an isotropic substrate with flexoelectricity were investigated by Yang et al. [130]. It was found that flexoelectricity has a profound effect on the phase velocity of Love wave and causes the wave attenuation in the piezoelectric guided layer with nanoscale thickness. Furthermore, Hrytsyna et al. studied the Love wave propagation in a layered piezoelectric structure based on the strain gradient theory [131], in which flexoelectricity, higher-order stress, and micro-inertial effect were considered. The numerical results revealed that flexoelectricity increases the phase velocity of Love wave, while the micro-inertial effect reduces its value. Moreover, these effects become more significant for Love waves with smaller wavelength and guided layer with smaller thickness. Singhal et al. performed a comparative study on Love wave propagating in different piezoelectric material plates weakly bonded with a pre-stressed elastic plate with flexoelectricity [132]. The numerical results demonstrated that flexoelectricity has a notable influence on the wave velocity of Love wave, and the flexoelectric effect on wave propagation is significantly affected by the piezoelectric layer’s thickness, initial stress, interface imperfect parameter, and piezoelectric materials. One recent interesting work accomplished by Shen et al. focused on the longitudinal wave propagating in one-dimensional detuned phononic crystals with the flexoelectric effect [133]. They found that increasing the layer thickness detuning (random disordered) and flexoelectric coefficient detuning linearly widens the band gap, and the sensitivity of flexoelectric coefficient detuning is much higher than that of thickness detuning.

Figure 10. Lamb wave propagation in a piezoelectric plate with flexoelectricity and strain gradient elasticity [129]. The acronyms PE, SGE, and FE stand for the piezoelectric effect, strain gradient effect, and flexoelectric effect, respectively. f is the flexoelectric coefficient and l is the characteristic length. (a) variation of the phase velocity versus wavenumber for different flexoelectric coefficients; (b) variation of the phase velocity versus wavenumber for different characteristic lengths of strain gradient elasticity. (Reproduced with permission from Yang et al. [129]. Copyright 2018 by IOP Publishing).

Size-dependent waves due to the surface effect

Stimulated by the studies on wave propagation in elastic media with surface effect [134,135], wave propagation behaviors in piezoelectric nanostructures have been recently investigated by a few research groups using the advanced theories of surface piezoelectricity.

Chen [46] modeled the surface of a piezoelectric half-space as a thin piezoelectric layer with an extremely small thickness, and presented the dispersion relation of BG wave propagating in a piezoceramic half-space through the transfer matrix method. It was found that surface effect makes BG wave slightly dispersive and lowers its phase velocity. Different from Chen’s work, Zhang et al. [136] and Zhang et al. [137] performed the analyses of Love and Rayleigh-type surface waves propagating in a PNF over an elastic half-space via the surface piezoelectricity model, respectively, in which the thickness of surface layer was ignored. The numerical results showed that, owing to the surface effect, the dispersive properties of surface waves exhibit a prominent dependence on the surface parameters and the thickness of the PNF. Also, based on the surface piezoelectricity model, Zhou and Chen [138] investigated the surface effect on the propagation behaviors of surface waves, including the Rayleigh and BG waves, propagating in a generally anisotropic piezoelectric half-space. They revealed that the decreasing influence of surface effect on the surface wave velocity becomes more remarkable as the wavenumber and material intrinsic length increase.

In addition to the surface wave propagating in piezoelectric nanostructures, many efforts have been devoted toward the size-dependent bulk waves due to the surface effect. For example, following the method proposed by Chen [46], Wu et al. [139] developed the surface magneto-electro-elasticity model and investigated the surface effect on the anti-plane shear horizontal (SH) wave propagating in a magneto-electro-elastic nanoplate via Stroh formalism. The results indicated that the dispersive relations of the anti-symmetric and symmetric SH waves depend on the thickness of surface layer (see Figure 11(a and b)), the surface material parameters (see Figure 11(c and d)), and the considered SH wave mode branches (see Figure 11). Moreover, the influence of $r_h$ (thickness ratio between the surface layer and bulk layer) on the dispersive properties of SH waves is more conspicuous than $r_c$ (elastic constant ratio between the surface layer and bulk layer). In addition, by using the surface piezoelectricity model, the surface effect on SH wave propagating in piezoelectric plates was studied by Zhang et al. [140] and Zhang et al. [141]. The two studies both revealed that, owing to the surface effect, the propagation properties of SH waves become remarkably size-dependent when the plate thickness is comparable to the material intrinsic length. In addition to the SH wave, the surface effect on Lamb wave propagating in PNPs was investigated by Zhang et al. based on the surface piezoelectricity model [142]. The numerical results indicated that, due to the surface effect, the dispersive modes exhibit obvious size-dependent behaviors for the nanoscale PNP and the phase velocity of the Lamb waves remarkably decreases. Furthermore, Zhou developed a two-dimensional theory based on the surface piezoelectricity model and first-order shear deformation theory, and then studied the propagation of Lamb wave in a piezoelectric cylindrical shell [143]. Numerical results revealed that the surface effect plays a significant role in the dispersion of Lamb waves when the shell thickness is comparable to the material intrinsic length. The similar conclusion was drawn by Rexy et al. [144] through investigating the flexural wave propagating in a piezoelectric nanofiber based on the Timoshenko beam model and surface piezoelectricity theory. There also exist a few works on bandgap properties of piezoelectric phononic crystal (PC) nanobeams with surface effect by using the Timoshenko and Euler-Bernoulli beam models as well as surface piezoelectricity theory [145–147]. In Refs. [145] and [146], the results showed that the surface effect has a significant influence on the band structure of a PC nanobeam, and the surface parameters can help slightly tune the frequencies and widths of the considered bandgaps. Moreover, the material intrinsic length $l_s$ has a greater influence on the bandgaps than the residual surface stress ${\sigma }_x^0$ (see Figure 12(a and b)), which demonstrated that the effects of surface elasticity and surface piezoelectricity on the bandgaps are more prominent than the residual surface stress. It can be noted from Figure 12(c and d) that the surface effect on the band structures of the piezoelectric PC nanobeam can be significantly affected by the considered beam models in Ref [147].

Figure 11. Surface effect on the dispersion curves of the first five SH wave modes of a magneto-electro-elastic plate [139]: (a) different values of $r_h$ for the anti-symmetric SH modes; (b) different values of $r_h$ for the symmetric SH modes; (c) different values of $r_c$ for the anti-symmetric SH modes; (d) different values of $r_c$ for the symmetric SH modes. $r_h$ represents the thickness ratio between the surface layer and bulk layer. $r_c$ represents the elastic constant ratio between the surface layer and bulk layer. (Reproduced with permission from Wu et al. [139]. Copyright 2015 by IOP Publishing).

Figure 12. Surface effect on the bandgap properties of a piezoelectric PC nanobeam [145,147]: (a) influence of the surface residual stress ${\sigma }_x^0$ on the starting frequencies and widths of the first four bandgaps; (b) influence of the material intrinsic length $l_s$ on the starting frequencies and widths of the first four bandgaps; (c) band structure of a PC Timoshenko beam; (d) band structure of a PC Euler-Bernoulli beam. (Reproduced with permission from Qian et al. [145]. Copyright 2018 by American Institute of Physics AIP, and reproduced with permission from Qian et al. [147]. Copyright 2021 by Elsevier).

Size-dependent waves due to the nonlocal effect

Based on the nonlocal elasticity theory established by Eringen, size-dependent waves propagating in various piezoelectric nanostructures have been systematically investigated in recent years.

Some attention from researchers has been paid to the surface wave propagating in piezoelectric media due to their diverse technological applications. Based on nonlocal piezoelectricity, Tung [148] investigated the Rayleigh-type waves propagating in a transversely isotropic piezoelectric half-space, and they found that the increase in the nonlocal parameter significantly raises the phase velocity of Rayleigh waves. Also, the propagation of BG waves in a piezoelectric layer overlying a piezoelectric half-space was systematically studied by Sharma and Kumar [149], and the influences of the nonlocal parameter and electrically boundary conditions on the phase velocity and group velocity were discussed in detail. The numerical results demonstrated that the dispersive relations of BG wave are dependent on the nonlocal parameter for both the electrically open and shorted conditions. Specifically, the nonlocal effect causes a critical frequency, beyond which BG wave cannot propagate in the piezoelectric medium, and the nonlocal parameter has a decaying effect on the critical frequency.

In addition to the surface waves, bulk waves propagating in piezoelectric nanostructures have also attracted numerous interests from the academia. Ghorbanpour et al. investigated the size-dependent shear vertical (SV) wave propagating in a double-piezoelectric nanobeam-based system by using the nonlocal Euler-Bernoulli beam theory [150]. The results revealed that the nonlocal parameter has a remarkable influence on the phase velocity at large wavenumbers for the considered three cases (in-phase, out-of-phase, and one beam fixed). Ma et al. developed the nonlocal Euler-Bernoulli and Timoshenko beam models, and studied the dispersive behaviors of flexural waves propagating in a magneto-electro-elastic (MEE) nanobeam under thermo-magneto-electro-mechanical loads [151]. It was found that the dispersive properties of flexural waves significantly depend on the nonlocal parameter and beam models (see Figure 13(a)). Specifically, with the increase of the nonlocal parameter, the frequency decreases slowly at smaller wavenumbers, while it decreases rapidly at larger wavenumbers. Moreover, the frequency predicted by the Euler beam model is always higher than that predicted by the Timoshenko beam model for the same nonlocal parameter. Apart from the beam-like structures, a few works on the size-dependent waves propagating in plate-like structures have been reported. Ma et al. performed the analysis of bulk wave propagation in a PNP based on the nonlocal Kirchhoff and Mindlin plate theories under thermo-electro-mechanical loads [152]. The results showed that, similar to waves in the PNBs, the dispersion relations of bulk waves in the PNPs are notably affected by the nonlocal parameter and the considered plate models (see Figure 13(b)). By employing the Legendre polynomial method, Liu et al. studied Lamb and SH waves in a PNP based on the nonlocal piezoelectricity theory [153]. They found that the nonlocal effect decreases the wavenumbers of the purely real Lamb wave modes, while it strengthens the attenuation of the purely imaginary Lamb wave modes. For SH waves, the nonlocal effect makes the first SH wave mode dispersive and decreases the escape frequency (at which the phase velocity is zero and beyond which the elastic wave cannot propagate) of SH waves. In addition, some works focus on the size-dependent waves propagating in piezoelectric composite nanostructures. Arani et al. incorporated the quasi-3D sinusoidal theory into the nonlocal piezoelectricity theory, and investigated the bulk wave propagating in FGPM composite plates reinforced by single-walled carbon nanotubes [154]. Numerical results revealed that the phase velocity predicted by the nonlocal piezoelectricity theory is lower than that predicted by the classical continuum theory, and the increase of the nonlocal parameter decreases the cutoff frequencies (at which the wavenumber approaches zero or the phase velocity approaches to infinity) and escape frequencies. The similar conclusions were drawn in Ref [155] by investigating the bulk wave propagating in a stratified composite via the nonlocal piezoelectricity theory. Furthermore, the reflection and transmission of elastic waves in a piezoelectric plate sandwiched by two solid half-spaces were studied by Liu et al. using the nonlocal piezoelectricity theory [156]. Chen et al. proceeded the propagation analysis of the size-dependent bulk wave in an MEE layered plates by incorporating the nonlocal theory into the linear MEE theory [157]. It was found that the nonlocal parameter has a notable influence on the dispersive relations of Lamb and SH waves as well as the distributions of physical fields.

Figure 13. Dispersive relations of piezoelectric nanobeams [151] in (a) based on different beam models and dispersive relations of piezoelectric nanoplates [152] in (b) based on different plate models under different nonlocal parameters $e_{0}a$. (Reproduced with permission from Ma et al. [151]. Copyright 2017 by Elsevier, and reproduced with permission from Ma et al. [152]. Copyright 2018 by World Scientific).

It is worth noting that some research groups have reported their studies on the size-dependent waves propagating in periodic piezoelectric layered structures or piezoelectric PC structures due to the nonlocal effect. Chen et al. presented the band structures of SH waves in periodic piezoelectric layered structures based on the nonlocal piezoelectricity theory [158]. Yan et al. carried out the similar work with the imperfect interface taken into account [159]. They both found that the nonlocal effect causes a cutoff frequency in the band structures, beyond which the elastic waves cannot propagate through the periodic layered structure. Moreover, the cutoff frequency of the band structure is affected by the nonlocal parameter and interface property. The propagation of bulk waves in periodic piezoelectric composites was examined by Yan et al. using the nonlocal piezoelectricity theory [160]. The cutoff frequency caused by the nonlocal effect was also observed, which can be tuned by adjusting the internal or external characteristic lengths as well as the volume fraction. The same research groups further investigated the in-plane elastic wave propagating in periodic layered piezoelectric structures [161] and periodic piezoelectric/piezomagnetic laminates [162]. The influences of the piezoelectric/piezomagnetic coefficients (see Figure 14(a and b)) and the nonlocal parameter (see Figure 14(c and d)) on the band structures were systematically discussed. They found that altering these factors can tune the band structures, wave localization degree, and cutoff frequency (see Figure 14). In addition, another research group [163,164] considered the piezoelectric PC nanobeam and nanoplate made of piezoelectric material and epoxy, and the bandgap properties in these two nanostructures were studied by using the nonlocal Euler-Bernoulli beam and Kirchhoff plate theories, respectively. The numerical results indicated that the tuning of the starting frequency and bandwidth of the bandgaps for the PC nanobeam and nanoplate can be achieved by adjusting the nonlocal parameter.

Figure 14. Localization factor spectra of the periodic piezoelectric/piezomagnetic laminates [162]. (a) variations of the localization factor versus the nondimensional frequency ${\mathrm{\Omega }}_{Te}$ and piezoelectric coefficient; (b) variations of the localization factor versus ${\mathrm{\Omega }}_{Te}$ and piezomagnetic coefficient; (c) variations of the localization factor versus ${\mathrm{\Omega }}_{Te}$ and the nonlocal parameter R for the normal incidence of P wave; (d) variations of the localization factor versus ${\mathrm{\Omega }}_{Te}$ and R for the normal incidence of SV wave. The black dash line represents the cutoff frequency, beyond which the elastic waves cannot propagate in the periodic piezoelectric/piezomagnetic laminates. (Reproduced with permission from Chen et al. [162]. Copyright 2019 by Elsevier).

Size-dependent waves due to the comprehensive effect

Similar to the size-dependent vibrations, an individual small-scale effect does not suffice to predict the overall size-dependent wave behaviors in structures at the nanoscale. Therefore, the comprehensive theoretical frameworks by incorporating some or all of the effects mentioned above have been recently developed. In this subsection, the advances in the size-dependent waves predicted by these comprehensive continuum theories are reviewed.

Based on the surface piezoelectricity model and nonlocal piezoelectricity theory, Zhang et al. investigated the dispersive characteristics of the size-dependent plane waves propagating in a PNP [165]. It was found that the coupling influences of surface piezoelectricity and nonlocal parameter on the dispersive relations are more pronounced in comparison with each individual effect. With the same modified continuum theory, Zang et al. studied the propagation properties of the longitudinal wave in a PNP [166]. The numerical results indicated that the nonlocal parameter has a significant decreasing effect on the phase velocity of the longitudinal waves, while the surface effect on the phase velocity is neglectable. The surface and nonlocal effects on the bulk wave propagating in an FG PNR were investigated by Arefi [167] using the Love rod model and GM theory. The simulation results revealed that the surface and nonlocal effects on the dispersive relations of the nanorod are dependent on the wavenumber and material gradient index.

Many efforts have been devoted toward the coupling influences of the gradient piezoelectricity and nonlocal piezoelectricity on wave propagations in piezoelectric nanostructures by using different modified continuum theories. For example, Mawassy et al. performed the wave propagation analysis in piezoelectric composites by using the nonlocal flexoelectricity theory [168]. It was found that the bulk waves in piezoelectric composites with flexoelectricity are dispersive and the nonlocal parameter reduces the frequencies of the bulk waves. Masoumi et al. studied the flexoelectric effect on plane wave propagating in a PNB through the nonlocal strain gradient theory (NSGT) [169]. The results revealed that flexoelectricity lowers the phase velocity of the plane waves (including the bending, longitudinal, and shear waves), and the flexoelectric effect on the wave dispersive behaviors is obviously size-dependent. Without considering flexoelectricity, Ebrahimi et al. proceeded the analytical modeling of plane waves propagating in a piezoelectric double-layered nanobeam system [170] by using the NSGT directly. It was found that the phase velocity of plane waves in this system rises with the increase of the length scale parameter and the decrease of the nonlocal parameter. Habibi et al. employed the NSGT to investigate the wave propagation properties of a size-dependent laminated composite coupled with a piezoelectric actuator [171]. The results indicated that, although individual nonlocal effect and individual strain gradient elasticity cause the obvious decrease and increase of phase velocity, respectively, their coupling influences predicted by the NSGT exhibit a gentle decrease in the phase velocity. Furthermore, Hu et al. [172] explored the wave motion problem of a sandwiched PNP under thermo-electric loads via the NSGT. They found that the nonlocal parameter reduces the wave frequency (i.e. softening effect), while the length scale parameter related to the strain gradient elasticity increases the wave frequency (i.e. hardening effect). The same research group further investigated the wave propagation in a sandwiched PNP with thermo-electro-moisture changes by using the higher-order NSGT [173]. The results showed that the higher-order nonlocal parameter has a weaker softening effect on the wave frequencies than the low-order nonlocal parameter.

There also exist a few works on the size-dependent waves with the gradient piezoelectricity, surface piezoelectricity, and nonlocal piezoelectricity all taken into account. Based on the Kirchhoff plate model, Ebrahimi and Dabbagh dealt with the propagation problem of bulk waves in a PNP by incorporating the surface piezoelectricity model into the NSGT [174]. The simulation results demonstrated that the nonlocal parameter has a decreasing effect on the frequencies of bulk waves, while the surface effect and length scale parameter related to the strain gradient elasticity have an increasing influence on the wave frequencies. With the Love rod model, Arefi and Zenkour presented the analytical solutions for the longitudinal wave propagating in an FG PNR by incorporating surface elasticity into the NSGT [175]. Furthermore, based on the Euler-Bernoulli beam model, Amiri et al. investigated the wave propagation in viscous-fluid-conveying PNT by using the surface piezoelectricity model and the NSGT [176]. The numerical results in Refs. [175] and [176] also validated the conclusions drawn in Ref [174]. In a word, the comprehensive continuum theories considering the gradient, surface, and nonlocal effects simultaneously may provide more accurate predictions of the size-dependent behaviors of waves propagating in various piezoelectric nanostructures than those considering any individual effect only.

Based on the above-mentioned references, the size-dependent vibrations and waves can be obviously observed in piezoelectric structures at nanoscale. Therefore, the geometric size (such as the thickness or radius) of piezoelectric structures is usually selected as several to hundreds of nanometers, and the transition size may be determined through the parametric study. The crucial material coefficients related to the size-dependent phenomena still need to be measured or determined by experiments or atomistic simulations. At the end of this review, the structural sizes and characteristic parameters (e.g. the flexoelectric coefficient, characteristic length parameters in strain gradient theory, surface parameters, and nonlocal parameters) are summarized in Table 6 according to some representative literatures. We hope this table could provide the researchers a convenient and fast reference to the selection of these characteristic parameters in their future studies on size-dependent mechanical properties of piezoelectric materials/structures.

Table 6. Summary of geometric sizes and characteristic parameters for three advanced theories of piezoelectricity. f represents the flexoelectric coefficient. l₀, l₁, and l₂ represent the length scale parameters associated with the dilatation, deviatoric stretch, and symmetric rotation gradients, respectively, in strain gradient theory. ${\sigma }^s$, c^s, and e^s represent surface residual stress, surface elastic constant, and surface piezoelectric constant, respectively. l_s is usually the surface layer thickness or material intrinsic length. $\tau$ represents the nonlocal parameter and h is the thickness of plate and unit-cell. (L) represents that the parameters used in the references come from the literatures, and (T) represents that they are the artificial testing parameters. Acronyms: PNW (piezoelectric nanowire), PNB (piezoelectric nanobeam), PNP (piezoelectric nanoplate), PPC (periodically piezoelectric composite), SM (surface moduli), BM (bulk moduli).

Structures	Materials	Geometric sizes	Characteristic parameters	References
PNB & PNP	BaTiO3	10 ~ 1000 nm	f11 = −0.013V, f13 = 5V, f19 = 10V, f14 = 5V (L^[177,178^])	[55,56,58]
PNW	ZnO	25 nm	f11 = f12 = f44 = 10^−9V (T)	[59]
PNB&PNP	Strontium Titanate	2 ~ 100 nm	f12 = −1.3V, f14 = −1.5V, f44 = −0.28V (L^[179^])	[60,61]
PNB	BaTiO3/PVDF	5 ~ 100 nm	fB = 1V, fP = 5V(T); l0 = l1 = l2 = 17.6$\mu \mathrm{m}$ (L^[7^])	[66]
PNB	BaTiO3/PVDF	20 ~ 100 nm	f13B = 5V, f13P = 1V (T)	[67]
PNB	BaTiO3/SrTiO3	10 ~50 nm	f3113B = 5V, f3113S = 10V (L^[58,180^])	[69]
PNB	PZT-4/PZT-5H	1 nm	l0 = l1 = l2 = 17.6 $\mu \mathrm{m}$ (T)	[65]
PNB	PZT-4/PZT-5A	10 ~ 50 nm	f3113-4 = 5V, f3113-5A = 1V (T)	[68]
PNB & PNP	PZT-5H	1 ~ 150 nm	$c_{11}^s=c_{12}^s=7.56\mathrm{N}/\mathrm{m},e_{31}^s=e_{32}^s=-3\times {10}^{-8}\mathrm{N}/\mathrm{m}$ (L^[43^]) ${\sigma }_{11}^s=0.1\sim 1\mathrm{N}/\mathrm{m},c_{12}^s=3.3\mathrm{N}/\mathrm{m},c_{66}^s=2.13\mathrm{N}/\mathrm{m}$ (T)	[73–76,78,80,142]
PNP	PZT-5H	10 ~ 150 nm	$c_{11}^s=7.56\mathrm{N}/\mathrm{m},e_{31}^s=-3\times {10}^{-8}\mathrm{N}/\mathrm{m}$ (L^[43^]) $c_{12}^s=5.23\mathrm{N}/\mathrm{m},c_{44}^s=1.26\mathrm{N}/\mathrm{m}$ (T)	[77]
PNB	AlN	10 ~ 10^5nm	$c_{11}^s=114.1\mathrm{N}/\mathrm{m}$ (L^[181^]) $e_{31}^s=-1.93\times {10}^{-10}\mathrm{N}/\mathrm{m},{\rho }^s=1.09\times {10}^{-7}\mathrm{k}\mathrm{g}/{\mathrm{m}}^2$ (T)	[82]
PNP	PZT-5H & ZnO	10 ~ 1000 nm	SM = ls×BM (L^[182,183^])	[81,83,86,140,141,145]
PNB & PNP	\	0.5 ~ 10 nm	$\tau$= 0 ~ 4nm (T)	[88–96,151–153,163]
PNP & PPC	\	\	$\tau /h=0.03\sim 0.18$ (T)	[157,158,160,162]

Conclusions

This paper provides a review on the recent advances in the study of size-dependent vibrations and waves in various piezoelectric nanostructures due to the individual or comprehensive influences of gradient piezoelectricity, surface piezoelectricity, and nonlocal piezoelectricity. To reasonably predict those novel size-dependent characteristics of piezoelectric materials, the advanced theories of gradient piezoelectricity, surface piezoelectricity, and nonlocal piezoelectricity have been developed based on the classical continuum mechanics framework. These modified continuum theories have been widely employed to investigate the size-dependent behaviors of linear vibrations and waves in piezoelectric materials/nanostructures. A general conclusion can be drawn that the gradient, surface, and nonlocal parameters have significant influences on the behaviors of vibrations and waves, and these effects could be enhanced as the structural size decreases down to the nanoscale. In comparison with the past researches, prominent advances have been achieved in recent years, which are summarized below:

1. The comprehensive theoretical frameworks, which take some or all of the gradient effect, surface effect, and nonlocal effect into consideration, have been developed, which may provide more accurate predictions of the size-dependent vibrations and waves than the theories considering any individual effect only.

2. The modified continuum models of novel piezoelectric materials such as the FGPMs , piezoelectric composites, and piezoelectric semiconductor materials have been reported recently. It can be concluded that the size-dependent characteristics of vibrations and waves may be significantly affected by the material gradient index, material homogeneity, and semiconductor property.

3. The size-dependent vibrations and waves in novel piezoelectric nanostructures such as periodic piezoelectric laminates, piezoelectric phononic crystals, and curved structures, have also attracted a lot of research interests. These investigations could help shape the practically important strategies, which can be used, for instance, to enhance the frequency response and tune the wave propagation behaviors in novel piezoelectric nanodevices.

In spite of the substantial achievements that have been made, the following significant issues still remain to be addressed in future studies.

First, owing to the different small-scale effects, the obvious deviations between the results predicted by different modified continuum theories can be observed. Moreover, the existing parametric studies based on the artificial small-scale parameters and material constants may just qualitatively predict the size-dependent properties of vibrations and waves in piezoelectric materials/nanostructures. The quantitative and consistent results for the size-dependent vibrations and waves still need validation and verification via the precious and supportive experimental data or molecular dynamics simulation [7,184–186].

Second, it is of great value and demand to study size-dependent vibrations and waves in real 3D piezoelectric structures, because the 3D results could provide theoretical benchmarks for the ones obtained from the approximate theoretical models (e.g. the Mindlin plate and Kirchhoff plate models) [54,187,188], and determine the range of their applicability.

Third, the reports on the size-dependent vibrations of piezoelectric nanostructures mainly focus on vibration response of the lower-order modes such as the flexure and in-plane extension modes, which are widely used in PNB-, PNW-, and PNR-based nanodevices. However, owing to the crucial applications in radio-frequency telecommunication and high-sensitivity sensing, the PNP-based nanodevices operating with higher-order modes (for instance, thickness-shear and thickness-extension modes), have also attracted increasing interests in recent years [189–193]. Hence, the small-scale effects on vibration response of the higher-order modes should also be investigated in future researches.

Fourth, more comprehensive continuum theories, which incorporate, say, the thermo-magneto-electro-mechanical models into the modified continuum theories of the gradient, surface, and nonlocal piezoelectricity, should be established to explore the all-sided influence of small-scale and multi-physics coupling on the size-dependent properties of vibrations and waves in novel MEMS/NEMS structures.

Last, dielectric elastomers have recently received considerable attention from the academia and industry due to their advantages of low actuation voltage and large deformation under electric stimuli [194]. The vibration responses and wave motions in dielectric elastomer devices can be efficiently tuned by the external electro-mechanical loads [195–197]. For nanoscale dielectric elastomer devices, the small-scale effect could be enhanced by the large deformation, and in turn may have a more remarkable influence on the size-dependent vibrations and waves as well as the tunability of device performance under electro-mechanical loads [198]. Therefore, investigation on the size-dependent properties of dielectric elastomer nanodevices under external loads is also an interesting and meaningful topic.

Acknowledgments

The work is supported by the National Natural Science Foundation of China [grant numbers 12192210, 12192211 and 11872329], the 111 Project [grant number B21034], the Natural Science Foundation of Zhejiang Province [grant number LD21A020001], and the National Postdoctoral Program for Innovative Talents (grant number BX2021261). Partial support from the Shenzhen Scientific and Technological Fund for R&D, PR China (grant number 2021Szvup152) is also acknowledged.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the National Natural Science Foundation of Zhejiang Province [LD21A020001]; National Natural Science Foundation of China [12192210]; National Natural Science Foundation of China [12192211]; 111 Project [B21034]; Shenzhen Scientific and Technological Fund for R&D, PR China [2021Szvup152]; National Postdoctoral Program for Innovative Talents [BX2021261]; National Natural Science Foundation of China [11872329].