A systematic design of multifunctional lattice structures with energy absorption and phononic bandgap by topology and parameter optimization

ABSTRACT

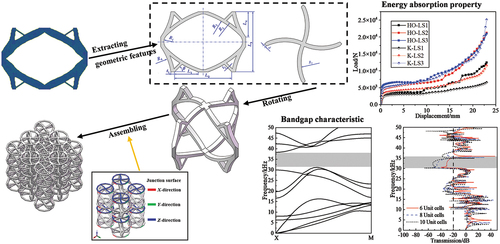
Lattice structure can realize excellent multifunctional characteristics because of its huge design space, and the cellular configuration directly affects the lattice structural performance and lightweight. A novel energy-absorbing multifunctional lattice structure with phononic bandgap is presented by topology and parameter optimization in this paper. First, the two-dimensional (2D) cellular configuration is lightweight designed by using independent continuous mapping (ICM) topology optimization method. The 2D cell is reconstructed by geometric parameters and rotated into a three-dimensional (3D) cell by using chiral shape to achieve bandgap. Subsequently, the surrogated model with energy absorption as the object and first-order natural frequency as the constraint is established to optimize a parametric 3D cell based on the Response Surface Methodology (RSM). Finally, the lattice structures are assembled with dodecagonal staggered arrangements to avoid the deformation interference among the adjacent cells. In addition, the lattice structural energy absorption and bandgap characteristics are analyzed and discussed. Compared to Kelvin lattice structure, the optimal lattice structure shows significant improvement in energy absorption efficiency. Besides, the proposed design also performs well in damping characteristics of the high-frequency and wide-bandgap. The lattice structural optimization design framework has great meaning to achieve the equipment structural lightweight and multi-function in the aerospace field.

GRAPHICAL ABSTRACT

KEYWORDS:

• Multifunctional lattice structure
• energy absorption
• phononic bandgap
• topology optimization
• parameter optimization

1. Introduction

Lattice structures have been widely used in the aerospace [1], biomedical [2–4] and other fields because of their high ratio of strength, high energy absorption, or vibration isolation. Therefore, extensive research has been conducted on the configuration design and property evaluation of lattice structures. Cellular configuration design is very important because the performance of the lattice structure is closely related to the geometric features of a cell. The traditional cellular configurations studied are mainly focused on body-centered cubic [5], face-centered cubic [6] and their combined deformed structures [7,8]. Furthermore, configurations with certain mechanical properties, such as negative Poisson’s ratio [9,10], compression and torsion [11,12], multi-stable switching [13], and negative thermal expansion [14,15], have been designed owing to the high designability of lattice structures. However, it is necessary to design multifunctional lattice structures to ensure efficient and stable work of the mechanical system, with the diversification of engineering requirements. The design of multifunctional lattice structures has difficulties of interdisciplinary comparing with the single performance lattice structure, such as huge amount of calculation, high complexity of model establishment and solution, prominent coupling effect, etc. Hence, a systematic structural design method is needed to be developed to achieve multifunctional lattice structure.

The methods for designing lattice structures are summarized into three types, including bionic design inspired by nature, empirical design based on the deformation principle and structural optimization design using algorithms. Bionic design is an imitation of structures with specific properties and rules in nature, such that the resulting structures can reproduce these properties [16–18]. Empirical design establishes a relationship between the structural geometric parameters and the required property during structural deformation by using the mechanical equilibrium equation, and the lattice structural property can be adjusted with the help of the established relationship [19–22]. Structural optimization design involves the setting of objectives and constraints based on the optimization method and calculates the design variables iteratively by using an optimization algorithm until an optimal solution meeting the constraints is realized [23–27]. Many studies have been conducted on artificially designed lattice structures based on the principle of functional structure deformation. However, few studies have been focused on designing lattice structures using a systematic structural optimization design method. Structural optimization design is classified as topology, shape, and parameter optimization. A configuration with the optimal material distribution is generated by topology optimization in the conceptual design stage [28–30]. The mechanical properties can be further improved by detailed design of geometry shape and parameters optimization. Topology optimization has higher design freedom, more innovative configurations, and greater economic benefits. Therefore, the topology optimization is key to an innovative lattice structural design.

In recent decades, the research of topology optimization methods has attracted many scholars, the typical methods of continuum topology optimization are the homogenization method [31], evolutionary structure optimization method [32], SIMP method [33,34], phase field method [35], level set method [36–38], moving deformable component method [39], and independent continuous mapping (ICM) method [40,41]. Homogenization theory [42,43] is a common analysis method to study periodic structures. The homogenization theory generally takes the flexibility as the optimization goal, introduces the hollow cell microstructure, and takes the unit cell size as the design variable. In addition, the homogenization method determines the existence of the microstructure by the change of the cell size in the optimization process, and allows the existence of the intermediate size unit cell, so that the topology optimization model and the size optimization model are unified and continuous. However, the sensitivity calculation becomes complicated due to the existence of density and orientation variables in the optimization model. It is still difficult to establish a topology optimization model based on the homogenization theory with the object of energy absorption and phononic bandgap. And the checkerboard phenomenon is easy to appear in the process of solving the optimization model, which affects structural continuity. Hence, the cellular configuration of the lattice structure is explored via the ICM method in this work. Generally, the optimization model of the ICM method is established with the goal of lightweight structure and the constraint of mechanical performance. The independent continuous topological variables are introduced to indicate the existence or absence of material and used to approximate discrete topological variables. A filtering function is implemented to recognize the relation between the topological variables and structural mechanical performances. Then, the topology optimization model is solved via the dual sequential quadratic programming algorithm to reduce the complexity of finite element calculation [44].

The research studies on energy-absorbing lattice structures are relatively comprehensive, in terms of both configuration and material. In terms of configuration, in addition to the body-centered cubic structures [45], there also exist ring [46], Kelvin [47], diamond [48] and bionic lattice structures [49,50]. Many scholars have also analyzed the energy absorption performance of gradient lattice structures [51–53]. The development of additive manufacturing has played a role in promoting further research on lattice structures, thus facilitating the application of a variety of materials to the study of lattice structures, such as aluminum alloys [54], cobalt-chromium alloys [55], steel [56] and other metals, resins [57] and other polymer materials, and fiber-reinforced composite materials [58]. Recently, the bandgap analysis of lattice structures combined with phononic crystals has received significant attention and has become the research hotspot, which has important meanings to study the structural performance of vibration isolation, noise reduction, and wave absorption. The bandgap characteristic reflects the vibrational damping property of the structure, which prevents the propagation of elastic waves in a certain frequency domain. According to the boundary, lattice structures with phononic bandgap are divided into one-dimensional [59], two-dimensional [60,61] and three-dimensional structures [62]. Recently, the chiral structure [63,64] has been proven to not only have negative Poisson’s ratio, but also the potential to achieve band gaps due to their asymmetry. In addition, lattice structures with bandgap and other functions are designed, such as negative thermal expansion lattice structure with bandgap [65] and multi-stable lattice structure with bandgap [66].

Recently, scholars begin to pay attention to the study of multifunctional lattice structures with phonon bandgap and energy absorption. Jiang et al. [67] added elastic strut connections to the face-centered cube frame, which realized the bandgap function of the energy-absorbing lattice structure. Zhang et al. [68] designed a layered lattice structure with vibration isolation and energy absorption based on the idea of layered design. However, at present, there is no systematic optimization method to design this multifunctional lattice structure. Directly using topology optimization to obtain the final structure is the most ideal design form. However, the combination of these two properties exists in interdisciplinary problems of mechanics and acoustics in lattice structural design, which is mainly manifested in the establishment of the model and the coupling effect. The mechanical problem is to analyze the energy absorption capacity of the structure under large deformation, and the acoustic problem is to investigate the propagation characteristics of elastic waves in the structure. Hence, it is still difficult to characterize these two properties simultaneously. In addition, how to apply boundary conditions to the base structure to analyze the two properties also needs further consideration. In this study, the multifunction of the lattice structure is realized by step-by-step design. This design strategy simplifies the complex problem of two performance coupling, which also avoids the large amount of calculation and iterative non-convergence in the design process. A topology optimization model with displacement constraints is established based on the ICM method and solved to obtain a lightweight conceptual structure. The bandgap is realized by combining chiral rotation deformation and geometric parameters with better performance and is obtained by parameter optimization. The results of two performance analyses show that the design method is feasible.

This paper is composed of four sections as follows. The process of lattice structure design is described in section 2, including topology optimization, parameter optimization, and arrangement design. In section 3, the compression process of the lattice structure is analyzed, and the energy absorption capacity of two kinds of lattice structures composed of Hybrid Optimization-Cell and Kelvin cell are compared. In section 4, the phononic bandgap characteristics of lattice structures are analyzed via numerical simulations and the influence of cellular parameters on the bandgap frequency and width is discussed. Conclusions are provided in Section 5.

2. Lattice structure design

A novel structural design framework combining topology optimization and parameter optimization is proposed to design an energy absorption lattice structure with damping performance. The design process is divided into three steps, including topology optimization design, parameter optimization design, and assemble design of the cells.

2.1 Topology optimization design

The cellular configuration with energy absorption is explored by the ICM method. The design domain of the cell is a rectangle with the sizes of 14 mm × 10 mm, as shown in Figure 2(a). Aluminum alloy is a selected material with an elastic modulus of 72.4 GPa, a density of 2800 kg/m³, and Poisson’s ratio of 0.33. Symmetrical fixed constraints are applied to the midpoints on the two vertical edges of the rectangle, and a vertical downward point load F = 1000 N is imposed at the midpoints and 1/7 side lengths from the end points on the two horizontal edges. The design domain is divided into 14,000 shell elements. The structural volume is considered as the objective and two horizontal edge midpoints of the base structure are set as the displacement constraints of key nodes. The topology optimization model is established as follows:

(1) $\left\{\begin{array}{c}Findt\in E^L\\ minV=V\left(t\right)\\ \mathrm{s}.\mathrm{t}.u_j\left(t\right)\le {\bar{u}}_j\left(j=1,\dots ,J\right)\\ t_{min}\le t_i\le 1\left(i=1,\dots ,L\right)\end{array}\right.$(1)

where $t$ is the topological variable vector, $E^L$ the design variable space, and $V(t)$ the volume of the topological configuration, respectively; $u_j\left(t\right)$ the key nodal displacements, ${\bar{u}}_j$ the upper bound of the constraint value, and$J$ the number of displacement constraints of key nodes, respectively; $L$ the number of topological variables, and $t_{min}$ the lower bound of the topological variables, respectively.

In order to obtain the standard quadratic programming model of Equation (1)(1) $\left\{\begin{array}{c}Findt\in E^L\\ minV=V\left(t\right)\\ \mathrm{s}.\mathrm{t}.u_j\left(t\right)\le {\bar{u}}_j\left(j=1,\dots ,J\right)\\ t_{min}\le t_i\le 1\left(i=1,\dots ,L\right)\end{array}\right.$(1) , the explicit relationship between the objective and topology variables is established by the second-order Taylor expansion and the explicit function of constraints is obtained via the first-order Taylor expansion. Then, the standardized model is solved via using the dual sequence quadratic programming algorithm [40].

Figure 1. Iterative history of topology configuration and its structural volume ratio.

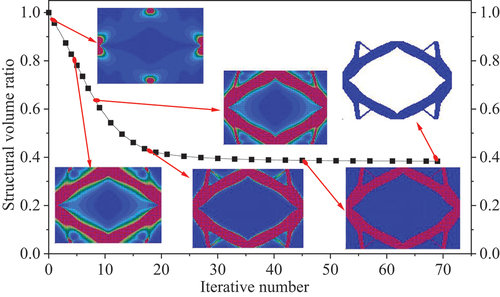
The iterative history of topology configuration and its structural volume ratio are presented in Figure 1. The topology optimization converges after 69 iteration steps. The structural volume ratio decreases rapidly at the beginning of the iteration, but the rate of decrease begins to slowdown when the iteration reaches step 10. After iteration to step 36, the volume ratio is almost unchanged, and the final value is 0.384. A highly lightweight configuration is obtained by topology optimization.

Figure 2 shows the design process of the lattice structure. A smooth topological configuration is presented in Figure 2(b). A parametric two-dimensional (2D) cell is obtained via reconstructing a geometric model of the topological configuration, as illustrated in Figure 2(c). The 2D cell is then rotated into a three-dimensional (3D) cell with reference to the chiral structure shown in Figure 2(d) to design the cell with phononic bandgap. Table 1 lists the geometric parameters of the 2D cell and its chiral structure. The conceptual design of a 3D cell named Topology Optimization-Cell (TO-C) is displayed in Figure 2(e), and the thickness of the 3D cell is determined by the chiral structure parameter δ. In addition, the parameters of TO-C are further optimized, which is described in section 2.2. The lattice structure is assembled by cells in a dodecagonal staggered layout, which is chosen in section 2.3.

Figure 2. Lattice structure design process. (a) Design domain of topology optimization; (b) Topology optimization configuration; (c) Parameterized two-dimensional cell; (d) Chiral structure; (e) Conceptual design of three-dimensional cell (Topology Optimization-Cell); (f) Detail design of three-dimensional (Hybrid Optimization-Cell); (g) Lattice structure assembled by cells.

Table 1. Geometric parameters of the 2D cell and chiral structure.

Geometric parameters
L1	4.35 mm	R1	1.5 mm
L2	9.5 mm	R2	15 mm
L3	10 mm	R3	14.5 mm
L4	4.6 mm	R4	10 mm
t1	0.6 mm	R5	8 mm
t2	0.4 mm	θ	45°
δ	0.5 mm

2.2 Parameter optimization design

The above parameterized 2D lattice structure cell is constructed via a topology optimization method and a series of deformation designs. Parameter optimization is carried out to obtain a 3D cell with better mechanical properties.

The lattice structure material is aluminum alloy 2014-T4 and the material properties are as follows: Young’s modulus of 72.4 GPa, density of 2800 kg/m³, Poisson’s ratio of 0.33, yield stress of 290 MPa, ultimate strength of 470 MPa and elongation of 10%. The constitutive model of the material is an ideal elastic-plastic model. The stress–strain relationship is linear elastic when the stress is less than the yield stress. The material yield occurs when the stress is equal to the yield stress, and the stress value remains with the increase of strain. Quasi-static compression and vibration modal analysis of the cell are implemented by the numerical simulation to study the energy absorption and frequency characteristic of TO-C. Figure 3 shows the quasi-static compression performance, vibration mode, and parameter effects of TO-C. From the load–displacement curve illustrated in Figure 3(a), the compression process includes three stages: elastic, platform, and dense stage. The displacement from 0 mm to approximately 0.9 mm occurs in the elastic stage. The load increases rapidly with the increase of displacement in this stage, and with the further compression, the rising trend of load becomes slower due to the bending of the main support rod. The displacement values from 0.9 mm to approximately 4.0 mm are in the platform stage and basically maintain a height as the displacement value increases. It begins to enter the dense stage after the displacement reaches 4.0 mm, and the load increases rapidly again as the displacement increases. A fixed constraint is imposed on the bottom of the cell, and a vibration modal analysis is performed. The vibrational mode is shown in Figure 3(b) and the cellular first-order natural frequency value is 7323.6 Hz.

Figure 3. Quasi-static compression history, vibration mode and parameters effects of TO-C. (a) Quasi-static compression load–displacement curve of cell. (b) Vibration mode. (c) Variation curve of energy absorption and first-order natural frequency with θ. (d) Variation curve of energy absorption and first-order natural frequency with R₂. (e) Variation curve of energy absorption and first-order natural frequency with R₅.

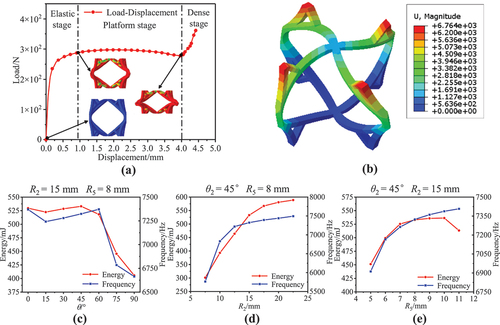
Figure 3(c)-(e) presents the effects of cellular parameters θ, R₂, and R₅ on the compressed energy absorption and first-order natural frequency, respectively. θ ranges from 0° to 90° with the spacing of 15°; R₂ ranges from 7.5 mm to 22.5 mm with a spacing of 2.5 mm; R₅ ranges from 5 mm to 11 mm with a spacing of 1 mm. It is found that the cellular energy absorption surges with the increase in R₂, increases at first with the increase in R₅, and begins to decrease after R₅ reaches the value of 10 mm. The change of energy absorption as θ is complex: it decreases when the value of θ is less than 15°, increases between 15° and 45°, and decreases rapidly when the value of θ is greater than 45°. The variation in the first-order natural frequency with θ is like that in energy absorption and increases with the increase in R₂ and R₅. In addition, the influence of θ on the two properties is less than that of the other two parameters.

When the frequency of the external load is consistent with the natural frequency, structural resonance will be induced. This situation can be avoided by increasing the cell structural natural frequency. And then, the parameters of the cell are optimized by using the response surface methodology (RSM), which is an optimization method of fitting the functional relationship between influencing factors and response values via using multiple regression equations [69,70]. The parameter optimization model is established by taking the maximum energy absorption as the objective, first-order natural frequency as the constraint:

(2) $\left\{\begin{array}{c}\mathrm{F}\mathrm{i}\mathrm{n}\mathrm{d}x\in E^T\\ max\hspace{0.17em}E(x)\\ \mathrm{s}.\mathrm{t}{f}_1(x)\ge \underset{\_}{f_1}\hspace{0.17em}\\ \hspace{0.17em}\underset{\_}{x_i}\le x_i\le \overline{x_i}\hspace{0.17em}(i=1,\dots ,T)\end{array}\right.$(2)

where x is the design variable vector, $E^T$ the design variable space, and $E\left(x\right)$ the function of the energy absorption with respect to cellular geometric parameters, respectively. $T$is the number of design variables, $f_1\left(x\right)$ the function of the first-order natural frequency with respect to cellular geometric parameters, and $\underset{\_}{f_1}$the first-order natural frequency constraint value, respectively. $\underset{\_}{x_i}$ and $\overline{x_i}$ are the lower and upper bounds of the design variables, respectively. The number of design variables $T$ is three, including the TO-C geometric parameters θ, R₂, and R₅.

Before function fitting, a certain amount of sample data needs to be prepared. Twenty sample points are randomly selected by the super-Latin cube method. The first-order natural frequency and energy absorption responses of the sample points are obtained via numerical simulations. The 20 sample points and the response values of the energy absorption and first-order natural frequency are shown in Table 2.

Table 2. Sample points and response values.

θ/°	R2/mm	R5/mm	f1/Hz	E/mJ
65.25	11.63	7.55	7086.8	434.36
78.75	12.38	5.15	6510.8	419.12
20.25	19.13	10.55	7421.3	562.652
42.75	7.88	6.95	5920.9	391.96
60.75	14.63	6.65	7267.3	488.82
15.75	9.38	8.15	6800.1	428.91
29.25	21.38	7.25	7398.3	570.71
56.25	22.13	5.75	7400.4	548.19
69.75	17.63	8.75	7480	560.63
6.75	18.38	8.45	7369.4	539.07
24.75	10.88	10.85	7119.2	417.19
87.75	8.63	9.65	6288.8	376.34
83.25	16.88	6.05	7300.4	513.06
74.25	13.13	7.85	7301.2	483.49
11.25	13.88	9.05	7247.3	494.61
33.75	16.13	9.35	7370.9	544.27
51.75	15.38	6.35	7245.6	519.5
2.25	20.63	10.25	7470.4	568.22
47.25	19.88	9.95	7492.2	569.07
38.25	10.13	5.45	6543.4	435.63

Based on the data in Table 2, the response polynomial relationship between the first-order natural frequency and absorbed energy with respect to the three parameters is obtained as follows:

(3) $\begin{array}{rl}& f_1(\theta ,R_2^{\hspace{0.17em}},R_5^{\hspace{0.17em}})=-0.001096{\theta }^3+1.988547R_2^3+21.595421R_5^3+0.279952{\theta }^2-100.234306R_2^2\\ & -530.369332R_5^2+0.991417\theta R_2^{\hspace{0.17em}}+2.167941\theta R_5^{\hspace{0.17em}}+5.419269R_2^{\hspace{0.17em}}{R}_5^{\hspace{0.17em}}\\ & -49.283053\theta +1597.448985R_2^{\hspace{0.17em}}+4125.65061R_5^{\hspace{0.17em}}-11274.235692\end{array}$(3)

(4) $\begin{array}{rl}& E(\theta ,R_2^{\hspace{0.17em}},R_5^{\hspace{0.17em}})=0.000148{\theta }^3-0.036076R_2^3+0.269733R_5^3-0.019962{\theta }^2+0.984224R_2^2\\ & -8.234241R_5^2+0.068585\theta R_2^{\hspace{0.17em}}+0.195294\theta R_5^{\hspace{0.17em}}+1.253182R_2^{\hspace{0.17em}}{R}_5^{\hspace{0.17em}}\\ & -2.019122\theta -2.448181R_2^{\hspace{0.17em}}+53.342192R_5^{\hspace{0.17em}}+265.028761\end{array}$(4)

The complex correlation coefficient $R^2$and revised complex correlation coefficient $R_{adj}^2$ are introduced to evaluate the accuracy of the fitting formula. The closer these two values are to 1, the better the fitting accuracy [71]. $R^2$and $R_{adj}^2$ of the first-order natural frequency fitting formula are 0.991 and 0.975, respectively. Furthermore, $R^2$and $R_{adj}^2$ of the energy absorption fitting formula are 0.986 and 0.961, respectively. Therefore, the response surface fitting formulas of the first-order natural frequency and energy absorption satisfy the accuracy requirements.

The surrogated model is solved by using the Non-linear Programming by the Quadratic Lagrangian (NLPQL) algorithm. The algorithm solution settings are given as follows: the initial values of the TO-C geometric parameters θ, L₂, and R₂ are [45°, 15, 8], and the first-order natural frequency constraint value is 7700 Hz. The convergent accuracy of the optimization solution is set to 1 × 10⁻⁶.

After 75 iterations, the optimal parameter combination [50.72°, 21.52, 9.79] is obtained. The cell designed through topology optimization and parameter optimization is called the Hybrid Optimization-Cell (HO-C), as shown in Figure 2(f). Table 3 presents parameter changes of TO-C and HO-C. The energy absorption increases from 533.073 mJ to 596.114 mJ with a growth rate 11.8%. The first-order natural frequency raises from 5.1% from 7323.6 Hz to 7700 Hz with a growth rate 5.1%. In addition, the natural frequency of the cell is related to its phononic bandgap. The influence is analyzed in detail in section 4.1.

Table 3. Comparison of TO-C and HO-C.

	θ/°	R2/mm	R5/mm	f1/Hz	E/mJ
TO-C	45	15	8	7323.6	533.073
HO-C	50.716	21.52	9.791	7700	596.114
Variation	12.7%	43.5%	22.4%	5.1%	11.8%

To verify the accuracy of the parameter optimization structure, the 3D cell is reconstructed and simulated using the optimized parameters. The numerical analysis results of the frequency and absorbed energy absorption are 7517.5 Hz and 595.312 mJ, with errors of 2.37% and 0.13%, respectively.

2.3 Assemble design

The lattice structural mechanical properties are not only closely related to the cells, but also affected by the interaction among them. The deformation of the cell structure along the cross direction is large during the compression process, and a suitable arrangement could ensure the normal deformation of the lattice structure during the compression process. The arranged lattice structures are named the Topology Optimization-Lattice Structure (TO-LS) and the Hybrid Optimization-Lattice Structure (HO-LS), HO-LS as shown in Figure 2(g).

Figure 4 shows three arrangements of lattice structures formed by cells. Figure 4(a) presents the TO-LS assembled by a direct linear periodic arrangement, where the red arrow indicates the direction of the large deformation of the cell. It is evident from Figure 4(d) that the transverse deformation of the four adjacent cells is concentrated in one position, which results in stress concentration of the lattice structure. The lattice structure is assembled in an octagonal staggered arrangement to avoid large deformation of adjacent cells in the same direction, as shown in Figure 4(b). Although this arrangement prevents the direct influence of adjacent cells, as compression progresses, geometric interference occurs in the transverse deformation of diagonal cells, as indicated by the black circle in Figure 4(e). Assembling cells using these two arrangements destroys the programmability of lattice structures.

Figure 4. Arrangements. (a) Linear arrangement. (b) Octagonal staggered arrangement. (c) Dodecagonal staggered arrangement. (d) the compressive deformation stress cloud diagram with linear arrangement. (e) the compressive deformation stress cloud diagram with octagonal staggered arrangement. (f) the compressive deformation stress cloud diagram with dodecagonal staggered arrangement.

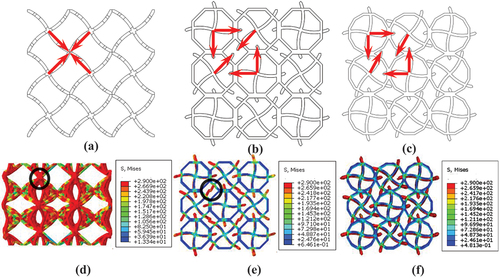
The final choice of dodecagon staggered arrangement to make cell and lattice structure satisfy certain law of energy absorption, as shown in Figure 4(c). Figure 4(f) illustrates top view of the compressive deformation stress cloud diagram and it shows that the compression deformation of each cell is no longer affected by the adjacent cells. The energy absorption performance of the single-layer lattice structure is analyzed by numerical simulations to verify the lattice structural programmability in this arrangement. When the compression ratio of the single-layer lattice structure is 20%, the energy absorption is 4890.19 mJ. Theoretically, there is a multiple relationship between the lattice structural energy absorption and cellular energy absorption, and the coefficient is the number of the cells, which is 9. Hence, the energy absorption theoretical value of the single-layer lattice structure is 4797.657 mJ, which is basically consistent with the value of numerical simulation.

3. Energy absorption property

In this section, the energy absorption property of a 3 × 3 × 3 lattice structure is discussed in the process of quasi-static compression. The deformation of the lattice structure is first analyzed by compression stress cloud diagram. Then, the optimal lattice structures are compared with Kelvin lattice structure (K-LS) [72] in the energy absorption capacity because Kelvin lattice structure has high compressive strain rate and long-stage interval of energy absorption platform.

3.1 Compression performance

The mechanical properties of HO-LS with the dodecagonal staggered arrangement are studied. Table 4 presents the front and top views of the stress cloud diagram, with a compression ratio of 10%, 20%, 30%, and 40%, respectively. From the top views, it can be found that the lattice structural stress distribution is relatively even when it is compressed, and the lattice structure layers flip slightly when the strain reaches 30%. The front views presented in Table 4 show that the deformation of each layer is almost identical during quasi-static compression.

Table 4. Top and front views of the HO-LS compression stress cloud diagram.

3.2 Comparison of energy absorption

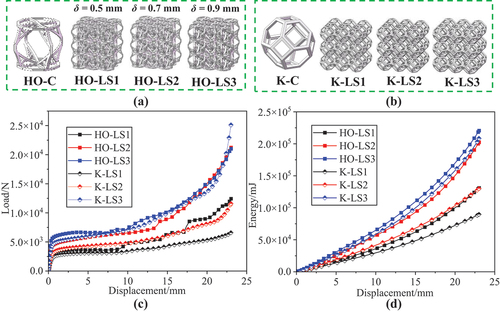
The compression-energy absorption performances of HO-LS and K-LS with different volume ratios are compared. HO-LS with different volume ratios is obtained by changing the parameter δ of HO-C. The δ values of 0.5 mm, 0.7 mm, and 0.9 mm are selected here, and the corresponding lattice structures are presented in Figure 5(a). And K-LS with the same volume ratio as HO-LS is established, as shown in Figure 5(b).

Figure 5. Compression properties of HO-LS and K-LS with different volume ratios. (a) HO-LS. (b) K-LS. (c) Compression load–displacement curve of HO-LS and K-LS. (d) Compression energy absorption curve of HO-LS and K-LS.

The mechanical properties of lattice structures under quasi-static compression of up to 80% are analyzed without considering failure, and the compression performance is characterized by load – displacement curves and energy–displacement curves.

It can be found from the load–displacement curves in Figure 5(c) that both HO-LS and KO-LS with different volume ratios have a long compression platform stage. In this stage, the height of the platform increases but the length of the platform becomes shorter with the increase in the volume ratio. The lattice structures enter the dense stage when the amount of their structural compression is approximately 30%. The rods inside the cell are toppled with the increase in displacement at this stage. Hence, the load–displacement curves show oscillation phenomenon. The energy–displacement curves are shown in Figure 5(d), where the linear part corresponds to the platform stage and the rapidly growing part corresponds to the dense stage.

In addition, the load–displacement curves show that the stiffness of HO-LS is usually greater than that of K-LS with the same volume ratio. The energydisplacement curves are more intuitive to compare the energy absorption properties of the two lattice structures, and it is obvious that the HO-LS has higher energy absorption efficiency. The results indicate that the presented lattice structural optimization design framework is effective in achieving a lattice structure with excellent energy absorption performance.

4. Bandgap property

The damping performance is evaluated using bandgap and transmission characteristics of the elastic wave propagation in the structure. The phononic bandgap properties of the designed lattice structure are verified by the energy band structure and transmission characteristic curve. In addition, the influence of cellular geometric parameters on the frequency and width is analyzed and discussed.

4.1. Bandgap and transmission analysis

Bandgap is a range of frequencies in which the propagation of elastic waves is inhibited [67]. A simplified triangular Brillouin region is presented in Figure 6(a). The designed lattice structure is anisotropic, and there are two main directions: longitudinal (loading direction) and transverse. The setting of the chiral structure by rotational deformation is used to realize the bandgap in the loading direction. Therefore, the lattice structure designed is anisotropic, and only the bandgap characteristic in the X-M direction is studied. Figure 7 shows the bandgap properties of two lattice structures (TO-LS and HO-LS). As shown in Figure 7(a),(c), TO-C has an apparent X-M bandgap between 31 kHz and 38 kHz, while HO-C has an X-M bandgap between 33 kHz and 41 kHz. HO-C has higher bandgap frequency and wider bandwidth than TO-C.

Figure 6. The region of Bloch wave vector transmission and a model of analyzing transmission characteristic (a) Illustration of the Brillouin region. (b) the beam consisting of the six cells (excited by simple harmonics at one end).

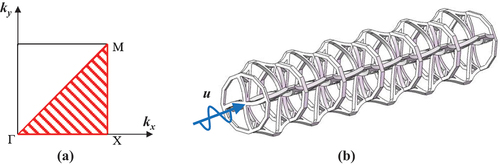
Figure 7. Bandgap and transmission characteristic. (a) X-M energy band structure diagram of TO-C. (b) Transmission characteristic curve of TO-Beam. (c) X-M energy band structure diagram of HO-C. (d) Transmission characteristic curve of HO-Beam.

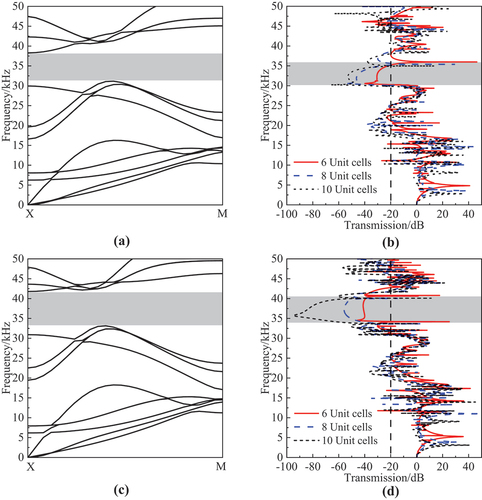
The transmission characteristic curve of the beam comprising six, eight, and ten cells along the X-M direction are analyzed to further characterize the damping property of the lattice structure in the bandgap frequency range. The beam with six cells is presented in Figure 6(b). A simple harmonic wave excitation is applied at one end of the beam, and the displacement frequency response function is obtained via finite-element calculations with different excitation frequencies:

(5) $T=20{log}_{10}(\frac{\left|A_{out}\right|}{\left|A_{in}\right|})$(5)

where $T$ is the transmission of the structure, $\left|A_{in}\right|$ the displacements of the input under excitation, and $\left|A_{out}\right|$ the displacement of the output under excitation, respectively. The transmission characteristic curves are illustrated by scanning the $T$ in the frequency range of the energy band structure diagrams, which is illustrated in Figure 7(b),(d). The broadband damping region almost completely matches the bandgap of the energy band structure diagram on considering an attenuation of −20 dB as the standard. In addition, it can be found that with the increase in the number of cells, the smaller the transmission value is, the more obvious the damping capacity is.

4.2. Parametric analysis

The comparison of the cell structural bandgap before and after the parameter optimization in 4.1 also indicates that the cell geometric parameters have an effect on the bandgap. The bandgap influence of the cellular parameters is analyzed in this section. The selected parameters are δ, θ, R₂, and R₅. The range of δ is from 0.3 mm to 0.9 mm with an interval of 0.2 mm. The values of the other three parameters and corresponding rules are the same as those of section 2.2. Figure 8 shows the influence of the cellular geometric parameters on the bandgap frequency and bandgap width.

Figure 8. Variation of bandgap frequency and bandwidth with cellular geometric parameters. (a) Bandgap frequency of TO-C varying with θ. (b) Bandgap width of TO-C varying with θ. (c) Bandgap frequency of TO-C varying with R₂. (d) Bandgap width of TO-C varying with R₂. (e) Bandgap frequency of TO-C varying with R₅. (f) Bandgap width of TO-C varying with R₅.

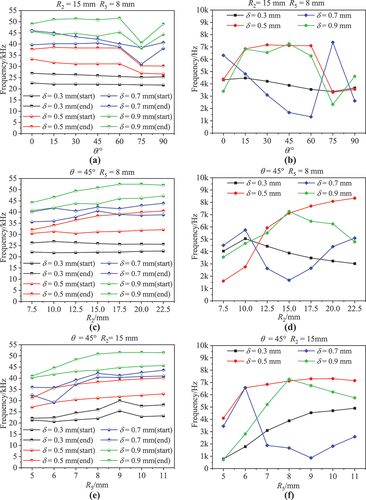
Figure 8(a) presents the influence of θ on the bandgap frequency. It is observed that a smaller value of θ has a little effect on the bandgap frequency. However, when the value of θ is 75°, the bandgap frequency exhibits an obvious downward mutation. Figure 8(c) presents the effect of R₂ on the bandgap frequency. It can be observed that the bandgap frequency grows with R₂. Similarly, the bandgap frequency also increases with R₅, as shown in Figure 8(e). From the three images, it is apparent that the bandgap frequency increases significantly with δ. However, when δ is 0.7 mm, the bandgap frequency curve of TO-C is oscillatory. The abrupt change in the bandgap frequency occurs because the specific parameter values of the cell structure could affect other parameters.

The width of the bandgap is determined by the bandgap start and end frequencies. Therefore, an abrupt change in the bandgap frequency causes a sudden change in the influence of the bandgap width parameters. Figure 8(b),(d),(f) present the effects of three parameters on the bandgap width of TO-C. It is observed that the bandgap width of TO-C for the same δ value is similarly affected by the three parameters. In addition, it is surprising that the bandgap frequency of the lattice structure is abrupt when the parameter value increases to a certain value.

5. Conclusions

This article proposes a lattice structural optimization design framework. A lattice structure with excellent energy absorption and phononic bandgap is designed by combining topology optimization, chiral rotation deformation, and parameter optimization. The design process of the lattice structure is described systematically, and its energy absorption and bandgap properties are analyzed. The main conclusions are as follows:

1. By assembling HO-C cells into a lattice structure in a dodecagonal-staggered arrangement, the energy-absorbing programmability can be guaranteed because the geometric interference among cells can be avoided when the lattice structure is compressed.

2. By comparing the energy absorption performance of HO-LS and K-LS with different volume ratios, the method combined with topology and parameter optimization is effective and feasible in designing a lattice with a good energy absorption characteristic. In addition, the platform height of load–displacement curves increases and the platform length decreases with the increase in the structure volume ratio.

3. Both HO-LS and K-LS show that the lattices designed by rotation deformation with reference to the chiral structure usually possess damping characteristics of high-frequency and wide-bandgap. The frequency range of the phononic bandgap can be adjusted by changing the geometric parameters of the cell.

This study provides a systematic method for the exploration of lightweight multifunctional lattice structure in the aerospace field. In addition, the phononic bandgap involves the frequency value and the width, which is more complicated than the natural frequency in the cell optimization design. The authors will further explore the parallel optimization design of the energy-absorbing lattice structure by adding bandgap properties to the optimization elements.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (11872080, 12202008) and the Natural Science Foundation of Beijing, China (3192005).

Disclosure statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Funding

The work was supported by the National Natural Science Foundation of China [11872080, 12202008]; Natural Science Foundation of Beijing Municipality [3192005]