Nanocomposites with auxetic nanotubes

Abstract

The effect of extreme and negative Poisson's ratio (auxetic) behavior from non-reconstructed defective (NRD) carbon nanotubes on the mechanical properties of nanocomposites is demonstrated. NRD carbon nanotubes (CNTs) produced by electronic or ion irradiation are metastable structures, which however can exist at low temperatures or when surrounded by an external medium (e.g. CNT nanoropes of matrix in a composite). The defective nanotubes were modeled using an equivalent atomistic-continuum formulation for the mechanical properties of the C–C bond that provides both the effective mechanical properties of the atomic link and the thickness of the bond itself. The defective CNTs are modeled as truss-type finite elements, with the defective atoms selected using a random Latin hypercube algorithm. The mechanical properties (Young's modulus, shear and bulk modulus, as well as Poisson's ratios) are obtained using uniaxial tensile loading simulations. The defective nanotubes not only exhibit negative Poisson's ratio (PR), but also extreme positive PR values based on the percentage of defective atoms, radius and aspect ratio of the tubes. Hashin–Shritkman bounds are used to calculate the effective properties of nanocomposites with different matrix combinations and CNT inclusions. Based on the properties of the defective CNTs, extreme values of bulk and shear modulus for the nanocomposites are recorded.

Keywords:

• carbon nanotube
• auxetic behavior
• defect
• nanocomposite

1. Introduction

The existence of negative Poisson's ratio (NPR) inclusions has been hailed as a possible way to increase the fracture resistance and toughness of nanocomposites [1]. In isotropic, homogeneous and thermodynamically stable materials, the Poisson's ratio (PR) varies between –1 and 0.5, where the higher bound corresponds to an incompressible (rubber-like) solid, while the negative limit is related to a solid with infinite shear. In anisotropic materials, the Poisson's ratios can vary beyond the above bounds, the reciprocity relation between PRs and Young's moduli being the only thermodynamic constraint for special orthotropic materials, for example [2]. The negative Poisson's ratio (NPR), or auxetic behavior, was observed experimentally in iron pyrite [3] in the first half of the 20th century, and subsequently confirmed for 69% of the cubic elemental metals and some fcc rare gas solids, when stretched along the specific [110] off-axis direction [4]. Artificially-made materials and structures exhibiting NPR behavior have been manufactured as open cell foams [5], long-fibre composites [6], microporous polymers [7] and honeycomb structures [8,9]. Current nanomechanical models predict the Poisson's ratio of single-wall carbon nanotubes (SWCNTs) varying between 0.29 and 0.16, along with the chirality of the nanostructure [10,11]. At the nanoscale level, the possibility of having carbon nanotube structures with NPR behavior has been reported by Jindal and Jindal [12] and Tao, Alderson, and Alderson [13], suggesting that weakening of the C–C bond strength and variation of its length could lead us to obtain this unusual property. Ab initio simulations from Van Lier, Vam Alsenoy, Van Doren, and Geerlings [14] have shown that marginally NPR behavior (–0.032) could be achieved in closed short (9,0) SWCNTs. Yakobson and Couchman [15] have also draw attention to the fact that NPR could be achieved in CNT bundles when an extension of an entangled mat in one direction releases a relative glide of the CNTs filaments at their crossing. Evidence of this type of in-plane negative Poisson's ratio (PR) behavior has been recently discovered in buckypapers, with mixed MWCNT–SWCNT arrays, with PR values up to –0.3 for nanotube's average orientations of 50° in the CNT sheet [16]. In this work, we point out at the extreme and auxetic Poisson's ratio behavior in non-reconstructed defective (NRD) single-walled carbon nanotubes (SWCNTs), and its impact on the overall mechanical properties of nanocomposites made with these unusual inclusions. NRD nanotubes arise due to the presence of non-reconstructed vacancies (NRV) [17]. In vacancy defects, there are only two axially orientations mutually distinguishable at 2π/3. Although metastable, the non-reconstructed SWCNT configurations can be present at low temperatures and low dose irradiation [18], as well as in configurations with dangling bonds surrounded by a polymer matrix or in MWCNTs and bundles of SWCNTs [19]. A lattice configuration similar to the one of NRVs has been hinted as a possible deformation mechanism to generate auxetic and extreme Poisson's ratio in open cell foams [20] and centrosymmetric honeycombs [21]. We simulate the mechanical behavior of the NRD carbon nanotubes using a specific atomistic-structural mechanics model for equivalent mechanical properties of the C–C bonds. Lattice finite element models representing the nanotubes are then developed, with the C–C bonds represented by beams with the equivalent mechanical properties calculated with the above approach. The impact of the NRD presence is assessed through Monte Carlo simulations (12,300 hits), providing information about the sensitivity of the mechanical properties (Young's modulus, Poisson's ratio, shear and flexural moduli) versus the CNT aspect ratio, diameter and percentage of defects over total number of atoms. The mechanical properties and their statistical distributions are then used in homogenisation techniques [22,23] to assess the change of the nanocomposite mechanical properties over the pristine configuration.

2. NRD carbon nanotubes models and results

Structural mechanics approaches have been extensively used to simulate the mechanical properties of carbon nanotubes and graphene [24,25]. Tserpes and Papanikos [26] have proposed closed-form solutions to calculate the equivalent mechanical properties for the C–C bond equating an harmonic potential (AMBER force model) with the mechanical strain energies associated to hinging, stretching and out-of-plane bending of an equivalent Euler–Bernoulli beam. The method proposed [26] yields a C–C bond thickness of 0.140 nm, for an equilibrium length of 0.142 nm, clearly outside the validity of the Euler–Bernoulli beam in terms of slenderness of the aspect ratio. We have proposed an alternative approach to calculate the equivalent mechanical properties of the C–C bond, based on a Timoshenko beam with deep shear deformation [27]. The harmonic potential expressed in terms of AMBER force field is

(1a, 1b, 1c)

where k_r , k _θ and k _τ are, respectively, the force constants related to bond stretching, bending and torsional stiffness (k_r  = 6.52 × 10⁻⁷ N nm⁻¹, k _θ = 8.76 × 10⁻¹⁰ N nm rad⁻², and k _τ = 2.78 × 10⁻¹⁰ N nm⁻¹ rad⁻²). The mechanical strain energies associated to the Timoshenko beam deformation and their equivalence with the chemical potentials are expressed in the following way:

(2a, 2b, 2c)

where Δβ and 2α are, respectively, the end beam rotation and bond angle variation, whereas ΔL is the stretch deformation of the bond. The other parameters are the equivalent isotropic mechanical properties of the bond (Young's modulus, E, and shear modulus, G), as well as the geometry of the bond beam (cross-section, A, inertia moment, I, and polar moment of inertia, J). The major difference between the previous approach [26] is the formulation of the bending strain energy (2c) in terms of shear deformation constant Φ[28], which is a function of the Poisson's ratio, ν for the equivalent material of the C–C bond. Equating the energies as per 2a–2c we obtain a nonlinear system of equations with the variables constituted by the equilibrium length L, the thickness d and the Poisson's ratio ν. For an equilibrium length of 0.142 nm and the requirement of isotropic material for the bond [G = E / 2 / (1 + ν)], the nonlinear system can be solved using a Marquardt algorithm [29]. The identified thickness for the C–C bond is 0.084 nm, with a Poisson's ratio ν = 0.0032, similar to the PR of cork [30]. The 0.084 nm value of thickness is well in line with the one provided by different MD simulations [31,27]. SWCNT models were assembled using finite element 3D structural beams equivalent to C–C bonds for different armchair configurations with chiral index n = 6, 13, 20, 27. The lengths of the carbon nanotubes were varying, with aspect ratios (tube length/diameter) of 5, 10, 15 and 20. The vacancies were simulated selecting atoms using a random Latin hypercube sampling technique, and deactivating the connected C–C bonds providing the 120° axial directions for the single defect. The defective CNTs were modeled using four different percentages of vacancies over the total number of atoms in a single carbon nanotube – 0.5%, 1.0%, 1.5% and 2.0%, providing a structure with distributed NRDs. For the uniaxial loading, the nanotubes were clamped at one end, and subjected to a uniaxial strain of 0.1% under a nonlinear geometric loading condition. The homogenised radial strain for the carbon nanotube was calculated as , where S is the surface of the tube. The Young's modulus and Poisson's ratio ν_rz were estimated using the definitions for tubular cellular structures [32]. The shear modulus was derived using the approach illustrated by Tserpes and Papanikos [26], with an imposed set of rotations and clamed DOFs at the opposite end of the nanotube. For each nanotube configuration, 200 Monte Carlo sampling of vacancies were performed, providing a total of 12,800 simulations for armchair tubes.

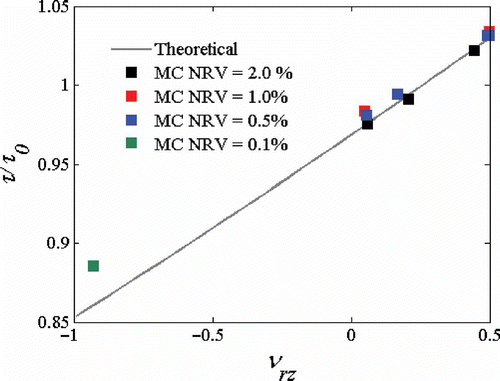
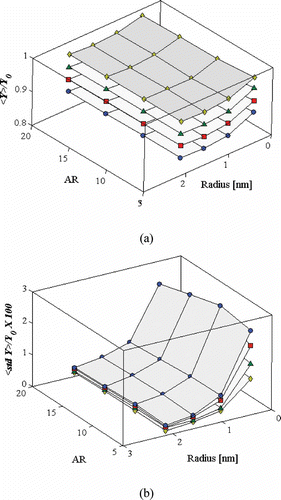
The presence of the non-reconstructed defects provides a general decrease of the Young's modulus, depending mildly on the radius and aspect ratio of the nanotubes, but strongly on the percentage of vacancies (Figure 1a). For example, in armchair tubes with aspect ratio 5, for a defects percentage of 0.5%, the mean value of the ratio between defected and pristine Young's modulus varies between 0.995 for a radius of 0.41 nm to 0.958 for a tube diameter of 3.2 nm, to slightly increase to 0.961 for a radius of 2.13 nm. Sammalkorpi et al. [17] observe a Y/Y ₀ ratio up to 0.97 in (5,5) nanotubes with triple vacancies. The ratio between the standard deviation of the Young's modulus versus Y ₀ shows dependences versus the radius R and aspect ratio (AR) of R ⁻¹ and AR ^−1/2, respectively, with values ranging from 0.01% for a vacancy percentage of 0.5, to 0.026% for a NRV percentage of 2. We have noticed that the mean of the standard deviation versus the mean of the Young's modulus is confined between a maximum of 2.7% for a radius of 0.43 nm, aspect ratio of 5 and NRV percentage of 2, to a minimum of 0.3 % for radiuses of 1.7 nm, maximum aspect ratio of 20 and vacancies percentage of 0.5 (Figure 1b). In contrast, the Poisson's ratio, ν_rz, shows large variations, depending on the tube geometry, the percentage and the location of vacancies.

Figure 1. (a) Mean Young's modulus ratio and (b) standard deviation of Young's modulus ratio for armchair (n,n). • = 2% NRV; ▪ = 1.5% NRV; ▴= 1% NRV; ◊ = 0.5% NRV.

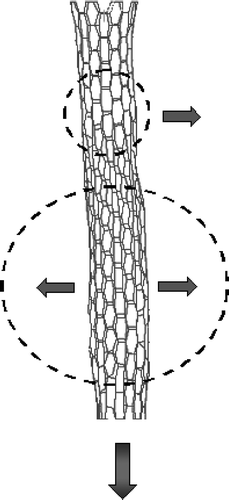
From our observations, the NPR is normally induced by defects close to the ends of the tube, and concurrently in the middle of the CNT length, as shown in Figure 2 for a (6,0) nanotube. The NRVs close to the ends provide an amplification of the Saint–Venant effects on the loading conditions, causing out-of-plane rotations of the C–C bonds connected to the vacancies, and local radial expansion of the nanotube under a positive axial strain (Figure 3). When the NRVs were located on average four to five cells away from the ends, the mechanical behaviors of the defected nanotubes were the opposite, with local radial contractions under a global positive axial strain, and therefore a positive Poisson's ratio effect.

Figure 2. Zigzag (6,0) nanotube (AR = 10, 2% NRD).

Figure 3. Auxetic (6,0) nanotube (ν = –0.932).

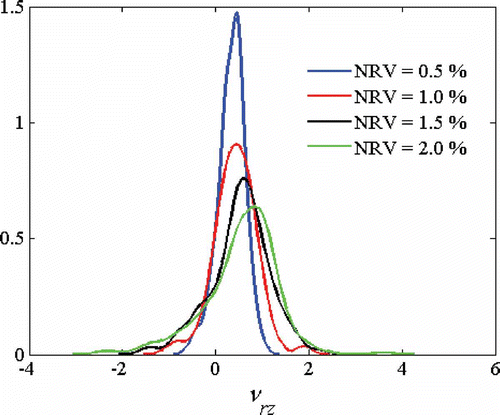
Pristine single-wall nanotubes have Poisson's ratios (ν_rz) values varying with their chirality in ranges between 0.29 to 0.16 [10,11]. The non-reconstructed defective nanotubes showed significant variations in terms of magnitude and sign, for given chirality, aspect ratio and percentage of NRVs. The probability density functions associated to the Poisson's ratio showed significant levels of skewness and, in general, a non-Gaussian distribution. For armchair tubes (6,6) and aspect ratio of 5, the mean Poisson's ratio varies between 0.22 at a NRV percentage of 0.5, to 0.59 for NRV = 2% (Figure 4). The Poisson's ratio ν_rz of the pristine nanotube is 0.29. The standard deviations (Figure 5) are significantly large, ranging from 0.66–2.14 to 3–3.6 times the mean values. With the maximum aspect ratio considered in this study (20), the probability density distributions for the Poisson's ratio show even higher average value and standard deviation discrepancies from the pristine nanotube values. The extreme Poisson's ratios recorded in these simulations make the NRD nanotubes anisotropic materials, like tubular auxetic truss structures studied previously by some of the authors, albeit with larger ν_rz values available [32]. The percentage of negative Poisson's ratios varies according to the nanotube chirality, aspect ratio and vacancy ratios. Auxetic nanotubes vary between a 12.5% for an armchair (6,6) at aspect ratio of 5 and NRV of 0.5%, to 28% for (26,26), aspect ratio 20 and NRV of 2%. The percentage of auxetic nanotubes for a given radius appears to be linearly dependent on the tube aspect ratio, and proportional to NRV ^½ for the vacancies. The mean values for the positive and negative PR values for a given tube aspect ratio appear also linearly dependent on the percentage of vacancies, as well as proportional to R ⁻¹. For the minimum vacancies ratio considered in this study, the positive mean Poisson's ratio is reported to be 1.04 for the same aspect ratio and tube radius (AR = 20 and R = 1.278 nm respectively).

Figure 4. Probability density functions for ν_rz in (n,n) tubes (R = 0.426 nm, AR = 5).

Figure 5. Distribution of the standard deviations for (n,n) configurations (pristine ν_rz between 0.29 and 0.16).

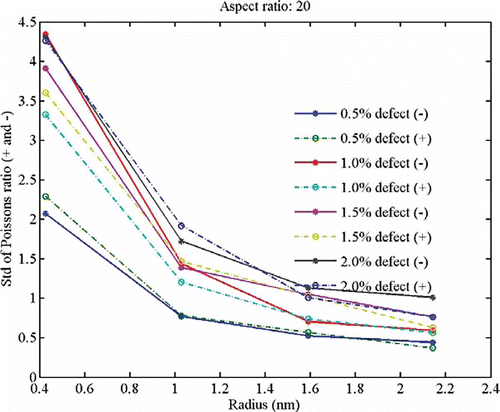
For the auxetic CNTs, the average Poisson's ratios range between –9.1 for n = 6 and NRV = 2.0% to –0.87 for n = 27 and NRV = 0.5%. The distribution of the standard deviations (Figure 4b) again follows the inverse radius dependence and linear proportionality with the vacancies percentage. The standard deviations for the auxetic nanotubes follow a similar trend, with a general decrease of 12–15% compared to the positive Poisson's ratio nanotubes.

3. Composite with NRD nanoinclusions

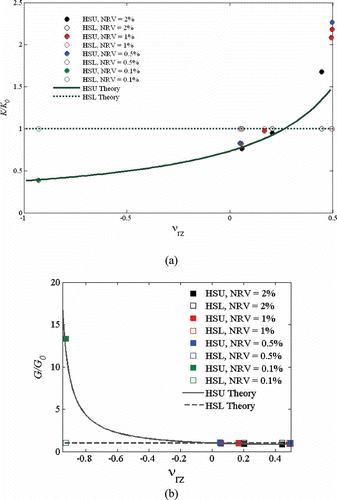
The effect of nanoinclusions on the behavior of composites is often evaluated as first approximation with the calculation of upper and lower Hashin–Shritkman bounds (HSU and HSL) [22] valid for biphase composites with circular spheres. Let us consider a nanocomposite made with pristine SWCNTs of Y = 1.71 TPa and ν_rz = 0.16 [11] embedded in an epoxy matrix (E _m = 2.5 GPa, ν_m = 0.25), with a volume fraction of 7%. As showed in the previous section, the main characteristic of the NRD nanotubes is the large fluctuation in terms of Poisson's ratio, but a fairly stable slight decrease of the axial stiffness, between 85% and 95% of the pristine nanotube value. Figures 6a and 6b show, respectively, the variation of the upper and lower bounds for the nanocomposite with different Poisson's ratios of the CNTs. The analytical HSU and HSL bounds are calculated considering a stable Young's modulus stiffness for the CNT equal to 90% of the one of the pristine tube, but varying the Poisson's ratio ν_rz between –1 and 0.5 (isotropic material interval). The analytical formulae are compared with the bounds calculated with the effective Young's modulus and Poisson's ratio from the Monte Carlo simulations, and normalised with the bounds corresponding to the pristine nanocomposite configuration. The normalised upper bound of the bulk modulus related to the simulated FE CNTs configuration (Figure 6a) follows the analytical approximation quite closely, although when the Poisson's ratio is close to the upper bound (0.5) the MC simulations provide a significant enhancement compared to the theoretical prediction. For that specific case, the HSU bound is between 2.1 and 2.3 times higher than the one of the pristine nanotube configuration of reference. The normalised bulk lower bound is unchanged compared to the base reference, showing that the presence of anomalous CNT Poisson's ratio does not affect that particular mechanical property. Also for the lower bound of the shear modulus (Figure 6b) there is no change compared to the pristine configuration, while the upper bound closely follows the analytical approximation, with a 14-fold increase of the HSU bound for a ν_rz = –0.92 compared to the base reference nanocomposite. The strong increase in the upper bound is recorded for all the auxetic (negative Poisson's ratio) CNT configurations.

Figure 6. HS bounds for the NRD nanocomposite (a) bulk modulus and (b) shear modulus.

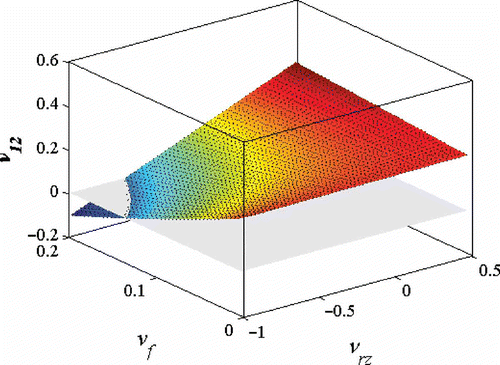
The mechanical properties of unidirectional reinforced nanocomposites can be evaluated using the Hashin–Rosen formulations [23], in particular the in-plane Poisson's ratio ν₁₂ (Figure 7). The onset of auxeticity for the whole composite starts for NRD CNTs having a Poisson's ratio of –0.6 and a volume fraction of 20%. For lower volume fractions the required negative ν_rz for the CNTs increase, with a minimum v_f  = 14% for a nanotube Poisson's ratio of –0.99. Although possible from a theoretical point of view, the likelihood of producing unidirectional auxetic nanocomposites with NRD nanotubes is low. We have observed that the percentage of auxetic configurations identified during the Monte Carlo simulations varies between 14% for aspect ratios of 5 and defect percentages of 0.1, to a maximum of 25% for the highest diameter nanotubes, highest aspect ratio and 2% of defects. The Hashin–Rosen formulations imply that the 100% of the nanotubes would be auxetic.

Figure 7. In-plane Poisson's ratio, ν₁₂, for unidirectional reinforced nanocomposites versus volume fraction and CNT Poisson's ratio.

A specific domain where the presence of auxetic fibres in reinforced composites could provide some benefit is the fibre pullout. Negative Poisson's ratio fibres show a significant increase in pullout force, as recorded in polypropylene fibres [33] and auxetic polyethylene yarns [34]. We use the nanofibre pullout model proposed by Xiao and Liao [35] modified for SWCNTs to calculate the membrane force and maximum interfacial shear stress between the surrounding matrix and the nanotube, taking as reference the nanocomposite configuration used for the HS bounds (Figure 8). For a given traction force (100 N/m) and a friction coefficient of 0.3 between nanotube and matrix [35], the maximum interfacial shear stress is increased for the extreme positive Poisson's ratio configurations (maximum 4% for the specific nanotube type considered). Alleviation of maximum shear stresses is provided for the auxetic nanotube configurations, with a theoretical decrease of 15% when considering NRD CNTs with average 10% of stiffness reduction compared to their pristine configuration. The results from the finite element Monte Carlo simulations fit the theoretical trend line well. The maximum interfacial shear stress decrease is also accompanied by the specific auxetic deformation mechanism, where the fibre tends to oppose the external force pullout by expanding radially against the matrix [33].

Figure 8. Maximum interfacial shear stress ratio during pullout of the NRD nanofibres.

4. Conclusions

In this work, we have shown a deformation mechanism leading to an auxetic (negative Poisson's ratio) behavior in single-wall carbon nanotubes. The non-reconstructed defective (NRD) nanotubes can be created by ion and/or electronic irradiation, although they have to be stabilised at low temperature and/or in a surrounding matrix. Whereas the axial stiffness is only slightly decreased and shows a Gaussian-type distribution according to the radius of the nanotube, its aspect ratio and percentage of defects, the Poisson's ratio shows large fluctuation, also beyond the internal (–1, 0.5) of the classical elasticity.

Whereas the NRD nanotubes are in general anisotropic, we focus in this study on the implication on using NRD CNTs with isotropic behavior, to evaluate the impact of this type of nanoinclusions in composites with isotropic phases. The Hashin–Shritkman bounds of composites with NRD inclusions are significantly enhanced compared to the values of the pristine nanotube reference configuration. The maximum interfacial shear stress during fibre pullout also seems to decrease for the auxetic nanotube configurations. We also show a theoretical possibility to obtain an auxetic in-plane nanocomposite with unidirectional reinforcement. Future work will focus on the assessment of the strong anisotropy of the inclusions, and identify design maps for the possible use of these interesting nanostructures.

Acknowledgments

FS acknowledges the support in CPU time from the EU FP6 STRP01364 CHISMACOMB project.