Using geographically weighted regression to solve the areal interpolation problem

Abstract

Areal interpolation is used to transfer attribute information from the initial set of source units with known values to the target units with unknown values before subsequent spatial analysis can occur. The areal units with unknown attribute information can be either at a finer scale or misaligned with respect to the source data layer. This article presents and describes a geographically weighted regression (GWR) method for solving areal interpolation problems for nested areal units and misaligned areal units. Population data, selected as the attribute information, are interpolated from census tracts to block groups (a finer scale) and pseudo-tracts (misaligned from tracts but at the same approximate scale). Root mean square error, adjusted root mean square error, and mean absolute error are calculated to evaluate the performance of the interpolation methods. The land cover data derived from Landsat Thematic Mapper Satellite Imagery with a 30×30 m spatial resolution are applied to as the ancillary data to describe the underlying distribution of population. To evaluate the utility of GWR as an areal interpolation method, the simple areal weighting method, a dasymetric method, and different ordinary least squares regression methods are used in this article as comparison methods. Results suggest that GWR is a better interpolator for the misaligned data problem than for the finer scale data problem. The latter is a result of issues associated with the scaling step to ensure the pycnophylatic property required in areal interpolation.

Keywords:

• geographically weighted regression
• areal interpolation
• spatial interpolation

1. Introduction

Geographical Information Systems (GIS) are tools for geo-registering, integrating, and analyzing spatial data from disparate sources. For a variety of reasons, individual data are often aggregated into areal units, but when data come from different sources for the same geographic domain, they often involve alternative spatial aggregations resulting in different sets of areal units. The scale of aggregation as well as the delineation of areal units at a given scale is a critical decision in all GIS applications because the results of a subsequent spatial analysis depend largely on the spatial units used. This is known as the modifiable areal unit problem (Openshaw and Taylor 1981).

In these instances, data values must then be estimated for a common geography from the available information. Areal interpolation is the process of transferring attribute values from one partitioning of space to a different one (Goodchild and Lam 1980, Lam 1983, Flowerdew and Green 1989). In a polygonal system, an attribute value can be either spatially extensive such as a count of items present or spatially extensive such as the density of items present. Given two known polygonal (or zonal) geographies, one geography is referred to as the source layer and the other as the target layer. Normally, a data value exists for the source zones but not for the target zones. The data values for the source zones are used to estimate values for the same attribute with respect to the target zones. The development of GIS has also increased the need for areal interpolation, because totally new polygons are generated by using GIS through tools such as spatial buffering and polygon overlay. The spatial attributes of the new objects, such as area and perimeter, are easily calculated within a GIS because measurement is a basic function of these systems. However, the estimation of nonspatial attributes is difficult because the underlying spatial distribution of these attributes is unknown; areal interpolation is used to reallocate the nonspatial data to newly created objects.

2. Approaches to areal interpolation

Spatial interpolation methods are divided into point interpolation methods and areal interpolation methods (Lam 1983). Point interpolation is normally used to estimate unknown values from a sample of an attribute that varies continuously over space. Point interpolators include methods such as inverse weighted distance, kriging, and trend surface analysis (Lam 1983). Areal interpolation is used to reaggregate entity data into a different areal partition of space. Although the two types of spatial interpolation solve very different geographic problems, point interpolators can also be used to reaggregating data under certain conditions as described below.

Areal interpolators are further divided into simple interpolators and intelligent interpolators. Simple areal interpolation methods refer to transferring data from source zones to target zones without using supplementary data (Okabe and Sadahiro 1997). The original simple areal interpolation is the pycnophylactic method proposed by Tobler (1979) to create a smooth density surface from a three-dimensional density polygonal prism for the purpose of isopleth mapping. Because densities are estimated for individual grid cells, Tobler noted that the method can also be used as a method to transfer variable values from source zones to target zones reaggregating the grid cells into the new spatial partition. The term pycnophylactic refers to the volume-preserving property of the method. Unlike point interpolation, areal interpolation requires that no volume of the original polygon prism is lost in the interpolation process and that none of the total count of items in the source layer is lost in the target layer. The pycnophylactic interpolation procedure using regular grids was later extended to a surface representation based on a triangulated irregular network by Rase (2001).

Another simple areal interpolation using spatially extensive attributes is areal weighting, based on the geometric overlay of the source and target zones. In areal weighting, the data value for each intersection area is in the same proportion to the data value of its associated source zone as its area is to the area of that source zone (Goodchild and Lam 1980). Spatially intensive attributes must first be converted to their spatially extensive counterparts before areal weighting is performed. Because area weighting is inherently volume preserving and can be easily implemented using polygon overlay operations, the method can be incorporated into most GIS software packages (Xie 1995) and areal weighting is widely used in practice (Langford 2006).

A third type of simple areal interpolation is based on point-based areal interpolation (Lam 1983). This approach requires intensive data, so spatially extensive attributes are first converted into density values. A control point for each source zone is identified (usually the centroid) and the density value is assigned to that point. A smooth surface of the attribute variable is interpolated to a regular grid of points using one of the different point interpolation methods (Lam 1983, Xie 1995). The density value for each grid cell is converted back to a count value and the values are reaggregated to the target layer. Lam (1983) had noted that the interpolated values depend greatly on the choice of the control point and that point-based interpolators are not volume preserving. However, the volume-preserving property can be imposed by proportionally scaling the original estimated values to match the original volume of each source zone, a practice used in many areal interpolation techniques.

In contrast to simple procedures, intelligent areal interpolation methods use some form of ancillary data related to interpolated attribute data to improve estimation accuracy (Langford et al. 1991, Langford 2006). Ancillary data are used to infer the internal structure of attribute data distribution within source zones such as land use patterns. For estimating population it is reasonable to assume that people are concentrated in residential areas or within a certain distance of roads. The estimated population of the target polygon based on its internal structure should be more accurate than that derived by a simple areal interpolation method. Exactly what ancillary information is used, and how it is used, varies from one method to another. Although any ancillary data could be used, population has often been correlated with remotely sensed data either classified in an urban/nonurban dichotomy, or classified as land use/land cover types, or individual pixel reflectance values (Wu et al. 2005). Data regarding road networks have also been used (Xie 1995, Mrozinski and Cromley 1999).

Langford (2006) has subdivided intelligent areal interpolators into dasymetric methods versus statistical methods. The term ‘dasymetric’, which means density measuring, was used by Wright (1936) to describe a method for mapping population densities when more information is known regarding the underlying distribution of population. The simplest dasymetric interpolation method is the binary dasymetric method used by Fisher and Langford (1996) to interpolate population density in western Leicestershire. They divided the necessary land use information obtained from satellite imagery into residential and nonresidential uses. A binary mask of residential pixels is overlaid against the source layer to find the number of residential pixels within each source zone, so that the population of each residential pixel can be determined proportionate to the number of residential pixels rather than the total number of pixels in a source zone as in a simple interpolation. An alternative binary method was developed by Mrozinski and Cromley (1999) in which only the area within a specified distance of a road could have population. Their method also applied an iterative smoothing operator to the pixels before estimating the population for the target areas. Xie (1995) also used network information in the areal interpolation process. Using the length of road, a road's feature class code, or the number of houses associated with the line segments of a road network as weights, Xie allocated the population to target zones. Of these weights, the one based on the feature class code provided the best estimation (Xie 1995).

Eicher and Brewer (2001) evaluated several dasymetric approaches to areal interpolation: (1) grid and polygon binary methods, (2) polygon and grid three-class methods, and (3) the limiting variable method. They found that the interpolation result using the limiting variable method, which had the lowest overall error, closely resembled the result from the three-class method, and both of these methods performed slightly better than the binary method. Langford (2006) noted that there is little evidence to suggest that intelligent interpolation methods have been widely adopted within the GIS community, despite the fact that these methods have substantial improvements in estimation accuracy compared with simple areal interpolation. He argued that this is because the polygon overlay tool is readily available in most GIS packages, encouraging the widespread use of the areal weighting method, and that areal weighting does not require the additional data resources that are needed in the intelligent methods.

In statistical methods, a functional relationship is established between the ancillary data and the values being estimated usually in the form of some type of regression. Langford et al. (1991) expressed population as a function of the pixel counts for each land cover type using ordinary least squares (OLS) regression. They proposed three models: a shotgun model, a focused model, and a simple model. In the shotgun model, the independent land cover variables included industrial, dense population, residential, unpopulated, and agriculture land cover categories. There were two logical flaws with the shotgun model. First, the regression model had an intercept, which means that even if there is no residential cover, population can still exist. Second, the estimated population can be negative. To address these problems, the focused model population was regressed with no intercept against only two land cover variables, dense population and residential. Finally in the simple model, the dense population and residential land cover categories were further aggregated to one variable, and population was then regressed on this variable with zero intercept. They found that the shotgun model has the best fit, followed by the focused model and simple model; however, the difference between the shotgun and focused model was not statistically significant.

Reibel and Agrawal (2007) used the regression interpolation methods developed by Langford et al. (1991) to estimate population in eastern Los Angeles County using the National Land Cover Dataset (NLCD) from the US Geological Survey. They divided the NLCD data into high intensity urban, low intensity, and suburban residential. Once the weight of each land cover type was obtained by using OLS regression, they used these values to generate a population surface with respect to the NLCD data layer's grid. As in most regression-based models, the estimated population in each cell must be adjusted by multiplying the ratio of its respective source zone's observed population to the source zone's estimated population to preserve the total in the target layer.

Flowerdew and Green (1989) proposed a Poisson model to interpolate count variables using ancillary binary data for target zones because this form of regression is theoretically preferable for modeling counts, and negative population estimates could be avoided. Binary variables distinguish different types of ancillary data used in the model. The Poisson parameter for each type is estimated by two separate Poisson regressions performed on the source zones and then applied to target zones for each type, respectively. If one target zone has both types of ancillary data, the expected count data would be the combination of the two parameters based on a weighting scheme.

Flowerdew and Green (1991) then improved their Poisson model by adapting the expectation and maximum-likelihood (EM) algorithm, which was originally developed by Dempster et al. (1977), to solve problems of missing data. The EM algorithm contains two iterative steps. The E-step computes the conditional expectation of the missing data given the model and observed data and the M-step fits the model by maximum likelihood to the complete dataset including the estimates made in the E-step. These steps are repeated until convergence. The EM interpolation technique loosens the restriction of binary variables for the target zone in the Poisson model to other types of variables such as multi-categorical and interval-scale variables. Flowerdew and Green (1994) later extended the EM method to deal with continuous variables having a normal distribution.

Overall, the statistical models have been found to underperform compared with dasymetric models (Fisher and Langford 1995), because the parameters on which the estimates are based are globally fitted to source zones whereas dasymetric estimates are based on local parameters. To overcome the global nature of regression, Yuan et al. (1997) developed a regional model that regressed population against land cover types in each county of their study area. The regional model outperformed the globe regression model, based on R ² values, in three of the four counties. However, Langford (2006) pointed out there is no guideline for how to divide a study area into subregions before applying a more local regression model. As administrative units, the county boundaries used by Yuan et al. (1997) are determined independently of the underlying distribution of population. Furthermore, any variation in the local model parameters between counties indicates that some spatial variation exists in the relationship between population density and land cover. Attributes such as population distribution probably exhibit spatial nonstationarity because population densities vary by urban area and within land cover types. Geographically weighted regression (GWR), developed by Fotheringham et al. (1992) to model spatially varying relationships, may be a more appropriate statistical tool for areal interpolation. The next two sections describe the data and methodology for testing GWR as an areal interpolation technique.

3. Study area and data

In this study, two types of analyses are performed on data from Hartford County, Connecticut. In 2000, Hartford County had a population of 857,183. In the first analysis, population counts for the 222 census tracts are used to estimate the population of the 666 block groups nested within the tracts. This analysis examines the problem of using areal interpolation across scales. In the second analysis, census tract population counts are used to estimate the population of an alternative geography of 193 polygons at the same scale. This analysis examines the problem of using areal interpolation for a different spatial partition at a similar scale. The alternative geography of 193 polygons was compiled by dissolving the block group layer into this new geography based on block group contiguity. The actual population of these pseudo-tracts is the sum of the population of the block groups that formed each unit. Census 2000 data were used in this study to compile both the population values and the tract and block group boundaries. The Summary File 1 count of persons was downloaded from the Connecticut Data Server at the University of Connecticut, and the geographic boundary files were acquired from the Map and Geographic Information Center (MAGIC) at the University of Connecticut.

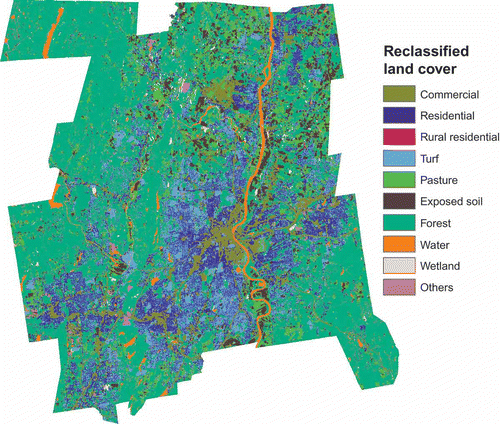
The Hartford County region is characterized by various types of land use, including residential areas with different housing densities, commercial and industrial districts, and open spaces. The population is not evenly distributed within the region. This is an important consideration when using ancillary data with the GWR model. One of the goals of this study is to determine if such a model can account for spatial variation throughout the extent of the study area. The pre-classified land cover data used in this study were derived by Civco et al. (1998) from Landsat Thematic Mapper Satellite Imagery with a 30×30 m spatial resolution. This dataset was selected over national datasets such as the NLCD because its land cover classification accuracy is higher (Civco et al. 1998). The Connecticut statewide classification was produced through the hierarchical approach. In this approach the pixels from the satellite imagery were separated into general land cover groupings based on the spectral characteristics of each land cover group. The purpose of this classification was to focus signature selection training on spectrally similar categories, thereby reducing the number of signatures and subsequent classes containing mixed land cover types. The groups belong to three broad categories: vegetation, water and wetlands, and urban and barren. Finally, selective filtering using a 3-by-3 majority filter was applied 6 different times to generate the final 28 classes in the initial land cover map (Civco et al. 1998). Land cover categories that may not be significantly different with respect to the population distribution were collapsed such that the initial land cover map was reclassified from 28 original categories into 10 final categories: (1) commercial, industrial and pavement, (2) residential, (3) rural residential, (4) turf, (5) pasture, (6) exposed soil, (7) forest, (8) water, (9) wetland, and (10) other. Figure 1 shows the spatial distribution of the reclassified land cover categories. The zonal statistical tool in ArcGIS 9.3 was then used to calculate the number of cells of each land cover type within each census geographic unit.

Figure 1. The remotely sensed land cover distribution for Hartford County.

4. Methodology

Results from GWR-based areal interpolation are evaluated against results from areal weighting interpolation, dasymetric interpolation, and OLS regression. For the dasymetric interpolation, the distribution of residential and rural residential land covers is combined as a binary control layer in which population is assumed to be located within their area. For the OLS regression method, Langford et al. (1991) indicated that three considerations influence the analysis and selection of independent variables. First, there is a conflict between a desire to maximize the fit obtained by including as many terms as possible and simple logic, which suggests that the correct form of any fitted model should only include residential land cover without an intercept term. In the latter case, the coefficient in such a model can be directly interpreted as the population density per pixel. Second, because the dependent variable (population) is count data, the interpolated results should be nonnegative. Third, although R ² can be used to indicate the global fit of a regression model, it is also important to examine the model performance based on the interpolation results.

In this study, three OLS models with different independent variables are proposed for comparison. In OLS method 1, tract population is the dependent variable and the 10 independent variables are the pixel count of the 10 land cover types at the tract level. In OLS method 2, no intercept is permitted, tract population is again the dependent variable, and the two independent variables are the pixel counts for residential and rural residential land cover at the tract level. In this model, the regression coefficients are interpreted as the density of population in each pixel of the specified land cover. Finally, in OLS method 3, no intercept is permitted, tract population is the dependent variable, and the single independent variable is the sum of pixel counts of the residential and rural residential variables at the tract level.

GWR was developed by Fotheringham et al. (1992) to handle spatial nonstationarity in functional relationships. Spatial nonstationarity indicates that the measurement of a relationship would vary if it is taken in different parts of the study area. General OLS regression assumes spatial stationarity in which the relationships are the same everywhere in the study area. OLS regression is a global model, and the estimated parameters are location independent. A typical OLS regression model is

(1)

where y is the dependent variable, X_i s are the set of the independent variables, β _i s are the estimated parameters, and ε is the residual. For spatial data, it assumes a stationary spatial process because the estimated parameters are constant everywhere. Any geographic variation in the relationships is confined to the error term.

GWR is a local statistical technique to analyze spatial variations in relationships. Assume (u,v) are the coordinates of the position of some data point in the study area. The GWR model is

(2)

GWR uses weighted least squares regression in which the weights are a function of distance from location (u,v). Weights are chosen such that those observations near the predicted point where the parameter estimates are desired have more influence on the result than observations farther away.

In this approach, the locations for predicting the regression parameters do not have to be the same as the locations of the observed data. Second, because the model assumes point information for both the observed information as well as the predicted information, it is inherently a point-based areal interpolator. As such, Lam's (1983) criticisms of point-based areal interpolation apply to GWR as well. All initial estimates are rescaled to preserve the population total at the tract level. If the data were for actual point locations, GWR could produce a continuous distribution of regression coefficients by estimating parameter values over a fine grid of (u,v) locations. This approach would be appropriate if the data represented measurement at point locations. In the case of areal interpolation, the data have been aggregated into areal units and polygon centroids are used to represent the distribution as weighted points. Second, the finer the spatial distribution of prediction points, the greater the computational burden as separate regressions are calculated at each (u,v) location. For this study, the centroids of the census tracts are used as the control points. When estimating block group populations, the regression coefficients are then predicted for both census tract centroids and block group centroids. Predicting at tract centroids assumes that the regression coefficient estimates do not vary within each tract whereas predicting at the block group centroids permits spatial variation in the regression parameters within each tract. When estimating pseudo-tract populations, the regression coefficients are then predicted for both census tract centroids and pseudo-tract centroids. Predicting at tract centroids again assumes that the regression coefficient estimates do not vary within each tract whereas predicting at the block group centroids assumes no spatial variation in the regression parameters within each pseudo-tract.

The regression coefficients are calculated and then used to estimate the population of the intersection units formed by the overlay of the source and target layers. The rescaling step is performed by summing the estimated population values for the intersection units by the tract for which they are subunits. A proportion factor is calculated by dividing the actual population of the tract by the estimated sum. Each population value for an intersection unit is then multiplied by the proportion factor.

The GWR tool in the Spatial Statistics Toolbox of ArcGIS 9.3.1 is used to estimate the GWR models and to display the results of the analysis. Using the GWR tool eliminates the need to transfer tabular data back and forth between the GIS software and the statistical package because the tool uses the native shapefile format of the geographic data files. For each analysis, a total of 12 GWR models were run. To examine the influence of the size of the neighborhood, six models were run using 50 neighbors and six were run using 120 neighbors. As neighborhood size increases, the GWR parameter estimates are more spatially similar and approach the OLS parameter estimates. When estimating block group population, six of the runs used the tract centroids for calculating the regression parameters and the other six runs used the block group centroids. When estimating pseudo-tract populations, six runs used the tract centroids and six runs used the pseudo-tract centroids for estimating the regression parameters. Finally, four GWR models used the same independent variables and an intercept term as in OLS1; four models used the two independent variables and no intercept as in OLS2, and four models used the single independent variable and no intercept as in OLS3. In naming each model, the number of neighbors precedes the term GWR, the matching OLS number follows term GWR, and TRCT, BLKG, or PTRC comes last, referencing whether tract centroids, block group centroids, or pseudo-tract centroids, respectively, were used as the prediction locations. Thus 160 GWR2 BLKG refers to the GWR model using 160 neighbors, two independent variables with no intercept, and block group centroids are the locations for predicting the regression parameters.

Finally, the accuracy of each interpolation method is measured based on three diagnostics: the root mean square (RMS) error (Fisher and Langford 1995), the adjusted root mean square (Adj-RMS) error (Gregory 2002), and the mean absolute error (MAE). The RMS error is calculated as the square root of the squared average difference between the estimated values of population versus the actual population value. The RMS error gives an overall evaluation of the global performance of the areal interpolation method. The Adj-RMS error standardizes errors for each target zone due to the variation of the value of the variables in each target zone. The MAE is calculated as the average of the absolute deviation between the estimated and actual values.

5. Results

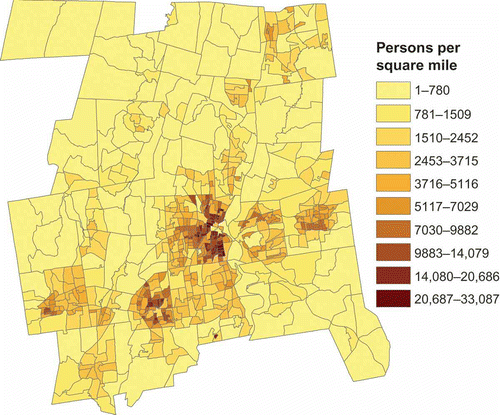
As expected the relationship between population and land cover exhibited spatial nonstationarity. Figure 2 displays the actual spatial distribution of population density. The highest densities are in the center and lower left of center of the map. Figure 3 shows the spatial distribution of the regression coefficients for the 50 GWR2 BLKG model. These coefficients represent the per pixel population density of the residential land cover in Figure 3a and of rural residential land cover in Figure 3b. The higher per pixel density values given in Figure 3a are generally located in the areas where the overall population density is highest in Figure 2. In contrast, the per pixel density values for rural residential are the highest in the lower right and the lowest in the center. In OLS2, per pixel density values are the same everywhere.

Figure 2. Spatial distribution of population density at the block group level.

Figure 3. Spatial distribution of the GWR coefficient at the block group level in the 50 GWR2 BLKG model: (a) for residential land cover; (b) for rural residential land cover.

Table 1 presents the accuracy assessment for the block group population estimates. Examining the interpolation results before the scaling step is applied (Table 1), it is clear that the parsimonious use of just one or two independent variables without an intercept gives a better initial estimation. The OLS1 and the four GWR1 models had the worst estimates among all of the models. The GWR2 and GWR3 models overall did better than their OLS2 and OLS3 counterparts. With the exception of the adjusted RMS values, the GWR estimates were more accurate than either the OLS2 estimates or the OLS3 estimates. Being able to generate local regression coefficients produced better results than one global set of coefficients. A related result was that the GWR models that used 50 neighbors usually were more accurate than their 160 neighbor counterparts. The more the neighbors, the closer the local coefficients will approximate the global coefficients. Finally, using the 222 tract centroids as the estimation points rather than the 666 block group points did not matter. Within the local areas, there was not enough difference in coefficient values to generate very different estimates. After the scaling step to achieve the pycnophylatic property was applied to the initial estimates, the results were quite different. The areal weighting and dasymetric models are now included in these comparisons because they are volume preserving by definition. Using RMS error as the accuracy metric, the OLS1 model was now the most accurate, followed by the two GWR1 models with 160 neighbors and the dasymetric model. The models with more independent variables and an intercept were better estimators in the final analysis.

Table 1. Results of the block group interpolation

	RMS	Rank	Adj-RMS	Rank	MAE	Rank
Before scaling
OLS1	1310.54	13	38.711	13	1241	12
OLS2	679.02	9	14.742	5	490	10
OLS3	679.10	10	14.993	6	489	9
50 GWR1 TRCT	1197.67	12	37.723	11	1072	11
50 GWR1 BLKG	1195.58	11	38.588	12	1282	13
160 GWR1 TRCT	1395.24	14	40.358	14	1328	14
160 GWR1 BLKG	1395.14	15	40.796	15	1328	15
50 GWR2 TRCT	616.42	2	6.554	1	356	3
50 GWR2 BLKG	614.53	1	7.751	2	356	4
160 GWR2 TRCT	656.83	6	11.784	3	352	1
160 GWR2 BLKG	656.81	5	11.977	4	352	2
50 GWR3 TRCT	621.42	4	21.090	10	445	6
50 GWR3 BLKG	620.08	3	20.259	9	443	5
160 GWR3 TRCT	663.47	7	16.683	8	474	7
160 GWR3 BLKG	663.59	8	16.664	7	474	8
After scaling
Areal weighting	562.22	17	23.666	17	407	13
Dasymetric	343.20	4	14.015	11	237	1
OLS1	335.01	1	15.390	16	249	2
OLS2	515.90	12	13.826	8	354	12
OLS3	514.95	14	14.000	10	353	9
50 GWR1 TRCT	366.26	5	12.720	6	268	5
50 GWR1 BLKG	367.24	6	12.180	5	271	6
160 GWR1 TRCT	339.61	2	14.945	14	251	3
160 GWR1 BLKG	339.81	3	15.022	15	251	4
50 GWR2 TRCT	516.40	16	5.965	1	438	15
50 GWR2 BLKG	515.36	15	6.428	2	436	14
160 GWR2 TRCT	512.84	7	10.963	3	471	16
160 GWR2 BLKG	513.26	8	10.982	4	471	17
50 GWR3 TRCT	514.60	10	14.019	12	353	7
50 GWR3 BLKG	514.57	9	12.955	7	354	10
160 GWR3 TRCT	514.64	11	14.020	13	353	8
160 GWR3 BLKG	514.98	13	13.904	9	354	11
Note: RMS, root mean square; MAE, mean absolute error.

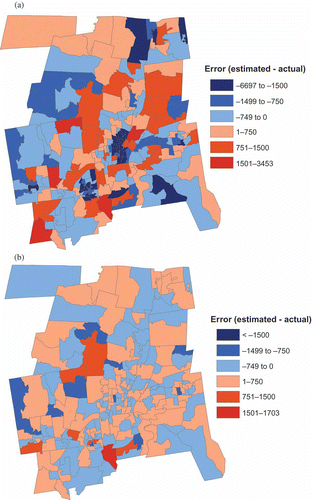
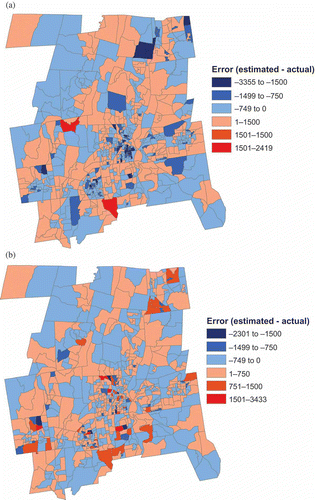
To understand why this reversal of fit occurred, it is necessary to examine the spatial distribution of the error associated with the initial estimates. There are two types of error: overestimation and underestimation. The best estimator before scaling was the 50 GWR2 BLKG model. The spatial distribution of its errors presented in Figure 4a is balanced between error associated with overestimation and underestimation. Most tracts have both overestimated values as well as underestimated values. In summing the block group values within a tract together, these errors would tend to cancel each other out and the tract level error would be less than the magnitude of the error at the block group level. Second, some block group estimates would be made worse by the scaling. Suppose that the total population of a tract was initially overestimated. Each initial block group estimate would be multiplied by a number less than one so that the new sum of block group populations would match the tract population. Any block group that was initially underestimated would now be even more underestimated. In Figure 4b, most block groups improved in the magnitude of their error but some had greater error than before. In addition, because there was more underestimation than overestimation initially, the range of the underestimation decreased from (–3355,0) to (–2301,0). Conversely, the range of the overestimation increased from (0,2419) to (0,3433).

Figure 4. Spatial distribution of error by block group for the 50 GWR2 BLKG model (a) before scaling, (b) after scaling.

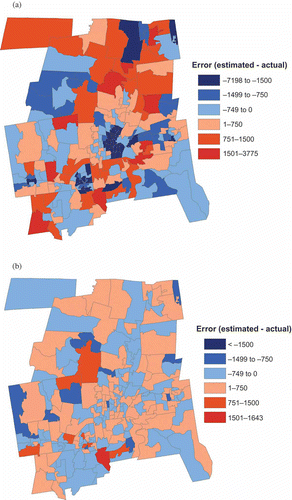
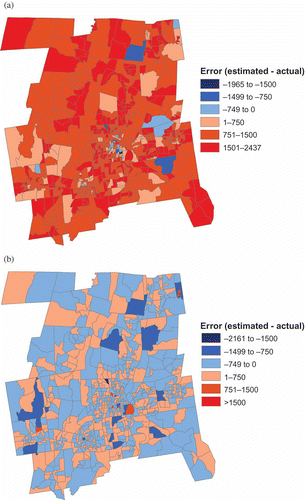
On the other hand, the OLS1 model was one of the worst estimators initially. However, the spatial distribution of its initial error (Figure 5a) shows that the population of most block groups is overestimated so that all block groups within most of the tracts have the same type of error: overestimation. In summing the block group values within a tract together, the sum of errors at the block group level would be the same magnitude as the tract level error. Second, the magnitude of the error for all block groups within each tract having the same type of error would be improved because they are all scaled in the same direction. In the case of only overestimation error, the block group values would all be reduced. Some of the previously overestimated block groups may now be underestimated as can be seen by comparing Figure 5a with b, but the magnitude of the final error would not be greater than before. In Figure 5b no block group is overestimated by more than 1500 people, whereas most block groups in Figure 5a belong in that map class.

Figure 5. Spatial distribution of error by block group for the OLS1 model (a) before scaling, (b) after scaling.

The results of the alternative geography interpolation were somewhat the same but also very different. The pseudo-tract layer was overlaid against the tract layer and the estimations were made for the 444 intersection polygons. The various areal interpolation methods were used to first estimate the population of these polygons which were then summed to the pseudo-tract level. The accuracy statistics were then applied to these initial estimates (Table 2). Before the scaling step is applied, the use of just one or two independent variables without an intercept again gives a better initial estimation. The OLS1 and four GWR1 models again had the worst estimates among all of the models. The GWR2 and GWR3 models again did better than their OLS1 and OLS2 counterparts and the GWR models that used 50 neighbors were more accurate than their 160 neighbor counterparts. Finally, using the tract centroids as the estimation points rather than the pseudo-tract centroids did matter this time. Holding other factors constant, using the pseudo-tract centroids produced more accurate results.

Table 2. Results of pseudo-tract interpolation

	RMS	Rank	Adj-RMS	Rank	MAE	Rank
Before scaling
OLS1	2530.80	13	0.740	13	2281	13
OLS2	1774.31	9	0.352	9	1225	9
OLS3	1777.05	10	0.353	10	1226	10
50 GWR1 TRCT	2248.56	12	0.658	12	1939	12
50 GWR1 PTRC	2229.40	11	0.657	11	1926	11
160 GWR1 TRCT	2678.01	15	0.784	15	2450	15
160 GWR1 PTRC	2674.72	14	0.783	14	2448	14
50 GWR2 TRCT	1445.73	3	0.295	3	984	3
50 GWR2 PTRC	1436.43	2	0.294	2	975	1
160 GWR2 TRCT	1642.93	6	0.325	6	1107	6
160 GWR2 PTRC	1641.56	5	0.325	5	1105	5
50 GWR3 TRCT	1445.96	4	0.296	4	991	4
50 GWR3 PTRC	1434.79	1	0.294	1	982	2
160 GWR3 TRCT	1685.50	8	0.335	8	1131	8
160 GWR3 PTRC	1684.50	7	0.334	7	1130	7
After scaling
Areal weighting	951.94	17	0.247	17	703	17
Dasymetric	485.56	5	0.131	5	380	7
OLS1	661.38	12	0.167	12	521	12
OLS2	484.89	3	0.131	3	380	5
OLS3	485.56	6	0.131	6	380	8
50 GWR1 TRCT	709.86	15	0.174	15	543	15
50 GWR1 PTRC	723.42	16	0.180	16	554	16
160 GWR1 TRCT	675.39	14	0.170	14	530	14
160 GWR1 PTRC	675.00	13	0.170	13	528	13
50 GWR2 TRCT	487.11	9	0.132	9	376	3
50 GWR2 PTRC	485.62	8	0.132	8	379	4
160 GWR2 TRCT	476.52	1	0.129	1	373	1
160 GWR2 PTRC	478.17	2	0.130	2	374	2
50 GWR3 TRCT	485.61	7	0.131	7	381	9
50 GWR3 PTRC	487.57	10	0.132	10	385	11
160 GWR3 TRCT	485.52	4	0.131	4	380	6
160 GWR3 PTRC	489.07	11	0.132	11	382	10
Note: RMS, root mean square; MAE, mean absolute error.

The largest change in results from the first analysis came after the scaling step was applied. The 160 GWR2 TRCT model ranked first in each accuracy measurement but it only moved from 6th best whereas in the block group analysis the OLS1 went from 13th to 1st. Neither the OLS1 models nor the GWR1 models improved their relative ranking as they did in the block group estimation and areal weighting was again the worst. In general, all of the GWR2 and GWR3 models performed about the same, with their RMS errors ranging from 477 to 489. The spatial distribution of the estimation error before and after scaling was the reason for the lack of a major change. The error map for the 50 GWR3 PTRC model with the best RMS error before scaling (Figure 6a) is again balanced between error associated with overestimation and underestimation but is somewhat more clustered than before. After scaling, every pseudo-tract improved in its accuracy (Figure 6b). The 160 GWR2 TRCT model, the most accurate after scaling, also had a balance between error associated with overestimation and underestimation before scaling (Figure 7a) but these errors were more severe than for the 50 GWR3 PTRC model. After scaling (Figure 7b), however, there were fewer extreme errors and most pseudo-tracts fell into the classes closer to zero error (–749 to 0 and 1 to 750). These differences from the earlier analysis are probably the result of the fact that while the estimations were done at the intersection polygon level, these estimates were then summed to the pseudo-tract level before the accuracy measures were calculated. In the misaligned data problem, the lack of a scale change greatly influences the results after the scaling step.

Figure 6. Spatial distribution of error by pseudo-tract for the 50 GWR3 PTRC model (a) before scaling, (b) after scaling.

Figure 7. Spatial distribution of error by pseudo-tract for the 160 GWR2 PTRC model (a) before scaling, (b) after scaling.

6. Conclusions

GWR is a suitable technique for areal interpolation. Among the statistical approaches, it has the potential to replace global estimators such as OLS regression. However, as a point-based interpolator it is somewhat susceptible to the choice of the center point locations of both the control points and the predicted points. A more important problem is that it is not a volume-preserving interpolator without the addition of a scaling step. When calculating values for an alternative geography, the scaling step is not as much of a problem because the values estimated at the finer level of intersection polygons are then summed together cancelling out overestimations and underestimations. However, when estimating values for a different scale, its higher accuracy in local estimates can work against estimate improvement following the scaling step. Because the initial values are more balanced in the amount of overestimation versus underestimation, the magnitude of the error at the finer scale is greater than the level of error used by the scaling step and some estimates are worse than their initial value. Future research into using GWR as an areal interpolator should focus on incorporating the pycnophylatic property either directly into GWR or developing an alternative to simple proportional scaling for ensuring that the original population count is preserved by the interpolator.