Local ordered weighted averaging in GIS-based multicriteria analysis

Abstract

The Ordered Weighted Averaging (OWA) is a multicriteria combination procedure. An underlying assumption of the conventional or global OWA model is the spatial homogeneity of its parameters. This paper presents a spatially explicit or local form of OWA. The local model is based on the range sensitivity principle, which suggests that criterion weights depend on spatially variable range of criterion values. The local GIS-OWA procedure is used in a case study of evaluating socio-economic status in London, Ontario. The case study compares the global and local GIS-OWA methods. While the results of conventional GIS-OWA are essentially unmappable (with exception of the overall OWA scores), the results of local OWA modelling can be mapped and examined with GIS.

Keywords:

• GIS
• multicriteria analysis
• local ordered weighted averaging

1. Introduction

GIS-based multicriteria analysis is a set of procedures for combining criterion maps and preferences with respect to the relative importance of criteria (Carver 1991; Malczewski 1999, 2006a; Chakhar and Mousseau 2008; Greene et al. 2011). The Ordered Weighted Averaging (OWA) is a class of multicriteria combination procedures (Yager 1988). It includes the most often used GIS-based map combination models: the Weighted Linear Combination (WLC) and Boolean overlay operators such as intersection (AND) and union (OR) (Jiang and Eastman 2000). The GIS-based OWA method is often employed for analysing land-use suitability (e.g., Eastman 1997; Jiang and Eastman 2000; Malczewski 2006b, Taleai et al. 2007; Boroushaki and Malczewski 2008; Chen, Khan, and Paydar 2010; Rajabi, Mansourian, and Talei 2011). The use of GIS-OWA has been demonstrated in a variety of socio-economic applications including residential-quantity evaluation (e.g., Malczewski and Rinner 2005; Stimson et al. 2006), health-care research (Clements, Pfeiffer, and Martin 2006; Bell, Schuurman, and Hayes 2007), and tourism (Rinner and Malczewski 2002; Rinner and Raubal 2004). GIS-OWA has also been applied in a wide variety of environmental study domains such as: environmental monitoring (Carrara et al. 2008), conservation planning (Malczewski et al. 2003; Thackrah et al. 2004; Valente and Vettorazzi 2008), landslide-hazard management (Gorsevski, Jankowski, and Gessler 2006; Feizizadeh, Blaschke, and Nazmfar, forthcoming; Feizizadeh and Blaschke 2013), earthquake-hazard vulnerability (Rashed and Weeks 2003), water-resource management (Makropoulos and Butler 2006; Makropoulos et al. 2007; Chen and Paydar 2012; Zhou, Xu, and Shi 2012), seismic-risk assessment (Martins, e Silva, and Cabral 2012), geological-favourability evaluation (Araújo and Macedo 2002), and landfill location (Gemitzi et al. 2006; Gorsevski et al. 2012).

There are three main input components of GIS-OWA: (1) criterion or attribute maps (and associated value functions or standardization procedures), (2) criterion weights (and associated procedures for defining preferences with respect to relative importance of criteria), and (3) order weights (and associated degree of ORness of the OWA operator). These components can be incorporated into GIS-OWA to make the OWA operators spatially implicit or explicit. Accordingly, the GIS-OWA approaches can be categorized into two groups. The first group of methods uses the conventional (spatially implicit) OWA operators to process geospatial data and to combine the data with agent’s (decision maker’s) preferences (e.g., Jiang and Eastman 2000; Malczewski et al. 2003; Rashed and Weeks 2003; Bell, Schuurman, and Hayes 2007). This type of research does not take into account the fact that the agent’s preferences can vary from one location to another. Unless a geographical space is uniform, every location has some degree of uniqueness relative to the other locations. Spatial heterogeneity implies that the agent’s preferences estimated for an entire study area may not adequately describe the preferences at any given location within that area (Feick and Hall 2004; Ligmann-Zielinska and Jankowski 2008, 2012; Malczewski 2011).

The second group of GIS-OWA approaches is based on the assumption of heterogeneous agent’s preferences. A very little research has been done in this area of GIS-OWA applications. Makropoulos and Butler (2006) developed a spatially explicit GIS-OWA model, termed spatial OWA (SOWA), by making one of the OWA parameters spatially variable. Specifically, the spatially heterogeneous preferences were operationalized using the concept of spatially variable order weights (and associated measures of ORness). This implies that different types of OWA can be applied to different locations depending on their characteristics (Makropoulos and Butler 2006; Makropoulos et al. 2007).

The procedure proposed in this paper falls into the second category of GIS-OWA methods. It uses the range sensitively principle (Malczewski 2011) as a central concept for developing the local form of OWA. The principle suggests that the criterion weights depend on the range of criterion values: a criterion that has a large range of values should be given relatively greater weight than a criterion characterized by a small range of values (Keeney and Raiffa 1976). The spatial heterogeneity of criterion weights is operationalized by introducing the concept of neighbourhood to the criterion-weighting procedure. Specifically, the criterion weights are determined based on the local (or neighbourhood) range of criterion values.

The remainder of the paper is organized as follows: Section 2 defines the conventional or global GIS-OWA operator and discusses the three main components of the model. Section 3 presents the local form of GIS-OWA. A case study of evaluating socio-economic status of neighbourhoods is presented in Section 4.

2. Global OWA

2.1. Definition

For a given set of criteria maps, OWA is a map combination procedure that associates with the maps of two types of weights: a set of criteria weights, w₁, w₂,…,w_n, (0 ≤ w_k ≤ 1, and , k = 1,2,…,n), and a set of order weights λ₁, λ₂, …, λ_n (0 ≤ λ_k ≤ 1, and ). Given the set of attribute values a_i1, a_i2, …, a_in at the i-th location (i = 1,2, …, m), OWA can be defined as follows (Yagger 1988; Malczewski 2006b):

(1)

where OWA_i is the overall value (evaluation score) of the i-th location, s_i, or the (x_i, y_i) coordinates (for the sake of simplicity a single subscript, i, is used to indicate the i-th location); and u_k is the criterion weight, w_k, (see Section 2.3) reordered according to the attribute value, z_ik ; z_i1 ≥ z_i2 ≥ …≥ z_in is the sequence obtained by reordering of the standardized attribute values by means of a value function; that is, for the k-th criterion the attributes, a_1k, a_2k, …, a_mk are transformed to v_k(a₁), v_k(a₂), …, v_k(a_m) using a value function approach (see Section 2.2). The reordering procedure associates an order weight, λ_k, with a particular ordered ‘position’ of the attribute values a_i1, a_i2,…, a_in. The first-order weight, λ₁, is assigned to the maximum attribute value for the i-th location; λ₂ is associated with the next smaller value for the same location, and so on; λ_n is assigned to the smallest attribute value (see Section 2.4).

Equation (1) can be recognized as the conventional WLC with modified criterion weights (Malczewski 2000). The weights are obtained by multiplying the criterion weights by the order weights. For example, given a set of criterion values at the i-th location on the k-th criterion, v_k(a_i) = (0.1, 0.8, 1.0, 0.4), a set of order weights, λ_k = 0.25 for all k, and the following set of criteria weights, w_k = (0.2, 0.4, 0.3, 0.1),  = 0.68 (see Table 1).

Table 1. Example: computing OWA.

k	Criterion values vk(ai)	Criterion weights wk	Ordered criterion values zik	Reordered criterion weights uk	Order weights λk	λk uk	λk uk zik
1	0.1	0.2	1.0	0.3	0.25	0.075	0.075	0.30
2	0.8	0.4	0.8	0.4	0.25	0.100	0.080	0.32
3	1.0	0.3	0.4	0.1	0.25	0.025	0.010	0.04
4	0.4	0.1	0.1	0.2	0.25	0.050	0.005	0.02
Σ						0.250		0.68

With different sets of order weights, one can generate a wide range of OWA operators including the most often used GIS-base map combination procedures: the WLC model and Boolean overlay AND and OR operators (Yager 1988; Jiang and Eastman 2000). The AND and OR operators represent the extreme cases of OWA and they correspond to the MIN and MAX operators, respectively. The order weights associated with the MIN operator are: λ_n = 1, and λ_k = 0 for all other weights. Given the order weights, OWA_i(MIN) = MIN_k{v₁(a_i), v₂(a_i), …, v_n(a_i)}. The following weights are associated with the MAX operator: λ₁ = 1, and λ_k = 0 for all other weights, and consequently OWA_i(MAX) = MAX_k{v₁(a_i), v₂(a_i), …, v_n(a_i)}. For the computational example in Table 1, OWA_i(MIN) = 0.1 and OWA_i(MAX) = 1.0. Assigning equal order weights (that is, for k = 1, 2, …, n) results in the conventional WLC, which is situated at the mid-point on the continuum ranging from the MIN to MAX operators (Yager 1988). Thus, One can verify that the conventional WLC_i = (0.1 × 0.2) + (0.8  × 0.4) + (1.0 × 0.3) + (0.4 × 0.1) = 0.68.

2.2. Value function

The value function, v_k(a_i), is a representation of the agent’s preferences. It converts different levels of the k-th attribute into value scores measured on a scale from 0 to 1. Given the level of the k-th attribute for the i-th alternative, a_ik, the value function, v_k(a_i), is the worth or desirability of that alternative with respect to that criterion. There are a number of techniques for assessing value function (Keeney and Raiffa 1976; Hwang and Yoon 1981; Massam 1988; Malczewski 1999). The most often used GIS-based approach is the score-range procedure. This method transforms the criterion values into normalized (value) scores, v_k(a_i), as follows:

(2)

where and are the minimum and maximum criterion values for the k-th criterion, respectively, and is the range of the k-th criterion values; r_k > 0. The standardized score values, v_k(a_i), range from 0 to 1, with 0 is the value of the least-desirable outcome and 1 is the most-desirable score. Since the range in Equation (2) is defined for the whole study area, the r_k value is referred to as the global range. Consequently, v_k(a_i) is the global value function.

2.3. Criterion weights

There are a number of methods for estimating the criterion weights (Hwang and Yoon 1981; Massam 1988; Malczewski 1999; Raphael 1996). Irrespective of the method, the resulting weights should account for: (1) the changes in the range of variation for each evaluation criterion, and (2) the different degrees of importance being attached to these ranges of variation; that is, the difference between the maximum and minimum values for a given criterion (Keeney and Raiffa 1976; Hwang and Yoon 1981; Hobbs and Meier 2000). The significance of these requirements is that the criterion weights are related to the corresponding value functions. To demonstrate the relationships between the criterion weights and ranges, let us consider two locations, s₁ and s₂, evaluated by means of two criteria to be maximized; that is, s₁ = {a₁₁, a₁₂} and s₂ = {a₂₁, a₂₂}. If one is indifferent between the two decision alternatives, then for an additive value function (e.g., OWA_i(WLC)) the overall value of s₁ should be the same as the value of s₂ (Hobbs and Meier 2000); that is,

(3)

Using the definition of value function in Equations (2) and (3) is rewritten as follows:

(4)

After some algebra, we obtain:

(5)

and

(6)

Thus, the relationship between the criterion weights (the trade-off between criteria) is a function of the criterion ranges. Notice also that the concept of global criterion weight (and trade-off) makes an assumption about uniformity of preferences over whole study area irrespectively of the spatial heterogeneity that can be present due to social, economic, political, environmental, or other contextual factors.

2.4. Order weights

The generality of OWA is related to its capability to implement a wide range of combination operators by selecting appropriate order weights (Yager 1988; Jiang and Eastman 2000). Therefore, a key issue associated with using OWA is the method for defining the order weights. Several methods have been suggested in the literature (for an overview see Grabisch, Orlovski, and Yager 1998). Here, we will focus on the maximum entropy approach. O’Hagan (1990) argues that Shannon’s theory of communication (Shannon and Weaver 1949) provides a sound theoretical base for computing the optimal OWA weights. He suggests that the approach for determining the weights should be related to the degree of ORness and the measure of dispersion (entropy). The measure of ORness is defined as follows (Yager 1988):

(7)

The value of α ranges from 0 to 1. It measures the degree to which an OWA operator is similar to the logical OR (or MAX) operator. α = 0 for λ_k = 1 and all other weights are equal to 0; the value of α = 0.5 for λ_k = n⁻¹; and α = 1 for λ_n = 1 and all other λ_k weights are equal to 0.

The OWA operators can also be characterized by the dispersion measure (O’Hagan 1990). The normalized form of the dispersion measure is defined as follows:

(8)

The φ value is a measure of the order weight dispersion. It ranges from 0 to 1; φ = 0 for λ_k = 1 and all other weights are equal to 0; the value of φ  = 1 for λ_k = n⁻¹ for k = 1, 2,…, n.

The set of order weights is obtained by solving the following non-linear mathematical programming problem:

(9)

subject to:

(10)

The solutions to the problems (9) and (10) result in a set of order weights that maximizes the level of dispersion.

3. Local form of OWA

In the global OWA model (Equation (1)), a criterion weight, w_k, is intricately related to corresponding value function, v_k(a_i) (see Section 2.3). Specifically, to meaningfully estimate of the weight requires that at least the range of criterion values is specified (Keeney and Raiffa 1976; Hwang and Yoon 1981). The interrelated concepts of the criterion range (value function) and criterion weight provide the foundation for developing the local form of OWA. The relationship is encapsulated in the range sensitive principle (e.g., Keeney and Raiffa 1976; Fischer 1995). The principle suggests that, other things being equal, the greater the range of values for the k-th criterion, the grater the weight, w_k, should be assigned to that criterion (e.g., Fischer 1995). Thus, the criterion weights vary as a function of the range of criterion values, r_k. The local criterion value range is defined as follows:

(11)

where r_kq > 0, and and are the minimum and maximum values of the k-th criterion in the q-th subset of locations (neighbourhood), respectively (q = 1, 2, …, g). Thus, the local OWA modelling requires that a given study area be divided into neighbourhoods (zones or regions). This study uses the concept of moving window with a specified threshold distance for defining a neighbourhood (see Section 4.1). Given the q-th neighbourhood, the local form of OWA is defined as follows:

(12)

where OWA_iq is the overall value of the i-th alternative estimated locally (in the q-th neighbourhood); λ_k, is the order weight associated with the k-th criterion; z_i1q ≥ z_i2q ≥ …≥ z_inq is the sequence obtained by reordering of the standardized attribute values measured by means of the local value function v_k(a_iq) (see Equation (14)); and u_kq is the local criterion weight, w_kq, reordered according to the attribute value, z_ikq. The local criterion weight, w_kq, for the k-th criterion is defined as a function of the global weight, w_k, the global range, r_k, and the local range, r_kq. Specifically, the normalized form of the criterion weight is defined by:

(13)

where is the unnormalized local weight value of the k-th criterion in the q-th neighbourhood.

The local value function, v_k(a_iq), converts different levels of the k-th attribute associated with the i-th location in the q-th neighbourhood. It transforms the attribute values into standardized scores as follows:

(14)

where and are the minimum and maximum criterion values for the k-th criterion in the q-th neighbourhood, respectively; and r_kq is the local range (see Equation (11)). The standardized values of v_k(a_iq) range from 0 to 1, with 0 being the value of the least-desirable outcome and 1 is the value assigned to the most-desirable alternative in the q-th neighbourhood.

4. Case study: socio-economic status of neighbourhoods

The aim of this case study is to demonstrate the use of global and local OWA methods for evaluating socio-economic status of neighbourhoods. The study area is the City of London, Ontario. The problem of evaluating socio-economic conditions of residential neighbourhoods (and related problem of measuring quality of life or residential quality) provides a good example of a situation in which one has to combine a number of evaluation criteria (indicators) to obtain a composite measure of socio-economic status. Many studies rely on multivariate statistics and/or multicriteria evaluation procedures (e.g., Can 1992; Raphael 1996, CUISR (Community-University Institute for Social Research) 2000; FCM 2001; Massam 2002; Malczewski and Rinner 2005). The Federation of Canadian Municipalities (FCM) provides a reporting system to monitor the quality of life in Canadian municipalities (FCM (Federation of Canadian Municipalities) 1999, FCM (Federation of Canadian Municipalities) 2001). The project is known as the quality of life reporting system (QOLRS). The selection of evaluation criteria for this case study of assessing socio-economic status in London is based on QOLRS. The set of criteria includes: a_i1 = median household income ($), a_i2 = incidence of low income (% of population 15 years and over), a_i3 = employment rate (% population 15 years and over), a_i4 = average value of dwelling ($), a_i5 = university education (% population 15 years and over), and a_i6 = residential burglary (relative risk ratio). The census dissemination area is the basic unit of the analysis (Statistics Canada 2006). There are 494 census dissemination areas within the study area; thus, i = 1, 2,…, 494.

4.1. The input parameters for local OWA

The local form of OWA model requires the following inputs: global criterion weights, w_k, and order weights, λ_k, and the neighbourhood schemes. The global criterion weights, w_k, were defined using the pairwise comparison method (Saaty 1980; Malczewski 1999). A selection of several hypothetical scenarios of pairwise comparisons was considered (see Liu 2013). This study focuses on one of the scenarios, which resulted in the following set of global criterion weights: w₁ = 0.25, w₂ = 0.18, w₃ = 0.15, w₄ = 0.14, w₅ = 0.13, and w₆ = 0.14.

The order weights, λ_k, were obtained by solving the mathematical programming problem (9), and (10) for a given value of α and n = 6 (the number of criteria maps) using LINDO package (LINDO 2012). One can obtain a vast number of sets of order weights (map combination operators) by varying the parameter α. Each set of weights is associated with an optimal (maximum) value of dispersion. Table 2 shows the results for selected values of α.

Table 2. Optimal order weights (λ_k) for selected values of the α parameter and the number of criteria n = 6.

α	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
λ1	0.000	0.003	0.021	0.054	0.003	0.167	0.497	0.347	0.478	0.664	1.000
λ2	0.000	0.009	0.039	0.079	0.075	0.167	0.241	0.240	0.255	0.224	0.000
λ3	0.000	0.025	0.072	0.114	0.075	0.167	0.109	0.165	0.136	0.075	0.000
λ4	0.000	0.075	0.136	0.165	0.109	0.167	0.075	0.114	0.072	0.025	0.000
λ5	0.000	0.224	0.255	0.240	0.241	0.167	0.075	0.079	0.039	0.009	0.000
λ6	1.000	0.664	0.478	0.347	0.497	0.167	0.003	0.054	0.021	0.003	0.000
φ	0.000	0.532	0.763	0.901	0.970	1.000	0.970	0.901	0.763	0.532	0.000

In this case study, the q-th neighbourhood is defined using the concept of moving windows (O’Sullivan and Unwin 2010). It consists of a focal location (census dissemination area) and locations (areas) in its vicinity. The i-th location is the focal alternative and the set of neighbouring locations defined by the (x_j, y_j) coordinates (j = 1, 2,…, p; p < m). There are many methods for defining the shape and size of moving windows (Lloyd 2010; O’Sullivan and Unwin 2010). Given the distance, d_ij, between two locations, s_i and s_j, and some threshold distance, d, the neighbourhood (window), q, is defined as follows: j ∈ q if d_ij ≤ d, and j∉ q otherwise; that is, for a given value of d all points (centroids of census dissemination areas) within the threshold band are included into the neighbourhood. This case study uses the threshold distance d = 2400 m. The choice of d is based on two considerations. First, the local form of OWA requires that the distance threshold is large enough to ensure all census dissemination areas have at least one neighbour and the local range, r_kq, is greater than zero (see Equation (11)). Second, the value of d is selected based on the previous research on spatial patterns of crime and socio-economic status in London (see Malczewski and Poetz 2005).

4.2. Results and discussion

While the results of global OWA are unmappable with the exception of the criterion values and overall OWA scores, the local OWA models provide a wealth of information about the spatial patterns of the model components (such as criterion values, ranges, weights, trade-offs) and the overall OWA scores. Notice that for each value of α the OWA procedure results in a set of spatial outputs. Theoretically, one can generate a massive number of maps showing the results of local OWA. This study presents a selection of maps to demonstrate the key concepts of OWA.

4.2.1. Global and local value functions

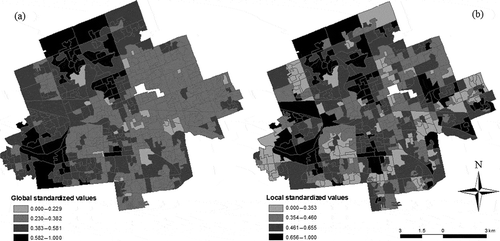
The standardized criterion scores are generated according to the global and local value functions (Equations (2) and (14)), respectively. The global value function, v_k(a_i), converts different levels of the k-th attribute into standardized score taking into account the global range for the k-th criterion (see Section 2.2), while the local range for the q-th neighbourhood is the base for obtaining the local value function, v_k(a_iq). As expected, the global value function procedure results in identifying a general spatial trend, while the local method generates a ‘localized’ spatial arrangement of criterion values. The results for the average-value-of-dwelling criterion provide a representative illustration of the spatial patterns of global and local standardized values (see Figure 1). Three features of those patterns deserve attention. First, the pattern of standardized values, according to the local OWA model, is substantially different from the pattern of the global standardized values. Second, the highest criterion values are located in the west and north sectors of the city and they tend to decline as one moves eastward and southward (Figure 1(a)). This spatial trend is based on the global range representing the absolute (global) minimum and maximum values of the criterion. The high values tend to cluster around the absolute maximum located in the north-west part of the city, and the low-value-housing tend to cluster in the vicinity of the absolute minimum value located in the east sector of London. Third, the spatial pattern generated by the local model shows that the high and low values tend to be ‘evenly’ dispersed across the city (Figure 1(b)). It points to the high and low values of the standardized scores. The pattern is based on the local range representing the relative minimum and maximum criterion values. The relative extreme values can be found in all sectors of the city irrespectively of the absolute criterion values; that is, an area characterized by a relatively low value can be located in the north-west sector of the city, and relatively high criterion values can be found in the east end of London.

Figure 1. Evaluating socio-economic status of neighbourhoods in the City of London, Ontario: spatial patterns of standardized scores the average-value-of-dwelling criterion generated by (a) global value function, v₄(a_i), and (b) local value function, v₄(a_iq).

4.2.2. Spatial patterns of local weights

The values of global criterion weights, w_k, are constant over the study area. Unlike the global criterion weights, the local weights vary from one location to another. Figure 2 shows the spatial patterns of local weights. The patterns represent the spatial distributions of preferences about relative importance of a given criterion. Specifically, the global weights, w_k, are adjusted locally according the changes of the local ranges, r_kq, relative to the global ranges, r_k. For example, while the local weight for the median-income criterion w₁ = 0.25; the local weights, w_1q, range from 0.145 to 0.410 (see Figure 2(a)). The highest values of these weights tend to cluster in the west end of the city. This implies that these areas are characterized by a relatively higher importance of median income as compared to the whole study area. The lowest values of the criterion are located in the central and east parts of London. The low values of the local weights indicated that the criterion is relatively less important locally as compared to the global criterion weighting.

Figure 2. Evaluating socio-economic status of neighbourhoods in the City of London, Ontario: spatial patterns of local criterion weights. (a) Median household income, w_1q, (b) incidence of low income, w_2q, (c) employment rate, w_3q, (d) average value of dwelling, w_4q, (e) university education, w_5q, and (f) residential burglary, w_6q.

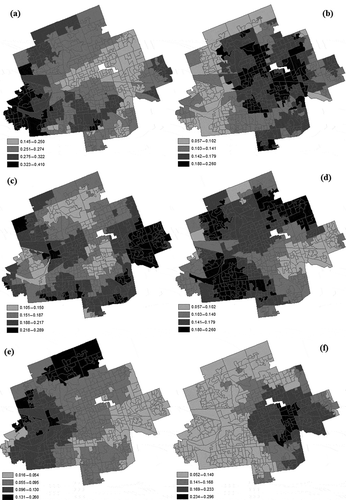
Notice that in general the relationships between the local weights follows the relationship between the global weights; that is, one would expect the following: if w₁ > w₂, then w_1q > w_2q. However, in some situations the local weights can be very different from the global weights. For example, a comparison of the spatial pattern of local weights for the criterion of median income (Figure 2(a)) and employment (Figure 2(c)) reveals that in some areas of the east section of London the employment criterion is relatively more important than the criterion of median income (that is, w_1q < w_3q), although the reverse is true globally (that is, w₁ = 0.25 > w₃ = 0.15). One can arrive at similar conclusions by making pairwise comparisons of the spatial patterns of local weights. In general, the local structure of the six criteria (the set of local criterion weights) can be substantially different as compared to the global structure (the set of global criterion weights).

The analysis of spatial patterns of local trade-offs between criteria provides further insights into the nature of local preference structure. Table 3 shows the global trade-offs and the average values of local trade-offs for each pair of the six criteria. The results suggest that the values of global trade-offs are similar to the average local trade-offs. For example, the trade-off between the median-income and employment criteria measured by the ratio of w₁/w₃ = 0.25/0.15 = 1.67. This implies that the median-income criterion is relatively more important than the employment criterion, and consequently one would be willing to trade-off 1.67 units of employment for one unit of median income. It is useful to compare the global trade-off to the average value of local trade-off. For example, the average local trade-off between the median-income and employment criteria is obtained by Σ(w_1q/w_3q)/494 = 1.45 (see Table 3). Thus, on average, the local trade-off is slightly different from the global value of trade-off. Similar conclusion can be reach by comparing the trade-off values for each pair of the criteria. In general, however, the local trade-offs depend on the local situation and they can be substantially different from the global trade-off for a given pair of criteria.

Table 3. Evaluating socio-economic status of neighbourhoods in the City of London, Ontario: the global trade-offs and the average values of local trade-offs.

Criterion	OWA model	ai1	ai2	ai3	ai4	ai5	ai6
ai1	Global	1.00	1.39	1.67	1.79	1.92	1.79
	Local	1.00	1.48	1.45	1.90	2.05	2.22
ai2	Global	0.72	1.00	1.20	1.29	1.38	1.29
	Local	0.76	1.00	1.04	1.40	1.59	1.46
ai3	Global	0.60	0.83	1.00	1.07	1.15	1.07
	Local	0.75	1.05	1.00	1.39	1.80	1.53
ai4	Global	0.56	0.78	0.93	1.00	1.08	1.00
	Local	0.60	0.86	0.84	1.00	1.27	1.30
ai5	Global	0.52	0.72	0.87	0.93	1.00	0.93
	Local	0.31	0.48	0.46	0.55	1.00	0.74
ai6	Global	0.56	0.78	0.93	1.00	1.08	1.00
	Local	0.59	0.76	0.79	1.14	1.57	1.00

Note: a_i1 = median household income, a_i2 = incidence of low income, a_i3 = employment rate, a_i4 = average value of dwelling, a_i5 = university education, and a_i6 = residential burglary.

The local trade-off is related to the magnitude of criterion values variation locally. Specifically, it is a function of the local ranges (see Section 2.3). The larger the local range of the k-th criterion relative to the other criterion ranges, the higher the value of local weights. Figure 3 presents the spatial pattern of local trade-offs between the median-income and employment criteria (w_1q/w_3q). As expected, the values of w_1q/w_3q is greater than 1.00 in most neighbourhoods of the city, which implies that the median-income criterion is relatively more important than the employment criterion. There are two areas in the north and west part of London characterized by the local trade-offs greater than the global value (that is, w_1q/w_3q > 1.67). This suggests that the median criterion in the north and west sections of the city is relatively more impotent locally then globally. There is also a sizeable pocket of trade-offs w_1q/w_3q < 1.00 in the east sector of London. In contrast to the global relationship between the two criteria, this indicates that the employment criterion is relatively most important than the median-income criterion in that part of the city.

Figure 3. Evaluating socio-economic status of neighbourhoods in the City of London, Ontario: spatial patterns local criterion ranges of: (a) median income, r_1q (b) employment rate, r_3q, and (c) the local trade-offs between the median-income and employment criteria (w_1q/w_3q).

4.2.3. Spatial patterns of global and local OWA scores

Theoretically, one can obtain an enormous number of map combination operators (or evaluation strategies) by varying the α parameter (see Section 2.4). Here, we limit our analysis to a selection of α  = {0.0, 0.5, 1.0}, and the optimal set of order weights (see Table 2). Figure 4 shows three evaluation strategies. Each strategy is associated with a given value of α. For α = 0.0, the criterion maps are combined by the AND operator. This combination operator is referred to as the worst-case evaluation scenario because it assigns the lowest value to each location. Increasing the value of α from 0.0 to 0.5 corresponds to the situations in which relatively higher and higher order weights are assigned to the higher ranking criterion values at the expense of assigning smaller order weights to the lower ranking criterion values at a given location. For α = 0.5, the criterion maps are combined according to the conventional WLC model. Increasing the value of α from 0.5 to 1.0 implies that greater and greater order weights are assigned to the higher criterion values at the expense of assigning smaller weights to the smaller criterion values at a given location. For α = 1.0, the criterion maps are combined by the OR operator. This represents the best-case scenario; that is, the highest possible value is selected at each location (Jiang and Eastman 2000; Malczewski et al. 2003).

Figure 4. Evaluating socio-economic status of neighbourhoods in the City of London, Ontario: spatial patterns the overall global and local OWA values for: (a) and (d) α = 0.0; (b) and (e) α = 0.5; (c) and (f) α = 1.0.

The spatial patterns of socio-economic status generated by the global OWA is characterized by a west–east division (see Figures 4). In general, the values of global OWA scores tend to be lower in the eastern portion of the city. This observation suggests that the pattern of socio-economic status in London can be described using the notion of the dual city, which identifies a polarization of the city into two distinct geographical areas according to the socio-economic status (Malczewski and Poetz 2005). In London, one can identify the contrast between the west and north-west areas of high socio-economic status and the east section of the city characterized by low socio-economic status. Although this pattern can be observed for each of the global OWA model, it is especially noticeable for the results of AND operator. The west–east division becomes less and less evident along with increasing the value of α from 0.0 to 1.0.

The results of the local OWA provide us with further insights into the spatial pattern of socio-economic status in London (see Figure 4). The patterns of local OWA scores exhibit substantially different characteristics than those obtained using the global OWA models, and they show, as expected, a much greater degree of local variability. While the global OWA operators identify the global spatial trend in terms of absolute values (that is, the global minimum and maximum values), the local OWA models generate spatial patterns of relative socio-economic values. The local spatial patterns highlight relatively high and low OWA scores locally. While the local patterns of OWA preserve, to some degree, the main feature (spatial tend) of the spatial distribution of global OWA scores, they also show local variability of socio-economic status. This observation is especially evident for the local pattern generated by the AND model (see Figure 4(d)). In this case, one can identify a general spatial trend and local variability of OWA scores. However, these characteristics of the spatial distribution of local OWA scores tend to be less and less noticeable along with increasing the α value from 0.0 to 1.0. These results are confirmed by an analysis of the Moran’s I coefficients for the spatial patterns of OWA scores (Table 4). One can derive two general remarks from examining the spatial autocorrelation statistics. First, the values of Moran’s I coefficients for all patterns are statistically significant indicating high degree of spatial autocorrelation. However, the coefficients for the global OWA scores are consistently higher than those for the local counterparts. Second, the Moran’s I coefficients gradually decline along with increasing the value of α. For example, the Moran’s I coefficients of the spatial patterns generated by the AND operator are 0.502 and 0.301 for the global and local OWA models, respectively; while the corresponding coefficients for the OR model are 0.254 and 0.115. These comparisons indicate that the clustering of similar values tends to decline along with increasing the value of α.

Table 4. Evaluating socio-economic status of neighbourhoods in the City of London, Ontario: the Moran’s I coefficients of the spatial patterns of global and local OWA scores for selected values of α (see Figure 4).

α	Moran’s I
	Global OWA	Local OWA
0.0	0.502	0.301
0.1	0.495	0.297
0.2	0.482	0.293
0.3	0.469	0.289
0.4	0.456	0.285
0.5	0.444	0.283
0.6	0.402	0.241
0.7	0.334	0.205
0.8	0.295	0.157
0.9	0.271	0.138
1.0	0.254	0.115

Note: All coefficients are statistically significant at p < 0.000.

5. Conclusion

The main aim of this paper was to develop a local form of GIS-OWA. This was achieved by introducing the range sensitivity principle into the global OWA model. The concept of range sensitivity provided a platform for ‘localizing’ value functions and criterion weights. The local form of OWA was then integrated with a procedure for obtaining an optimal set of order weights. The fact that the order weights are obtained by specifying a single parameter α is one of the major advantages of GIS-OWA. By specifying suitable parameter α (a set of order weights) it is possible to change the form of map combination procedures from the AND combination through all intermediate types (including conventional WLC) to the OR model.

While the previous research on GIS-OWA (Makropoulos and Butler 2006) focused on incorporating spatially explicit parameter α into the global GIS-OWA model, the proposed model presents an approach for developing the local form of GIS-OWA based on the concepts of spatially explicit value functions and criterion weights. These two approaches are complementary. One can suggest that an integration of these two modelling frameworks would provide a further advancement of research on the local form GIS-OWA. The local form of GIS-OWA opens up new opportunities for spatial analysis. The results of conventional GIS-OWA are unmappable with exception of the overall OWA scores. The results of local OWA modelling can be mapped and further examined with GIS. The local form of OWA provides a tool for place-based analysis. The elements of the local model are localized providing detailed information about neighbourhoods. Specifically, an analysis of the spatial distribution of local criterion weights and local value functions can provide new insights into the nature of spatial patterns. The spatially distributed parameters of local OWA can be used for examining the local preferences with respect to relative importance of evaluation criteria as well as the local trade-offs between criteria. The outcomes of local OWA are potentially useful in targeting priority areas for informing local planning and socio-economic policies development. The results suggest that the socio-economic status related policies should be informed by an understanding of contextual factors, which should be examined locally, and different policies should be applied in different neighbourhoods of the city.