A method for finding a least-cost corridor on an ordinal-scaled raster cost surface

ABSTRACT

The least-cost path problem is a widely studied problems in geographic information science. In raster space, the problem is to find a path that accumulates the least amount of cost between two locations based on the assumptions that the path is a one-dimensional object (represented by a string of cells) and that the cost (per unit length) is measured on a quantitative scale. Efficient methods are available for solution of this problem when at least one of these assumptions is upheld. This is not the case when the path has a width and is a two-dimensional object called a corridor (represented by a swath of cells) and the cost (per unit area) is measured on an ordinal scale. In this paper, we propose one additional model that characterizes a least-cost corridor on an ordinal-scaled raster cost surface – or a least ordinal-scaled cost corridor for short – and show that it can be transformed into an instance of a multiobjective optimization problem known as the preferred path problem with a lexicographic preference relation and solved accordingly. The model is tested through computational experiments with artificial landscape data as well as real-world data. Results show that least ordinal-scaled cost corridors are guaranteed to contain smaller areas of higher cost than conventional least-cost corridors at the expense of more elongated and winding forms. The least ordinal-scaled cost corridor problem has computational complexity of O(n^2.5) in the worst case, resulting in a longer computational time than least-cost corridors. However, this difference is smaller in practice.

KEYWORDS:

• Raster cost surface
• wide path
• multiobjective shortest path problem
• preferred path problem
• scales of measurement

1. Introduction

The least-cost path problem is one of the most widely studied problems in geographic information science. It is a source of theoretical exploration and has a variety of practical applications ranging from the placement of highways (Lombard and Church 1993; Yu, Lee, and Munro-Stasiuk 2003; Scaparra, Church, and Medrano 2014) and pipelines (Huber and Church 1985; Feldman et al. 1995; Bagli, Geneletti, and Orsi 2011) to siting for wildlife corridors (Adriaensen et al. 2003; Chetkiewicz and Boyce 2009; Rayfield, Fortin, and Fall 2010). The least-cost path problem and its solution methods are dependent on how the underlying surface is represented. When solved in digital devices, two-dimensional (2D) cost surfaces may be discretized into regions of constant cost and their least-cost paths into polylines. This vector version of the problem is known as the ‘weighted region problem’ (Mitchell and Papadimitriou 1991). However, it cannot be solved exactly in polynomial time (De Carufel et al. 2012). When a 2D cost surface is discretized into a grid of regular (commonly rectangular, hexagonal, or triangular (Carr, Olsen, and White 1992; Birch, Oom, and Beecham 2007; Dale 2000; Sahr 2011)) shaped cells, each of which is assigned a value representing the cost per unit length, we have a raster version of the problem that seeks a path that accumulates the smallest amount of cost while connecting a source cell and a destination cell. Furthermore, vector and raster data may be extended from 2D to three-dimensions (3D). In such cases, a 3D least-cost path problem is considered (Eklund, Kirkby, and Pollitt 1996; Scott 1994; Wagner and Scott 1995).

The 2D raster-based least-cost path problem relies on two (sometimes implicit) assumptions. First, the cost values assigned to the cells are measured on a scale that allows them to be meaningfully multiplied and added. Second, the path is a one-dimensional object, which has length but not width. These assumptions together justify the representation of a path as a sequence of adjacent cells and the calculation of its accumulated cost as the sum of the cost-weighted distance between each pair of consecutive cells (i.e. the product of the distance between the centres of those cells and the mean of their cost values) in that sequence, where two cells are said to be adjacent if they share a cell side or a cell corner, that is, if one can be translated to the other in an orthogonal or diagonal one-cell step.

The two assumptions also motivate an efficient solution method for the problem. It converts a raster cost surface to a graph in which nodes represent cells and arcs represent pairs of adjacent cells, and equates the length of each arc with the cost-weighted distance between the corresponding cells. A least-cost path on the original cost surface corresponds to a shortest path in the derived graph, which can be searched for by any classic shortest path algorithm such as the one by Dijkstra (1959). Dijkstra’s algorithm in its original form has a complexity of O(n²) where n represents the number of nodes (or cells in the present context). It has a better complexity with an advanced data structure such as a priority queue or heap (Ahuja, Magnanti, and Orlin 1993), and its actual computation time may be shortened with a heuristic such as A* (Hart, Nilsson, and Raphael 1968).

The validity of the quantitative cost assumption may be questioned unless it is certain that the cost values have been measured on a ratio scale, such as travel time per unit distance (Mulrooney et al. 2017) or travel cost per unit distance (Hallett and McDermott 2011). Significantly, in many applications of the least-cost path problem, cost is estimated by classifying one or more qualitative attributes such as land cover type (Ray, Lehmann, and Joly 2002; Chardon, Ariaensen, and Matthysen 2003; Driezen et al. 2007; Stevenson-Holt et al. 2014). Although this process may take advantage of opinions and judgements of experts in the relevant fields (O’Brien et al. 2006; Gonzales and Gergel 2007; LaRue and Nielsen 2008; Chetkiewicz and Boyce 2009), it does not necessarily guarantee accurate or consistent results (see Rayfield, Fortin, and Fall (2010), Zeller, McGarigal, and Whiteley (2012), Ligmann-Zielinska and Jankowski (2014) for reviews).

If sufficient information is not available for quantification of cost, one alternative is to measure cost on an ordinal scale and assign each cell a ranking (Graham 2001; Rabinowitz and Zeller 2010). Numerical values may be used to encode these rankings but they are arbitrary. Thus, if a conventional least-cost path is searched for over such a cost surface, its location or length may not be accurate or consistent because they are affected by the superfluous magnitudes assigned to essentially ordinal-scaled cost values (see Schadt et al. 2002; Larkin et al. 2004; Driezen et al. 2007; Gonzales and Gergel 2007; Rayfield, Fortin, and Fall 2010; Murekatete and Shirabe 2020 for discussions). Such paths would be considered to be derived without attention to the true cost value. For this reason, the currently available methods for delineating least-cost paths would not reasonably apply when the cost values are not certainly measured on a ratio scale. However, one could consider a situation where the cost values are not measured on a ratio scale, but there exist some knowledge how much more preferred one value is than another. As such, there are many variations of this problem that fall between knowing exact ratio scale measurements of cost and using an ordinal scale to rank values as discussed above. For example, O’Brien et al. (2006) used a plus/minus score to score different landcover types with their perceived level of suitability for woodland caribou habitat, and then order them accordingly. In another example, researchers used ranked variables and attributes derived from expert surveys to determine the relative weight of variables and attributes in order to score suitability (LaRue and Nielsen 2008). Each variation could potentially necessitate a new problem formulation and solution.

Still, it is possible to consider a variant of the least-cost path problem that addresses the assumption that there is no knowledge of how much one value is preferred over another and does not rely on the availability of quantitative cost. In their attempt to rank-order paths situated on an ordinal-scaled raster cost surface, for example, Murekatete and Shirabe (2020) employed a tie-breaker of two paths that measures, for each path, the (geometric) length of the segment consisting of cells of each cost value and regards the one having the shorter segment of the highest cost value as less cost. If the two paths are tied, the same procedure is performed with the second highest cost value, and if necessary, it is repeated with each of the lower cost values until the tie is broken. This is analogous to the one based on which participating countries in the Olympic Games are ranked in the number of first gold, then silver, and finally bronze medals. With this tie-breaker, the problem can be transformed into a tractable multicriteria shortest path problem (to be reviewed in the next section) and solved as such (Murekatete and Shirabe 2020). It was found that their solution intersected fewer cells deemed ‘undesirable’ than the traditional least-cost paths did. Such an approach to the least-cost path problem could provide planners, researchers, and geographers with an additional tool in a set of useful algorithms. For each use case, a user should evaluate the conditions of the problem, the desired outcome, and the significance of potential errors in delineation of a path, and then choose the most appropriate from the available tools.

The validity of the one-dimensional path assumption is another concern. Paths found on raster surfaces often represent real world entities that have significant widths, such as highways (McHarg 1969, Gårds and Oscarsson 2019), railways (Arulrajah et al. 2009; Kalliainen and Kolisoja 2013), and pathways for animal movement (Singleton 2002; LaRue and Nielsen 2008). These examples suggest that some paths are actually two-dimensional objects characterized by their width as well as their length, and therefore should be evaluated in terms of their cost-weighted area in the least-cost path problem, or more fittingly, the least-cost corridor problem.

The least-cost corridor problem has been approached by a variety of methods in the literature. One creates a buffer around a least-cost path by half the desired corridor width (LaRue and Nielsen 2008). Another involves smoothing the cost surface using a radius equal to half the desired width and finding a least-cost path on the smoothed cost surface as the centerline of a least-cost corridor on the original cost surface (Huber and Church 1985). Yet another resamples the cost surface in order to make the resolution of a cell match the required width (see Gonçalves (2010) for an example). These approaches are straightforward and easy to perform but their accuracy is uncertain. On the other hand, Gonçalves (2010) explicitly modelled a corridor as a ‘wide path’, which is a region swept by a one-dimensional string of cells called ‘path-front’, and converted the least-cost corridor problem into a shortest path problem in a graph where path-fronts (or various forms) are represented as nodes and transitions between path fronts are represented as arcs and solved it as such. This approach effectively finds a least-cost corridor with a specified width, but it quickly becomes inefficient as the width increases (which, in turn, increases the number of forms of path-fronts exponentially). Shirabe (2016) replaced a path front with a two-dimensional group of cells arranged in an octagonal form in sweeping a corridor, which turned out to be a more scalable approach. Although there are a number of approaches to the least-cost corridor problem, as named above, unfortunately there is no exploration in current literature as to whether any of them works when quantitative information on cost is not available.

The purpose of this paper is to propose a model that characterizes a least-cost corridor on an ordinal-scaled raster cost surface and an efficient method for it solution. The rest of the paper is structured as follows. Section 2 reviews two path/corridor optimization problems, on which the design of our model is based, as described in Section 3. The performance of the model was tested through computational experiments with synthetic data and real-world data, and their results are reported in Sections 4 and 5, respectively. Section 6 discusses findings and implications of the experiments and application. Section 7 concludes the paper.

2. Preliminaries

We review two optimization problems that motivate our formulation and solution of the least ordinal-scaled cost corridor problem: the preferred path problem with a lexicographic preference relation and the least-cost corridor problem.

2.1. Preferred path problem with a lexicographic preference relation

Suppose a path, P, in a graph, G, such that each arc (i, j) has an ordered set of q lengths, {$l_1\left(i,j\right)$, … , $l_q\left(i,j\right)$}. Then, consider an ordered set of q lengths, {$l_1\left(P\right)$, … , $l_q\left(P\right)$}, of P that are defined as follows.

(1) $l_k\left(P\right)={\sum }_{\left(i,j\right)\in P}{l}_k\left(i,j\right)\mathrm{\forall }k\in \left\{1,\dots ..,q\right\}$(1)

If the multiple lengths of each arc can be reduced to a single length, G becomes a usual graph and affords the classic shortest path problem. Otherwise, we have a multicriteria shortest path problem that may not be tractable unless paths are compared in some special ways.

A ‘lexicographic preference relation’ (Perny and Spanjaard 2005) is one such comparison that makes the problem tractable. It defines the order of preference of two paths in the following manner. A path, P, is preferred to another path, Q, if P’s first length is shorter than Q’s. If their first lengths are equal, P is preferred to Q if P’s second length is shorter than Q’s. This tie-breaker is repeated with a subsequent length at a time until the tie is broken. A lexicographic preference relation is formally expressed as follows.

P is preferred to Q if and only if

(2) $l_k\left(P\right)<l_k\left(Q\right)\mathrm{\exists }k\in \left\{1,\dots ..,q\right\}$(2)

(3) $l_j\left(P\right)=l_j\left(Q\right)\mathrm{\forall }j<k$(3)

The ‘preferred path problem’ (Perny and Spanjaard 2005) with a lexicographic preference relation is defined accordingly.

Table

Problem 1: The preferred path problem with a lexicographic preference relation Given a graph of nodes and arcs with each arc having a set of lengths arranged in descending order, find a path starting with a specified source node and ending with a specified destination node such that no such path is preferred to it according to Equations (2)(2) $l_k\left(P\right)<l_k\left(Q\right)\mathrm{\exists }k\in \left\{1,\dots ..,q\right\}$(2) and (3(3) $l_j\left(P\right)=l_j\left(Q\right)\mathrm{\forall }j<k$(3) ).

Problem 1 generalizes the classic shortest path problem and can be solved by a minor modification of Dijkstra’s algorithm with a complexity of O(n²q), where n is the number of nodes and q is the number of lengths of each arc (see, e.g. Murekatete and Shirabe (2021) for pseudocode).

2.2. Least-cost corridor problem

According to the terminology of Tomlin (1990), a neighbourhood is a set of cells that is arranged in a specified form.

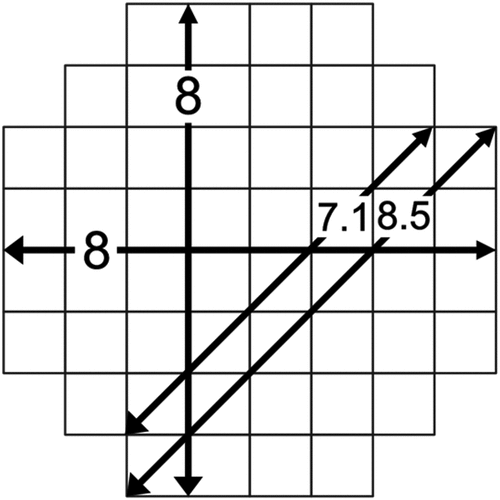
In his formulation of the least-cost corridor problem, Shirabe (2016) constructs neighbourhoods of a ‘(w,d)-form’, that is, a w-by-w block of cells, where w is the desired corridor width in number of cells from which d rows are diagonally removed from each corner. In particular, d is set to the largest integer that is not greater than $\frac{2-\surd 2}{2}$w in order to minimize the differences in the lateral and diagonal widths of the form and make the form as regular as possible. As illustrated in Figure 1, given the nature of rectangular cells, the lateral widths are consistently equal to w, whereas the diagonal widths alternate between two values around w.

Figure 1. A neighborhood of the (8,2)-form (set of cells). Measurements of the lateral and diagonal widths are displayed at each of the double arrows.

A corridor is then defined as a sequence of adjacent neighbourhoods of the same (w,d)-form (determined by a specified corridor width) (see Figure 2 for an example), where two neighbourhoods are said to be adjacent to each other if one neighbourhood can be translated to the other in an orthogonal or diagonal one-cell step (see Figure 3).

Figure 2. Example of a corridor defined as a sequence of adjacent neighborhoods between two neighborhoods (enclosed by bold lines). All neighborhoods in this example have the same (8,2)-form.

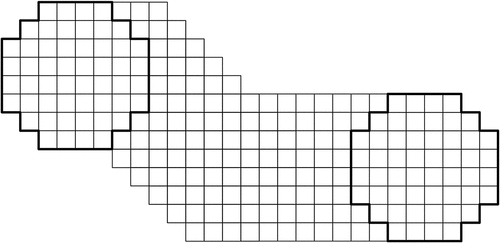
Figure 3. Pairs of a neighborhood (set of empty cells) and each of its adjacent neighborhoods (enclosed by bold lines) and their corresponding crescents (shaded).

The quality of a corridor is evaluated in terms of its cost-weighted area. Let P be a corridor and U(P) be all the cells that are in at least one neighbourhood in P. The cost-weighted area of P, $a\left(P\right)$, is defined as:

(4) $a\left(P\right)=\sum _{i\in U\left(P\right)}{f}_i{a}_i$(4)

where a_i is the (geometric) area of cell i and f_i is the cost per unit area in cell i.

With a corridor and its cost-weighted area defined above, the least-cost corridor problem is defined as follows.

Table

Problem 2: The least-cost corridor problem Given a raster cost surface on which each cell has a value representing its cost per unit area, find a sequence of adjacent neighbourhoods of a specified form starting with a specified source neighbourhood and ending with a specified destination neighbourhood such that no such sequence has a smaller cost-weighted area than it does.

A corridor, P, has another property, cumulative cost-weighted area, $\bar{a}\left(P\right)$. Letting N_s be the first neighbourhood in P, it is defined as:

(5) $\bar{a}\left(P\right)={\sum }_{i\in N_s}{f}_i{a}_i+{\sum }_{\left(N_i,N_j\right)\in P}a\left(N_i,N_j\right)$(5)

where

(6) $a\left(N_i,N_j\right)={\sum }_{k\in N_j\mathrm{\setminus }{N}_i}{f}_k{a}_k$(6)

In Equation (6)(6) $a\left(N_i,N_j\right)={\sum }_{k\in N_j\mathrm{\setminus }{N}_i}{f}_k{a}_k$(6) , $N_j\mathrm{\setminus }{N}_i$ represents the set difference – referred to here as a ‘crescent’ for its shape (see Figure 3 for examples)—of two adjacent neighbourhoods, N_i and N_j, and $a\left(N_i,N_j\right)$ denotes its cost-weighted area. It is important to note that if a corridor, P, does not self-intersect, i.e. none of its crescent intersect any other crescent or the first neighbourhood of it, then U(P) = $N_s\cup \left({\text{U}}_{\left(N_i,N_j\right)\in P}{\text{N}}_{\text{j}}\backslash {\text{N}}_{\text{i}}\right)$ and $a\left(P\right)=\bar{a}\left(P\right)$.

The cumulative cost-weighted area and its possible equality to the cost-weighted area motivate the following procedure for solving Problem 2. First, convert the raster cost surface into a graph in which each node represents a neighbourhood and each arc represents a crescent derived from a pair of adjacent neighbourhoods, and assign each arc the cost-weighted area of the corresponding crescent. Then, search the graph for a shortest path between the nodes corresponding to the source neighbourhood and the destination neighbourhood, and select the cells of the corridor that the shortest path corresponds to. Since the number of nodes in the graph is smaller than or equal to the number, n, of cells in the cost surface, the graph search takes O(n²) time if Dijkstra’s algorithm is employed.

The procedure described above does not guarantee to generate a corridor without self-intersection. However, results from the computational experiments by Shirabe (2016) suggest that it is rare to occur.

3. Method

The least-cost corridor problem on an ordinal-scaled cost surface – or the least ordinal-scaled cost corridor problem – is introduced here in terms of formulation and solution.

3.1. Formulation

To evaluate a corridor situated on an ordinal-scaled cost surface, we measure the subarea of it corresponding to each cost value separately, instead of aggregating them. Suppose that the cost surface has q different cost values, which are arranged in the descending order. Let P be a corridor (i.e. a sequence of adjacent neighbourhoods of the same (w,d)-form), N_s be the first neighbourhood of P, and U(P) be all the cells that are in at least one neighbourhood of P. Then, consider the subset of U(P) that consists of only cells with the kth cost value. The (geometric) area of this subset is referred to as the kth area, $a_k\left(P\right)$, of P, and formally defined as:

(7) $a_k\left(P\right)=\sum i\in U\left(P\right)a_{k\left(i\right)}\forall k\in \left\{1,\dots \mathrm{..},q\right\}$(7)

where a_k(i) is the area of cell i with the kth cost value.

Although we do not have quantitative information on the ordinal-scaled cost surface, we know that its kth cost value is higher than its (k + 1)th cost value. Then, we assume the most conservative assumption: the magnitude of the difference between two consecutive cost values is arbitrarily large. This leads us to the following relation for two corridors. A corridor, P, is preferred to another corridor, Q, if P has a smaller 1st area than Q. If the two corridors have equal 1st areas, P is preferred to Q if P has a smaller 2nd area than Q. The tie-breaker is repeated with a subsequent area at a time until the tie is broken. This is a lexicographic preference relation, which is formally defined as:

P is preferred to Q if and only if

(8) $a_k\left(P\right)<a_k\left(Q\right)\mathrm{\exists }k\in \left\{1,\dots ..,q\right\}$(8)

(9) $a_j\left(P\right)=a_j\left(Q\right)\mathrm{\forall }j<k$(9)

Accordingly, the least ordinal-scaled cost corridor problem is formulated as a special case of the preferred path problem with a lexicographic preference relation as follows.

Table

Problem 3: The least ordinal-scaled cost corridor problem Given an ordinal-scaled raster cost surface with q different cost values arranged in the descending order, find a sequence of adjacent neighbourhoods of a specified form starting with a specified source neighbourhood and ending with a specified destination neighbourhood such that no such sequence is preferred to it according to Equations (8)(8) $a_k\left(P\right)<a_k\left(Q\right)\mathrm{\exists }k\in \left\{1,\dots ..,q\right\}$(8) and (9(9) $a_j\left(P\right)=a_j\left(Q\right)\mathrm{\forall }j<k$(9) ).

3.2. Solution

To design a method for solving the least ordinal-scaled cost corridor problem presented as Problem 3, we first define the kth cumulative area, ${\bar{a}}_k\left(P\right)$, of a corridor, P, as:

(10) $\overline{ }{a}_k\left(P\right)=\sum i\in N_s{a}_{k\left(i\right)}+\sum \left(N_i,N_j\right)\in P{a}_k\left(N_i,N_j\right)\forall k\in \left\{1,\dots \mathrm{..},q\right\}$(10)

where $a_k\left(N_i,N_j\right)$ is the kth area of the crescent, $N_j\mathrm{\setminus }{N}_i$, derived from two adjacent neighbourhoods, N_i and N_j, which is defined as:

(11) $a_k\left(N_i,N_j\right)=\sum i\in N_j\backslash N_i{a}_{k\left(i\right)}\forall k\in \left\{1,\dots \mathrm{..},q\right\}$(11)

As stated in Section 2.2, if a corridor, P, does not self-intersect, then while any two of its first neighbourhood $N_s$ and crescents $N_j\mathrm{\setminus }{N}_i$ (for all $\left(N_i,N_j\right)\in P$) does not intersect each other, the union of all of them is equal to $U\left(P\right)$, which here implies that P’s kth cumulative area (defined by Equation (10))(10) $\overline{ }{a}_k\left(P\right)=\sum i\in N_s{a}_{k\left(i\right)}+\sum \left(N_i,N_j\right)\in P{a}_k\left(N_i,N_j\right)\forall k\in \left\{1,\dots \mathrm{..},q\right\}$(10) is equal to its kth area (defined by Equation (7))(7) $a_k\left(P\right)=\sum i\in U\left(P\right)a_{k\left(i\right)}\forall k\in \left\{1,\dots \mathrm{..},q\right\}$(7) for every k.

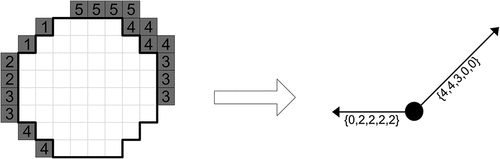
This suggests a possible application of the procedure used for the least-cost corridor problem (Problem 2) that converts the raster cost surface into a graph in which nodes represent neighbourhoods and arcs represent crescents derived from adjacent neighbourhoods. The only difference here is that each arc is assigned an ordered set of q lengths, the kth of which represents the kth area of the corresponding crescent (see Figure 4 for an example). The conversion takes O(nqw) time where n and q are the numbers of cells and of unique values, respectively, of the cost surface and w is the corridor width. This is because for each of n cells, it visits each of a constant number of cells adjacent to that cell, and for each of these visits, it loops through the corresponding crescent whose number of cells is proportional to w, and counts, for each of the q values, the number of cells that have that value.

Figure 4. An example of conversion of crescents (shaded) on a raster cost surface with five different values (5, 4, 3, 2, and 1) to arcs (arrows) of a graph each having five lengths (bracketed). Note that a node (dot) of the graph corresponds to a neighborhood (enclosed by bold line) on the raster cost surface. Note also that the number in each cell in the crescent represents the cost value of that cell.

Table

The general procedure of the proposed solution would then be as follows.
Step 1: Convert the raster grid to a graph for specified (w,d)-form which contains a node representing each neighbourhood and a set of set two arcs (one in each direction) between adjacent neighbourhoods.
Step 2: Calculate and set the weight of each arc using Equation (11)(11) $a_k\left(N_i,N_j\right)=\sum i\in N_j\backslash N_i{a}_{k\left(i\right)}\forall k\in \left\{1,\dots \mathrm{..},q\right\}$(11) .
Step 3: Find the most preferred path from an origin node to a destination node in the graph using the modification of Dijkstra’s algorithm for the preferred path problem with a lexicographic relation (Problem 1).
Step 4: Using the preferred path in the graph, identify the corresponding corridor in the original cost grid.

The graph search takes O(n²q) time, as the number of nodes of the graph is less than or equal to the number of cells of the cost surface, and the number of lengths of each arc of the graph is equal to the number of unique values in the cost surface. It must be acknowledged, however, that the output corridor is not guaranteed to be without self-intersection, so that its kth area is not guaranteed to be equal to the kth length of the most preferred path. Therefore, the presented procedure is a heuristic. In practice, however, resulting corridors are highly unlikely to self-intersect, as demonstrated in the computational experiments reported in the next two sections.

4. Experiments

We conducted two computational experiments. The first experiment (Experiment 1) was designed to examine the qualities of the proposed model of a least ordinal-scaled cost corridor. The second experiment (Experiment 2) was designed to evaluate the computational efficiency of the proposed method for its solution. We included a comparison of the proposed model and the existing least-cost corridor model in both experiments. This is because existing models remain available to be used instead of, alongside, or in connection with the proposed model although cost values may be measured on an ordinal scale.

4.1. Data

4.1.1. Experiment 1

In Experiment 1, we accessed two sets of artificial landscape data created by Seegmiller et al. (2020) for similarly designed experiments with the existing least-cost corridor model. The artificial landscape data was created using the NLMpy PYTHON software package (Etherington et al. 2015), which implements a number of algorithms to generate neutral landscape models (NLMs) encoded in raster format with various types of spatial patterns. Each of the two sets comprised 100 NLMs, each consisting of 500 rows and 500 columns and containing fractional values ranging from 0 to 1.

The first set of 100 NLMs was generated with the ‘mid-point displacement method’ (Fournier et al. 1982) to simulate real-world surfaces, referred to as ‘cloudy’ (Murekatete and Shirabe 2020), whose values change gradually with varying degrees of autocorrelation (see Figure 5(a) for an example). The frequency distribution of cell values in each cloudy NLM took the form of a bell-shape curve across the value range. The second set of 100 NLMs, referred to as ‘patchy’ (Murekatete and Shirabe 2020), was generated with the ‘modified random clusters method’ (Saura and Marténez-Millén 2000) to simulate real-world surfaces consisting of regions of constant values (see Figure 5(b) for an example). The frequency distribution of cell values in each patchy NLM was uniform across the value range.

Figure 5. Examples of (a) cloudy and (b) patchy neutral landscape models. Note that the darker shades represent higher values.

4.1.2. Experiment 2

In Experiment 2, we accessed three additional sets of cloudy NLMs with three different grid sizes, i.e. 250-by-250, 500-by-500, and 750-by-750, from Seegmiller et al. (2021). Each of the three sets comprised 100 NLMs, each containing fractional values ranging from 0 to 1.

4.2. Procedure

In both experiments involved a large number of instances of the least ordinal-scaled cost corridor problem and of the least-cost corridor problem created by systematically varying the number of unique cost values, the corridor width, and the grid size. Details of this procedure are described below.

4.2.1. Experiment 1

In Experiment 1, we performed the following tasks for the set of 100 cloudy NLMs, as well as for the set of 100 patchy NLMs.

4.2.1.1. Creation of cost grids

We first divided the value range 0 to 1 defined for all NLMs into five intervals of equal length. Next, we mapped five integer values, representing cost, starting with 1 and ending with 100 with a constant (or as constant as possible) increment to those intervals. Then, we converted each of the 100 NLMs into a cost grid by assigning each cell one of those cost values corresponding to the NLM value of that cell. This resulted in 100 cost grids with five unique cost values ranging from 1 to 100. Similarly, we created four additional sets of 100 cost grids with 10, 20, 50, and 100 unique cost values ranging from 1 to 100. Note that because of the random nature of the NLM creation process, there were some NLMs whose values did not populate all the defined intervals, which caused the resulting cost grids to contain slightly fewer unique values than they were supposed to.

4.2.1.2. Instantiation of problems

We defined 25 problem types by combining each of the five sets of cost grids having 5, 10, 20, 50, and 100 unique values and each of five corridor widths including 5, 10, 20, 40, and 80 cells. These corridor widths were chosen to span five different widths increasing exponentially to represent a large range of different widths. An example is one of finding a corridor with a width of five cells on a cost grid of 100 unique values. For each such problem type, we fixed a source and destination pair at the upper-left and lower-right corners of the grid, and created 100 instances, one for each of the 100 cost grids. This resulted in 2500 problem instances.

4.2.1.3. Solution of problems

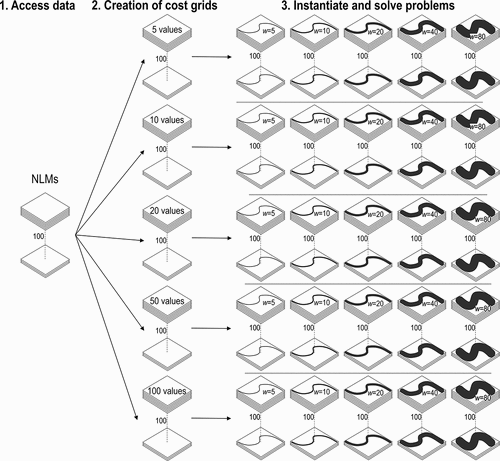
We solved each of the 2500 problem instances as a least ordinal-scaled cost corridor problem with the solution method presented in Section 3 and as a least-cost corridor problem with the solution method reviewed in Section 2. Both solutions involved the routine for converting a cost grid to a graph and Dijkstra’s algorithm (with a priority queue) for searching the graph for a shortest path, which were coded in Java and executed on a 3.40 GHz Intel Core i7–6700 CPU processor with 32.8 GM of Ram. This resulted in 2500 least-cost corridors and 2500 least ordinal-scaled cost corridors. The workflow of the steps outlined above is schematically illustrated in Figure 6.

Figure 6. Workflow of the three steps for Experiment 1. Step 1 was accessing neutral landscape models (NLM). Step 2 was to convert them to ordinal scaled cost grids with 5, 10, 20, 50, and 100 unique values. Step 3 was to instantiate the problems with corridors with widths of 5, 10, 20, 40, and 80 cells and then solve those problems.

4.2.1.4. Analyses of areas of corridors

For each of the 2500 least ordinal-scaled cost corridors and each of the 2500 least-cost corridors, we calculated the area of it that intersected cells of each unique cost value as well as its total area in terms of number of cells. We did not include the cells in the source or destination in this calculation because they were predetermined and should not affect qualities of the corridor.

4.2.1.5. Analyses of sinuosity of corridors

We also analysed the shape and length of each of the 2500 least ordinal-scaled cost corridors and each of the 2500 least-cost corridors. We had anticipated that both least ordinal-scaled cost corridors and least-cost corridors would tend to twist and turn to avoid costly cells, which were not uniformly distributed. To see if there was any difference between the two types of corridors in this tendency, we calculated the sinuosity of each corridor as the ratio of the length of its centerline to that of the straight line between its source and destination. Given the anticipated sinuosity, we had suspected that corridors might self-intersect. Therefore, we checked for self-intersection in all the corridors.

4.2.2. Experiment 2

In Experiment 2, we first defined 15 problem types in almost the same manner as in Experiment 1, using the same corridor widths but only three numbers, 10, 50, and 100, of unique cost values were considered. Then, we derived a cost grid from each NLM in the three sets of 100 NLMs (each set corresponding to one of three grid sizes) and created an instance of each of the 15 problem types with that cost grid. This resulted in 1500 problem instances for each of the three grid sizes. Then, we solved each problem instance as a least ordinal-scaled cost corridor problem and as a least-cost corridor problem as we did in Experiment 1. For each solution, we measured the time to convert the cost grid to a graph and the time to run the shortest path algorithm in the graph.

5. Results

5.1. Experiment 1

We report results of Experiment 1 with cloudy cost grids and with patchy cost grids separately. To facilitate the presentation, we use the following convention.

• The segment of a corridor that consists of cells whose cost values are not in the highest p% but in the highest q(>p)% of a given set of cost values is referred to as the ‘p%-q% segment’ of that corridor. For example, the 0–10% segment of a corridor in a cost grid with 50 unique values consist of cells with cost values of 92, 94, 96, 98, or 100.

• The area of the ‘p%-q% segment’ of a corridor is measured in terms of number of cells and called the ‘p%-q% area’ of that corridor.

5.1.1. Cloudy grids

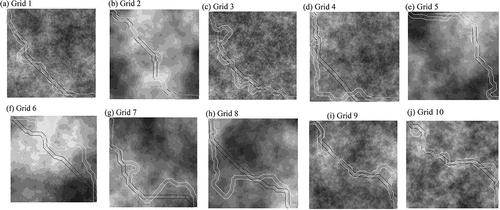
A visual inspection of corridors generated in the experiment suggested that least ordinal-scaled cost corridors tended to take more turns than least-cost corridors to avoid costly cells (see Figure 7 for an example). This was confirmed by the numerical results presented below.

Figure 7. Example of a least ordinal-scaled cost corridor (outlined in white) and a least-cost corridor (outlined in black) with w=20 between their common source and destination generated on a cloudy cost grid with 10 unique values. (a)-(j) represent the first ten cloudy cost grids used in the experiment. Note that the darker shades represent higher cost values.

Tables 1(a,b) summarize all the 2500 least ordinal-scaled corridors and the 2500 least-cost corridors, respectively, in terms of the average 0–10% to 90–100% areas of 100 instances of each problem type (specified by the number of unique cost values and the corridor width associated with the corresponding row). For example, the bottom-left cell of Table 1(a) indicates that the average 0–10% area of the 100 least ordinal-scaled cost corridors with a width of 80 cells in cost grids with 100 unique values was six cells. Note that for those problem types with five unique cost values (corresponding to the first five rows), only five segments (i.e. 0–20% to 80–100% segments) were considered instead of the 10 segments (i.e. 0–10% to 90–100% areas), because each of the five cost values was 20% of the cost value range. For example, the top-right cell of Table 1(b) indicates that the average 80–100% area of the 100 least-cost corridors with a width of five cells in cost grids with five unique values was 888 cells. The most costly segments of the least ordinal-scaled cost corridors tended to be significantly smaller than that of the least-cost corridors for any problem type (compare each row of the first column in Table 1(a,b)).

Table 1. Average segment areas of (a) the 100 least ordinal-scaled cost corridors and (b) the 100 least-cost corridors for each problem type on cloudy cost grids.

					0%-10%		10%-20%	20%-30%		30%-40%	40%-50%	50%-60%				60%-70%		70%-80%	80%-90%			90%-100%		Total
(a). Least ordinal-scaled cost corridors
Number of Unique Values	5	Width		5	32			274			1407					2227			918					4858
				10	67			603			2998					4393			1738					9799
				20	128			1282			6012					7901			2982					18306
				40	232			2633			11477					13961			4719					33022
				80	336			5395			20752					22004			6509					54996
	10	Width		5	2	31		100		208	535	1057				1268	1237		773	250				5462
				10	4	66		196		461	1173	2114				2465	2325		1421	456				10682
				20	5	129		414		1064	2385	4047				4433	4025		2463	727				19692
				40	4	248		804		2152	4870	7583				7903	6699		3859	974				35097
				80	6	358		1395		4170	8708	12463				12296	10087		5411	1229				56122
	20	Width		5	3	33		114		225	588	1153				1355	1302		828	279				5881
				10	4	69		231		512	1277	2310				2608	2378		1504	488				11382
				20	5	135		440		1092	2448	4186				4596	4079		2504	743				20228
				40	4	252		816		2316	4904	7638				7956	6869		3965	1001				35720
				80	6	359		1415		4254	8896	12627				12440	10183		5435	1247				56863
	50	Width		5	3	36		120		250	635	1222				1416	1373		866	302				6222
				10	4	72		233		568	1305	2353				2651	2430		1531	496				11642
				20	5	141		454		1159	2538	4306				4660	4118		2529	766				20676
				40	4	255		826		2316	5060	7823				8087	6910		3945	1014				36238
				80	6	362		1436		4280	8954	12669				12504	10210		5409	1250				57080
	100	Width		5	3	38		122		261	647	1239				1441	1387		858	300				6295
				10	4	75		237		587	1344	2419				2687	2447		1545	505				11851
				20	5	144		465		1190	2651	4400				4702	4112		2509	760				20939
				40	4	257		841		2405	5094	7894				8023	6800		3912	1026				36256
				80	6	366		1463		4369	9127	12811				12458	10104		5378	1252				57334
(b). Least-cost corridors
Number of Unique Values	5		Width	5	50				316		1203				1640				888				4096
				10	98				685		2565				3359				1680				8387
				20	183				1438		5097				6177				2828				15723
				40	315				2925		9899				11200				4467				28806
				80	559				5751		17789				18131				6193				48424
	10		Width	5	7	44			108	221	486		747		822		804		551		254		4044
				10	13	92			206	475	1051		1597		1696		1608		1113		453		8303
				20	17	189			424	1004	2119		3061		3217		2915		1931		663		15540
				40	24	331			868	2150	4167		5749		5833		5110		3213		902		28347
				80	49	559			1814	4330	7717		9810		9542		7993		4616		1065		47495
	20		Width	5	7	52			116	221	482		745		824		787		538		227		3999
				10	14	88			219	480	1056		1591		1713		1590		1066		400		8217
				20	16	182			446	1039	2123		3030		3209		2881		1897		597		15420
				40	27	371			927	2186	4134		5679		5779		4999		3157		825		28085
				80	49	566			1844	4425	7834		9794		9305		7803		4458		1012		47089
	50		Width	5	6	52			117	224	477		765		815		784		528		208		3976
				10	12	92			223	479	1052		1607		1707		1589		1054		386		8202
				20	16	182			450	1045	2120		3052		3198		2875		1875		576		15389
				40	28	372			929	2203	4139		5707		5766		4978		3111		804		28036
				80	49	570			1845	4527	7813		9808		9261		7739		4354		952		46919
	100		Width	5	6	52			120	233	493		754		802		778		520		199		3958
				10	13	89			225	495	1069		1604		1699		1576		1037		382		8189
				20	16	199			463	1046	2147		3056		3183		2823		1841		556		15329
				40	28	373			940	2246	4212		5713		5700		4889		3070		796		27966
				80	50	587			1913	4685	7978		9733		8969		7504		4257		943		46619

Each row of Table 1(a,b) conveys that both the least ordinal-scaled cost corridors and the least-cost corridors generally had left-skewed distributions of segment areas, and their average 0;.–10% (or 0–20%) areas were disproportionally small. Another similarity of the two types of corridors was that each of their average segment areas (except the 0–10% area of the least ordinal-scaled cost corridors) increased with corridor width, but it remained almost the same even as the number of unique values increased. The former can be seen by scanning any five rows having the same number of unique values, and the latter by scanning any five rows having the same corridor width. A notable difference, on the other hand, was that the least ordinal-scaled cost corridors generally had a smaller average 0–10% (or 0–20%) area but larger average 40–50% (or 40–60%), … , 90–100% (or 80–100%) areas than the least-cost corridors.

Table 2(a,b) presents the average sinuosity of the 100 least ordinal-scaled cost corridors and of the 100 least-cost corridors, respectively, for each of the 25 problem types on cloudy cost grids. The former was higher than the latter for all problem types. The average sinuosity of both types of corridors generally decreased with corridor width (to a smaller degree with the least-cost corridors). The number of unique cost values, however, had mixed effects. While the average sinuosity of the least ordinal-scaled cost corridors increased with number of unique cost values, that of the least-cost corridors decreased with it but only slightly.

Table 2. Average sinuosities of (a) the 100 least ordinal-scaled cost corridors and (b) the 100 least-cost corridors for each problem type on cloudy cost grids.

(a) Least Ordinal-Scaled Cost Corridors
				Least ordinal-scaled cost corridor
Number of Unique Values	5	Width	5	1.40
			10	1.39
			20	1.36
			40	1.31
			80	1.27
	10	Width	5	1.57
			10	1.51
			20	1.46
			40	1.39
			80	1.29
	20	Width	5	1.69
			10	1.61
			20	1.50
			40	1.42
			80	1.30
	50	Width	5	1.79
			10	1.65
			20	1.53
			40	1.44
			80	1.31
	100	Width	5	1.81
			10	1.67
			20	1.55
			40	1.44
			80	1.31
(b) Least-Cost Corridors
				Least ordinal-scaled cost corridor
Number of Unique Values	5	Width	5	1.18
			10	1.19
			20	1.17
			40	1.15
			80	1.13
	10	Width	5	1.17
			10	1.17
			20	1.15
			40	1.14
			80	1.11
	20	Width	5	1.16
			10	1.16
			20	1.15
			40	1.13
			80	1.10
	50	Width	5	1.15
			10	1.16
			20	1.14
			40	1.12
			80	1.10
	100	Width	5	1.14
			10	1.16
			20	1.14
			40	1.12
			80	1.09

Note: the sinuosities are measured as the ratio of the length of the geometric distance of the least-cost ordinal scaled corridor over the geometric straight line distance between the source and destination.

Lastly, none of the 2500 least ordinal-scaled corridors and the 2500 least corridors self-intersected.

5.1.2. Patchy grids

A visual comparison of least ordinal-scaled cost corridors and least-cost corridors (see Figure 8 as an example) suggested that the former turned more to avoid costly cells. To show this numerically, as done with those generated in cloudy cost grids, the 100 least ordinal-scaled cost corridors and the 100 least-cost corridors were summarized in terms of the average 0–10% (or 0–20%) to 90–100% (80–100%) areas (Table 3) and of the average sinuosity (Table 4) for each of the 25 problem types.

Figure 8. Example of a least ordinal-scaled cost corridor (outlined in white) and a least-cost corridor (outlined in black) with w=20 between their common source and destination generated on a patchy cost grid with 10 unique values. (a)-(j) represent the first ten patchy cost grids used in the experiment. Note that the darker shades represent higher cost values.

Table 3. Average segment areas of (a) the 100 least ordinal-scaled cost corridors and (b) the 100 least-cost corridors for each problem type on patchy cost grids.

(a). Least ordinal-scaled cost corridors
				0%-10%	10%-20%	20%-30%	30%-40%	40%-50%	50%-60%	60%-70%	70%-80%	80%-90%	90%-100%	Total
Number of Unique Values	5	Width	5	42		140		786		1785		2681		5435
			10	80		411		2053		3694		4901		11139
			20	176		1778		4801		6585		7657		20997
			40	995		6311		8909		9824		10045		36083
			80	4531		11805		12078		12356		12377		53146
	10	Width	5	20	27	48	123	321	576	825	1085	1232	1440	5697
			10	34	63	128	457	942	1347	1737	2174	2265	2722	11869
			20	59	179	688	1562	2221	2810	3115	3687	3544	4121	21986
			40	181	1541	2930	3856	4389	4527	4904	4885	4617	5139	36969
			80	1323	4931	5756	6315	5959	6624	6318	6109	6034	6806	56175
	20	Width	5	20	29	49	138	336	569	840	1082	1202	1489	5753
			10	34	67	142	483	943	1391	1742	2230	2322	2769	12121
			20	66	240	795	1572	2216	2857	3221	3681	3531	3890	22069
			40	269	1711	2941	4123	4562	4743	5023	4879	4692	5097	38041
			80	1880	5068	5843	6277	6094	6535	6446	6287	5956	6749	57134
	50	Width	5	20	29	50	149	354	603	832	1080	1238	1485	5839
			10	35	76	157	534	956	1421	1708	2217	2368	2764	12237
			20	75	270	851	1643	2323	2973	3285	3625	3670	4149	22864
			40	336	1766	3060	4175	4605	4711	5119	4920	4652	4798	38142
			80	2203	5151	5995	5895	6158	6297	6499	6430	6062	6646	57338
	100	Width	5	21	31	58	183	409	666	910	1156	1364	1479	6276
			10	35	81	173	621	1105	1562	1855	2305	2582	2795	13115
			20	76	303	929	1777	2498	3120	3485	3775	3989	4038	23991
			40	355	1869	3373	4278	4852	4961	5056	5154	4975	4517	39391
			80	2483	5416	6271	6334	6872	6679	6763	6697	6704	6813	61032
(b). Least-cost corridors
				0%-10%	10%-20%	20%-30%	30%-40%	40%-50%	50%-60%	60%-70%	70%-80%	80%-90%	90%-100%	Total
Number of Unique Values	5	Width	5	102		190		424		1092		2742		4550
			10	256		441		972		2305		5260		9235
			20	724		1191		2210		4590		8328		17043
			40	2544		3483		4787		7876		10715		29405
			80	6544		7583		8930		11175		12200		46432
	10	Width	5	48	58	82	113	187	267	426	678	967	1608	4434
			10	114	153	200	270	403	600	925	1389	1904	3026	8985
			20	353	427	552	702	909	1328	1861	2599	3286	4604	16622
			40	1211	1366	1676	1799	2238	2732	3512	4268	4419	5761	28982
			80	3101	3485	3690	3951	4232	4738	5300	5672	5442	6436	46047
	20	Width	5	47	65	86	113	187	265	436	680	931	1566	4377
			10	127	170	201	262	404	588	909	1397	1873	2971	8901
			20	350	436	558	741	924	1355	1842	2503	3216	4495	16421
			40	1225	1357	1696	1848	2291	2777	3433	4106	4277	5672	28682
			80	3112	3512	3714	3945	4218	4740	5235	5635	5428	6360	45900
	50	Width	5	49	61	83	119	187	292	420	681	939	1506	4337
			10	126	162	207	270	405	624	897	1386	1903	2903	8883
			20	340	439	566	759	902	1403	1839	2520	3217	4432	16418
			40	1241	1391	1678	1855	2286	2800	3397	4149	4259	5599	28655
			80	3107	3555	3751	3957	4206	4724	5190	5636	5540	6296	45963
	100	Width	5	49	63	90	139	223	306	470	781	1093	1620	4832
			10	129	166	228	292	486	669	983	1600	2186	3001	9740
			20	354	446	634	809	1044	1480	1980	2857	3640	4503	17746
			40	1277	1408	1806	1902	2510	2986	3719	4322	4875	5389	30195
			80	3213	3648	3965	3931	4758	4909	5463	5724	5767	6471	47849

Table 4. Average sinuosities of (a) the 100 least ordinal-scaled cost corridors and (b) the 100 least-cost corridors for each problem type on patchy cost grids.

(a) Least Ordinal-Scaled Cost Corridors
				Least ordinal-scaled cost corridor
Number of Unique Values	5	Width	5	1.57
			10	1.58
			20	1.55
			40	1.43
			80	1.23
	10	Width	5	1.64
			10	1.68
			20	1.62
			40	1.47
			80	1.30
	20	Width	5	1.66
			10	1.72
			20	1.63
			40	1.51
			80	1.32
	50	Width	5	1.67
			10	1.72
			20	1.68
			40	1.51
			80	1.32
	100	Width	5	1.67
			10	1.73
			20	1.68
			40	1.51
			80	1.35
(b) Least-Cost Corridors
				Least ordinal-scaled cost corridor
Number of Unique Values	5	Width	5	1.31
			10	1.31
			20	1.26
			40	1.18
			80	1.09
	10	Width	5	1.28
			10	1.27
			20	1.23
			40	1.16
			80	1.08
	20	Width	5	1.26
			10	1.26
			20	1.22
			40	1.15
			80	1.08
	50	Width	5	1.24
			10	1.25
			20	1.21
			40	1.14
			80	1.08
	100	Width	5	1.24
			10	1.24
			20	1.21
			40	1.14
			80	1.08

Note: the sinuosities are measured as the ratio of the length of the geometric distance of the least-cost ordinal scaled corridor over the geometric straight line distance between the source and destination.

Each row of Table 3(a,b) shows that for both the least ordinal-scaled cost corridors and least-cost corridors, the average 0–10% (or 0–20%) area was smallest and increased from left to right across the columns. Notably, the least ordinal-scaled cost corridors generally had a smaller average 0–10% (or 0–20%) area and larger average 40–50% (or 40–60%), … , 90–100% (or 80–100%) areas than the least-cost corridors. As for the effects of the two defining parameters of a problem type, all the average segment areas increased with corridor width and changed only slightly with number of unique cost values, for both types of corridors.

Table 4(a,b) indicate that the least ordinal-scaled cost corridors had a larger average sinuosity than the least-cost corridors for all problem types, and that the average sinuosity of both types of corridors generally decreased with as the corridor width increased but did not change much with number of unique cost values. The most costly segments of the least ordinal-scaled cost corridors tended to be significantly smaller than that of the least-cost corridors for any problem type (compare each row of the first column in Tables 3(a) and 1(b)).

Lastly, none of the 2500 least ordinal-scaled corridors and the 2500 least corridors self-intersected.

5.2. Experiment 2

Table 5(a,b) present the average running times for converting a cost grid to a graph and searching the graph for a shortest path to find a least ordinal-scaled cost corridor and a least-cost corridor, respectively, for the 100 instances of each of the 15 problem types (specified by the number of unique cost values and the corridor width associated with the corresponding row). Note that the former running time is referred to here as ‘G2 G’ time and the latter as ‘SP’ time.

Table 5. Average running times for grid to graph conversion and shortest path search in seconds of (a) the 100 least ordinal-scaled cost corridors and (b) the 100 least-cost corridors for each problem type and grid size.

(a) Least ordinal-scaled cost corridors
				Grid Size
				250-by-250		500-by-500		750-by-750
				G2G	SP	G2G	SP	G2G	SP
Number of Unique Values	10	Width	5	0.25	0.11	1.00	0.82	2.49	2.48
			10	0.39	0.10	1.63	0.65	3.88	2.00
			20	0.70	0.08	3.12	0.51	7.10	1.56
			40	1.41	0.06	6.81	0.36	16.27	1.20
			80	2.82	0.04	16.46	0.25	41.85	0.87
	50	Width	5	0.62	0.17	2.59	1.15	5.93	3.52
			10	0.78	0.15	3.31	0.91	7.38	2.70
			20	1.10	0.12	4.81	0.71	10.76	2.11
			40	1.81	0.09	8.53	0.51	20.05	1.63
			80	3.11	0.05	18.03	0.35	45.57	1.19
	100	Width	5	1.08	0.21	4.68	1.41	10.44	4.10
			10	1.28	0.19	5.48	1.11	12.08	3.22
			20	1.59	0.16	6.98	0.87	15.74	2.59
			40	2.24	0.11	10.53	0.66	24.73	2.03
			80	3.47	0.07	19.72	0.46	50.32	1.53
(b) Least-cost corridors
				Grid Size
				250-by-250		500-by-500		750-by-750
				G2G	SP	G2G	SP	G2G	SP
Number of Unique Values	10	Width	5	0.08	0.06	0.34	0.28	0.79	0.69
			10	0.18	0.07	0.71	0.29	1.92	0.71
			20	0.44	0.06	1.87	0.27	4.26	0.62
			40	1.09	0.05	4.89	0.21	11.80	0.56
			80	2.48	0.03	13.65	0.15	34.50	0.46
	50	Width	5	0.08	0.06	0.33	0.27	0.86	0.71
			10	0.17	0.06	0.71	0.30	2.03	0.75
			20	0.41	0.06	1.87	0.21	4.39	0.65
			40	1.05	0.05	4.91	0.21	12.21	0.58
			80	2.43	0.03	13.66	0.15	34.71	0.46
	100	Width	5	0.08	0.06	0.33	0.27	0.82	0.68
			10	0.17	0.07	0.71	0.30	2.03	0.75
			20	0.43	0.06	1.93	0.22	4.33	0.64
			40	1.09	0.05	4.97	0.21	11.85	0.56
			80	2.41	0.03	13.81	0.15	34.47	0.46

For all problem types, the least ordinal-scaled cost corridors had longer average G2 G time and SP time than the least-cost corridors. Still, their computational behaviours were similar in the following aspects. First, their average G2 G times increased almost linearly with grid size and corridor width. Second, their average SP times increased faster than linearly with grid size and decreased with increasing corridor width but only slightly. A major difference between the two types of corridors was that while both average G2 G time and SP time for the least ordinal-scaled cost corridors increased almost linearly with number of unique cost values, those for the least-cost corridors were not affected by it.

Finally, it is worth mentioning that for both types of corridors the G2 G time significantly dominated the SP time.

6. Demonstration

With the goal of demonstrating the proposed model’s practical value, we applied it to a 2019 study by Gärds and Oscarsson (2019), which explored the possibility of alternative alignment of the existing highway between two Swedish cities, Jönköping and Huskvarna. The major task was to identify a promising location for a right-of-way of 400 metres required for a highway route between two specified locations.

6.1. Data

In the study, waterbodies, slope, proximity to buildings, and land cover were found relevant factors to placement of the highway, which led to four respective raster cost surfaces created as follows.

• Waterbody cost surface – derived from a land cover map, where water bodies were masked, and near shore and rivers were assigned cost values between 0 and 1.

• Slope cost surface – derived from an elevation map, classified into six slope ranges, with each given a score of 0, 3, 5, 7, 10, and 25 based on the per cent slope and its relevant slope criteria. Those scores were then transformed to a standardized cost between 0 and 1 using a linear scaling method.

• Land cover cost surface – derived from a land cover map with 11 land cover types. The values were reclassified to combine similar land cover types, resulting in six land covers. The land cover classes were then ranked in order of preference for construction and assigned cost between 0 and 1.

• Proximity to buildings cost surface – derived from a map of building footprints. Euclidean distance from buildings was calculated, and the distance was classified into four bins. Each bin was given an ordered score between 0 and 3 based on the relevant proximity to building criteria. Finally, the scores were transformed to a standardized cost between 0 and 1 using a linear scaling method.

All the four cost surfaces had the same spatial extent (1320 rows and 700 columns) and resolution (20 metres) and were combined into a single composite cost surface by calculating a weighted sum of their cost values on a cell-by-cell basis. The weight of each cost surface was determined by applying the analytical hierarchy process (see Eastman, Kyem, and Toledano 1993 for an outline of its procedure) to the relative importance of each factor perceived by the involved planners. The cost surface contained 69 different values ranging from 0 to 820, and as seen in Table 6, their distribution was heavily skewed to the left.

Table 6. Frequency distribution of cost values over the study area.

	0% − 10%	10% − 20%	20% − 30%	30% − 40%	40% − 50%	50% − 60%	60% − 70%	70% − 80%	80% − 90%	90% − 100%	Total
Number of Cells in Cost Surface	531	233	624	57233	5267	9087	275870	416879	77624	41838	885186

Note: The range of the cost values was divided into 10 intervals (indicated by the 0%-10% to 90%-100% columns) of equal length.

6.2. Problem

Given the cost surface with a resolution of 20 metres and the two terminal locations, the task of aligning the highway right-of-way of 400 metres was seen as a problem of finding a least-cost corridor with a width of 20 cells between two terminal neighbourhoods. In the original study, the cost values were assumed to be measured on a ratio scale. In this demonstration, we were interested in how different a solution might result if this assumption were to be violated.

Thus, we solved the highway alignment problem as a least ordinal-scaled cost corridor problem and as a least-cost corridor problem using the methods described in the preceding sections. Then, we evaluated the two output corridors in terms of their segment areas (i.e. the 0–10% segment to the 90–100% segment) and sinuosity.

7. Results

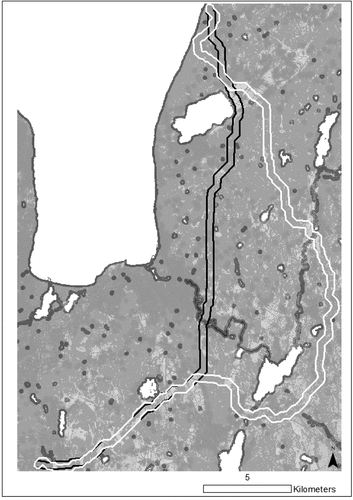
Figure 9 shows the least ordinal-scaled cost corridor and the least-cost corridor generated. When visually inspected, we saw that the former had many small turns, as well as one large turn avoiding a stretch of more costly cells. This differed from the least-cost corridor, which had few small turns and no large turns. This was reflected in the sinuosities of the two corridors: 1.75 for the least ordinal-scaled cost corridor and 1.22 for the least-cost corridor.

Figure 9. The least ordinal-scaled cost corridor (outlined in white) and the least-cost corridor model (outlined in black) between the two terminal locations. Note that the darker shades represent higher cost values, and white represents prohibited areas.

Table 7 presents the 0–10% to 90–100% areas of the two corridors. Both corridors avoided costly cells, as the least ordinal-scaled cost corridor completely avoided those cells with the top 20% highest cost values and the least-cost corridor contained only two such cells. A major difference was that the least ordinal-scaled cost corridor did not contain a single cell until the 30–40% value range, whereas the least-cost corridor already contained cells in the more costly value ranges. However, the former had a larger area overall than the latter, by 1.44 times.

Table 7. Areas of segments of the least ordinal-scaled cost corridor and the least-cost corridor.

	0% − 10%	10% − 20%	20% − 30%	30% − 40%	40% − 50%	50% − 60%	60% − 70%	70% − 80%	80% − 90%	90% − 100%	Total
Least Ordinal-Scaled Cost Corridor	0	0	0	42	0	108	3834	32601	6701	5424	48710
Least-Cost Corridor	2	0	43	148	0	36	5159	19824	4421	4201	33834

Note that the area of each segment of a corridor is measured in terms of number of cells.

As for the computational cost, the grid-to-graph conversion took 31.61 and 23.51 s for the least ordinal-scaled cost corridor model and the least-cost corridor model, respectively. A larger difference was seen in the shortest path search, as the former model took 7.22 and the latter model took 0.91 s.

8. Discussion

8.1. Qualities

The results presented in Tables 1 and 3 suggest that the proposed least ordinal-scaled cost corridor model produces corridors which avoid high-cost cells. The area of least ordinal-scaled cost corridors containing cells with the 10% most costly values is small in absolute and proportional terms, making up a significantly smaller proportion of the corridors than the rest of values in the cost surface. While this is also true for least-cost corridors, the area of least ordinal-scaled cost corridors containing the most costly values tends to be smaller than that of least-cost corridors (the 0–10% areas and 10–20% areas in Tables 1 and 3).

It was found that the overall areas of least ordinal-scaled cost corridors were larger than those of least-cost corridors. This was most likely because the former corridors took more turns to sidestep high-cost cells, which resulted in a higher sinuosities (see Tables 2 and 4) and larger areas of cells with less costly values (see Tables 1 and 3). An implication of this is that if the foremost desire is to minimize values which are ordered as more costly than others, the least ordinal-scaled cost corridors will be preferable to least-cost corridors, but at the cost of the corridor potentially being longer overall. Without knowing the differences in cost values, however, it is not certain that longer least ordinal-scaled cost corridors will cost more than their least-cost counterparts.

There were no instances of self-intersection in the experiments or the demonstration, despite the increase in sinuosity in the least ordinal-scaled cost corridors. However, it is not certain that self-intersection will never happen. This is because as the number of unique values increases, least ordinal-scaled cost corridors may take more turns and have a higher sinuosity, as seen with those corridors found in cloudy cost surfaces (see Table 2). The chance of a corridor self-intersecting increases with its sinuosity. Therefore, we may not see self-intersecting corridor on cost surfaces with small number of unique values, such as those derived from land cover data, which are unlikely to go beyond the number tested in this paper. For example, the United Nations Food and Agriculture Organization’s Land Cover Classification System has identified just 22 land cover classes for the entire globe (Di Gregorio and Jansen 2005), and the United States Geological Survey defines 16 land cover classes in the National Land Cover Database for the United States (Yang et al. 2018).

Another finding was that the ability to avoid high-cost cells was affected by the frequency distribution of values in the cost surface (as observed by Murekatete and Shirabe (2018) with least-cost paths). This was well illustrated by the least ordinal-scaled cost corridors found on cloudy cost surfaces that contained a smaller area in the least costly value range (see the second-to-last column of each row in Table 1(a)). The same was seen with the least ordinal-scaled cost corridor found in the demonstration (see the second-to-last column of Table 7). This might seem counterintuitive because avoiding more costly cells would normally result in a larger area of less costly cells. The unexpectedly small area of less costly cells in those corridors is explained by the fact that the corresponding cost surfaces had a significantly small number of less costly cells.

8.2. Efficiency

Both the grid-to-graph (G2 G) conversion and the shortest path (SP) search for least ordinal-scaled cost corridors took longer than those for least-cost corridors. The time it takes for the G2 G conversion time for both the least ordinal-scale cost corridors and the least-cost corridors increased almost linearly with the number of nodes in the graph. This can be explained by their computational complexities of the G2 G conversion, which are O(nqw) and O(nw) for least ordinal-scaled cost corridor and the least-cost corridor, respectively, where n is the number of cells in the cost surface, q is the number of unique values, and w is the corridor width. Similarly, the SP time for both least ordinal-scaled cost corridors and least-cost corridors increased faster than linearly with the number of nodes in the graph. This can be explained again by their computational complexities of the SP search, which are O(n²q) and O(n²) for the least ordinal-scaled cost corridor and least-cost corridor, respectively. However, both G2 G time and SP time for least ordinal-scaled cost corridors became longer as the number of unique values in the cost surface increased, whereas those for least-cost corridors did not, which was expected given the presence and absence of q in their respective complexities. What was unexpected, however, was that the SP search for both least ordinal-scaled cost corridors and least-cost corridors had slightly smaller running times as the width of the corridors grew. This is explained by the fact that as the width of the corridor increases, there are fewer valid neighbourhoods in the raster cost surface, and therefore fewer nodes in the graph.

Given the additional dependence on the number of unique values in the cost surface (q) in both the G2 G conversion and SP search, the running time of least ordinal-scaled cost corridors runs the risk of becoming significantly longer if the number of unique values in the cost surface becomes too large. As discussed above, it is expected that many cost surfaces are derived from land cover maps, and therefore the number of values in a cost surface will remain the same even as the size of the surface grows. This does not rule out cases in which the cost surface has been derived from more than one factor and may result in a larger number of unique values, similar to those in the application demonstration.

The G2 G conversion dominates the processing time for least ordinal-scaled cost corridors and least-cost corridors in this study. However, in a similar experiment by Shirabe (2016), the average running time for the G2 G conversion for a least-cost corridor was not much. For example, it was 0.27 s when the dimensions of the cost surface were 500-by-500, there were 100 unique cost values, and the corridor width was 80, compared to 13.81 s in Experiment 2. This led us to believe the longer running times of the G2 G conversions in Experiment 2 was most likely because our implementation of the models was not optimal. This suggests that the running time of the G2 G conversion could be significantly reduced.

Though we have identified the problem on a two-dimensional raster grid with rectangular (square) cells, and developed the algorithm accordingly, this problem is potentially seen on other data types. For example, in future work we could see adapting the heuristic for vector data or raster grids with other shapes of cells. Additionally, we could extend the 3D least-cost corridor introduced in Seegmiller (2021) using a 3D neighbourhood form to a 3D least ordinal-scaled cost corridor. Finally, to further test the method currently proposed, we may consider using a parallel algorithm with openMP or GPU in the future.

9. Conclusions

We have introduced a new variant of the least-path problem called ‘the least ordinal-scaled cost corridor problem’, in which the values of a cost surface are not quantitatively measured and a path has width as well as length. We have formulated it as a special case of the preferred path problem with a lexicographic preference relation and solved it as such. Through computational experiments, we have found that least ordinal-scaled cost corridors effectively avoid costly cells, but at the expense of elongating their forms and increasing the running time in comparison to least-cost corridors. As demonstrated with a real-world example of highway alignment, the least ordinal-scaled cost corridor problem holds promise as an alternative to existing optimal routing models when there is not full information on the data and cost evaluation involves high degrees of subjectivity and uncertainty.

Acknowledgments

The authors thank the editor and anonymous reviewers for their valuable and constructive comments on earlier drafts of the article. Any errors remain, of course, the sole responsibility of the authors. This work was supported by the Swedish Research Council Formas under Grant 942-2015-1513.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The work was supported by the Swedish Research Council [942-2015-1513].