Circulatory System Based Optimization (CSBO): an expert multilevel biologically inspired meta-heuristic algorithm

ABSTRACT

The optimization problems are becoming more complicated, requiring new and efficient optimization techniques to solve them. Many bio-inspired meta-heuristic algorithms have emerged in the last decade to solve these complex problems as most of these algorithms may be trapped into local optima and could not effectively solve all types of optimization problems. Hence, researchers are still trying to develop new and better optimization algorithms. This paper introduces a novel biologically-based optimization algorithm called circulatory system-based optimization (CSBO). CSBO is modeled based on the function of the body’s blood vessels with two distinctive circuits, i.e. pulmonary and systemic circuits. The proposed CSBO algorithm is tested on a wide variety of complex functions of the real world and validated with the standard meta-heuristic algorithms. The results indicate that the CSBO algorithm successfully achieves the optimal solutions and avoids local optima. Note that the source code of the CSBO algorithm is publicly available at http://www.optim-app.com/projects/csbo.

KEYWORDS:

• Circulatory System Based Optimization (CSBO)
• complex optimization functions
• optimization
• biologically inspired algorithm
• and real-world problems

1. Introduction

Optimizing the design process is one of the most critical topics most engineers and inventors consider. A typical design can be optimized if its parameters are selected appropriately. Optimization is a mathematical tool that selects the best decision from the available set of possible solutions to achieve the ideal goal. After defining the problem variables, it is considered a function called the objective function. Physical conditions are then displayed as constraints on the problem. Then, the optimal solution is obtained by solving the resulting model using optimization methods (Radosavljević, 2018).

Generally, an optimization problem, whether it is a minimization or maximization, can be described as follows (Radosavljević, 2018): (1) $\begin{array}{r}\text{Minimize}z=F(\mathit{x})\end{array}$(1) Subject to: (2) $\begin{array}{rl}{g}_i(\mathit{x})& \le 0;i=1,2,\dots ,n\end{array}$(2) (3) $\begin{array}{rl}{h}_j(\mathit{x})& =0;j=1,2,\dots ,m\end{array}$(3) (4) $\begin{array}{rl}{x}_d^l\le x_d& \le x_d^u;d=1,2,\dots ,D.\end{array}$(4)

In the above equation, $F(\mathit{x})$ represents the objective function of a typical optimization problem, $\mathit{x}$ is the vector of variables with D dimension, i.e. the algorithm inputs. $g_i(\mathit{x})$ and $h_j(\mathit{x})$ vectors are the inequality and equality constraints of the problem, and n and m parameters are the number of the inequality and equality constraints, respectively.

Optimization problems from different application perspectives can be divided into the following different categories:

• Static and dynamic: If the objective function varies with time, the optimization problem is dynamic; otherwise, it is static.

• Constrained and unconstrained: A constrained optimization problem involves variables restricted to a specific set or constraint, and an unconstrained optimization problem concerns variables that are not restricted.

• Linear or non-linear: The objective function and constraints of linear optimization problems are linear functions of the design variables.

• Discrete and continuous: A discrete optimization problem has certain discrete control variables. On the other hand, in a continuous problem, the values of the variables are continuous.

• Random and non-random: In an optimization problem, depending on whether the variables are real, binary, or random values, the problem is divided into different categories of true, binary, or random.

• Single and multi-objective: A problem can have multiple objective functions. Each of them requires the setting of specific control parameters.

The optimization problems’ methods are divided into four categories: counting, computational, innovative, and meta-heuristic methods. As with dynamic programming, counting expands the scope of the search space in each iteration because there is only one point in the domain space of the objective function at a time. Computational methods interface applied mathematics, statistics, information science, and engineering. It emphasizes analytically intractable problems of classical and quantum computations. Researchers are interested in developing computational and mathematical methods to quantify, analyze, and understand recent applications in more complicated systems. Unlike the mathematical methods with a mathematical basis and the convergence of algorithms, the innovative and meta-heuristic methods are proven (where the problem is convex) and may not have proper convergence. Suppose the objective function is not convex or concave in solving optimization problems. In that case, there is almost no mathematical algorithm to guarantee the optimal global solution. Therefore, different optimization methods and a new stochastic algorithm have been established. In these methods, a close and acceptable optimal solution is obtained in a limited and acceptable time. These methods are random and inspired by nature and physical processes. Due to the drawbacks of the mathematical methods, evolutionary methods have been proposed for optimization problems. Among them, the following algorithms have been introduced. Finally, but certainly not least, developing novel algorithms is a prominent area of research for many researchers. Evolutionary events, the collective behavior of species (swarm intelligence approaches), physical laws, and human-related concepts can all serve as inspiration for developing a new algorithm. Indeed, the inspired meta-heuristic algorithms are classified into four subclasses as a primary classification (Mirjalili, 2016):

• Natural evolutionary processes or occurrences inspire evolutionary algorithms (EAs): such as using the behavior of flora for artificial flora algorithm (AFA) (L. Cheng et al., 2018), plant intelligence (Akyol & Alatas, 2017), virulence optimization algorithm (VOA), and an optimization strategy inspired by the ideal process through which viruses attack bodily cells (Jaderyan & Khotanlou, 2016), evolution strategies (ESs), a sub-class of nature-inspired direct search (Rechenberg, 1989). Genetic algorithms (GAs) are search heuristics inspired by Charles Darwin’s theory of natural evolution (Holland, 1992). An opposition-based high dimensional optimization algorithm (OHDA) unique feature is its angular movement in response to very few samples, enabling successful search in high dimensions (GhaemiDizaji et al., 2020). An artificial infectious disease algorithm via the SEIQR epidemic model (G. Huang, 2016) aims to show the relationship of an infectious disease to an optimization algorithm. Mouth brooding fish algorithm (Jahani & Chizari, 2018) models organisms’ symbiotic interaction tactics to live and reproduce in an environment and finds the optimal answer by using mouth brooding fish movement, dispersion, and protection patterns. Colonial competitive differential evolution (CCDE), which is based on mathematical modeling of socio-political evolution (Ghasemi et al., 2016), tree growth algorithm (TGA) that replicates the fight for food and light among trees (Cheraghalipour et al., 2018), invasive tumor growth (ITGA) achieved by abnormal cells detaching from the tumor bulk because of a decrease in or complete lack of intercellular adhesion molecules (Tang et al., 2015), slime mould algorithm (SMA) that inspired via the foraging and diffusion conduct of slime mould (Li et al., 2020), and invasive weed optimization (IWO) that mimics weed colony’s behavior (Mehrabian & Lucas, 2006).

• Swarm Intelligence Algorithms (SIAs) development: Simulating natural patterns and behaviors in nature is one of the primary goals of SIAs. Fitness dependent optimizer (FDO), which simulates the behavior of the bee swarm in order to locate better colonies (Abdullah & Ahmed, 2019), lion optimization algorithm (LOA) that inspired by lions’ unique lifestyle and social behavior (Yazdani & Jolai, 2016), monarch butterfly optimization (MBO) that inspired via idealizing and simplifying the travel of monarch butterflies (Wang et al., 2019), yellow saddle goatfish algorithm, an optimization model motivated by yellow saddle goatfish hunting behavior involving chaser and blocker fish (Zaldívar et al., 2018), Aquila optimizer (AO) that inspired via the Aquila’s strategies in nature during the process of catching the prey (Abualigah et al., 2021), sailfish optimizer (SO) influenced by a group of hunting sailfish (Shadravan et al., 2019), moth search algorithm (MSA) that motivated via the Lévy flights and phototaxis of the moths (Wang, 2018), ant colony optimization (ACO) (Dorigo & di Caro, 1999), kidney-inspired algorithm (KA) making a novel population-based algorithm informed by the human kidney mechanism (Jaddi et al., 2017), artificial hummingbird algorithm (AHA) that mimics the intelligent foraging behaviors and flight skills of hummingbirds (Zhao et al., 2022), a naturalistic approach to Harris hawks optimization (HHO) (Heidari et al., 2019), artificial ecosystem-based optimization (AEO), a population-based optimizer that mimics three unique traits of live organisms (Zhao et al., 2020), Chameleon swarm algorithm (CSA) that mimics the dynamic skills of chameleons when hunting and navigating for food sources (Braik 2021), crow search algorithm (CSA) motivated by crows’ social smart tendency for hiding food (Askarzadeh, 2016), cooperation search algorithm (CSA) taking cues from modern business teamwork (Feng et al., 2021), grasshopper optimization algorithm (GOA) based on the natural foraging and swarming activity of grasshoppers (Saremi et al., 2017), COOT algorithm motivated by the dynamic behavior of the population of birds (Naruei & Keynia, 2021), black widow optimization algorithm (BWOA) prompted by black widow spider mating rituals (Hayyolalam & Kazem, 2020), JAYA algorithm a gradient-free optimization technique (R. Rao, 2016), tunicate swarm algorithm (TSA), which mimics tunicate navigation and foraging turbojet engines and swarming behavior (Kaur et al., 2020), chimp optimization algorithm (COA) influenced by chimps’ individuality and sexual motivation (Khishe & Mosavi, 2020), pity beetle algorithm (PBA) based on a beetle’s aggregation habit (Kallioras et al., 2018), emperor penguin optimizer (EPO) resembles emperor penguin huddling (Dhiman & Kumar, 2018), ludo game-based met-heuristics (P. R. Singh et al., 2019), which uses two or four players to imitate the game ludo to update distinct swarm intelligent characteristics, Fox optimization algorithm (RFO) which uses a mathematical model of red fox hunting, developing population, searching for food, and habits (Połap & Woźniak, 2021), galactic swarm optimization (GSO) via motion between stars (Muthiah-Nakarajan & Noel, 2016), parasitism–predation algorithm (PPA) to tackle the challenges of low convergence and the constraint of dimensionality of enormous data (A.-A. A. Mohamed et al., 2020), earthworm optimization algorithm (EWA) via the butterfly adjusting operation and migration operation (Wang et al., 2018), Barnacle mating habits in nature served as inspiration for BMO (Sulaiman et al., 2020), a biological-inspired optimization algorithm named squirrel search algorithm (SSA) (Jain et al., 2019), colony predation algorithm (CPA) based on animals to avoid enemies (Tu et al., 2021), wild geese algorithm (WGA) which natural life and death in the wild is its basis (Ghasemi et al., 2021), hunger games search (HGS) which mimics the behavioral choice and hunger-driven activities of animals (Yang et al., 2021), bald eagle search optimization algorithm (BESO) an innovative, based on bald eagles’ hunting tactics or social conduct when searching for fish (Alsattar et al., 2020), phasor particle swarm optimization (PPSO) based on a phasor-theoretic model of particle design variables with a phase angle (Ghasemi et al., 2019), elephant herding optimization (EHO) which mimics the herding behavior of elephants (Wang et al., 2015), buttery optimization algorithm (BOA) that imitates the natural foraging and mating activities of butterflies (Sharma et al., 2021).

• Physics-Inspired algorithms (PIAs): Yin-Yang-pair optimization (YYO) algorithm via physical event or specific tool (Punnathanam & Kotecha, 2016), an algorithm by Franklin’s and Coulomb’s laws theory, i.e. the CFA optimizer (Ghasemi et al., 2018), gradient-based optimizer (GBO) which uses Newton’s approach to investigate the search domain using a number of vectors and two major operators (Ahmadianfar et al., 2020), electromagnetic field optimization (EFO) that the behavior of electromagnets with varying polarities and a natural ratio called the golden ratio is its basis (Abedinpourshotorban et al., 2016), weIghted meaN oF vectOrs (INFO) which uses a solid structure and updating the vectors’ position (Ahmadianfar et al., 2022), wind driven optimization (WDO) algorithm which updates the velocity and position of wind-controlled air parcels regarding the physical equations that control air motion (Bayraktar et al., 2013), Lévy flight distribution (LFD) (Houssein et al., 2020), Equilibrium optimizer (EO) a revolutionary optimization technique for the implementation of control volume mass balance models (Faramarzi et al., 2020), simulated annealing (SA) a method involves metalworking process of heating and cooling a material to change its physical qualities (Kirkpatrick et al., 1983), supernova optimizer (SO) motivated by supernova phenomena (Hudaib & Fakhouri, 2018), dynamic differential annealed optimization (DDAO) (Ghafil & Jármai, 2020), henry gas solubility optimization (HGSO) encouraged by Henry’s law (Hashim et al., 2019), artificial chemical reaction optimizer (ACRO), which is designed to be inspired by chemical reactions (Alatas, 2011), water evaporation optimization (WEO) that simulates the evaporation of water molecules on a solid surface with varying wettability (Kaveh & Bakhshpoori, 2016), rain-fall optimization based on behavior of raindrops (Kaboli et al., 2017), gases Brownian motion optimization (GBMO) motivated by gas Brownian movement and turbulent rotational motion (Abdechiri et al., 2013), atom search optimization (ASO) basis of the basic of molecular dynamics (Zhao et al., 2019), turbulent flow of water-based optimization (TFWO) fascinated by whirlpools formed in turbulent water flow (Ghasemi et al., 2020), thermal exchange optimization (TEO) based on Newton’s law of cooling (Kaveh & Dadras, 2017), heat transfer search (HTS) which the law of thermodynamics and heat transfer are its basis (Patel & Savsani, 2015), RUNge Kutta algorithm (RUN) which the law of the Runge Kutta (RK) method and the mathematical foundations (Ahmadianfar et al., 2021), weighted superposition attraction (WSA) in which agents create a superposition that causes other solution vectors to follow (Baykasoğlu & Akpinar, 2017), and gravitational search algorithm (GSA) based on mass exchanges and gravity (Rashedi et al., 2009).

• Human/social-related Algorithms (HSAs): political optimizer (PO) replicating the human political process (Askari et al., 2020), a very optimistic method (Vommi & Vemula, 2018) employing two factors; luck and effort, future search algorithm (FSA) which mimics the person’s life (Elsisi, 2019), volleyball premier league algorithm (VPLA) that works through interacting and competing among volleyball teams (Moghdani & Salimifard, 2018), path planning algorithm (PPA) to find a sequence of valid configurations (Zhou et al., 2017), pathfinder algorithm (PA) that tries to solve the graph theory’s shortest path problem (Yapici & Cetinkaya, 2019), teaching–learning-based optimization (TLBO) algorithm that examines a teacher’s impact on students (R.V. Rao et al., 2011), imperialist competitive algorithm (ICA) suggests an optimization method influenced by imperialism (Atashpaz-Gargari & Lucas, 2007), collective decision optimization (CDO) that human social behavior based on decision-making traits is its basis (Q. Zhang et al., 2017), and queuing search algorithm (QSA) which is stimulated from human doings in queuing process (J. Zhang et al., 2018).

As mentioned above, many optimization algorithms have been proposed recently. As stated by no free lunch theorems (Wolpert & Macready, 1997), the real-world deal with a wide range of complex problems with different objective functions. Therefore, the inherent nature of algorithms may have the best functionality for several functions. However, it suffers from performing well for several other problems. No single algorithm can effectively solve a wide variety of real-world problems, which is the fundamental reason for presenting these new algorithms. For example, the problems addressed in CEC 2014 functions consist of 30 different test functions: unimodal, simple multimodal, hybrid, and composition. In CEC 2014, it has attempted to design these 30 test functions to cover a wide range of real-world problems, such as engineering design and economic load dispatch in small to large-scale systems. Therefore, researchers need an algorithm that can cover a broader range of problems to rank excellently for every 30 test functions.

On the other hand, time is a significant factor in many optimization problems. Therefore, a new algorithm that is powerful and robust and has a reasonable speed to reach an acceptable optimal solution is required. Besides, each optimization algorithm has several control parameters that the user must determine their values according to his experience, which is sometimes time-consuming and questionable. Therefore, a simple and robust algorithm is required to give the optimal and reasonable result with lower control parameters. In other words, the need for a comprehensive and robust algorithm is well felt in all branches of science. This article introduces an algorithm called CSBO that can achieve these goals.

The CEC 2005, CEC 2014, and CEC 2017 standard test functions are utilized in this paper to demonstrate the effectiveness of the CSBO. These standard test functions cover a wide range of functions, such as multimodal, multimodal, and hybrid functions. We compare the results with several modern and standard algorithms at each optimization stage to show the algorithm’s performance.

Briefly, the advantages of the proposed algorithm can be listed below:

• A new meta-heuristic algorithm inspired by regular body function

• Ability to perform effectively for a wide range of real-world functions

• Having a special competitive performance compared to modern and standard algorithms

The remainder of this article is summarized as follows: the conceptual and mathematical formulations of the CSBO algorithm are introduced in Section 2. In Section 3, the performance of the proposed algorithm is benchmarked on real-world test functions. The application of the proposed algorithm for solving some engineering optimization problems with complicated search spaces is investigated in Section 4. Finally, Section 5 represents some essential conclusions.

2. Circulatory System Based Optimization (CSBO) algorithm

Modeling is one of the most important branches of engineering that is a good way to study the behavior of a system (Ghasemi et al., 2021). Models are representations of different systems. With the help of the model, the effect of different factors on the system can be simulated. Of course, models must predict the behavior of different systems and functions of each problem in different conditions.

2.1. Regular circulatory system

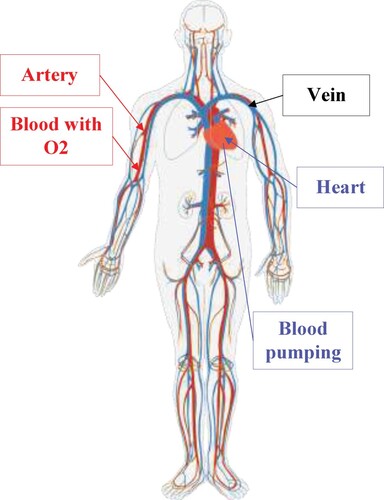
This article presents a new powerful optimizer using the circulatory system function model. The heart is a fantastic organ that pumps oxygen and nutrient-rich blood through the human body to sustain life. The heart is an essential part of the cardiovascular system, called the circulatory system. It contains all elastic, muscular tubes (vessels) that carry blood from the heart to the body and back to it.

Blood is vital for the body. In addition to carrying fresh oxygen from the lungs and nutrients to the body’s tissues, it also eliminates the body’s waste products, including carbon dioxide, away from the tissues. This circulation is necessary to sustain life and promote the health of all parts of the body.

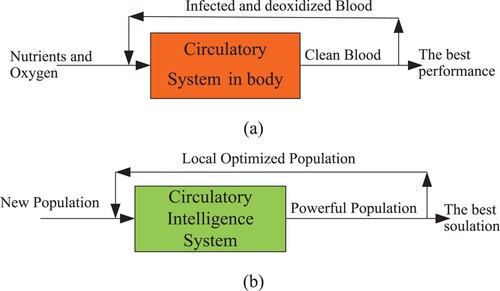
According to the simple inspiration model from the circulatory system of the body’s regular performance in Figure 1, the body’s blood vessels are functionally divided into two distinctive circuits: the pulmonary circuit and the systemic circuit. The pump for the pulmonary circuit, which circulates blood through the lungs, is the right ventricle. The left ventricle is the pump for the systemic circuit, which provides the blood supply for the body’s tissue cells. Pulmonary circulation transports oxygen-poor blood from the right ventricle to the lungs, where the blood picks up a new blood supply. Then it returns the oxygen-rich blood to the left atrium.

Figure 1. A simple inspiration model from the circulatory system for modeling CSBO (‘Pixabay.com,’ n.d.).

Blood is considered a Newtonian fluid in most cases. The main variables of the circulatory system are flow, pressure, and volume. Pressure-flow modeling of the circulatory system can be examined from two perspectives, beating and non-beating, which is considered in a model inspired by the beating perspective.

Arteries and veins are considered cylindrical vessels whose walls have elastic properties. To stimulate blood flow in most models, the momentum continuity (Fan et al., 2009), known as the Navier-Stokes equations (Johnston et al., 2006), is used with the assumption of constant density and viscosity. The Newtonian fluid can be expressed in the following general form regardless of several gravitations. (5) $\begin{array}{rl}\rho \left(\frac{\mathrm{\partial }v}{\mathrm{\partial }t}+v-\mathrm{\nabla }v\right)& =-\mathrm{\nabla }P-\mathrm{\nabla }.\tau \end{array}$(5) (6) $\begin{array}{rl}\Delta \overrightarrow{U}& =0\end{array}$(6) Where $\rho$ is the fluid density, $v$ is the velocity vector, $P$ is the pressure, t represents time, and $\tau$ is the stress tensor.

The systemic circulation provides the functional blood supply to all body tissue. It carries oxygen and nutrients to the cells and picks up carbon dioxide and waste products. Systemic circulation carries oxygenated blood from the left ventricle, through the arteries, to the capillaries in the body’s tissues. From the tissue capillaries, the deoxygenated blood returns through a system of veins to the right atrium of the heart. It then moves into the right ventricle, and the above cycle is repeated, equivalent to one iteration in our proposed algorithm.

In this algorithm, we have modeled two pulmonary and systemic circuits as two separate groups with two different optimization cycles. They are equivalent to specific functions modeled on a specific type of population.

Here, this process of the circulatory system is equivalent to the generation of a more substantial population and elimination of a weaker population in the optimization algorithm. The mathematical modeling of the CSBO optimization process is explained in the following sections.

2.2. Circulatory system regular performance as an intelligent systematic algorithm: CSBO

In the mathematical modeling of new meta-heuristic optimization algorithms, many hypotheses based on the inspiration of the phenomenon may be considered. In this section, we briefly explain how to model the circulatory system function as an optimizer and implement the proposed CSBO algorithm.

In the CSBO algorithm, like any other meta-heuristic optimization algorithm, at first, an initial population is generated based on a random function within the problem range, which here represents the mass of blood droplets. The position of the blood droplets represents the possible solutions to an optimization problem in the search space, and the circulatory system acts as an operator of this population to refine and strengthen them and eliminate the weaker population. In other words, the solution (blood) quality in the search space (body) is improved throughout an iterative process based on the functionality of the blood’s circularity system in the body.

In the proposed algorithm, the pulmonary circulation deals with deoxygenated blood, which is equivalent to the weaker population, and the systematic circulation deals with oxygenated blood, which is equivalent to the population with a better target value. In other words, it deals with a better population. The ith blood mass (BM_i) (or ith individual of the population in CSBO) will move based on its position. In other words, it will be directed to a more optimal position; otherwise, it will maintain its current position. Figure 2 shows how the evolutionary process of the blood in the circulatory system equivalently can be modeled as an optimizer system. Also, Table 1 shows, in detail, how the elements or functions of the circulatory system are modeled in the proposed CSBO algorithm.

Figure 2. The blood circulatory (a) and equivalent optimizer (b) process.

Table 1. The equivalent concepts of the circulatory system and CSBO algorithm.

Element or function in the circulatory system	The equivalent concept in the CSBO algorithm
Blood mass	Algorithm population
Blood movement in the body	Population movement within the problem range
Cleaner blood with more oxygen	Objective function
Circulation cycle	Algorithm iteration
Deoxygenated blood	Weaker population
Oxygenated blood	Stronger population
Blood purification	Population composition
Blood pumping	Changing the population position
CO2 separation from blood	Crossover
Pulmonary and systemic circulations	Population separation

2.3. The mathematical modeling of the CSBO algorithm

At first, the CSBO algorithm, like any other meta-heuristic algorithm, starts with an initial population or blood masses $B{M}_i=(B{m}_{i,1},B{m}_{i,2},\dots ,B{m}_{i,D})$ for a typical problem with the number of dimensions D (d= 1:D), which randomly generates between the minimum $B{M}_{\text{min}}=(B{m}_{\text{min,1}},B{m}_{min,2},\dots ,B{m}_{min,D})$ and maximum $B{M}_{\text{max}}=(B{m}_{max,1},B{m}_{max,2},\dots ,B{m}_{max,D})$ values of the problem parameters range as follows: (7) $\begin{array}{rl}B{M}_i& =B{M}_{\text{min}}+rand(1,D)\\ & \times (B{M}_{\text{max}}-B{M}_{\text{min}});i=1:Npop.\end{array}$(7) This initial population, as mentioned earlier, plays the same role as blood particles or masses in the body.

2.3.1. Movement of blood mass in the veins

The ith blood mass in the veins, BM_i, moves based on the imposed force or pressure. The mass always moves in a direction that has more optimal conditions. Therefore, the value of its objective function (amount of force or pressure) decreases. We can model the clogged arteries in the heart as trapping in locally optimal solutions. We like this situation not to happen like in the real world. As the body continues to work, the algorithm will continue its optimization process well. This step of the circulatory cycle is modeled based on the particle positions and their objective function values as follows: (8) $\begin{array}{rl}B{M}_i^{new}& =B{M}_i+K_{i1}\times p_i\times (B{M}_i-B{M}_1)\\ & +K_{23}\times p_i\times (B{M}_3-B{M}_2)\end{array}$(8) (9) $\begin{array}{rl}{K}_{ij}& =\frac{F(B{M}_j)-F(B{M}_i)}{|F(B{M}_j)-F(B{M}_i)|+\epsilon }\\ & =\{\begin{array}{l}1;F(B{M}_i)<F(B{M}_j)\\ -1;F(B{M}_i)>F(B{M}_j)\\ 0;F(B{M}_i)=F(B{M}_j)\end{array}\end{array}$(9) In fact, $K_{ij}$ determines the direction of movement of the ith blood mass (BM_i) in the arteries. p_i is a value between 0 and 1 and depends on the problem dimensions. It determines the amount of displacement and moves toward a better value in each circulation cycle.

2.3.2. Population or blood mass flow in pulmonary circulation

As mentioned earlier, the pulmonary circulation deals with deoxygenated blood, equivalent to the weaker population in optimization. In fact, in the CSBO, at each iteration, the population is sorted, and NR numbers of the weakest population enter the pulmonary circulation and are directed to the lungs to gain oxygen (10) $\begin{array}{r}B{M}_i^{new}=B{M}_i+\left(\frac{randn}{it}\right)\times randc(1,D),i=1:NR\end{array}$(10) In (7), randn denotes the random normal number, it indicates the current algorithm iteration, randc indicates the random vector from the Cauchy probability distribution, and D is the number of the optimization problem dimension. The pulmonary circulation also changes the $p_i$ for this population as follows: (11) $\begin{array}{r}{p}_i=rand(1,D),i=1:NR\end{array}$(11)

2.3.3. Population or blood mass flow in systematic circulation

As mentioned, NR numbers of the weakest sorted population enter the pulmonary circulation. The rest of the population (NL = Npop-NR) that have a better fit value enter the systematic circulation with a new amount in order to circulate through the body, as modeled below: (12) $\begin{array}{r}B{M}_{i,j}^{new}=B{M}_{1,j}+p_i\ast (B{M}_{3,j}-B{M}_{2,j})\end{array}$(12) The systematic circulation also corrects the $p_i$ for this group of population as follows: (13) $\begin{array}{r}{p}_i=\frac{F(B{M}_i)-F_{\text{Worst}}}{F_{\text{Best}}-F_{\text{Worst}}},i=1:NL\end{array}$(13) where $F_{\text{Worst}}$ and $F_{\text{Best}}$ are the worst and best values of cost function obtained until the current iteration.

The cycle of optimization will be continued for the specified number of iterations. Similar to other meta-heuristic algorithms, each member of the population will accept the new position if it gets a better value of the fitness function.

The CSBO algorithm pseudo-code is summarized in Algorithm 1.

3. The competitive study based on the standard real-world benchmark functions: CEC 2005, CEC 2014, and CEC 2017 benchmarks

Table

In order to confirm the functionality of our proposed inspired approach, named CSBO algorithm, a test bed of well-known 14 CEC 2005, 30 CEC 2014 and 29 CEC 2017 benchmarks functions is employed in the following experiments.

3.1. CEC2005 benchmark functions

In this section, the first fourteen CEC 2005 popular test functions (Y. Wang et al., 2011) have been utilized to show the performance of the proposed algorithm. These functions, which have been used in a wide variety of optimization articles in recent years, are shown in Table 2.

Table 2. Summary of the selected 14 test functions from CEC 2005 (Y. Wang et al., 2011) for testing CSBO for global real-parameter optimization (F_min = 0).

Real-parameter unimodal test functions:		[BSmin, BSmax]
Shifted Sphere	$F1=\sum _{i=1}^D{z}_i^2$, the o = [o1, o2, … , oD] (the shifted global optimum) for all functions. Moreover, the $z=x-o$ for all shifted functions and all shifted Rotated functions.	[−100, 100] ^D
Shifted Schwefel’s Problem 1.2	$F2=\sum _{i=1}^D{\left(\sum _{j=1}^i{z}_j\right)}^2$.	[−100, 100] ^D
Shifted Rotated High Conditioned Elliptic	$F3=\sum _{i=1}^D({10}^6{)}^{\frac{i-1}{D-1}}{z}_i^2$, where $z=(x-o)\ast M$, and the M: orthogonal matrix.	[−100, 100] ^D
Shifted Schwefel’s Problem 1.2 with Noise in Fitness	$F4=\left(\sum _{i=1}^D{\left(\sum _{j=1}^i{z}_j\right)}^2\right)\ast (1+0.4|N(0,1)|)$.	[−100, 100] ^D
Schwefel’s Problem 2.6 with Global Optimum on Bounds	$F5=max\{|A_{i}x-B_i|\}$, the A is a D*D matrix, Ai is the ith row of A. Bi = Ai * o. o is a D*1 vector, and oi is a random number in the range [−100, 100].	[−100, 100] ^D
Real-parameter multimodal test functions:
Shifted Rosenbrock’s	$F6=\sum _{i=1}^{D-1}(100(z_i^2-z_{i+1}{)}^2+(z_i-1{)}^2),z=x-o+1.$	[−100, 100] ^D
Shifted Rotated Griewank’s without Bounds	$F7=\frac{1}{4000}\sum _{i=1}^D(z_i{)}^2-\prod _{i=1}^D\cos \left(\frac{z_i}{\sqrt{i}}\right)+1$, $z=(x-o)\ast M$, $M=M^{,}(1+0.3|N(0,1)|)$. M' is the linear transformation matrix, condition number = 3 orthogonal matrix.	[−600, 600] ^D
Shifted Rotated Ackley’s with Global Optimum on Bounds	$F8=-20exp(-0.2\sqrt{D^{-1}\sum _{i=1}^D{z}_i^2})-exp\left(D^{-1}\sum _{i-1}^D\cos (2\pi z_i)\right)+20+e$, $z=(x-o)\ast M$.	[−32, 32] ^D
Shifted Rastrigin’s	$F9=\sum _{i=1}^D(z_i^2-10\cos (2\pi z_i)+10)$, $z=x-o$.	[−5, 5] ^D
Shifted Rotated Rastrigin’s	$F10=\sum _{i=1}^D(z_i^2-10\cos (2\pi z_i)+10)$, $z=(x-o)\ast M$.	[−5, 5] ^D
Shifted Rotated Weierstrass	.	[−0.5, 0.5] ^D
Schwefel’s Problem 2.1	$\begin{array}{rl}F12& =\sum _{i=1}^D(A_i-B_i(x){)}^2,\\ A_i& =\sum _{j=1}^D(a_{ij}\sin {\alpha }_j+b_{ij}\cos {\alpha }_j),\\ B_i(x)& =\sum _{j=1}^D(a_{ij}\sin x_j+b_{ij}\cos x_j),\end{array}$.aij, bij are random integer numbers in the range [−100,100], α is a random number from [−π,π ].	[−π, π]^D
Real parameter expanded multimodal test functions:
Shifted Expanded Griewank’s plus Rosenbrock’s Function	$\begin{array}{rl}F13& =F8(F2(z_1,z_2))+\dots +F8(F2(z_{D-1},z_D))\\ & +.F8(F2(z_D,z_1))+,z=x-o+1.\end{array}$	[−3, 1] ^D
Shifted Rotated Expanded Schaffer’s F6 Function	$\begin{array}{rl}F14& =F6(z_1,z_2)+\dots +F6(z_{D-1},z_D)\\ & +.F6(z_D,z_1)+,z=(x-o)\ast M.\end{array}$, $z=(x-o)\ast M$	[−100, 100] ^D

3.1.1. Number of population in CSBO algorithm

This section selects five different populations for our algorithm and then runs the optimization function. These populations are 30, 45, 60, 75 and 90. The same computer did all the simulations 30 times per test function and 300,000 function evaluations (NFEs) (Y. Wang et al., 2011) with 30 dimensions.

The simulation results with NR = 15 are given in Table 3. In the last column, three indexes are shown in which Nb (the number of the best results) is the number of tries that the algorithm obtained the best results in comparison with other studied algorithms, Nw (the number of the worst results) is the number of tries that the algorithm obtained the worst results compared to other studied algorithms and Mr (the mean rank) is the average rank of all obtained tries among all the test functions. According to this Table 3, the algorithm can perform well with different populations. For example, the population of 45 could be an appropriate choice for D = 30. We chose this number for the rest of our work.

Table 3. Summary of the results for CSBO from CEC2005 with D = 30 and NR = Npop/3.

		Npop = 30	Npop = 45	Npop = 60	Npop = 75	Npop = 90
Functions		Mean ± Std.R	Mean ± Std.R	Mean ± Std.R	Mean ± Std.R	Mean ± Std.R
Unimodal	F1	0 .0 ± 0 .0	0 .0 ± 0 .0	0 .0 ± 0 .0	0 .0 ± 0 .0	0 .0 ± 0 .0
		1	1	1	1	1
	F2	2.03E −23 ± 3.38E −23	2.69E −21 ± 4.38E −21	1.43E −17 ± 2.26E −17	1.42E −14 ± 3.46E −14	8.94E −13 ± 1.33E −12
		1	2	3	4	5
	F3	34640 ± 20429	35093 ± 23108	60587 ± 30084	48267 ± 26321	76693 ± 36766
		1	2	4	3	5
	F4	27.84 ± 31.1	0.581 ± 0.942	0.0629 ± 0.102	0.0134 ± 0.0349	0.00829 ± 0.0155
		5	4	3	2	1
	F5	740 ± 537	149 ± 193	340 ± 509	55.88 ± 77.4	116.9 ± 229
		5	3	4	1	2
Basic multimodal	F6	2.14 ± 2.06	0.532 ± 1.40	0.553 ± 1.41	0.70 ± 1.23	3.42 ± 2.88
		4	1	2	3	5
	F7	0.0272 ± 0.0245	0.0177 ± 0.0145	0.020 ± 0.0173	0.0128 ± 0.0144	0.00607 ± 0.00919
		5	3	4	2	1
	F8	20.95 ± 0.0524	20.95 ± 0.0463	20.96 ± 0.0355	20.96 ± 0.0451	20.96 ± 0.0479
		1	1	2	2	2
	F9	1.66E −15 ± 1.83E −15	0 .0 ± 0 .0	0 .0 ± 0 .0	0 .0 ± 0 .0	0 .0 ± 0 .0
		2	1	1	1	1
	F10	71.77 ± 10.74	83.44 ± 12.06	84.5 ± 10.88	87.18 ± 11.23	94.95 ± 10.18
		1	2	3	4	5
	F11	31.06 ± 1.33	30.37 ± 1.53	30.79 ± 0.914	31.53 ± 1.27	31.77 ± 1.42
		3	1	2	4	5
	F12	41256 ± 6491	22139 ± 23412	49124 ± 17694	56649 ± 7280	64075 ± 11207
		2	1	3	4	5
Expanded multimodal	F13	2.7 ± 0.243	3.09 ± 0.302	3.34 ± 0.314	3.51 ± 0.288	3.90 ± 0.415
		1	2	3	4	5
	F14	12.84 ± 0.204	12.91 ± 0.21	12.87 ± 0.32	12.98 ± 0.192	13.07 ± 0.225
		1	3	2	4	5
Nb/Nw/Mr		7/4/2.36	6/0/1.93	2/1/2.64	3/1/2.79	4/9/3.43

3.1.2. Effect of NR on CSBO performance analysis

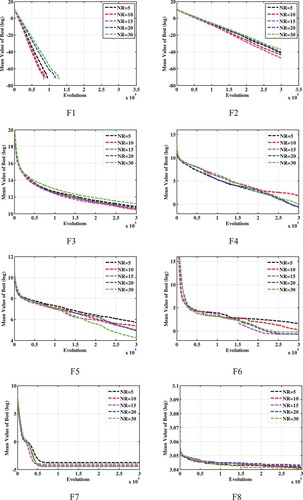
In this section, we consider different values of NR, i.e. 5, 10, 15, 20 and 30, to assess the algorithm’s effectiveness. All the simulations were done by taking 45 populations. From the results, it is evident that different values of NR have a negligible effect on CSBO. For F2, F3, F6, F9, F11, and F14, NR = 15 leads to better performance. However, the efficiency of CSBO deteriorates quickly with the decrease of NR to 5 for more text functions (except F1 and F14). For the rest values of NR (10, 20, and 30), CSBO has approximately the same performance as NR = 15. Therefore, according to Table 4, NR = Npop/3 is an appropriate choice for our algorithm.

Table 4. Summary of the results CSBO for CEC2005 test functions for testing different NR with Npop = 45 and D = 30.

NR		5	10	15	20	30
Functions		Mean ± Std.R	Mean ± Std.R	Mean ± Std.R	Mean ± Std.R	Mean ± Std.R
Unimodal	F1	0.0 ± 0.0	0.0 ± 0.0	0.0 ± 0.0	0.0 ± 0.0	0.0 ± 0.0
		1	1	1	1	1
	F2	1.01E−18 ± 2.51E−18	1.14E−19 ± 2.66E−19	2.69E−21 ± 4.38E−21	4.00E−18 ± 6.12E−18	7.62E−17 ± 1.94E−16
		3	2	1	4	5
	F3	52056 ± 33375	390224 ± 27925	35093 ± 23108	45437 ± 24326	72386 ± 41031
		4	2	1	3	5
	F4	0.526 ± 0.672	5.15 ± 19	0.581 ± 0.942	0.545 ± 1.81	0.99 ± 1.46
		2	5	3	1	4
	F5	304 ± 354	220 ± 273	149 ± 193	139 ± 249	70.2 ± 134
		5	4	3	2	1
Basic multimodal	F6	5.05 ± 2.95	1.40 ± 1.81	0.532 ± 1.40	0.532 ± 1.40	0.797 ± 1.65
		34	23	11	41	52
	F7	0.0228 ± 0.0115	0.0130 ± 0.0133	0.0177 ± 0.0145	0.0121 ± 0.00914	0.0112 ± 0.0119
		5	3	4	2	1
	F8	20.94 ± 0.0546	20.92 ± 0.0644	20.95 ± 0.0463	20.97 ± 0.0421	20.91 ± 0.0706
		3	2	4	5	1
	F9	9.47E−16 ± 1.63E−15	1.18E−16 ± 4.59E−16	0.0 ± 0.0	0.0 ± 0.0	0.0 ± 0.0
		3	2	1	1	1
	F10	88.2 ± 15.2	81.8 ± 10.1	83.44 ± 12.06	89.82 ± 10.76	89.07 ± 10.76
		3	1	2	5	4
	F11	30.7 ± 1.15	30.4 ± 1.76	30.37 ± 1.53	32.05 ± 1.49	32.2 ± 1.64
	F12	41046 ± 14303	37680 ± 8969	22139 ± 23412	45986 ± 11205	20768 ± 24578
		4	3	2	5	1
Expanded multimodal	F13	2.95 ± 0.235	2.94 ± 0.273	3.09 ± 0.302	3.43 ± 0.109	3.40 ± 0.205
		2	1	3	5	4
	F14	12.91 ± 0.192	12.91 ± 0.166	12.91 ± 0.21	13.03 ± 0.157	13.00 ± 0.195
		1	1	1	3	2
Nb/Nw/Mr		2/4/3.07	4/1/2.29	7/0/2.0	4/5/3.0	6/3/2.64

R denotes the algorithm ranking in the corresponding function compared to other algorithms in Table 4, in which 1 and 5 indicate the best and worst rank, respectively, and this is true for all parts of this paper.

In Figure 3, the summary of the CSBO convergence curves has been shown based on the results given in Table 4 to optimize CEC2005 functions. As it is clear from these curves, the CSBO has a decent convergence speed for most functions. According to the figures, although the convergence characteristic of NR = 5 for the F9 curve has the highest convergence rate, its final solution is inferior compared to other NR values. On the other hand, NR = 15 has the best convergence characteristic. Moreover, the convergence rates for the NR = 10 and 30 and even NR = 5 are also acceptable.

Figure 3. The convergence rates of CSBO in different NR values of Table 4.

3.1.3. Comparison with other algorithms

This section proposes the test functions obtained by the CSBO algorithm compared with other standard algorithms in related articles, as shown in Table 5 with NFEs: 3.00E + 05 for D = 30 and 500,000 for D = 50. The parameter setting of some competitor algorithms, in this case, is given in Table 6. In this table, the plus sign (+) represents that other algorithms outperform the offered CSBO, the minus sign (−) denotes that other algorithms underperform the proposed CSBO, and the equal sign (=) shows the same functionality.

Table 5. Summary of the results for CEC2005 test functions for different algorithms with D = 30 and NFEs = 3.00E + 05.

		GL-25	HRCGA	EPSDE	SaDE	SLPSO	APSO	FIPS	CSBO
Functions		MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R
Unimodal	F1	5.60E−27	2.10E−13	0.0	0.0	1.00E−13	7.20E−14	1.30E + 02	0.00.01
		1.76E−26	7.29E−13	0.0	0.0	1.74E−13	1.38E−13	2.47E + 03
		2/–	5/–	1/=	1/=	4/–	3/–	6/–
	F2	4.04E + 01	1.17E + 01	4.23E−26	8.26E−06	1.82E−02	1.40E−06	1.72E + 02	2.69E−214.38E−212
		6.28E + 01	1.03E + 02	4.07E−261/+	1.65E−054/–	9.53E−025/–	1.57E−053/–	4.44E + 02
		7/–	6/–					8/–
	F3	2.19E + 06	8.01E−13	8.74E + 05	4.27E + 05	1.19E−13	7.39E−14	8.87E + 03	3.51E + 042.31E + 045
		1.08E + 06	4.99E−12	3.28E + 06	2.08E + 05	1.47E−13	1.43E−13	2.62E + 05
		8/–	3/+	7/–	6/–	2/+	1/+	4/+
	F4	9.07E + 02	1.31E + 03	3.49E + 02	1.77E + 02	1.16E + 04	9.46E + 02	7.70E + 02	5.81E−019.42E−011
		4.25E + 02	3.62E + 037/–	2.23E + 03	2.67E + 02	2.99E + 04	3.30E + 03	2.81E + 03
		5/–		3/–	2/–	8/–	6/–	4/–
	F5	2.51E + 03	NA	1.40E + 03	3.25E + 03	NA	NA	NA	1.49E + 021.93E + 021
		1.96E + 02		7.12E + 02	5.90E + 02
		3/–		2/–	4/–
Basic multimodal	F6	2.15E + 01	8.59E + 00	6.38E−01	5.31E + 01	1.07E + 01	2.99E + 01	3.56E + 06	5.32E−011.40E + 001
		1.17E + 00	6.50E + 01	1.49E + 002/–	3.25E + 01	1.40E + 02	1.68E + 02	8.31E + 07
		5/–	3/–		7/–	4/–	6/–	8/–
	F7	2.78E−02	NA	1.77E−02	1.57E−02	NA	NA	NA	1.77E−021.45E−022
		3.62E−02		1.34E−02	1.38E−02
		3/–		2/=	1/+
	F8	2.09E + 01	2.11E + 01	2.09E + 01	2.09E + 01	2.04E + 01	2.12E + 01	2.10E + 01	20.954.63E−023
		5.94E−02	3.08E−01	5.81E−02	4.95E−02	8.46E−01	3.57E−01	2.68E−01
		2/+	5/–	2/+	2/+	1/+	6/–	4/–
	F9	2.45E + 01	2.99E + 01	3.98E−02	2.39E−01	1.17E−13	5.74E + 00	4.81E + 01	0.00.01
		7.35E + 00	4.87E + 01	1.99E−01	4.33E−01	1.79E−13	9.09E + 00	5.71E + 01
		6/–	7/–	3/–	4/–	2/–	5/–	8/–
	F10	1.42E + 02	1.07E + 02	5.36E + 01	4.72E + 01	1.15E + 02	1.33E + 02	1.90E + 02	8.34E + 011.21E + 013
		6.45E + 01	4.07E + 02	3.03E + 01	1.01E + 01	2.49E + 02	3.00E + 02	6.04E + 01
		7/–	4/–	2/+	1/+	5/–	6/–	8/–
	F11	3.27E + 01	1.67E + 01	3.56E + 01	1.65E + 01	3.29E + 01	3.04E + 01	3.75E + 01	3.03E + 011.53E + 003
		7.79E + 00	4.37E + 01	3.88E + 00	2.42E + 00	1.45E + 01	2.51E + 01	1.03E + 02
		5/–	2/+	7/–	1/+	6/–	4/–	8/–
	F12	6.53E + 04	NA	3.58E + 04	3.02E + 03	NA	NA	NA	2.21E + 042.34E + 042
		4.69E + 04		7.05E + 03	2.33E + 03
		4/–		3/–	1/+
Expandedmultimodal	F13	6.23E + 00	NA	1.94E + 00	3.94E + 00	NA	NA	NA	3.09E + 003.02E−012
		4.88E + 00		1.46E−01	2.81E−01
		4/–		1/+	3/–
	F14	1.31E + 011.84E−01	NA	1.35E + 01	1.26E + 01	NA	NA	NA	1.29E + 012.10E−012
		3/–		2.09E−01	2.83E−01
				4/–	1/+
+/–/=		1/13/0	2/7/0	4/8/2	6/7/1	2/7/0	1/8/0	1/8/0	–
Mr/Final rank		4.5714/6	4.6667/7	2.8571/3	2.7143/2	4.2222/4	4.4444/5	6.4444/8	2.0714/1

NA: Not Available.

Table 6. The parameter setting of different algorithms.

Algorithm	Comparison
GL-25	PG = 25%, NF^G = 250, NM^G = 500, NF^L = 5, NM^L = 100.
HRCGA	PG = 25%, NF^G = 200, NM^G = 400, NF^L = 5, NM^L = 100.
EPSDE	Each member in the initial population is assigned a mutation strategy and parameter values randomly selected from the respective pools. The mutation strategy and parameter values produce better offspring survive while those who fail to produce better offspring are reinitialized.
SaDE	The F values are randomly generated with a mean and standard deviation of 0.5 and 0.3. The mutation strategy and the parameter CR are self-adapted based on their previous performance.
SLPSO	ω = 0.9 − 0.5 ∗$\frac{Iter}{Ite{r}_{\text{max}}}$, η = 1.496, γ = 0.01.
APSO	ω = [0.4, 0.9], η1 + η1 = [3, 4] with adapting tuning and global star for population topology.
FIPS	χ = 0.7298, $\sum c_i$ = 4.1 with local URing for population topology.

We compared our algorithm with GL-25 (global and local real-coded genetic algorithms based on parent-centric crossover operators) (Y. Wang et al., 2011), HRCGA (real-coded genetic algorithm) (C. Li et al., 2011), EPSDE (an ensemble of trial vector generation approaches and control parameters of DE) (Y. Wang et al., 2011), SaDE (DE with strategy adaptation) (Y. Wang et al., 2011), SLPSO (self-learning particle swarm optimizer) (C. Li et al., 2011), APSO (an adaptive PSO) (C. Li et al., 2011) and FIPS or FIPSO (a fully informed PSO) (C. Li et al., 2011). Although the proposed algorithm is basic, it can conquer other algorithms in the same circumstance, which shows its effectiveness as a novel solution for optimization problems. The ‘–’, ‘’, and ‘=’ denote that the performance of the corresponding algorithm is worse than, better than, and similar to that of CSBO, respectively.

From Table 5, it can be found that SaDE and EPSDE generally have similar performance after CSBO. FIPS algorithm has the worst performance among all in this table. In addition, PSO and GA have the same average ranking. Moreover, SaDE has the most comparable performance to CSBO in the test functions of F6 and F14. It should be noted that SaDE is an enhanced evolved algorithm, while CSBO is the first version of its kind.

3.2. CEC 2014 benchmark functions

This section investigates the results of implementing the CSBO on CEC 2014 benchmark functions.

3.2.1. CSBO initial evaluation in comparison with original classical algorithms

In order to verify the performance of the proposed CSBO algorithm compared to other algorithms, we have selected the CEC2014 functions in this section. These are real-world modeled optimization functions. CEC 2014 functions (unimodal, simple multimodal, hybrid, and composition benchmark tests) (J. J. Liang et al., 2013) have been used successfully in many recent articles and, therefore, in this paper to test the performance of the proposed CSBO algorithm, we have used them. These functions are described (Liang et al., 2013).

In this section, we have selected two dimensions, 30 and 50, with 30 runs for each test function. The number of evolutions in all parts of the article is 300,000 and 500,000 for two dimensions, 30 and 50, respectively. Also, Npop and NR for these two dimensions are set at 45 and 15 and 60 and 20, respectively. The parameter setting of some of the competitor algorithms is given in Table 7.

Table 7 Parameters of some competitors for CEC2014 test functions.

Algorithm	Parameter settings
LDWPSO	Npop = 40, inertia weight w linearly decreasing from 0.9 to 0.4, acceleration coefficients c1 = c2 = 2, Global topology
FIPSO	Npop = 40, χ = 0.729, $\sum c_i$ = 4.1 with local URing for population topology.
BLPSO	Npop = 40, inertia weight w linearly decreasing from 0.9 to 0.2, acceleration coefficients c1 = c2 = 1.496, the maximum possible immigration and emigration rates I = E = 1.
GL-25	PG = 25%, NF^G = 250, NM^G = 500, NF^L = 5, NM^L = 100.
RCBBOG	Npop = 100, maximum habitat probability mmax = 0.005, maximum possible immigration and emigration rates I = E = 1, linear migration model
GBABC	Npop = 60, limit = 100, crossover probability CR = 0.3.

The simulation results for D = 30 are given in Table 8, compared to the robust and modern algorithms in (X. Chen et al., 2017) e.g. LDWPSO (linearly decreasing inertia weight PSO), FIPSO or FIPS, BLPSO (biogeography-based learning PSO), RCBBOG (real code biogeography-based optimization with Gaussian mutation), GL-25, and GBABC (Gaussian bare-bones artificial bee colony). Both tables clearly show that the proposed CSBO algorithm has defeated all other algorithms for most functions (F1, F2, F3, F4, F13, F15, F17, F18, F20, F F21, F22, F24, F25, F26, F28, and F30). In addition, increasing the dimension of the functions could not significantly affect CSBO. Interestingly, the proposed algorithm never had the worst performance and rank for both dimensions among the algorithms, indicating the robustness and reliability of the CSBO. Nevertheless, to mention that the two algorithms, GBABC and BLPSO, overcame the CSBO for 7 and 8 test functions of D = 30, respectively, which is normal.

Table 8. Summary of the results for CEC2014 test functions for different algorithms with D = 30 and NFEs = 3.00E + 05.

		LDWPSO	FIPSO	BLPSO	RCBBOG	GL-25	GBABC	CSBO
Function		MeanStd.R/Win	MeanStd.R/Win	MeanStd.R/Win	MeanStd.R/Win	MeanStd.R/Win	MeanStd.R/Win	MeanStd.R
F1	Unimodal	3.41E + 06	1.01E + 07	2.99E + 06	3.77E + 06	8.52E + 05	9.61E + 06	1.06E + 04
		3.69E + 06	3.81E + 067/−	1.10E + 06	2.16E + 065/−	9.84E + 05	2.90E + 06	1.06E + 04
		4/−		3/−		2/−	6/−	1
F2		3.02E + 01	3.08E + 03	5.09E + 03	9.36E + 03	3.37E + 03	2.03E + 01	8.72E−143.64E−14
		5.14E + 01	2.97E + 034/−	4.25E + 03	1.08E + 047/−	5.27E + 03	5.97E + 01	1
		3/−		6/−		5/−	2/−
F3		9.31E + 01	1.85E + 03	3.67E + 00	1.53E + 04	2.18E−01	9.70E + 01	4.60E−3
		1.04E + 02	9.64E + 026/−	1.16E + 01	1.19E + 047/−	6.56E−01	1.42E + 02	1.56E−21
		4/−		3/−		2/−	5/−
F4	Simplemultimodal	1.39E + 02	1.99E + 02	2.68E + 01	7.70E + 01	9.17E + 01	3.52E + 01	4.43E + 00
		3.72E + 01	2.36E + 017/−	3.47E + 01	3.37E + 014/−	1.02E + 01	3.32E + 01	1.67E + 01
		6/−		2/−		5/−	3/−	1
F5		2.09E + 01	2.09E + 01	2.08E + 01	2.00E + 01	2.10E + 01	2.04E + 01	2.04E + 01
		8.97E−02	5.66E−024/−	7.01E−02	4.44E−031/+	3.45E−02	3.44E−02	4.98E−022
		4/−		3/−		5/−	2/=
F6		1.08E + 01	6.25E + 00	9.37E−06	2.09E + 01	7.25E + 00	5.74E + 00	6.05E + 00
		2.50E + 00	2.56E + 00	3.20E−05	2.94E + 00	3.61E + 00	2.07E + 00	6.61E + 00
		6/−	4/−	1/+	7/−	5/−	2/+	3
F7		1.50E−02	1.25E−04	9.47E−14	1.98E−02	1.70E−11	2.77E−13	2.62E−3
		1.33E−02	6.15E−04	4.31E−14	2.75E−02	4.41E−11	9.76E−14	8.33E−3
		6/−	4/+	1/+	7/−	3/+	2/+	5
F8		1.93E + 01	4.97E + 01	2.32E−01	2.83E + 01	2.38E + 01	1.78E−13	6.63E−02 2.27E−01
		4.58E + 00	1.04E + 01	5.65E−01	7.33E + 00	6.23E + 00	6.46E−14	2
		4/−	7/−	3/−	6/−	5/−	1/+
F9		5.75E + 01	1.45E + 02	3.54E + 01	5.54E + 01	5.39E + 01	4.86E + 01	5.45E + 01
		1.73E + 01	1.16E + 01	6.93E + 00	1.51E + 01	5.34E + 01	1.03E + 01	7.29E + 00
		6/−	7/−	1/+	5/−	3/+	2/+	4
F10		4.59E + 02	2.13E + 03	8.83E + 01	1.61E + 02	1.11E + 03	1.01E + 00	9.55E + 00
		2.16E + 02	5.09E + 02	6.48E + 01	1.22E + 02	4.57E + 02	7.56E−01	3.00E + 00
		5/−	7/−	3/−	4/−	6/−	1/+	2
F11		2.93E + 03	6.11E + 03	2.08E + 03	3.22E + 03	5.55E + 03	2.65E + 03	2.51E + 03
		8.68E + 02	3.63E + 02	3.82E + 02	5.42E + 02	2.13E + 03	2.73E + 02	2.30E + 03
		4/−	7/−	1/+	5/−	6/−	3/−	2
F12		1.75E + 00	2.48E + 00	8.83E−01	2.29E−01	2.96E + 00	5.81E−01	5.01E−01
		5.16E−01	2.73E−01	1.49E−01	1.17E−01	1.93E−01	7.65E−02	1.00E−01
		5/−	6/−	4/−	1/+	7/−	3/−	2
F13		4.81E−01	2.96E−01	2.21E−01	3.85E−01	3.22E−01	1.70E−01	1.62E−01
		1.32E−01	3.33E−02	2.85E−02	9.87E−02	4.93E−02	2.59E−02	3.89E−02
		7/−	4/−	3/−	6/−	5/−	2/−	1
F14		3.01E−01	2.85E−01	2.14E−01	4.77E−01	2.95E−01	9.57E−02	2.07E−01
		4.65E−02	3.16E−02	2.88E−02	2.24E−01	2.80E−02	2.05E−02	3.15E−02
		6/−	4/−	3/−	7/−	5/−	1/+	2
F15		7.60E + 00	1.50E + 01	7.41E + 00	4.37E + 01	1.27E + 01	5.43E + 00	4.86E + 00
		2.56E + 00	9.32E−01	8.49E−01	1.49E + 01	5.13E + 00	1.17E + 00	7.73E−01
		4/−	6/−	3/−	7/−	5/−	2/−	1
F16		1.08E + 01	1.18E + 01	9.67E + 00	1.18E + 01	1.21E + 01	1.08E + 01	1.08E + 01
		8.30E−01	3.17E−01	4.92E−01	7.54E−01	3.10E−01	3.42E−01	3.31E−01
		2/=	3/−	1/+	3/−	4/−	2/=	2
F17	Hybrid	3.07E + 05	4.20E + 05	1.86E + 05	1.13E + 06	1.68E + 05	9.94E + 05	1.64E + 03
		1.75E + 05	2.19E + 05	1.11E + 05	7.61E + 05	8.63E + 04	4.81E + 05	1.15E + 03
		4/−	5/−	3/−	7/−	2/−	6/−	1
F18		2.31E + 03	2.94E + 03	9.05E + 02	3.67E + 03	2.34E + 02	2.24E + 03	5.64E + 01
		2.30E + 03	3.37E + 03	1.20E + 03	4.95E + 03	2.28E + 02	2.79E + 03	4.16E + 01
		5/−	6/−	3/−	7/−	2/−	4/−	1
F19		6.98E + 00	5.72E + 00	3.74E + 00	1.49E + 01	5.01E + 00	4.90E + 00	4.45E + 00
		2.55E + 006/−	1.45E + 005/−	6.12E−011/+	1.11E + 017/−	5.63E−014/−	7.26E−013/−	9.81E−012
F20		4.87E + 02	2.23E + 03	3.12E + 02	3.83E + 04	1.62E + 02	1.36E + 03	2.80E + 01
		2.91E + 02	1.28E + 03	3.48E + 02	1.81E + 04	6.32E + 01	7.13E + 02	1.86E + 01
		4/−	6/−	3/−	7/−	2/−	5/−	1
F21		8.77E + 04	9.08E + 04	3.85E + 04	4.35E + 05	6.21E + 04	1.11E + 05	3.11E + 02
		6.75E + 04	5.86E + 04	3.19E + 04	3.50E + 05	2.82E + 04	5.50E + 04	1.05E + 02
		4/−	5/−	2/−	7/−	3/−	6/−	1
F22		1.99E + 02	1.71E + 02	1.16E + 02	4.90E + 02	1.53E + 02	1.29E + 02	1.05E + 02
		1.34E + 02	9.30E + 01	6.86E + 01	1.97E + 02	4.95E + 01	7.45E + 01	8.05E + 01
		6/−	5/−	2/−	7/−	4/−	3/−	1
F23	Composition	3.15E + 02	3.16E + 02	3.15E + 02	3.15E + 02	3.15E + 02	3.12E + 02	3.15E + 02
		1.46E−01	3.33E−01	6.11E−13	1.68E−02	2.68E−09	1.79E + 01	8.22E−13
		2/=	3/−	2/=	2/=	2/=	1/+	2
F24		2.31E + 02	2.24E + 02	2.22E + 02	2.47E + 02	2.22E + 02	2.03E + 02	2.01E + 02
		7.12E + 00	5.95E−01	7.39E−01	4.37E + 00	4.75E−01	5.39E + 00	4.51E + 00
		5/−	4/−	3/−	6/−	3/−	2/−	1
F25		2.08E + 02	2.08E + 02	2.05E + 02	2.15E + 02	2.07E + 02	2.08E + 02	2.03E + 02
		1.75E + 00	1.08E + 00	4.41E−01	6.88E + 00	1.31E + 00	9.34E−01	7.64E−01
		4/−	4/−	2/−	5/−	3/−	4/−	1
F26		1.17E + 02	1.00E + 02	1.04E + 02	1.01E + 02	1.00E + 02	1.00E + 02	1.00E + 02
		3.79E + 01	4.48E−02	1.82E + 01	1.48E−01	4.36E−02	4.85E−02	6.71E−02
		4/−	1/=	3/−	2/−	1/=	1/=	1
F27		5.46E + 02	3.33E + 02	3.08E + 02	6.89E + 02	3.02E + 02	4.03E + 02	3.14E + 02
		1.06E + 02	4.96E + 01	2.94E + 01	2.20E + 02	6.65E−01	1.01E + 00	5.23E + 01
		6/−	3/+	2/+	7/−	1/+	5/−	4
F28		1.20E + 03	1.30E + 03	7.87E + 02	1.14E + 03	8.92E + 02	7.96E + 02	7.43E + 02
		3.30E + 02	7.72E + 01	5.22E + 01	2.44E + 02	2.65E + 01	4.57E + 01	5.08E + 015
		6/−	7/−	2/−	5/−	4/−	3/−	1
F29		1.26E + 03	4.01E + 03	1.39E + 03	1.50E + 03	1.02E + 03	1.12E + 03	1.34E + 03
		8.50E + 02	1.85E + 03	1.39E + 02	3.29E + 02	1.06E + 02	1.99E + 02	3.00E + 03
		3/+	7/−	5/−	6/−	1/+	2/+	4
F30		3.59E + 03	4.40E + 03	1.19E + 03	4.20E + 03	1.26E + 03	2.02E + 03	1.11E + 03
		1.68E + 03	1.60E + 03	2.49E + 02	4.67E + 03	2.66E + 02	6.95E + 02	9.41E + 02
		5/−	7/−	2/−	6/−	3/−	4/−	1
+/−/=		1/27/2	2/27/1	7/22/1	2/27/1	4/24/2	8/19/3	#
Nb/Nw/Mr		0/2/4.6667	1/10/5.1667	6/0/2.5333	2/15/5.4333	2/2/3.60	5/0/2.9333	16/0/1.80
Final rank		5	6	2	7	4	3	1

Examining the table results, we find that although CSBO has obtained inappropriate rankings (rank 4) for the three functions 9, 27 and 29, it has a partial difference with the best mean result. For example, for function 29, the best mean result is 1.02E+ 03 obtained by the ultra-modern genetic algorithm GL-25, while this result for CSBO is 1.34E+ 03, which is acceptable. Although CSBO did its worst performance with a rank of 5 for function 7, it got the best solution for 16 test functions. Based on the last three rows of the table, we can consider it a strong and appropriate emerging algorithm.

Table 9 contains the simulation results for the LDWPSO, FIPSO, BLPSO, RCBBOG, GL-25, and GBABC in (X. Chen et al., 2017) and CSBO (this study) algorithms for D = 50. According to this table, the Mr value for a dimension size of 30 is 1.8, while the value for a dimension of 50 is 2.0333. It demonstrates that increasing the dimension reduces the performance of CSBO. Furthermore, it shows that the performance of CSBO partially decreases by increasing the dimension. Nevertheless, it still has the first ranking with the best functionality for half of the test functions without any worst results.

Table 9. Summary of the results for CEC 2014 test functions for different algorithms with D=50 and NFEs=5.00E + 05.

Function		LDWPSO	FIPSO	BLPSO	RCBBOG	GL-25	GBABC	CSBO
F1	Unimodal	6.54E + 06	3.43E + 07	5.10E + 06	3.35E + 06	2.14E + 06	8.82E + 06	1.86E + 05
		5.07E + 06	9.04E + 06	1.28E + 06	1.39E + 06	2.03E + 06	1.85E + 06	9.81E + 04
		5/−	7/−	4/−	3/−	2/−	6/−	1
F2		3.32E + 03	2.97E + 04	3.44E + 03	3.52E + 03	2.29E + 03	5.74E + 03	2.20E + 03
		4.67E + 03	3.10E + 04	2.35E + 03	4.81E + 03	1.17E + 03	7.08E + 03	3.06E + 03
		3/−	7/−	4/−	5/−	2/−	6/−	1
F3		2.93E + 03	1.15E + 04	4.23E + 01	3.41E + 04	3.41E + 02	1.35E + 03	1.06E + 02
		2.16E + 03	2.39E + 03	8.97E + 01	1.66E + 04	4.32E + 02	1.02E + 03	1.48E + 02
		5/−	6/−	1/+	7/−	3/−	4/−	2
F4	Simple	1.89E + 02	2.68E + 02	8.64E + 01	9.76E + 01	9.54E + 01	8.75E + 01	3.00E + 01
	Multimodal	5.58E + 01	3.70E + 01	5.04E + 00	3.40E + 01	1.55E + 00	2.68E + 01	3.25E + 01
		6/−	7/−	2/−	5/−	4/−	3/−	1
F5		2.11E + 01	2.11E + 01	2.09E + 01	2.00E + 01	2.12E + 01	2.06E + 01	2.03E + 01
		7.13E−02	3.65E−02	5.07E−02	5.33E−05	2.01E−02	3.93E−02	2.63E−02
		5/−	5/−	4/−	1/+	6/−	3/−	2
F6		2.60E + 01	2.02E + 01	9.22E−02	4.13E + 01	3.80E + 00	1.38E + 01	2.27E + 01
		4.37E + 00	5.56E + 00	3.21E−01	5.60E + 00	3.26E + 00	3.83E + 00	2.71E + 00
		6/−	4/+	1/+	7/−	2/+	3/+	5
F7		9.11E−03	6.07E−05	2.92E−13	1.42E−02	1.57E−08	8.53E−13	4.93E−05
		9.46E−03	1.72E−04	6.46E−14	7.10E−03	4.57E−08	5.12E−13	1.91E−04
		6/−	5/−	1/+	7/−	3/+	2/+	4
F8		4.79E + 01	1.60E + 02	4.97E−01	5.78E + 01	5.09E + 01	4.17E−13	2.61E + 01
		1.17E + 01	1.70E + 01	8.16E−01	1.07E + 01	9.19E + 00	6.89E−14	2.53E + 00
		4/−	7/−	2/+	6/−	5/−	1/+	3
F9		1.38E + 02	3.25E + 02	7.10E + 01	1.06E + 02	1.12E + 02	1.11E + 02	1.08E + 02
		2.28E + 01	1.80E + 01	9.02E + 00	2.48E + 01	1.06E + 02	1.83E + 01	9.95E + 00
		6/−	7/−	1/+	2/+	5/−	4/−	3
F10		1.09E + 03	6.63E + 03	3.63E + 02	5.54E + 02	2.52E + 03	3.75E + 00	9.28E + 02
		4.06E + 02	5.84E + 02	1.81E + 02	2.92E + 02	8.26E + 02	2.30E + 00	1.07E + 02
		5/−	7/−	2/+	3/+	6/−	1/+	4
F11		6.12E + 03	1.26E + 04	4.46E + 03	5.79E + 03	1.29E + 04	5.92E + 03	5.57E + 03
		2.42E + 03	3.03E + 02	4.77E + 02	8.05E + 02	1.51E + 03	3.86E + 02	3.80E + 02
		5/−	6/−	1/+	3/−	7/−	4/−	2
F12		2.65E + 00	3.36E + 00	8.77E−01	2.49E−01	3.81E + 00	6.96E−01	1.03E + 00
		5.62E−01	2.69E−01	1.18E−01	8.51E−02	2.06E−01	6.71E−02	7.71E−02
		5/−	6/−	3/+	1/+	7/−	2/+	4
F13		5.83E−01	4.41E−01	2.86E−01	5.26E−01	4.54E−01	2.21E−01	2.15E−01
		1.19E−01	4.78E−02	3.72E−02	1.20E−01	5.48E−02	3.42E−02	4.52E−02
		7/−	4/−	3/−	6/−	5/−	2/−	1
F14		4.07E−01	3.48E−01	2.65E−01	5.47E−01	3.45E−01	1.12E−01	3.31E−01
		1.91E−01	3.81E−02	2.42E−02	2.50E−01	2.89E−02	1.55E−02	3.56E−02
		6/−	5/−	2/+	7/−	4/−	1/+	3
F15		1.88E + 01	3.22E + 01	1.48E + 01	9.56E + 01	2.29E + 01	1.27E + 01	1.22E + 01
		6.07E + 00	1.41E + 00	1.33E + 00	1.96E + 01	1.22E + 01	2.73E + 00	1.19E + 00
		3/−	6/−	2/−	7/−	5/−	4/−	1
F16		2.08E + 01	2.15E + 01	1.82E + 01	2.13E + 01	2.16E + 01	1.99E + 01	2.03E + 01
		8.41E−01	3.10E−01	4.73E−01	6.47E−01	3.34E−01	3.26E−01	2.85E−01
		4/−	6/−	1/+	5/−	7/−	2/+	3
F17	Hybrid	5.52E + 05	1.78E + 06	5.97E + 05	9.61E + 05	4.50E + 05	2.52E + 06	8.36E + 03
		4.48E + 05	7.18E + 05	2.10E + 05	5.13E + 05	2.06E + 05	1.14E + 06	3.70E + 03
		3/−	6/−	4/−	5/−	2/−	7/−	1
F18		5.38E + 02	1.18E + 03	3.73E + 02	1.33E + 03	5.04E + 02	1.21E + 03	2.80E + 02
		4.59E + 02	9.53E + 02	3.68E + 02	1.28E + 03	2.72E + 02	1.08E + 03	2.91E + 02
		4/−	5/−	2/−	7/−	3/−	6/−	1
F19		4.37E + 01	6.51E + 01	2.16E + 01	2.27E + 01	3.44E + 01	1.36E + 01	1.21E + 01
		2.82E + 01	1.91E + 01	9.78E + 00	5.28E + 00	5.67E + 00	2.93E + 00	1.60E + 00
		6/−	7/−	3/−	4/−	5/−	2/−	1
F20		1.52E + 03	1.86E + 03	2.57E + 02	7.82E + 04	4.30E + 02	5.24E + 03	1.05E + 02
		7.99E + 02	6.23E + 02	1.41E + 02	3.66E + 04	2.34E + 02	1.63E + 03	4.26E + 01
		4/−	5/−	2/−	7/−	3/−	6/−	1
F21		3.51E + 0	1.19E + 06	3.80E + 0	1.42E + 06	3.55E + 0	1.64E + 0	1.97E + 03
		52.56E + 05	4.72E + 05	51.44E + 05	7.65E + 05	51.56E + 05	65.15E + 05	1.88E + 03
		2/−	5/−	4/−	6/−	3/−	7/−	1
F22		8.20E + 02	1.02E + 03	2.64E + 02	1.11E + 03	6.00E + 02	4.10E + 02	3.98E + 02
		2.65E + 02	2.84E + 02	1.30E + 02	3.82E + 02	4.25E + 02	1.74E + 02	1.64E + 02
		5/−	6/−	1/+	7/−	4/−	3/−	2
F23	Composition	3.45E + 02	3.51E + 02	3.44E + 02	3.44E + 02	3.44E + 02	3.39E + 02	3.44E + 02
		7.79E−01	1.26E + 00	2.56E−13	2.60E−04	2.07E−09	2.63E + 01	3.80E−13
		3/−	4/−	2/=	2/=	2/=	1/+	2
F24		2.76E + 02	2.58E + 02	2.58E + 02	2.98E + 02	2.60E + 02	2.49E + 02	2.54E + 02
		3.71E + 00	4.02E + 00	4.07E + 00	7.16E + 00	4.97E + 00	1.64E + 01	2.15E + 00
		5/−	3/−	3/−	6/−	4/−	1/+	2
F25		2.19E + 02	2.21E + 02	2.10E + 02	2.27E + 02	2.18E + 02	2.17E + 02	2.08E + 02
		3.29E + 00	2.16E + 00	7.36E−01	9.51E + 00	2.86E + 00	1.85E + 00	4.36E + 00
		5/−	6/−	2/−	7/−	4/−	3/−	1
F26		1.37E + 02	1.39E + 02	1.47E + 02	1.40E + 02	1.17E + 02	1.00E + 02	1.00E + 02
		4.91E + 01	5.11E + 01	5.08E + 01	4.96E + 01	3.78E + 01	8.14E−02	4.21E−02
		3/−	4/−	6/−	5/−	2/−	1/=	1
F27		1.01E + 03	6.99E + 02	3.24E + 02	1.33E + 03	3.33E + 02	6.18E + 02	2.71E + 02
		8.97E + 01	1.80E + 02	2.85E + 01	9.56E + 01	2.79E + 01	1.71E + 02	6.51E + 01
		6/−	5/−	2/−	7/−	3/−	4/−	1
F28		2.26E + 03	2.88E + 03	1.14E + 03	1.84E + 03	1.29E + 03	1.23E + 03	1.11E + 03
		6.77E + 02	2.18E + 02	4.20E + 01	2.47E + 02	8.01E + 01	9.26E + 01	6.12E + 01
		6/−	7/−	2/−	5/−	4/−	3/−	1
F29		1.36E + 07	2.62E + 04	1.36E + 03	2.39E + 03	1.41E + 03	1.32E + 03	6.50E + 03
		4.24E + 07	1.31E + 04	1.82E + 02	7.93E + 02	1.22E + 02	2.69E + 02	1.83E + 04
		7/−	6/−	2/+	4/+	3/+	1/+	5
F30		3.17E + 04	5.20E + 04	9.09E + 03	1.33E + 04	9.91E + 03	9.41E + 03	8.95E + 03
		1.04E + 04	1.10E + 04	3.05E + 02	2.03E + 03	3.17E + 02	5.36E + 02	4.96E + 02
		6/−	7/−	2/−	5/−	4/−	3/−	1
+/−/=		0/30/0	1/29/0	12/17/1	5/24/1	3/26/1	10/19/1	#
Nb/Nw/Mr		0/2/4.8667	0/10/5.7000	7/1/2.3667	2/11/5.0667	0/4/3.9667	7/2/3.2000	15/0/2.0333
Final rank		5	7	2	6	4	3	1

3.2.2. A comparison of CSBO with the state-of-the-art PSO algorithms (PSOs)

In this section, to better demonstrate the performance of the proposed CSBO, we compare our results with a novel example of PSO called promotional particle swarm optimizer (PPSO) (L. Zhang et al., 2021), which has been recently introduced, as well as ten other modern and basic algorithms. The ten state-of-the-art PSO algorithms (L. Zhang et al., 2021) are included: GPSO (global version PSO with inertia weight) (Eberhart & Kennedy, 1995), FIPS-URing (FIPS with URing topology) (Mendes et al., 2004), DMS-PSO (a dynamic multiswarm PSO) (J.-J. Liang & Suganthan, 2005), CLPSO (a comprehensive learning PSO) (J. J. Liang et al., 2006), MLPSO (a multilayer PSO) (L. Wang et al., 2014), SLPSO (a social learning PSO) (R. Cheng & Jin, 2015), DTTPSO (a dynamic tournament topology strategy in PSO) (L. Wang et al., 2016), HFPSO (a hybrid firefly and PSO algorithm) (Aydilek, 2018), PhaPSO (a phasor PSO) (Ghasemi et al., 2019), and XPSO (an expanded PSO) (Xia et al., 2020).

The results for dimension 30 are given in Table 10 based on the mean value and standard deviation. The winning sign is defined by +, indicating the CSBO has won over the competitor algorithm in that function. In addition, the minus sign – and equity sign = show the failure and the same performance of CSBO compared to the corresponding algorithm. Total statistical results are given in Figures 4 and 5. As can be seen from the results of the first three unimodal functions and simple multimodal function F4, CSBO results are significant and superior to PSOs. On the other hand, the performance of the proposed algorithm for the last three test functions, F28, F29 and F30, which are composition test functions, is average and relatively poor compared to PSOs. CSBO scored the worst ranking of 7 for these three test functions.

Figure 4. The competitive results of CSBO and PSOs CEC 2014 test functions.

Figure 5. The number of the best and worst results of CSBO and PSOs.

Table 10. A comparison of CSBO with the state-of-the-art PSOs for CEC 2014 functions with NFEs=3.00E + 05.

	F1			F2			F3
Optimizer	Mean	Std.	R/Win	Mean	Std.	R/Win	Mean	Std.	R/Win
GPSO	1.85E + 06	1.17E + 06	8/+	8.87E + 02	1.69E + 03	5/+	8.74E + 01	1.24E + 02	6/+
FIPS-URing	6.27E + 07	2.08E + 07	12/+	4.05E + 04	3.30E + 04	11/+	5.47E + 04	2.46E + 04	12/+
DMS-PSO	1.34E + 07	3.76E + 06	11/+	2.09E + 05	7.68E + 05	12/+	4.07E + 03	1.25E + 03	9/+
CLPSO	7.62E + 06	3.93E + 06	10/+	2.09E + 03	2.62E + 03	7/+	1.08E + 01	9.35E + 00	4/+
MLPSO	5.32E + 05	3.74E + 05	6/+	6.00E −01	2.12E + 00	2/+	8.20E + 00	1.79E + 01	3/+
SLPSO	5.09E + 05	3.84E + 05	5/+	1.08E + 04	1.09E + 04	10/+	7.14E + 03	7.36E + 03	11/+
DTTPSO	1.05E + 05	5.20E + 04	2/+	8.38E + 03	3.54E + 03	9/+	4.30E + 03	1.89E + 03	10/+
HFPSO	3.98E + 05	2.80E + 05	4/+	2.34E + 03	8.74E + 03	8/+	1.89E + 00	4.00E + 00	2/+
PhaPSO	1.31E + 06	1.70E + 06	7/+	1.16E + 03	6.29E + 03	6/+	1.61E + 03	8.81E + 03	8/+
XPSO	3.69E + 06	4.85E + 06	9/+	3.21E + 02	5.99E + 02	4/+	1.72E + 01	2.06E + 01	5/+
PPSO	2.47E + 05	1.32E + 05	3/+	3.00E + 01	3.65E + 01	3/+	1.67E + 02	2.05E + 02	7/+
CSBO	1 . 06E + 04	1 . 06E + 04	1/#	8 . 72E −14	3 . 64E −14	1/#	4 . 60E −03	1 . 56E −02	1/#
	F4			F5			F6
GPSO	2.82E + 01	1.09E + 01	7/+	2.08E + 01	7.55E −02	6/+	6.74E + 00	2.00E + 00	5/+
FIPS-URing	2.66E + 01	4.98E −01	5/+	2.10E + 01	5.21E −02	8/+	3.81E + 01	1.60E + 00	12/+
DMS-PSO	2.79E + 01	8.03E −01	6/+	2.06E + 01	6.24E −02	4/+	8.70E + 00	1.39E + 00	7/+
CLPSO	9.01E + 01	4.54E + 01	11/+	2.04E + 01	1.26E −01	3/=	5.45E + 00	3.26E + 00	2/−
MLPSO	1.26E + 01	1.15E + 01	2/+	2.07E + 01	2.27E −01	5/+	1.50E + 01	4.03E + 00	10/+
SLPSO	3.17E + 01	2.83E + 01	9/+	2.09E + 01	5.08E −02	7/+	8 . 54E −01	9 . 31E −01	1 /−
DTTPSO	1.61E + 01	2.22E + 01	3/+	2.09E + 01	5.42E −02	7/+	8.84E + 00	1.87E + 00	8/+
HFPSO	2.94E + 01	4.42E + 01	8/+	2 . 00E + 01	2 . 22E −02	1 /−	9.73E + 00	3.96E + 00	9/+
PhaPSO	7.67E + 01	4.15E + 01	10/+	2.01E + 01	1.79E −01	2/−	2.68E + 01	3.44E + 00	11/+
XPSO	1.21E + 02	4.89E + 01	12/+	2.09E + 01	1.17E −01	7/+	5.48E + 00	2.41E + 00	3/−
PPSO	2.14E + 01	1.03E + 01	4/+	2.04E + 01	3.50E −01	3/=	7.60E + 00	2.01E + 00	6/+
CSBO	4 . 43E + 00	1 . 67E + 01	1 /#	2.04E + 01	4.98E −02	3/#	6.05E + 00	6.61E + 00	4/#
	F7			F8			F9
GPSO	1.35E −02	1.58E −02	10/+	2.35E + 01	5.71E + 00	5/+	6.11E + 01	1.76E + 01	6/+
FIPS-URing	8 . 99E −05	2.95E −04	1 /−	8.75E + 01	1.21E + 01	12/+	1.66E + 02	1.14E + 01	11/+
DMS-PSO	2.01E −01	1.65E −01	12/+	5.55E + 01	5.64E + 00	9/+	7.82E + 01	9.22E + 00	8/+
CLPSO	1.90E −03	5.23E −03	5/−	3.58E + 00	1.95E + 00	2/+	3.89E + 01	1.09E + 01	2/−
MLPSO	5.58E −03	7.64E −03	7/+	4.22E + 01	8.59E + 00	7/+	7.06E + 01	2.06E + 01	7/+
SLPSO	1.56E −03	4.41E −03	4/−	1.66E + 01	3.51E + 00	3/+	1 . 78E + 01	5.38E + 00	1 /−
DTTPSO	7.38E −04	4.04E −03	2/−	7.99E + 01	1.12E + 01	11/+	7.88E + 01	1.02E + 01	9/+
HFPSO	1.11E −02	1.13E −02	9/+	5.37E + 01	1.87E + 01	8/+	7.91E + 01	2.54E + 01	10/+
PhaPSO	1.65E −02	1.90E −02	11/+	7.01E + 01	1.79E + 01	10/+	1.72E + 02	2.87E + 01	12/+
XPSO	9.67E −03	1.31E −02	8/+	2.59E + 01	9.44E + 00	6/+	4.17E + 01	1.27E + 01	3/−
PPSO	8.22E −04	2.53E −03	3/−	2.21E + 01	6.99E + 00	4/+	4.80E + 01	1.14E + 01	4/−
CSBO	2.62E −03	8.33E −03	6/#	6 . 63E −02	2.27E −01	1 /#	5.45E + 01	7.29E + 00	5/#
	F10			F11			F12
GPSO	6.41E + 02	1.91E + 02	6/+	2.69E + 03	6.26E + 02	6/+	1.25E + 00	7.00E −01	8/+
FIPS-URing	6.57E + 03	2.44E + 02	12/+	7.68E + 03	2.66E + 02	12/+	2.41E + 00	2.21E −01	11/+
DMS-PSO	2.00E + 03	3.03E + 02	11/+	3.42E + 03	2.48E + 02	10/+	8.51E −01	1.82E −01	6/+
CLPSO	3.46E + 01	4.93E + 01	2/+	2.12E + 03	5.02E + 02	2/−	4.22E −01	9.48E −02	2/−
MLPSO	9.48E + 02	3.11E + 02	7/+	3.28E + 03	6.92E + 02	9/+	1.22E + 00	6.02E −01	7/+
SLPSO	2.96E + 02	1.89E + 02	3/+	8 . 72E + 02	4.50E + 02	1 /−	2.38E + 00	3.45E −01	10/+
DTTPSO	1.42E + 03	3.64E + 02	9/+	2.40E + 03	3.81E + 02	3/−	2.46E + 00	2.57E −01	12/+
HFPSO	1.13E + 03	3.25E + 02	8/+	2.88E + 03	7.25E + 02	7/+	2 . 95E −01	1.33E −01	1 /−
PhaPSO	1.64E + 03	6.92E + 02	10/+	3.80E + 03	5.69E + 02	11/+	6.77E −01	3.77E −01	4/+
XPSO	5.58E + 02	2.07E + 02	5/+	2.43E + 03	8.79E + 02	4/−	1.80E + 00	6.92E −01	9/+
PPSO	5.28E + 02	2.52E + 02	4/+	2.89E + 03	6.88E + 02	8/+	7.52E −01	3.01E −01	5/+
CSBO	9 . 55E + 00	3.00E + 00	1 /#	2.51E + 03	2.30E + 03	5/#	5.01E −01	1.00E −01	3/#
	F13			F14			F15
GPSO	4.00E −01	9.24E −02	11/+	4.03E −01	2.65E −01	10/+	6.51E + 00	2.40E + 00	7/+
FIPS-URing	3.74E −01	5.25E −02	10/+	3.14E −01	4.46E −02	6/+	1.55E + 01	8.97E −01	11/+
DMS-PSO	2.93E −01	4.76E −02	7/+	2.64E −01	1.47E −01	4/+	1.52E + 01	1.52E + 00	10/+
CLPSO	2.56E −01	4.59E −02	6/+	2.50E −01	3.56E −02	3/+	6.63E + 00	1.24E + 00	8/+
MLPSO	3.20E −01	9.57E −02	8/+	3.69E −01	1.68E −01	9/+	5.38E + 00	2.11E + 00	5/+
SLPSO	1.68E −01	2.92E −02	2/+	4.16E −01	7.44E −02	11/+	8.08E + 00	4.88E + 00	9/+
DTTPSO	2.10E −01	4.49E −02	3/+	2.68E −01	3.83E −02	5/+	2 . 77E + 00	7.56E −01	1 /−
HFPSO	3.67E −01	9.58E −02	9/+	4.35E −01	2.65E −01	12/+	5.79E + 00	1.85E + 00	6/+
PhaPSO	5.43E −01	1.25E −01	12/+	3.35E −01	1.37E −01	8/+	3.28E + 01	1.32E + 00	12/+
XPSO	2.53E −01	6.01E −02	5/+	3.19E −01	1.79E −01	7/+	4.17E + 00	1.16E + 00	3/−
PPSO	2.23E −01	6.73E −02	4/+	2.48E −01	4.08E −02	2/+	4.09E + 00	1.40E + 00	2/−
CSBO	1 . 62E −01	3.89E −02	1 /#	2 . 07E −01	3.15E −02	1 /#	4.86E + 00	7.73E −01	4/#
GPSO	1.09E + 01	7.37E −01	5/+	2.69E + 05	1.87E + 05	9/+	5.85E + 03	7.73E + 03	11/+
FIPS-URing	1.33E + 01	1.51E −01	12/+	1.62E + 06	3.98E + 05	12/+	1.62E + 05	1.29E + 05	12/+
DMS-PSO	1.07E + 01	4.32E −01	3/−	3.24E + 05	1.98E + 05	10/+	1.49E + 03	2.08E + 03	7/+
CLPSO	1.05E + 01	5.52E −01	2/−	6.81E + 05	4.45E + 05	11/+	1.22E + 03	1.47E + 03	6/+
MLPSO	1.17E + 01	4.78E −01	9/+	8.81E + 04	8.08E + 04	5/+	4.72E + 03	5.28E + 03	10/+
SLPSO	1.20E + 01	3.05E −01	10/+	1.07E + 05	6.27E + 04	8/+	7.38E + 02	8.67E + 02	4/+
DTTPSO	1.12E + 01	4.13E −01	7/+	2.88E + 04	1.22E + 04	2/+	3.45E + 02	3.26E + 02	3/+
HFPSO	1.13E + 01	6.52E −01	8/+	7.12E + 04	5.30E + 04	4/+	3.83E + 03	6.38E + 03	8/+
PhaPSO	1.22E + 01	5.35E −01	11/+	8.99E + 04	3.70E + 05	6/+	1.17E + 02	5.44E + 01	2/+
XPSO	1 . 03E + 01	8.41E −01	1 /−	1.05E + 05	9.82E + 04	7/+	3.99E + 03	3.90E + 03	9/+
PPSO	1.09E + 01	5.63E −01	5/+	5.09E + 04	2.99E + 04	3/+	1.02E + 03	1.22E + 03	5/+
CSBO	1.08E + 01	3.31E −01	4/#	1 . 64E + 03	1.15E + 03	1 /#	5 . 64E + 01	4.16E + 01	1 /#
	F19			F20			F21
GPSO	1.02E + 01	2.40E + 00	9/+	4.13E + 02	1.63E + 02	4/+	9.27E + 04	7.66E + 04	11/+
FIPS-URing	1.75E + 01	7.88E −01	11/+	2.68E +0 4	7.75E + 03	12/+	6.46E + 05	2.68E + 05	12/+
DMS-PSO	1.29E + 01	1.00E + 00	10/+	9.03E + 02	3.22E + 02	6/+	8.66E + 04	4.13E + 04	9/+
CLPSO	6.57E + 00	1.75E + 00	3/+	9.24E + 02	5.74E + 02	7/+	9.10E + 04	8.53E + 04	10/+
MLPSO	7.34E + 00	3.40E + 00	7/+	1.06E + 03	1.03E + 03	8/+	4.82E + 04	4.54E + 04	7/+
SLPSO	7.16E + 00	1.21E + 00	6/+	2.35E + 04	1.38E + 04	11/+	7.36E + 04	6.03E + 04	8/+
DTTPSO	6.89E + 00	1.57E + 00	5/+	1.34E + 04	3.38E + 03	10/+	3.73E + 04	1.63E + 04	5/+
HFPSO	9.44E + 00	1.99E + 00	8/+	3.65E + 02	4.24E + 02	3/+	2.99E + 04	2.04E + 04	4/+
PhaPSO	1.92E + 01	1.48E + 01	12/+	4.17E + 02	1.39E + 03	5/+	2.47E + 04	1.15E + 05	3/+
XPSO	6.78E + 00	1.33E + 00	4/+	2.43E + 02	8.77E + 01	2/+	3.94E + 04	4.05E + 04	6/+
PPSO	6.38E + 00	2.31E + 00	2/+	1.76E + 03	1.34E + 03	9/+	2.11E + 04	1.42E + 04	2/+
CSBO	4 . 45E + 00	9.81E −01	1 /#	2 . 80E + 01	1.86E + 01	1 /#	3 . 11E + 02	1.05E + 02	1 /#
	F22			F23			F24
GPSO	3.12E + 02	1.13E + 02	8/+	3.14E + 02	9.70E −13	2/−	2.27E + 02	8.35E + 00	9/+
FIPS-URing	4.53E + 02	1.29E + 02	10/+	3.14E + 02	1.18E −02	2/−	2.24E + 02	6.49E −01	6/+
DMS-PSO	1.52E + 02	6.79E + 01	2/+	3.14E + 02	4.75E −02	2/−	2.30E + 02	1.90E + 00	11/+
CLPSO	1.86E + 02	9.18E + 01	3/+	3.15E + 02	2.22E −12	3/=	2.25E + 02	2.70E + 00	7/+
MLPSO	2.40E + 02	1.45E + 02	6/+	3.14E + 02	8.06E −13	2/−	2.36E + 02	7.73E + 00	12/+
SLPSO	2.08E + 02	1.06E + 02	5/+	3.15E + 02	1.28E −12	3/=	2.29E + 02	5.78E + 00	10/+
DTTPSO	4.96E + 02	1.48E + 02	11/+	3.14E + 02	5.47E −13	2/−	2.23E + 02	9.48E −01	5/+
HFPSO	4.14E + 02	1.28E + 02	9/+	3.15E + 02	8.61E −13	3/=	2.16E + 02	1.13E + 01	3/+
PhaPSO	5.85E + 02	2.36E + 02	12/+	3 . 08E + 02	2.94E + 01	1 /−	2 . 00E + 02	3.69E −02	1 /−
XPSO	2.90E + 02	9.98E + 01	7/+	3.16E + 02	1.71E −01	4/+	2.22E + 02	7.06E + 00	4/+
PPSO	2.03E + 02	9.58E + 01	4/+	3.14E + 02	4.85E −13	2/−	2.26E + 02	1.93E + 00	8/+
CSBO	1 . 05E + 02	8.05E + 01	1 /#	3.15E + 02	8.22E −13	3/#	2.01E + 02	4.51E + 00	2/#
	F25			F26			F27
GPSO	2.01E + 02	3.11E −01	2/−	1.37E + 02	4.89E + 01	6/+	4.71E + 02	7.57E + 01	6/+
FIPS-URing	2.10E + 02	2.65E + 00	8/+	1 . 00E + 02	4.44E −02	1 /=	1.29E + 03	3.39E + 01	11/+
DMS-PSO	2.05E + 02	7.13E −01	4/+	1.04E + 02	1.83E + 01	3/+	4.71E + 02	6.68E + 01	6/+
CLPSO	2.08E + 02	1.21E + 00	7/+	1.04E + 02	1.83E + 01	3/+	4.02E + 02	2.53E + 01	3/+
MLPSO	2 . 00E + 02	1.25E −01	1 −	1 . 00E + 02	8.15E −02	1 /=	6.81E + 02	1.56E + 02	9/+
SLPSO	2.06E + 02	1.82E + 00	5/+	1.17E + 02	3.79E + 01	5/+	3.70E + 02	6.17E + 01	2/+
DTTPSO	2 . 00E + 02	8.44E −14	1 /−	1.95E + 02	1.60E + 01	8/+	5.73E + 02	9.43E + 01	7/+
HFPSO	2.07E +0 2	3.81E + 00	6/+	1.47E + 02	5.05E + 01	7/+	6.48E + 02	1.50E + 02	8/+
PhaPSO	2 . 00E + 02	1.53E −08	1 /−	1.01E + 02	1.36E −01	2/+	8.99E + 02	4.45E + 02	10/+
XPSO	2.08E + 02	2.11E + 00	7/+	1.10E + 02	5.07E + 01	4/+	4.52E + 02	7.58E + 01	4/+
PPSO	2 . 00E + 02	4.13E −02	1 /−	1 . 00E + 02	5.85E −02	1 /=	4.67E + 02	5.58E + 01	5/+
CSBO	2.03E + 02	7.64E −01	3/#	1 . 00E + 02	6.71E −02	1 /#	3 . 14E + 02	5.23E + 01	1 /#
	F28			F29			F30
GPSO	4.06E + 02	2.81E + 01	4/−	2.11E + 02	2.29E + 00	3/−	7.22E + 02	2.08E + 02	3/−
FIPS-URing	3.98E + 02	2.88E + 00	2/−	2.25E + 02	1.77E + 00	5/−	8.88E + 02	2.09E + 02	6/−
DMS-PSO	3 . 96E + 02	1.89E + 01	1 /−	2.15E + 02	1.13E + 00	4/−	7.67E + 02	1.76E + 02	4/−
CLPSO	8.17E + 02	4.10E + 01	8/+	1.38E + 03	3.14E + 02	8/+	2.94E +0 3	8.83E + 03	8/+
MLPSO	4.13E + 02	1.46E + 01	5/−	2.09E + 02	3.01E + 00	2/−	6.14E + 02	2.47E + 02	2 /−
SLPSO	9.30E + 02	1.41E + 02	9/+	1.73E + 03	4.91E + 02	9/+	3.23E + 03	1.06E + 03	11/+
DTTPSO	5.97E + 02	3.86E + 02	6/−	6.59E + 02	4.44E + 02	6/−	7.87E + 02	2.74E + 02	5/−
HFPSO	1.61E + 03	4.57E + 02	11/+	7.41E + 06	8.60E + 06	11/+	2.95E + 03	1.82E + 03	9/+
PhaPSO	1.98E + 03	6.27E + 02	12/+	9.13E + 07	6.38E + 07	12/+	3.49E + 04	5.85E + 04	12/+
XPSO	1.32E + 03	3.49E + 02	10/+	5.63E + 05	3.08E + 06	10/+	3.11E + 03	1.59E + 03	10/+
PPSO	4.05E + 02	6.26E + 00	3/−	2 . 06E + 02	9.70E −01	1 /−	4 . 62E + 02	1.24E + 02	1 /−
CSBO	7.43E + 02	5.08E + 01	7/#	1.34E + 03	3.00E + 03	7/#	1.11E + 03	9.41E + 02	7/#

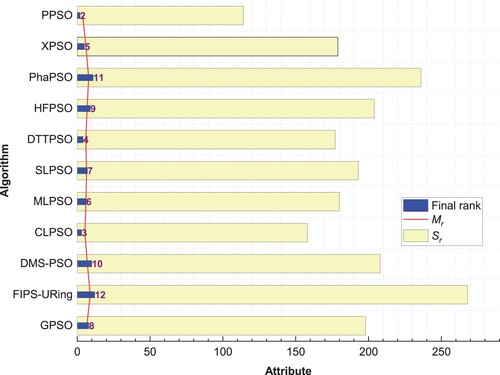
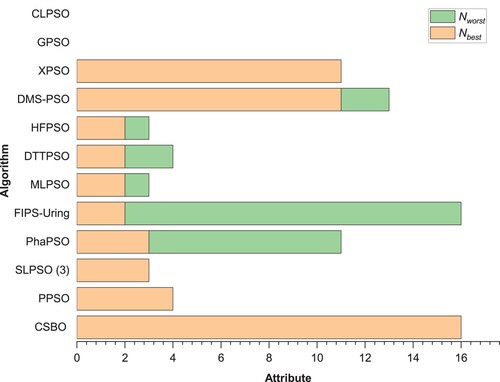
Looking at Figure 4, where S_r is the sum of the total rank of the algorithm, CSBO, with an average rank of 2.6333, is the decisive winner of this comparative study. Its closest algorithm is PPSO, with an average rank of 3.80, which is a significant difference. This Figure shows that FIPS-URing is the weakest algorithm. Figure 5 also lists the top-down algorithms based on the number of functions with the best value or rank 1 (N_best) and the number of times they have the weakest rank (N_worst). CSBO has a rank of 1 for 16 functions, while its nearest competitor, PPSO, ranks 1 in only four functions. In addition, GPSO and CLPSO did not get the best value or worst value for any function. The proposed CSBO, SLPSO, and PPSO algorithms never got the worst value, which is a great advantage for these algorithms. Moreover, although FIPS-Uring obtained the best value for two functions; it got the worst value 14 times, which shows its deficiency.

We use Wilcoxon’s test to determine whether two algorithms behave significantly differently (Ghosh et al., 2012). The p-values for applying Wilcoxon’s test on CSBO and PSOs are shown in Table 11. The p-values less than 0.05 (the significance level) are in boldface. Because of the data, it is clear that CSBO outperforms the other eleven PSO algorithms. Furthermore, although CSBO is not significantly superior to PPSO, it outperforms it on an average ranking basis.

Table 11. The competitive results of Wilcoxon’s test and performance of CLBO versus PSOs.

	The optimization performance of CSBO is			CSBO versus
Corresponding algorithm	Worse (−) than	better ( +) than	Similar (=) with	p-values
GPSO	5	25	0	4.1889E −07
FIPS-URing	5	24	1	7.1008E −08
DMS-PSO	5	25	0	1.3208E −06
CLPSO	6	22	2	1.5075E −04
MLPSO	5	24	1	1.3244E −05
SLPSO	4	25	1	1.9634E −05
DTTPSO	8	22	0	4.6240E −05
HFPSO	2	27	1	9.1531E −07
PhaPSO	4	26	0	2.8199E −06
XPSO	5	25	0	7.0172E −06
PPSO	8	20	2	0.0167

In addition, by looking closely at Table 11, we can see that CSBO has defeated all PSOs for most of the test functions. The most important competitor of CSBO is the PPSO algorithm, which is a very modern algorithm introduced in 2021. Although CSBO has a worse result than DTTPSO for 8 test functions, it has succeeded in 22 functions instead, which is a significant difference.

3.2.3. A comparison of CSBO with the popular inspired optimization algorithms (IOAs):

In this section, to identify CSBO compared to inspirational algorithms as well as their improved versions, the results of several other algorithms published in recent articles with conditions similar to CSBO with dimension 30 for the same cec2014 have been demonstrated as shown in Table 12, and the comparative study has been accomplished. These algorithms are included: mTLBO (a modified TLBO) (X. Chen et al., 2018; Satapathy & Naik, 2014), m-SCA (a hybrid self-adaptive sine cosine algorithm with opposition based learning) (Gupta & Deep, 2019), MG-SCA (a memory guided SCA) (Gupta et al., 2020), NIWTLBO (a nonlinear inertia weighted TLBO) (X. Chen et al., 2018; Wu et al., 2015), CBSA (a new constraint backtracking search optimization algorithm) (Dai et al., 2020), TOGPEAe (an improved grey prediction evolution algorithm based on topological opposition based learning) (Dai et al., 2020), HMCTLBO (hierarchical multi-swarm cooperative TLBO) (F. Zou et al., 2017), DIRECT-L (deterministic global search optimization algorithms with locally-biased version) (Gablonsky & Kelley, 2001), OptBees (Bee-inspired algorithm) (Maia et al., 2014), SOO + BOBYQA (simultaneous optimistic optimization with BOBYQA) (Preux et al., 2014), NRGA (non-uniform mapping in real-coded GAs) (Yashesh et al., 2014), WOA (whale optimization algorithm) (Mirjalili & Lewis, 2016), GWO (Grey wolf optimizer) (Mirjalili et al., 2014), MFO (Mirjalili, 2015), and LJA (Jaya with Levy flight) (Iacca et al., 2021) In addition, the parameter settings of some of these algorithms are given in Table 13.

Table 12. A comparison of CSBO with the state-of-the-art IOAs for CEC 2014 functions with NFEs=3.00E + 05.

	F1			F2			F3
Optimizer	Mean	Std.	R/Win	Mean	Std.	R/Win	Mean	Std.	R/Win
mTLBO	6.46E + 07	4.03E + 07	13/+	1.18E + 09	1.52E + 09	12/+	4.68E + 00	1.73E + 01	3/+
m-SCA	2.26E + 07	6.35E + 06	8/+	8.11E + 07	5.59E + 07	9/+	2.59E + 04	6.43E + 03	12/+
MG-SCA	2.92E + 07	2.07E + 07	9/+	2.26E + 09	1.69E + 09	14/+	1.77E + 04	6.63E + 03	11/+
NIWTLBO	4.95E + 05	3.70E + 05	3/+	1.78E + 02	2.49E + 02	5/+	2.52E + 01	5.73E + 01	5/+
CBSA	4.12E + 07	1.19E + 07	11/+	3.20E + 08	6.61E + 07	10/+	2.37E + 03	1.03E + 03	6/+
TOGPEAe	6.54E + 06	3.49E + 06	7/+	1.79E + 07	2.26E + 07	8/+	5.47E + 03	4.07E + 03	8/+
HMCTLBO	1.11E + 06	2.39E + 05	5/+	1.93E −13	3.71E −14	2/+	9.47E + 00	1.27E + 01	4/+
DIRECT-L	1.99E + 08	1.19E −07	16/+	3.62E + 08	5.98E −08	11/+	1.10E + 04	9.09E −12	10/+
OptBees	8.57E + 04	3.01E + 05	2/+	3.21E −12	1.13E −11	3/+	8.41E −03	3.73E −02	2/+
SOO + BOBYQA	2.67E + 06	0.00E + 00	6/+	9.96E + 01	3.41E −13	4/+	7.84E + 03	9.09E −12	9/+
NRGA	5.74E + 05	2.87E + 05	4/+	9.28E + 03	3.91E + 03	6/+	4.58E + 03	3.76E + 03	7/+
WOA	3.16E + 07	1.38E + 07	10/+	3.10E + 06	2.12E + 06	7/+	3.52E + 04	2.18E + 04	14/+
GWO	6.90E + 07	5.38E + 07	14/+	2.18E + 09	2.47E + 09	13/+	3.12E + 04	8.60E + 03	13/+
MFO	7.59E + 07	9.77E + 07	15/+	1.36E + 10	8.42E + 09	16/+	8.99E + 04	4.98E + 04	16/+
LJA	6.31E + 07	1.87E + 07	12/+	4.77E + 09	6.03E + 08	15/+	6.91E + 04	1.07E + 04	15/+
CSBO	1 . 06E + 04	1.06E + 04	1 /#	8 . 72E −14	3.64E −14	1 /#	4 . 60E −03	1.56E −02	1 /#
	F4			F5			F6
mTLBO	3.85E + 02	1.17E + 02	14/+	2.09E + 01	5.60e–02	4/+	2.42E + 01	2.27E + 00	12/+
m-SCA	1.83E + 02	2.58E + 01	10/+	2.09E + 01	7.07E −02	4/+	1.46E + 01	3.35E + 00	6/+
MG-SCA	2.76E + 02	6.55E + 01	13/+	2.04E + 01	1.44E −01	2/=	1.94E + 01	2.89E + 00	9/+
NIWTLBO	9.32E + 01	3.17E + 01	7/ +	2.09E + 01	4.68e–02	4/+	2.88E + 01	3.01E + 00	13/+
CBSA	1.56E + 02	2.13E + 01	9/+	4.14E + 01	9.01E + 00	5/+	9.93E + 01	1.09E + 01	16/+
TOGPEAe	1.44E + 02	4.37E + 01	8/+	2.05E + 01	3.56E −01	3/+	2.16E + 01	3.46E + 00	10/+
HMCTLBO	5.91E + 01	3.06E + 01	4/+	2 . 00E + 01	1.38E + 02	1 /–	1.41E + 01	1.19E −05	5/+
DIRECT-L	8.90E + 01	2.27E −13	6/+	2 . 00E + 01	3.41E −13	1 /–	9.00E + 00	5.68E −13	3/+
OptBees	1.26E + 01	1.36E + 01	2/+	2 . 00E + 01	1.01E −05	1 /–	1.64E + 01	3.41E + 00	7/+
SOO + BOBYQA	3.68E + 01	0.00E + 00	3/+	2 . 00E + 01	0.00E + 00	1 /–	1 . 91E + 00	5.68E −13	1 /–
NRGA	8.06E + 01	3.10E + 01	5/+	2 . 00E + 01	1.10E −04	1 /–	1.78E + 01	2.18E + 00	8/+
WOA	1.95E + 02	4.74E + 01	11/+	2.04E + 01	1.64E −01	2/=	3.60E + 01	4.05E + 00	15/+
GWO	2.62E + 02	8.96E + 01	12/+	2.09E + 01	4.80E −02	4/+	1.39E + 01	2.24E + 00	4/+
MFO	1.14E + 03	1.13E + 03	16/+	2.04E + 01	1.75E −01	2/=	2.40E + 01	3.33E + 00	11/+
LJA	4.08E + 02	5.38E + 01	15/+	2.09E + 01	4.97e–02	4/+	3.39E + 01	1.29E + 00	14/+
CSBO	4 . 43E + 00	1.67E + 01	1 /#	2.04E + 01	4.98E −02	2/#	6.05E + 00	6.61E + 00	2/#
	F7			F8			F9
mTLBO	6.00E + 01	2.36E + 01	15/+	1.16E + 02	2.46E + 01	10/+	1.25E + 02	2.89E + 01	7/+
m-SCA	2.01E + 00	4.62E −01	10/+	1.10E + 02	1.24E + 01	9/+	1.31E + 02	9.81E + 00	8/+
MG-SCA	1.99E + 01	1.18E + 01	14/+	1.07E + 02	2.14E + 01	8/+	1.39E + 02	2.56E + 01	11/+
NIWTLBO	3.15E −01	1.42E + 00	5/+	1.42E + 02	1.96E + 01	12/+	1.72E + 02	2.15E + 01	13/+
CBSA	4.00E + 00	6.84E −01	11/+	1.86E + 01	1.86E + 00	3/+	9.56E + 01	9.56E + 00	5/+
TOGPEAe	1.40E + 00	3.12E −01	9/+	5.89E + 01	1.80E + 01	5/+	7.22E + 01	2.17E + 01	4/+
HMCTLBO	2.21E −02	1.02E −13	3/+	1.24E + 02	0.00E + 00	11/+	1.66E + 02	2.82E −11	12/+
DIRECT-L	9.33E −01	4.55E −13	7/+	5.89E + 01	5.68E −13	5/+	1.32E + 02	6.82E −13	9/+
OptBees	3.75E −02	3.78E −02	4/+	1 . 14E −13	2.70E −13	1 /−	1.37E + 02	3.21E + 01	10/+
SOO + BOBYQA	4.09E −01	2.27E −13	6/+	9.25E + 01	3.41E −13	7/+	5.97E + 01	0.00E + 00	3/+
NRGA	1.59E −02	1.59E −02	2/+	2.66E + 01	7.72E + 00	4/+	4 . 57E + 01	1.33E + 01	1 /−
WOA	9.99E −01	7.38E −02	8/+	1.93E + 02	4.43E + 01	14/+	2.26E + 02	5.27E + 01	15/+
GWO	1.84E + 01	1.44E + 01	13/+	7.77E + 01	1.86E + 01	6/+	9.62E + 01	2.59E + 01	6/+
MFO	1.17E + 02	6.91E + 01	16/+	1.43E + 02	3.81E + 01	13/+	2.23E + 02	6.06E + 01	14/+
LJA	1.58E + 01	2.80E + 00	12/+	2.24E + 02	9.93E + 00	15/+	2.61E + 02	1.47E + 01	16/+
CSBO	2 . 62E −03	8.33E −03	1 /#	6.63E −02	2.27E −01	2/#	5.45E + 01	7.29E + 00	2/#
	F10			F11			F12
mTLBO	2.87E + 03	6.57E + 02	8/+	3.28E + 03	5.48E + 02	7/+	2.50E + 00	2.66E −01	16/+
m-SCA	3.58E + 03	4.72E + 02	12/+	4.93E + 03	4.71E + 02	15/+	1.76E + 00	2.89E −01	13/+
MG-SCA	2.82E + 03	6.83E + 02	7/+	3.30E + 03	6.26E + 02	8/+	6.33E −01	3.36E −01	8/+
NIWTLBO	3.15E + 03	4.38E + 02	9/+	3.05E + 03	7.21E + 02	6/+	1.93E + 00	6.19e–01	14/+
CBSA	1.35E + 02	2.35E + 01	2/+	2.80E + 03	2.58E + 02	4/+	4.72E −01	6.66E −02	6/−
TOGPEAe	3.79E + 03	1.91E + 03	13/+	4.53E + 03	1.45E + 03	13/+	7.74E −01	1.10E + 00	9/+
HMCTLBO	1.63E + 03	1.14E −02	5/+	4.46E + 03	7.13E + 01	12/+	8.83E −01	2.04E −02	10/+
DIRECT-L	3.17E + 03	4.55E −12	10/+	3.98E + 03	2.73E −12	10/+	1.92E −01	1.36E −12	4/−
OptBees	1.04E + 03	2.50E + 02	3/+	2.72E + 03	5.63E + 02	3/+	1.81E −01	6.06E −02	3/−
SOO + BOBYQA	2.13E + 03	9.09E −13	6/+	2 . 09E + 03	9.09E −13	1 /−	3 . 00E −02	6.82E −13	1 /−
NRGA	1.07E + 03	4.56E + 02	4/+	3.41E + 03	6.43E + 02	9/+	1.51E −01	7.04E −02	2/−
WOA	4.04E + 03	6.57E + 02	14/+	4.82E + 03	9.06E + 02	14/+	1.63E + 00	4.22E −01	12/+
GWO	2.13E + 03	6.62E + 02	6/+	2.81E + 03	9.41E + 02	5/+	1.52E + 00	1.19E + 00	11/+
MFO	3.47E + 03	8.85E + 02	11/+	4.15E + 03	6.90E + 02	11/+	4.33E −01	2.64E −01	5/−
LJA	5.68E + 03	3.95E + 02	15/+	6.88E + 03	3.12E + 02	16/+	2.49E + 00	2.73e–01	15/+
CSBO	9 . 55E + 00	3.00E + 00	1 /#	2.51E + 03	2.30E + 03	2/#	5.01E −01	1.00E −01	7/#
mTLBO	1.77E + 00	9.83E −01	15/+	2.04E + 01	8.51E + 00	12/+	1.20E + 03	1.46E + 03	15/+
m-SCA	3.86E −01	5.92E −02	5/+	2.65E −01	2.94E −02	6/+	1.52E + 01	1.47E + 00	4/+
MG-SCA	5.51E −01	8.94E −02	11/+	2.34E + 00	3.31E + 00	13/+	8.72E + 01	1.01E + 02	12/+
NIWTLBO	5.93E −01	1.44E −01	13/+	2.91E −01	1.67E −01	10/+	1.74E + 02	2.96E + 02	14/+
CBSA	3.89E −01	5.27E −02	6/+	2.83E −01	3.87E −02	9/+	1.99E + 01	2.08E + 00	5/+
TOGPEAe	4.93E −01	1.15E −01	8/+	2.63E −01	5.02E −02	5/+	2.43E + 01	7.54E + 00	7/+
HMCTLBO	3.45E −01	6.36E −03	4/+	2.15E −01	1.18E −03	3/+	2.63E + 01	1.48E + 01	8/+
DIRECT-L	5.16E −01	9.09E −13	9/+	2.81E −01	9.09E −13	8/+	3.91E + 01	0.00E + 00	9/+
OptBees	5.61E −01	1.46E −01	12/+	4.00E −01	2.29E −02	11/+	1.27E + 01	6.86E + 00	2/+
SOO + BOBYQA	3.40E −01	1.59E −12	3/+	2.80E −01	3.15E −13	7/+	2.17E + 01	1.14E −12	6/+
NRGA	2.81E −01	5.59E −02	2/+	1 . 87E −01	2.64E −02	1 /−	1.37E + 01	4.78E + 00	3/+
WOA	5.27E −01	1.26E −01	10/+	2.55E −01	4.84E −02	4/+	7.00E + 01	1.99E + 01	11/+
GWO	4.42E −01	2.94E −01	7/+	4.54E + 00	8.41E + 00	16/+	1.25E + 02	3.19E + 02	13/+
MFO	2.21E + 00	1.34E + 00	16/+	3.54E + 01	2.47E + 01	14/+	2.23E + 05	5.77E +0 5	16/+
LJA	1.08E + 00	1.19E −01	14/+	4.33E + 00	1.70E + 00	15/+	5.05E + 01	9.36E + 00	10/+
CSBO	1 . 62E −01	3.89E −02	1 /#	2.07E −01	3.15E −02	2/#	4 . 86E + 00	7.73E −01	1 /#
	F16			F17			F18
mTLBO	1.11E + 01	7.48E −01	5/+	6.56E + 05	1.24E + 06	9/+	1.92E + 04	8.10E + 04	10/+
m-SCA	1.20E + 01	2.89E −01	8/+	5.99E + 05	3.59E + 05	8/+	1.61E + 05	8.25E + 04	12/+
MG-SCA	1.16E + 01	6.91E −01	7/+	9.56E + 05	7.62E + 05	10/+	1.48E + 05	9.00E + 05	11/+
NIWTLBO	1.16E + 01	4.92e–01	7/+	2.52E + 04	3.08E + 04	2/+	2.06E + 03	2.34E + 03	5/+
CBSA	1.05E + 01	3.26E −01	2/−	3.46E + 06	1.54E + 06	14/+	4.54E + 06	1.89E + 06	13/+
TOGPEAe	1.23E + 01	6.54E −01	10/+	7.12E + 04	5.59E + 04	6/+	3.07E + 03	3.05E + 03	6/+
HMCTLBO	1.16E + 01	2.52E −05	7/+	6.10E + 04	5.48E + 04	5/+	3.43E + 03	2.23E + 01	7/+
DIRECT-L	1.22E + 01	1.36E −12	9/+	1.73E + 07	0.00E + 00	16/+	3.96E + 03	5.46E −12	8/+
OptBees	1.09E + 01	6.84E −01	4/+	2.74E + 04	4.00E + 04	3/+	1.96E + 02	4.72E + 02	3/+
SOO + BOBYQA	9 . 81E + 00	1.14E −12	1 /−	4.21E + 04	1.46E −11	4/+	4 . 16E + 01	1.59E −12	1 /−
NRGA	1.15E + 01	6.67E −01	6/+	2.35E + 05	1.18E + 05	7/+	5.50E + 02	7.09E + 02	4/+
WOA	1.25E + 01	4.48E −01	11/+	3.56E + 06	2.52E + 06	15/+	1.50E + 04	5.01E + 04	9/+
GWO	1.09E + 01	5.81E −01	4/+	1.40E + 06	1.56E + 06	11/+	9.21E + 06	1.98E + 07	15/+
MFO	1.27E + 01	5.33E −01	12/+	3.39E + 06	4.07E + 06	13/+	5.19E + 06	3.61E + 07	14/+
LJA	1.28E + 01	1.78E −01	13/+	2.63E + 06	9.76E +0 5	12/+	1.26E + 07	1.06E + 07	16/+
CSBO	1.08E + 01	3.31E −01	3/#	1 . 64E + 03	1.15E + 03	1 /#	5.64E + 01	4.16E + 01	2/#
	F19			F20			F21
mTLBO	8.02E + 01	3.50E + 01	16/+	2.72E + 02	1.21E + 02	2/+	3.18E + 04	2.86E + 04	7/+
m-SCA	1.93E + 01	5.95E + 00	7/+	1.22E + 04	3.70E + 03	11/+	1.10E + 05	5.66E + 04	8/+
MG-SCA	2.28E + 01	1.43E + 01	9/+	4.24E + 03	3.82E + 03	7/+	2.35E + 05	2.39E + 05	10/+
NIWTLBO	2.30E + 01	1.40E + 01	10/+	3.75E + 02	1.56E + 02	3/+	1.44E + 04	8.91E + 03	3/+
CBSA	2.04E + 01	5.81E + 00	8/+	6.95E + 03	3.35E + 03	8/+	6.64E + 05	2.63E + 05	11/+
TOGPEAe	1.60E + 01	1.80E + 01	5/+	3.31E + 03	3.67E + 03	6/+	1.73E + 04	1.74E + 04	5/+
HMCTLBO	8.97E + 00	3.52E −03	3/+	4.81E + 02	4.61E + 01	4/+	4.81E + 02	4.61E + 01	2/+
DIRECT-L	4.77E + 01	9.09E −13	13/+	4.90E + 04	3.64E −11	15/+	4.85E + 06	4.66E −09	16/+
OptBees	7.90E + 00	1.86E + 00	2/+	8.53E + 02	7.71E + 02	5/+	1.74E + 04	1.80E + 04	6/+
SOO + BOBYQA	1.63E + 01	1.82E −12	6/+	3.44E + 04	2.18E −11	14/+	1.54E + 04	0.00E + 00	4/+
NRGA	1.37E + 01	1.29E + 00	4/+	1.14E + 04	5.56E + 03	10/+	1.81E + 05	9.42E + 04	9/+
WOA	5.07E + 01	3.83E + 01	14/+	2.29E + 04	1.95E + 04	13/+	1.17E + 06	9.72E + 05	15/+
GWO	4.34E + 01	2.62E + 01	12/+	1.34E + 04	9.03E + 03	12/+	7.16E + 05	1.26E + 06	13/+
MFO	7.36E + 01	5.32E + 01	15/+	5.67E + 04	4.34E + 04	16/+	7.83E + 05	1.18E + 06	14/+
LJA	3.78E + 01	3.45E + 01	11/+	9.92E + 03	3.69E + 03	9/+	6.94E + 05	2.03E + 05	12/+
CSBO	4 . 45E + 00	9.81E −01	1 /#	2 . 80E + 01	1.86E + 01	1 /#	3 . 11E + 02	1.05E + 02	1 /#
	F22			F23			F24
mTLBO	5.32E + 02	2.09E + 02	8/+	3.53E + 02	1.98E + 01	9/+	2 . 00E + 02	7.93E −04	1 /−
m-SCA	2.57E + 02	5.71E + 01	3/+	3.21E + 02	1.58E + 00	5/+	2 . 00E + 02	4.29E −02	1 /−
MG-SCA	3.39E + 02	1.78E + 02	4/+	3.29E + 02	4.03E + 00	6/+	2 . 00E + 02	1.56E −03	1 /−
NIWTLBO	6.41E + 02	2.93E + 02	11/+	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	1.99E −05	1 /−
CBSA	4.19E + 02	1.04E + 02	7/+	2.26E + 02	4.77E + 01	3/−	2 . 00E + 02	5.57E −04	1 /−
TOGPEAe	6.87E + 02	1.65E + 02	12/+	2.16E + 01	3.46E + 00	2/−	3.17E + 02	1.93E + 00	8/+
HMCTLBO	6.23E + 02	4.32E −02	10/+	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	5.69E −04	1 /−
DIRECT-L	1.04E + 03	4.55E −12	16/+	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	0.00E + 00	1 /−
OptBees	2.32E + 02	9.16E + 01	2/+	3.15E + 02	6.59E −02	4/=	2.36E + 02	5.42E + 00	5/+
SOO + BOBYQA	9.56E + 02	4.55E −13	15/+	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	0.00E + 00	1 /−
NRGA	4.07E + 02	1.29E + 02	6/+	3.15E + 02	1.35E −03	4/=	2.28E + 02	4.21E + 00	4/+
WOA	8.13E + 02	2.70E + 02	13/+	3.35E + 02	9.16E + 00	7/+	2.06E + 02	5.12E + 00	3/+
GWO	3.78E + 02	1.65E + 02	5/+	3.35E + 02	1.04E + 01	7/+	2 . 00E + 02	8.23E −04	1 /−
MFO	8.67E + 02	2.29E + 02	14/+	3.71E + 02	3.98E + 01	10/+	2.76E + 02	2.73E + 01	7/+
LJA	5.47E + 02	1.05E + 02	9/+	3.43E + 02	3.41E + 00	8/+	2.57E + 02	4.04E + 00	6/+
CSBO	1 . 05E + 02	8.05E + 01	1 /#	3.15E + 02	8.22E −13	4/#	2.01E + 02	4.51E + 00	2/#
mTLBO	2.04E + 02	7.51E + 00	4/+	1.41E + 02	4.93E + 01	5/+	9.40E + 02	2.48E + 02	14/+
m-SCA	2.01E + 02	3.19E + 00	2/−	1 . 00E + 02	5.40E −02	1 /=	4.33E + 02	2.01E + 01	7/+
MG-SCA	2.11E + 02	2.82E + 00	7/+	1.01E + 02	1.53E −01	2/+	8.19E + 02	9.17E + 01	11/+
NIWTLBO	2 . 00E + 02	0.00E + 00	1 /−	1.90E + 02	3.03E + 01	7/+	5.24E + 02	2.76E + 02	8/+
CBSA	2 . 00E + 02	8.04E −09	1 /−	1 . 00E + 02	4.88E −02	1 /=	3.62E + 02	9.59E + 01	5/+
TOGPEAe	2.09E + 02	7.21E + 00	5/+	1.04E + 02	1.83E + 01	4/+	9.26E + 02	8.92E + 01	13/+
HMCTLBO	2 . 00E + 02	0.00E + 00	1 /−	1 . 00E + 02	9.73E −03	1 /=	2.80E + 02	1.10E + 02	2/−
DIRECT-L	2 . 00E + 02	0.00E + 00	1 /−	2.00E + 02	0.00E + 00	8/+	2 . 00E + 02	0.00E + 00	1 /−
OptBees	2.01E + 02	1.67E −01	2/−	1.01E + 02	1.71E −01	2/+	4.02E + 02	9.67E −01	6/+
SOO + BOBYQA	2 . 00E + 02	0.00E + 00	1 /−	2.00E + 02	0.00E + 00	8/+	2 . 00E +0 2	0.00E + 00	1 /−
NRGA	2.11E + 02	1.68E + 00	7/+	1 . 00E + 02	9.24E −02	1 /=	5.88E + 02	1.70E + 02	9/+
WOA	2.16E + 02	1.60E + 01	9/+	1 . 00E + 02	1.10E −01	1 /=	1.08E + 03	3.71E + 02	16/+
GWO	2.10E + 02	5.34E + 00	6/+	1.47E + 02	5.02E + 01	6/+	6.16E + 02	1.20E + 02	10/+
MFO	2.14E + 02	7.65E + 00	8/+	1.03E + 02	1.50E + 00	3/+	9.21E + 02	2.23E + 02	12/+
LJA	2.16E + 02	2.58E + 00	9/+	1.01E + 02	1.02E −01	2/+	9.86E + 02	2.48E + 02	15/+
CSBO	2.03E + 02	7.64E −01	3/#	1 . 00E + 02	6.71E −02	1 /#	3.14E + 02	5.23E + 01	3/#
	F28			F29			F30
mTLBO	2.36E + 03	5.34E + 02	13/+	5.45E + 06	1.21E + 07	16/+	8.61E + 04	6.81E + 04	14/+
m-SCA	1.05E + 03	2.74E + 02	6/+	4.44E + 04	1.77E + 04	8/+	3.48E + 04	1.05E + 04	10/+
MG-SCA	9.68E + 02	1.06E + 02	5/+	1.19E + 06	3.25E + 06	11/+	1.92E + 04	8.25E + 03	9/+
NIWTLBO	1.88E + 03	3.98E + 02	12/+	9.18E + 05	3.58E + 06	9/+	2.93E + 03	7.84E + 02	6/+
CBSA	5.74E + 02	4.65E + 02	3/−	3.37E + 04	1.09E + 04	7/+	1.38E + 04	3.52E + 03	8/+
TOGPEAe	1.58E + 03	2.22E + 02	10/+	2.09E + 03	5.16E + 02	6/+	1.09E + 04	6.80E + 03	7/+
HMCTLBO	2 . 00E + 02	0.00E + 00	1 /−	1.97E + 06	3.68E −10	13/+	1.43E + 03	1.70E −03	4/+
DIRECT-L	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	0.00E + 00	1 /−
OptBees	4.31E + 02	1.51E + 01	2/−	2.16E + 02	1.16E + 00	2/−	5.93E + 02	9.77E + 01	2/−
SOO + BOBYQA	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	0.00E + 00	1 /−	2 . 00E + 02	0.00E + 00	1 /−
NRGA	1.59E + 03	5.70E + 02	11/+	1.32E + 03	2.08E + 02	4/+	2.89E + 03	5.43E + 02	5/+
WOA	2.38E + 03	4.88E + 02	14/+	4.85E + 06	4.82E +0 6	15/+	8.38E + 04	6.11E + 04	13/+
GWO	1.20E + 03	2.62E + 02	9/+	1.29E + 06	4.28E + 06	12/+	5.20E + 04	3.15E + 04	11/+
MFO	1.12E + 03	1.57E + 02	7/+	3.06E + 06	3.62E + 06	14/+	5.89E + 04	5.40E + 04	12/+
LJA	1.13E + 03	6.63E + 01	8/+	9.82E + 05	2.07E + 06	10/+	1.09E + 04	4.24E + 03	7/+
CSBO	7.43E + 02	5.08E + 01	4/#	1.34E + 03	3.00E + 03	5/#	1.11E + 03	9.41E + 02	3/#

Table 13. The parameters of some state-of-the-art IOAs for CEC 2014 test functions.

Algorithm	Parameter settings with NFEs = 3.00E + 05
mTLBO	Npop = 50
m-SCA	Npop = 30, jumping rate = 0.1, Self-adaptation rate = [0, 1].
NIWTLBO	Npop = 50, inertia weight w= 0∼1.0
CBSA	Npop = 50.
TOGPEAe	Npop = 50, δ = [0.001, 0.1].
HMCTLBO	Npop = 50, the subswarm size was empirically set to 5, the regrouping period P was also empirically set to 5, the sampling size was set to 10, and the range of each hypercube dimension was twice the range of the corresponding dimension of the learners.
DIRECT-L	tolerance = 0:0, volper = 0:0, sigmaper = 0:0, maxDim = 64, maxDivs = 3; 000, maxDepth = 600.
WOA	Npop = 30, a1 = [2 0]; a2 = [−2 −1]; b = 1
GWO	Npop = 30, convergence constant a = [2 0] (linear reduction)
MFO	Npop = 30, a = [−2 −1]; b = 1
LJA	Npop = 150, β = 1.8

As in the previous section, CSBO has impressive performance for the first four test functions compared to other algorithms or IOAs. The worst rank obtained, which is a middle rank, is 7 for the test function 12 or Shifted and rotated Katsuura function, which is equal to 5.01E − 01, and the best value and the second-best value for this test function are obtained by SOO + BOBYQA and NRGA, respectively, which are equal to 3.00 E − 02 and 1.51E − 01. On the other hand, the worst solutions obtained by m-SCA, NIWTLBO, LJA and mTLBO were 1.76E + 00, 1.93E + 00, 2.49E + 00 and 2.50E + 00. Given these results, it can be said that the solutions obtained by CSBO are acceptable results. At the same time, it can become a more robust algorithm with some modifications.

Note for Table 12: The ‘–’, ‘’, and ‘=’ denote that the performance of CSBO is worse than, better than, and similar to that of the corresponding algorithm, respectively.

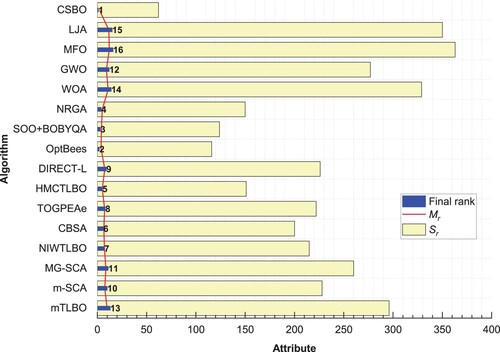
Summary of statistical results from CSBOs and IOAs are given in Figures 6 and 7. A quick look at Figure 6 reveals that CSBO deservedly is the best and most reliable algorithm. The closest algorithm to CSBO is the OptBees algorithm, with an average value of 3.8667, a difference of 1.8 from the average value of CSBO, which is a considerable difference. WOA, LJA and MFO (three new and trendy algorithms) are the worst rankings, with averages of 10.9667, 11.6667 and 12.1000, which are difficult to accept in a few conditions.

Figure 6. The competitive results of CLBO and IOAs on CEC 2014 test functions.

Figure 7. The competitive results of CLBO and IOAs according to the N_best and N_worst.

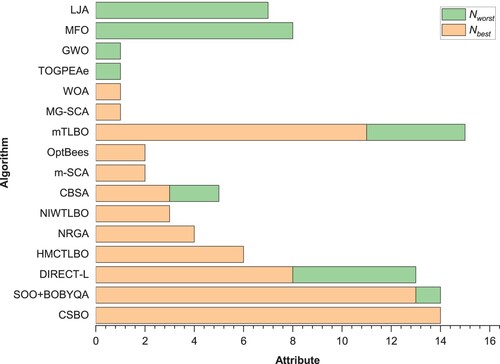
On the other hand, looking carefully at Figure 7, it can be seen that CSBO got the best solutions for 14 test functions here and never got the worst ranking. As mentioned, the worst ranking was 7, which was within acceptable limits. The modern algorithms SOO + BOBYQA and DIRECT-L obtained the best solutions for 13 and 8 functions in this study. At the same time, SOO + BOBYQA once and DIRECT-L five times got the worst solutions, which indicates the valuable functionality of our proposed CSBO.

It is clear from the figure that the two algorithms, LJA and MFO, which have never had the best solution, are in the red. Their solution has been the worst for most functions compared to other algorithms.

Table 14 compares the p-values of CSBO with fifteen other modern optimization techniques when Wilcoxon’s test is used. The p-values less than 0.05 (the significance level) are in boldface. As a result of the data, it is clear that CSBO outperforms other algorithms. Although CSBO is not statistically superior to the rest of the SOO + BOBYQA, it exceeds this on an average ranking basis. Furthermore, this table demonstrates that CSBO significantly outperforms all other algorithms. The most comparable strategy is SOO + BOBYQA, which achieved the most significant outcomes in 13 situations but failed in 17 cases compared to CSBO.

Table 14. The competitive results of Wilcoxon’s test and performance of CLBO versus IOAs.

	The performance of CSBO is			CSBO versus
Corresponding algorithm	worse (−) than	better (+) than	similar (=) with	p-values
mTLBO	1	29	0	2.7481E −09
m-SCA	2	27	1	2.4574E −08
MG-SCA	1	28	1	3.4868E −09
NIWTLBO	3	27	0	3.9661E −07
CBSA	6	23	1	1.0287E −06
TOGPEAe	1	29	0	7.3761E −10
HMCTLBO	6	23	1	3.6196E −04
DIRECT-L	9	21	0	1.1745E −04
OptBees	7	22	1	6.7900E −04
SOO + BOBYQA	13	17	0	0.0677
NRGA	4	24	2	1.8467E −05
WOA	0	28	2	1.4888E −09
GWO	1	29	0	1.0465E −09
MFO	1	28	1	1.5008E −10
LJA	0	30	0	1.0172E −10

3.3. CEC 2017 benchmark functions

In order to verify the performance of the proposed CSBO algorithm compared to other algorithms, we have selected the CEC2017 functions in this section. These are real-world modeled optimization functions. CEC 2017 functions (unimodal, simple multimodal, hybrid, and composition benchmark tests) (Wu et al., 2017) have been used successfully in many recent articles and, therefore, in this paper to test the performance of the proposed CSBO algorithm, we have used them.

In this section, we have selected 30-dimension with 30 runs for each test function. The number of evolutions in all parts of the article is 300,000. Also, the population and NR set at 45 and 15, respectively. The parameter settings of some competitors, in this case, are given in Table 15.

Table 15. The parameter settings of some competitors for CEC 2017 test functions.

Algorithm	Parameter settings with NFEs = 3.00E + 05
AWPSO	w = [0.9 0.4] (linear reduction), a = 0.000035, b = 0.5, c = 0, d = 1.5
GSA	Npop = 100, G0 = 100, α = 20
GWO	Npop = 100, convergence constant a = [2 0] (linear reduction)
SCA	a = 2, r1 = a – Iter × (a / Itermax), r2 = 2 × π × rand(), r3 = 2 × rand(), r4 = rand()
EHO	clan = 5, α = 0.5, β = 0.1
BOA	p = 0.8, α = 0.1, c = 0.01
BA	Npop = 50, the pulse rate (r), the factors updating α and γ are set to 0.9.
HHO	Npop = 30, C = [0, 2], E = [−2,2]
GOMGBO	Npop = 30,
HGS	Npop = 50.

The simulation results for D = 30 are given in Table 16, compared to the robust and modern algorithms in the recent literature, e.g. AWPSO (a sigmoid-function-based adaptive weighted particle swarm optimizer PSO) (Wei et al., 2020), GSA and GWO (Lei et al., 2020), SCA, EHO and BOA (Li & Wang, 2021), BA (Alsalibi et al., 2021), HHO (Hu et al., 2022), GOMGBO (Gaussian bare-bones mechanism GBO) (Qiao et al., 2021) and HGS (Izci et al., 2022). From both tables, it is clear that CSBO has defeated all other algorithms for most functions (F1, F3, F4, F6, F7, F9, F11, F12, F13, F14, F15, F17, F18, F19, F21, F23, F24, F27, F28, and F30). Interestingly, CSBO never had the worst performance and rank for CEC 2017 among the algorithms, indicating the robustness and reliability of the CSBO. Nevertheless, to mention that the two algorithms, HGS and GOMGBO, overcame the CSBO for the 8 and 2 functions of CEC 2017, which is normal.

Table 16. Summary of the results for CEC2017 test functions for different algorithms with D = 30 and NFEs = 3.00E + 05.

	AWPSO	GSA	GWO	SCA	EHO	BOA	BA	HHO	GOMGBO	HGS	CSBO
Function	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R/Win	MeanStd. R
F1	2.46E + 09	1.90E + 03	1.72E + 03	1.25E + 10	2.68E + 10	4.47E + 10	3.37E+11	1.04E + 07	6.28E + 01	6.92E + 03	3.13E−09
	2.67E + 09	1.03E + 03	8.91E + 08	2.94E + 09	5.87E + 09	6.73E + 09	3.48E + 09	1.87E+06	1.13E + 02	4.50E + 03	1.40E−08
	7/+	4/+	3/+	8/+	9/+	10/+	11/+	6/+	2/+	5/+	1
F3	1.00E + 04	8.27E + 04	2.82E + 04	3.47E + 04	7.23E + 04	6.48E + 04	2.85E + 09	4.85E + 03	1.40E−01	4.07E + 00	2.93E−13
	2.12E + 04	4.33E + 03	9.70E + 03	7.52E + 03	9.76E + 03	9.30E + 03	4.62E + 08	1.70E + 03	3.00E−01	4.14E−01	1.28E−13
	5/+	10/+	6/+	7/+	9/+	8/+	11/+	4/+	2/+	3/+	1
F4	2.81E + 02	1.42E + 02	1.70E + 02	1.05E + 03	4.60E + 03	1.94E + 04	3.54E + 04	1.25E + 02	6.93E + 01	1.63E + 01	1.26E + 01
	1.76E + 02	1.59E + 01	4.98E + 01	3.75E + 02	3.91E + 02	3.77E + 03	1.36E + 03	2.36E + 01	3.42E + 01	1.75E + 01	1.50E + 01
	7/+	5/+	6/+	8/+	9/+	10/+	11/+	4/+	3/+	2/+	1
F5	8.15E+01	2.26E + 02	9.20E + 01	2.73E + 02	3.34E + 02	3.71E + 02	5.26E + 03	2.30E + 02	8.06E + 01	3.11E + 01	6.55E + 01
	2.75E + 01	2.01E + 01	2.63E + 01	2.24E + 01	1.80E + 01	2.33E + 01	2.13E + 01	2.98E + 01	2.01E + 01	8.25E + 00	8.00E + 00
	4/+	6/+	5/+	8/+	9/+	10/+	11/+	7/+	3/+	1/−	2
F6	4.12E + 00	5.00E + 01	4.00E + 00	4.90E + 01	7.10E + 01	7.00E + 01	6.85E + 02	6.34E + 01	3.60E−01	8.60E−01	2.79E−13
	3.05E + 00	2.75E + 00	2.33E + 00	5.20E + 00	6.00E + 00	9.54E + 00	6.55E + 00	5.40E + 00	7.83E−01	5.88E−01	6.88E−14
	5/+	7/+	4/+	6/+	10/+	9/+	11/+	8/+	2/+	3/+	1
F7	1.12E + 02	8.70E + 01	1.35E + 02	4.40E + 02	7.30E + 02	6.10E + 02	1.80E + 03	5.30E + 02	1.02E + 02	3.92E + 01	3.86E + 01
	2.23E + 01	1.19E + 01	4.95E + 01	4.15E + 01	4.43E + 01	5.58E + 01	1.63E + 02	8.35E + 01	2.43E + 01	1.06E + 01	6.39E + 00
	5/+	3/+	6/+	7/+	10/+	9/+	11/+	8/+	4/+	2/+	1
F8	8.02E + 01	1.51E + 02	8.10E + 01	2.50E + 02	3.00E + 02	3.00E + 02	1.65E + 04	1.69E + 02	7.76E + 01	1.95E + 01	6.70E + 01
	2.33E + 01	1.31E + 01	1.25E + 01	1.62E + 01	2.15E + 01	1.85E + 01	3.98E + 01	2.33E + 01	2.30E + 01	6.80E + 00	8.11E + 00
	4/+	6/+	5/+	8/+	9/+	9/+	10/+	7/+	3/+	1/−	2
F9	3.52E + 02	2.03E + 03	2.80E + 02	4.81E + 03	8.48E + 03	8.45E + 03	1.01E + 04	5.86E + 03	6.89E + 01	7.60E−01	9.95E−02
	4.08E + 02	3.92E + 02	1.39E + 02	1.43E+03	1.20E + 03	1.03E + 03	1.69E + 03	5.95E + 02	6.47E + 01	2.63E + 00	1.79E−01
	5/+	6/+	4/+	7/+	10/+	9/+	11/+	8/+	3/+	2/+	1
F10	2.85E + 03	3.87E + 03	2.73E + 03	7.04E + 03	7.15E + 03	7.49E + 03	9.88E + 04	4.39E + 03	3.04E + 03	6.08E + 02	2.76E + 03
	6.26E + 02	4.34E + 02	5.49E + 02	3.42E + 02	3.14E + 02	2.75E + 02	7.65E + 03	6.57E + 02	6.73E + 02	2.82E + 02	2.66E + 02
	4/+	6/+	2/−	8/+	9/+	10/+	11/+	7/+	5/+	1/−	3
F11	2.00E + 02	3.50E + 02	4.10E + 02	1.05E + 03	1.03E + 03	4.51E + 03	3.46E + 04	1.52E + 02	4.83E + 01	4.26E + 01	3.96E + 01
	1.11E + 02	8.92E + 01	4.42E + 02	2.65E + 02	1.46E + 02	1.83E + 03	3.37E + 03	3.99E + 01	2.18E + 01	4.52E + 01	3.22E + 01
	5/+	6/+	7/+	9/+	8/+	10/+	11/+	4/+	3/+	2/+	1
F12	1.61E + 08	1.03E + 07	3.31E + 07	1.13E + 09	3.17E + 09	1.05E + 10	3.95E + 09	9.24E + 06	3.32E + 04	1.89E + 04	1.69E + 04
	3.26E + 08	1.93E + 07	3.81E + 07	2.52E + 08	5.20E + 08	3.41E+09	9.45E + 07	5.95E + 06	3.77E + 04	2.05E + 04	1.15E + 04
	7/+	5/+	6/+	8/+	9/+	11/+	10/+	4/+	3/+	2/+	1
F13	3.91E + 07	2.97E + 04	6.63E + 06	3.87E + 08	1.06E + 09	6.52E + 09	4.17E + 09	3.14E + 05	1.12E + 04	1.03E + 04	1.04E + 02
	1.93E + 08	6.45E + 03	2.33E + 07	1.24E + 08	2.71E + 08	3.65E + 09	6.17E + 08	1.17E + 05	1.71E + 04	6.78E + 03	1.03E + 02
	7/+	4/+	6/+	8/+	9/+	11/+	10/+	5/+	3/+	2/+	1
F14	1.79E + 04	4.73E + 05	7.96E + 04	1.42E + 05	1.79E + 05	9.60E + 05	1.35E + 07	5.19E + 04	1.09E + 03	1.15E + 03	3.81E + 01
	3.34E+04	1.31E + 05	1.76E + 05	8.76E + 04	7.54E + 04	1.84E + 06	1.65E + 06	1.03E + 05	1.23E + 03	1.63E + 03	9.38E + 00
	4/+	9/+	6/+	7/+	8/+	10/+	11/+	5/+	2/+	3/+	1
F15	4.20E + 04	1.02E + 04	2.43E + 05	1.19E + 07	2.60E + 07	1.35E + 08	1.73E + 08	6.89E + 04	3.91E + 03	2.79E + 03	2.49E + 01
	6.34E + 04	1.93E + 03	5.82E + 05	1.07E + 07	1.04E + 07	1.80E + 08	6.11E + 07	6.59E + 04	6.88E + 03	2.78E + 03	1.98E + 01
	5/+	4/+	7/+	8/+	9/+	10/+	11/+	6/+	3/+	2/+	1
F16	8.18E + 02	1.58E + 03	7.20E + 02	2.01E + 03	2.57E + 03	4.58E + 03	4.46E + 04	1.60E + 03	8.85E + 02	1.60E + 02	4.17E + 02
	2.88E + 02	2.84E + 02	2.39E + 02	3.47E + 02	1.94E + 02	1.38E + 03	2.96E + 02	3.65E + 02	2.64E + 02	1.36E + 02	1.62E + 02
	4/+	6/+	3/+	8/+	9/+	10/+	11/+	7/+	5/+	1/−	2
F17	3.11E + 02	1.20E + 03	2.30E + 02	7.10E + 02	8.90E + 02	6.17E + 03	3.07E + 04	9.54E + 02	3.56E + 02	6.05E + 01	5.40E + 01
	1.58E + 02	1.70E + 02	1.16E + 02	1.88E + 02	1.65E+02	5.38E + 03	1.82E + 02	2.84E + 02	1.65E + 02	4.70E + 01	1.85E + 01
	4/+	9/+	3/+	6/+	7/+	10/+	11/+	8/+	5/+	2/+	1
F18	5.66E + 05	3.18E + 05	7.73E + 05	3.92E + 06	1.38E + 06	1.08E + 07	2.26E + 09	8.29E + 05	5.42E + 04	2.22E + 04	1.46E + 02
	1.02E + 06	1.76E + 05	1.40E + 06	2.66E + 06	6.64E + 05	1.50E + 07	1.98E + 07	7.16E + 05	3.69E + 04	1.44E + 04	1.34E + 02
	5/+	4/+	6/+	9/+	8/+	10/+	11/+	7/+	3/+	2/+	1
F19	2.47E + 05	1.23E + 04	2.04E + 05	2.13E + 07	6.23E + 07	2.64E + 08	1.66E + 09	2.41E + 05	4.40E + 03	9.80E + 03	1.29E + 01
	7.76E + 05	5.13E + 03	3.88E + 05	1.10E + 07	2.53E + 07	2.69E + 08	6.24E + 07	1.77E + 05	9.07E + 03	1.11E + 04	4.28E + 00
	7/+	4/+	5/+	8/+	9/+	10/+	11/+	6/+	2/+	3/+	1
F20	2.99E + 02	1.03E + 03	3.30E + 02	6.30E + 02	5.80E + 02	8.40E + 02	3.96E + 03	7.37E + 02	3.33E + 02	2.16E + 01	1.15E + 02
	1.27E + 02	2.36E + 02	1.66E + 02	1.01E + 02	7.75E + 01	1.04E + 02	1.36E + 02	2.12E + 02	1.74E + 02	1.13E + 01	6.21E + 01
	3/+	10/+	4/+	7/+	6/+	9/+	11/+	8/+	5/+	1/−	2
F21	2.94E + 02	4.60E + 02	2.70E + 02	4.50E + 02	5.00E + 02	3.90E + 02	2.87E + 03	4.60E + 02	2.67E + 02	2.71E + 02	2.63E + 02
	1.75E + 01	1.95E + 01	1.85E + 01	1.50E + 01	1.60E + 01	1.51E + 02	2.55E + 01	5.25E + 01	2.01E + 01	3.40E + 01	6.46E + 00
	6/+	9/+	3/+	8/+	10/+	7/+	5/+	9/+	2/+	4/+	1
F22	2.12E + 03	4.19E + 03	2.27E + 03	5.98E + 03	2.99E + 03	2.20E + 03	5.33E + 04	4.23E + 03	4.40E + 02	1.13E + 02	7.36E + 02
	1.46E + 03	1.69E + 03	1.45E + 03	2.36E + 03	3.14E + 02	7.00E + 02	1.70E + 03	1.77E + 03	1.05E + 03	1.07E + 02	1.55E + 03
	4/+	8/+	6/+	10/+	7/+	5/+	11/+	9/+	2/−	1/−	3
F23	5.90E + 02	1.26E + 03	4.30E + 02	6.80E + 02	9.90E + 02	9.00E + 02	3.37E + 04	8.07E + 02	4.45E + 02	3.24E + 02	3.10E + 02
	7.49E + 01	1.23E + 02	3.04E + 01	2.64E + 01	5.15E + 01	1.23E + 02	4.95E + 02	1.05E + 02	3.05E + 01	6.42E + 00	6.04E + 00
	5/+	10/+	3/+	6/+	9/+	8/+	11/+	7/+	4/+	2/+	1
F24	7.13E + 02	8.90E + 02	5.00E + 02	7.60E + 02	1.08E + 03	1.37E + 03	5.77E + 04	1.05E + 03	5.14E + 02	3.79E + 02	3.65E + 02
	1.18E + 02	5.57E + 01	4.70E + 01	2.46E + 01	6.37E + 01	1.67E + 02	5.19E + 05	1.47E + 02	2.84E + 01	1.26E + 01	1.42E + 01
	5/+	7/+	3/+	6/+	9/+	10/+	11/+	8/+	4/+	2/+	1
F25	4.11E + 02	4.30E + 02	4.60E + 02	6.70E + 02	2.22E + 03	3.15E + 03	4.95E + 05	4.10E + 02	3.78E + 02	4.33E + 02	3.89E + 02
	7.28E + 01	1.22E + 01	2.69E + 01	7.39E + 01	5.33E + 02	4.64E + 02	4.86E + 07	2.02E + 01	2.15E + 00	3.37E + 01	8.53E + 00
	5/+	6/+	7/+	8/+	9/+	10/+	11/+	4/+	1/−	3/+	2
F26	2.29E + 03	4.26E + 03	1.83E + 03	4.33E + 03	6.00E + 03	7.80E + 03	7.85E + 04	3.75E + 03	1.90E + 03	6.38E + 02	1.65E + 03
	7.62E + 02	8.95E + 02	2.45E + 02	3.06E + 02	5.87E + 02	1.17E + 03	6.76E + 02	2.12E + 03	5.09E + 02	4.37E + 02	1.49E + 02
	5/+	7/+	3/+	8/+	9/+	10/+	11/+	6/+	4/+	1/−	2
F27	6.09E + 02	1.97E + 03	5.30E + 02	6.90E + 02	1.23E + 03	1.06E + 03	3.65E + 04	6.31E + 02	5.00E + 02	3.96E + 02	3.06E + 02
	9.38E + 01	3.21E + 02	1.78E + 01	2.60E + 01	9.38E + 01	1.35E + 02	6.75E + 01	6.78E + 01	1.37E−04	1.74E + 01	8.64E + 00
	5/+	10/+	4/+	7/+	9/+	8/+	11/+	6/+	3/+	2/+	1
F28	6.06E + 02	5.10E + 02	5.30E + 02	1.03E + 03	2.29E + 03	5.05E + 03	5.64E + 04	4.52E + 02	4.71E + 02	4.56E + 02	3.51E + 02
	1.60E + 02	4.94E + 01	4.83E + 01	1.63E + 02	3.00E + 02	5.08E + 02	4.33E + 02	2.65E + 01	5.64E + 01	1.45E + 02	6.60E + 01
	7/+	5/+	6/+	8/+	9/+	10/+	11/+	2/+	4/+	3/+	1
F29	5.19E + 02	1.81E + 03	8.10E + 02	1.69E + 03	2.30E + 03	6.47E + 03	5.46E + 04	1.37E + 03	6.93E + 02	3.37E + 02	4.20E + 02
	1.70E + 02	2.10E + 02	1.26E + 02	2.52E + 02	2.14E + 02	2.74E + 03	3.57E + 02	2.96E + 02	1.88E + 02	5.64E + 01	7.66E + 01
	3/+	8/+	5/+	7/+	9/+	10/+	11/+	6/+	4/+	1/−	2
F30	5.15E + 05	1.67E + 05	3.90E + 06	7.06E + 07	8.97E + 07	5.74E + 08	1.65E + 09	1.65E + 06	4.59E + 03	3.56E + 05	2.11E + 03
	9.02E + 05	1.24E + 05	3.10E + 06	3.47E + 07	3.04E + 07	3.63E + 08	6.31E + 07	8.27E + 05	3.39E + 03	5.45E + 05	1.64E + 02
	5/+	3/+	7/+	8/+	9/+	10/+	11/+	6/+	2/+	4/+	1
+/−/=	29/0/0	29/0/0	28/1/0	29/0/0	29/0/0	29/0/0	29/0/0	29/0/0	27/2/0	21/8/0
Nb/Nw/Mr	0/0/5.0690	0/0/6.4483	0/0/4.8621	0/0/7.6207	0/1/8.7931	0/2/9.4138	0/26/10.6897	0/0/6.2759	1/0/3.1379	8/0/2.1724	20/0/1.3793
Final rank	5	7	4	8	9	10	11	6	3	2	1

Although CSBO obtained indicates inappropriate rankings (rank 3) for the two functions, 10 and 22, the last three rows of Table 16 reveal that CSBO is a robust and appropriate emerging algorithm.

3.4. CSBO complexity

The CSBO method was applied in MATLAB 7.6, and the simulation was performed on a Pentium IV E5200 PC equipped with 2 GB of RAM. The CSBO algorithm was used to evaluate all test functions in the CEC 2014 competition (J. J. Liang et al., 2013). The algorithm was executed 30 times for each test problem for a total number of 10,000 × D function evaluations. The convergence speed of the CSBO algorithm is determined according to the procedure provided in (J. J. Liang et al., 2013). T₀ denotes the execution time of the following scheme in Table 17: $\begin{array}{l}\mathit{f}\mathit{o}\mathit{r}\mathbf{i}\text{ = 1:1000000}\\ x=0.55+\left(double()i;x\text{ + }\frac{x}{2}\sqrt{x}\right)\\ x=\log (x);x=e^x;x=\frac{x}{(x+2)};\\ \mathit{e}\mathit{n}\mathit{d}\end{array}$ T₁ is the time required to compute F18 for 200 000 evaluations, whereas T₂ denotes the time required to run the suggested technique for 200 000 evaluations. T₂ is assessed five times, and the mean of the five evaluations is represented by ${\stackrel{⌢}{T}}_2$. As a final point, the complexity of the algorithm is represented as ${\stackrel{⌢}{T}}_2$, T₁, and (${\stackrel{⌢}{T}}_2$−T₁)/T₀.

Table 17. CSBO Complexity.

D	T0	T1	${\stackrel{⌢}{T}}_2$	(${\stackrel{⌢}{T}}_2$−T1)/T0
30	0.2503	2.5411	3.4201	3.5118
50	0.2504	5.0096	6.6204	6.4329

In addition, the computational cost of CSBO is mainly determined by three processes: blood particle initialization, fitness assessment, and blood particle update. The computing complexity of the initialization procedure is O (Npop), where Npop is the number of blood particles. The updating CSBO has a computational cost of O (Itermax × Npop) + O (Itermax × Npop × D), which is comprised of searching for the optimal position and updating the location vectors of all the blood particles, where Itermax is the maximum number of iterations and D is the dimension of the particular issues. As a result, CSBO’s computational complexity is O (Npop × (Itermax + Itermax × D + 1)).

4. Application of CSBO algorithm for engineering optimization problems

In the second phase study, some experiments were accomplished to compare the proposed CSBO algorithm with other obtained optimal best results for solving various manufacturing parameter optimization problems such as the engineering design optimization, the parameter estimation for frequency-modulated (FM) sound waves, and the maximizing of the reliability in the engineering systems.

Over the last few years, population-based swarm intelligence based on various EAs has attracted much interest among researchers in the related fields for the optimal solutions such as the optimal solutions of various types of manufacturing parameters and engineering design optimization problems in order to improve the system’s features like performance and cost. A variety of manufacturing topics can be defined as optimization problems with many nonlinear characteristics and the inequality (or equality) and nonlinear (or linear) optimization constraints. Product and process design, tuning manufacturing parameters, scheduling and production planning are some examples of this area.

Therefore, to attain desired product quality with high efficiency, it is urgent to use optimization methods to handle the manufacturing development. Since manufacturing processes are going to be more complicated and also the products’ quality must satisfy high standards, the investigation of improved methods for solving these problems is highly explored, and it is still an ongoing subject in the current competitive market (G. Zhang et al., 2013).

In the recent years, various optimization heuristic techniques and EAs have been applied to solve manufacturing parameter and engineering design optimization problems, such as harmony search (HS) (Lee & Geem, 2005), genetic algorithms (GAs) (Coello & Montes, 2002); (Dhadwal et al., 2014); (Pasandideh et al., 2013), the various optimization heuristic techniques of the differential evolution (DE) algorithm for constrained optimization such as the hybrid DE algorithms (Liao, 2010), a cultural DE (CDE) (Becerra & Coello, 2006), the DE with dynamic stochastic selection (DSS-MDE) (M. Zhang et al., 2008), the co-evolutionary DE (CoDE) (F. Huang et al., 2007), a modified DE (COMDE) (A. W. Mohamed & Sabry, 2012), the evaluating DE (de Melo & Carosio, 2012), a new hybrid DE (Yildiz, 2013a), a DE and tissue membrane systems (DETPS) algorithm (C. Li et al., 2011), an improved constrained DE (Gong et al., 2014), a dual-population DE with coevolution (Gao et al., 2014), the various techniques of PSO algorithm for constrained manufacturing parameter optimization such as a unified PSO (UPSO) algorithm (Parsopoulos & Vrahatis, 2005), a co-evolutionary PSO (CPSO) algorithm (Q. He & Wang, 2007b), a hybrid algorithm of PSO with DE (PSO-DE) (Liu et al., 2010), an improved vector PSO (Sun et al., 2011), the ABC optimization algorithms ((Brajevic et al., 2011); (G. Li et al., 2012); (Tsai, 2014); (Brajevic & Tuba, 2013); (A. Singh & Sundar, 2011); (Brajevic, 2015)), the TLBO optimization algorithm ((Yildiz, 2013b); (Yu et al., 2016); (Maity & Mishra, 2018)), cuckoo search (CS) algorithm (Gandomi, Yang, and Alavi, 2013), Jaya algorithm (R. V. Rao & Waghmare, 2017) and etc.

4.1. The constrained engineering design optimization using CSBO

In order to verify the results of the proposed CSBO algorithm on the constrained engineering design applications, three problems from the competitive study are chosen: optimal design of a tension/compression spring, the three-bar truss and the pressure vessel to minimize the total cost of the manufacturing and design. The population size and the maximum number of iterations have been chosen to be 45, 400 for three-bar truss, and 5000 for pressure vessel and tension/compression spring optimal design problems, respectively, with 30 independent runs for the CSBO algorithm, which are summarized as follows. In recent years, it should be noted that many researchers have examined these engineering problems in different studies. Thus, we just investigated the cases considering all the limitations and conditions.

4.1.1. Problem 1: the tension/compression spring design problem

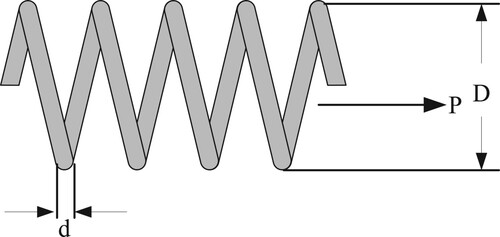
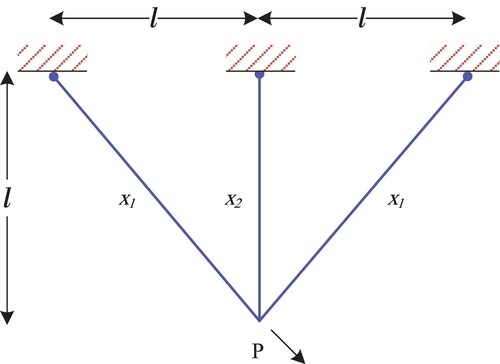
The tension/compression problem aims to minimize the tension/compression spring’s weight regarding constraints on the minimum deflection, shear stress, surge frequency, diameter, and design variables, as shown in Figure 8 (Arora, 2004). This problem includes one linear and three nonlinear inequality constraints and three continuous design variables. In addition, tre are three continuous variables, including the wire diameter x₁(d) with region 0.05 ≤ x₁≤2, the mean coil diameter x₂(D) with region 0.25 ≤ x₂≤1.3, and the number of active coils x₃ (P) with region 2 ≤ x₃≤15 (Akay & Karaboga, 2012; Coello & Montes, 2002).

Figure 8. The optimal design of tension/compression spring problem.

The mathematical formulation of the tension/compression spring optimal design problem can be given as follows (Q. He & Wang, 2007b) and (Yu et al., 2016):

Minimize: (14) $\begin{array}{r}{F}_1(X)=(x_3+2)x_2{x}_1^2.\end{array}$(14) Subject to: (15) $\begin{array}{rl}{g}_1(X)& =1-\frac{x_2^3{x}_3}{71785x_1^4}\le 0,\end{array}$(15) (16) $\begin{array}{rl}{g}_2(X)& =\frac{4x_2^2-x_1{x}_2}{12566(x_1^3{x}_2-x_1^4)}+\frac{1}{5108x_1^2}-1\le 0,\end{array}$(16) (17) $\begin{array}{rl}{g}_3(X)& =1-\frac{140.45x_1}{x_2^2{x}_3}\le 0,\end{array}$(17) (18) $\begin{array}{rl}{g}_4(X)& =\frac{x_1+x_2}{1.5}-1\le 0.\end{array}$(18)

The simulation results achieved by the proposed CSBO algorithm compared to GA (Coello & Montes, 2002), CPSO (Q. He & Wang, 2007b), CDE (F. Huang et al., 2007), DELC (L. Wang & Li, 2010), ABC (Akay & Karaboga, 2012), UABC (Brajevic & Tuba, 2013), ITLBO (Yu et al., 2016), CSA (Askarzadeh, 2016), EO (Faramarzi et al., 2020), water cycle algorithm (WCA) (Eskandar et al., 2012), Bat algorithm (BA) (Gandomi, Yang, Alavi, and Talatahari, 2013), HEA-ACT (Y. Wang et al., 2009), spotted hyena optimizer (SHO) (Dhiman et al., 2021), chaotic water cycle algorithm (CWCA III) (Heidari et al., 2017), and virus colony search (VCS) (Jain et al., 2019) algorithms are listed in Table 18. The simulation results show that the proposed CSBO algorithm is better and more robust for the tension/compression spring optimal design problem.

Table 18. Comparison of the best results for tension/compression spring problem by algorithms.

Variable	GA	CPSO	CDE	DELC	ABC	UABC	ITLBO	CSBO
x1(d)	0.051989	0.051728	0.051609	0.3567177413	0.051749	0.051691	0.051689	0 . 0517303564
x2(D)	0.363965	0.357644	0.354714	0.0516890611	0.358179	0.356769	0.356723	0 . 357710461
x3 (P)	10.890522	11.244543	11.410831	11.2889656626	11.203763	11.285988	11.288662	11 . 231171877
g1(X)	−0.000013	−0.000845	−0.000039	NA	0.0	0.0	0.0	−1 . 0154E −05
g2(X)	−0.000021	−1.260E −05	−0.000183	NA	0.0	0.0	0.0	−3 . 4846E −06
g3(X)	−4.061338	−4.051300	−4.048627	NA	−4.056663	−4.053886	−4.053796	−4 . 05567
g4(X)	−0.722698	−0.727090	−0.729118	NA	−0.726713	−0.727694	−0.727725	−0 . 72704
Best	0.0126810	0.0126747	0.0126702	0.012665233	0.012665	0.012665	0.012665	0 . 012665
Mean	0.0127420	0.012730	0.012703	0.012665267	0.012709	0.012683	0.012666224	0 . 012665
Worst	0.012973	0.012924	0.012790	0.012665575	NA	NA	0.012673454	0 . 012666
Std.	5.90E −05	5.1985E −05	2.70E −05	1.3E −07	0.012813	3.31E −05	2.12E −06	4 . 38E −14
Variable	CSA	EO	WCA	HEAA	BA	CWCA III	VCS	SHO
x1(d)	0.0516890284	0.05161991	0.051680	0.051689	0.05169	0.0517091014	0.051685684	0.051144
x2(D)	0.3567169544	0.355054381	0.356522	0.356729	0.35673	0.3571073363	0.3566365087	0.343751
x3 (P)	11.2890117993	11.38796759	11.30041	11.288293	11.2885	11.2708257743	1.293729668245	12.0955
g1(X)	−4.441E −16	NA	−1.65E −13	−3.96E −10	0.0	NA	−5.2916E −11	NA
g2(X)	−4.1078E −15	NA	−7.9E −14	−3.59E −10	0.0	NA	−2.672E −11	NA
g3(X)	−4.05378408	NA	−4.0534	−4.053808	−4.0538	NA	−4.0536252	NA
g4(X)	−0.72772934	NA	−0.7279	−0.727720	−0.7277	NA	−0.727785	NA
Best	0.012665	0.012666	0.012665	0.012665	0.012665	0.012671577	0.012665	0.0126740
Mean	0.012666	0.013017	0.012746	0.012665	0.013501	0.013401730	0.012720	0.012684106
Worst	0.012667	0.013997	0.012952	0.012665	0.016895	0.016810785	0.012996	0.012715185
Std.	1.36E −06	3.91E −04	8.06E −05	1.4E −09	0.001420	0.4578E −03	6.527E −05	0.000027

In fact, CSBO could obtain the standard deviation of 4.38E −14, which is an outstanding result. Although other algorithms could result in an optimal global solution, they all have the worse Std. compared to CSBO.

4.1.2. Problem 2: the three-bar truss design problem

The three-bar truss structure design, as shown in Figure 9, is a continuous constrained nonlinear optimization problem in which the objective is to minimize structure volume by using two continuous design variables x₁ and x₂ with region 0 ≤ x₁≤1, and 2 with region 0 ≤ x₂≤1, along with three nonlinear inequality constraints. The mathematical formulation of the three-bar truss structure optimal design problem can be defined as follows (Brajevic & Tuba, 2013):

Figure 9. The three-bar truss structure optimal design problem.

Minimize: (19) $\begin{array}{r}{F}_2(X)=100\times \left(2\sqrt{2}{x}_1+x_2\right).\end{array}$(19) Subject to: (20) $\begin{array}{rl}{g}_1(X)& =P\times \frac{\sqrt{2}{x}_1+x_2}{\sqrt{2}{x}_1^2+2x_1{x}_2}-\sigma \le 0,\end{array}$(20) (21) $\begin{array}{rl}{g}_2(X)& =P\times \frac{x_2}{\sqrt{2}{x}_1^2+2x_1{x}_2}-\sigma \le 0,\end{array}$(21) (22) $\begin{array}{rl}{g}_3(X)& =P\times \frac{1}{\sqrt{2}{x}_2+x_1}-\sigma \le 0,\end{array}$(22)

The best-obtained simulation results from the proposed CSBO algorithm are listed in Table 19, which are compared to various earlier algorithms including SBO (Ray & Liew, 2003), DSS-MDE (M. Zhang et al., 2008), HEA-ACT (Y. Wang et al., 2009), PSO-DE (Liu et al., 2010), COMDE (F. Huang et al., 2007), UABC (Brajevic & Tuba, 2013), CSA (Askarzadeh, 2016), WCA (Eskandar et al., 2012), water strider algorithm (WSA) (Kaveh & Eslamlou, 2020), ICA (Atashpaz-Gargari & Lucas, 2007), (Kaveh & Eslamlou, 2020), salp swarm algorithm (SSA) (Kaveh & Eslamlou, 2020), (Mirjalili et al., 2017), neural network algorithm (NNA) (Kaveh & Eslamlou, 2020), (Sadollah et al., 2018), and biogeography-based optimization (BBO) (Kaveh & Eslamlou, 2020), (Simon, 2008) algorithms. The results indicate that the CSBO algorithm is quite competitive and effective for optimal design of the three-bar truss structure. It is worth mentioning that this is a simple problem with only two dimensions and could be solved easily by most algorithms.

Table 19. Comparison of the best results for the three-bar truss structure optimal design problem.

Variable	SBO	DSS-MDE	HEA-ACT	PSO-DE	COMDE	UABC	CSBO
x1	0.7886210370	0.7886751359	0.7886803456	0.788675134746	NA	0.788675	0.788675107937
x2	0.4084013340	0.4082482868	0.4082335517	0.408248290037	NA	0.408248	0.408248365867
g1(X)	NA	NA	NA	NA	NA	0.000	−2.5199842
g2(X)	NA	NA	NA	NA	NA	−1.464102	−1.4641015
g3(X)	NA	NA	NA	NA	NA	−0.535898	−0.5358985
Best	263.8958466	263.8958434	263.895843	263.89584338	263.8958434	263.895843	263 . 895843377
Mean	263.90335672	263.8981518	263.895843	263.89584338	263.8958434	263.895843	263 . 895843377
Worst	263.96975638	263.95226	263.895843	263.89584338	263.8958434	NA	263 . 895843382
Std.	NA	9.19E −03	8.3E −12	4.5E −10	5.34E −13	0.0	6 . 83E −18
Variable	CSA	WCA	WSA	ICA	SSA	NNA	BBO
x1	0.7886751284	0.788651	0.788683	0.788625	0.788683	0.788639	0.789066
x2	0.4082483080	0.408316	0.408227	0.408389	0.408265	0.40835	0.408227
g1(X)	−1.6875E −14	0.0000	NA	NA	NA	NA	NA
g2(X)	−1.46410	−1.464024	NA	NA	NA	NA	NA
g3(X)	−0.5358984	−0.535975	NA	NA	NA	NA	NA
Best	263.895843377	263.895843	263.89584340	263.89584519	263.89584346	263.89584432	263.89665288
Mean	263.895843377	263.895903	263.89606687	263.89932689	263.89635079	263.89739164	264.50214578
Worst	263.895843377	263.896201	263.89743217	263.91413326	263.90188334	263.90537191	267.74884623
Std.	1.0123E −10	8.71E −05	0.00031196	0.00411693	0.00093128	0.00245495	0.88058464

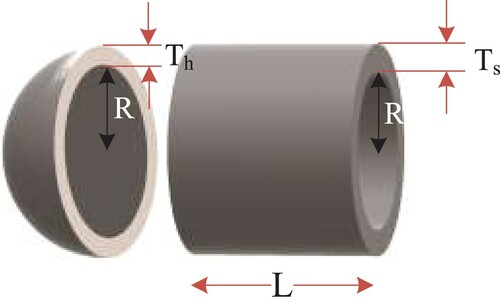
4.1.3. Problem 3: the pressure vessel optimization problem

In the pressure vessel optimal design, as shown in Figure 10, the optimization problem objective function is to minimize the total cost (F₃(X)), containing the material cost, forming and welding of a cylindrical vessel structure. There are two discrete design variables, the thickness of the shell (x₁ or T_s ) with region 1 ≤ x₁≤99 and the thickness of the head (x₂ or T_h ) with region 1 ≤ x₂≤99, in which the design variables x₁ and x₂ are integer multiples of 0.0625. In addition, two continuous design variables, including the inner radius (x₃ or R ) with region 10 ≤ x₃≤200, and the length of the cylindrical section of the vessel, not including the head (x₄ or L ) with region 10 ≤ x₄≤200 are the other variables (Q. He & Wang, 2007b) and (Brajevic & Tuba, 2013). Therefore, the optimal design problem can be expressed as follows (Q. He & Wang, 2007b):

Figure 10. The pressure vessel optimal design problem.

Minimize: (23) $\begin{array}{rl}{F}_3(X)& =0.6224x_1{x}_3{x}_4+1.7781x_2{x}_3^2\\ & +3.1661x_1^2{x}_4+19.84x_1^2{x}_3.\end{array}$(23) Subject to: (24) $\begin{array}{rl}{g}_1(X)& =-x_1+0.0193x_3\le 0,\end{array}$(24) (25) $\begin{array}{rl}{g}_2(X)& =-x_2+0.00954x_3\le 0,\end{array}$(25) (26) $\begin{array}{rl}{g}_3(X)& =-\pi x_3^2{x}_4-\frac{4}{3}\pi x_3^3+1296000\le 0,\end{array}$(26) (27) $\begin{array}{rl}{g}_4(X)& =x_4-240\le 0,\end{array}$(27)

The best-achieved simulation results by the proposed CSBO algorithm in comparison with GA (Coello & Montes, 2002), CPSO (Q. He & Wang, 2007b), CDE (F. Huang et al., 2007), CB-ABC (Brajevic, 2015), ABC (Akay & Karaboga, 2012), UABC (Brajevic & Tuba, 2013), CSA (Askarzadeh, 2016), EO (Faramarzi et al., 2020), BA (Gandomi, Yang, Alavi, & Talatahari, 2013), Gaussian quantum-behaved particle swarm optimization (G-QPSO) (Eskandar et al., 2012), (dos Santos Coelho, 2010), hybrid particle swarm optimization (HPSO) (Eskandar et al., 2012), (Q. He & Wang, 2007a), moth-flame optimization (MFO) (Mirjalili, 2015), and GSA (Mirjalili, 2015), (Rashedi et al., 2009) algorithms are listed in Table 20. The simulation results demonstrate that the proposed CSBO algorithm is quite competitive and robust for different optimal design problems. The CSBO algorithm could obtain the same best, worst, and mean values for different cases, which leads to optimal global solutions. On the other hand, although other methods could result in the best solution, they suffer from large Std., which affects their performance in different circumstances.

Table 20. Comparison of the best results for the pressure vessel optimal design problem.

Variable	GA	CPSO	CDE	CB-ABC	ABC	UABC	CSBO
x1	0.8125	0.8125	0.8125	NA	0.8125	0.8125	0.8125
x2	0.4375	0.4375	0.4375	NA	0.4375	0.4375	0.4375
x3	42.097398	42.091266	42.098411	NA	42.098446	42.098446	42.098445596
x4	176.654050	176.746500	176.63769	NA	176.636596	176.636596	1.76636595842
g1(X)	−0.000020	−0.000139	−6.677E −07	NA	0.000	−0.000	0.0
g2(X)	−0.035891	−0.035949	−0.035881	NA	−0.035881	−0.035881	−0.035881
g3(X)	−27.886075	−116.3827	−3.683016	NA	−0.000226	−0.000	−3.4924E −010
g4(X)	−63.345953	−63.2535	−63.36231	NA	−63.363404	−63.363404	−63.3634
Best	6059.9463	6061.0777	6059.7340	6059.714335	6059.714339	6059.714335	6059 . 714335
Mean	6177.2533	6147.1332	6085.2303	6126.623676	6245.308144	6192.116211	6059 . 714335
Worst	6469.3220	6363.8041	6371.0455	NA	NA	NA	6059 . 714335
Std.	130.9297	86.4545	43.0130	1.14E + 02	2.05E + 02	2.04E + 02	6 . 68E −16
Variable	CSA	EO	G-QPSO	HPSO	BA	MFO	GSA
x1	0.8125	0.8125	0.8125	0.8125	0.8125	0.8125	1.1250
x2	0.4375	0.4375	0.4375	0.4375	0.4375	0.4375	0.6250
x3	42.09844539	42.0984456	42.0984	42.0984	42.0984456	42.098445	55.988659
x4	176.63659855	176.636596	176.6372	176.6366	176.6365958	176.636596	84.4542025
g1(X)	−4.0241E −09	NA	−8.79E −07	−8.80E −07	NA	NA	NA
g2(X)	−0.03588083	NA	−3.58E −02	−3.58E −02	NA	NA	NA
g3(X)	−7.1227E −04	NA	−0.2179	−3.1226	NA	NA	NA
g4(X)	−63.3634015	NA	−63.3628	−63.3634	NA	NA	NA
Best	6059.7143634	6059.7143	6059.7208	6059.7143	6059.714335	6059.7143	8538.8359
Mean	6342.4991	6668.114	6440.3786	6099.9323	6179.1300	NA	NA
Worst	7332.8416	7544.4925	7544.4925	6288.6770	6318.95	NA	NA
Std.	130.9297	566.24	448.4711	86.2000	137.223	NA	NA

4.2. Parameter estimation for FM sound waves

In this section, the proposed CSBO algorithm with Iter_max = 5000 and the population size of Npop = 45 is used to estimate the optimal parameters of an FM sound wave synthesis.

The highly complex multimodal FM sound synthesis optimization problem is significant in numerous recent music systems (Das & Suganthan, 2010). Estimating the optimal parameters of an FM sound wave synthesis is a D-dimensional optimization problem. This paper considershe case of D = 6 based on (Das & Suganthan, 2010). The 6 dimensional vector has six components: X = [x₁(a₁), x₂(ω₁), x₃(a₂), x₄(ω₂), x₅(a₃), x₆(ω₃)] with region −6.5 ≤ X ≤ 6.35 for all variables. The equations are given for the estimated and objective sound wave are given as follows for 100 times (t = 1:100) (C. Li et al., 2011): (28) $\begin{array}{rl}y(t)& =x_1\sin (x_{2}t\theta +x_3\sin (x_{4}t\theta +x_5\sin (x_{6}t\theta )))\end{array}$(28) (29) $\begin{array}{rl}{y}_0(t)& =1.0\times \sin (0.5t\theta -1.5\ast \sin (4.8t\theta \\ & +2.0\ast \sin (4.9t\theta )))\end{array}$(29) Where $\theta =\frac{2\pi }{100}$.

The optimization problem objective function is defined as the summation of square errors between $y(t)$ (the estimated wave) and $y_0(t)$ (the target wave) as shown below, with optimum value F₄(X) = 0: (30) $\begin{array}{r}{F}_4(X)=\sum _{t=0}^{100}{(y(t)-y_0(t))}^2.\end{array}$(30) The comparison between the best results obtained from the CSBO algorithm with the best results reported in (C. Li et al., 2011), such as SLPSO, APSO, CLPSO, CPSOH, FIPS, SPSO, JADE, HRCGA, HRCGA, FPSO, TRIBES-D, and G-CMA-ES, is given in Table 21. As it is evident, the CSBO algorithm outperforms all other proposed algorithms (for all four factors, i.e. Best, Worst, Mean and Std.). Furthermore, test solution obtained from the CSBO algorithm compared to very new algorithms such as gorilla troops optimizer (GTO) (Abdollahzadeh et al., 2021), and tunicate swarm algorithm (TSA) (Kaur et al., 2020), is shown in Table 22, which confirms the ability and efficient performance of the proposed CSBO algorithm compared to TSA and GTO.

Table 21. Comparison of the CSBO best results with the best results reported in (C. Li et al., 2011).

Algorithms	Best	Mean	Worst	Std.
SLPSO	0.0	4.18	13.79	26.99
APSO	0.0	11.33	34.22	41.13
CLPSO	0.007	3.82	14.08	23.53
CPSOH	3.45	27.08	42.52	60.61
FIPS	0.0	5.93	15.11	25.75
SPSO	0.0	9.88	18.27	33.85
JADE	0.0	7.55	13.92	26.18
HRCGA	0.0	8.41	17.59	32.54
FPSO	0.0	5.22	15.82	28.31
TRIBES-D	2.22	14.68	22.24	4.57
G-CMA-ES	3.326	38.75	55.09	16.77
CSBO	0 . 0	1 . 332	10 . 75	3 . 64

Table 22. The best solution results from the CSBO and state-of-the-art algorithms for F4(X).

Variable	CSBO	GTO (Abdollahzadeh et al., 2021)	TSA (Abdollahzadeh et al., 2021)
x1	1 . 0	−1.00	0.3415
x2	0 . 50	−5.0	4.7881
x3	−1 . 50	−1.5	1.4309
x4	4 . 80	4.80	0.1158
x5	2 . 0	2.0	0.0975
x6	4 . 90	4.90	0.5480
$F_4(X)=F_4([x_1,x_2,x_3,x_4,x_5,x_6])$	0 . 0	2.2811E −27	25.1052

4.3. Reliability-redundancy allocation optimization (RRAO) problem

The main purpose of reliability-redundancy constraint and nonlinear optimization problems is to augment the system reliability (maximization of the overall system reliability) using component reliabilities (r = (r₁, r₂, … , r_m)) and redundancy allocation number (n = (n₁, n₂, … , n_m)) optimization vectors for subsystems of the system, X = [r, n]. The nonlinear mixed-integer programming model of this problem can be formulated by selecting the reliability of the system as the objective function to be maximized by considering multiple nonlinear constraints as expressed below: (31) $\begin{array}{r}\text{Maximize}{R}_s=F(r,n)\end{array}$(31) (32) $\begin{array}{r}\begin{array}{l}\text{subject}\text{to}g(r,n)\le l\\ 0\le r_d\le 1,n_d\in Z^{+}\\ \text{(positive integer in the discrete space),}0\le d\le m.\end{array}\end{array}$(32) where R_s is the reliability of different systems, F(.) and g(.) are the objective and constraint functions for the RRAO problem of the overall parallel-series systems, respectively. The g(.) is usually associated with system cost, volume and weight. r = (r₁, r₂, … , r_m) and n = (n₁, n₂, … , n_m) are the component reliabilities and redundancy allocation number vectors for system subsystems, including m subsystems, respectively, and l is the system resource limitation.

4.3.1. A real-world example: the maximizing of the reliability of the over-speed protection system of a gas turbine

The over-speed detection has an important role in mechanical and electrical systems. When an over-speed happens, it is vital to halt the fuel source by utilizing a few control valves (V₁ to V₄). The over-speed protection system of a gas turbine for RRAP optimization mixed-integer non-linear problem is depicted in Figure 11. The input parameters of the over-speed protection system are summarized in Table 23 (T.-C. Chen, 2006).

Figure 11. The diagram block for the over-speed protection system of a gas turbine (T.-C. Chen, 2006; Ghavidel et al., 2018).

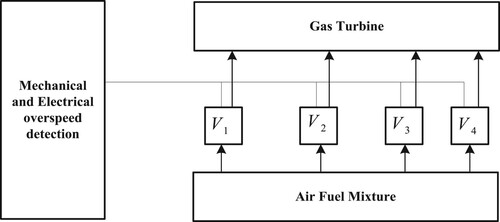
Table 23. Data of the fourth test system (T.-C. Chen, 2006; Ghavidel et al., 2018).

Stage	10^5 × ${\alpha }_d$	${\beta }_d$	$w_d{v}_d^2$	$w_d$	V	C	W
1	1.0	1.5	1	6	250	400	1000 h
2	2.3	1.5	2	6
3	0.3	1.5	3	8
4	2.3	1.5	2	7

This reliability optimization (maximization) problem can be formulated as follows: (33) $\begin{array}{r}\text{Maximize}{F}_5(r,n)=\prod _{d=1}^m[1-{(1-r_d)}^{n_d}]\\ 0.5\le r_d\le (1-{10}^{-6}),0\le d\le m\\ 1\le n_d\le 10,\in Z^{+}\\ \text{(positive integer in the discrete space)}.\end{array}$(33) The system constraints include:

1. The combination of weight, volume and redundancy allocation constraints: (34) $\begin{array}{r}{g}_1(r,n)=\sum _{d=1}^m{v}_d^2{n}_d^2\le V\end{array}$(34) where, v_d is the volume of d^th subsystem for all components, V is the upper volume limit of the subsystem’s products.

2. The system cost constraint: (35) $\begin{array}{r}\begin{array}{l}{g}_2(r,n)=\sum _{d=1}^{m}C(r_d)[n_d+e^{0.25n_d}]\le C,\\ C(r_d)={\alpha }_d{\left(-\frac{T}{\ln r_d}\right)}^{{\beta }_d}.\end{array}\end{array}$(35) where, C parameter is the upper-cost limit of the system and $C(r_d)$ is the cost for all components with reliability rd at dth stage. T is the operating time in which the components are working.

3. The system weight constraint: (36) $\begin{array}{r}{g}_3(r,n)=\sum _{d=1}^m{w}_d{n}_d{e}^{0.25n_d}\le W\end{array}$(36)

In Table 24, the best results obtained from the CSBO algorithm with Iter_max = 3000 and the population size of Npop = 45 compared to many previous reported works are given. It is obvious from this table that the CSBO algorithm outperforms in comparison with other algorithms such as IA (Ghavidel et al., 2018), a novel global harmony search (EGHS) (D. Zou et al., 2011), a particle-based simplified swarm optimization (PSSO) (C.-L. Huang, 2015), a new modified ICA based on attraction and repulsion concepts (AR-ICA) (Afonso et al., 2013), a new artificial fish optimizer (NAFSA) (Q. He et al., 2015) and a novel hybrid of PSO and GA (GA-PSO) (Sheikhalishahi et al., 2013) for maximization optimization problems.

Table 24. Comparison of best results obtained of CSBO with some of the previously reported results.

Variable	IA	EGHS	PSSO	AR-ICA	NAFSA	GA-PSO	CSBO
r1	0.903800	0.900925066	0.90166461	0.90148988	0.90160779120	0.901628	0.901614621
r2	0.874992	0.851636929	0.88817296	0.85003526	0.84993077684	0.888230	0.849921181
r3	0.919898	0.948079849	0.94821033	0.94812952	0.94814603278	0.948121	0.948141545
r4	0.890609	0.887654500	0.84987084	0.88823833	0.88821809379	0.849921	0.88822282
n1	5	5	5	5	5	5	5
n2	5	6	5	5	6	5	6
n3	5	4	4	4	4	4	4
n4	5	5	6	5	6	6	5
Best	0.999942	0.99995463	0.99995467	0.999954673	0.99995467467	0.99995467	0 . 99995468
g1	50	55	NA	55	55	55	55
g2	0.002152	0.00000105	NA	0.00213782	4.5195E −07	0.000006	2.3180E −009
g3	28.803701	24.80188272	NA	24.8018827	24.802	15.363463	24.80188
MPI (%)	21.853	9.847E −02	1.03E −02	3.699E −03	1.496E −05	1.03E −02	NA
Mean	NA	0.99993588	0.9999416669	0.99993804	0.99995075542	0.99995467	0 . 99995468
Worst	NA	0.99985315	0.99986938	0.99982276	NA	0.99995467	0 . 99995468
Std	NA	2.2E −05	1.61E −5	0.00002204	4.43E −06	1.0E −16	3 . 38E −24

4.4. Discussions and prospect of the future

On the CEC 2005, CEC 2014 and CEC 2017 standard benchmarks and five popular real-world engineering issues, the proposed CSBO algorithm is compared to other well-known nature-inspired algorithms. The statistical analysis of the benchmark functions demonstrates that this method can produce promising and competitive outcomes. Additionally, it was discovered that CSBO is capable of performing well in exploration and exploitation in real-parameter (shifted) multimodal and enlarged multimodal functions, as well as in real-parameter unimodal functions. Additionally, the findings of the real-parameter composite and hybrid functions demonstrate that the CSBO strikes an appropriate balance between exploration and exploitation. Additionally, CSBO’s average optimized outcomes and standard deviation on average results are comparable to those generated by other optimization methods. Convergence speed comparisons further demonstrate the provided algorithm’s rapid convergence capability. It would be fascinating to apply CSBO to other optimization issues in many science and engineering sectors in the future. Numerous study directions can be offered for future works. First, we investigate various spirals’ influence Second, a binary implementation of CSBO may be an intriguing future project. Finally, it is recommended to provide certain operators for solving multi-objective algorithms utilizing CSBO. Another intriguing issue would be conducting additional research on the NR parameter value to decide it automatically without user control.

5. Conclusion

In this article, we presented a new meta-heuristic optimization algorithm inspired by the functionality of the circulatory system in the human body named the Circulatory System Based Optimization (CSBO) algorithm. The performance and mathematical modeling of CSBO and its functionality as an optimizer were presented. CSBO was tested and optimized on a wide variety of complex real-world functions compared with many well-known optimization algorithms. Various test functions, including unimodal, multimodal, hybrid, and composition standard benchmarks of the CEC 2005, CEC 2014 and CEC 2017 were used to test the performance of the proposed algorithm. The results showed the higher performance of CSBO compared to the state-of-the-art algorithms in terms of exploration, exploitation, local optima avoidance, and convergence manner. Also, a dimensional scalability analysis was conducted for CSBO, including 30 and 50 dimensions of the CEC2014, and the results indicated that CSBO could efficiently search the feasible space to find the optimal or near-optimal solutions. Finally, CSBO was applied to several different practical engineering problems. These engineering problems are included: the tension/compression spring design, the three-bar truss design, the pressure vessel design, the parameter estimation for FM sound waves, and the reliability-redundancy allocation optimization. The simulation results indicated that CSBO is quite competitive and robust for optimal design problems compared with many modern and advanced optimization algorithms in the recent literature. Therefore, CSBO can be considered a modern and robust algorithm for future studies and optimization applications.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2022R1A4A3032838) and in part by the Chung-Ang University Research Grants in 2021.