Combining entrepreneurship and mathematics in primary school – what happens?

ABSTRACT

This article reports on an educational design research study exploring the potential of combining entrepreneurship and mathematics – two of the key competencies stressed as important in a society of lifelong learning. The aim of the study was to explore what happens when entrepreneurship is integrated into mathematics lessons. Eight Swedish primary schools were involved in the iterative design wherein researchers and teachers together planned, implemented, and evaluated lessons. The results indicate that combining entrepreneurial and mathematical competencies may produce a win-win situation. Entrepreneurial competencies can be of value when students are learning mathematics, and at the same time mathematics teaching can be organised so that students develop both mathematical and entrepreneurial competencies.

KEYWORDS:

• Entrepreneurial competencies
• mathematical competencies
• design research
• primary school

Introduction

This article reports on an educational design research study exploring the potential of combining the teaching of entrepreneurial and mathematical competencies in Swedish primary schools [1]. Entrepreneurial and mathematical competencies are two of the key competencies the European Community stresses as important in a society of lifelong learning (EU, 2007). Mathematics is well established in educational settings, and interest in entrepreneurial competencies has increased around the world since the European Community began to emphasise them. The interest in entrepreneurial competencies in an educational context is not so much about starting companies as it is about giving all students opportunities to develop abilities that characterise entrepreneurs. According to Holmgren and From (2005), this emphasis on entrepreneurial competencies is part of an ongoing “neo-liberal orientated” (p. 387) education process sweeping through Europe. This process is visible in all levels across European educational systems, and similar processes can be seen in the United States. The joint belief is that entrepreneurial competencies, like mathematical competencies, will contribute to individuals’ future success in society, no matter what kind of work they do (EU, 2007; Holmgren & From, 2005).

Figure 1. Summary of the analysis process

Thus, it seems to be generally assumed that entrepreneurship is something positive, and the increased interest in entrepreneurial competencies in educational settings is seldom problematised (Holmgren & From, 2005). However, based on a research overview, Leffler and Svedberg (2010) state that there are no longitudinal studies that show any effects, positive or negative, of the increased interest in entrepreneurial competencies in schools. Furthermore, there are very few studies on entrepreneurial competencies taught in conjunction with core subjects in general nor in primary school in particular. For example, there are no previously published studies on teaching where entrepreneurial and mathematical competencies are combined. The few studies focused on the combination between entrepreneurial competencies and other subjects seldom focus on the holistic nature of a given subject but instead focuses on parts of a subject being integrated into entrepreneurial projects. Such studies indicate problems when entrepreneurship is combined with subjects instead of worked with in isolation (Davidsen & Sørensen, 2015). Despite this, they (ibid) claim that any given subject can be organised as entrepreneurial learning. However, a fair question is what happens to the learning competencies of the subject? According to Holmgren and From (2005), subjects seem to become subordinated when teachers are focusing on entrepreneurial competencies. Based on this, the research question we ask in this article is: What happens to mathematics education when entrepreneurship is integrated into the mathematics lessons? Instead of taking an unconsidered stance, we try to investigate both the positive and negative potential of combining entrepreneurial and mathematical competencies in Swedish primary-school education. Thus, the starting point for this article is mathematics teaching and the aim is to add to the research on the teaching and learning of mathematics in primary school. Mathematics teachers can gain insight about possibilities and reservations regarding the integration of entrepreneurial competencies into mathematics lessons from this article.

Entrepreneurship in educational settings

Even though both policy documents and the literature promote entrepreneurial education, there is no consensus about what entrepreneurial education really is or whether entrepreneurship can be taught at all. A recent review on entrepreneurship in school contexts in Finland, Iceland and Sweden, showed various understandings of the concept (Dal, Elo, Leffler, Svedberg, & Westerberg, 2016). However, what seems to be agreed on in this context is that entrepreneurship is something positive and that one should teach for entrepreneurship, not about entrepreneurship (Dal et al., 2016; Holmgren & From, 2005). These two approaches – for and about – are also found in a study on the implementation of entrepreneurship in Swedish upper secondary school. This study shows that such an implementation can become an issue of teaching in, about, or for entrepreneurship. Teaching in entrepreneurship implies practical and theoretical education about how to start companies; teaching about entrepreneurship implies the theoretical study of entrepreneurship as a phenomenon; and teaching for entrepreneurship implies learning in which the students participate in activities in social contexts that allow them to have influence on and responsibility for the process (Karlsson, 2009).

The increased emphasis on entrepreneurship in international policy and educational research has led to diversity in regard to the attributes and the essence of entrepreneurial learning with multiple, sometimes fragmented, conceptualisations and definitions (Wang & Chugh, 2014). Examples are entrepreneurial perspective (Kuratko, 2005), entrepreneurial mindset (Davidsen & Sørensen, 2015; Sarasvathy, 2009), entrepreneurial orientation (Lumpkin & Dess, 1996) and entrepreneur’s characteristics (Westerberg, Singh, & Häckner, 1997). Recognising this diversity of conceptualisations and definitions, we, in line with many other researchers, focus on attributes of entrepreneurial learning (Lindh, 2017). In line with Jones and Iredale (2014), we focus on enterprise education which includes the capabilities, behaviours and skills needed to function effectively as a consumer, citizen, employee or self-employed person in a flexible market economy. Based on an overview, Holmgren and From (2005) point to creativity, innovation, risk taking, opportunity spotting, self-motivation, and the ability to cope with uncertainty as entrepreneurial capabilities, behaviours and skills. Similarly, when stressing entrepreneurship as important in a society of lifelong learning, the European community emphasises the ability to turn ideas into action, which involves taking initiative, autonomy, creativity, risk taking, innovation, and project management. According to the European community, competencies such as these are to be developed through continuous learning adapted to students’ age (EU, 2007).

As mentioned above, the European community’s emphasis on entrepreneurial competency has increased the attention directed towards entrepreneurship in different national educational settings. In 2009, the Swedish government published a national Strategy for Entrepreneurship in the Educational Area (Government Offices of Sweden, 2009). Starting companies is mentioned in the strategy, but similar to the approach recommended by the European community, the emphasis is on general competencies that characterise entrepreneurs. This is particularly evident for primary school where competencies such as creativity, responsibility, curiosity, and self-confidence are given prominence. One part of the strategy was to include the importance of entrepreneurial competencies in all guiding documents in elementary school, and when a new Swedish primary-school curriculum was implemented in 2011, entrepreneurship was to permeate all primary-school teaching (National Agency for Education, 2011a).

The school should stimulate pupils’ creativity, curiosity and self-confidence, as well as their desire to explore their own ideas and solve problems. Pupils should have the opportunity to take initiatives and responsibility, and develop their ability to work both independently and together with others. The school in doing this should contribute to pupils developing attitudes that promote entrepreneurship. (National Agency for Education, 2011a, p.11)

As presented above, there is a range of conceptualisations and definitions of entrepreneurial education used in policy documents and research. Based on the European community, the Swedish national curriculum, and research literature on entrepreneurship (Holmgren & From, 2005; Jeffrey & Craft, 2004; Leffler & Svedberg, 2010; Lumpkin & Dess, 1996; Sarasvathy & Venkataraman, 2011; Westerberg et al., 1997), the study presented in this article has focused on the following six entrepreneurial competencies: creativity, ability to take responsibility, courage, ability to take initiative, tolerance for ambiguity, and ability to collaborate. The first four (creativity, ability to take responsibility, courage, and ability to take initiative) were chosen based on research on entrepreneurial orientation (Lumpkin & Dess, 1996) while the two last (tolerance for ambiguity and ability to collaborate) were chosen based on research on entrepreneur’s characteristics (Westerberg et al., 1997).

Creativity is about finding new, for the individual, solutions to new and old problems and is well researched as positive in both entrepreneurial and mathematics education research. Creativity is often emphasised as the most central aspect of entrepreneurial orientation as it involves engaging in and supporting new ideas and experimental processes (Lumpkin & Dess, 1996). One major characteristic of creativity is possibility thinking, which is about finding alternatives when obstacles are encountered (Craft, 2002). Jeffrey and Craft (2004) define creativity as innovation, ownership, control, and relevance. In this study, ownership and control are instead included in a different competency, the ability to take responsibility, both for oneself and others. Lumpkin and Dess (1996) describe the ability to take responsibility as individuals independent bringing forth and realising ideas or visions. To be able to take responsibility, students must be given autonomy, which is about handing control back to the learner. Courage is a basic concept in entrepreneurial orientation since entrepreneurship initially was linked to self-employment and thus a greater personal risk (Lumpkin & Dess, 1996). It is about stepping out of one’s comfort zone into situations the individual is not fully comfortable with. Having courage does not necessarily imply that the individual likes to step out of the comfort zone but that s/he is willing to undertake the action to achieve a desired goal (Sarasvathy (2001). Ability to take initiative is about being proactive, which, just like ability to take responsibility, is dependent on autonomy. Being proactive implies taking actions towards future problems instead of waiting for a leader (for example a teacher) to set the agenda (Lumpkin & Dess, 1996; Sarasvathy, 2001).

Tolerance for ambiguity is about acting in situations where the scope of action is not fixed in advance. As part of the entrepreneur’s characteristics, this competency includes the ability to act on opportunities and in situations that are characterised by complexity without obvious solutions (Westerberg et al., 1997). It can, for example, entail working on an ambiguous task that is not fully understood. Finally, the ability to collaborate involves both sharing and absorbing ideas and knowledge to solve tasks and is considered as a key competency for being able to work in society in the coming years. When entrepreneurial learning was included in the Swedish curriculum the emphasis was on entrepreneurship as a social process through which individuals collaborate to transform ideas into solutions. The ability to collaborate implies seeing others as collaborators rather than competitors and includes mutual exchange as well as concrete collaborative projects (Sarasvathy, 2001).

The role of these entrepreneurial competencies in this study is to be understood as teaching for entrepreneurship in combination with a subject, thus teaching for entrepreneurial and mathematical competencies – in the same lesson.

Mathematics in educational settings

When stressing mathematical competencies as important in a society of lifelong learning, the European community emphasises the ability to solve problems in everyday situations (EU, 2007). Similarities can be seen in the Swedish national curriculum where mathematics is described as a “creative, reflective, problem-solving activity” (National Agency for Education, 2011a, p.62). Describing mathematics in terms of creativity, reflection, and problem-solving can be seen in contrast to a national inspection of mathematics teaching undertaken in 2009, which showed that mathematics teaching was dominated by individual calculating, offering limited opportunities for students to develop their ability to solve problems (Swedish Schools Inspectorate, 2009).

Approaches to teaching mathematics differ, both between and within countries, but the western European countries, at least, share in common a focus on competencies where mathematical competence means “the ability to develop and apply mathematical thinking in order to solve a range of problems in everyday situations” (EU, 2007, p.8). This focus on competencies is visible in the Swedish national curriculum, where it is stated that mathematics education essentially should give students opportunities to develop the following five competencies:

• formulate and solve problems using mathematics and also assess selected strategies and methods,

• use and analyse mathematical concepts and their interrelationships,

• choose and use appropriate mathematical methods to perform calculations and solve routine tasks,

• apply and follow mathematical reasoning, and

• use mathematical forms of expression to discuss, reason and give an account of questions, calculations and conclusions.

(National Agency for Education, 2011a, p.59)

To formulate and solve problems using mathematics and also assess selected strategies and methods is about working with problem-solving tasks, which are defined as tasks where the method or methods for solving are not known by the problem solver beforehand. Problem-solving tasks are considered to be cognitively demanding, enabling conceptual understanding, which is understood to be opposed to memorising rules and procedures (Heyd-Metzuyanim, Smith, Bill, & Resnick, 2016). In a problem-solving approach, students have to investigate new ways of thinking where creativity and tolerance for ambiguity are often emphasised as important abilities (Lesh & Zawojewski, 2007). Thus, a problem-solving approach in mathematics teaching has similarities with education for entrepreneurship as presented above.

The competency to use and analyse mathematical concepts and their interrelationships is about having knowledge of mathematical concepts and their relationships to one another and to be able to use and apply this knowledge when working on mathematical tasks (National Agency for Education, 2011b). Knowledge of an interrelationship implies making links between different concepts, for example by using causal or logical reasoning (Boesen et al., 2014). The competency also includes the ability to use and coordinate different kinds of representations, for example pictures, symbols, graphs and formulas (National Agency for Education, 2011b).

To choose and use appropriate mathematical methods to perform calculations and solve routine tasks implies being able to identify the method best suited to solving a specific task. Mathematical methods include mental and written calculations as well as the use of calculators or other digital technologies. The competency also implies the ability to use procedures such as making measurements or constructing tables and coordinate systems (National Agency for Education, 2011b).

To apply and follow mathematical reasoning is the explicit act of justifying choices and conclusions by mathematical arguments, which involves understanding mathematical relationships (Boesen et al., 2014). Reasoning can involve both informal and formal mathematical arguments where a proof can be seen as the strictest form of reasoning. However, proofs are not included in the Swedish curriculum for primary school (National Agency for Education, 2011b).

Finally, to use mathematical forms of expression to discuss, reason and give an account of questions, calculations and conclusions means exchanging information with others about mathematical ideas and thoughts by using different forms of expression. The competency also implies the ability to switch between different forms of expression (National Agency for Education, 2011b).

These competencies will be used to analyse empirical examples further on in the article. The question to be investigated is what happens with mathematics lessons when entrepreneurship is integrated into them? As mentioned, the Swedish curriculum stresses that entrepreneurship is to permeate all teaching in primary school. But what if the mathematics lessons don’t become better – or what if they even become worse? Why then would entrepreneurship permeate mathematics teaching in primary school?

Methodological and theoretical framing

The study was conducted within the frames of educational design research. This is not a fixed method but a genre of inquiry in which solutions to complex educational “problems” are developed in iterative design cycles through collaboration between researchers and practitioners (McKenney & Reeves, 2012). In this study, the complex educational “problem” is the question of what happens to mathematics lessons when entrepreneurship is integrated? Each iterative design cycle included the modification of a mathematics lesson into which entrepreneurial competencies were merged, implementation of this lesson, and retrospective analysis of the lesson. Typically, the goal in design research is to develop design propositions, which include the specifications of what a design should look when it reaches a desired situation (McKenney & Reeves, 2012). However, in this study the desired situation was not known in advance, hence the iterative design became more explorative. When the study was begun, it was not known whether bringing entrepreneurship into mathematics lessons was something desirable or not; that is what was to be investigated. Of course, we wanted the developed lessons to become “good mathematics lessons” but we did not know if this would be the case in advance as we did not know what would happen when the entrepreneurial competencies were integrated.

To be able to understand what happens with mathematics lessons when entrepreneurship was integrated, we took a sociocultural perspective on learning, where context is not something to be acted upon but something to be interacted with. Students’ possibilities for learning depend on the activities we invite them to participate in, and learning is indicated by the students changing the ways they participate in these activities (Rogoff, 2003; Wertsch, 1998). Thus, how we arrange mathematics activities influences what the students are invited to participate in, and thereby influences their possibilities for learning mathematics. When entrepreneurial competencies were integrated into the mathematics lessons, it changed what the students were invited to participate in and by that also changed their possibilities for learning mathematics.

The study

Nine researchers from mathematics education and entrepreneurship as well as approximately 30 teachers (varying slightly over the two years of the study) from eight primary schools (children aged 6 to 12) were involved in the study. As in several other countries (Tatto, Lerman, & Novotná, 2009), these primary school teachers were educated as generalists, teaching several subjects, one of which being mathematics. At these eight schools, iterative design cycles (including the modification of mathematics lessons to include entrepreneurial competencies, implementation of these lessons, and retrospective analysis of the lessons) were frequently conducted in the classes during one school year. Approximately, each class at these eight schools were involved in six design cycles (varied slightly based on the length of the design cycles) during the study. The starting point for the two empirical examples selected for this article was a set of mathematics lessons that were already planned by the teachers without any consideration of entrepreneurial competencies. These lessons were then modified based on the six entrepreneurial competencies presented in the previous section; that is creativity, tolerance for ambiguity, courage, ability to take initiative, ability to collaborate, and ability to take responsibility. The two selected lessons are from two different design cycles in two different classes at two different schools. Together the two lessons illustrate the findings from the entire study in the eight schools. The two teachers involved in the empirical examples presented in this article were educated for the grades they were teaching. All requirements for information, approval, confidentiality, and appliance advocated by the Swedish Research Council (2008) were followed.

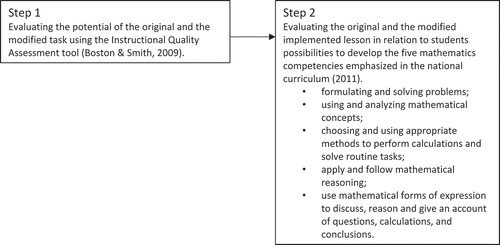
The analysis of the all the lessons within the design cycles was conducted in two steps. First, we evaluated the potential of the task (both the ordinary lesson plan and the modified lesson plan) based on how it was phrased verbally and in text by the teachers. In order to investigate what happened with the pre-planned mathematics task when entrepreneurship was integrated, we used the Instructional Quality Assessment Toolkit (Boston & Smith, 2009; Heyd-Metzuyanim et al., 2016). This tool provides a score of 1–4 on the cognitive demand of a task (Table 1). We used the tool to compare the task as it was phrased in the previously planned lessons with how it became phrased when entrepreneurship was integrated.

Table 1. The prominent task features in the instructional quality assessment tool as presented by Boston and Smith (2009).

Level of cognitive demand	Prominent features
Level 1: memorisation task	The task is not ambiguous, it demands only producing or committing previously learned facts or rules.
Level 2: Procedures without connection task	The task is to be solved with a specifically taught and called for procedure requiring no explanation.
Level 3: Procedures with connections task	The task demands the use of procedures that cannot be used mindlessly. Focus on concepts and ideas, often several representations are included.
Level 4: Doing mathematics task	The task is unpredictable and requires complex and non-algorithmic thinking, the task require students to explore and understand concepts, processes and relationships.

What is intended with a mathematics task is often rather different from how the task turns out in classrooms. This is due to the fact that teachers’ introduction of a task and/or organisation of the lesson sometimes reduces or even eliminates the potential of the task (Mason & Johnston-Wilder, 2006; Smith & Stein, 2014). Thus, a high cognitive level of a task is a necessary but not a sufficient condition for conceptual mathematics teaching (Clarke et al., 2013; Heyd-Metzuyanim et al., 2016). In order to evaluate how the task was implemented in the classroom, the second step in the analysis was to evaluate how the lesson turned out. The researchers were present during the lessons, taking notes. After each lesson, the researchers and the teachers met for an evaluation. The evaluation focused on what had been possible for the students to learn during the lesson and how the changes that were made to the ordinary lesson plan may have contributed, positively or negatively. The evaluation of the ordinary lesson plan was a theoretical evaluation as this lesson was never conducted while the evaluation of the modified lesson plan was based on observations of the implemented lesson. Inspired by Boesen et al. (2014), we evaluated the lesson based on opportunities to learn the five mathematics competencies emphasised in the Swedish national curriculum. The analysis process is summarised in Figure 1.

Results

As mentioned, two lessons will be used as examples as the results are presented. These two examples are chosen as they represent the main findings from the analysis of all the lessons in the study. In line with the theoretical framing of the study the focus is on what the students are invited to participate in and, based on that, what becomes possible for them to learn. The two lessons presented here are to be understood as examples of lessons analysed and similar analysis has been made of all lessons within the study. It is on the wholeness of that analysis that the conclusions and implications in the last section is based on.

In the results the pre-modified plan for each lesson will be presented first, followed by a description and evaluation of the modifications made. Then follows an evaluation on what was made possible for the students to learn during the lessons.

Example 1: describing geometrical figures

The first example is a lesson that was conducted in a sixth-grade classroom, which implies that the students were 12 years old. The majority of the students in this classroom did not have Swedish as their native language, which why they lacked the Swedish words for several mathematical concepts. Based on this, each mathematics lesson most often began with the teacher explaining the mathematical concepts to be used. The goal of this selected lesson was for the students to describe geometrical figures in as much detail as possible. Examples of figures were parallelograms, rhombi, and pyramids. The original plan was to, as usual in this class, start with a collective inventory of “useful Swedish concepts” on the board. After that, each student was to be handed a picture of a geometrical figure with the task of writing a description of the figure in as much detail as possible.

When modifying this lesson to integrate entrepreneurial competencies, the initial collective inventory of “useful concepts” was removed. In order to promote creativity, ability to take initiative, and tolerance for ambiguity, the students were instead handed a picture of a geometrical figure and told that they were to describe the figure in as much written detail as possible and that it should be possible for their classmates to draw the figure based on their descriptions. After writing their descriptions, the students were to read them aloud, one by one. This part of the lesson was intended to promote courage. As the students were reading their descriptions, the other students were to draw the figure described on small whiteboards. For each figure, a joint evaluation was to be made by the class in collaboration, considering questions such as: Was it possible to draw the figure based on the description? Which concepts were useful? and Which other concepts could also have been useful? After each evaluation, the students who had not already read their descriptions were to be given an opportunity to change or add to their descriptions. Thus, the descriptions could become more detailed and more precise as the lesson went on. Finally, at the end of the lesson, all the concepts used by the students were to be collected on the board. Making this list, the students would have a joint responsibility for the concepts that were included.

The analysis of the ordinary lesson plan compared to the modified plan using the Instructional Quality Assessment tool (Boston & Smith, 2009) showed that the task had changed from a level 1 (memorisation task) to a level 4 (doing mathematics task).

The next step was to evaluate students’ possibility to learn the five mathematics competencies emphasised in the Swedish national curriculum. An analysis of the original lesson plan determined that it covered (at least in part) two of the five mathematics competencies emphasised in the national curriculum – to use and analyse mathematical concepts (write descriptions) and to use mathematical forms of expression to give an account of questions (write descriptions). The implementation of the modified lesson went on accordingly to the lesson plan. An analysis of the modified lesson, as it was implemented in the classroom, indicated possibilities for students to develop their ability to solve a problem (how to describe the figure at hand without having knowledge of which concepts were possible or suitable to use in advance), use and analyse mathematical concepts (writing and drawing), apply and follow mathematical reasoning (joint evaluation after each description), and use mathematical forms of expression to discuss, reason, and give an account of questions (write, read, and evaluate descriptions). Thus, an analysis of the modified lesson in relation to the five mathematical competencies indicates the potential for students to develop their abilities regarding four of the five mathematics competencies. A summary is presented in Table 2.

Table 2. Summary of the analysis of the ordinary and modified lesson in example 1.

Mathematical competencies	The ordinary lesson	The modified lesson
problem solving		how to describe the figure at hand without in beforehand having knowledge of which concepts being possible or suitable to use.
analyse mathematical concepts	write descriptions based on pre-presented concepts	Write descriptions and draw figures based on classmates’ descriptions
choose and use appropriate mathematical methods
apply and follow mathematical reasoning		joint evaluation of descriptions
use mathematical forms of expression to discuss, reason, and give an account of questions, calculations, and conclusions	write descriptions based on pre-presented concepts	write, read, and evaluate descriptions

Example 2: knowing the answer – finding the questions

The second example is a lesson that was conducted in all grades at one school, which implies that the students were six to 12 years old. The goal of this lesson was for the students to use the correct rules of arithmetic when solving written word-problems. For younger students, only addition and subtraction were to be included in the word tasks; for the older students, multiplication and division were also included. The original plan was to provide the students with a number of word-problems for them to solve.

When modifying this lesson to integrate entrepreneurial competencies, the initial set of word-problems to be solved was exchanged for one number; the students were then to create several word problems that would arrive at that number as the answer. The number varied according to grade. For example, for grade one the answer was 7; whereas in grade five the students could choose to work with the answer 45 or 96. The change of the task was to challenge tolerance for ambiguity as this was a new kind of task for the students. Furthermore, the infinite possibilities of solutions were to promote creativity and make it possible for the students to take their own initiatives. In the lower grades the students were to produce word-problems involving addition and subtraction for the given answer. In the lower grades the students were also to develop word-problems involving multiplication and division. The youngest students were to draw their word-problems, while the others were to write theirs. The students were to work in pairs (ability to collaborate) to produce one word-problem for each rule of arithmetic. At the end of the lesson, each pair of students were to present their word-problems to the rest of the class (courage). The reason for seeing this as courage is that most students expressed that this was something that they were not used to why they felt insecure and nervous. Each word-problem was to be evaluated in terms of whether it was suitable for the given rule of arithmetic. Thus, in this last part of the lesson, the students were to collaborate and take responsibility for their own learning and their classmates’.

The analysis of the ordinary lesson plan compared to the modified plan using the Instructional Quality Assessment Toolkit (Boston & Smith, 2009) showed that the task had changed from level 2 (procedures without connection task) to level 4 (doing mathematics task).

The implementation of the modified lesson went according to the lesson plan. During the lesson the students struggled a lot, especially since they had to think in reverse to be able to construct their word-problems. To produce a division task, they had to think in terms of multiplication or addition and vice versa. Thus, the students struggled with using their previous mathematical knowledge in, for them, a new setting (creativity, tolerance for ambiguity). While they worked, the students sometimes took their own initiatives; for example, some students started to use calculators to check that their word-problems were correct

An analysis of the original lesson plan determined that it covered one of the five mathematics competencies emphasised in the national curriculum, with the potential for students to develop their ability to choose and use appropriate methods to perform calculations (use the correct rule of arithmetic). An analysis of the implementation of the modified lesson indicated possibilities for students to develop their ability to solve a problem (previous mathematical knowledge in a new setting), use and analyse mathematical concepts (draw or write suitable word-problems), choose and use appropriate mathematical methods (draw or write suitable word-problems), apply and follow mathematical reasoning (produce tasks in pairs and evaluation with the whole class), and use mathematical forms of expression to discuss, reason, and give an account of questions, calculations, and conclusions (producing, presenting, and evaluating word-problems). Thus, an analysis indicates possibilities for students to develop their abilities regarding all five of the competencies. A summary is presented in Table 3.

Table 3. Summary of the analysis of the ordinary and modified lesson in example 2.

Mathematical competences	The ordinary lesson	The modified lesson
problem solving		previous mathematical knowledge is to be used in a new – not obvious – setting
analyse mathematical concepts		draw or write suitable word-problems
choose and use appropriate mathematical methods	use the correct rule of arithmetic	draw or write suitable word-problems suitable for different rules of arithmetic
apply and follow mathematical reasoning		produce tasks in pairs and evaluate tasks in whole class
use mathematical forms of expression to discuss, reason, and give an account of questions, calculations, and conclusions		producing, presenting, and evaluating word-problems suitable for different rules of arithmetic

Conclusion and discussion

This last section will address the question focused on in this article: What happens to mathematics education when entrepreneurship is integrated into the lessons? The analysis of the modified lessons presented in this article indicates that the integration of entrepreneurial competencies into the mathematics lessons changed what the students were invited to participate in and, in that way, what became possible for them to learn. For example, when analysing the modified first lesson, it was stated that during the modified lesson the students had had opportunities to develop the six entrepreneurial competencies as intended. The conclusion was also reached that the modifications had increased opportunities for students to learn how to describe geometrical figures. During the lesson the students experienced the importance of details and correct concepts as well as which concepts were required or desirable to describe each figure. They did not present their descriptions merely for the sake of showcasing but were instead given agency to disagree, change their work and that of others, and discuss mathematical concepts. Furthermore, by adding the drawing component to the lesson, the students also had to interpret concepts used by others and experience the ambiguity of some of the concepts used. To summarise example 1, the modification of the lesson to be more in line with the six entrepreneurial competencies increased opportunities for students to learn the mathematics competencies emphasised in the national curriculum from two competencies to four, and the competency that was only partially addressed in the original lesson plan became fully covered in the new one.

When analysing the second modified lesson, it was stated that the students had had opportunities to develop the six entrepreneurial competencies as intended. When analysing the mathematics, it was concluded that the modifications had led to a task that looked quite narrow at first glance, but it turned out that, as students worked with it, the task offered them opportunities to develop a wide range of mathematical competencies. Producing the word-problems involved the students in even more and deeper mathematical discussions than the teachers had anticipated. These discussions, for example, included relationships between different rules of arithmetic and algorithms. To summarise, the modification of the lesson in line with the six entrepreneurial competencies increased opportunities for students to learn the mathematics competencies emphasised in the national curriculum from one competency to five.

What was found to be similar between the two lessons – and between further lessons developed within the study – was that the integration of entrepreneurial competencies changed the mathematical possibilities. The analysis using the Instructional Quality Assessment Toolkit (Boston & Smith, 2009) showed that the majority of the modified lessons within the study developed to level 4, which indicates performing a mathematics task. By promoting creativity, ability to take initiative, and tolerance for ambiguity, the tasks became more open and possible to solve in different ways. To promote ability to collaborate, the students worked together in different constellations, and thus they had opportunities to formulate and solve problems using mathematics; analyse mathematical concepts and their interrelationships; andapply and follow mathematical reasoning as well as mathematical forms of expression to discuss, reason, and give an account of questions, calculations, and conclusions. All of these are emphasised as what is essential for Swedish students to develop through mathematics education in primary school (National Agency for Education, 2011a). In order to promote the ability to take responsibility and courage, both lessons ended with joint presentations and discussions. In these, many mathematical issues were further elaborated as the students assessed selected strategies and methods and further analysed mathematical concepts and their interrelationships. Also, these competencies are emphasised in the curriculum for primary school mathematics in Sweden (National Agency for Education, 2011a).

Taken together, it appears that the integration of entrepreneurial competencies into the mathematics lessons within the study developed the lessons into lessons characterised as problem-solving lessons. Several national and international studies report how curricular reforms focusing on mathematical competencies in mathematics education seldom result in pedagogical changes in the teaching of mathematics in schools. This is often explained as teachers’ having difficulties with identifying the meaning of the messages of the different reforms (Boesen et al., 2014; Ross, McDougall, & Hogaboam-Gray, 2002). Based on the results of this study, we could argue that the focus on entrepreneurial competencies helps the teachers to implement the message of the reformed curriculum with its focus on mathematical competencies in a way that has not been seen in research where teachers have been asked to focus solely on the mathematical competencies (Boesen et al., 2014). Although it can be argued that the designs of the modified lessons given as examples in this article have been known and promoted in mathematics education for a long time, they were not the initial choice of mathematics lessons for these teachers. It was not until creativity, tolerance for ambiguity, courage, ability to take initiative, ability to collaborate, and ability to take responsibility were introduced as important competencies in and of themselves that these teachers planned and implemented these kinds of mathematics lessons. As previous described, studies have shown that teachers often reduce “the problem” in problem-solving lessons, by for example giving the students hints or instructions for solving the tasks (Mason & Johnston-Wilder, 2006; Smith & Stein, 2014). The emphasis on entrepreneurial competencies within this study seem to have helped the teachers not to eliminate the potential of the modified lessons. This can be connected to how the teachers themselves expressed how integrating entrepreneurial competencies forced them to organise their mathematics lessons differently. The differences they expressed was giving fewer instructions in the form of recipes for the students to follow, instead providing more conceptual tasks with room for students’ autonomy, creativity and initiative (Palmér, Johansson, & Karlsson, 2018). This is in line with the results from Davidsen and Sørensen (2015) where they state that: “Entrepreneurship as a learning philosophy affects the whole school system and especially how teachers in practice organise their teaching” (14).

It is, of course, possible that the positive results in the study do not solely rely on the integration of entrepreneurial competencies into the mathematics lessons. During the study, the teachers’ prerequisites for planning their lesson differed from the usual, i.e. they had more time to plan and the planning was made in a collaborative setting with colleagues and researchers. During the lessons, both the teacher and a researcher were present in the classroom. Furthermore, a selection of entrepreneurial competencies different from the ones used in this study would possibly have led to different results. Additionally, Holmgren and From (2005) stress that positive connections towards, for example, creativity and ability to take initiative vary between times, cultures, contexts, and practices. It is on the basis of such constant fluctuation that the results of the study presented here need to be understood as possible working premises rather than conclusions.

However, despite this, we will end by concluding that, based on the analysis of all lessons within the study with the two lessons presented in the article to be understood as examples, the integration of entrepreneurial competencies into the mathematics lessons seems to have increased opportunities for the learning of mathematics in line with how mathematics competencies are described in the curriculum. The kind of lessons presented in this article are not unique and have been known and promoted in mathematics education for a long time, but their connections to entrepreneurial competencies have not been highlighted. Thus, the results of this study indicate that combining mathematical and entrepreneurial competencies may produce a win-win situation where students can develop both in the same lesson. In a retrospective perspective, some possible links could be seen in advance, for example regarding creativity (Craft, 2002) and tolerance for ambiguity (Lesh & Zawojewski, 2007); however, regardless of this, the implementation of the study was explorative. At the same time as the study shows that creativity, tolerance for ambiguity, courage, ability to take initiative, ability to collaborate, and ability to take responsibility can be of positive value when students are learning mathematics; the study has also shown the importance of a mathematical foundation in the lessons for this to happen. The analysis in this article is on mathematics lessons into which entrepreneurial competencies were integrated. We also tried the opposite, to integrate mathematical competencies into general entrepreneurial project, but this did not generate similar positive outcomes. Thus, to summarise, an integration of entrepreneurial competencies into mathematics lessons may develop the lessons towards the creative, reflective, problem-solving activities as described in the Swedish curriculum (National Agency for Education, 2011a). However, for that to happen, the mathematical foundation of the lessons must be firmly established before entrepreneurial competencies are implemented. This study also supports further study in this field, including investigating if the results are transferable to other grades and/or subjects and how a selection of entrepreneurial competencies different from the ones used in this study would possibly lead to different results.

Additional information

Funding

The study was funded by the Kamprad Family Foundation ref # [20132036]

Notes on contributors

Hanna Palmér

Hanna Palmér is associate professor in mathematics education at Linnaeus University in Sweden. Her research is focused on mathematics teaching and learning in preschool, preschool class and primary school. Of special interest is problem solving in mathematics, digital technology in mathematics education, entrepreneurial competences and professional identity development of mathematics teachers.

Maria Johansson

Maria Johansson has a PhD in mathematics and also one in mathematics education. Her PhD in mathematics education focused on issues to do with mathematics in preschool, particularly to do with the professional development of preschool teachers and childcare workers. She is an Associate Professor at Luleå University in Sweden where she works in teacher education. Her research interests are wide ranging, covering both mathematics and mathematics education for a range of ages.