The development of the cycle model and its effect on mathematics learning using GeoGebra mathematical software

ABSTRACT

This article presents an instructional technology-based cycle model intended to support and facilitate the teaching and learning of mathematics, particularly calculus. The study used quantitative methods with quasi-experimental research that uses non-randomised assignments of the study group that are categorised into experimental and control groups including 36 and 30 students in the control and experimental groups, respectively, at a university in Ethiopia. A pre-test was administered to the experimental and control groups before the intervention (statistical control over the groups) to identify students’ abilities in the two groups. Based on nine steps, Vygotsky’s theory of learning model was implemented in the classroom using GeoGebra software. The findings suggest that the GeoGebra classroom-oriented approach to learning differential calculus, using the cycle model, had a positive effect on students’ conceptual understanding and a very positive effect on their procedural understanding. The article recommends that using the cycle model of instruction in the teaching and learning of calculus can bring important benefits to different stages of schooling in the Ethiopian context and beyond.

KEYWORDS:

• GeoGebra
• calculus
• cycle model
• mathematics learning
• conceptual understanding
• procedural understanding
• zone of proximal development

Introduction

The present century has been marked by rapid technological developments; the learning environment has thus undergone irreversible changes, and individuals can learn whatever they choose, as long as they have access to technology that is paired with their skills to use it effectively. Technology has become the foundation of this modern industrial society’s so-called Fourth Industrial Revolution (4IR) and its ever-increasing global demand for scholars in the 21st century. Meanwhile, integrating technology into higher education has become a non-negotiable imperative. Technology-based instruction aims to stimulate students’ active participation, purposeful learning, and task-oriented activities. The integration of technological aids, specifically in the teaching of mathematics, is a move away from teacher-centred instruction towards a learning-centred approach in which the student’s conceptualisation of subject matter takes centre stage.

Implementing information and communications technology (ICT) in teaching and learning mathematics Has been slower in the classroom than expected. Some factors hampering the implementation of new educational technologies are mentioned by researchers such as De Witte and Rogge (2014), and Agyei and Voogt (2010). Agyei and Voogt (2010) point out that the slow implementation of educational technology may result from a lack of teacher professional development.

De Witte and Rogge (2014) argue that the computer shortage in schools restricts technology use. Similarly, Safdar, Yousuf, Parveen, and Behlol (2011) believe that the financial outlay and resources required by these technologies are responsible for their slow integration of technology in education intended to expedite and enhance the mastering of subject content. So and Kim (2009) argue that the success of integrating technology in education rests on the benefits it holds for the educator. However, studies on the use of technology in mathematics learning have revealed different findings in terms of improvement (or not) in learning. For instance, Biagi and Loi (2013), Goodison (2002), and Hourigan and O’Donoghue (2009) found that the use of technology did not lead to any visible improvements in mathematics learning. In contrast, several scholars have reported gaps in the use of technology in teaching in the mathematics classroom (Curri, 2012; Miller & Glover, 2007; Novotná & Jančařík, 2018; Tay, Lim, Lim, & Koh, 2012). However, another study revealed that one of the best methods of enhancing student achievements in various mathematical topics, for instance, calculus, is using technology in the teaching and learning process (Eyyam & Yaratan, 2014).

Calculus has a broad range of applications in disciplines such as economics, engineering, science, business, computer science, and information systems (Mendezaba & Tindowen, 2018). As a branch of mathematics, the concepts embedded in calculus are abstract and complex (Gordon, 2004; Sahin, Cavlazoglu, & Zeytuncu, 2015; Zachariades et al., 2007). As such, students need higher-order thinking skills to cope with calculus. Sahin et al. (2015) argue that calculus is often the main reason for the failure of students at the undergraduate level because of the way these students have been trained. In their study, Bressoud, Ghedamsi, Martinez-Luaces, and Törner (2016) and Curri (2012) found that students’ difficulties with calculus emerged between secondary school and tertiary education.

Tall, Smith, and Piez (2008, p. 207) argue that “calculus can be taught more by using technology from all fields of mathematics”. In a series of research studies demonstrating the power of Tall (1986, 1990, 2003, 2013) found that digital technology enhanced visualisation skills enabling programming language (in Ethiopia, a current course known as Python has recently been added), and improved students’ understanding of the concepts of calculus. Tall (2019, August) points out that digital technology enhances the teaching and learning of calculus by allowing students to make fast and accurate numerical calculations, manipulate symbols, and create dynamic figures that help them to visualise abstract concepts.

Several researchers have demonstrated that most difficulties encountered by students in calculus arise from a poor understanding of function concepts (Breidenbach, Dubinsky, Hawks, & Nichols, 1992; Williams, 1991). To explore these difficulties, educators have resorted in their teaching to instructional multimedia such as graphic software (Lavicza, 2010; Robutti, 2010); computerised algebraic systems (Durán, Pérez, & Varona, 2014; Mignotte, 1992; Ozguiin-Koca, 2010) or a combination of both (Antohe, 2009; Dikovic, 2009; Hohenwarter & Jones, 2007; Hohenwarter & Lavicza, 2009).

Effective teaching programmes in the 21st century are characterised by technology integration in education (Machaba & Bedada, 2022; Pierson, 2001). Gündüz and Odabasi’s (2004) study revealed that we could no longer regard the integration of technologies in the learning environment in the classroom as an option; it is an obligation in the information age. This use of technology in the classroom requires thorough planning of it should be used to facilitate mathematical understanding (Zhao, Pugh, Sheldon, & Byers, 2002).

In this study, we investigated the effect on students’ learning of mathematics, and specifically of calculus, of GeoGebra mathematical software by applying the nine steps of the cycle model which was developed by the first author in his doctoral study (Bedada, 2021). GeoGebra was used in this study as it is open-source software, it is simple to use, and anybody can download the software free from the internet. Although there are currently several technologies available to enhance the teaching and learning of mathematics, the choice of the most appropriate technological tool can be difficult (Ruthven, Hennessy, & Brindley, 2004).

Research problem, AIM, and research questions

In Ethiopia, little research has been done on integrating technology into mathematics teaching at either the school or university level (Machaba & Bedada, 2022), especially in teaching with open-access software like GeoGebra (Bedada & Machaba, 2022a). Teaching in Ethiopia is still traditional and teacher-centred, not consistent with Common Core State Standards that do not recommend traditional teaching and learning approaches (Alabdulaziz, Aldossary, Alyahya, & Althubiti, 2021). Thus, this study developed a new cycle model, implemented it in the study area, and investigated its fruitfulness for teaching differential calculus (DC) by technology. In the words of Dewey (2016, as cited in Turkmen, 2006, p. 72), “if we teach today’s students as we taught yesterday’s, we rob them of tomorrow” (p.1). Thus, in the present study, the general objective was to elaborate on the development of the cycle model and investigate its effects on university students’ calculus learning by using GeoGebra mathematical software. Therefore, the objectives of this study are twofold. The first objective of this study is to investigate the effectiveness of the use of GeoGebra mathematics software with the help of cycle model in enhancing students’ differential calculus conceptual understanding. The second objective is to investigate the improvement of students’ procedural understanding in differential calculus through the application of GeoGebra mathematical software using the cycle model. The objectives are considered achieved if students who were exposed to the GeoGebra mathematical software using the cycle model in the teaching and learning of differential calculus outperform students in the group without this technology and are taught through conventional lecturing.

Students’ proficiency in mathematics education

Learning theories influenced the evolution of mathematics education. These theories can be classified under the two umbrella terms, behaviourism and constructivism. The method of transmission of mathematics knowledge differs in these theories of learning. Behaviourism combines explicit teaching and direct instruction as a method of knowledge transmission, sometimes known as a traditional teaching method. In constructivism, knowledge is constructed when it is imposed or integrated into existing knowledge. This mechanism is known as the active teaching method (Hechter, 2020). We constantly develop and organise our knowledge both in daily life and at school. Reactivating previously taught information while learning something new is thought (imposed or integrated into existing knowledge) to be the key to successful knowledge construction (van Kesteren, Krabbendam, & Meeter, 2018).

In social constructivist theory, the learning process is cooperative, and knowledge is created not only through the interaction of teacher and student in the environment (psychologically) but also by students themselves (intra-psychologically) (Churcher, Downs, & Tewksbury, 2014).

Vygotsky believed that knowledge was made within the process of communication and interaction with others and scaffolding would lead to the storage of information in the mind and used by the students in the environment (the basis of the developed cycle model) at a later date (Vygotsky, 1978b).

As mathematics is considered to be a difficult subject (Kinnari, 2010); the reviewed literature argues that the use of technology may facilitate the transmission of mathematical knowledge in the classroom, so this study employed the use of GeoGebra together with traditional/conventional methods that are “embedded in culture, human experience and social interaction” (Hechter, 2020, p. 5) with the help of a newly developed model (Bedada, 2021; Bedada & Machaba, 2022c).

Mathematics task activities commonly occur within the classroom while social interaction takes place. Tasks are the basis for students’ classroom learning (Stein & Smith, 2011). Tasks that need students to recall steps in a monotonous manner led to one type of student thinking [multiple choice question types]; tasks that require students to think theoretically and encourage them to make connections leading to different ways of thinking [working out problem questions]. Students who have difficulty linking statistical words or calculations with their graphical, tabular, or other representations may improve with the help of technology (Ocal, 2017). In general, in mathematics, the recognition of students’ starting level (proficiency) by using a pre-test of differential calculus containing the tasks of two types of knowledge (conceptual and procedural) can lay the foundation for successful learning situations in the environment (Kinnari, 2010).

In general, students’ recognition starting level or proficiency refers to their fluency in both types of knowledge (conceptual and procedural understanding) that can be discretely measured, quantified, and stratified using the tasks of differential calculus before and after an intervention (Ellis & Berry, 2005; Kilpatrick, 2001). The term mathematical proficiency has been referred to as mathematical literacy by Kilpatrick (2001), who posits five strands of mathematical proficiency. These are conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition. This study concentrated on the two types of knowledge known as conceptual understanding and procedural understanding. These are defined by Kilpatrick (2001) as:

• Conceptual understanding–students’ grasp of mathematical concepts, operations, and relations, knowledge that students understand.

• Procedural understanding–students’ skills to follow mathematical procedures and whether they use them flexibly, accurately, efficiently, and appropriately.

Developing tasks for mathematics proficiency

If mathematics is dealt with as a priori knowledge in the classroom, based on objective reasoning alone, without considering the experiences of students with mathematics or the meaning they make of what they have learned, developing these tasks can be accomplished by delivering a pre- and post-test which allows teachers to identify students’ mathematics achievement by a discretely measured, quantified, and stratified delivered pre and post-test (Ellis & Berry, 2005). Hence, the activities given to the students may be developed depending on the concepts of the two types of understanding – conceptual and procedural understanding.

Next, let us look at the examples of questions constructed by the first author that were categorised into procedural and conceptual types of questions and how the GeoGebra applet was employed within the classroom setting.

Question 1: What is the value of $\underset{x\to 0}{lim}\frac{sin5x}{2x}$

a. $\frac{5}{2}$

b. $\frac{2}{5}$

c. $1$

d. $\frac{1}{2}$

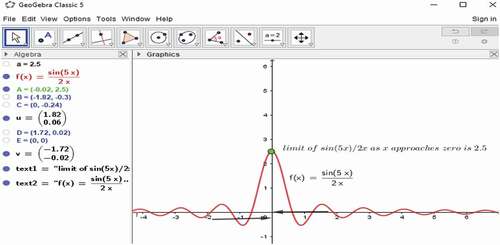
For this question, the students need to recall the formula of a special limit by using previous knowledge to compute the answer. The question is thus categorised as a conceptual test. The teacher may need to inform their students using the GeoGebra applet to find the answer, as illustrated in Figure 1.

Figure 1. Graph of $f\left(x\right)=\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left(5x\right)}{2x}$

To find the sketched graph, students first need to write the function $f\left(x\right)=\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left(5x\right)}{2x}$ at the input menu bar of GeoGebra and then press the enter key on the keyboard. After that, students must write limit (f, point) = limit ($\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left(5x\right)}{2x},0)$, then press the enter key.

Note that this step holds for all other functions to enter into the GeoGebra menu unless the function is defined in piecewise form.

Question 3: Find the values of a&b such that the diving board function is continuous

$f(x)=\left\{\begin{array}{c}2,x\le -1\\ ax+b,-1<x\le 3\\ -2,x\ge 3\end{array}\right\}$

a. $b=1,a=-1$

b. $a=1,b=-1$

c. $a=2,b=-2$

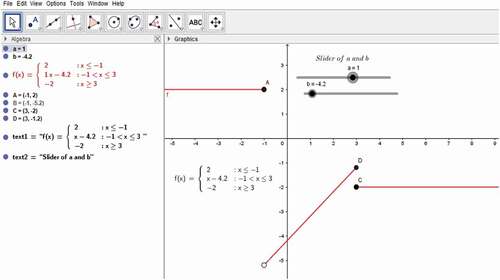
This question needs manipulations to get the answer and is thus categorised as a procedural test types. However, GeoGebra can tell us how to find the constants. To write such diving board functions, students need to write if (conditions, then) in the GeoGebra input menu bar in which the ‘condition’ stands for each condition of the corresponding given function and “then” stands for the corresponding function. In addition, as the dividing board function contains constants, we need to have a slider, say a and b, from GeoGebra to indicate the constants are considered variables. Hence, students need to write: if $(x\le -1,2,1<x\le 3,ax+b,x\ge 3,-2)$.

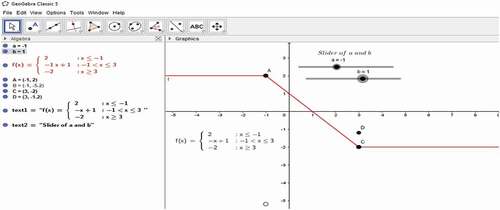
We see that this graph in Figure 2 is not continuous as the graphs have a jump, and we can read from the slider when the values of the constants are a = 1, and b = −4.2, the function has a jump. But, by moving the two sliders to the back and front, we find the exact values of a and b at which the function is continuous. From this, the graph could be depicted as in Figure 3.

Figure 2. Graph of diving board function

Figure 3. Values where the function is continuous

This graph showed that the diving board function is continuous when the values of a = −1 and b = 1.

Teaching and learning differential calculus

Arango et al. (2015) argue that explaining differential calculus traditionally can be dry and off-putting for students. They believe that the use of technology may render explanations more fruitful. As technology continues to develop astonishingly, teaching and learning calculus becomes more accessible and more possible. Technology has migrated from large mainframes to portable desktop computers, calculators, laptops, and notebooks, while manual input of data, arithmetic, and the subsequent creation of graphs have been replaced by automated calculations and graphs. This makes technology available anywhere, anytime.

A study conducted in Brazil by Nobre et al. (2016) found that calculus (and how it was taught) was the primary cause of failure among college and university students. Traditionally, students experience calculus as difficult, hard to understand, and daunting. Innovative methods and approaches are needed to make teaching and learning calculus more effective (Charles-Ogan & Ibibo, 2018; Lasut, 2015). As early as the end of the last century, Rochowicz (1996) identified calculus as the subject that prevents many students from completing courses in science and engineering. According to his research, the calculus curriculum was outdated (even then) and needed to be revised to align with a technologically oriented educational curriculum.

The rapid growth of technology in the 21st century is ongoing, and studies on the effect of combining technology and calculus instruction have also increased. Tall et al. (2008) identify the dynamic nature of both technology and calculus as the reason for this increased interest in such research. Recognising the importance of calculus as the backbone of many science courses, other scholars (Durán et al., 2014; Lavicza, 2010; Mignotte, 1992; Ozguiin-Koca, 2010; Robutti, 2010) have argued that technology has the potential to simplify complex calculus concepts and is gaining ground as a research interest.

The potential of technology in education to promote constructivist instruction, which this study has adopted (Bedada & Machaba, 2022a), is particularly appealing. Huang, Spector, and Yang (2019) list the characteristics of constructivist learning as follows:

• Instruction is student-centred.

• Learners actively construct internal psychological representations.

• Learning comprises the reorganisation and reconstruction of old knowledge and the meaningful construction of new knowledge.

• Learning is not only individualised, but involves language-centred social interaction, communication, and cooperation.

• Learning must be situationally embedded to support meaningful learning.

• The construction of meaning requires appropriate resources.

Material and method

Theoretical framework

The theoretical framework of this study is grounded in Vygotsky’s theory of learning and extends to the Zone of Proximal Development. The study outlines how communication between students and technology, students and their peers (among students), and students and teachers (more knowledgeable adults) affect the learning of mathematics, particularly calculus, with GeoGebra software. Using this theoretical framework, the researcher developed a model to observe how using GeoGebra/technology in differential calculus relates to Vygotsky’s ideas of the Zone of Proximal Development (ZPD) and scaffolding patterns (Wood, Bruner, & Ross, 1976).

Overview of Vygotsky’s theory of learning

Social interaction plays a significant role in student learning at school and in the wider environment. In this learning landscape, learning occurs both at school from the teacher or instructor and other people in the environment (world), that is, from the human to the world of the object/technology (Lantolf & Appel, 1994). To this end, the sociocultural environment or milieu is the central idea in Vygotsky’s theory of learning. His theory of cognitive development is based on a child’s ability to learn things socially with the tools at hand (hands, hammers, computers) and to learn from culturally based signs (language, writing, mathematics). Modern technology or digital technology enhances human abilities to learn, especially in calculus, and emphasises the interaction of technology and humans that enables them to increase their capacity to process expressions numerically, manipulate symbolically, create new theories and represent ideas visually (Tall, 2013). Thus, this study used Vygotsky’s theory of learning principles of social interactions by allowing students to interact with each other when using GeoGebra software with the help of the cycle model.

Zone of proximal development and learning mathematics by using technology

The zone of proximal (potential) development (ZPD) is the gap between what a student can do independently and what they could potentially do with support (guidance) and assistance (Daniels, 2001). Vygotsky (1984) divided ZPD into two categories of intellect: actual intellect, the distance between the actual developmental level as indicated by independent problem-solving ability, and potential intellect, indicated by problem-solving ability with adult guidance or in collaboration with more capable peers. In the present study, the more capable peers were the teachers. Students in the ZPD zone can be successful with instructional guidance (Blake & Pope, 2008).

The development [origin] of the cycle model

According to Bedada and Machaba

The concept of student brain enrichment continues to be an important theoretical component of brain-based learning. Within a certain setting, people (students) learn knowledge (both conceptual and procedural knowledge) in a specific pattern. The potential of technology in education is to promote constructivist instruction is particularly appealing. Within a given setting in the education system classroom setting, brain-based learning is a way of attaining knowledge from the more knowledgeable others (most of the time [the] teacher). To cope with the expected brain-based learning, the role of the teacher is found in the first phase. The role of the teacher lay in identifying both environment and student ability, designing, guiding, helping, assisting, facilitating, giving feedback, evaluating, and motivating students to use their learning in the classroom and environment after they had developed their understanding (internalisation) for externalisation. In this regard, Vygotskian theory holds that cognitive development can be described as a process of internalising culturally transmitted knowledge (that can be held by scaffolding) in the cycle model (containing nine steps), in which the exposure to cultural models (cyclical model) stimulates a gradual internal process of knowledge growth (in both conceptual and procedural understanding) in students learning differential calculus with the help of GeoGebra. (Bedada & Machaba, 2022b, p. 4)

Today, there are various learning and teaching models in the 21st century or the fourth industrial revolution era. One example of the model that helps educators in the instructional process is the ASSURE model with the help of technology. According to the ASSURE model, phases consist of analysis, state objectives, select instructional materials, utilisation materials, required students, and evaluation, and the model is regarded as the first step in the analysis, which is identifying students’ characteristics on entering the programme (Baran, 2010). However, in Vygotsky’s (1978b) conceptualisation, the term “mediator” is defined as the ladder between an environmental stimulus and an individual response to this stimulus. In the present study, this is referred to as the environment and the individual area of the cycle model of teaching mathematics using GeoGebra. Our brains make meaning of the environment and integrate neuronal information from our senses and existing memories into a single phenomenon; in the case of mathematics, we can consider ethnomathematics. For all teaching and learning, identification of the area/environment is mandatory. For instance, we cannot implement teaching with technology at low infrastructure schools unless the school infrastructures are identified first. In most descriptions of learning, the starting point of learning is the interaction of students with their environment (e.g. the scaffolding of students with the help of GeoGebra).

Vygotsky (1978a) believed that knowledge is created within the process of communication and interaction with others and scaffolding would lead to the storage of information in the mind for use by the students in the environment. Within the model, there is the relationship between an environmental stimulus and individual response to the stimulus as well as the ladder between environment stimulus (GeoGebra) and students learning differential calculus. Young, Reynolds, and Walberg (1996) analysed students’ achievements about individual and institutional factors. At the individual level, factors that might affect students’ achievements include their background, attitudes towards science, the time they are exposed to instruction, home environment, and parental involvement. Similarly, Singh et al. (2002) argue that students’ achievement in mathematics and science is affected by attitude, motivation, and academic time, the greatest influence being the time spent on homework. Homework has the advantage that students grapple with ideas on their own but receive feedback (stages of the cycle model) from their teacher in the classroom – an effective means of assisting performance and facilitating learning in the Zone of Proximal Development (ZPD) (Tharp, 1993).

Within the environment, a variety of objects that may be human (students) or human-created tools (the content of the lesson and technology) may occur. Indeed, culture (ethnomathematics) is naturally part of an environment. Students are actors in the learning process and interact with the environment. In Vygotskian theory (1978), this interaction is known as sociocultural interaction. When human-created objects such as GeoGebra are introduced into the interaction process, interaction may be between student-teacher or student-student. In this model, student-teacher interaction is guided (scaffolded) by the technology of GeoGebra. Those students who are guided by more knowledgeable ones (MKOs), most of whom will be teachers, will internalise the concepts (self-reflection) in the environment. When the self-reflection that occurs during internalisation is reflected in the environment, for example in the reproduction of culture, externalisation will immediately take place. For example, the creation of new artefacts is made possible by its transformation like that of human growth and understanding of required activities (Vygotsky, 1978b; Vygotsky, Leont’ev, & Luria, 1999). If a well-designed model and activities are implemented in classroom teaching and learning, externalisation will be optimum (Vygotsky et al., 1999). The teacher-guided students in such environments become new teachers, and if these newly qualified teachers apply these activities themselves, the process becomes cyclical. In this study, this cyclical process is referred to as the hypothesised cycle model. A learning cycle is not a teaching method, instead, it is a process of teaching and learning (Marek, Gerber, & Cavallo, 1999).

In summary, studies have shown that in the Zone of Proximal Development learning can be scaffolded equally by using interactive teaching methods or by using technology. In Vygotsky’s theory of learning, students learn a given course (such as calculus) first by interacting with a more knowledgeable person, in this case, the teacher. Gradually, the student internalises the knowledge and engages in activities independently using tools in the given environment. As students’ abilities grow, scaffolding is progressively decreased, an important aspect of ZPD. In other words, where students interact with each other, cooperative learning takes place, and the assistance of the individual occurs during these activities. For these reasons, this study uses nine steps in the implementation of the hypothesised cyclical model in classroom learning and teaching of calculus. Table 1 shows the nine stages of the developed cycle model with the activities to be done in each stage.

Table 1. Stages of the cycle model.

Stages	Name of the stages	Activities
1	Environment	Identification of area (environment) (such as laboratory class setting).
2	Individual behaviour	Identification of individual areas (teacher professional development and student ability, perception). As the researcher was a teacher, the MKO applies, thus teaching and learning can take place. The pre-test was used to identify students’ abilities.
3	State objectives	State objectives of teaching a lesson with Technology/GeoGebra (by using review literature).
4	Design	Design teaching materials (lesson plan that is compatible with GeoGebra)
5	Implementation	Implementation of a lesson plan in the classroom (start scaffolding student-student, teacher-student interaction)
6	Feedback	Get feedback from students (responses). This feedback could be in the form of an intermediate test, post-test and interview
7	Evaluation	Evaluation of whether the method achieved what was intended. Comparison of abilities before and after the intervention
8	Internalisation and externalisation	Disseminate and practice the knowledge they obtained in the next stages of the cycle model, Stage 9
9	Environment	Practising the knowledge they obtained within the environment by becoming a MKO (such as teachers, and other experts according to the types of intervention given)

Source: Bedada and Machaba (2022b, p. 4).

Methodology

The study used quantitative methods with quasi-experimental research using non-randomised assignments of the study group categorised into experimental and control groups (Shadish & Luellen, 2005). The study included 36 and 30 numbers of students in control and experimental groups, respectively. A pre-test was administered to the experimental and control groups before intervention for the sake of identifying the abilities of students in the two groups.

Data sources and data collection instruments

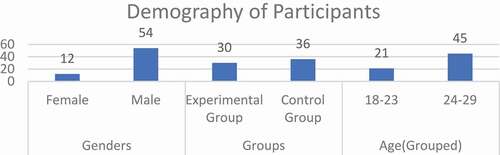
Mathematics learning first-year students at Wachemo University were the sources of data for the study. The demographics of the participants are indicated in Figure 1. The first author constructed 20 multiple-choice items and four problems to be solved that were used for the pre-test before the intervention and the post-test after the intervention from differential calculus topics (Mcmillan & Schumacher, 2014). After the pilot study, the researcher narrowed this down to 18 multiple-choice items and two problems, with 20 questions in total. The quantitative data were collected using the differential calculus achievement test. The demographic information of the participants is reflected in Figure 4.

Figure 4. Participants’ demographic information.

Results

Issues of reliability and validity

A quantitative research study generally uses what is termed a pilot study to increase the validity and reliability of a study. Pilot studies are sometimes also referred to as feasibility studies. Thus, this study used a pilot study to increase the validity and reliability of the data collection instrument. The pilot study was conducted to check the reliability of the test items that would be used in the main study. Students who volunteered to participate in the pilot study were third-year mathematics students at Wachemo University in the second semester of 2020. These were the first- and second-year calculus course students who had already passed this course. These students had graduated in 2020 before the main study was conducted. A test and questionnaires were administered to 15 students. However, for this article, we only report on the data from a test (Bedada & Machaba, 2022b).

Cronbach’s alpha value and inter-item correlations were computed to examine the deficit in items (very simple or very difficult questions that disturb another test on student’s achievement), to assess whether the DCAT test score was reliable. The pilot study revealed that the Cronbach alpha value for DCAT was 0.716 after deleting four items, two each from both categories of questions (conceptual and procedural understanding). Three of these items were found to have low inter-item correlations with the whole scale, affecting the reliability of the complete test, and one further item was removed by SPSS as the item had zero variance. Thus, in the main study, students’ achievement and their understanding of calculus were investigated using 20 DCAT items. The researcher divided the tests into a conceptual and procedural understanding depending on the nature of the constructed tests. Procedural questions are questions that can be obtained by following steps, whereas conceptual questions are questions that can be resolved by remembering only the formula or logic. Each category of understanding (conceptual and procedural) consisted of 10 question items.

If the value of Cronbach’s alpha of an item is equal to or greater than 0.5, then the item is considered acceptable, implying that it is reasonably reliable (Salvucci, Walter, Conley, Fink, & Saba, 1997; Taber, 2018).

Data analysis and interpretation

Analysis of group differences in the pre-test of differential calculus achievement

Scores obtained from the pre-test were analysed by applying an independent sample T-test, which compares the means of the two groups as shown in Table 3 below. To ensure the use of the T-test (Elliott & Woodward, 2007), the researcher computed the normality of the pre-test recorded data, and the pre-test was normally distributed in both groups in the study as the significance level in both tests was greater than 0.5 Please see Table 3. Table 2 shows that the summary of item analysis of DCAT of both types of knowledge [procedural and conceptual].

Table 2. Summary of item analysis of DCAT.

Item analysis
Tests	Difficulty index (P)	Reliability Coefficient (KR-20)	Remark
Procedural (P) test items	0.2131	0.649	Four items needed to be revised (Q9,11,14,19) as all were marginal and difficult items.
Conceptual (C) test items	0.213	0.525	Three items needed to be revised: Q12 was a poor and very difficult item; Q16 was average in terms of difficulty and a poor item in terms of differentiation between students, and Q4 was a very difficult item and only marginally useful for identifying students). In addition, one item (Q15) was rejected and replaced as it had a negative discrimination index and was very difficult (Sharma, 2021).

Table 3. Normality of pre-test.

	Group	Kolmogorov-Smirnov			Shapiro-Wilk
		Statistic	Df	Sig.	Statistic	df	Sig.
Pre-test	Experimental	.119	30	.200	.946	30	.133
	Control	.145	36	.055	.957	36	.172

Source: Bedada and Machaba (2022b, p. 7)

Analysis of group differences in post-test of differential calculus

Table 4 shows a mean difference of 0.33333 between Group 1 (M = 27.000) and Group 2 (M = 26.6667). This difference indicates that the two groups were very similar as the difference was not significant at 0.05 (p = 0.898 > 0.05) (see Table 5). Students in the two groups had similar academic backgrounds.

Table 4. Overall descriptive statistics of the two groups’ proficiency in differential calculus before the intervention.

Groups	Differential calculus achievement (Before intervention)
	N	Mean	SD	Std. Error
Experimental	30	27.0000	9.96546	1.81944
Control	36	26.6667	10.82326	1.80388
Total	66	26.8182	10.36400	1.27572

Source: Bedada and Machaba (2022b, p. 6)

Table 5. Overall one-way analysis of variance summary table comparing groups’ achievement in differential calculus before intervention.

Differential Calculus Achievement Test (Before Intervention)
	Sum of Squares	Df	Mean Square	F	Sig.
Between Groups	1.818	1	1.818	.017	.898
Within Groups	6980.000	64	109.063
Total	6981.818	65

Source: Bedada and Machaba (2022b, p. 7)

The uniformity in the results of the two groups was a good starting point for the researchers to be able to deduce whether the intervention had an effect. Hence, if the experimental group scored higher than the control group on the post-test, the researcher could assume that the differences had occurred because of the treatment in the study, by controlling other confounding variables. The one-way ANOVA is summarised in Table 5.

The results in Table 5 show that there was a statistically non-significant difference in pre-test differential calculus achievement (F (1,64) = 0.017, p = 0.898 > 0.05). As the study concentrated on both types of knowledge (conceptual and procedural), the researchers had to investigate the initial knowledge of students before intervention in the individual area of the cycle model.

Analysis of group differences in post-test of differential calculus

After the intervention (implementation stages of cycle model [Stage 4] and other stages of the cycle model, identification of the area (environment) (laboratory class), the identification of individual areas, stating objectives of teaching a lesson with GeoGebra (using review literature), designing teaching materials [lesson plan that is compatible with GeoGebra]), that ranges from Stage 1 through Stage 4 of the cycle model, respectively, had been completed, the post-test was administered to both the experimental and the control group, forming part of the feedback stages of cycle model.

The recorded post-test scores achieved after the intervention were analysed and are reflected in Table 6.

Table 6. Overall descriptive statistics for two groups on differential calculus achievement after the treatment.

Comparison of Pre-test Scores and Post-test Scores of Groups
Interventions		Pre-test Scores	Post-test Scores
Experimental (N = 30)	Mean	27.0000	41.1667
	Std. Deviation	9.96546	13.81424
Control (N = 36)	Mean	26.6667	31.1111
	Std. Deviation	10.82326	11.40871
Total	Mean	26.8182	35.6818
	Std. Deviation	10.36400	13.44179

Source: Source: Bedada and Machaba (2022b, p. 10)

Table 6 shows that the mean score of the experimental Group 1 in the post-test was M = 41.1667 and that of the control Group 2 was M = 31.1111; the mean difference between the two groups was 10.05556, indicating that the scores of the two groups were significantly different at 0.05 (p 0.002 < 0.05) after the intervention. Again, the study investigated which groups come with a difference in both types of knowledge. Table 7 shows the level of proficiency in terms of students’ conceptual and procedural understanding in differential calculus achievement when taught using GeoGebra (experimental Group 1) using the stages of the cycle model and when taught through conventional lecturing (Control Group 2).

Table 7. Descriptive analysis of student proficiency in conceptual and procedural understanding.

Pre-test conceptual-procedural, Post-test conceptual and post-test procedural with Groups
Groups		Pre-test Conceptual	Pre-test Procedural	Post-test Conceptual	Post-test Procedural
Experimental	Mean	16.3333	10.6667	16.8333	24.3333
	Std. Deviation	6.55656	5.83292	8.14559	7.51244
Control	Mean	13.8889	12.7778	20.0000	11.2500
	Std. Deviation	7.28120	5.90937	9.56183	8.39855
Total	Mean	15.0000	11.8182	18.5606	17.1970
	Std. Deviation	7.01646	5.92494	9.01986	10.30791

Source: Bedada and Machaba (2022b, p. 7)

Table 7 shows that students’ conceptual and procedural understanding of the differential calculus material in GeoGebra Mathematical software-assisted learning had improved. In contrast, students’ conceptual and procedural understanding of the differential calculus material in the control group indicated improvement only in conceptual understanding. In the case of procedural understanding, nothing had changed, or understanding had diminished slightly. Further statistical tests were required on the post-test data. Firstly, a normality test was done on the results obtained from the post-test of differential calculus proficiency. The reason for carrying out further analysis was to determine whether the data were normally distributed, allowing me to choose the right types of tests for the data distributions (e. g. parametric such as a t-test or non-parametric such as a Mann-Whitney test) (Elliott & Woodward, 2007). Thus, the descriptive analysis of the normality test of the post-test data was computed and tabulated in Table 8.

Table 8. Descriptive analysis of normality test of post-test data.

Tests of Normality of post-test
	Groups	Kolmogorov-Smirnov			Shapiro-Wilk
		Statistic	Df	Sig.	Statistic	df	Sig.
Post-test Scores	Experimental	.139	30	.144	.924	30	.033
	Control	.128	36	.145	.962	36	.253

The results in Table 8 indicate that the data were normally distributed for the value of p = 0.144 and p = 0.145, respectively, for the experimental and control group in learning differential calculus and were greater than 0.05 in the Kolmogorov-Smirnov test. In contrast, the Shapiro-Wilk test in Table 8 indicates that the data in the experimental group were not normally distributed as the p-value was less than 0.05; however, the data for the control group were normally distributed. Thus, further investigation using another test was required. Table 9 reflects the post-test data normality test for both types of understanding to determine for which types of proficiency the data were not normally distributed.

Table 9. Descriptive analysis of normality test of post-test proficiency data.

Tests of Normality
Post-test	Groups	Kolmogorov-Smirnov			Shapiro-Wilk
		Statistic	Df	Sig.	Statistic	df	Sig.
Conceptual	Experimental	.199	30	.004	.909	30	.014
	Control	.144	36	.057	.970	36	.434
Procedural	Experimental	.251	30	.000	.887	30	.004
	Control	.145	36	.055	.923	36	.016

Table 9 shows that data from the post-tests of both types of knowledge in the experimental group were not normally distributed; on the other hand, in the control group, these data were normally distributed. As no data were normally distributed in this section, the non-parametric test used was the Mann-Whitney U test (Elliott & Woodward, 2007). The results of the Mann-Whitney test on students’ achievement in differential calculus are reported in Table 10.

Table 10. Mann-Whitney U test on students’ scores in differential calculus.

Time Groups		N	Effect size(r)	Mean Rank	Median	Sum of Ranks	Z-value	U	P
Pre-test conceptual	Experimental	30	.19	37.42	15	1122.50	−1.551	422.5	.121
	Control	36		30.24	15	1088.50
	Total	66
Pre-test procedural	Experimental	30	.71	30.03	10	901.00	−1.385	436	.166
	Control	36		36.39	15	1310.00
	Total	66
Post-test Conceptual	Experimental	30	.72	29.93	17.5	898.00	−1.397	433	.163
	Control	36		36.47	20	1313.00
	Total	66
Post-test Procedural	Experimental	30	.83	47.10	20	1413.00	−6.729	132	.000
	Control	36		22.17	10	798.00
	Total	66

From Table 10, the Mann-Whitney U test showed that procedural proficiency/understanding was statistically significant in both experimental (Md = 20, n = 30) and control groups (Md = 10, n = 36) after the intervention (U = 132, z = −6.729, p < 0.05); students’ scores in the post-test of conceptual understanding of differential calculus in the experimental group (Md = 17.5, n = 30) and control group (Md = 20, n = 36) did not show any visible significant difference between the two (U = 433, z = −1.397, p = 0.163 > 0.05). The pre-intervention procedural understanding of differential calculus of students in the experimental group (Md = 10, n = 30) and of those in the control group (Md = 15, n = 36), (U = 436, z = −1.385, r = .71, p = .166 > 0.05); the conceptual understanding of differential calculus of students in the experimental group (Md = 15, n = 30) and students in the control group (Md = 15, n = 36), (U = 422.5, z = – 1.551, r = .19, p = 0.121 > 0.05) post-intervention also showed no visible significant difference. However, using computed effect size (ES), which can be calculated as $r=\frac{z}{\surd N}$, where N is the total number of participants and z is the z-value computed by SPSS, the groups had small to moderate differences in terms of pre-test conceptual, and procedural, and post-test conceptual understanding of differential calculus in both groups (Rice & Harris, 2005). Table 11 indicates the interpretation of the effect size computed.

Table 11. Interpretation of the effect sizes.

Observations	Computed effect size	Percentile gain	Interpretation
Pre-test – post-test	−1.7	46%	Improvement is high as the value is greater than Cohen’s d standard of 0.8.
Pre-C – Post-C	−0.06	2%	Improvement is low as the value is smaller than Cohen’s d standard 0.2.
Pre-P – Post-P	−2.35	49%	Improvement is high as the value is greater than Cohen’s d standard of 0.8.

The next stages of the cycle model are the evaluation stages that contain whether the programme that the educator(s) employed for a teaching and learning process by technology is achieved or not by using all stages of the cycle model from Stages 1(environment) to 8(evaluation). Lastly, the Internalisation and Externalisation stages of the cycle model were followed. It was anticipated that students in the experimental group would internalise the GeoGebra mathematical software and externalise their knowledge in the environment with their mentors or students after they had completed their studies at university. Vygotsky’s concept of internalisation is a model of learning alienated activities, interconnected dialogic processes (scaffolding) (i.e. decontextualised) in which the individual uses sociocultural practices (teaching and learning of differential calculus with the aid of the GeoGebra mathematical software) through engagement with these interconnections (activities designed by Tharp, 1993; Smith, Dockrell, & Tomlinson, 1997).

Those students who had internalised the activities were expected to externalise the activities again in the school environment, which is known as communities of practice. This stage was similar to Stage 1 of the cycle model, but participants were now familiar with the environment and the activities they had engaged in during the treatment.

Discussion and findings

The combination of the two mathematical proficiencies of students in the understanding of differential calculus in the experimental group showed great improvement, with an effect size of d = 1.7 and with a percentile gain of 46%. Students in the experimental group showed great improvement in procedural understanding, with an effect size of d = 1.2 and a percentile gain of 49%. However, in a conceptual understanding of differential calculus, the students showed only slight improvement with an effect size of d = 0.02 and a percentile gain of 2%. These findings indicate that using GeoGebra for teaching DC helped students improve their procedural understanding more than their conceptual understanding, which contrasts with the findings of Ocal (2017).

The analysis of post-test data using the Mann-Whitney U test indicated that procedural proficiency/understanding was statistically significantly different in the two groups (U = 132, z = −6.729, p < 0.05), whereas student’s proficiency in procedural understanding of differential calculus after the intervention (U = 433,z = −1.397, p = 0.163 > 0.05), and procedural understanding of differential calculus before the intervention (U = 422.5, z = – 1.551, p = 0.121 > 0.05) showed no significant visible difference (U = 436, z = −1.385, p = .166 > 0.05) between the groups. Using computed ES, the groups showed small to moderate differences in terms of pre-intervention conceptual and procedural and post-intervention conceptual understanding of differential calculus, indicating that there was a relationship between the two (Rice & Harris, 2005). In addition, when observing both types of knowledge in each group, the findings revealed that in the experimental group, students’ differential calculus proficiency (conceptual: median = 15 to median = 17.5, and procedural: median = 10 to median = 20) had increased as had the students’ overall scores (Dikovic, 2009). In the experimental group, procedural understanding of differential calculus had increased more than conceptual understanding as GeoGebra enables students’ visualisation of changes to variables. The transformation of procedural to conceptual understanding requires a gradual integral reconstruction of students’ perceptions towards the use of GeoGebra, even though the students expressed positive perceptions towards the use of GeoGebra during the study (Attorps, Björk, & Radic, 2011; Bedada & Machaba, 2022c). Therefore, the findings indicated that instruction with GeoGebra positively affected students’ scores in both conceptual and procedural understanding of differential calculus, contrary to the findings of Ocal (2017), who reported that GeoGebra did not affect procedural understanding. However, procedural understanding can be considered the mediator between conceptual understanding and student achievement (Zulnaidi & Zamri, 2017). In contrast, proficiency in procedural understanding was slightly diminished in the control group (median = 15 to median = 10), whereas proficiency in conceptual understanding of differential calculus was increased (median = 15 to median = 20). The findings by Handelsman et al. (2004), Hurd (1998) and Williams, Papierno, Makel, and Ceci (2004) revealed that courses focused more on memorisation and less on conceptual understanding and computational/procedural understanding of the material at the college level.

Finally, this study revealed that students in the experimental group were more advantaged than those in the control group regarding both types of proficiency. These findings are in keeping with those of several earlier studies on overall student achievement (Akanmu, 2015; Alkhateeb & Al-Duwairi, 2019; Arbain & Shukor, 2015; Doğan & Içel, 2011; Hutkemri, 2014; Jelatu, 2018; Nobre et al., 2016; Ocal, 2017; Preiner, 2008; Rohaeti & Bernard, 2018; Saha, Ayub, & Tarmizic, 2010; Tatar, 2013; Thambi & Eu, 2013; Zulnaidi & Zamri, 2017).

This model could contribute to the improvements of student achievement in terms of both types of knowledge (conceptual and procedural) and, in particular, the relationship between the two types of mathematical proficiency, known as the iterative views of Rittle-Johnson (2017). The two types of knowledge (conceptual and procedural understanding) can be seen as bidirectional, iterative views, which means that improvements in one type of knowledge lead to improvements in the other (Nordlander, 2021; Rittle-Johnson, 2017). Both conceptual and procedural understanding lead to high achievement in calculus and interact with each other (Hoyles & Forman, 1995; Rittle-Johnson, 2017).

Conclusion

This study shed light on the use and effect of GeoGebra in teaching and learning differential calculus in the Ethiopian context. It was conducted when the Ministry of Science and Higher Education (MOSHE) became aware of the fourth industrial revolution and was making efforts to expand technology integration at every stage of schooling, especially at the university level (PASET Forum, 2019). Learners in the 21st century need technical support in the learning process because of the advancements made in technology for teaching and learning. A GeoGebra-oriented classroom uses one of these technologies that can be implemented in the classroom.

The findings of the present study suggest that the cycle model that emanated from the study for learning and teaching could improve students’ procedural and conceptual understanding. The study satisfied the principles of the fourth educational revolution, which are that the teaching and learning process should be reshaped (Ally & Wark, 2020) and consistent with Common Core State Standards that do not recommend traditional teaching and learning approaches (Alabdulaziz et al., 2021). The present study thus produced the cycle model for teaching and learning differential calculus using technology (Koehler & Mishra, 2009). The findings of the study reveal that the improvement of both proficiencies was the result of the scaffolding of student and teacher activities, such as explaining (defining the problem), feedback, rearranging (as the software is dynamic and the teacher can change a given question as many times as they want to) and modifying and modelling lesson learning within the classroom, by GeoGebra.

In summary, we strongly believe that the use of GeoGebra had a positive impact on visualisation through self-exploration and social interaction when learning differential calculus by using instructional technology known as the cycle model.

Authors’ contributions

Tola Bekene Bedada: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data and wrote the paper. Prof. M.F. Machaba: Supervisor to the main author and contributed to the writing of the paper.

Acknowledgments

I am grateful to all the enumerators (at the Mathematics Department of Wachemo University and the University of South Africa) and participants of the study who participated in the completion of this study. I also thank my PhD thesis supervisor Prof. M. F. Machaba. All views and results of this study are only those of the authors.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data and materials used in the current study are available from the corresponding author upon request.

Additional information

Funding

The authors have not received any financial support for this research.

Notes on contributors

Tola Bekene Bedada

Tola Bekene Bedada was born in 1987 at Arsi zone, Ethiopia, and graduated with his BEd in Mathematics from Debre Markos University in 2009 and his Master’s in mathematics education from Addis Ababa University in 2011. He completed his PhD in Mathematics Education in 2021 and currently workng in Wachemo University,Ethiopia. Hisresearch interests are instructional technology in Mathematics Education and learners’ misconceptions.

M.F. Machaba

Prof. France Machaba, DEd, was born in Alldays, South Africa, on 5 April 1974. He holds a Doctoral degree in Mathematics Education from Tshwane University of Technology (TUT) (2014), a Master’s degree in Education from Tshwane University of Technology (2003), a BTech (Educational Management, 1999) and a BTech in Natural Science (Mathematics & Physics, 2000) also from TUT and a BSc (Hons) (Mathematics Education) from Wits University (2005). His research interests are in Teaching and learning of Mathematical Literacy alongside Mathematics, investigation of learners’ misconceptions in understanding mathematics concepts, and the usage of everyday context in the teaching and learning of Mathematics.