Neuronal spike-train responses in the presence of threshold noise

Abstract

The variability of neuronal firing has been an intense topic of study for many years. From a modelling perspective it has often been studied in conductance based spiking models with the use of additive or multiplicative noise terms to represent channel fluctuations or the stochastic nature of neurotransmitter release. Here we propose an alternative approach using a simple leaky integrate-and-fire model with a noisy threshold. Initially, we develop a mathematical treatment of the neuronal response to periodic forcing using tools from linear response theory and use this to highlight how a noisy threshold can enhance downstream signal reconstruction. We further develop a more general framework for understanding the responses to large amplitude forcing based on a calculation of first passage times. This is ideally suited to understanding stochastic mode-locking, for which we numerically determine the Arnol'd tongue structure. An examination of data from regularly firing stellate neurons within the ventral cochlear nucleus, responding to sinusoidally amplitude modulated pure tones, shows tongue structures consistent with these predictions and highlights that stochastic, as opposed to deterministic, mode-locking is utilised at the level of the single stellate cell to faithfully encode periodic stimuli.

Keywords:

• stochastic mode-locking
• integrate-and-fire
• threshold noise
• auditory processing
• ventral cochlear nucleus

 Introduction

A vast body of work has been devoted to understanding the variability of single neuron response to repeated stimuli, especially as regards the consequences for neural coding (Mainen and Sejnowski 1995; Nowak et al. 1997; Beierholm et al. 2001; Fellous et al. 2001). For a recent perspective on this within the computational neuroscience community we refer the reader to Longtin and Rinzel (2009). The source of spike-train variability is often linked to noise which can arise across a broad range of spatial and temporal scales. Examples of stochastic processes within the single neuron include the dynamics of gene regulatory networks, ranging up to channel kinetics and neurotransmitter release. Recent work has begun to quantify these, and other, sources of noise and uncover how they contribute to trial-to-trial variability (Faisal et al. 2008). Theoretical work in this area has greatly benefited from the use of techniques from nonlinear dynamics and statistical physics (Holden 1976; Tuckwell 1989; Lindner et al. 2004) and is still an active area of research (Laing and Lord 2010). In this paper, we are primarily interested in the variable times of generation of action potentials in response to a given input, as opposed to spontaneous action potentials. The latter are often thought of as arising from intrinsic channel fluctuations in an excitable system (Chow and White 2000), whereas for strongly driven systems extrinsic fluctuations are more important. Although it is common to model the generation of action potential timings through a stochastic point process (Rieke et al. 1999) we shall favour the use of a mechanistic model that retains a clear notion of a voltage threshold for spike generation. The simplest class of models of this type are those of integrate-and-fire (IF) type. The dynamics of these noiseless models subject to periodic forcing has been developed in Coombes and Bressloff (1999), using the language of Arnol'd tongues, building on the seminal work of Keener et al. (1981). Obviously these are deterministic dynamical systems models that are unlikely to generate variable firing times without some additional stochastic component. This is often introduced as an additive or multiplicative noise source in the current drive to the model in order to mimic the effects of channel fluctuations or the stochastic nature of neurotransmitter release. Numerical studies of sinusoidally forced IF models with additive zero-mean Gaussian white noise have been pursued in Hunter et al. (1998) to show a resonance-related enhancement in spike time reliability that decreases as the relative amplitude of the fluctuations increases. Similar studies of quasi-periodically forced noisy IF models have also been performed by Tiesinga (2002) who showed that neuronal reliability is strongly influenced by the location of Arnol'd tongues in parameter space. Mathematical techniques for studying periodically forced noisy IF models have been developed by many authors using techniques from statistical physics (mainly for Langevin and Fokker-Planck equations) (Burkitt and Clark 2000; Plesser and Gerstner 2000; Brunel et al. 2001; Verechtchaguina et al. 2006; Kostur et al. 2007; Schwalger and Schimansky-Geier 2008) as well as the numerical analysis of an appropriate stochastic phase transition operator (Tateno et al. 1995; Shimokawa et al. 2000). However, noise at the axon hillock (connecting the cell body to the axon and being the primary site of action-potential initiation) is another mechanism that may underlie spike variability. The source of this noise is once again due to channel noise (despite the comparatively large number of ion channels that are present at these sites). Stochastic simulations suggest that it is the number of ion channels open at the action potential threshold that determines its timing precision and that the resulting variability in spike timing is larger for weaker driving signals, for which the likelihood of the membrane potential reaching the action potential threshold is more affected by channel noise (Schneidman et al. 1998). Because of this it would seem natural to model firing variability at the axon hillock via a random modulation of the threshold in an IF model. Indeed such a model has already been shown to be capable of representing the responses of H1 cells in the visual system of the fly (Gestri et al. 1980). H1 cells are directionally selective and their mean response has been shown to encode reliably the velocity contrast of drifting gratings. Importantly, threshold noise is a natural model that can cover a broad spectrum of biophysical sources of stochasticity in a phenomenological fashion. From a functional perspective it is probably of less consequence as to how one models noise as opposed to recognising that in some form or other it underlies spike-train variability (assuming the model also accurately fits data). As well as providing a convenient description for such behaviour, noisy threshold models are in fact mathematically and computationally easier to deal with than models with random current injection (Lindner et al. 2005) and have been analysed in the context of optimal linear signal estimation by Gabbiani and Koch (1996, 2001) and Steinmetz et al. (2001).

In the next section, we introduce the IF model and the form of threshold noise that we shall study throughout this paper. Then we develop a linear response theory for the determination of firing patterns in the regime of small amplitude periodic forcing. Here we review work of Knight (1972a, 1972b, 2008) and use simulations to show that a population of uncoupled leaky IF neurons with sufficient threshold noise can faithfully encode a stimulus in the network firing rate. We then develop a novel method for the determination of first passage times in IF systems with threshold noise based on the notion of a Rice expansion. This allows us to work in the regime of large amplitude periodic forcing to determine inter-spike interval (ISI) histograms. Numerical simulations of the stochastic model are used to confirm the validity of our calculations. We also numerically explore the patterns of ISIs throughout parameter space and determine how increasing the level of noise modifies the landscape for stochastic mode-locking. We then show that data from stellate cells in the ventral cochlear nucleus are very well explained by an IF model with threshold noise, which supports the hypothesis that stochastic, as opposed to deterministic, mode-locking is utilised at the level of the single chopper cell to encode periodic stimuli. This leads to a tentative proposal concerning the role of stochasticity in coding different aspects of the stimulus envelope in these neurons. Finally we give a brief summary and discussion of the work in this paper.

1. The model

The evolution of the voltage V in a linear (leaky) IF model is given by

where I(t) is an injected current. An action potential is said to occur whenever the membrane potential V reaches some threshold V _th. The set of action potential firing times are defined by

The corresponding set of inter-spike intervals (ISIs) is given by . Immediately after a firing event the system undergoes a discontinuous reset such that . Hence, the flow generated by the IF process is discontinuous at the firing times t=T _n . Introducing the membrane time-constant and absorbing a factor of g _L within the definition of I(t) the deterministic solution of Equation (1) may be written

where

In this paper we shall focus on periodic forcing with . A simple calculation gives

In the case that the threshold V _th is a constant, the properties (existence and stability) of mode-locked solutions can be explicitly calculated (Coombes and Bressloff 1999). By a mode-locked solution we mean here that the spike train generated in response to a periodic signal shows a repeating pattern of p clustered spikes, which repeat at integer multiples q of the stimulus period. The explicit construction of borders in parameter space that define the instabilities of mode-locked states, labelled p:q, can be used to build up the so-called Arnol'd tongue structure for the model. For example a 1:1 mode-locked state fires with period at a phase φ∈[0, 1) determined by the solution of with , which from Equation (3) gives

Here we have used the fact that G is a Δ-periodic function. From the form of Equations (5) and (6) we see quite clearly that in the limit (so that the model is a perfect integrator) then the neuron could lock to the signal at any arbitrary phase as long as . Hence, there is a big difference in the behaviour of perfect and leaky IF models. A perfect integrator could show variability in its phase-locking to a periodic signal (depending on initial data) though a leaky integrator could not (as it would always lock to the phase φ determined by Equation (6)). However, to incorporate the effect of threshold noise we shall move away from a completely deterministic description and reinterpret the threshold for firing as a random variable, such that , where ξ is drawn from a distribution ρ(ξ). In this case, the probability of the neuron firing when the membrane potential is equal to V is

where H is a Heaviside function. A common choice for the distribution of thresholds is one that reproduces the Little model (Little 1974; Little and Shaw 1978) with ρ=f′ and . Here the temperature parameter β controls the width of the bell-shaped distribution for ρ and we have simply that . Other sigmoidal forms for the probability of firing can be generated by choosing bell shaped distributions for ρ. Throughout the rest of this paper we shall work with the Gaussian choice

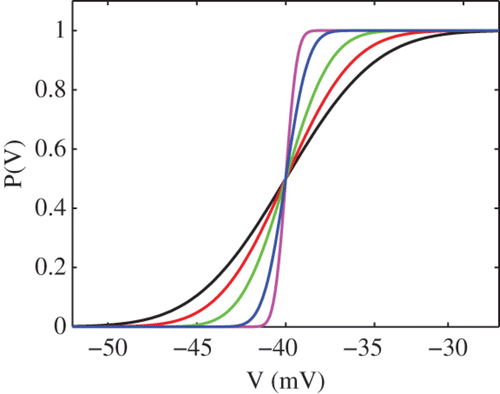
The probability of firing in a model with Gaussian threshold noise defined by Equation (8) is shown in Figure 1. For the rest of this study we shall represent the fluctuating threshold by a stochastic process Φ(t) whose stationary probability distribution around the mean V _th is given by Equation (8) with a temporal correlation function . Since , Φ(t) is differentiable in the mean-square sense, so that threshold crossings are well defined. The numerical scheme that we have developed for the implementation of this IF model with a stochastic threshold is given in Appendix 1.

Figure 1. The probability of firing in a model with Gaussian threshold noise. Here V _th=−40 mV and σ=4 mV⁻¹ (black), σ=3 mV⁻¹ (red), σ=2 mV⁻¹ (green), σ=1 mV⁻¹ (blue) and σ=0.5 mV⁻¹ (magenta).

1. Linear response theory

To gain an understanding of the response properties of a periodically forced leaky IF neuron model (both with and without noise) it is first useful to develop a linear response theory. In fact this has already been done in a very beautiful paper by Knight (1972a), who focused on stochastic effects that can be modelled by choosing an appropriate distribution for the ISIs. In this section we shall review the techniques of Knight for both single unit and population responses (as well as their relation), though focusing more closely on threshold noise and how it enforces a specific ISI distribution. For a recent discussion on how to analyse networks of nonlinear IF neurons we refer the reader to Richardson (2008).

1 Deterministic single unit response

Consider , with corresponding changes , and . Here . For a frequency we have the corresponding change , so that . Expanding the firing map , with V(t) given by Equation (3), to first order gives

From Equation (4) we note that if I(t) is slowly varying then with G′(t) ∼ 0. In this case we have from Equation (9) the simpler relationship that

Fixing t=T _n+1 and writing the instantaneous period T _n+1−T _n as Δ(t) gives

For I(t)=I ₀, , , and then

which is independent of t. Here . We interpret Equation (12) as the deterministic single unit response gain function, which gives the corresponding change in frequency as a function of the change in the drive. Note that for a perfect integrator () then Equation (12) has zeros when , , and .

1 Deterministic population response

Consider a population density ρ(V, t) for a large uncoupled network indexed by i=1, …, N:

The dynamics for ρ(V, t) can be written in terms of a conservation law:

for some flux J(V, t). The population firing rate, r(t), can be identified with the flux through V=V _th, namely

In an asynchronous state the density ρ(V, t) is a time-independent constant ρ₀. Hence, for a pure integrator with τ V˙=I

and the signal can be reconstructed from the population rate. This has recently been termed the faithful copy property by Knight (2008). Since asynchrony underlies this coding property it is interesting to note that a recent theoretical study has shown that recurrent neural networks are capable of generating such states despite substantial amounts of shared input (and also retain low mean spiking correlations) (Renart et al. 2010). For a constant signal I=I ₀ we have simply that . A linear perturbation analysis can be performed by considering and in which case it may be shown that (see Appendix 2)

For a model that deviates from Equation (17) the implication would be that signal reconstruction from the population rate is not optimal.

1 Relationship between single unit rate and population rate

Consider a large uncoupled network of N spiking neurons with a population firing rate r(t). In an asynchronous state over one ISI, Δ(t), of a single neuron all neurons in the network must fire once. Hence

A linear response theory may be developed by letting , and expanding Equation (18) to first order around . This yields

which is valid for any model described by Equation (18). Note the divergence of when . To obtain the variation in r in terms of the variation in I we write

where is model dependent. Using Equation (12) for a leaky integrator we find

We see that only in the limit and do we recover the relationship (17), suggesting that signal reconstruction for a network of (uncoupled) leaky IF neurons is poor especially near resonances where . Obviously one way to compensate is to work with membrane models that are not leaky. However, physiologically this does not seem to be the preferred choice. Rather we will next show that threshold noise is a natural way to flatten Equation (21) and improve the ability of a network to reconstruct an input signal.

1 Stochastic encoding

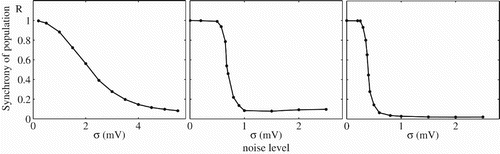
Noise may be thought to serve two purposes for uncoupled leaky IF networks: (i) to combat the tendency to synchronise and promote asynchronous states (which are better for signal reconstruction at the network level), and (ii) to diminish resonances (and again lead to better signal reconstruction). To establish the former property we perform simulations of N=1000 uncoupled leaky IF neurons with increasing levels of threshold noise and track the Pinsky–Rinzel measure of synchrony (Pinsky and Rinzel 1995). This is defined with the introduction of a set of phases, φ _k (j, m), associated with the firing times of the jth neuron:

Here the T _k (j, m) represent the set of firing times of neurons i≠j that occur on the interval . The number of such events will be denoted by A(j, m) with . For a set of phases with n=A(j, m) and fixed (j, m) we introduce the order parameter

An overall measure of synchrony, R, is defined by averaging R(Φ) over all neurons and firing events in some time window. Perfect synchrony would correspond to R=1 and asynchrony to R=0. Figure 2 confirms the conjecture that increasing the threshold noise strength does indeed promote asynchronous network states. In this plot we vary the ratio of the driving frequency to the natural frequency of the neuron, , as well as the amplitude of forcing, a, and show that in all cases synchrony drops off with increasing variance of the noisy threshold.

Figure 2. Loss of synchrony with increasing noise strength in a network of 1000 uncoupled leaky IF neurons for different values of the ratio of the driving frequency to the natural frequency of the neuron, s_ω ≡ ω/ω₀, and the amplitude of forcing, a. Parameter values are (left) s_ω=1.1, a=1, (middle) s_ω=2.2, a=2, (right) s_ω=3.1, a=1.5. Other parameter values are η=2 ms, I ₀=2.4, V _L=V _R=−60 mV, V _th=−40 mV and τ=10 ms.

To establish the second conjecture regarding the ability of noise to diminish resonances we present the following mathematical analysis (making use of linear response theory). In the presence of threshold noise the instantaneous ISI is a random variable defined, from Equation (3), according to

For the case of a constant drive with I=I ₀ the ISI is simply defined by

where for a constant drive G(t)=I ₀ for all t. From the linear response theory in the Deterministic single unit response section with I=I ₀, we have an explicit form for as

Denote the probability density for Δ as and the corresponding distribution for Δ₀ as . The mean value of is thus

Introducing the function , allows us to write Equation (27) in the form

As we did for the noise free case in the Relationship between single unit rate and population rate section, above, we next show how to calculate a population response (uncoupled) in the presence of noise.

Denote the probability density that a single neuron fires at time t after firing at t−Δ as . Denote the number of firings in the population between t and t−Δ as n(Δ, t), which is related to the population rate r(t) as

The number of neurons in the network then satisfies

Performing a linear response analysis according to and gives

where is an average with respect to the perturbation of the distribution:

For and using we find

Identifying then using Equations (28) and (33) gives the result

Noting that the denominator in Equation (34) cannot equal zero, and resonances (where s_ω is integer) are suppressed. In the noise free limit (when the distribution for ψ₀ is a delta-Dirac function centred at the value of Δ₀ defined by Equation (25) with ξ=0), we recover the deterministic result (Equation (21)) with .

To compute Equation (34) it is necessary to evaluate for the given distribution of threshold noise. To do this we note that , where , so that we may write

with defined by Equation (25). By differentiation of Equation (25) we see

Hence,

which may be evaluated numerically. A plot of the amplitude of Equation (34) for various levels of noise is shown in Figure 3.

Figure 3. A plot of the amplitude of the population response function |δ r/δ I|/r ₀ for a leaky integrator network as a function of s_ω≡ω/ω₀ for σ=0.01 (black), σ=0.1 (green), σ=0.15 (blue), σ=0.2 (red) and σ=0.25 (magenta). The response function becomes progressively flatter and resonances are abolished as the blow up around s_ω=1 on the right illustrates. Other parameter values are V _L=V _R=−60 mV, V _th=−40 mV, τ=10 ms and I ₀=2.3.

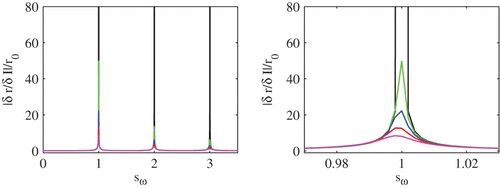
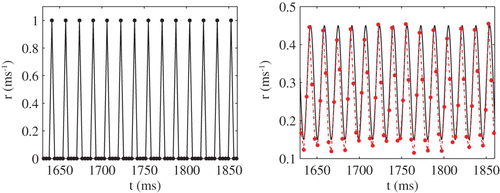
The linear response theory that we have reviewed here is limited in that it can only treat small amplitude periodic signals. However, to establish whether the faithful copy property can be achieved for large amplitude forcing we resort to direct numerical simulations. In Figure 4 we show results of a study of 1000 uncoupled IF neurons with threshold noise for both small and large noise strengths. In the low noise case phase-locking to the periodic driving signal dominates and the neurons operate in synchrony. The network firing rate is able to track the frequency of the drive but not its specific temporal shape. In contrast, high levels of noise promote asynchrony (see Figure 2), and the network rate accurately reflects the shape of the sinusoidal driving force.

Figure 4. Network rate r (dots) for σ=0.001 mV (left) and σ=5.5 mV (right) in the 1:1 case for s_ω=1.1 and a=1. The solid black line in the right panel corresponds to the oscillating input signal. Other parameter values are η=2 ms, I ₀=2.4, V _L=V _R=−60 mV, V _th=−40 mV and τ=10 ms.

In the next section we move beyond linear response theory by developing the calculation of first passage times in IF systems with threshold noise. Moreover, we will broaden our discussion to include the properties of other mode-locked states, and not just the 1:1.

1. First passage times

The observation that neurons generate voltage spikes as soon as the membrane potential reaches a critical value has led to the identification of ISIs with first passage times (Gerstein and Mandelbrot 1964; Capocelli and Ricciardi 1971). Generally, a first passage time corresponds to the time that a stochastic process needs to reach a predefined boundary given some initial data. Hence, the first passage time is a random variable. Since the neuron is reset to a fixed value after eliciting a spike, each ISI presents a realisation of a first passage time, so that the distribution of first passage times is identical to the ISI distribution. The most common approaches to quantify first passage times have assumed a constant threshold, e.g. Ricciardi and Sato (1988), but see Tuckwell and Wan (1984) for a contribution involving a deterministically moving barrier and Tateno and Jimbo (2000) for an IF model with periodically varying threshold (though constant drive). In contrast, we here consider a fluctuating threshold in the presence of a deterministic membrane potential.

1 Solution for varying boundary

Since we have chosen the fluctuating threshold to be a stationary Gaussian process Φ(t) (see Introduction), then the calculation of the ISI distribution is equivalent to computing the first passage time of this process through the deterministically evolving trace of the membrane potential. Following ideas of Rice (1944), the probability that Φ(t) crosses through the boundary V(t) in the interval [t, t+d t] is given by

where denotes the joint probability that the random threshold crosses the voltage trace from above in the intervals , \ldots, conditioned on . A closed form expression for W _n follows readily as (Ricciardi and Sato 1983; Verechtchaguina et al. 2006)

with V _k =V(t _k ) and . The probability describes all trajectories with and , k=1, …, n conditioned on . Since Φ(t) is a Gaussian process, the unconditioned joint probability p _2n (q) with , , takes the form

Here, we introduced the mean vector , and the symmetric correlation matrix Γ_2n with entries

where . The conditional joint probability then follows from Bayes’ theorem as

where Γ_2n+1 is the correlation matrix for the 2n+1 dimensional vector (φ₀, q). The matrix Λ_2n results from crossing out the first column and the first row of , and we have set with . To gain a first insight into ISI distributions, we compute the leading term in Equation (38), which results in

where , , and

Since the exact time evolution of the membrane potential enters the calculation of W ₁, its value depends on the initial phase ψ₀ of the input current, which we take as in this section. Suppose we start from a fixed value of ψ₀, then the resulting ISI distribution for the first threshold crossing gives rise to a distribution of phases at reset. Therefore, the ISI distribution at the second threshold crossing F ₂(V(t), t) is the weighted average

Here we have dropped the dependence of W ₁ on the initial value of the random threshold assuming that the correlation time of Φ(t) is much shorter than any ISI. Since Equation (45) determines the phases of the input current at the second reset, we introduce the operator 𝒦 defined through . Therefore, the phase distribution at the nth reset is given by

If Equation (46) possesses a stable fixed point, i.e. a stable distribution g ^☆ such that , then the full ISI distribution is given by

The existence of an invariant distribution g ^☆ follows from e.g. (Tateno 1998). The right column in Figure 5 shows ISI distributions from direct numerical simulations and from the evaluation of W ₁ employing the iteration outlined above. The frequency of the drive is given by , where ω₀ is the frequency of the unforced neuron (see Deterministic single unit response section above). The analytical results follow closely the simulated distributions for various sets of parameter values. Upon decreasing the strength of the fluctuations, we find narrower distributions. Note that the ISI time at the maximum of the distribution corresponds to the deterministic period. Since the distributions shown in Figure 5 have a single peak they describe stochastic phase-locked states in which there is only a single phase, namely that the neuron fires only one spike per q cycles of forcing. In other parameter and noise regimes different responses are possible where the neuron fires p spikes per q cycles of forcing, and in this instance we would expect to see p peaks in the distribution of ISIs, as illustrated in Figures 6 and 7. The changes in the peak structure of the ISI distribution may be used to define phenomenological stochastic bifurcations, often referred to as P-bifurcations (Arnold 1998). Characterising P-bifurcations is one practical method to detect changes in the behaviour of noisy neural systems (Doi et al. 1998; Tateno 1998, 2002; Tateno and Pakdaman 2004), and the method we have developed here is ideally suited to this since it can be used to numerically estimate the stationary ISI distribution. However, it is beyond the scope of our intention to pursue this here as we would need to go to higher order in the Rice expansion to get an accurate representation of the stationary ISI distributions of p:q states. Rather to gain an understanding of the type of stochastic bifurcations that can be supported in a IF model with threshold noise we next turn to direct numerical simulations of the spiking model and show how responses can be organised in parameter space using the notion of Arnol'd tongues.

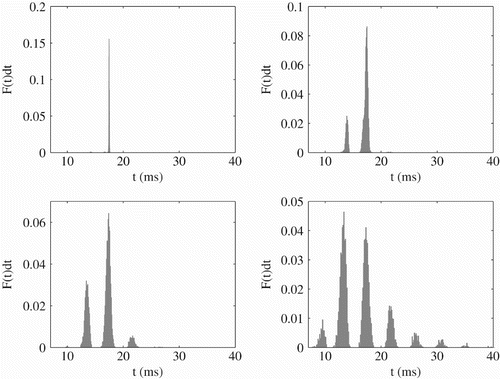
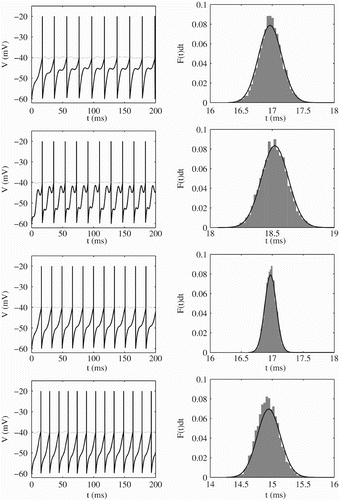
Figure 5. Left: Membrane potential (solid black line) and threshold (dotted black line) for different sinusoidal drive. Right: ISI distribution corresponding to the trajectories on the left; analytical results (solid black line) and histograms from direct numerical simulations (grey bars). Parameter values are from top to bottom η=2 ms, σ=0.2, s_ω=1.2, a=1, I ₀=2.3; η=2 ms, σ=0.2, s_ω=2.2, a=2, I ₀=2.3; η=2 ms, σ=0.1, s_ω=1.2, a=1, I ₀=2.3; η=2 ms, σ=0.2, s_ω=1.2, a=1, I ₀=2.4. Other parameter values are V _L=V _R=−60 mV, V _th=−40 mV and τ=10 ms.

Figure 6. ISI distribution for different noise strengths: σ=0.1 (top left), σ=0.5 (top right), σ=1 (bottom left), σ=2 (bottom right). The deterministic dynamics shows a 1:4 mode-locked state. Other parameter values are η=2 ms, s_ω=4.1, a _v =2.25, I ₀=2.4, V _L=V _R=−60 mV, V _th=−40 mV and τ=10 ms.

Figure 7. ISI distribution when the deterministic dynamics shows a 2:1 mode-locked state. Parameter values are σ=0.5, s_ω=0.5, a=1, η=2 ms, I ₀=2.4, V _L=V _R=−60 mV, V _th=−40 mV and τ=10 ms.

1 Tongue structure

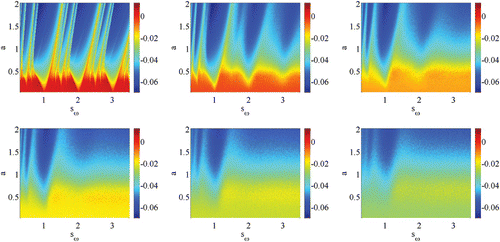
The phenomenon of mode-locking has been intensely studied in the context of the periodic forcing of nonlinear oscillators, with the standard circle map providing a canonical model, see for example Boyland (1986). For deterministic periodically forced IF models the firing map is known to support regions of parameter space where the firing rate takes the value p/q, where . These regions are referred to as Arnol'd tongues, and describe recurring firing patterns for which a neuron fires p spikes for every q cycles of a periodic injected current (p:q mode-locked states). With an increase of the amplitude of the driving current from zero Arnol'd tongues typically open as a wedge, centred at points in parameter space where the natural frequency of the neuron is rationally related to the forcing frequency. In between tongues quasi-periodic behaviour, emanating from irrational points on the amplitude/frequency-ratio axis, are observed. The tongue borders are defined in terms of instabilities of solutions with rational firing rate, and have been calculated in Coombes and Bressloff (1999). In the presence of noise it would be natural to calculate such borders using the notion of P-bifurcations described in the previous section. However, it is equally useful to simply scan through parameter space and collect some useful measure of the output of a simulated neuron. One natural response measure would be the average firing rate. However, within a tongue this would show no variation, even though the ISI distribution would change shape (though not develop new peaks). In a deterministic setting one alternative measure would be the Liapunov exponent. For an IF model this can be written in closed form as a function of the derivative of the voltage and threshold just before and after firing (Coombes 1999). Since our choice of threshold noise is differentiable this formula may also be applied in the stochastic setting. Although its strict interpretation as a Liapunov exponent would no longer be valid it does provide some measure of response more subtle than a simple calculation of the average firing rate. We write this response measure as

where and are the time derivative of V just after and just before the mth firing event, respectively, and ˙Φ is the time derivative of Φ. Figure 8 shows a sequence of Arnol'd tongue structures with an increasing level of noise. For low noise tongue structures are easily identifiable, with the dominant ones being 1:q, emanating from the points where . The action of the noise is to erode small tongues with the 1:1 state being the most persistent.

Figure 8. Plots of the Liapunov exponent in the (a, s_ω) plane showing Arnol'd tongues for σ=0, 0.5, 1, 1.5, 2, 2.5 parameter values are η=2 ms, I ₀=2.3, V _L=V _R=−60 mV, V _th=−40 mV and τ=10 ms.

1. Application to auditory processing

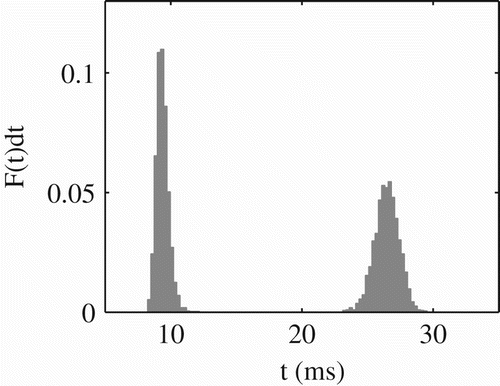
We have seen how the characteristics of threshold noise in IF models affects the coding of periodic inputs at the population level. We now relate this theory back to a specific example of sensory coding, in the brainstem of the auditory pathway. Encoding in the peripheral auditory system is inherently noisy. It is therefore an important question what the role of this noise is in terms of stimulus encoding. We show that the instantiation of stochasticity in the neural threshold can reproduce with remarkable accuracy the responses of a cell where the dominant source of noise is at the input. We then go on to tentatively propose how the degree of stochasticity might affect stimulus coding in different sub-populations of cells. To place this theoretical work in context, we begin with a simplified account of the sensory processes leading to the stimulus encoding. The cochlea can be thought of as an ‘array of band pass filters’ (Holdsworth et al. 1988). These filters are implemented mechanically by a flexible membrane in the cochlea, the basilar membrane. The time varying motion of the basilar membrane is converted to electrical activity by the inner hair cells (IHCs). IHC receptor potentials follow the oscillatory motion, but are half wave rectified and low-pass filtered, with a cut-off between 2–5 kHz (Johnson 1980; Palmer and Russell 1986). In high-frequency channels, therefore, a demodulation or ‘envelope extraction’ occurs. A high-frequency (>5 kHz) pure tone that is sinusoidally amplitude modulated will produce IHC depolarisation with a d.c. component and a sinusoidal a.c. component. IHC depolarisation drives stochastic neurotransmitter release at synapses between the IHC and the auditory nerve fibre. The resulting action potentials reflect the time-varying nature of the IHC membrane fluctuations. The auditory nerve fibres project into the ipsilateral cochlear nucleus (CN), that is located in the brainstem. The ventral division of the CN (VCN) (Rose et al. 1959; Osen 1969; Hackney et al. 1990)) might be described as a kind of ‘auditory pre-processor’, splitting the input into multiple pathways each of which emphasises a particular aspect of the stimulus. One particular morphological class of VCN neurons is the stellate cell. Stellate cells have a small number of fairly thick dendrites, with numerous small synapses from auditory nerve fibres (Smith and Rhode 1989). Injecting current into a stellate cell causes the cell to fire regularly for the duration of the current and below threshold the relationship between the injected current amplitude and the intracellular voltage is linear (Oertel 1983). Electrophysiologically, many of these cells are classified as ‘choppers’, because in response to a pure tone they fire regularly, not unlike during current injection (Rhode and Smith 1986). Membrane capacitance confers a temporal integration lasting several milliseconds and their numerous inputs serve to average out some of the stochasticity of the input nerve firings (Oertel 1985). However, stellate cells also vary in how regularly they fire (Young et al. 1988; Blackburn and Sachs 1989). Cells which fire precisely at preferred times throughout a sound stimulus are sub-classified as ‘sustained’ choppers, whilst others which only fire regularly at the beginning of the response (10–20 ms) are classified as ‘transient’ choppers (see Blackburn and Sachs 1989). Some VCN neurons fire mainly at the onset of a sound. Many of these appear also to be stellate cells (Smith and Rhode 1989; Palmer et al. 2003), and possess similar electrical (Oertel et al. 1990) and temporal integration properties (Palmer et al. 1996). Unlike other stellate cells, they are extremely densely innervated on their soma (Smith and Rhode 1989). With many small inputs and little dendritic filtering, these cells act as coincidence detectors which is a major factor in generating a response at the beginning of a stimulus (Sumner et al. 2009), when all input auditory nerve fibres are firing. Although onset units fire mainly at the onset of a pure tone, they fire very reliably and regularly in response to periodic stimuli, such as AM tones, vowels and harmonic complexes (Winter et al. 2003). The sub-threshold linearity of stellate cells means that they are well characterised by linear IF models. Such models have been used to emulate chopper responses (Arle and Kim 1991; Hewitt and Meddis 1993) and onset responses (Kalluri and Delgutte 2003; Sumner et al. 2009). IF models also provide a good approximation of the responses of these cells to envelope fluctuations, such as sinusoidal amplitude modulation (Hewitt et al. 1992). Recently it was further confirmed that the behaviour of stellate cells in the VCN is well modelled by IF neurons by demonstrating the stochastic mode-locked behaviour, seen in the above analysis, in their response to AM tones and other complex stimuli such as vowels (Laudanski et al. 2010).

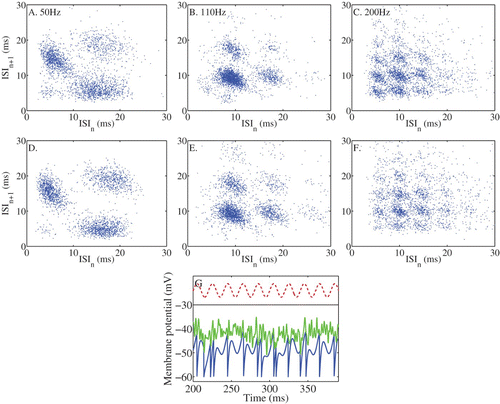
An IF model driven by a sinusoidal input with a d.c. component, as used for the analysis presented in this paper, offers a good first approximation of these cells’ responses to an amplitude modulated tone stimulus. In the upper row of Figure 9 we show an example of the responses of a chopper unit to an amplitude modulated tone with modulation rates of different frequencies (see Laudanski et al. 2010 for details). The spiking patterns are represented here as pairs of intervals, in an inter-spike interval scattergram. These representations reveal pairs of intervals that indicate the presence of stochastic mode-locked states. In the lower row of panels we show an IF model with a noisy threshold in which the parameters have been set so as to approximate the responses of the cell, when periodically forced with a sinusoid. It demonstrates a good correspondence with the data despite lacking a realistic simulation of auditory nerve inputs. The bottom panel shows, for a short time period in response to the 50 Hz modulation rate, the evolution of the membrane potential (action potentials are not shown) and the stochastic threshold. Thus, the simple models upon which the presented analysis is based, appear to be able to reproduce the spike patterns seen in real VCN stellate cells. The instantiation of the noise as either input noise or threshold noise is clearly not crucial, and ‘threshold-noise’ based IF neurons appear to offer a convenient formalism for investigating population coding in VCN stellate cells. Assuming that variation in the degree of stochasticity has a similar impact on coding in these cells as the presented analysis, we can speculate on the role of noise on envelope coding in these neurons. Laudanski et al. (2010) found considerable variation in the degree of complexity in the modes of firing in VCN neurons. More-complex mode-locking properties (precise intervals at modes other than 1:1) were seen in choppers and onset units which fired more regularly in response to pure tones. We would predict that a population of the less regularly firing chopper units, and thus a population showing less complex modes of firing to a periodic signal, would actually encode stimulus envelope more faithfully. Onset cells, in general, showed less high order modes, but this was attributable not to a lack of regular responding, but because they locked (or phase locked) almost perfectly to the fundamental of a complex signal with a 1:1 mode (Winter et al. 2003). A population of such onset cells should, like the more regular chopper units, show a poor representation of the stimulus envelope. However, they may in turn provide a nonlinear coding (i.e. feature emphasis) of certain aspects of the envelope, such as the fundamental period or its harmonics. Thus, the theory of Knight (1972a, 1972b, 2008), together with the theoretical insights into the role of noise in stimulus encoding, presented here and elsewhere, raises the possibility that the range of response regularity seen across stellate cells in the VCN might be contributing (even usefully) to the different envelope coding properties at the population level.

Figure 9. A-C. ISI scattergrams of the responses of a VCN chopper unit to amplitude modulated tones. The tone was 3 s long, with a frequency the same as the characteristic frequency of the unit, 50 dB above the CF threshold. AM depth was 100% and frequency was as indicated. D-F. The responses of a stochastic-threshold IF model fitted to the data. The model parameters were: sinuisodal input: a=0.7, I ₀=1.5 mV, threshold noise: σ=2.7, η=0.75 ms, IF parameters: τ=3.18 ms, V _L=V _R=−60 mV, V _th=−42 mV. G. An example of the evolution of the membrane potential of the model (blue) for the 50 Hz modulation rate, the stochastic threshold (green) and the modulated input on an arbitrary scale.

1. Discussion

In this paper we have introduced a form of threshold noise into the leaky IF model and shown how it can be analysed, first using linear response theory and then by developing a novel calculation of first passage times using a Rice expansion. Direct numerical simulations of the model in response to sinusoidal forcing were shown to be organised in parameter space in accordance with a tongue structure inherited from the noise-free model. With increasing threshold noise this structure was eroded in the sense that narrow tongues became less identifiable. However, this structure is the one recently recognised to exist in data from stellate units of the ventral cochlear nucleus in response to amplitude-modulated tones. Indeed we were able to choose model and noise parameters to fit this data and thus show that a theory of stochastic mode-locking can be used to understand stellate responses across a wide range of stimulus conditions. Moreover, by revisiting original arguments of Knight (1972a, 1972b) it is intriguing to think that stellate cells might in fact be utilising noise to achieve asynchrony at the population level, allowing the faithful encoding of a stimulus envelope in the population firing rate. Interestingly a general approach to the reconstruction of sensory stimuli with leaky IF neurons with random thresholds has recently been developed by Lazar and Pnevmatikakis (2009) making use of a reproducing kernel Hilbert space framework.

Acknowledgements

R. Thul is supported by a Leverhulme Trust Early Career Fellowship. J. Laudanski was supported by a Marie Curie Early Stage Researcher Training Fellowship from the European Commission (EC Contract No. MEST-CT-2005-020723). Alan Palmer and Chris Sumner are supported by the Medical Research Council (UK).

Appendix 1

In the numerical simulations we combined a second order scheme for the membrane potential (Hansel et al. 1998) with a spectral method for the fluctuating threshold. The latter is based on the spectral decomposition of a stochastic process (Papoulis and Pillai 2002)

which can be rewritten as (Shinozuka and Deodatis 1991)

with and for sufficiently small but finite . The independent random phases α _k are uniformly distributed on [0, 2π], and we have introduced the Fourier transform of the correlation function as

Equation (51) measures the spectral power associated with each frequency ω, and we can usually assume that S(ω) decays towards zero for high frequencies. Note that the decay is Gaussian in the case of a Gaussian correlation function. This decrease in power introduces a cut-off frequency ω _u defined by

for . Setting , we find from Equation (50) an approximation [Xtilde](t) of the random process X(t) given by

where we have to enforce the condition A ₀=0 for S(0)≠0 to insure that the mean and the autocorrelation of the approximate stochastic process [Xtilde](t) match those of the original process X(t) (Shinozuka and Deodatis 1991). To generate sample paths of [Xtilde](t), we introduce a temporal discretisation Δ t and rewrite Equation (53) as

with for . It follows from Equation (50) that X(t) has a period of , so that and Δ t are related by due to T=M Δ t. Moreover, the sampling theorem leads to the condition , which in turn gives rise to M≥2 N. An efficient way to compute a sample path of [Xtilde](t) is by the use of fast Fourier transforms, since Equation (54) expresses [Xtilde](t) as the inverse Fourier transform of a function B(ω) that is sampled at points B _n . Note that B _n =0 for as we assume for n>N.

Appendix 2

Variation of the flux with , gives . Using (14) we may differentiate δ J to obtain

Letting , and we obtain the ordinary differential equation

Integrating between V=V _R and V=V _th and using the fact that gives Equation (17).