Stochastic sensitivity analysis of noise-induced excitement in a prey–predator plankton system

Abstract

In this paper, the excitable Truscott–Brindley dynamical model of the interacting populations under environmental noise is considered. We study a probabilistic mechanism of the noise-induced outbreaks in a zone of stable deterministic equilibria. The stochastic sensitivity functions technique and method of confidence ellipses are applied for the description of the spatial arrangement of random states near the deterministic attractor. The effectiveness of our method for the constructive analysis of the stochastic excitement in Truscott–Brindley model is demonstrated. A critical value for the intensity of noise-generating noise-induced outbreaks is estimated.

Keywords:

• noise-induced excitement
• prey–predator system
• stochastic sensitivity function

Introduction

The interaction between nonlinearity and stochasticity in dynamical systems can generate unexpected phenomena, which have no analogue in the deterministic case. Very often, even small background noise induces new regimes of dynamics with various random transitions (Horsthemke and Lefever 1984; Baltanas et al. 2002; Lindner et al. 2004; Anishchenko et al. 2007). The last decade has witnessed an increasing number of investigations in the analysis of noise-induced phenomena in biological systems (Allen 2003; Spagnolo et al. 2004; Ridolfi et al. 2011). Dynamical models of the interacting populations are characterized by a wide variety of nonlinear laws (Holling 1959; Murray 1989; Bazykin 1998; May 2001). Environmental noise is an inevitable attribute of any living system. Abrupt catastrophic shifts in ecosystems can be caused by small deterministic disturbances and stochastic fluctuations (Scheffer et al. 2001; Rietkerk et al. 2004). Theoretically, such shifts can be attributed to alternative stable ecosystem states, nonuniformity of phase portraits, and sensitivity of boundaries of basins of attraction. The catastrophic responses to a changing environment intensify near bifurcation points where ecosystems are highly excitable.

A constructive influence of noise has been observed in many excitable biophysical systems (Pikovsky and Kurths 1997; Lindner et al. 2004; Freund et al. 2006; Sieber et al. 2007; Muratov and Vanden-Eijnden 2008; Li et al. 2011). Usually, a noise-induced excitement is connected with the multistability of the corresponding deterministic model. Because of random disturbances, a phase trajectory can cross a separatrix between basins of the attraction of coexisting attractors and exhibit a new dynamical regime (Kraut et al. 1999; Scheffer et al. 2001). A classic example of such phenomena in ecosystems is a noise-induced extinction in the stochastic population models with an Allee effect (Dennis 2002; Sun et al. 2009; Bashkirtseva and Ryashko 2011).

However, the multistability is not a necessary condition of the excitability (Lindner et al. 2004). In the Truscott–Brindley (TB) model of prey–predator plankton system, a single attractor (stable equilibrium or limit cycle) has been observed (Truscott and Brindley 1994). Nevertheless, this population model exhibits a phenomenon of the excitability. Noise-induced oscillations with the coherent resonance in this system have been investigated by Sieber et al. (2007). Because of the excitability, a stochastic TB model under seasonal forcing behaves as a trigger with a switching between the bloom and nonbloom modes (Freund et al. 2006). The phenomenon of the pattern formation (‘patchy invasion’) in a spatiotemporal TB model has been investigated by Morozov and Petrovskii (2009). Studies of the extended models of plankton blooms were carried out by Clother and Brindley (1999), Biktashev et al. (2003), and Huppert et al. (2004).

For the deterministic TB model, the underlying mathematical reason of the excitability is an essential nonuniformity of the phase portrait. The equilibrium of this model is characterized by a high sensitivity to variations of initial conditions. If the initial deviation is small, the system quickly relaxes back into the stable equilibrium. Once the deviation reaches a certain threshold, a large excursion of the trajectory is observed.

Random disturbances initiate the transition of the trajectory to the excitability zone and generate new outbreak. The aim of this study is to investigate the mechanism of the interaction between stochasticity and nonlinear geometrical peculiarities of the phase portrait of a TB model.

The main tool for the analysis of noise-induced phenomena is a direct numerical simulation of random trajectories. In fact, this time-consuming method allows to present only the after-effects of noises. For investigating the underlying probabilistic mechanisms of the noise-induced phenomena, analytical approaches are required.

The Kolmogorov–Fokker–Planck equation gives the most detailed probabilistic description of stochastic dynamics. However, the direct use of this equation is technically very difficult even for the simplest possible situations. Therefore, asymptotic methods and approximations are commonly used (Lindner et al. 2004; Anishchenko et al. 2007). The quasipotential method is well known (Freidlin and Wentzell 1984; Dembo and Zeitouni 1995), and in the context of this method, a stochastic sensitivity function (SSF) technique for the probabilistic description of stochastic attractors has been explained by Mil'shtein and Ryashko (1995), Bashkirtseva and Ryashko (2000, 2004, 2009), Ryashko et al. (2009), and Bashkirtseva et al. (2010). The SSF technique has been successfully applied to the analysis of the stochastic limit cycles for randomly forced Brusselator (Bashkirtseva and Ryashko 2000), noise-induced transitions between periodic attractors of the Lorenz model (Bashkirtseva and Ryashko 2009), and backward stochastic bifurcations in the Roessler system (Bashkirtseva et al. 2010).

In this paper, we demonstrate how the method of confidence ellipses that is based on the SSF technique can be applied to investigate the probabilistic mechanism of the noise-induced outbreaks in the stochastically forced TB model. A theoretical background of the general SSF technique for stochastic equilibria is briefly discussed, and then a constructive description of the method of confidence ellipses is presented. Finally, the application of this theoretical approach to the analysis of the noise-induced excitement of TB model is discussed.

Stochastic sensitivity of equilibria: confidence ellipses

For many processes in population dynamics, the basic mathematical model is a nonlinear deterministic system of ordinary differential equations:

where x is a n-vector and f(x) is a n-vector function. Suppose that Equation (1) has a stable equilibrium x¯. A classical analysis of the local stability of this equilibrium is based on the linear approximation system and corresponding Lyapunov exponents , where λ _i are eigenvalues of the matrix .

A system of stochastic differential equations (in Ito's or Stratonovich's sense)

is a traditional mathematical model allowing to study the quantitative description of the results of random disturbances. Here w(t) is a n-dimensional Wiener process, σ (x) is a n×n-matrix function of disturbances, and ϵ is a scalar parameter of the noise intensity.

For the stable equilibrium (λ<0), under the random disturbances, the stochastic states of the forced system (2) are concentrated around x¯ and form a corresponding stochastic equilibrium with a stationary probabilistic distribution . The detailed description of this random distribution is given by the stationary Kolmogorov–Fokker–Planck equation:

In a general case, the analytical research of this equation is a very difficult. Under these circumstances, for a small noise, asymptotics based on the quasipotential v(x)=− are actively used (Freidlin and Wentzell 1984; Dembo and Zeitouni 1995). The function v(x) is governed by the Hamilton–Jacobi equation:

where v(x¯)=0 and v(x)>0 for x≠x¯.

For a small noise, one can write the approximation of as follows:

In the stability analysis, a constructive approximation (Mil'shtein and Ryashko 1995) of the quasipotential in a small neighborhood of the deterministic equilibrium x¯ is required. Since v(x¯)=0 and , the first nonzero term of the Taylor expansion for v(x) is quadratic: , where V is a positive definite n×n-matrix. This quadratic approximation (Mil'shtein and Ryashko 1995) of the quasipotential allows to present an asymptotic of the stationary distribution in the Gaussian form

with the covariance matrix , where W=V ⁻¹. For the exponentially stable equilibrium x¯, the matrix W is a unique solution of the matrix equation

This matrix W is an SSF of the equilibrium x¯.

For a two-dimensional case, this matrix characterizes a spatial arrangement and size of the confidence ellipse

which describes the dispersion of the random states of the stochastic system (2) around the stable equilibrium x¯. Here ϵ is a noise intensity, , and P is a fiducial probability. This means that the random states belong to the interior of this ellipse with the probability P (see Figure 6 for illustration).

Figure 6. Random states and a confidence ellipse for a=7.3, ϵ=0.0005, and P=0.95.

Let and be, respectively, the eigenvalues and the corresponding normalized eigenvectors of the stochastic sensitivity matrix W of the equilibrium . For the coordinates and , the equation of the confidence ellipse can be written in a standard form:

Coordinates x ₁ and x ₂ of this confidence ellipse in the phase plane can be written in a parametrical form:

The method of confidence ellipses presented here for stable equilibrium has been successfully used for the constructive description of the confidence domains around limit cycles. This technique has been applied to the analysis of the noise-induced extinction in the population model with Allee effect (Bashkirtseva and Ryashko 2011) to investigate the probabilistic mechanism of noise-induced transitions between limit cycles of the Lorenz model (Bashkirtseva and Ryashko 2009). This approach has been extended by Ryashko et al. (2009) as a method of confidence tori. The probabilistic asymptotics of the escape of random trajectories from covariance tubes have been studied in the analysis of fast–slow stochastic dynamical systems (Berglund et al. 2012).

Analysis of noise-induced excitement in TB plankton system

Let us consider a stochastically forced system

where w _i (t), i=1, 2, are independent Wiener processes and ϵ is a noise intensity. For , this system is a well-known deterministic TB model (Truscott and Brindley 1994) for the prey–predator dynamics of phytoplankton x and zooplankton y. This system models the logistic growth of the phytoplankton with an intrinsic rate r and Holling-type III grazing with maximum rate a ²/b ² as well as natural mortality of zooplankton with rate m. A small parameter δ reflects a high sensitivity and fast response of the phytoplankton population to environmental changes. Noise-induced phenomena for this stochastic system have been studied by Freund et al. (2006) and Sieber et al. (2007) using the method of direct numerical simulation of random trajectories. Freund et al. (2006) analyzed a trigger mechanism of the noise-induced switching between the bloom and nonbloom modes for TB model under the periodic seasonal forcing. Sieber et al. (2007) investigated the noise-induced prey–predator oscillations and coherence resonance for extended TB model with the phytoplankton population splitting into a susceptible and an infected part.

In this study, for the stochastically forced TB model (4), we applied the method of confidence ellipses based on the SSF technique to study the noise-induced excitement.

First, consider the unforced deterministic system (4) with . For , this system has a nontrivial equilibrium:

We study the dynamics of the system (4) for the fixed set of parameters δ=0.01, r=m=1, b=7, and a∈7.1 10. The choice of the small value δ means a high excitability (Sieber et al. 2007) of the deterministic system. As for the main dynamical features including the mechanism of the excitability and the bifurcation, this population model is similar to the well-studied excitable FitzHugh–Nagumo model of the neuron activity (see Pikovsky and Kurths 1997; Lindner and Schimansky-Geier 1999; Volkov et al. 2003; Lindner et al. 2004; Muratov and Vanden-Eijnden 2008; Berglund and Landon 2011).

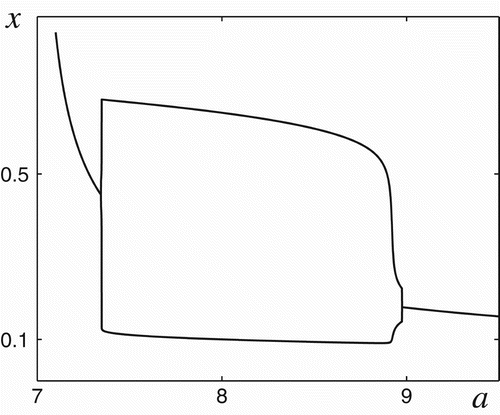
For , this system demonstrates Hopf bifurcation at the points a ₁=7.345 and a ₂=8.975. In the intervals [7.1, a ₁) and (a ₂, 10], the equilibrium is stable. In the interval (a ₁, a ₂), this equilibrium is unstable and the deterministic system has a stable limit cycle. Note that a transition zone from small- to large-amplitude cycles is very narrow. One can see this in Figure 1, where extremal values of the variable x are plotted for considered attractors (equilibria and cycles). In this narrow zone, TB model exhibits Canard oscillations. Here, even a small variation in the parameter a leads to large changes in the form and size of the limit cycle.

Figure 1. Attractors of the deterministic Truscott–Brindley system.

We will now focus on the neighborhood of the Hopf bifurcation point a ₁=7.345. In Figure 2(a), a phase portrait of the deterministic system with the stable equilibrium (black circle) for a=7.3<a ₁ is plotted. Dashed line indicates a nullcline [xdot]=0. As one can see, the phase portrait around the equilibrium in Figure 2(a) is extremely nonuniform. Because of nonlinearity, this equilibrium is characterized by a high sensitivity to variations of initial conditions. Even small deviations result in small-amplitude trajectories that correspond to the subthreshold response: the system quickly relaxes back into the stable equilibrium. If we take initial deviations larger than some threshold, large-amplitude trajectories appear. It corresponds to the suprathreshold response with the outbreak: a large excursion of the trajectory is observed. Note that in this case (a=7.3) a phase trajectory of the outbreak is close to the limit cycle (a=7.35) shown in Figure 3(a).

Figure 2. Truscott–Brindley system (4) with a=7.3: (a) a deterministic phase portrait (ϵ=0), and random trajectories for (b) ϵ=0.001 and (c) ϵ=0.003.

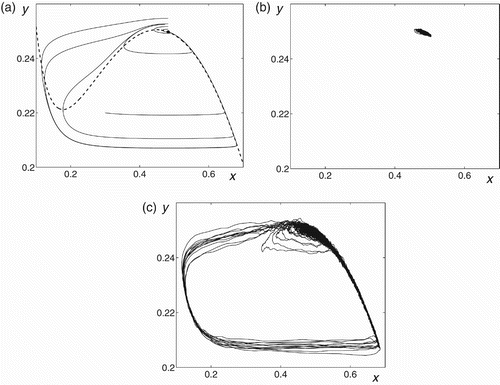
Figure 3. Truscott–Brindley system (4) with a=7.35: (a) a deterministic limit cycle (ϵ=0), and random trajectories for (b) ϵ=0.001 and (c) ϵ=0.003.

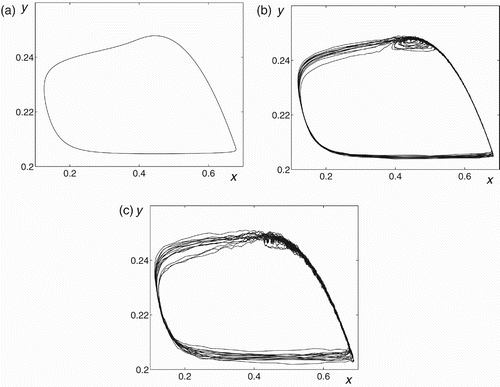
Random trajectories of the stochastically forced model leave the deterministic attractor and form a corresponding stochastic attractor around it. Results of the direct numerical simulations of the stochastic system (4) with and are plotted in Figure 2(b) and 2(c) for a=7.3 and in Figure 3(b) and 3(c) for a=7.35. For a numerical simulation of random trajectories, an appropriate stochastic component of random disturbances was introduced in the deterministic fourth-order Runge–Kutta scheme on each time step. As one can see in Figures 2(b) and 3(b), the random trajectories forced by small noise are concentrated near the corresponding deterministic attractors. Here, random trajectories form the stochastic equilibrium (Figure 2(b)) and the stochastic cycle (Figure 3(b)). As the noise intensity increases, the dispersion of random states grows. Here, the model (4) demonstrates a phenomenon of the noise-induced generation of oscillations with high amplitude in the zone of stable equilibria. Indeed, in Figure 2(c), for , the random trajectories look like stochastic cycle. This stochastic attractor is similar to the stochastic cycle presented in Figure 3(c). The aim of this study is to elaborate a constructive method for the probabilistic analysis of this phenomenon.

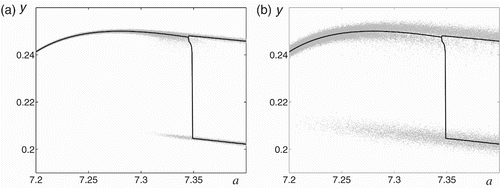
Consider how a form of stochastic attractors depends on the parameter a and noise intensity ϵ. Stochastic attractors (grey color) and deterministic attractors (black color) are presented for two values of the noise intensity (Figure 4(a)) and (Figure 4(b)) on the interval around the bifurcation point a ₁. Here, Poincaré section points of stochastic trajectories and deterministic attractors with a vertical line x=x¯ are plotted. We can see how the random disturbances deform the attractors of the dynamical system. These deformations are mainly observed at the left of the bifurcation point a ₁, and only in this zone the phenomenon of the noise-induced excitement occurs.

Figure 4. Deterministic (black) and stochastic (grey) attractors for (a) ϵ=0.001 (b) and ϵ=0.005.

A dispersion of random states around the stable equilibrium on the interval [7.2, a ₁) is nonuniform. This feature can be explained with the help of the SSF technique. The stochastic sensitivity of the equilibrium can be characterized by the stochastic sensitivity matrix

This matrix can be found directly from Equation (3). For the system (4), matrices and have the following elements:

The matrix equation (3) for the elements can be rewritten in the following form:

Hence, the elements of the stochastic sensitivity matrix W for the system (4) are as follows:

Elements w ₁₁ and w ₂₂ define the stochastic sensitivity of the equilibrium along x- and y-axes, and w ₁₂=w ₂₁ reflects the covariation. Figure 5 shows values w ₁₁ (a) and w ₂₂ (a) of the SSF matrix W(a) for equilibria . As one can see, . This means that for the zone of equilibria, the stochastic sensitivity of the phytoplankton is a lot more than the stochastic sensitivity of the zooplankton. Both w ₁₁ (a) and w ₂₂ (a) essentially grow near the bifurcation point a ₁. Large values of w ₁₁ and w ₂₂ signalize about the possible noise-induced excitement. However, for the constructive analysis of this phenomenon, we must know a spatial arrangement of the random states in the stochastic attractor.

Figure 5. Stochastic sensitivity of equilibria.

For investigating the stochastic equilibria on the basis of SSF technique, we use the confidence ellipses method. These ellipses are simple geometrical models for the description of a configurational arrangement of random states near the stable equilibrium.

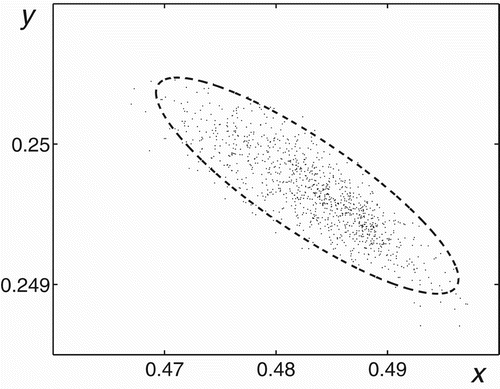
The random states of the system (4) for a=7.3 and and the corresponding confidence ellipse with the fiducial probability P=0.95 are plotted in Figure 6. As one can see, results of the direct numerical simulation agree with the SSF technique.

To apply the method of confidence ellipses to the analysis of noise-induced excitement, we must know the geometrical features of the phase portrait of the deterministic system. Nonlinearity of the considered deterministic model divides dynamics into two types (Truscott and Brindley 1994). First, the solution with initial conditions close to the stable equilibrium uniformly tends to this equilibrium (subthreshold regime). Second, the solution with initial conditions sufficiently far from the equilibrium has a typical outbreak (suprathreshold regime). In the deterministic model, these two regimes of dynamics are definitely separated. In a stochastic case, noise-induced transitions between these two regimes can be observed. We analyzed these transitions using the method of confidence ellipses.

Consider a mutual arrangement of the confidence ellipses and the deterministic phase curves in the neighborhood of the stable equilibrium. For a small noise, the confidence ellipses are localized near the stable equilibrium in the subthreshold zone. As the noise intensity increases, the confidence ellipses expand and begin to occupy the suprathreshold zone. This means that the random trajectories of the forced system with high probability can exceed the bounds of the unexcitable regime and exhibit large-amplitude stochastic oscillations. The noise intensity that corresponds to the onset of this occupation can be used as an estimation of the critical value .

The phase trajectories of the deterministic TB system are plotted for a=7.2 and a=7.3 in Figures 7(a) and 7(b), respectively. Along with the deterministic phase portraits, a set of confidence ellipses with the fixed fiducial probability P=0.95 for corresponding equilibria is shown for three noise intensity values: (small), (middle), and (large).

Figure 7. Phase trajectories of the deterministic Truscott–Brindley system and confidence ellipses with ϵ=0.001 (small), ϵ=0.003 (middle), ϵ=0.005 (large), P=0.95 for (a) a=7.2 and (b) a=7.3.

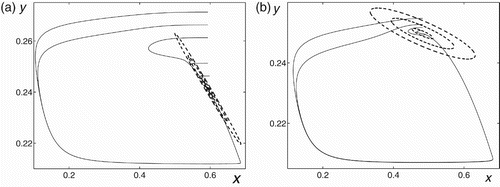
As we can see, for a=7.2, all confidence ellipses with embrace initial conditions corresponding to the first type of dynamics with small amplitude oscillations (see Figures 7(a) and 8(a)). Here the critical value . In Figure 7(b) for a=7.3, a small ellipse with lies in a subthreshold zone too. Confidence ellipses with occupy a zone of initial conditions corresponding to the second type of dynamics with outbreak oscillations (see Figures 7(b) and 8(b)). Here . 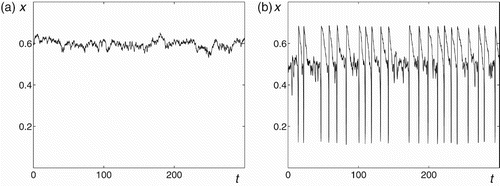It is worth noting that these results of the estimation of the critical value of the noise intensity agree with direct numerical simulations (Figure 8).

Figure 8. Time series of the stochastic Truscott–Brindley system with ϵ=0.003 for (a) a=7.2 and (b) a=7.3.

So, the confidence ellipses method provides a descriptive parametrical analysis of the interaction between nonlinearity and stochasticity for this concrete dynamical population model. With the help of this method, one can estimate numerically the critical value of the noise intensity generating noise-induced oscillations of large amplitude in a zone of the stable deterministic equilibria.

Conclusions

In this paper, we have studied the effects of additive noise on excitable TB dynamical model of the prey–predator plankton populations. The remarkable feature of the dynamics of this model is that a small noise generates large-amplitude oscillations even in the parametrical zone where the deterministic system has a single stable equilibrium. We show that this phenomenon can be explained by the high stochastic sensitivity of this equilibrium. We study a probabilistic mechanism of these noise-induced outbreaks with the help of the SSF technique and the method of confidence ellipses.

Our approach is based on the geometrical analysis of the mutual arrangement of the confidence ellipses and the deterministic phase curves near the stable equilibria. For a small noise, the confidence ellipses are localized near the stable equilibrium in the subthreshold zone, where the trajectories of the deterministic model uniformly tend to equilibrium. So, the random trajectories of the stochastic model oscillate with a small dispersion. As the noise intensity increases, the confidence ellipses expand and begin to occupy the suprathreshold zone, where the trajectories of the deterministic model exhibit outbreaks. In this case, for the stochastic model, a generation of large-amplitude random oscillations occurs. The noise intensity critical value separating these two regimes is estimated by the suggested method of confidence ellipses. Note that this method allows to avoid time-consuming direct numerical simulations of the random trajectories in investigating noise-induced phenomena.

Thus, the SSF technique is a useful analytical tool for the prediction and quantitative analysis of noise-induced excitement for stochastically forced nonlinear dynamical models. It is worth noting that in this paper we demonstrated our method for particularly for the TB system only. This is a simple model of the complicated processes going in ecosystems. Nevertheless, it appears that the SSF technique is capable of catching essential features and probabilistic mechanisms of shifts in ecosystems.

Acknowledgements

This work was partially supported by Grant RFBR10-01-96022_ural and Federal Target Program Grant No. 1.1099.2011.