Abstract
The paper first discusses the recently reported fractional-order Lorenz system, analyzes it by using the frequency-domain approximation method and the time-domain approximation method, and finds its chaotic dynamics when the order of the fractional-order system varies from 2.8 to 2.9 in steps of 0.1. Especially for the fractional-order Lorenz system of the order as low as 2.9, the results obtained by the frequency-domain method are consistent with those obtained by the time-domain method. Some Lyapunov exponent diagrams, bifurcation diagrams, and phase orbits diagrams have also been shown to verify the chaotic dynamics of the fractional-order Lorenz system. Then, an analog circuit for the fractional-order Lorenz system of the order as low as 2.9 is designed to confirm its chaotic dynamic, the results from circuit experiment show that it is chaotic.
1. Introduction
The research for the theory of the fractional integrals and derivatives has begun to attract more and more attention since 1960. Generally, chaotic cannot be found in continuous autonomous systems whose order is less than three. However, with the development of fractional calculus, some fractional-order systems whose dimensions are less than three are reported to display chaotic motion recently, such as the fractional Chua's circuit (Hartley, Lorenzo, & Qammer, Citation1995), the fractional Rössler system (Li & Chen, Citation2004), the fractional Lorenz system (Grigorenko & Grigorenko, Citation2003), the fractional Chen system (Lu & Chen, Citation2006), the fractional-modified Duffing system (Ge & Qu, Citation2007), and so on (Ahmad & Sprott, Citation2003; Chen, Liu, Wang, & Li, Citation2008; Huang, Zhao, Wang, & Li, Citation2012; Li, Liao, & Lou, Citation2012; Lu, Citation2006; Pan, Zhou, Zhou, & Sun, Citation2011; Ahmad, Citation2005; Wang, Huang, & Zhao, Citation2012). All these works may bring new motivation for the research on the theory and application of chaos.
However, most of the above researches only display chaotic dynamics of some fractional-order systems by phase portraits, Lyapunov exponents for fixing system parameters, bifurcations, and Poincaré section. Compared with the integer-order chaotic systems, these seem insufficient for showing chaotic characteristics of the fractional-order systems. Therefore, the paper studies the fractional-order Lorenz system, gives its Lyapunov exponents diagram which changes with system parameter, and designs an analog circuit which displays its chaotic behavior from physical implementation. Our work may help to display the chaotic characteristic of the fractional-order Lorenz system from different points of view.
Grigorenko and Grigorenko (Citation2003) reported the fractional-order Lorenz system, and gave a conclusion that chaotic dynamic cannot be found when system dimension of the fractional-order Lorenz is less than or equal to 2.91. Subsequently, Li and Chen (Citation2004) reported some mistakes. In 2009, Yu discussed Hopf bifurcation behavior and showed the phase orbits when system dimension is 2.96 (Yu, Li, Wang, & Yu, Citation2009). Recently, Jia, Chen, and Xue (Citation2013) found chaos existed in the lower dimensional fractional-order Lorenz system. However, they only discuss its chaotic dynamics when the fractional orders α, β, and γ are same. Therefore, the paper will further discuss its chaotic dynamics when the fractional orders α, β, and γ are different.
2. Fractional-order Lorenz system
Grigorenko and Grigorenko (Citation2003) reported the fractional-order Lorenz system
where a, b, and c is system parameters, α, β, and γ is the fractional order.
Generally, computing a fractional differential equation is complex and difficult work, therefore, approximation methods are often adopted to analyze some fractional-order systems numerically such as the time-domain approximation methods and the frequency-domain The former are more reliable to show chaos, the latter is more convenient for circuit implementation. In order to display its chaotic characteristics from different point of view, the two approximation methods will be used to display the chaotic dynamic of the fractional-order Lorenz in this paper.
Let a=10, , c=28, α=0.9, β=1, and
, based on the frequency-domain approximation method, using approximation function (Ahmad & Sprott, Citation2003)
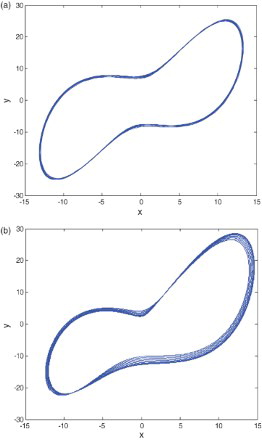
Fig. 1. Chaotic attractor of the fractional-order Lorenz system based on the frequency-domain approximation method.
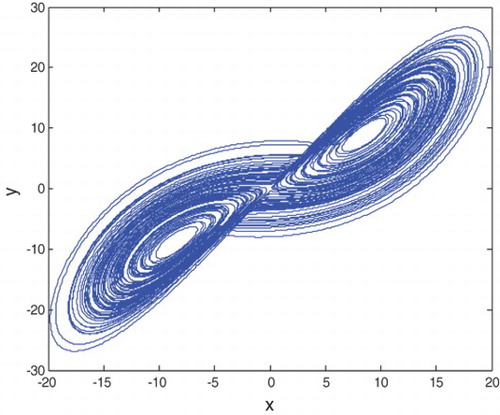
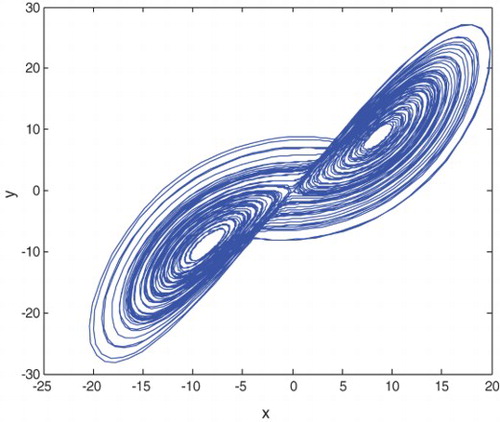
Under the same condition, based on the time-domain approximation method, using the advised Adams–Bashforth–Moulton method, a same chaotic attractor can also be found, as shown in . That is, the chaotic dynamic indeed exists in the fractional-order Lorenz system of the order as low as 2.9.
Fig. 2. Chaotic attractor of the fractional-order Lorenz system based on the time-domain approximation method.
2.1. Fractional-order Lorenz system of the order as low as 2.9
In order to show the chaotic behaviors of the fractional-order Lorenz system of the order as low as 2.9, when fixing , c=28, α=0.9, β=1, γ=1 and varying a, by using the both frequency-domain method and time-domain method, the paper computes Lyapunov exponents diagrams and bifurcation diagrams, as shown in . Furthermore, the paper analyses Lyapunov exponents diagram and bifurcation diagrams for the fractional-order Lorenz system, finds the results obtained by the frequency-domain method are consistent with those obtained by the time-domain method. That is, using the frequency-domain method, the paper gives Lyapunov exponents diagram and bifurcation diagram, as shown in (a) and 3(b), respectively. Generally speaking, when the system displays chaotic dynamics, its biggest Lyapunov exponent is larger than zero, the points in the corresponding bifurcation diagram are dense. When the system does not display chaotic dynamics, its biggest Lyapunov exponent is equal to or less than zero, the points in the corresponding bifurcation diagram are sparse or few. That is, (a) and 3(b) is consistent. Furthermore, when using the time-domain method to analyze the system, we only need to give bifurcation diagram. That is, it is enough for showing the consistence between the frequency-domain method and time-domain method to analyze bifurcation diagram, therefore, the paper only computes bifurcation diagram by using the time-domain method, as shown in (c), which is same as (b). By comparing (b) and 3(c), a conclusion can be obtained that the chaotic behaviors exist in the fractional-order Lorenz system of the order as low as 2.9, and the results are consistent when using the frequency-domain method and time-domain method.
Fig. 3. Lyapunov exponents diagram and bifurcations for the 2.9-order Lorenz system. (a) Lyapunov exponents diagram based on the frequency-domain method. (b) Bifurcation diagram based on the frequency-domain method. (c) Bifurcation diagram based on the time-domain method.
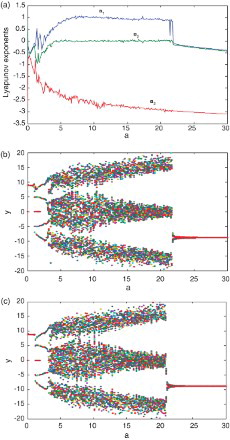
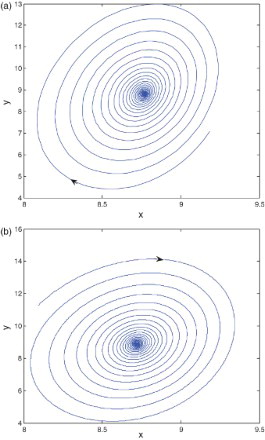
By analyzing Lyapunov exponents diagram and bifurcation diagrams in , the following results can be obtained for the fractional-order Lorenz system, when , c=28, α=0.9, β=1, γ=1 and varying a, the fractional system (1) can display the periodic attractors, and asymptotically stable orbits besides the chaotic attractors. Now let a=3, using the time-domain method and frequency-domain method, the fractional-order Lorenz system will show periodic attractors, as shown in (a) and 4(b), respectively. In addition, let a=1, using the time-domain method and frequency-domain method, the fractional-order Lorenz system will show asymptotically stable orbits, as shown in (a) and 5(b), respectively. That is, phase portraits are consistent when using two different approximation methods, and verify the analysis from Lyapunov exponents diagram and bifurcation diagram.
2.2. Fractional-order Lorenz system of the order as low as 2.8
When fixing , c=28, α=0.9, β=0.9, γ=1 and varying a, using the frequency-domain method, the paper also gives Lyapunov exponents diagram and bifurcation diagram, as shown in (a) and 6(b), respectively, and the Lyapunov exponents diagram is consistent with bifurcation diagram. By analyzing (a) and 6(b), a conclusion can be obtained that the chaotic dynamics exit in the fractional-order Lorenz system of the order as low as 2.8 when using the frequency-domain method.
Fig. 6. Lyapunov exponents diagram and bifurcation for 2.8-order Lorenz system. (a) Lyapunov exponents diagram based on the frequency-domain method. (b) Bifurcation diagram based on the frequency-domain method. (c) Bifurcation diagram based on the time-domain method.
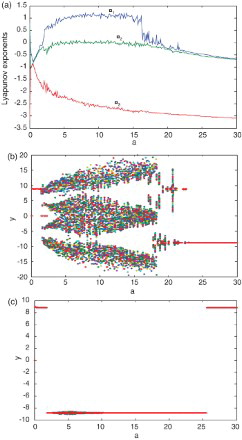
By comparing Lyapunov exponents diagram in (a) with that in (a), the following results can be obtained, when fixing , c=28 and a∈[2.5, 21.8], the 2.9-order Lorenz system displays chaotic dynamics; when fixing
, c=28, and a∈[2.5, 17.3], the 2.8-order Lorenz system also displays chaotic dynamics. That is, under the same condition, the chaotic range of the 2.9-order Lorenz system may be larger.
In addition, under the same condition, using the time-domain approximation methods, the paper also obtains another bifurcation diagram, as shown in (c). By analyzing (c), the chaos is not found for the fractional-order Lorenz system of the order as low as 2.8. That is, a conclusion can be obtained that the chaotic dynamics do not exist in the fractional-order Lorenz system of the order as low as 2.8 when using the time-domain method. Furthermore, when using the frequency-domain method and time-domain method, the 2.8-order Lorenz system displays different dynamics. The former shows that the system is chaotic, and the latter shows that the system is not chaotic. Which result is on earth true? This will need further study in the future.
3. Circuit design for the fractional-order Lorenz system
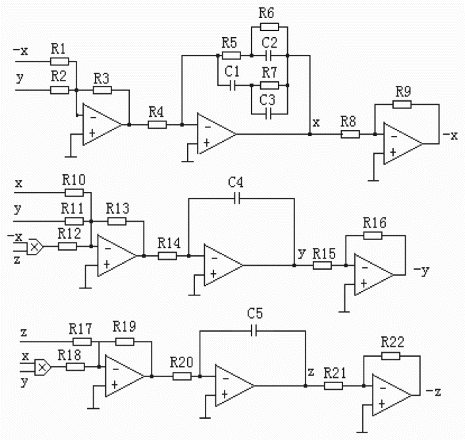
Although the fractional-order Lorenz system has been proved by the Lyapunov exponents, the numerical simulations and bifurcation diagrams, these seem insufficient to show complex dynamics of the fractional-order Lorenz system. Therefore, the paper also designs an analog circuit to implement the system by using resistors, capacitors, analog multipliers AD633, and analog operational amplifiers LF347N, as shown in . That is, the dynamics of the system are confirmed by physical implementation.
In the circuit, three state variables x, y, and z are implemented by three channels, respectively, the operations of addition, subtraction, and integration in every channel are performed by the operational amplifiers LF347Ns, and the nonlinear terms of system (1) are implemented by the analog multiplier AD633. In addition, based on fractional frequency-domain approximation (Ahmad & Sprott, Citation2003) and tree circuit approximation (Chen et al., Citation2008), an integration circuit for the fractional order α=0.9 is designed and used in the first channel of . and thus an analog circuit for the fractional-order Lorenz system of the order as low as 2.9 is finished. The resistors shown in are that ,
,
,
,
,
,
,
, R3 is adjusted, and capacitors are that
,
,
,
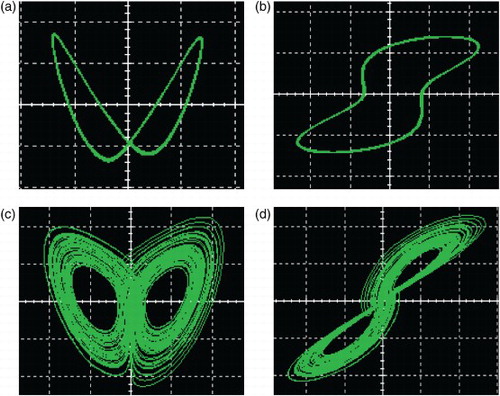
. When adjusting R3, phase portraits of some attractors can be observed by oscilloscope. Furthermore, when
, we can observe that periodic attractor in x−z plane is showed in (a) and periodic attractor in x−y plane is showed in (b); when
, we can observe chaotic attractor in x−z plane is showed in (c) and chaotic attractor in x−y plane is showed in (d); All these attractors observed by oscilloscope not only show the chaotic dynamics of the fractional-order Lorenz system of the order as low as 2.9, but also prove that analog circuit for the fractional-order system is well coincident with numerical simulations.
4. Conclusions
Using the frequency-domain approximation method, time-domain approximation method and numerical simulation analysis, the paper finds chaotic behaviors of the fractional-Lorenz system of the order as low as 2.8 and 2.9. That is, chaos exists in the fractional-order Lorenz system. Especially, chaotic dynamics are same for the fractional-order Lorenz system of the order as low as 2.9 when using the two different approximations. In addition, we also design an analog circuit to implement the fractional-order system, and the results from circuit experiment are well consistent with numerical simulation.
Acknowledgements
This work was supported in part by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11202148), the Natural Science Foundation of China (Grant No. 61174094), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20090031110029), and the Research Fund of Tianjin University of Science and Technology (Grant No. 20110124).
References
- Ahmad, W. M. (2005). Hyperchaos in fractional order nonlinear systems. Chaos Solitons & Fractals, 27 1459–1465. doi: 10.1016/j.chaos.2005.03.031
- Ahmad, W. M., & Sprott, J. C. (2003). Chaos in fractional-order autonomous nonlinear systems. Chaos, Solitons & Fractals, 16 339–351. doi: 10.1016/S0960-0779(02)00438-1
- Chen, X. R., Liu, C. X., Wang, F. Q., & Li, Y. X. (2008). Study on the fractional-order Liu chaotic system with circuit experiment and its control. Acta Physica Sinica 57(3), 1416–1422. Retrieved form http://wulixb.iphy.ac.cn
- Ge, Z. M., & Qu, C. Y. (2007). Chaos in a fractional-order modified duffing system. Chaos Solitons & Fractals 34 262–291. doi: 10.1016/j.chaos.2005.11.059
- Grigorenko, I., & Grigorenko, E. (2003). Chaotic dynamics of the fractional Lorenz system. Physical Review Letters 91(3), 034101-1-4. doi: 10.1103/PhysRevLett.91.034101
- Hartley, T. T., Lorenzo, C. F., & Qammer, H. K. (1995). Chaos in a fractional order Chua's system. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 42(8), 485–490. doi: 10.1109/81.404062
- Huang, X., Zhao, Z., Wang, Z., & Li, Y. X. (2012). Chaos and hyperchaos in fractional-order cellular neural networks. Neurocomputing, 94 13–21. doi: 10.1016/j.neucom.2012.01.011
- Jia, H. Y., Chen, Z. Q., & Xue, W. (2013). Analysis and circuit implementation for the fractional-order Lorenz system. Acta Physica Sinica, 14 140503. Retrieved from http://wulixb.iphy.ac.cn
- Li, C. G., & Chen, G. R. (2004). Chaos and hyperchaos in the fractional-order Rossler equations. Physica A, 341 55–61. doi: 10.1016/j.physa.2004.04.113
- Li, H. Q., Liao, X. F., & Lou, M. W. (2012). A novel non-equilibrium fractional-order chaotic system and its complete synchronization by circuit implementation. Nonlinear Dynamics, 68 137–149. doi: 10.1007/s11071-011-0210-4
- Lu, J. G. (2006). Chaotic dynamics of the fractional-order Lü system and its synchronization. Physics Letter A, 354 305–311. doi: 10.1016/j.physleta.2006.01.068
- Lu, J. G., & Chen, G. R. (2006). A note on the fractional-order Chen system. Chaos Solitons & Fractals, 27 685–688. doi: 10.1016/j.chaos.2005.04.037
- Pan, L., Zhou, W. N., Zhou, L., & Sun, K. H. (2011). Chaos synchronization between two different fractional-order hyperchaotic systems. Communications in Nonlinear Science and Numerical Simulation, 16 2628–2640. doi: 10.1016/j.cnsns.2010.09.016
- Wang, Z., Huang, X., & Zhao, Z. (2012). Synchronization of nonidentical chaotic fractional-order systems with different orders of fractional derivatives. Nonlinear Dynamics, 69 999–1007. doi: 10.1007/s11071-011-0322-x
- Yu, Y. G., Li, H. X., Wang, S., & Yu, J. Z. (2009). Dynamic analysis of a fractional-order Lorenz chaotic system. Chaos Solitons & Fractals, 42 1181–1189. doi: 10.1016/j.chaos.2009.03.016