Adaptive fuzzy terminal sliding-mode control of MEMS z-axis gyroscope with extended Kalman filter observer

Abstract

This paper presents a new terminal sliding-mode control (TSMC) for the micro electro-mechanical systems (MEMS) z-axis gyroscope. However, TSMC may chatter when uncertainty values are overestimated or may exhibit a steady-state error when uncertainty values are underestimated. In this paper, an adaptive fuzzy terminal sliding-mode controller is designed to retain the advantages of the terminal sliding-mode controller and to reduce the chattering occurred with the terminal sliding-mode controller. Stability analysis of the TSMC is presented in the presence of external disturbance and model uncertainties. Moreover, an extended Kalman filter (EKF) observer is designed to estimate the angular velocity and all of the gyroscope parameters and convergence analysis of the proposed EKF algorithm is presented. Numerical simulations using the nonlinear dynamic model of an MEMS z-axis gyroscope with uncertainties demonstrate the effectiveness of the approach in fast trajectory tracking problems and robustness in estimating the gyroscope parameters and also the angular velocity.

Keywords:

• fuzzy logic control
• MEMS gyroscope
• terminal sliding-mode control
• extended Kalman filter

1. Introduction

Micro electro-mechanical systems (MEMS) gyroscope, which is one of the micro-machined inertial sensors, and commonly used to measure the angular velocity in many areas including platform stabilization in space applications, activity monitoring in biomedical applications, sport equipment in consumer applications, robotics and machine and vibration monitoring in industrial applications, monitoring mechanical shock and vibration during transportation in automotive applications (Batur, Sreeramreddy, & Khasawneh, 2006; Fei & Batur, 2009).

Vibrational MEMS gyroscopes are capable of vibrating along two orthogonal axes and energy is transferred from one axis (referred to as drive axis) to the other axis (referred to as sense axis) through Coriolis forces, which is arising from a rotating reference frame and proportional to its rotation rate. The conventional mode of operation drives one of the axes of the gyroscope into a known oscillatory motion and then detects the Coriolis acceleration coupling along the sense axis, which is orthogonal to the drive axis. The response of the sense mode provides information about the unknown angular velocity. However, in practice, the fabrication imperfections and environmental variations are always present, resulting in parameter changes, mechanical couplings between two axes, and different kinds of noises along the axes which will degrade the sensitivity of the gyroscope. The angular velocity measurement and minimization of the cross coupling between two axes are challenging problems in vibrating gyroscopes. As a consequence, some kind of advanced control method is essential for improving the performance and stability of MEMS gyroscopes.

Over the last years, sliding-mode controllers have been proposed to control the MEMS gyroscope. Batur et al. (2006) developed a sliding-mode control for an MEMS gyroscope system combined with a force balancing control strategy to identify angular velocity. Fei and Batur (2009) derived an adaptive sliding-mode control (ASMC) with Proportional-Integral sliding surface for an MEMS gyroscope in order to enable the system to track the desired trajectory or reference model and to identify its angular velocity, but chattering phenomena still was a problem. Moghanni-Bavil-Olyaei, Ghanbari, and Keighobadi (2012) presented an adaptive fuzzy sliding-mode control (AFSMC) for an MEMS gyroscope to attenuate the chattering by replacing the discontinuous part in the reaching mode with a fuzzy logic control. However, faster trajectory tracking and convergence rate may be desired.

Terminal sliding-mode control (TSMC) is a particular case of the higher order sliding-mode control. This technique has been studied to further improve the control performances. Essentially, to achieve finite-time convergence and to give an asymptotic stability, in addition, it is an adequately solution of the systems with high order degrees. However, it has a major drawback of the sliding-mode control techniques such as the chattering phenomena (Cao, Chen, Chen, Zhao, & Fan, 2012; Nekoukar & Erfanian, 2011; Tzuu-Hseng & Yun-Cheng, 2010). Drawback of the chattering is significant in practical applications because it leads, e.g. to high moving of mechanical parts and heat losses in electrical power circuits. In the last few years, many applications have been developed for the improvement of the performance of the combination of fuzzy control, TSMC and adaptive control (Nekoukar & Erfanian, 2011; Tao, Taur, & Chan, 2004; Tzuu-Hseng & Yun-Cheng, 2010). Fuzzy control is a somewhat intelligent, cost-effective nonlinear control which can approximate any nonlinear function to any desired accuracy because of the universal approximation property (Passino & Yurkovitch, 1998). The main idea for the integration of the fuzzy idea and TSMC approach is to reduce the chattering phenomena which often occur in the sliding-mode control systems because of high frequency switching and it will often excite undesired dynamics of the system. A TSMC has been proposed for the MEMS gyroscope (Saif, Ebrahimi, & Vali, 2011), but the paper does not concern with input disturbances and uncertainties as well. Also, chattering has not been attenuated significantly.

On the other hand, an efficient observer is needed to measure the angular velocity through the control system. Kalman filter is an optimal estimator which minimizes the estimation error variance in the presence of the noises in measurement and inside the system (Shaked & De-Souza, 1995).

In this paper, we present a new TSMC for an MEMS z-axis gyroscope by concerning the input disturbances and uncertainties which uses a nonlinear sliding surface. Then, Fuzzy system is employed to approximate the sliding-mode reaching law. An extended Kalman filter (EKF) is derived for online updating the gyroscope parameters of the model and the angular velocity so that closed-loop stability and finite-time convergence of tracking errors and its derivatives can be guaranteed.

This paper is organized as follows: In Section 2, the mathematical model and the dynamics of an MEMS gyroscope is described. In Section 3, the adaptive fuzzy terminal sliding-mode control (AFTSMC) is developed. Section 4 presents an EKF observer to estimate the angular velocity and all of the gyroscope parameters. Simulation results are provided to validate the effectiveness of the proposed control system in Section 5. Conclusions are drawn in Section 6.

2. MEMS vibrational gyroscope model

2.1 Dynamics of MEMS gyroscope

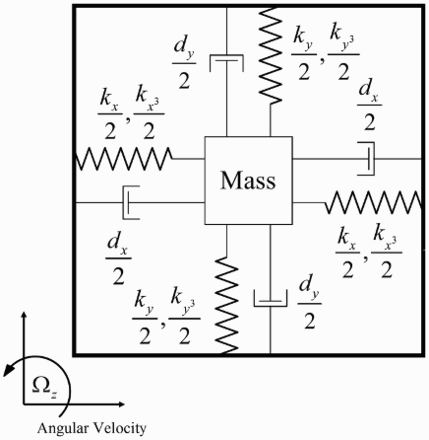
The schematic of an MEMS z-axis gyroscope is shown in Figure 1. This vibratory gyroscope includes a proof mass suspended by springs, an electrostatic actuation and sensing mechanisms for forcing an oscillatory motion and sensing the position and velocity of the proof mass. It is assumed that the table where the proof mass is mounted moves with a constant velocity and the gyroscope rotates at a slowly changing angular velocity about z-axis. The Coriolis force is generated in a direction perpendicular to the driving and rotational axes.

Figure 1. Dynamical model of MEMS z-axis gyroscope.

By using Lagrange's equation and with the assumptions stated above, the dynamics of gyroscope become as follows:

where x and y are two perpendicular axes in xy plane. The origin for x−y coordinates is at the center of the proof mass in the absence of the applied force. The fabrication imperfections are considered in the coupling spring and damping coefficients, and . The spring and damping terms along x and y axes are; , , , , and . The angular rate, , is perpendicular to the xy plane and it is assumed to be almost known. However, small unknown variations may occur in the corresponding nominal values. The accurate value of the proof mass, m is determined. and are the control forces along the x and y directions, respectively.

Dividing gyroscope dynamics (1) and (2) by the reference mass results in the following vector forms as

where

The variation of the angular rate is assumed negligible. Non-dimensionalizing the equations of motion of a gyroscope is useful because the numerical simulation is easy, even under the existence of large two time-scale differences in gyroscope dynamics. Using the dimensionless time, and dividing both sides of Equation (3) by reference frequency and length, and q₀ give the final form of the dimensionless equation of motion as follows:

By defining new parameters as the dimensionless representation of Equations (1) and (2) becomes

where

2.2 System description and control objectives

Consider the dynamics with parametric uncertainties and external disturbance as follows:

where and are the states of the MEMS gyroscope, Δ F denotes uncertain terms representing the un-modeled dynamics or structural variation of the system, , u(t) is the control input, d_m is matched disturbances. The states and the inputs, in Equation (7), are all deviations of the corresponding trajectories of the nonlinear system from a trim condition.

Assumption: The matched and unmatched lumped uncertainty and external disturbance Δ F and d_m are bounded by known positive parameters δ, such that and .

The control target for an MEMS gyroscope is to maintain the proof mass to oscillate in x and y directions at frequencies ω₁ and ω₂ and at amplitudes A₁ and A₂, respectively. These requirements can be stated as and . The purpose of the control scheme is to establish conditions that the unknown angular velocity Ω_z can be estimated. Equivalently, the control objective can be stated in terms of a reference model as follows:

where and .

The tracking error and its derivative are given as follows:

3. Adaptive fuzzy terminal sliding-mode control

3.1 TSMC design

In order to maintain the proof mass to track a smooth desired trajectory q_m in Equation (8), which includes desired proof mass oscillations in the actuation and sensing directions at given frequencies and amplitudes, the terminal sliding manifold is defined as follows:

where s=(s₁, s₂), and λ and γ are positive-definite constant matrices to be, respectively, selected, i.e. , . It should be noted that the finite-time convergence dynamic in TSMC depending on design parameters α, β, λ and γ in contrast with conventional sliding-mode control implies a swifter tracking capability in the MEMS z-axis gyroscope control problem. To ensure that the state of the system approaches the terminal sliding surface, first-time derivative of the sliding surface should be converged to zero as follows:

where . Setting to solve the equivalent control, u_eq, gives

In order to satisfy sliding condition despite uncertainty on the dynamics of the MEMS gyroscope, a discontinuous term across the terminal sliding surface is added to u_eq. Consequently, the non-singular TSMC law is proposed as follows:

where K_s is a positive-definite constant matrix. The last component of the control signal is designed to address the uncertainties and disturbances.

Substituting Equation (13) into Equation (7) yields

The tracking error equation now becomes

The dynamics of the terminal sliding surface s(t) is given as

By using , Equation (16) yields in the following simple form:

3.2 Stability analysis

The stability and robustness analysis of the proposed TSMC law in the presence of the matched and unmatched uncertainties and disturbances is accomplished by choosing a Lyapunov function as

Taking the time derivative of V(t) yields

Considering, , in which η is a positive fixed value, becomes negative semi-definite, i.e. . This implies that the trajectory reaches the terminal sliding surface in finite time and remains on the terminal sliding surface (Slotine & Li, 1991). From Equation (10), e(t) will also asymptotically converge to zero. Furthermore, using LaSalle's invariant set theorem, .

However, the differentiation of the terminal sliding surface in the stability derivation process will result in the singular condition due to the condition . But this control system presents the chattering problem caused by K_s and discontinuity of the sign function of the SMC at the reaching phase. In order to resolve this drawback, we will replace the reaching law by the fuzzy logic system which will be presented in the following section.

3.3 Adaptive fuzzy terminal sliding-mode control design

In order to remove the charting phenomena caused by the discontinuous part of , we aim to replace the constant K_s of commutation of discontinuous control parameter by the auto adjustable gain generated by the fuzzy logic controller and the sign function by another fuzzy logic controller.

The reaching law is designed as

where K_f is the normalization factor of the output variable, and u_f (t) is the output of the adaptive fuzzy terminal sliding-mode controller, which is determined in accordance with the normalized outputs of the TSMC, i.e. s(t) and . The fuzzy control rules can be represented as the mapping of the input linguistic variables s(t) and to the output linguistic variable u_f (t) as follows (Moghanni-Bavil-Olyaei et al., 2012):

where denotes the functional characteristics of the fuzzy linguistic decision schemes.

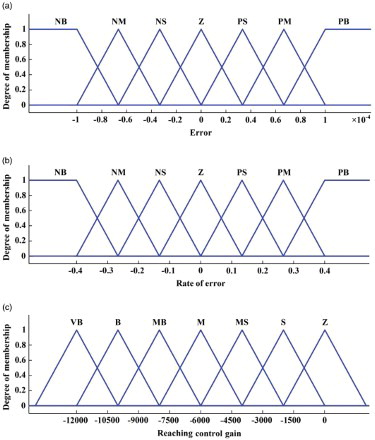
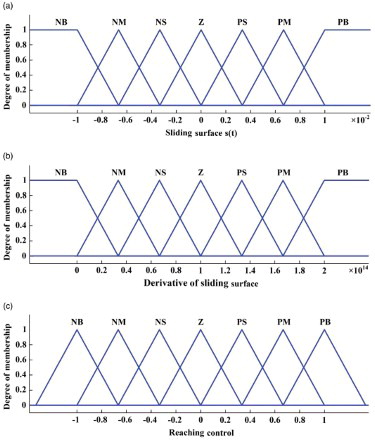
In order to choose the membership functions, the basic problem is to break the 0–1 modeling. Triangular membership functions are the first choices in every problem. However, if the situation is complex and deep, we might need a special type of membership function (Ross, 2010). In our problem, triangular membership functions can solve the difficulties. The ranges of the membership functions are selected based on a trial-and-error approach. The membership functions of input linguistic variables s(t) and and the membership functions of output linguistic variables u_f (t) and K_f are shown in Figures 2 and 3, respectively. They are decomposed into seven fuzzy partitions expressed as NB (Negative Big), NM (Negative Medium), NS (Negative Small), Z (Zero), PS (Positive Small), PM (Positive Medium) and PB (Positive Big). The fuzzy control surface of the output u_f (t) is shown in Figure 4. The fuzzy rules are extracted in such a way that the stability of the system would be satisfied and these rules contain the input–output relationships that define the control strategy. The linguistic fuzzy rules are defined heuristically in the following generic form: where , and Bⁱ are the membership functions in the ith IF–THEN rule corresponding to the input and output fuzzy sets, respectively. In the fuzzy inference engine, the intersection minimum and the center average defuzzification operations are used.

Figure 2. Membership functions (a) sliding surface, (b) derivative of sliding surface and (c) reaching control.

Figure 3. Membership functions (a) error, (b) rate of error and (c) reaching control gain.

Figure 4. Control forces by AFTSMC and comparison of adaptations by AFSMC and AFTSMC with EKF.

The IF–THEN rules of the MEMS gyroscope system are represented in Tables 1 and 2. In the fuzzy rule table, the rules are designed such that the following points are taken under consideration:

Table 1.  Rule base of AFSMC.

	NB	NM	NS	Z	PS	PM	PB
NB	NB	NB	NM	NS	PS	PS	PS
NM	NB	NM	NM	NS	PS	PS	PS
NS	NM	NM	NS	NS	PS	PS	PM
Z	NM	NM	NS	Z	PS	PM	PM
PS	NM	NS	NS	PS	PS	PM	PM
PM	NS	NS	NS	PS	PM	PM	PB
PB	NS	NS	NS	PS	PM	PB	PB

Table 2.  Rule base for adaptation of the reaching control gain K_f.

	NB	NM	NS	Z	PS	PM	PB
NB	M	MS	S	Z	S	MS	M
NM	MB	M	MS	S	MS	M	MB
NS	B	MB	M	MS	M	MB	B
Z	VB	B	MB	M	MB	B	VB
PS	B	MB	M	MS	M	MB	B
PM	MB	M	MS	S	MS	M	MB
PB	M	MS	S	Z	S	MS	M

Table 3.  The MEMS gyroscope parameters used in simulation.

Parameter	Value	Unit
M		kg
dx		Ns/m
dxy		Ns/m
dy		Ns/m
kx	80.98	N/m
kx3		N/m^3
kxy	5	N/m
ky	71.62	N/m
ky3		N/m^3
w0	1	kHz
q0		m

• (1) The output fuzzy sets are normalized in the interval (−1, 1), then .

• (2) When the product is positive, the membership value of u_f (t) is set such that its sign is the same as that of s(t), therefore the following inequality is insured:

This condition is required to achieve the system stability.

The AFTSMC law has been represented as follows:

4. Angular velocity estimation via EKF

It is known that the Kalman filter estimates the states of a linear system with additive state and output noises (Grover & Hwang, 1992). Due to the fact that the MEMS gyroscope dynamics equations are nonlinear, an EKF is required (Simon, 2006). The EKF is a discrete algorithm to estimate nonlinear dynamics affected by noise. Consider the nonlinear discrete dynamic system

where h is observation (measurement) matrix, w^(k) and v^(k+1) are the process and observation noises, respectively; both assumed as zero mean multivariate Gaussian noises.

We assume that the changes of parameters of the gyroscope are not as much as the angular velocity and we assume that they are known constants. By neglecting the centrifugal forces and cubic type stiffness, the linear dynamics of an MEMS z-axis gyroscope (7) is written in the following form:

where and . Then, the angular velocity will be calculated as . Let be the estimation error and u is replaced from Equation (13). The update law is designed as follows:

where ρ>0. It can be shown that the estimation error is uniformly ultimately bounded, where the gyroscope parameters are assumed to be known constants or slowly varying parameters.

Defining the extended state vector as

Allows writing the nonlinear discrete state representation of Equation (25) as

where T_s is the sampling time. The angular velocity observer, built in as Equation (3), is discretized such as

with ϕ^D calculated, for a generic quantity ϕ, as

From Equation (5), a suitable EKF can be designed which is effectively decoupled from the angular velocity observer as follows:

where K^(k) is the observer gain and ◯^(k) is an estimation of x^(k). By applying EKF to system of Equation (28), estimation equations in the EKF can be calculated as follows:

where Q^(k)>0 is process noise covariance, P^(k|k) is error covariance and A^(k) is Jacobin matrix of the state transition. Then, correction equations in the EKF are as follows:

where is the observation error, R^(k)>0 is covariance matrix of observation (measurement) noise, r^(k+1) is the current measurement of the nonlinear system and K^(k) is the Kalman filter gain.

4.1 Convergence analysis

In this subsection, we consider the convergence analysis of the algorithm. The dynamics of the a priori estimation error is governed by the following difference equation:

It may be noted that the over-bar notation has been introduced on error vectors and covariance matrices to emphasize that the expressions are for the noise-free case. It is further assumed that (Boutayeb, Rafaralahy, & Darouach, 1997; Reif & Unbehauen, 1999):

Assumption 1 A^(k+1) is non-singular for all k.

Assumption 2 There exists a, c, κ>0 such that , and , i.e. matrices A^(k+1), H^(k+1) and K^(k+1) are uniformly bounded.

Assumption 3 There exists p₁, p₂>0 such that and .

Then, by defining matrices

the following inequality can be proved using the matrix inversion lemma and the Riccati equations (Reif & Unbehauen, 1999)

If we choose the Lyapunov function as

then, using Equation (36), it follows that

Since matrix , we can conclude that the difference Equation (34) has asymptotically stable equilibrium point at the origin. Let q denote the smallest eigenvalue of Q^(k), then, using Assumptions 1–3 and using arguments similar to Reif and Unbehauen (1999), it follows that

i.e. the difference Equation (34) has globally asymptotically stable equilibrium point at the origin. If we further assume that p₂≥1, then following Reif and Unbehauen (1999), it can be shown that

which implies that the origin is an exponentially stable equilibrium point.

5. Simulation results

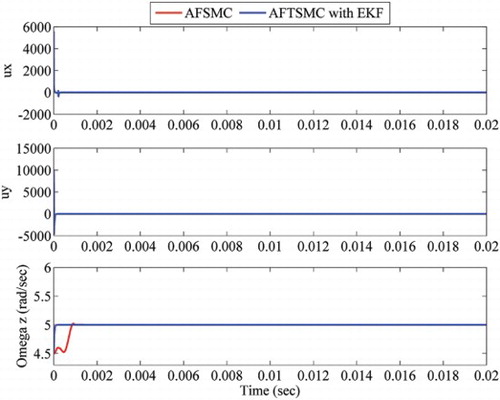
In this section, the performance of the proposed AFTSMC on a lumped MEMS gyroscope model is evaluated using simulation results in MATLAB/SIMULINK for tracking and estimating the angular rate, Ω_z, and gyroscope parameters. Results of simulations are shown in Figure 4. The simulation results are compared with the results of adaptive fuzzy SMC (Moghanni-Bavil-Olyaei et al., 2012).

The desired motion trajectories are and , where and . The modeling uncertainties, Δ F are considered as:±3% change in the spring and damping coefficients from corresponding nominal values, ±2% changes in the magnitude of coupling terms d_xy and ω_xy, and ±5% variations of Ω_z, which are modeled as random variables with zero mean and unity variance. The unknown angular velocity, Ω_z, is assumed to have an amplitude of 5.0 rad/s. Initial values for the reference model states are as follows: which are all in meters or meter per seconds. Parameters of the MEMS gyroscope are given in Table 1. Terminal sliding surface parameters are designed such that , , α=9 and β=5. Parameters of the observers are tuned as follows: with initial guess As shown in Figure 4, the chattering-free control effort and estimation performance of the proposed controller is significantly superior compared with that of the previous methods which makes it possible to achieve a faster response.

6. Conclusions

In this paper, we have considered a novel control system with novel observation system for an MEMS z-axis gyroscope, where it has been successfully applied for the control of the axes of the MEMS gyroscope on the desired directions and to estimate the unknown angular velocity and all of gyroscope parameters. The design has been proved to guarantee the closed-loop stability in the sense of Lyapunov method. It has been verified that the proposed controller has superior tracking performance and robustness to conventional ASMC and AFSMC in estimating the gyroscope parameters and also the angular velocity in the presence of input disturbances and model variations. Future works can be on the estimation of time-varying angular velocities.