Adaptive synchronization of fractional-order memristor-based Chua's system

Abstract

Adaptive synchronization of fractional-order memristor-based Chua's circuit is discussed in this paper. Two adaptive synchronization schemes are presented for the fractional-order memristor-based Chua's circuit based on the stability theory of fractional-order differential system, the drive–response concept and the adaptive control principle. Also the case of only one parameter known and the case of all the other parameters fully unknown are discussed. The results show that controller parameters can be adjusted to enhance the convergence rate of the error system. Finally, numerical simulations are drawn to demonstrate these results.

Keywords:

• fractional-order
• memristor
• Chua's circuit
• adaptive synchronization

1. Introduction

As Professor Chua pointed in 1971 (Chua, 1971), memristor is considered as the missing fourth passive circuit element. It has attracted many scientists to investigate the property of the memristor-based systems. The memristor-based systems (El-Sayed, Elsaid, Nour, & Elsonbaty, 2013; Wang, Wang, & Tan, 2011) display abundant dynamical behaviors such as bifurcation, chaos and so on, which are very complicated and have already been applied in other fields such as secure communication (Kinzel, Englert, & Kanter, 2010). Also researchers have discussed dynamical behavior and stability analysis of the fractional-order memristor-based Chua's circuit in Petráš (2010a). This system exhibits chaos phenomena under some special conditions. As an important and interesting behavior, synchronization has extensively been investigated. Many researchers have studied the synchronization of chaotic systems by adopting many schemes such as feedback control (Wu, Wen, & Zeng, 2012), impulsive control (Zhong, Yu, & Yu, 2010), sliding mode control (Yau, 2004), backstepping method (Song, Shen, & Chang, 2011) and so on. System structure and parameters are usually known in most methods. However, in fact, some parameters are uncertain or unavailable. Adaptive control principle (Wen, Zeng, & Huang, 2012) can be used to estimate the uncertain parameters of the system.

Motivated by the above discussion, two adaptive synchronization schemes are proposed for the fractional-order memristor-based Chua's circuit. In this paper two cases of only one parameter known and all the other parameters unknown are discussed. Also different controller functions and parameter update rules are proposed. The simulation results show that the parameters in the update rules can be chosen to enhance the convergence rate. This method can also be applied in the chaotic system without a memristor.

2. Fractional-order memristor-based systems

The fractional-order operator is the generalization of integer-order operator. There are three commonly used definition of the fractional-order differential operator: Grunwald–Letnikov, Riemann–Liouville and Caputo. These definitions can be found in Ding, Wang, and Ye (2012), Dong, Wang, and Gao (2013), Hu, Wang, Shen, and Gao (2013) and Kan, Wang, and Shu (2013). In this paper, we will study the dynamical behavior of fractional-order system with the Grunwald -Letnikov (GL) definition, which is defined as where [·] means the integer part. Therefore, in the rest of this paper, the notation D^q is chosen as GL fractional derivative operator for brevity's sake. General numerical solution of the fractional differential equation can be expressed as

where parameters are binomial coefficients, which is calculated with the following formula (Monje, Chen, Vinagre, Xue, & Feliu, 2010): For the memory term expressed in the above equation, we put v=1 for all k. In order to investigate the dynamical behavior, we will employ the following lemma.

lemma[(Zhao, Hu, & Liu, 2010)] 1

For fractional-order system D^qx=f(x), when fractional order q≤1, if there exists one positive matrix P such that function holds, the state x is asymptotically stable.

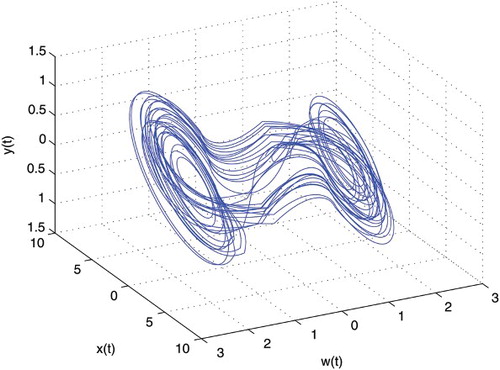
A new fractional-order memristor-based Chua's circuit has been proposed in Petráš (2010a):

where the piece-wise linear function W(ω) is given as where a, b>0. As pointed in Petráš (2010a), when parameters are taken as and fractional order q=0.97, this system displays chaotic attractors in the 3D state space which is shown in Figure 1.

Figure 1. Strange attractor of the memristor-based Chua's system (1).

3. Adaptive synchronization

Let system (1) be the drive system. In this section, according to the property of parameter α, we discuss two cases. Suppose other parameters are unknown.

3.1 Parameter α known

The response system is as follows:

where parameters and γˆ of the response system (2) are unknown and need to be estimated. The piece-wise linear function is given by It is easy to obtain the error system from Equations (1) and (2) as follows:

where e₁=x−◯, e₂=y−ŷ and e₃=z−zˆ, . The controller functions are designed as follows:

where k₁, k₂, k₃ and k₄ are adjustable parameters. Let . Then the update rules for three unknown parameters are designed as follows:

where k₅, k₆ and k₇ are adjustable parameters. are control gains of parameters , respectively. Thus, we have the following main result.

Theorem 1

For error system (3), when parameters are properly chosen so that the following linear matrix inequality holds:

where blocking matrices Σ₁1 and Σ₁2 are given by where then the fractional-order memristor-based Chua's systems (1) and (2) can be synchronized under the adaptive control of Equations (4) and (5).

Proof From Lemma 1, one can choose J function as follows: where , Then function J along trajectories of Equation (3) is calculated as where Q₁ is given in Equation (6). From Lemma 1, J function is negative, which implies that the state variables e₁, e₂, e₃ and e₄ are asymptotically stable and parameters and e_ζ are estimated with controller functions (4) and update rules (5). Thus response system (2) is synchronized with drive system (1).

3.2 Parameter α unknown

When parameter α is unknown, the response system is given by

where parameters and γˆ of response system (7) are unknown and need to be estimated. It is easy to obtain the error system from Equations (1) and (7) as follows:

The controller functions are designed as follows:

Let . Then the update rules for unknown parameters are designed as follows:

where k₅, k₆, k₇ and k₈ are the adjustable parameters. From the similar proof of Theorem 1, we obtain the following result.

Theorem 2

For error system (8), when parameters are properly chosen so that the following linear matrix inequality holds:

where blocking matrices Π₁ and Π₂ are given by where then the fractional-order memristor-based Chua's systems (1) and (7) can be synchronized under the adaptive control of Equation (9) and (10).

Proof From Lemma 1, one can choose another J function as follows: where , The similar proof can be referred to Theorem 1. Thus the response system (7) is synchronized with the drive system (1).

4. Numerical example

The numerical simulation is carried out by using the approximation on Grunwald–Letnikov method proposed in Petráš (2010b). And for the memory terms, a short memory principle is used.

4.1 Simulation with known α

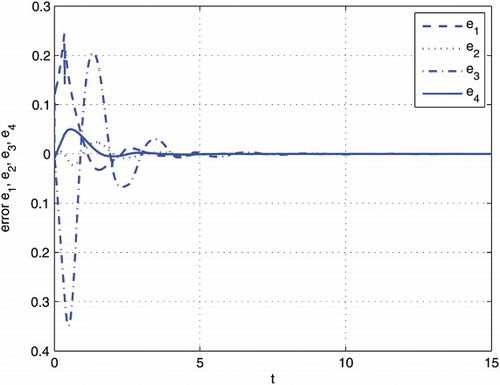
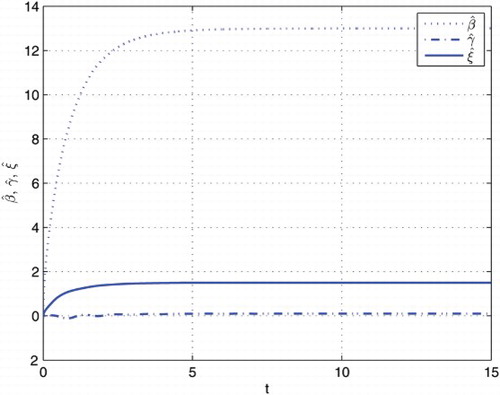
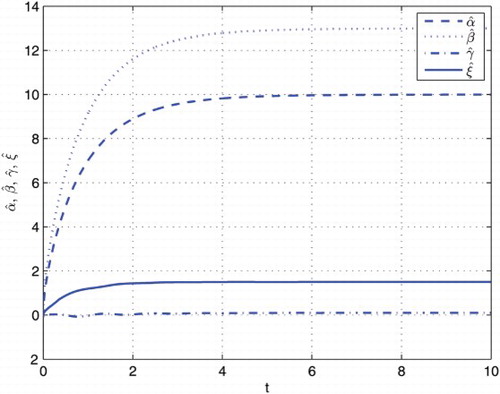
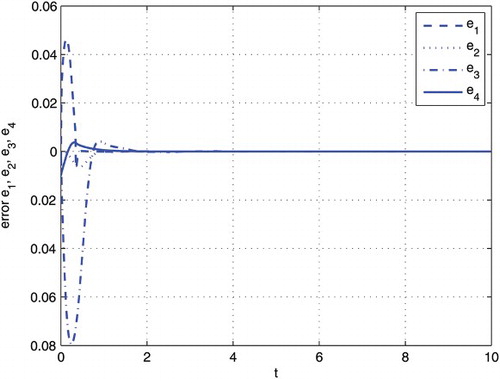
The initial states of the drive system and the response system are and , respectively. The parameters of the drive system are and q=0.97. Choose and k₄=2.5, the eigenvalues of matrix Σ₁ are −13.0831,−7.0534, −2.4484 and −0.9151. Also we choose k₅=1, k₆=1 and k₇=1. This can guarantee that the matrix Q₁ is negative. In addition, the initial values of parameters and e_ζ are and , respectively. Then the adaptive error states e₁, e₂, e₃ and e₄ and unknown parameters curve of and ζˆ are drawn in Figures 2 and 3, respectively.

Figure 2. Synchronization errors e₁, e₂, e₃ and e₄ with known α and θ=1, λ=1, τ=1.

Figure 3. Unknown parameters curve of βˆ, γˆ and ζˆ with known α and θ=1, λ=1, τ=1.

4.2 Simulation with unknown α

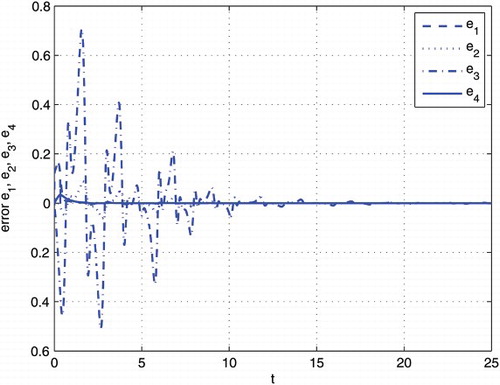
For unknown α, from Theorem 2, the similar parameters are the same as that in Section 4.1. Moreover, parameters are chosen as and k₄=2.5. Then the eigenvalues of matrix Π₁ are and −0.8261. Also we choose and k₈=1. This can guarantee the matrix Q₂ is negative. Take and τ=1. Then the synchronization errors e₁, e₂, e₃ and e₄ and unknown parameters of and ζ are drawn in Figures 4 and 5, respectively.

Figure 4. Synchronization errors e₁, e₂, e₃, and e₄ with unknown α and δ=1, θ=1, λ=1 and τ=1.

Figure 5. Unknown parameters curve of αˆ, βˆ, γˆ and ζˆ with unknown α and δ=1, θ=1, λ=1 and τ=1.

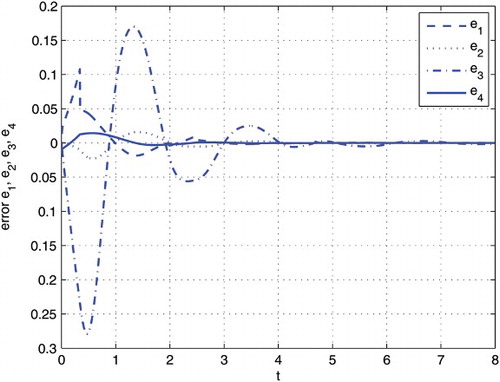
It is obvious that the convergence rate of synchronization errors and parameters and ζˆ are slower. In order to enhance the convergence rate, parameters and τ are revised as and τ=5. The corresponding synchronization errors are drawn in Figure 6.

Figure 6. Synchronization errors e₁, e₂, e₃ and e₄ with unknown α and δ=5, θ=5, λ=5 and τ=5.

4.3 Discussion with k₅=0, k₆=0, k₇=0 for known α

Figure 7 describes the synchronization errors with k₅=0, k₆=0 and k₇=0. It is obvious that the convergence rate of synchronization errors are slower than that of k₅=1, k₆=1 and k₇=1. Also in order to enhance the convergence rate, we choose and τ=15.

Figure 7. Synchronization errors e₁, e₂, e₃ and e₄ with known α and θ=15, λ=15 and τ=15.

5. Conclusions

With the intensive study on the fractional-order system and the memristor, the investigation on the fractional-order memristor-based system becomes the hot issue. The adaptive synchronization for the fractional-order memristor-based Chua's circuit has been investigated with unknown parameters. Some controller schemes and update rules for unknown parameters have been proposed to guarantee the adaptive synchronization. Finally, numerical simulation has been carried out to show the efficiency of the proposed schemes.

Acknowledgements

The authors are thankful to anonymous viewers for their valuable comments and suggestions to this paper. This work was supported by the National Natural Science Foundation of China under Grants 61304162, 61174216, 61074124, 61273183, 61374028 and the Talent Scientific Research Foundation of China Three Gorges University under Grant KJ2012B075.