ABSTRACT
In this paper, the problems of stability and stabilization are investigated for a class of nonlinear networked control systems (NCSs) in the presence of random delay. First, network-induced random delay is modelled as a Markov chain, and the resulting closed-loop system is transformed into a Markovian jump system. Then, sufficient conditions for stochastic stability and stabilization of the underlying systems are derived via a new linear matrix inequalities (LMIs) formulation. Moreover, the stabilizing output feedback controller design is achieved by assuming some elements in the transition probability matrix to be unknown or unavailable because of the complexity of the network. Finally, numerical examples and simulations are carried out to show the usefulness of the designed controller.
Introduction
Networked control systems (NCSs) are known as a control system communicating with sensors and actuators through a real-time network. Compared to the traditional point-to-point control systems, NCSs provide great advantages such as reduction of system wiring, ease of maintenance and diagnosis, and improvement of flexibility in system implementation (Ge, Tian, & Liu, Citation2007). Consequently, NCSs are applied in the various fields such as industrial automation, manufacturing plants, aircraft, heating, ventilating and air-conditioning systems, tele-robotic, remote surgery, unmanned aerial vehicles, and many other applications (Wang & Liu, Citation2008; Zhang, Gao, & Kaynak, Citation2013; Hespanha, Naghshtabrizi, & Xu, Citation2007). However, the analysis and design of NCSs are complex due to the insertion of the communication network in the feedback control loop (Zhang, Branicky, & Phillips, Citation2001; Tipsuwan & Chow, Citation2003).
Despite the great advantages, communication networks in control loops are encountering some problems such as data packet dropout and network-induced delays, which will deteriorate the system performance as well as the stability. Therefore, over the past decades, a great deal of attention has been paid to analyse how such issues affect on the NCSs performance. For NCSs with different network protocols, the network-induced delay may be constant, time-varying, or even random variable (Zhang et al., Citation2013).
In practical applications, most of the protocols (such as round-robin and Ethernet) used in NCS cannot ensure a constant delay. Thus, time-varying or random delays are considered in the most studies. For instance, in Luo, Wang, Wei, Alsaadi, and Hayat (Citation2016), an update matrix approach is developed to handle the time-varying yet periodic time delays resulting from the adoption of the round-robin protocol.
It should be noted that in the case of time-varying delays, the delay-range-dependent method is of less conservativeness compared with the delay-independent or delay-dependent results (Luo, Wang, Liang, Wei, & Alsaadi, Citation2016).
Recently, much attention has been paid to the modeling of random delay and data packet dropout with the Markov chain. Following that, the resulting closed-loop system will be known as a Markovian jump system (MJS), and one can use the well-known stability results of this specific class of systems to analyse such NCSs (Xiao, Hassibi, & How, Citation2000; Zhang, Shi, Chen, & Huang, Citation2005; Gao & Tang, Citation2011; Wu & Chen, Citation2007). It is noted that the behavior of such systems is determined by a transition probability matrix (TPM). Although the ideal knowledge on the transition probabilities simplifies the system analysis and design, obtaining completely known transition probabilities of a Markov chain practically are hard or even impossible due to the complexity of the network. Therefore, recent researches have been concentrated on the verification of the stability and stabilization conditions for this class of systems with uncertainties in transition probabilities. For this purpose, some approaches have been recently developed to overcome these uncertainties (Zhang & Boukas, Citation2009; Zhang & Lam, Citation2010; Braga, Morais, Oliveira, & Peres, Citation2013).
However, most of the results obtained in the aforementioned works have been concerned with linear systems. Evidently, it is important to investigate such problems for nonlinear systems (van de Wouw, Nešić, & Heemels, Citation2012; Zhang, Li, & Wang, Citation2015). Moreover, the full state of the plant cannot be directly measured, in practice. Therefore, it is more significant to exploit the output feedback controller for the NCSs design.
Summarizing the earlier discussion, in this paper, we are motivated to study the static-output feedback controller design for a class of nonlinear NCS involving random delay that is modeled via the MJSs approach with partly unknown transition probabilities. Besides, following obtained results in Zhang and Lam (Citation2010) to deal with unknown elements in TPM, we try to design the controller in a less conservative way, and new LMI-based sufficient conditions are derived to compute the controller gains.
The rest of the paper is organized as follows: in Section 2, the modeling of the network-induced random delay as a Markov chain is described. We review some related preliminaries on MJSs in Section 3, followed by a controller design procedure will provide for the stabilization of the closed-loop system via new linear matrix inequalities (LMIs). Section 4 provides a numerical example to validate proposed results. Finally, concluding remarks are given in Section 5.
Notation: The superscript ‘T’ and ‘−1’ stand for matrix transposition and the matrix inverse, respectively. stands for the n-dimensional Euclidean space,
is the set of
real matrices. The notation
implies that
is a real symmetric and positive-definite (semi-positive-definite) matrix.
and
denote identity matrix and zero matrix with appropriate dimensions, respectively.
represents the occurrence probability of the event
. Furthermore, the symmetric term, in a symmetric block matrix, is denoted by an asterisk, and
refers to the mathematical expectation operator.
Problem formulation
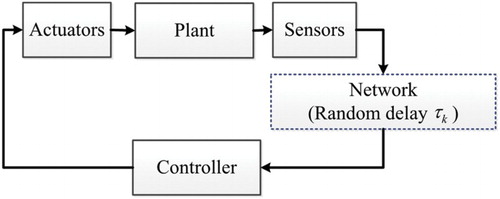
The NCS considered in this study is illustrated in . The considered structure includes three components: a nominal plant to be controlled, a network such as the Ethernet, and a controller. The nominal plant is described as follows:
(1)
where
and
are state vector and control input, respectively.
is the output vector and
represents the nonlinear function. The matrices
,
,
, and
are real constant matrices with appropriate dimensions. Moreover,
is full-row rank
.
The nonlinear function with
satisfies the following sector-bounded condition:
(2)
where
and
are constant real matrices with appropriate dimensions, and
. Note that the nonlinear function
is said to belong to the sector
.
Remark 2.1:
The sector-bounded condition (2) is a more general condition of nonlinearity than the widely investigated Lipschitz condition. Therefore, recently, noticeable achievements have been made on design and filtering problems for systems with the sector-bounded condition (Zhang et al., Citation2015; Wei, Wang, & Han, Citation2013).
The mode-dependent output feedback control law is defined as follows:
(3)
where
is assumed to be bounded and is modelled by a Markov chain taking values in a finite set
with transition probability from mode i at time k to mode j at time
,
, where
and
.
Remark 2.2:
This model is quite general, data packet dropout in the network can be included naturally by considering (Xiao et al., Citation2000). Especially, data packet dropout is seemed as a special case of the time delay.
For instant, assuming that , the TPM with partly unknown elements can be considered as follows:
where ‘
’ represents the unknown or unavailable elements. Let
be the column indices of the known and unknown elements, respectively, in the ith row in
as follows (Zhang & Lam, Citation2010):
Moreover, if , then it can be described as follows:
If we apply the control law (3) to system (1) and augment the state variable , then the closed-loop system is
(4)
where
and all elements in
are zero, except the
block which is equal to
.
Furthermore, for the nonlinear function satisfying the sector-bounded condition (2) results in
where
and
. One can rewrite this equation as follows:
Main results
In this section, firstly, the stochastic stability definition of the NCS modelled by MJS (4) is introduced. Based on these preliminaries, and by assuming partly known transition probabilities, some sufficient conditions are derived to guarantee the stochastic stability of this class of nonlinear NCS via new LMIs.
Definition 3.1:
The system (4) is stochastically stable, if for any initial state
and
.
We first investigate the stochastic stability result that serves as a theoretical basis for the subsequent design problem. In what follows, we define ,
, and
for brevity.
Theorem 3.1:
Consider the NCS in . For the given controller gain matrices the closed-loop system (4) is stochastically stable, if there exist matrices
satisfying the following equations:
(5)
where
Proof:
Choose a Lyapunov function candidate as
Then, we have
It follows that
(6)
On the other hand
Note that implies that
. Thus, Equation (6) can be rewritten as follows:
Obviously, the above inequality holds if and only if , and therefore, we have
where
and one can obtain that
which indicates that system (5) is stochastically stable according to Definition 3.1. This completes the proof of Theorem 3.1.
We are now in a position to deal with the static-output feedback controller design problem for the nonlinear NCS (1) with the effect of network-induced random delay.
Theorem 3.2:
Consider the closed-loop system (4), and let be a given scalar. A desired output feedback controller of the form (3) exists if there exist matrices
,
,
, and
satisfying
(7)
(8)
where
Furthermore, if is a feasible solution of Equations (7) and (8), then the controller gains in the form of (3) can be computed by
(9)
Proof:
At first, pre- and post-multiplying Equation (5) by and
, respectively. Then, by setting
and
, and using the Schur complement lemma, the following inequality is derived:
(10)
Since for
, it is easy to verify that, if equation (8) holds, the inequality (10) is satisfied. On the other hand, according to the definition
, we can obtain (7) and (9) readily, and the proof is then completed.
Because of the equality condition (7), the results of Theorem 3.2 still cannot be implemented directly by using numerical software. Therefore, we first introduce the relative lemma, and then based on this lemma, the existence conditions of the controller are developed in Corollary 3.1.
Lemma 3.1:
For with rank equal to p, there always exist orthogonal matrices
and
, for all
as follows:
(11)
where
,
and
, and
are the nonzero singular values of
.
Furthermore, if full-rank matrices exist in the following structure:
(12)
then there exist nonsingular matrices
satisfying Equation (7) (Gao & Tang, Citation2011).
Corollary 3.1:
The closed-loop system (5) is stochastically stable, if there exist matrices ,
,
,
, and
for
satisfying the LMIs (8), where
are defined by Equation (12). Furthermore, if there is a feasible solution, the controller gains
can be given by
(13)
where
and
are defined in Equation (11).
Numerical simulations
In this section, we evaluate the performance of the proposed controller through simulations.
Example 4.1:
Consider the nonlinear NCS (1) with parameters given as follows:
Besides the nonlinear function
is chosen as follows:
which satisfies the sector-bonded condition (2) with
Furthermore, the delay is modeled by a Markov chain with
and the three cases of the TPM are considered as .
Table 1. Different transition probability matrices.
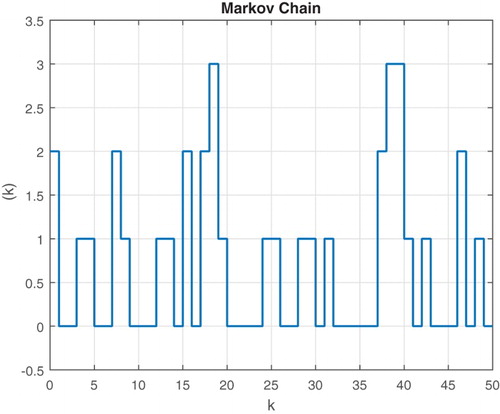
A possible system mode's evolution using the Case I TPM is given in .
By solving the LMIs in Corollary 3.1, we obtain the following mode-dependent controller gains ().
Table 2. Controller gains for different cases.
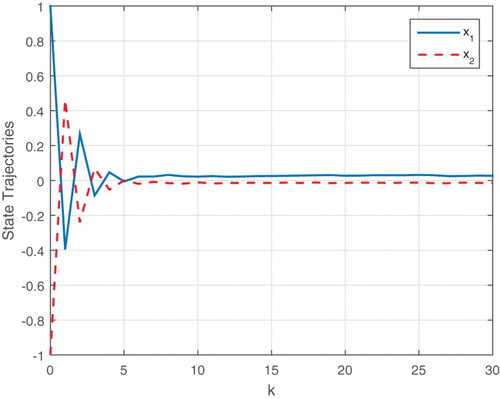
Our obtained controller can guarantee that the nonlinear NCS (1) is stochastically stable. Figures – show the system state response after 100 Monte Carlo simulations. In addition, the initial condition is assumed to be , and
. It can be seen that the system is stabilized and our proposed method is effective.
Figure 3. The system state trajectories with delay and by applying the designed output feedback controller (Case I).
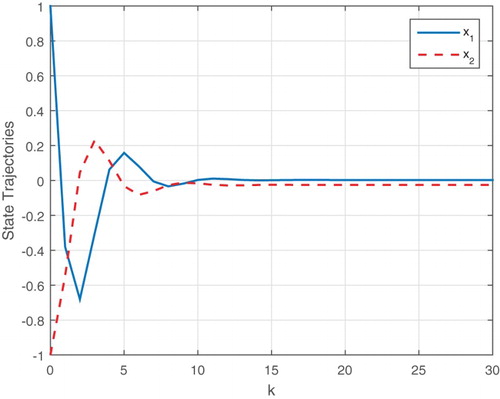
Figure 4. The system state trajectories with delay and by applying the designed output feedback controller (Case II).
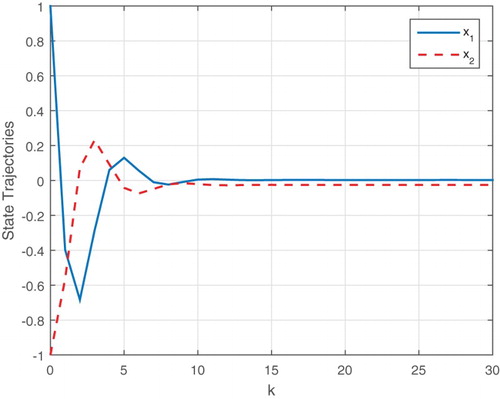
Figure 5. The system state trajectories with delay and by applying the designed output feedback controller (Case III).
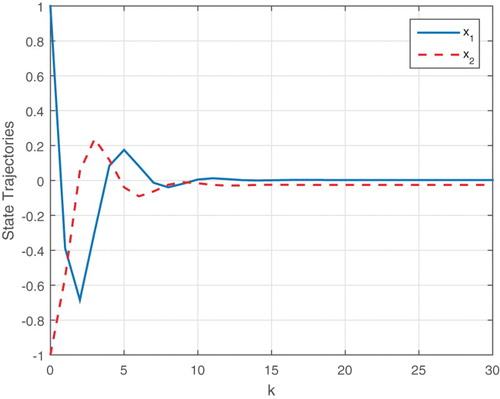
Example 4.2:
Consider the nonlinear NCS (1) with . The other system parameters and matrices are assumed to be the same as Example 4.1 with Case I TPM. Using Corollary 3.1, the computed controller gains are
depicts the state responses of the closed-loop system, from which we can see that the unstable system can be effectively stabilized with the designed feedback controller.
Conclusions
In this study, new LMI conditions have been proposed to design a stabilizing controller for a class of nonlinear NCSs involving random transmission delay. At first, by modeling the network-induced random delay as a Markov chain, the closed-loop system is transformed into a MJS with partly known TPM. Then, by employing the newly derived stochastic stability conditions, the static-output feedback controller has been designed such that the closed-loop system is stochastically stable. Finally, the effectiveness of the developed technique has been illustrated by a numerical example.
Disclosure statement
No potential conflict of interest was reported by the authors.
ORCiD
Jafar Zarei http://orcid.org/0000-0002-0135-8173
References
- Braga, M. F., Morais, C. F., Oliveira, R. C., & Peres, P. L. (2013). Robust stability and stabilization of discrete-time Markov jump linear systems with partly unknown transition probability matrix. American Control Conference (ACC) (pp. 6784–6789).
- Gao, S.-W., & Tang, G.-Y. (2011). Output feedback stabilization of networked control systems with random delays. Proceedings of the 18th IFAC World Congress (pp. 3250–3255).
- Ge, Y., Tian, L., & Liu, Z. (2007). Survey on the stability of networked control systems. Journal of Control Theory and Applications, 5(4), 374–379. doi: 10.1007/s11768-006-6137-5
- Hespanha, J. P., Naghshtabrizi, P., & Xu, Y. (2007). A survey of recent results in networked control systems. Proceedings of the IEEE, 95(1), 138–162. doi: 10.1109/JPROC.2006.887288
- Luo, Y., Wang, Z., Liang, J., Wei, G., & Alsaadi, F. E. (2016). H∞ control for 2-D fuzzy systems with interval time-varying delays and missing measurements. IEEE Transactions on Cybernetics, 1–12. doi: 10.1109/TCYB.2016.2514846
- Luo, Y., Wang, Z., Wei, G., Alsaadi, F. E., & Hayat, T. (2016). State estimation for a class of artificial neural networks with stochastically corrupted measurements under round-robin protocol. Neural Networks, 77, 70–79. doi: 10.1016/j.neunet.2016.01.001
- Tipsuwan, Y., & Chow, M.-Y. (2003). Control methodologies in networked control systems. Control Engineering Practice, 11(10), 1099–1111. doi: 10.1016/S0967-0661(03)00036-4
- Wang, F.-Y., & Liu, D. (Eds.). (2008). Networked control systems. London: Springer.
- Wei, G., Wang, L., & Han, F. (2013). A gain-scheduled approach to fault-tolerant control for discrete-time stochastic delayed systems with randomly occurring actuator faults. Systems Science & Control Engineering: An Open Access Journal, 1(1), 82–90. doi: 10.1080/21642583.2013.842509
- van de Wouw, N., Nešić, D., & Heemels, W. P. M. H. (2012). A discrete-time framework for stability analysis of nonlinear networked control systems. Automatica, 48(6), 1144–1153. doi: 10.1016/j.automatica.2012.03.005
- Wu, J., & Chen, T. (2007). Design of networked control systems with packet dropouts. IEEE Transactions on Automatic Control, 52(7), 1314–1319. doi: 10.1109/TAC.2007.900839
- Xiao, L., Hassibi, A., & How, J. P. (2000). Control with random communication delays via a discrete-time jump system approach. IEEE (pp. 2199–2204).
- Zhang, L., & Boukas, E.-K. (2009). Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica, 45(2), 463–468. doi: 10.1016/j.automatica.2008.08.010
- Zhang, L., Gao, H., & Kaynak, O. (2013). Network-induced constraints in networked control systems: A survey. IEEE Transactions on Industrial Informatics, 9(1), 403–416. doi: 10.1109/TII.2012.2219540
- Zhang, L., & Lam, J. (2010). Necessary and sufficient conditions for analysis and synthesis of Markov jump linear systems with incomplete transition descriptions. IEEE Transactions on Automatic Control, 55(7), 1695–1701. doi: 10.1109/TAC.2010.2046607
- Zhang, L., Shi, Y., Chen, T., & Huang, B. (2005). A new method for stabilization of networked control systems with random delays. IEEE Transactions on Automatic Control, 50(8), 1177–1181. doi: 10.1109/TAC.2005.852550
- Zhang, S., Li, Y., & Wang, Y. (2015). Fault detection for a class of non-linear networked control systems with data drift. IET Signal Processing, 9(2), 120–129. doi: 10.1049/iet-spr.2014.0055
- Zhang, W., Branicky, M. S., & Phillips, S. M. (2001). Stability of networked control systems. IEEE Control Systems Magazine, 21(1), 84–99. doi: 10.1109/37.898794