A delayed epidemic model of diseases through droplet infection and direct contact with saturation incidence and pulse vaccination

ABSTRACT

In this paper, we have considered a dynamical model of diseases that spread by droplet infection and also through direct contact with varying total population size and discrete time delay to become infectious. It is assumed that there is a latent period of the disease and an immune period of the recovered individuals. Pulse vaccination is an effective and important strategy for the elimination of infectious diseases and so we have analysed this model with pulse vaccination and saturation incidence rate. It is also assumed that the time lag due to lose of immunity of recovered individuals is equal to the interval between two pulses. We have defined two positive numbers and . It is proved that there exists an infection-free periodic solution which is globally attractive if and the disease is permanent if The important mathematical findings for the dynamical behaviour of the model are also numerically verified using MATLAB. Finally epidemiological implications of our analytical findings are addressed critically.

KEYWORDS:

• Droplet infection
• pulse vaccination
• saturation incidence rate
• permanence
• extinction

1. Introduction

Infectious diseases have tremendous influence on human life and are usually caused by pathogenic microorganisms, such as bacteria, viruses, parasites or fungi. The diseases can be spread directly or indirectly. In recent years, the spread of contagious diseases has been encountered largely by measures calculated to limit the more or less direct passage or carriage of infectious materials from the sick to others. Germs are transmitted primarily through direct or indirect contact, airborne or droplet secretion. Once transmitted, germs can survive for hours, even days in the environment, increasing the risk for infection significantly. Droplet infection is an infection transmitted from an infected person to an un-infected person through droplet secretions. We all produce these droplets after coughing or sneezing without covering our mouth and nose. The droplets travel through the air, and can either be breathed in, or land in a person's nose, mouth or eyes, which can cause an infection. The common cold is a viral infection of the upper respiratory tract and the virus (causing it) is typically transmitted through airborne droplets (aerosols), direct contact with infected nasal secretions or contaminated objects. Influenza can be spread in three main ways: (i) by direct transmission (when an infectious person sneezes mucus directly into the mouth, nose or eyes of another person); (ii) the airborne route (when someone inhales the aerosols produced by an infectious person coughing, sneezing or spitting) and (iii) through hand-to-mouth, hand-to-nose or hand-to-eye transmission (either from contaminated surfaces or from direct personal contact such as a hand-shake). Chickenpox is an airborne disease which spreads easily through coughing or sneezing of infectious individuals or through direct contact with secretions from the rash of an infectious person. A person having chickenpox is infectious 1–2 days before the rash appears and it remains contagious until all lesions have crusted over (this takes approximately 6 days). Mumps is a contagious disease that is spread from person to person through respiratory secretions, such as saliva from an infectious person. When an infectious person coughs or sneezes, the droplets aerosolize and can enter the mouth, nose or eyes of another person. Mumps can also be spread by sharing drinks and food. The virus causing it can also survive on surfaces and then be spread after contact in a similar manner. A person infected with mumps is contagious from approximately 6 days before the onset of symptoms until about 9 days after symptoms start and the incubation period (time until symptoms begin) is typically 16–18 days. Measles is a highly contagious viral disease and the virus causing it is spread by coughing and sneezing via close personal contact or direct contact with secretions.

Vaccination is a highly effective means of preventing these infections, one dose of vaccine does not protect all receivers because vaccine-induced immunity is lost after some period of time (Garly & Abay, 2003; Hethcote, 2000; Park, 2005; “Taber's Cyclopedic Medical Dictionary”, 1997). The waning for the vaccine-induced immunity suggested to specialists to implement booster course and it was seen that the booster programme enhanced the prevention rate from the disease. As for example, a clinical study on measles vaccination efficiency during an epidemic in Poland exhibits that the prevention caused by the first dose of vaccine was more than 90 and the prevention caused by the second dose of vaccine is more than 99 (Janaszek, Gay, & Gut, 2003).

Kribs-Zaleta and Martcheva (2002), Kribs-Zaleta and Velasco-Harnandez (2000), Moghadas (2004), Moghadas and Gumel (2003) and Hethcote (2000) analysed the effect of single dose vaccine programme applied to infectious individuals using mathematical modellings. Alexander, Moghadas, Rohani, and Summers (2006), Anderson and Grenfell (1986), Dietz (1981), Misra and Mishra (2009) and Paulo, Gomes, Casinhas, and Horta (2000) studied the impact of multiple dose vaccination programme on the dynamics of infectious diseases. Recently, Samanta (2011) has proposed and analysed a nonautonomous dynamical model of diseases that spread by droplet infection and also through direct contact with varying total population size and distributed time delay to become infectious.

The pulse vaccination strategy (PVS) consists of repeated application of vaccine at discrete time with equal interval in a population in contrast to the traditional constant vaccination (Gakkhar & Negi, 2008; Zhou & Liu, 2003). Compared to the proportional vaccination models, the study of pulse vaccination models is in its infancy (Zhou & Liu, 2003). At each vaccination time a constant fraction of the susceptible population is vaccinated successfully. Since 1993, attempts have been made to develop mathematical theory to control infectious diseases using pulse vaccination (Agur, Cojocaru, Mazor, Anderson, & Danon, 1993; Gakkhar & Negi, 2008). Nokes and Swinton (1995) discussed the control of childhood viral infections by PVS. Stone, Shulgin, and Agur (2000) presented a theoretical examination of the PVS in the SIR epidemic model and d'Onofrio (2002a, 2002b) analysed the use of pulse vaccination policy to eradicate infectious disease for SIR and SEIR epidemic models. Different types of vaccination policies and strategies combining pulse vaccination policy, treatment, pre-outbreak vaccination or isolation have already been introduced by several researchers (Babiuk, Babiuk, & Baca-Estrada, 2002; d'Onofrio, 2005; Gao, Chen, Nieto, & Torres, 2006; Gao, Chen, & Teng, 2007; Gjorrgjieva et al., 2005; Tang, Xiao, & Clancy, 2005; Wei & Chen, 2008; Zhang & Teng, 2008).

Epidemic models through ordinary differential equations were analysed by a number of scientists (Anderson & May, 1992; Brauer & Castillo-Chavez, 2001; Cai, Li, Ghosh, & Guo, 2009; Capasso, 1993; Diekmann & Heesterbeek, 2000; Kermack & Mckendrick, 1927; Ma, Song, & Takeuchi, 2004; Mena-Lorca & Hethcote, 1992; Meng, Chen, & Cheng, 2007; Naresh, Tripathi, & Omar, 2006; Takeuchi, Cui, Rinko, & Saito, 2006a, 2006b; Thieme, 2003; Zhang, Li, & Jin, 2015) to find the existence of the threshold values which distinguish whether the infectious disease will be going to die out, the local and global stability of the disease-free equilibrium and the endemic equilibrium, the existence of periodic solutions and the persistence of the disease.

In this paper we have considered a dynamical model of diseases that spread by droplet infection and also through direct contact with pulse vaccination and saturation incidence rate. It is assumed that the infection spreads through pathogens (bacteria and/or viruses) produced by droplets as well as by direct contact of individuals from infectious people. Also, it is assumed that there is a time lag due to incubation period of pathogens, i.e. the development of an infection from the time the pathogen enters the body until signs or symptoms first appear. It is also assumed that there is a time lag due to lose of immunity of recovered individuals which is equal to the interval between two pulses. However, the diseases incubate inside the host for a period of time before the host becomes infectious. Using a compartmental approach, it may be assumed that a susceptible individual first goes through a latent period (and is said to become exposed or in the class E) after infected. Because some successfully vaccinated susceptible individuals gradually lose their immunity after the bacterin (a suspension of killed or weakened bacteria used as a vaccine) is expired. We have introduced two threshold values and and further obtained that the disease will be going to extinct when and the disease will be permanent when . The important mathematical findings for the dynamical behaviour of the model are numerically verified using MATLAB and also epidemiological implications of our analytical findings are addressed critically in Section 5. The aim of the analysis of this model is to trace the parameters of interest for further study with a view to informing and assisting policy-maker in targeting prevention and treatment resources for maximum effectiveness.

2. Model derivation and preliminaries

In the following, we consider a dynamical model of diseases that spread by droplet infection and also through direct contact with discrete time delays and PVS which satisfies the following assumptions:

The underlying human population is split up into four classes (compartments), namely susceptible (S), exposed (infected but not yet infectious) (E), infectious (showing symptoms of disease) (I) and recovered (infectious people who have cleared (or recovered from) infection) (R). The compartment of pathogens (bacteria and/or viruses) which are produced by droplets of infectious individuals is denoted by P.

The susceptible population increases through birth and recovered hosts and decreases due to droplet infection, direct contact with infectious individuals, natural death and PVS.

Standard epidemiological models use a bilinear incidence rate based on the law of mass action (Anderson & May, 1979, 1992) and it is reasonable when the mixing of susceptible with infective (in infectious compartment) is considered to be homogeneous. If the population is saturated with infectious individuals, there are three types of incidence forms used in epidemiological model: the proportionate mixing incidence (Anderson & May, 1992; Cooke & van Den Driessche, 1996; Wang, 2002), nonlinear incidence (Hethcote & van Den Driessche, 1991; Hui & Chen, 2004) and saturation incidence (Anderson & May, 1992; May & Anderson, 1978) or (Ruan & Wang, 2003). Here incidence rates and have been considered.

The infectious class is increased by infection of susceptible. It is assumed that there is a time lag due to incubation period of pathogens, i.e. the development of an infection from the time the pathogen enters the body until signs or symptoms first appear. The infectious class is decreased through recovery from infection, by disease-related death and by natural death. Also, it is assumed that there is a time lag due to lose of immunity of recovered individuals which is equal to the interval between two pulses.

The infection spreads through pathogens produced by droplets from infectious people and also by direct contact with infectious individuals. Therefore, it is also assumed that the pathogen population has been generated through droplets of infectious people and is diminished due to natural death.

Thus, the following dynamical model of diseases that spread by droplet infection and direct contact with discrete time delays, saturation incidence and PVS is formulated: (1) where all coefficients are nonnegative constants. Here denotes the number of susceptible, denotes the number of exposed, denotes the number of infectious individuals, denotes the number of recovered and denotes the number of bacteria and/or viruses (pathogens) which are produced by droplets of infectious individuals. The pulse vaccination does not give life-long immunity, there is an immunity waning for the vaccination with the per capita immunity waning rate α, where implies that the recovered individuals would lose the immunity and implies that the recovered individuals is with the permanent immunity. Here, τ represents the latent period of the disease and in the term ‘’ denotes the immune period of recovered individuals. It is assumed that the immune period is equal to the interval between two pulses because some successfully vaccinated susceptible individuals gradually lose their immunity after the bacterin (a suspension of killed or weakened bacteria used as a vaccine) is expired (i.e. the period ). So, is also explained as the best time of losing immunity. Thus at time t, the proportion of the susceptible comes from the recovered compartment should be taken as . The probability that an individual in the immune period has survived is given by , where μ is the coefficient of natural death rate of all human classes. The influx of susceptible comes from two sources: a constant recruitment Λ and recovered hosts. The parameters are:

• : The coefficient of transmission rate from pathogens (bacteria and/or viruses) to susceptible humans through droplets due to droplet secretion and the rate of transmission of infection is of the form This is a more realistic incidence rate because .

• : The coefficient of transmission rate from pathogens (bacteria and/or viruses) to susceptible humans through direct contact with infectious person and the rate of transmission of infection is of the form This is a suitable incidence rate because .

• μ: The coefficient of natural death rate of all human classes.

• d: The coefficient of disease-related death rate of infective in infectious compartment.

• r: The coefficient of recovery rate of the individuals of the infectious class.

• τ: The constant latency period from the time of being infected (exposed) to the time of being infectious (capable of infecting others). The probability that an individual remains in the latency period (exposed class) at least t time units before becoming infectious is given by a step function with value 1 for and value zero for . The probability that an individual in the latency period has survived is given by . It is a more realistic probability distribution because it ensures that the death process is a Poisson process, which is a Markov process, with mean death rate μ.

• : The immune period of recovered individuals.

• η: The rate at which pathogens are produced by droplets of infectious individuals. Here we assume that and .

• δ: The natural death rate for pathogens that are produced by droplets of infectious individuals.

• : The fraction of susceptible who are vaccinated successfully at discrete time , which is called impulsive vaccination rate.

The total human population size can be determined by the following differential equation: (2) which is derived by adding first four equations of system (1(1) ). Therefore, (3)

Adding first five equations of system (1(1) ) we get, (4)

Let us simplify the model (1(1) ) as follows: (5) with initial conditions (6) where are nonnegative continuous functions on For a biological meaning, we further assume that The solution of system (5(5) ) and (6(6) ) is a piecewise continuous function is continuous on and exists. There exists a unique solution of (5(5) ) with initial conditions (6(6) ) since the right hand sides of Equation (5(5) ) and the pulse are smooth functions (Bainov & Simeonov, 1993, 1995; Lakshmikantham, Bainov, & Simeonov, 1989).

From biological considerations, we analyse systems (5(5) ) and (6(6) ) in the closed set (7) where represents the nonnegative cone of including its lower dimensional faces and It can be verified that G is positively invariant with respect to Equations (5(5) ) and (6(6) ).

Before starting our main results, we give the following four lemmas which will be essential for study.

Lemma 2.1

Kuang, 1993; Song & Chen, 2001

Consider the following equation: where for We have

Lemma 2.2

Kuang, 1993

Consider the following equation: where for We have

Lemma 2.3.

Consider the following impulsive differential equation: (8) where Then there exists a unique positive periodic solution of system (8(8) ) and is globally asymptotically stable.

Proof.

From the first equation of system (8(8) ) we get where is the initial value at time kT. Using the second equation of system (8(8) ) we have the following stroboscopic map: (9) where . Solving the following equation:

Since as 0<p<1 and b>0, the system (9(9) ) has a unique positive equilibrium which is globally asymptotically stable. Hence the corresponding periodic solution of system (8(8) ) is globally asymptotically stable. This completes the proof.

Lemma 2.4

Zhang & Teng, 2008

Consider the following impulsive differential equation: (10) where Then there exists a unique positive periodic solution with period of system (10(10) ) which is globally asymptotically stable.

3. Global stability of the disease-free periodic solution

In this section, we discuss the existence of the disease-free periodic solution of system (5(5) ), in which infectious individuals and pathogens are completely absent, that is, and Under this circumstances, system (5(5) ) reduces to the following impulsive system: (11)

From the third and sixth equations of system (11(11) ), we have .

Further, from the second and seventh equations of system (1(1) ) it follows that:

In the following, we shall show that the susceptible population and recovered population oscillate with period , in synchronization with the periodic impulsive vaccination strategy under some condition. Consider the following limit system of system (11(11) ) as per the previous discussions (12)

Using Lemma 2.4, the system (12(12) ) has a unique positive periodic solution with period if , which is globally asymptotically stable. Let us denote this periodic solution by . (13)

Theorem 3.1.

If and then the disease-free periodic solution of system (5(5) ) with initial conditions (6(6) ) is globally asymptotically stable.

Proof.

Since , we can choose small enough such that (14)

From the first and sixth equations of Equation (5(5) ), it follows that:

So, we consider the following comparison impulsive differential system: (15)

By Lemma 2.3, we know that the periodic solution of system (15(15) ) (16) is globally asymptotically stable. Let be the solution of system (5(5) ) with initial conditions (6(6) ) and . If be the solution of system (16(16) ) with initial value , then by the comparison theorem for impulsive differential equation (Lakshmikantham et al., 1989) there exists an integer such that (17)

Further, from the second and fifth equations of system (5(5) ), we have and (18)

Consider the following comparison equation: (19)

From Equation (14(14) ), we have (20)

Set be the solution of system (5(5) ) with initial conditions (6(6) ) and be the solution of Equation (19(19) ) with initial condition By the comparison theorem of differential equation and the positivity of solution (with ), we have (21)

Hence for any (sufficiently small), there exists a positive integer , where , such that Using the fourth equation of system (5(5) ), we get (22) Now,

So, by the comparison theorem, there exists an integer such that (23)

It follows from Equations (21(21) ) and (23(23) ) that there exists an integer such that (24)

Therefore, from the second equation of system (1(1) ), we have (25)

It is clear that there exists an integer such that (26)

Let . Therefore, using Equations (12(12) ), (24(24) ), (26(26) ) and the first equation of Equation (5(5) ), there exists an integer such that between two pulses (27)

Let us consider the following delayed differential equation: (28)

Using Equations (27(27) ), (28(28) ) and Lemma 2.2, we get () where is the solution of Equation (28(28) ) with initial condition for . Hence, there exists an integer such that (29)

As can be arbitrarily small, it follows from Equations (26(26) ) and (29(29) ) that (30)

Finally, it follows from Equations (21(21) ), (23(23) ) and (30(30) ) that if and , then the disease-free periodic solution of system (5(5) ) with initial conditions (6(6) ) is globally asymptotically stable. This completes the proof.

4. Permanence of the disease

In this section, we wish to discuss the permanence of the disease of system (5(5) ), this means that the long-term survival (i.e. will not vanish in time) of the sum of the numbers of infectious population and pathogen population () of system (5(5) ) with initial conditions (6(6) ). It demonstrates how the disease will be permanent (i.e. will not vanish in time) under some conditions.

Definition 1.

The disease in system (5(5) ) is said to be permanent, i.e. the long-term survival (will not vanish in time) of the sum of the numbers of infectious population and pathogen population () of system (5(5) ) with initial conditions (6(6) ), if there exists a positive constant m such that hold for any solution of Equation (5(5) ) with initial conditions (6(6) ).

Theorem 4.1.

If then there exists a positive constant m such that each positive solution of system (5(5) ) with initial conditions (6(6) ) satisfies for sufficiently large time t, where (31)

Proof.

From the second and fifth equations of system (5(5) ), we have (32) where .

Define, (33) Define, (34) for a sufficiently small

Let us claim that there exists a such that . Otherwise, there exists a such that . It follows from the first and sixth equations of Equation (5(5) ) (35)

Let us consider the following comparison impulsive differential system : (36)

By Lemma 2.3, we know that the periodic solution of system (36) is (37) which is globally asymptotically stable.

By the comparison theorem for impulsive differential equation (Lakshmikantham et al., 1989), there exists such that the following holds: (38) (39)

Otherwise, there exists a such that , where and However, from Equations (32), (34) and (38), we get (40)

So, we have got a contradiction and hence As a consequence of Equations (33), (34), (38) and (39), we get (41)

This is a contradiction because (42)

Therefore, we conclude for any , the inequality cannot hold for all Thus we are left to consider the following two cases:

1. for sufficiently large t;

2. oscillates about for sufficiently large t.

It is clear that if for sufficiently large t, then our desired result is obtained. So, we only need to consider the case (ii). Let (43)

Now, we will show that for sufficiently large t. Let and satisfy and for , where is sufficiently large such that for . It is clear that is uniformly continuous since the positive solution of Equation (5(5) ) is ultimately bounded and is not affected by impulsive effects. Hence there exists a constants , where and is independent of , such that for If , the required result is obtained. If since and , it follows that for . If ; we have for and by using the same arguments we can obtain for as the interval can be chosen arbitrarily. So, we can conclude that for sufficiently large t. On the basis of the previous discussions, the choice of m is independent of the positive solution of Equation (5(5) ) and hence any positive solution of Equation (5(5) ) satisfies for t large enough. This completes the proof.

Remark 1.

Unfortunately, we cannot establish the comparison of and . When , the dynamical behaviour of model (5(5) ) and (6(6) ) has not been clear. These works will be left as a part of our future consideration.

5. Numerical simulations and biological interpretations

Here we have done some numerical simulations using MATLAB. We first consider the case when using the parameter values given in Table 1. Using these parameter values, the movement paths of and are presented in Figure 1(a). This figure shows that the disease dies out when which supports our analytical result given in Theorem 3.1. Its epidemiological implication is that the infectious population vanishes, i.e. 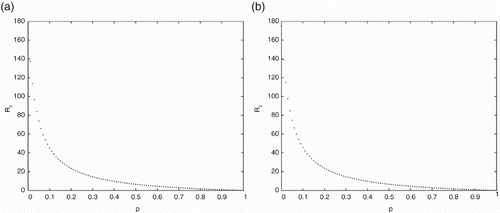the disease dies out when (see Figure 1(a)). In Figure 1(b), the effects of pulse vaccination on the threshold value is presented using the parameter values given in Table 1. It shows that the threshold values gradually decrease when the pulse vaccination rate increases. This implies that the strategy of pulse vaccination is very effective to eradicate the diseases spread by droplet infection and also through direct contact.

Figure 1. (a) Movement paths of and for (b) the effects of pulse vaccination on the threshold value with parameter values given in Table 1.

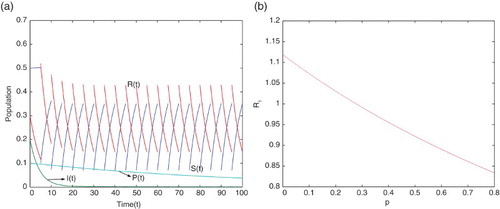
Table 1. Parameter values for figures 1(a), 1(b), 4(a) & 4(b).

Parameter	Values
Λ	0.1
	0.03
	0.01
	0.8
	0.7
μ	0.2
α	0.02
r	0.04
d	0.001
η	0.002
δ	0.01
	5
τ	0.1
p	0.8

Next, we consider the case when using the parameter values given in Table 2. Using these parameter values, the movement paths of and are presented in Figure 2(a). This figure shows that the disease will be permanent when which supports our analytical result given in Theorem 4.1. In Figure 2(b), the effects of pulse vaccination on the threshold value is presented using the parameter values given in Table 2. It shows that the threshold values gradually decrease when the pulse vaccination rate increases. This also implies that the strategy of pulse vaccination is very effective to eradicate the diseases.

Figure 2. (a) Movement paths of and for (b) the effects of pulse vaccination on the threshold value with parameter values given in Table 2.

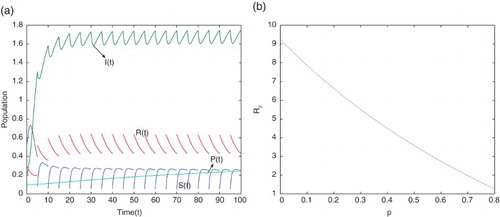
Table 2. Parameter values for figures 2(a), 2(b), 3(a), 3(b), 5(a) & 5(b).

Parameter	Values
Λ	0.5
	0.96
	0.95
	0.2
	0.1
μ	0.2
α	0.02
r	0.04
d	0.001
η	0.002
δ	0.01
	5
τ	0.1
p	0.8

We also consider the case when and with , , and other parameter values are values given in Table 2. Using these parameter values, the movement paths of and are presented in Figure 3(a). This figure shows that the disease dies out. For and where , and other parameter values are given in Table 2, the movement paths of and are presented in Figure 3(b). This figure shows that the disease is still permanent.

Figure 3. Movement paths of and (a) for and with and other parameter values are values given in Table 2, (b) for and where , and other parameter values are given in Table 2.

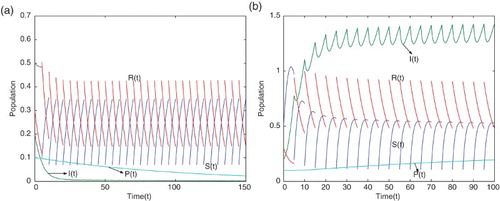
From the figures it is observed that a large pulse vaccination rate will lead to eradication of the diseases.

In Figure 4, the effects of pulse vaccination on the threshold value is presented using the parameter values given in Table 1. The effects of pulse vaccination on the threshold value is presented in Figure 5, using the parameter values given in Table 2. Figures 4 and 5 show that the threshold values and gradually decrease when the pulse vaccination rate increases. This implies that the strategy of pulse vaccination is very effective to eradicate the diseases.

Figure 4. The effects of pulse vaccination on the threshold value with parameter values given in Table 1 for (a) with delay and (b) without delay .

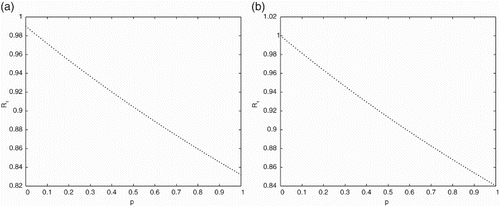
Figure 5. The effects of pulse vaccination on the threshold value with parameter values given in Table 2 for (a) with delay and (b) without delay .

From the figures it is observed that to eliminate the disease, the PVS and the time delay of disease should be considered at the same time.

Remark 2.

It is noticed that and . When , the dynamical behaviour of the epidemic model (5(5) ) and (6(6) ) has not been clear. This indicates that and cannot be unified as one parameter.

6. Conclusions

In this paper we have considered a dynamical model of diseases that spread by droplet infection due to droplet secretion and also through direct contact with discrete time delays, PVS and saturation incidence rate. The underlying human population is split up into four classes (compartments), namely susceptible (S), exposed (infected but not yet infectious) (E), infectious (showing symptoms of disease) (I) and recovered (infectious people who have cleared (or recovered from) infection) (R). The compartment of pathogens (bacteria and/or viruses) which are produced by droplet secretion of infectious individuals is denoted by P. The susceptible population increases through birth and recovered hosts and decreases due to droplet infection, direct contact with infectious individuals, natural death and PVS. The infected class is increased by infection of susceptible. It is assumed that there is a time lag due to incubation period of pathogens, i.e. the development of an infection from the time the pathogen enters the body until signs or symptoms first appear. The infected class is decreased through recovery from infection, by disease-related death and by natural death. The infection spreads through pathogens produced by droplets from infectious people and also by direct contact with infectious individuals. Therefore, it is assumed that the pathogen population has been generated through droplets of infectious people and is diminished due to natural death. It is also assumed that there is a time lag due to lose of immunity of recovered individuals which is identical to the interval between two pulses. Because some successfully vaccinated susceptible individuals gradually lose their immunity after the bacterin (a suspension of killed or weakened bacteria used as a vaccine) is expired. The most basic and important questions to ask for the systems in the theory of mathematical epidemiology are the persistence, extinctions, the existence of periodic solutions, global stability, etc. Here, we have established some sufficient conditions on the permanence and extinction of the disease by using inequality analytical technique. We have introduced two threshold values and and further obtained that the disease will be going to extinct when and the disease will be permanent when . The important mathematical findings for the dynamical behaviour of the diseases spread by droplet infection and also through direct contact are also numerically verified using MATLAB. It is observed that a large pulse vaccination rate will lead to eradication of the disease and when , the dynamical behaviour is not clear. The aim of the analysis of this model is to trace the parameters of interest for further study, with a view to informing and assisting policy-maker in targeting prevention and treatment resources for maximum effectiveness.

Acknowledgments

The authors are grateful to the anonymous referees and Professor Zidong Wang (Executive Editor) for their careful reading, valuable comments and helpful suggestions, which have helped them to improve the presentation of this work significantly. The first author is grateful to Prof. Javier Bracho Carpizo, Prof. Marcelo Aguilar and Prof. Ricardo Gomez Aiza, Institute of Mathematics, National Autonomous University of Mexico for their helps and encouragements.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The first author likes to thank TWAS, UNESCO and National Autonomous University of Mexico (UNAM) for financial support.