Robust H_∞ control for delayed systems with randomly varying nonlinearities under uncertain occurrence probability via sliding mode method

ABSTRACT

In this paper, we address the problem of robust sliding mode control (SMC) for a class of discrete-time stochastic systems with parameter uncertainties, time-varying delay and randomly varying nonlinearities (RVNs) under uncertain occurrence probability. Here, the norm-bounded parameter uncertainties are considered. The time-varying delay is bounded with known upper and lower bounds. In addition, the RVNs are depicted by using a Bernoulli distributed stochastic variable with uncertain occurrence probability. The aim of the paper is to provide an SMC method such that, for all parameter uncertainties, time-varying delay and RVNs, the robust asymptotic stability with a prescribed disturbance attenuation level is guaranteed for the sliding mode dynamics by providing a new sufficient condition. Moreover, the reachability analysis is carried out simultaneously, i.e. the states of the closed-loop system are driven onto a neighborhood of pre-designed sliding surface by synthesizing a robust sliding mode controller. Finally, the usefulness of the aforementioned control technique is verified by a numerical example.

KEYWORDS:

• Discrete delayed systems
• stochastic systems
• sliding mode control
• randomly varying no nlinearities
• uncertain occurrence probability

1. Introduction

Over the past decades, as a useful robust control method, the sliding mode control (SMC) has been extensively investigated and applied in engineering systems because of its attractive invariant properties (Choi, 2007; Davila, Fridman, & Levant, 2005; Foo & Rahman, 2010; Gao & Hung, 1993; Grema & Cao, 2017; Lee, Kim, & Sastry, 2009; Li, Yu, Hilton, & Liu, 2013), such as the insensitiveness to time-varying parameter perturbations and disturbances on prescribed sliding surface. According to the structural characteristic between various systems, a great number of methods have been proposed to copy with the robust control problems via SMC method, see e.g. Choi (2010), Hu, Wang, Niu, & Gao (2014), Gao, Wang, & Homaifa (1995) and Niu, Ho, & Lam (2005). Note that the digital control algorithms have commonly been used in the modern industrial fields, hence it has been prevalent for the SMC design of discrete control systems (Gao et al., 1995; Hu et al., 2014). For example, the robust SMC scheme has been given in Hu et al. (2014) for discrete-time nonlinear Markovian jump systems (MJSs). In Gao et al. (1995), the quasi-sliding mode has been discussed and the problems of the analysis and its engineering application have been extensively considered for discrete-time systems (Ma, Wang, Bo, & Guo, 2012).

As it is well known, the time-delays are often encountered in many physical systems during the signal transmissions, the signal judgment and computations (Bahreini & Zarei, 2016; Gholami & Binazadeh, 2018; Hu et al., 2014; Liu, Liu, Obaid, & Abbas, 2016; Yuan, Yuan, Wang, Guo, & Yang, 2017). The existence of the time-delays indeed leads to deteriorate the control system performance (Ding, Wang, Shen, & Dong, 2015; Hu, Wang, Gao, & Stergioulas, 2012a; Li, Dong, Han, Hou, & Li, 2017; Li, Shen, Liu, & Alsaadi, 2016; Niu & Ho, 2006). Hence, much effort has been devoted to eliminating the negative effects of time-delays onto whole system performance and a great number of SMC techniques have been developed for delayed systems with different types of time-delays, see e.g. Qi, Park, Cheng, & Kao (2017), Jiang, Kao, & Gao (2017), Hu, Wang, Gao, & Stergioulas (2012b) and Wu, Su, & Shi (2012). To be specific, the problem of robust stabilization has been tackled in Qi et al. (2017) for semi-MJSs with time-varying delays via SMC method. In Jiang et al. (2017), the integrator-based robust SMC method has been proposed for stochastic MJSs with slow time-varying delays. Recently, based on the delay-fractioning approach, a unified SMC framework has been established in Hu et al. (2012b) for discrete uncertain stochastic systems with mixed time-delays (discrete time-varying delays and distributed delays) and randomly occurring nonlinearities (RONs) satisfying the section-bounded conditions.

On the other hand, it is well known that additive nonlinearities and disturbances, if not properly addressed, may degrade the whole performance of the dynamical system (Hu, Liu, Ji, & Li, 2016; Hu, Wang, & Gao, 2011; Wang, Ding, Dong, & Shu, 2013; Wang, Wang, & Liu, 2010; Wang, Yaz, Schneider, & Yaz, 2017; Zou, Wang, Han, & Zhou, 2017). As such, a large number of control methods have been developed to tackle the SMC problem for systems with nonlinearities and disturbances, see e.g. Hu et al. (2011), Wang, Chan, Hsu, & Lee (2002) and Zhang, Su, & Lu (2015). The so-called RONs have first been introduced in Wang et al. (2010) to model the stochastic disturbances in networked environment. Subsequently, the robust SMC approach has been developed in Hu et al. (2011) for a class of stochastic systems with RONs via the delay-fractioning approach, where sufficient condition has been given to ensure the stability of sliding motion and proper SMC law has been synthesized. It is worth pointing out that the randomly varying nonlinearities (RVNs) have gained certain research interest especially in networked environment (Ding et al., 2015; Li et al., 2017). In particular, due to the inaccuracy of the statistical tests or other reasons, there is a need to model the RVNs with uncertain occurrence probability in a mathematical way (Zhang, Hu, Zhang, & Chen, 2017). Recently, the robust SMC method has been given in Zhang et al. (2017) for discrete systems with RVNs and time-varying delay. However, the robust SMC problem has not been addressed for discrete delayed stochastic systems with RVNs under uncertain occurrence probability, which motivates the current investigation with hope to further extend the existing result in Zhang et al. (2017).

Motivated by the above discussions, in this paper, we aim to solve the robust SMC problem for a class of discrete systems with parameter uncertainties, time-varying delay and RVNs under uncertain occurrence probability. A linear sliding surface is firstly defined. Then, sufficient conditions are established such that the system dynamics in the specified sliding surface is robustly asymptotically stable with a given performance, where the desired performance requirements can be realized by checking the feasibility of some LMIs and an equality constraint. Subsequently, a computational algorithm is presented to convert the original non-convex problem to an optimization one. The contributions of this paper can be listed as follows: (i) the systems addressed are more comprehensive, where the parameter uncertainties, time-varying delay as well as RVNs are considered in a same framework; (ii) the problem of SMC is discussed for addressed systems with RVNs under uncertain occurrence probability for the first time; and (iii) a new SMC scheme is provided to check the effects from the parameter uncertainties, time-varying delay, and RVNs under uncertain occurrence probability onto whole system performance. Finally, simulations are used to illustrate the usefulness of the proposed robust SMC scheme.

2. Problem formulation and preliminaries

Consider the following discrete uncertain system with time-varying delay and RVNs: (1) where is state of the system, is the control input, represents the controlled output, is the time-varying delay where and are known upper and lower bounds. denotes the matched nonlinearity. A, , B, C, , , , and are known matrices. is the exogenous disturbance.

The matrices and represent the mismatched norm-bounded uncertainties satisfying: (2) where , are known matrices, and are unknown matrices with . The are nonlinear functions satisfying the following sector-bounded conditions: (3) where matrices and are known matrices with proper dimensions and . is a 0-1 distributed stochastic variable with (4) where , is a known scalar, satisfies with ε being a certain constant and . Then, we have (5)

Remark 2.1

In (4(4) ), the stochastic variable obeying the Bernoulli distribution is introduced to characterize the so-called RVNs satisfying the sector-bounded conditions (3(3) ). Here, is utilized to characterize the uncertain occurrence probability, and the exact probability of may not easily be obtained probably due to the inaccuracy of the statistical tests or other reasons. Such a description can better reflect the case when the system is influenced by unpredictable factors, which would frequently happen in a probabilistic way. In fact, the introduction of could provide an extension of the description of RVNs within stochastic settings and the traditional modelling way of RVNs can be easily obtained by simply setting .

To proceed, we introduce the following assumptions.

Assumption 2.1

The nonlinear function is Euclidean norm-bounded.

Assumption 2.2

The matrix B is assumed to be full column rank.

The purpose of the paper is to propose a novel robust SMC law such that, for the simultaneous presence of norm-bounded uncertainties, time-varying delay, and RVNs under uncertain occurrence probability, both (Q1) and (Q2) can be satisfied, where

1. the state trajectories of system (1(1) ) are driven onto the designed sliding surface in finite time and, subsequently, the sliding motion is robustly asymptotically stable in mean square sense;

2. when , the output satisfies (6)

with and being a prescribed scalar.

Generally, we aim to design an SMC law by taking two steps: (i) design a discrete sliding surface and propose sufficient conditions to guarantee the robust asymptotic stability in mean square sense of the corresponding sliding mode dynamics with a prescribed performance; and (ii) synthesize the control law to guarantee the reachability of the sliding surface and restrict the system trajectories within a specified neighborhood of defined sliding surface thereafter.

Before ending this section, we give the following lemmas to facilitate further theoretical developments.

Lemma 2.1

For any real vectors a, b and matrix P>0 of appropriate dimensions, we have (7)

Lemma 2.2

Schur complement

Given constant matrices where and then if and only if (8)

Lemma 2.3

Let M and N be real matrices of compatible dimensions. Then for all F satisfying if and only if there exists a constant such that or, equivalently, (9)

3. Main results

In this section, we aim to deal with the design problem of robust sliding mode controller for addressed delayed systems in presence of parameter uncertainties, RVNs and external disturbances. A switching surface is firstly presented. Then, the robust asymptotic stability in mean square sense of the corresponding sliding mode dynamics with a pre-defined performance is ensured by providing a sufficient condition in terms of an LMI with an equality constraint. Subsequently, a computational algorithm is provided with help to convert the original non-convex problem into a minimization problem. In addition, a discrete sliding mode controller is presented to guarantee the reachability condition.

3.1. Switching surface

Similar to Hu et al. (2012a), we define the following linear switching function: (10) where constant matrix is designed later such that GB is non-singular and , here . In what follows, we select with P>0 to ensure the non-singularity of GB.

Note that the ideal quasi-sliding mode satisfies (11) Then, the equivalent control law can be derived from (1(1) ), (10(10) ) and (11(11) ) as follows: (12) Substituting (12(12) ) as into (1(1) ), the sliding mode dynamics equation is obtained as (13)

Now, we are ready to propose the robust asymptotic stability condition in mean square sense for the resulted closed-loop system (13(13) ) via the Lyapunov stability theorem.

Theorem 3.1

The sliding mode dynamics (13(13) ) with is robustly asymptotically stable in mean square sense if there exist matrices Q>0 and scalar satisfying (14) (15) where

Proof.

Choose the following Lyapunov-Krasovskii functional: (16)

where with P>0 and Q>0 being matrices to be determined. Then, the difference of along the system trajectory (13(13) ) can be expressed as (17) where (18) with . By applying Lemma 2.1, it follows that (19) (20) (21) (22) (23) Hence, substituting (19(19) )–(23(23) ) into (18(18) ) yields (24) Similarly, it can be inferred that (25) (26) Thus, it follows from (24(24) )–(26(26) ) that (27) where (28) Considering (3(3) ), we have (29) Then, it is not difficult to obtain (30) where (31) Subsequently, noting and employing Lemma 2.2, is equivalent to (32) where where are defined in (28(28) ), and are defined in (31(31) ).

Furthermore, rewrite matrix by (33) where By using Lemmas 2.2 and 2.3, it is obtained that matrix can guarantee matrix . Further, we imply , then . Therefore, it can be concluded that the sliding mode dynamics (13(13) ) is robustly asymptotically stable in mean square sense. Then, the proof of Theorem 3.1 is complete.

Subsequently, a unified framework is presented to ensure the robust mean-square asymptotic stability of the sliding mode dynamics (13(13) ) with a prescribed performance.

Theorem 3.2

For a pre-specified scalar the sliding mode dynamics (13(13) ) is robustly mean-square asymptotically stable with disturbance attenuation level γ if there exist matrices Q>0 and scalar satisfying (34) (35) where

Proof.

Clearly, implies . According to Theorem 3.1, the robust mean-square asymptotic stability of the sliding mode dynamics is achieved.

Next, let us handle the performance of the dynamics under consideration. Choose the same Lyapunov-Krasovskii functional as in Theorem 3.1. Then, the following inequality is derived by a similar difference calculation, (36) where (37) , and are defined below (35(35) ).

To copy with the performance analysis of the sliding mode dynamics (13(13) ), the following index is introduced: (38) Obviously, we aim to demonstrate when . It is easy to see that (39) where is defined in (28(28) ). From Lemmas 2.2 and 2.3, it is derived from (34(34) ) that and . Letting , we have (40) which completes the proof of Theorem 3.2.

Remark 3.1

In Theorem 3.2, a sufficient condition is given to ensure the robust mean-square asymptotic stability of the sliding mode dynamics with a prescribed performance. However, it is worth mentioning that there exists an equality constraint (35(35) ) and it is not easy to check the feasibility of the proposed method. Via the subsequent algorithm, a minimization problem is provided to verify the desired performance requirements.

3.2. Computational algorithm

It should be noted that the result in Theorem 3.2 is non-convex because of the equality constraint in (35(35) ). According to the method as in Niu et al. (2005); Niu, Ho, & Wang (2007), the equality can be equivalently described by . We now present the following inequality with . By utilizing the Schur complement, it follows that (41) Then, the original SMC problem is changed to following equivalent minimization problem: (42)

3.3. Design of sliding mode controller

In this subsection, based on the reaching condition in Gao et al. (1995), we are ready to synthesize an SMC law and conduct the reachability analysis of the specified sliding surface.

As in Gao et al. (1995), the desired performance can be achieved if the following reaching condition holds, (43) where, κ is the sampling period, and , here and are properly chosen scalars satisfying .

Recall that and in (2(2) ) and in Assumption 2.1 are bounded in terms of Euclidean norm. As in Hu et al. (2012b), set , and . Then , , and are also bounded. Naturally, we suppose that there exist known bounds , , , and satisfying (44) where , and are the ith element in , and , respectively. Define (45) Next, we are in a position to synthesize the discrete-time robust sliding mode controller and then ensure the reachability.

Theorem 3.3

Suppose that the problem (42(42) ) is solvable. If the sliding surface is presented by (10(10) ) with and P is the solution to (42(42) ), then the following sliding mode controller (46) can ensure the discrete reaching condition of specified sliding surface (10(10) ).

Proof.

The proof of this theorem is omitted for simplicity.

Remark 3.2

In this paper, the robust SMC problem has been studied for discrete stochastic systems with parameter uncertainties, time-varying delay and RVNs under uncertain occurrence probability. Up to know, new sufficient condition has been given to ensure the stability analysis of the sliding mode dynamics and the sliding mode controller has been designed, i.e. (Q1) and (Q2) have been satisfied, which ensure the desired performance requirements. Compared with published results, we need to deal with the difficulties from the parameter uncertainties, time-varying delay and RVNs simultaneously. Hence, we make efforts to attenuate the effects from mentioned factors onto whole system performance and propose an easy-to-verify sufficient criterion via the stochastic analysis technique. In particular, the related information of the mentioned factors is clearly reflected in Theorem 3.2, e.g. the matrices , and scalars , ε are there for RVNs subject to uncertain occurrence probability, the scalars and reflect the time-varying delay, and the matrices , , and account for the parameter uncertainties.

4. An illustrative example

In this section, we give an example to verify the effectiveness of the obtained method. Consider system (1(1) ) with the following parameters: In the simulation, set where and are the ith element of . Let , , , , , and Then, the solution to the minimization problem (42(42) ) can be expressed as

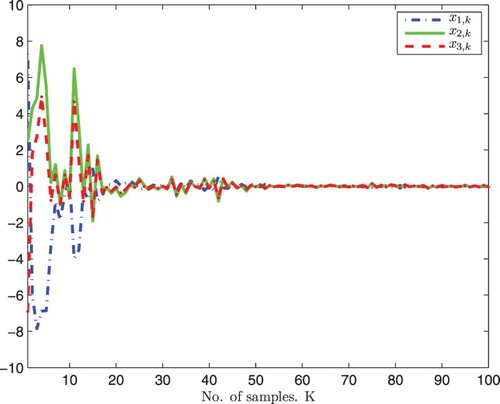
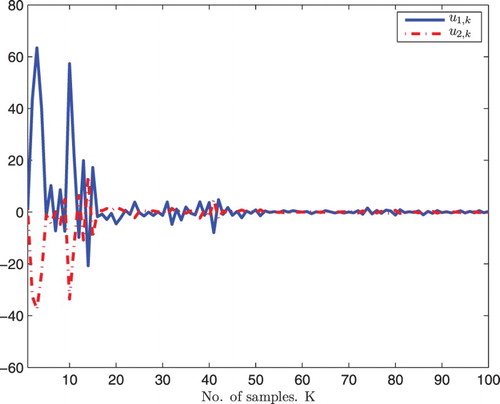
Selecting and , then all parameters in the sliding mode controller (46(46) ) are obtained. Then, the simulation results can be given in Figures 1–5. Among them, Figure 1 shows the state responses of the system where , and converge to a small neighborhood of zero quickly. The control input is plotted in Figure 3 and the time-delay is plotted in Figure 4. 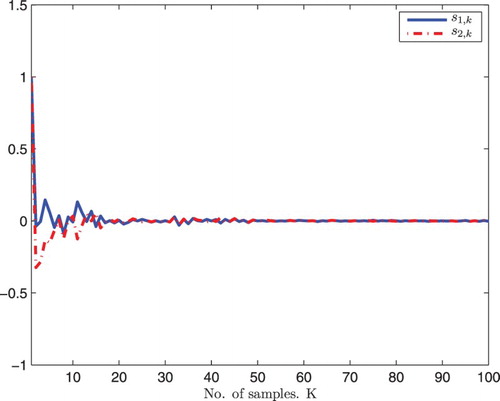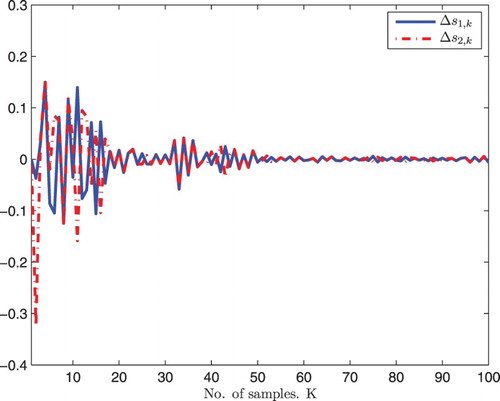Besides, the sliding mode function and signal are respectively presented in Figures 2 and 5. From the simulations, we can see that the control scheme obtained performs well.

Figure 1. The trajectory of state .

Figure 2. The trajectory of sliding variable .

Figure 3. The control signal .

Figure 4. The time-varying delay .

Figure 5. The signal .

5. Conclusions

In this paper, the robust SMC problem has been discussed for uncertain delayed systems with RVNs under uncertain occurrence probability. The phenomenon of RVNs has been modeled by a Bernoulli distributed stochastic variable with uncertain occurrence probability. Firstly, a linear sliding surface has been constructed. Secondly, sufficient conditions have been established to ensure robust mean-square asymptotic stability of the sliding mode dynamics with a prescribed performance. Subsequently, a minimization algorithm has been proposed for convenience of checking the feasibility of the proposed scheme and an SMC law has been constructed to ensure the reachability condition. It should be mentioned that the parameter matrices in the sliding surface and the synthesized SMC law can be obtained by solving an optimal problem. Finally, a numerical example has been given to demonstrate the feasibility of the obtained SMC scheme. It is worthwhile to point out that it is of significant importance to analyze and design the dynamical systems when the information is transmitted by limited network resources. Hence, further research topics include the extensions to the robust SMC problem for systems with communication protocols as in Zou, Wang, Gao, & Alsaadi (2017) and Zou, Wang, Hu, & Gao (2017), the event-triggered scheme in Dong, Wang, Shen, & Ding (2016) and the incomplete measurements in Geng, Liang, Liu, & Alsaadi (2018), Geng, Liang, Yang, Xu, & Pan (2017) and Geng, Wang, Cheng, & Alsaadi (2017) to improve the utilization of network resources.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Jun Hu http://orcid.org/0000-0002-7852-5064

Additional information

Funding

This work was supported in part by the National Natural Science Foundation of China under [grant number 61673141], the Fok Ying Tung Education Foundation of China under [grant number 151004], the University Nursing Program for Young Scholars with Creative Talents in Heilongjiang Province under [grant number UNPYSCT-2016029], the Postdoctoral Scientific Research Developmental Found of Heilongjiang Province of China under [grant number LBH-Q16120], the Science Funds for the Young Innovative Talents of HUST under [grant number 201508], and the Alexander von Humboldt Foundation of Germany.