Further results on robust H_∞ control design for uncertain time-delay systems with actuator delay: application to PMSG machine

ABSTRACT

The problem of robust state-feedback control design for a class of uncertain systems with two different time delays in the state vector and the input signal is investigated in this paper. The main feature of the paper is to develop a robust controller, which ensures the robust asymptotic stability of the system as well as the desired performance. By constructing a Lyapunov–Krasovskii functional, some sufficient conditions for the existence of the state-feedback controller is derived in terms of linear matrix inequalities. Numerical examples such as a wind energy conversion system model based on a permanent magnet synchronous generator model are provided to illustrate the effectiveness of the proposed method.

KEYWORDS:

• Robust control
• time-delay systems
• Lyapunov function
• input delay
• PMSG
• stability analysis

1. Introduction

The robust control design, as a well-known context, can handle model uncertainties and information constraints for dynamical systems have received a considerable amount of researchers’ interest in the past decades. Time delay, as one of the model complexity, can be found in various engineering systems such as chemical processes, biological systems, and economic systems. The problem of delay effects on the stability of systems including delays in the state, and/or input is of interest since the delay presence may induce complex behaviours (oscillation, instability, bad performances) for the schemes (Fiagbedzi & Pearson, 1986; Liu et al., 2017). Also uncertainty parametric are often the sources of instability and poor performance in many engineering systems, that considerable attention has been devoted to the problem of stability analysis and controller synthesis for uncertain systems (Mobayen & Baleanu, 2017).

In general, the stability criteria of time-delay systems (TDS) can be divided into two categories: delay-independent type (Pal & Negi, 2017; Zhang et al., 2017) and delay-dependent type (Lee, 2017; Aleksandrov et al., 2017; Pal & Negi, 2017). The earlier type is independent of delay size; and is generally conservative, especially when a delay is small. On the other hand, studies of delay-dependent criteria have focused mainly on identical delays in neutral and discrete terms (Aleksandrov, Hu, & Zhabko, 2014; Lu, Wu, & Bai, 2014; Yang, Wang, & Wang, 2017). Sun, Liu, and Chen (2009) studied the delay-dependent stability and stabilization criteria for neutral systems with time delays. The problem of robust stability of neutral systems with mixed time-varying delays has been studied in Lakshmananr, Senthilkumar, and Balasubramaniam (2011). Karimi and Gao (2010) presented a multiple delayed state-feedback control design for exponential synchronization problem of time-delay neural networks with multiple time-varying discrete delays. Karimi (2008) studied a convex optimization method for observer-based mixed control design of linear systems with time-varying state and output delays. Li, Jing, and Karimi (2014) studied the problem of output-feedback control for a class of active quarter-car suspension systems with time delay. Theoretically the controller can be solved by using the Lyapunov function method, however, there is no universal method to construct such kinds of Lyapunov functional. Sakthivel, Sakthivel, Selvaraj, and Karimi (2017) by using Lyapunov stability method and some integral inequality techniques a new set of sufficient conditions obtained in terms of linear matrix inequality (LMI) constraints to ensure the asymptotic stability of the considered system. The authors in Xie and Han (2008) presented a new method to obtain some robust stability conditions of uncertain linear systems with interval time-varying delay. This kind of approach can reduce the conservativeness compared with the existing results. Lyapunov theory is widely employed in the analysis and synthesis of a control system because of its effectiveness, and LMIs provide a powerful and efficient numerical tool for the stability analysis and computational aspects (Boyd, Ghaoui, Feron, & Balakrishnan, 1994).

Motivated by the above discussions, in this paper we have studied the problem of delay-dependent robust control for a class of uncertain systems with two different time-delay parameters in the state and input signals. The nonlinear uncertainties are supposed to be time-varying and norm bounded. A sufficient condition for the control problem is proposed in terms of the LMI approach using the Lyapunov functional. Numerical examples including a wind energy conversion system model based on a permanent magnet synchronous generator (PMSG) model are given to illustrate the feasibility and effectiveness of the proposed results.

The main contributions of the paper is twofold: (1) stability analysis and synthesis problems of dynamical system in the presence of mixed state and actuator delays which can reduce the conservativeness of the model to some extent from practical aspect; (2) dissemination of the stability analysis and synthesis results obtained in the paper on PMSG machine.

Notation. The notation in this paper is quite standard. The superscript ‘T’ stands for the transpose of a matrix; and denote an n-dimensional Euclidean space and the set of all nn real matrices, respectively; I is the identity matrix of appropriate dimension; is the Euclidean vector norm, and the symmetric terms in a symmetric matrix are denoted by *.

2. Problem formulation

In this section, a class of dynamical systems is considered with two different time-delay parameters in the state and control input as follows: (1a) (1b) (1c) where, are the state vector and the actuator output vector, respectively, and is the time delay in the state. are constant matrices with appropriate dimensions; the uncertainties , and represent the nonlinear perturbations with respect to the current state, the delayed states of the system and the actuator output, respectively. is a continuous vector-valued initial function and is an exogenous norm-bounded disturbance.

Before proceeding further, the following definitions and lemmas are reviewed.

Definition 2.1

The uncertain TDS of the form (1) is said to be robustly asymptotically stable in Lyapunov sense with an disturbance attenuation if system (1) with is robustly stable and moreover, under zero initial condition, there is (2)

Assumption 2.1

We suppose that the nonlinear uncertainties of the system, i.e. are bounded, i.e. (3a) (3b) (3c) where are positive scalars.

Remark 2.1

The nonlinear functions above can be interpreted as uncertainties in model dynamics representation and actuator mechanism in practice.

Lemma 2.1

(Schur complement). Let , be given matrices such that , then (4)

Lemma 2.2

Let , be real matrices of appropriate dimensions, and satisfying . Then, the following inequality holds for any constant :

The problem of control synthesis with the actuator delay we address here is as follows:

Given a prescribed level of disturbance attenuation and the actuator time-delay response d, find a control signal of the form with the actuation signal , where the matrix is to be determined in the sense of Definition 2.1.

3. performance analysis

In this section, we will focus on the asymptotic stability and performance analysis for the following system: (5a) (5b) (5c) where is a constant matrix with appropriate dimensions

Theorem 3.1

Under Definition 2.1 and Assumption 2.1, uncertain TDS (1) is asymptotically stable and fulfils performance condition (2) if there exist positive-definite matrices , and satisfying the following LMI: (6) where

Proof

Choose the following Lyapunov function: (7) with where, (i = 1, 2).

Calculating the time-derivative of we have the following time-derivatives of , that (8) (9) and (10) Then, from (7)–(9) and Assumption 2.1, one obtains (11) In the following, the disturbance attenuation in (2) can be written as (12) Considering we can obtain (13) From (10)–(12), it can be shown that (14) or where , and (15) With .

By using Schur complement in Lemma 1, we can rewrite (15) in the form of (5), which completes the proof.

4. Control design

This section is devoted to design the robust control for TDS in (1) in the presence of actuator delay.

Theorem 4.1

Consider uncertain TDS (1) with state delay and the actuator delay . The system (1) with a control input (16) is asymptotically stable and satisfies disturbance attenuation level , if there exist positive-definite matrices and matrix, and positive scalars such that the following LMI holds: (16) Then, the control feedback gain is obtained by (17)

Proof

By substituting the control signal (16) in (1), we have (18) According to Theorem 3.1 and by replacing with and with we can obtain (19) Because of nonlinear terms in (20) it should be changed to a linear form by pre-multiplying and post-multiplying to the matric inequality (20), and we can obtain (20) where .

Let and using Schur complement in Lemma 2.1. we can obtain the LMI in (17). This completes the proof.

Remark 4.1

The case of without input delay

Consider the following TDS with a delay in state vector only: (21a) (21b) (21c) Then, in the case of delay-free state-feedback control , the system (21a)–(21c) can be represented as (22a) (22b) (22c) Then, it can be similarly shown that the stability analysis and synthesis for system (22) will be met under a disturbance attenuation level if there exist positive-definite matrices , and matrix, and positive scalars such that the following LMI holds: (23) where . And, the control feedback gain is obtained by

5. Numerical example

In this section, the applicability of the proposed method is validated by three examples in the sequel.

Example 5.1

In this example, we consider the simulation of a wind energy conversion system model based on a PMSG model. It can be shown that by utilization of Park’s transformation to the (abc) coordinate frame PMSG model and linearizing the nonlinear model about an operating point, the following linear model in the d–q coordinate frame model can be obtained (Mittal, Sandhu, & Jain, 2012): (24) with and where and are the d- and q-axis stator voltage components; and are the d- and q-axis stator current components, respectively; and , are the stator inductance and resistance, respectively. is the flux, is the rotor electrical angular speed and P the number of the poles.

Assuming small deviation of resistance and inductance values from nominal corresponding values, we can represent the system (24) in the following form: (25) where and

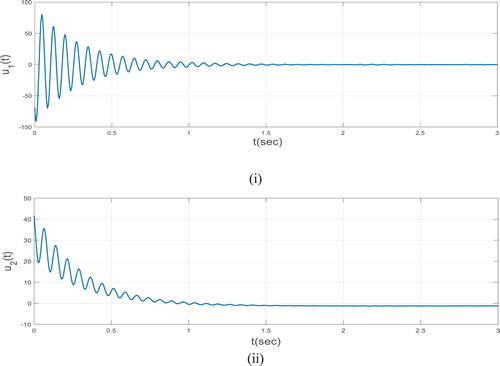
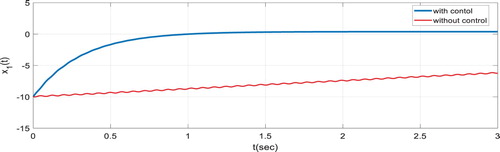
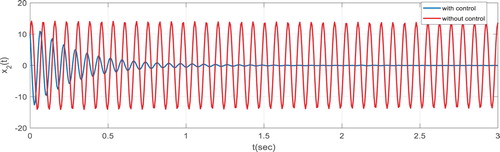
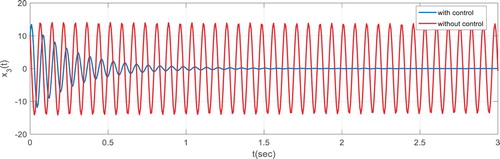
Consider the system (25) with the parameters of the WECS model in Table 1 and . For , , , by solving LMI (23) and in accordance to Remark 4.1, we can show the behaviour of input control signal in Figure 1 and state responses of both open-loop and closed-loop systems in Figures 2–4.

Figure 1. Input control signals.

Figure 2. State trajectory of d-axis current (with control–without control).

Figure 3. State trajectory of q-axis current (with control–without control).

Figure 4. State trajectory of rotational speed (with control–without control).

Table 1. WECS parameters.

	3.3 Ω
	41.56 ×  H
P	6
	4832 ×  V s

Example 5.2

Consider the system (1) with the following state-space matrices:

And , , .

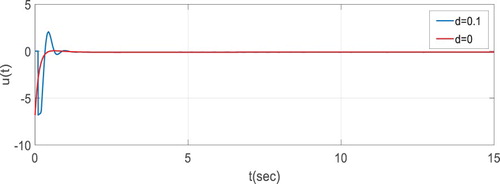
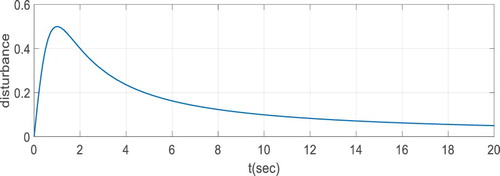
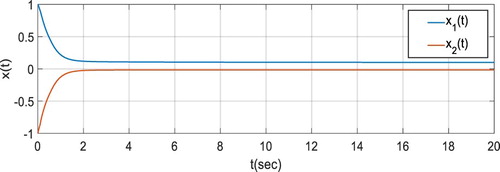
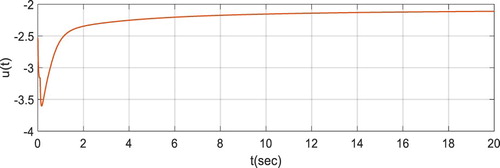
According to Theorem 4.1, the corresponding LMI is solved using Matlab LMI Toolbox, then the following solutions can be computed in the case of : With the state-feedback control gain  . In Figures 5–7, time behaviour of the disturbance, state system and control input are depicted. Both system stability and disturbance attention effect can be observed from the figures.

Figure 5 Time behaviour of the disturbance.

Figure 6. Time behaviour of state system.

Figure 7. Time behaviour of control input.

Example 5.3

Consider the model of system (22) with the following parameters: By choosing , and we can obtain a feasible solution to LMI (24), and compute the gain of state-feedback controller .

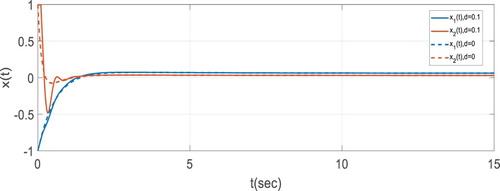
Then, for two different values of and we can show the behaviour of the states system and control input in Figures 8 and 9.

Figure 8. Time behaviour of states of system for two difference time delay.

Figure 9. Comparison of control input for two difference time delay.

5. Conclusion

In this paper, the problem of robust state-feedback control design for a class of uncertain systems with two different state delays has been considered. The Lyapunov stability theory and LMI have been used to guarantee the robust stabilization of the system under consideration. Also, a state-feedback controller has been explicitly computed. Moreover, an extension of the proposed problem to the case of delay in both the system state and input signals as the system actuator is presented and the corresponding control signal is developed. Finally, numerical examples such as a wind energy conversion system model based on a PMSG model are given to show the validity of the proposed methods. As further work, the method proposed in this paper will be examined within the event-triggered mechanism, see for instance Li, Shen, Liu, and Huang (2017), andWang, Wang, Shen, Li, and Alsaadi (2018).

Disclosure statement

No potential conflict of interest was reported by the author.