Novel identification algorithms for Hammerstein systems in ill-conditioned situations

Abstract

Two algorithms named Recursive Least Square algorithm for Ill-Conditioned situations (RLS-IC) and Multi Innovation Stochastic Gradient algorithm for Ill-Conditioned situations (MISG-IC) are proposed based on multi-innovation identification theory, least squares, stochastic gradient and singular value decomposition to identify Hammerstein systems in ill-conditioned situations. In ill-conditioned situations, identification algorithms based on classic least-squares and stochastic gradient lead to uncertain estimates and may be ineffective. Simulation examples show that the proposed algorithms are suitable for parameter estimation in Hammerstein nonlinear systems with ill-conditioned situations.

KEYWORDS:

• Nonlinear systems
• Hammerstein systems
• insufficient excitation
• multi-innovation identification theory
• singular value decomposition

1. Introduction

Since systems must be modelled very carefully in engineering studies, system identification is very important in engineering sciences (Chen & Hoo, 2013; Ding et al., 2014; Munyazikwiye et al., 2014). The identification of nonlinear systems is difficult and controversial and for this reason, engineers care about this area (Chaudhary & Raja, 2015; Ding, Wang, et al., 2016; Lin et al., 2015; Wang & Ding, 2015). The Hammerstein and Wiener models are a series combination of linear and nonlinear blocks. In a Hammerstein model, there is a static nonlinear block at first and then a dynamic linear block; however in a Wiener model, the order of the blocks will be changed. The Hammerstein model has been used in various fields of engineering and industrial sciences including bioelectric engineering, control engineering and chemical industries (Smith et al., 2007; Sung & Lee, 2004; Umoh & Ogunfunmi, 2010; Vörös, 1997; Wang & Zhang, 2015).

A common feature of most of the methods for the identification of Hammerstein systems is the creation of multipliers of linear and nonlinear block parameters in the parameters vector (Bai, 1998). This problem reduces the identification accuracy when the dimensions of parameter vectors are large. Some studies have been done in order to solve this problem in the identification of Hammerstein systems as follows. Shen et al. developed a parameters estimation algorithm for Hammerstein Multi-input Multi-output systems and presented an HGLS algorithm for the estimation of the parameters of the Hammerstein systems. In order to solve the problem of the cross-products between the parameters in the parameter vectors, a pseudo-linear identification model has been used by separating a key term from the output equation of the system (Shen & Ding, 2016). This algorithm has been inspired from the Least Squares algorithm (Ma, Xiong, et al., 2017; Shen & Ding, 2015). Mao et al. proposed an identification method for H–CARMA systems by using the adaptive filtering technique (Mao et al., 2016). Ding et al. obtained a new identification algorithm by using parameter separation, filtering technique and the multi-innovation identification theory, in order to solve the described problem and identification of Hammerstein systems (Mao & Ding, 2016). The Hammerstein model is a block-oriented model for describing systems. Researchers have investigated, saturation, preload, deadzone and backlash at the Hammerstein systems (Chen & Wang, 2015; Zhang et al., 2015). The linear block can be described by state space, transfer function, finite impulse response models (FIR) or infinite impulse response models (IIR) (Zhao et al., 2015; Zhao et al., 2016). In industry, time delay often exists in the inputs or outputs of systems. Some researchers have tried to identify Hammerstein systems with time delay. For example, Ma et al. presented an identification algorithm for Hammerstein systems with time delay in which systems are described by a state space model and the Kalman filter has been used for state estimation (Ma, Ding, et al., 2017). Zhang et al. modelled a nonlinear block with time delay by using neural network (Zhang et al., 2017). Some researchers have also identified time-delay systems using recursive algorithms (Atitallah et al., 2015; Elnaggar et al., 1989; Elnaggar et al., 1990).

Recursive least squares algorithm is one of the optimal methods for system identification. However, if excitation is insufficient, the covariance matrix becomes very large and the singularity problem will be created. A number of studies have been performed in the field of system identification in ill-conditioned situations by using singular value decomposition (SVD) and least squares (LS) algorithms (Deng et al., 2015; Zhang et al., 1994). A Damped Least Squares (DLS) method was also obtained for parameter estimation in ill-conditioned situations (Lambert, 1987). Some of the articles have examined the stability and convergence speed of the DLS method and derived a generalized Damped Least Squares (GDLS) algorithm (Evestedt & Medvedev, 2006; Yoo et al., 2003; Zengqiang et al., 2000). When excitation is sufficient, there are many methods to identify Hammerstein systems. Until now the issue of insufficient excitation for Hammerstein systems has not been investigated. In this paper, we will present new recursive algorithms by using eigenvector, eigenvalue, null space vector, least squares and multi-innovation identification theory for Hammerstein systems in ill-conditioned situations.

This article has the following structure. Section 2 introduces the identification problems for the Hammerstein systems with controlled autoregressive moving average (H-CARMA) model in ill-conditioned situations. Section 3 proposes a Recursive Least Square algorithm for Ill-Conditioned situations (RLS-IC). Section 4 proposes a Multi Innovation Stochastic Gradient algorithm for Ill-Conditioned (MISG-IC) situations. Section 5 provides an illustrative example and compares the performance of MISG-IC and RLS-IC algorithms. Finally, the conclusion is expressed in Section 6.

2. The problem description

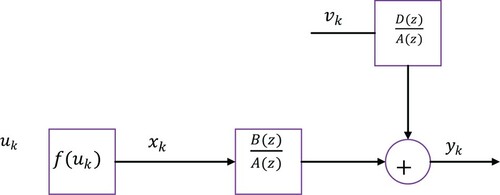
Let us introduce some notation. The symbol 1_n indicates a matrix of n × n dimension whose elements are all 1; the superscript T denotes the matrix/vector transpose; z & $z^{-1}$ represent shift operators: $z{y}_k=y_{k+1}$ and $z^{-1}{y}_k=y_{k-1}$; ${\hat{\theta }}_k$ denotes the estimation of $\theta$ at iteration k. Consider a Hammerstein controlled autoregressive moving average (H–CARMA) system shown in Figure 1.

Figure 1. The H-CARMA system.

The linear transfer function block and noise model are represented by G(z) and H(z). The relationship between input and output in a nonlinear block is expressed by $x_k=f(u_k)$. A(z), B(z) and D(z) are the polynomials in z, which are defined as $G(z)=A^{-1}(z)B(z)$ $H(z)=A^{-1}(z)D(z)$ $A(z)y_k=B(z)x_k+D(z)v_k$ $A(z)=1+a_1{z}^{-1}+\cdots +a_{na}{z}^{na}$ $B(z)=b_0+b_1{z}^{-1}+\cdots +b_{nb}{z}^{-nb}$ $D(z)=1+d_1{z}^{-1}+\cdots +d_{nd}{z}^{-nd}$

Assume that the system orders $n_a$, $n_b$ and $n_d$ are known. The nonlinear block can be modelled by Taylor series as follows: $x_k=f(u_k)={\sum }_{j=1}^m{\gamma }_j{u}_k^j$. The Hammerstein system is described in Equation (1). (1) $A(z)y_k=B(z)x_k+D(z)v_k$(1)

Then Equation (1) can be written as below: $\begin{array}{rl}{y}_k& =-a_1{y}_{k-1}-\cdots -a_{n_a}{y}_{k-n_a}+B(z)\sum _{j=1}^m{\gamma }_j{u}_k^j\\ & +v_k+d_1{v}_{k-1}+\cdots +d_{n_d}{v}_{k-n_d}\\ y_k& =-a_1{y}_{k-1}\cdots -a_{n_a}{y}_{k-n_a}+(B(z)-b_0)x_k\\ & +b_0\sum _{j=1}^m{\gamma }_j{u}_k^j+v_k+d_1{v}_{k-1}+\cdots +d_{n_d}{v}_{k-n_d}\end{array}$

Define the parameter vectors as $\theta =[a^T,b^T,{\gamma }^T,d^T{]}^T\in R^n,n=n_a+n_b+n_d+m+1$ $a=[a_1,a_2,\dots ,a_{n_a}{]}^T\in R^{n_a}$ $b=[b_0,b_1,b_2,\dots ,b_{n_b}{]}^T\in R^{n_b+1}$ $\gamma =[{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_m{]}^T\in R^m$ $d=[d_1,d_2,\dots ,d_{n_d}{]}^T\in R^{n_d}$

and the information vector and regression equations are given as (2) $\begin{array}{rl}{\varphi }_k& =[-y_{k-1},\dots ,-y_{k-n_a},x_{k-1},\dots x_{k-n_b},u_k,\dots ,\\ & \times u_k^m,v_{k-1},\dots ,v_{k-n_d}{]}^T\\ y_k& ={\varphi }_k^T{\theta }_k+v_k\end{array}$(2)

First, the cost function is defined as (3) $e_k=\sum _{j=1}^k{(y_k-{{\varphi }_k}^T{\hat{\theta }}_k)}^2$(3) The recursive equation for parameter estimation is given by (Weyer, 2001) (4) ${\hat{\theta }}_k={\hat{\theta }}_{k-1}+P_k{\varphi }_k(y_k-{{\varphi }_k}^T{\hat{\theta }}_{k-1})$(4) The recursive least squares algorithm can be implemented as follows: (5) $\begin{array}{rl}{K}_t& =P_k{\varphi }_k\end{array}$(5) (6) $\begin{array}{rl}{P}_k& =P_{k-1}-\frac{P_{k-1}.{\varphi }_k.{{\varphi }_k}^T.P_{k-1}}{1+{{\varphi }_k}^T.P_{k-1}.{\varphi }_k}\end{array}$(6) Due to insufficient excitation, the singularity problem will occur. Therefore, RLS algorithms could not be implemented for Hammerstein systems in ill-conditioned situations. Usually, recursive singular value decomposition has been used to solve the singularity problem in the recursive least squares algorithm (Liu et al., 2014; Zhang et al., 1994).

The recursive Least-Squares based on singular value decomposition (RLS-SVD) algorithm can be implemented in the ill-conditioned situations as follows. (7) $\begin{array}{rl}{K}_k& =\frac{H_{k-1}{D}_{k-1}^2{H}_{k-1}^T{\varphi }_k}{1+{\varphi }_k^T{H}_{k-1}{D}_{k-1}^2{H}_{k-1}^T{\varphi }_k}\end{array}$(7) (8) $\begin{array}{rl}\sum & =\left[\begin{array}{l}{{\varphi }_k}^T{H}_{k-1}\\ {D_{k-1}}^{-1}\end{array}\right]={\overline{H}}_{k-1}\left[\begin{array}{l}{D_{k-1}}^{-1}\\ 0\end{array}\right]{{\overline{V}}_{k-1}}^T\end{array}$(8) (9) $\begin{array}{rl}\sum ^T\sum & ={\overline{V}}_k[{\overline{D}}_k{]}^2{{\overline{V}}_k}^T\end{array}$(9)

$H_k$ and $D_k$can be updated as follows: (10) $\begin{array}{rl}{H}_k& =H_{k-1}{\overline{V}}_{k-1}\end{array}$(10) (11) $\begin{array}{rl}{D}_k& ={{\overline{D}}_{k-1}}^{-1}\end{array}$(11)

The SVD can be performed to obtain the appropriate initial values. (12) $\begin{array}{rl}U& =\left[{\varphi }_1\dots {\varphi }_P\right]\end{array}$(12) (13) $\begin{array}{rl}U& =Q\left(\begin{array}{c}S\\ 0\end{array}\right)V^T\end{array}$(13)

In addition, $P_0$ can be transformed as follows: (14) $P_0=(U^{T}U{)}^{-1}=(V{S}^2{V}^T{)}^{-1}$(14)

Note that (15) $\begin{array}{rl}{H}_0& =V\end{array}$(15) (16) $\begin{array}{rl}{D}_0& =S^{-1}\end{array}$(16)

In this paper, two methods will be presented with less estimation error in comparison with RLS-SVD to identify Hammerstein systems in ill-conditioned situations.

3. The RLS-IC algorithm for the H-CARMA system

The matrix $P_k$ in the forgetting factor recursive least squares (FF-RLS) algorithm is expressed according to Equation (17) (Ding, Xu, et al., 2016). Singular value decomposition of the positive semi definite matrix $P_k$ can be formulated as (17) $P_k=\lambda P_{k-1}+(\varphi {\varphi }^T{)}^{-1}$(17)

Assume that $U=\left[{\varphi }_1\begin{array}{cc}\dots & {\varphi }_P\end{array}\right]$. Because the system is in ill-conditioned situations, the covariance matrix is defined as (18) $P_k=\lambda P_{k-1}+(U^{T}U{)}^{-1}$(18)

Matrixes $V_{total}$ and ${V_{total}}^T$ are orthogonal. (19) $V_{total}{V_{total}}^T={V_{total}}^T{V}_{total}=I$(19)

Singular value decomposition of the positive semi definite matrix $U^{T}U$ can be formulated as (20) $U^{T}U=V_{total}\lambda {V_{total}}^T$(20)

First, the SVD has been performed to obtain the appropriate initial values. Singular value decomposition of the matrix $U^{T}U$ can be written as (21) $U^{T}U=\left[\begin{array}{cc}{V}_{null}& V_{eig}\end{array}\right]\left[\begin{array}{cc}{\lambda }_{null}& 0\\ 0& {\lambda }_{eig}\end{array}\right]\left[\begin{array}{c}{V_{null}}^T\\ {V_{eig}}^T\end{array}\right]$(21) where the matrixes ${\lambda }_{eig}$, ${\lambda }_{null}$ are diagonal matrixes and contain the non-zero eigenvalues and zero eigenvalues of $U^{T}U$. Since $V_{null}{\lambda }_{null}{V}_{null}^T=0$

Therefore, the matrix $U^{T}U$ can be simplified as follows: (22) $U^{T}U=V_{eig}{\lambda }_{eig}{V_{eig}}^T$(22)

The $V_{total}$ matrix can be assumed to be a transfer matrix to map the current space to an orthogonal one. (23) $z_k={V_{total}}^T{\varphi }_k=\left[\begin{array}{c}{V_{null}}^T\\ {V_{eig}}^T\end{array}\right]{\varphi }_k=\left[\begin{array}{c}0\\ {z_k}^{red}\end{array}\right]$(23) where the information vector of orthogonal space and the information vector of orthogonal reduced space are denoted by $z_k$ and ${z_k}^{red}$. The new cost function can be written based on orthogonal space as follows: (24) $S_{new}=(y_k-{\varphi }_k^T{V}_{eig}{V_{eig}}^T{\hat{\theta }}_K{)}^2=(y_k-z_k^T{\hat{\alpha }}_k{)}^2$(24) in which ${\hat{\alpha }}_k$ denotes the vector of estimated parameters in orthogonal space. The cost function on the orthogonal reduced space can be simplified as follows: (25) $\begin{array}{rl}{S}_{new}& ={(y_k-\left[\begin{array}{cc}0& Z_k^{red}\end{array}\right]\left[\begin{array}{c}{\hat{\alpha }}_k^0\\ {\hat{\alpha }}_k^{red}\end{array}\right])}^2\\ & =(y_k-Z{}_k^{re{d}^T}{\hat{\alpha }}_k^{red}{)}^2\end{array}$(25)

The recursive equation of estimated parameters in the transferred space in ill-conditioned situations can be obtained based on Equation (26) as follows: (26) $\begin{array}{rl}{\hat{\alpha }}_k^{red}& ={\hat{\alpha }}_{k-1}^{red}+P^{red}{z_k}^{red}(y_k-z{}_k^{re{d}^T}{\hat{\alpha }}_{k-1}^{red})\\ & ={\hat{\alpha }}_{k-1}^{red}+({V_{eig}}^T{P}_k{V}_{eig}{)}^{-1}{V_{eig}}^T{u}_k(y_k-Z{}_k^{re{d}^T}{\hat{\alpha }}_{k-1}^{red})\\ {\hat{\alpha }}_k^{red}& ={\hat{\alpha }}_{k-1}^{red}+({\lambda }_{eig}{)}^{-1}{V_{eig}}^T{E}_k\end{array}$(26) where (27) $\begin{array}{rl}{E}_k& ={\varphi }_k(y_k-z{}_k^{re{d}^T}{\hat{\alpha }}_{k-1}^{red})\end{array}$(27) (28) $\begin{array}{rl}{P}^{red}& =({z_k}^{red}{z}_k{}^{re{d}^T}{)}^{-1}\end{array}$(28) (29) $\begin{array}{rl}{z_k}^{red}& ={V_{eig}}^T{u}_k\end{array}$(29)

Since Equation (26) is in the orthogonal space, the recursive equation can be generalized to the original space by using Equation (30). (30) $\begin{array}{rl}{\hat{\theta }}_k& =V_k^{total}{\hat{\alpha }}_k=\left[\begin{array}{cc}{V}_{null}& V_{eig}\end{array}\right]\left[\begin{array}{c}\beta \\ {\hat{\alpha }}_k^{red}\end{array}\right]\\ & =V_{null}\beta +V_{eig}{\hat{\alpha }}_k^{red}\end{array}$(30) where (31) $\begin{array}{r}{V}_{eig}{\hat{\alpha }}_k^{red}={\hat{\theta }}_{k-1}+V_{eig}({\text{ƛ}}_{eig}{)}^{-1}{V_{eig}}^T{\varphi }_k(y_k-{u_k}^T{\hat{\theta }}_{k-1})\end{array}$(31) Therefore: (32) $\begin{array}{rl}{\hat{\theta }}_k& =V_{null}\beta +V_{eig}{\hat{\alpha }}_k^{red}={\hat{\theta }}_{k-1}+V_{null}\beta \\ & +V_{eig}({\text{ƛ}}_{eig}{)}^{-1}{V_{eig}}^T{\varphi }_k(y_k-{{\varphi }_k}^T{\hat{\theta }}_{k-1})\end{array}$(32) The cost function is defined as (33) $S_{\beta }=||{\hat{\theta }}_k-{\hat{\theta }}_{k-1}||$(33) Then the optimal value of β is calculated by minimizing the cost function as follows: (34) $\frac{\mathrm{\partial }{S}_{\beta }}{\mathrm{\partial }\beta }=0$(34) Therefore, the optimal value of β is obtained according to (35) $\begin{array}{rl}{\beta }^{\ast }& =-({V_{null}}^T{V}_{null}{)}^{-1}{V_{null}}^T{V}_{eig}({\lambda }_{eig}{)}^{-1}{V_{eig}}^T\\ & \times {\varphi }_k(y_k-{\varphi }^T{\hat{\theta }}_{k-1})\end{array}$(35) In consequence, the recursive least squares for ill-conditioned (RLS-IC) algorithm can be formulated as (36) $\begin{array}{rl}{\theta }_k^{\ast }& ={\theta }_{k-1}-V_{null}({V_{null}}^T{V}_{null}{)}^{-1}{V_{null}}^T{V}_{eig}({\lambda }_{eig}{)}^{-1}{V_{eig}}^T\\ & \times {\varphi }_k(y_k-{\varphi }^T{\hat{\theta }}_{k-1})+V_{eig}({\lambda }_{eig}{)}^{-1}{V_{eig}}^T\\ & \times {\varphi }_k(y_k-{\varphi }^T{\hat{\theta }}_{k-1})\end{array}$(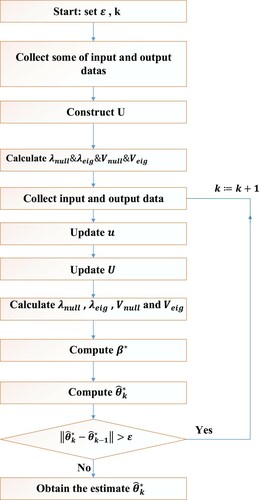36) Hammerstein nonlinear systems are identified in ill condition situations by using Equation (36). The flowchart of computing the parameter estimates of Hammerstein nonlinear systems in ill condition situations by the RLS-IC algorithm is shown in Figure 2.

Figure 2. The flowchart of the Recursive Least Square for Ill-Conditioned situation algorithm for computing ${\hat{\theta }}_k$.

4. The MISG- SIC algorithm for the H-CARMA system

Diversity in choice of P_k will lead to various identification methods. The matrix P_k in the forgetting factor recursive least squares (FF-RLS) algorithm and forgetting factor multi-innovation stochastic gradient (FF-MISG) algorithms are considered according to Equations (37) and (38) (Ding, Xu, et al., 2016). As the forgetting factor goes to unity, the FF-RLS algorithm reduces to the recursive least squares (RLS) algorithm: (37) $\begin{array}{rl}{P}_k& =\lambda P_{k-1}+(\varphi {\varphi }^T{)}^{-1}\end{array}$(37) (38) $\begin{array}{rl}{P}_k& =\lambda P_{k-1}+Trace(\varphi {\varphi }^T{)}^{-1}\end{array}$(38) The purpose of this section is to develop a Multi Innovation Stochastic Gradient algorithm for ill-conditioned situation for Hammerstein systems in the case of insufficient excitation. Thus the recursive equation (34) is rewritten as the recursive equation (39). (39) ${\theta }_k^{\ast }={\theta }_{k-1}+{R_k}^{-1}{\varphi }_k(y_k-{\varphi }^T{\hat{\theta }}_{k-1})$(39) where (40) $\begin{array}{r}{R_k}^{-1}=(I_n-V_{null}({V_{null}}^T{V}_{null}{)}^{-1}{V_{null}}^T)V_{eig}({\text{ƛ}}_{eig}{)}^{-1}{V_{eig}}^T\end{array}$(40) Therefore, Stochastic Gradient for Ill Conditioned (SG-IC) is obtained as (41)–(43) (41) $\begin{array}{rl}{\theta }_k^{\ast }& ={\theta }_{k-1}+r_k{\varphi }_k(y_k-{\varphi }^T{\hat{\theta }}_{k-1})\end{array}$(41) (42) $\begin{array}{rl}{r}_k& =\lambda r_k+{\lambda }_{1}trace({R_k}^{-1})\end{array}$(42) (43) $\begin{array}{rl}{\lambda }_1& =1-\lambda \end{array}$(43) where $\lambda$ indicates the forgetting factor and ${\lambda }_1$ denotes the correction factor. The innovation in the stochastic gradient algorithm is a scalar $e_k\in R$. (44) $e_k=y_k-{\varphi }^T{\hat{\theta }}_{k-1}$(44)

By using the gradient search, multi-innovation identification theory and equation (Hu et al., 2014) (41) the MISG-IC algorithm can be obtained for the Hammerstein nonlinear systems in ill-conditioned situations as follows: (45) $\begin{array}{rl}{\theta }_k^{\ast }& ={\theta }_{k-1}+r_k{\hat{\omega }}_{(k,s)}{E}_{(k,s)}\end{array}$(45) (46) $\begin{array}{rl}{r}_k& =\lambda r_k+{\lambda }_{1}trace({R_k}^{-1})\end{array}$(46) (47) $\begin{array}{rl}{\lambda }_1& =1-\lambda \end{array}$(47) (48) $\begin{array}{rl}{R_k}^{-1}& =(I_n-V_{null}({V_{null}}^T{V}_{null}{)}^{-1}{V_{null}}^T)V_{eig}({\text{ƛ}}_{eig}{)}^{-1}{V_{eig}}^T\end{array}$(48) (49) $\begin{array}{rl}{E}_{(k,s)}& =(Y_{(k,s)}-{{\hat{\omega }}_{(k,s)}}^T{\hat{\theta }}_{k-1})\end{array}$(49) (50) $\begin{array}{rl}{Y}_{(k,s)}& =[y_k,y_{k-1},\dots ,y_{k-s+1}{]}^T\end{array}$(50) (51) $\begin{array}{rl}{\omega }_{(k,s)}& =[{\hat{u}}_k,{\hat{u}}_{k-1},\dots ,{\hat{u}}_{k-s+1}]\end{array}$(51) (52) $\begin{array}{rl}{\hat{\varphi }}_k& =[-y_{k-1},\dots ,-y_{k-n_a},{\hat{x}}_{k-1},\dots ,{\hat{x}}_{k-n},u_k,\dots ,\\ & \times {u_k}^m,{\hat{v}}_{k-1},\dots ,{\hat{v}}_{k-n_d}{]}^T\end{array}$(52) (53) $\begin{array}{rl}{\hat{v}}_k& =y_k-{u_k}^T{\theta }_k\end{array}$(53) (54) $\begin{array}{rl}{\hat{x}}_k& ={\hat{\gamma }}_1{u}_k+{\hat{\gamma }}_2{u^2}_k+\cdots +{\hat{\gamma }}_m{u_k}^m\end{array}$(54)

The innovation in the multi-innovation stochastic gradient algorithms is a vector $E_{(k,s)}\in R^s$.

The estimation of θ can be obtained by using the MISG-IC algorithm in the following steps: Step 1: Select some groups of data to form the information matrix U and let k = 1, r(0)=1 and consider innovation length to be $s$. Step 2: Collect the input–output data to form ${\hat{\varphi }}_k$.

Step 3: Form ${\omega }_{(k,s)}$, $Y_{(k,s)}$ and $E_{(k,s)}$ using (51), (50), (49). Step 4: Calculate eigenvector, eigenvalue and null space vector of matrix U and create Equation (19). Step 5: Compute ${R_k}^{-1}$and $r_k$ by (48) and (46). Step 6: Update ${\hat{\theta }}_k$ according to (45). Step 7: Compute ${\hat{v}}_k$ and ${\hat{x}}_k$ according to (53) and (54). Step 8: Increase k by 1, go to step 1. New information vector replaces one column of information matrix, and information matrix is updated.

5. Simulation results

In this section, we present two numerical examples to illustrate the effectiveness of the RLS-IC algorithm and the MISG-IC algorithm for the H-CARMA system in ill-conditioned situations.

In this section, $\{u_k\}$ is taken as insufficient excitation, and $\{v_k\}$ as a white noise with zero mean and variance ${\sigma }^2=0.5$. Estimation error is calculated according to $\delta =\frac{||{\hat{\theta }}_k-{\theta }_k||}{||{\theta }_k||}$.

Example 1: Consider the following H-CARMA system: $A(z)y_k=B(z)x_k+D(z)v_k$ $A(z)=1+a_1{z}^{-1}=1+0.2z^{-1}$ $B(z)=1+b_1{z}^{-1}=1+0.3z^{-1}$ $x(k)={\gamma }_1{u}_k+{\gamma }_2{u_k}^2=0.8u_k+0.72{u_k}^2$

The parameters vector is assumed to be $\theta =[d_1,a_1,b_1,{\gamma }_2,{\gamma }_1{]}^T=[0.1,0.7,0.8,1,1.2{]}^T$

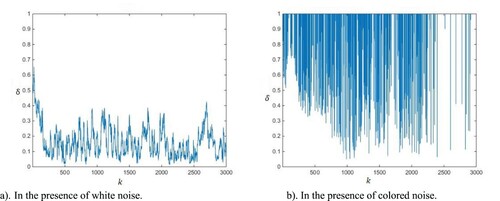
In this example, the Hammerstein system is identified in the case of insufficient excitation by using the RLS-SVD algorithm. At first, it is assumed that the output of the nonlinear block is measurable and the system is identified in the presence of white noise as well as coloured noise. The simulation results are shown in Figure 3. As it can be seen in the presence of coloured noise, the RLS-SVD method cannot estimate the parameters due to large estimation error.

Figure 3. The RLS-SVD estimation errors δ versus $k$.

Example 2: Consider the following H-CARMA system: $A(z)y_k=B(z)x_k+D(z)v_k$ $A(z)=1+a_1{z}^{-1}=1+0.7z^{-1}$ $B(z)=1+b_1{z}^{-1}=1+0.8z^{-1}$ $x_k={\gamma }_1{u}_k+{\gamma }_2{u_k}^2=1.2u_k+{u_k}^2$ $D(z)=1+0.1z^{-1}$

The parameters vector is assumed to be $\theta =[d_1,a_1,b_1,{\gamma }_2,{\gamma }_1{]}^T=[0.1,0.7,0.8,1,1.2{]}^T$

In this example, the RLS-IC and MISG-IC algorithms are applied to estimate the parameters of the Hammerstein systems in ill-conditioned situations. It is initially assumed that nonlinear block output is available. The estimation errors using the SG-IC algorithm in the presence of white noise and also coloured noise are shown in Figure 4. Then the output of the nonlinear block is assumed to be non-measurable and the system is identified in the presence of white noise as well as coloured noise. The results are shown in Figure 5. Estimation error is shown for different innovation lengths in Figure 6.

Figure 4. The SG-IC estimation errors δ versus k (the output of the nonlinear block can be measured).

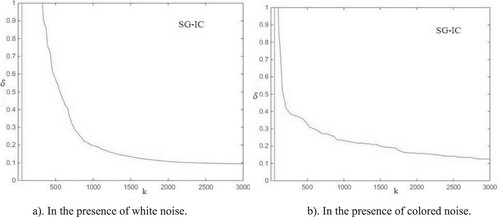
Figure 5. The SG-IC algorithm estimation errors δ versus k (the output of the nonlinear block cannot be measured).

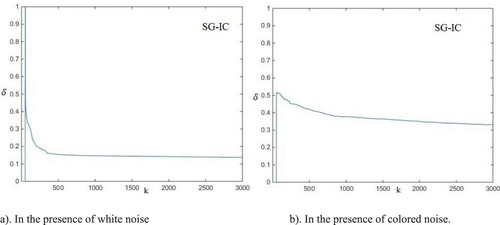
Figure 6. The RLS-IC and MISG-IC estimation errors δ versus k (the output of the nonlinear block cannot be measured).

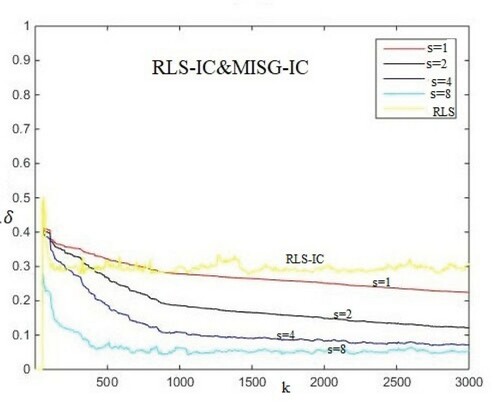
According to Figure 3, the RLS-SVD algorithm cannot identify the Hammerstein nonlinear systems very well in ill-conditioned situations. If it is assumed that we have access to nonlinear block output, the estimation error is still high, so it is not a good method for the identification of Hammerstein systems in ill-conditioned situations. But according to Figure 6, RLS-IC is a better way to identify Hammerstein systems in ill-conditioned situations, and the MISG-IC method is better than RLS-IC.

By increasing the innovation lengths, estimation error is greatly reduced. It can be seen that the proposed MISG-IC algorithm has a higher accuracy in comparison with the RLS-IC algorithm. Therefore, the MISG-IC algorithm is a more appropriate way to identify Hammerstein nonlinear systems in ill-conditioned situations.

6. Conclusion

This paper investigates the identification problem for Hammerstein systems assuming that the excitation is insufficient. RLS-IC and MISG-IC algorithms are proposed to identify such systems. Furthermore, the performance algorithms are compared. The simulation results show that the MISG-IC algorithm can estimate the system parameters in ill-conditioned situations better than the RLS-IC algorithm. The proposed algorithms can be extended to identify Hammerstein systems with time delay in ill-conditioned situations.

Disclosure statement

No potential conflict of interest was reported by the author(s).