Leader–follower consensus control for a nonlinear multi-agent robot system with input saturation and external disturbance

Abstract

This paper addresses the leader–follower consensus control problem for a nonlinear multi-agent robot system with control input constraint and external disturbances. Robot system is one of the most important practical systems in the industry. Due to the presence of disturbances in most practical systems, this paper considers the issue of finite-time leader–follower consensus control of the nonlinear multi-agent robot system along with actuator saturation and bounded disturbance. The modified terminal sliding mode control method is suggested for the system which is able to guarantee the stability of the overall system and fast finite-time leader–follower consensus control. For two different scenarios, the simulation of multi-agent robot system has been performed. The results show the effectiveness of the proposed control method.

KEYWORDS:

• Control input constraint
• robot system
• multi-agent system
• sliding mode control
• finite-time leader–follower consensus control

1. Introduction

Multi-agent systems has recently gotten to be an inclusive subject due to its wide requests in many areas, such as power systems, unmanned air vehicles, sensor networks, smart grids, biological systems, robotic teams, formation control, etc. (Hu et al., 2020; Hu et al., 2020; Hu et al., 2020; Li et al., 2011; Ma et al., 2015; Qin et al., 2014; Zhao et al., 2014; Zhao & Jia, 2015; Zhao & Jia, 2016). For getting an overall goal in multi-agent systems, the use of cooperative control is essential and the key idea is to design the distributed controllers on each agent by means of its local neighbouring information. That is, under a distributed local protocol, the agents can work cooperatively to achieve an overall goal. Especially, under the idea of cooperation, the agents in multi-agent systems only share information with their neighbours locally and attempt to reach an agreement to a certain degree.

Nowadays, attention to robust approaches in nonlinear, uncertain, and disturbed systems in various applications has increased dramatically (Shi et al., 2017; Wang, Zhu, et al., 2020; Wu et al., 2019; Xiong et al., 2016; Yu et al., 2020; Zhu et al., 2020). In the case of multi-agent systems, typical shared overall behaviours under cooperative control contain consensus (Chen et al., 2016; Feng et al., 2016; Hu et al., 2016; Wen et al., 2014), synchronization (Arenas et al., 2008; Lü et al., 2004; Pecora & Carroll, 1998), flocking (Olfati-Saber, 2006; Reynolds, 1987; Vicsek et al., 1995), and swarming (Yu et al., 2013), and much developments have been already realized. The consensus problem generally concerns about how a group of autonomous agents can reach to an agreement on position, velocity, or other certain quantity of criteria. Many of studied multi-agent systems are with single- or double-integrator dynamics (Meng et al., 2011; Qin et al., 2012; Wei, 2008; Wu et al., 2012; Yu et al., 2010).

In the study of consensus control, the convergence rate has been a significant topic. To be sure, this important performance index contains high interest for studying the effectiveness of a consensus protocol in the context of multi-agent systems. Most of consensus procedures concentrate on asymptotic convergence, where the settling time is unlimited. However, many applications require a high speed convergence commonly described by a finite-time control strategy (Huang et al., 2021; Wang, Huang, et al., 2020; Wang, Zhu, et al., 2020; Xiwei et al., 2009). Finite-time control allows some advantageous properties, such as good disturbance rejection and good robustness against uncertainties.

Another issue that needs to be addressed in consensus control is that in most practical control applications, such as those in robot manipulation and aerospace industry, the performance of the controller is directly related to the accuracy of the mathematical model and external disturbances. However, it is difficult to establish an appropriate mathematical model for a large number of nonlinear systems when the systems are complex and highly coupled nonlinear with uncertainties and external disturbances (Chen et al., 2020; Wang, 1999; Zhang et al., 2019) and there are some gaps between mathematical models and actual plant dynamics.

Also, in many practical dynamic systems, physical actuators saturation on hardware indicates an inevitable constraint of the control signal magnitude. Control saturation is one of the most common non-smooth nonlinearity that should be explicitly considered in the control design. The controllers that ignore actuator limitations may give rise to undesirable inaccuracy, severely degrade the performance of system, or even damage the stability of system (Leonessa et al., 2009). Hence, the controller design subjected to the control saturation and simultaneously achieving to higher performance is a very practical problem.

Most of the existing consensus protocols have been derived when there is no leader or when the leader is static. Nevertheless, in many missions, a dynamic leader is required. Many applications may require a dynamic leader, which could be virtual for its followers. Its behaviour is independent of the other agents. The leader-following consensus problem for multi-agent systems with Lipschitz nonlinear dynamics is discussed in (Xu et al., 2014). Also, the finite-time leader–follower consensus of nonlinear Lagrangian multi-agent systems is considered in (Sharifi & Yazdanpanah, 2020) with communication time delays and dynamic parameter uncertainties. Readers may refer to (Li et al., 2020; Qin et al., 2017; Qin et al., 2019; Yu et al., 2017) for a more comprehensive overview.

To the best of our knowledge, the input saturations are not frequently considered in the multi-robot systems control. In (Su et al., 2013), a low gain feedback control is proposed to avoid the saturation of the system, such that a semi-global leader–follower consensus of linear multi-agent system is achieved.

Furthermore, over the past few years, multi-agent robotic systems control has been become an important research area. In some cases, the network communication process between robotic agents is overlooked, and this case creates a dependency for each agent to maintain a permanent link with nearby units to be able to fulfil its goals. It is clear that in a real physical system network, the evolutions of multi-agent systems are unavoidably affected by disturbances and noises (Li et al., 2010; Lin et al., 2008; Liu & Jia, 2010).

The main concern is to find the effective coordination among autonomous agents to perform the task in order to achieve a high quality of overall performance.

For preventing such problems, sliding mode control (SMC) remains to be one of the most effective approaches in settling bounded disturbances and parameter variations (Edwards & Spurgeon, 1998; Utkin, 1992; Utkin et al., 1999). Typical SMC includes linear sliding-mode (LSM) control and terminal sliding-mode (TSM) control (Feng et al., 2002; Feng et al., 2013), where the former one is asymptotically stable while the second one is finite-time stable. TSM control can provide faster convergence and higher precision control than the traditional linear sliding mode control, nevertheless, it needs that a disturbance bound to be known.

The main purpose of this paper is to investigate the problem of finite-time leader–follower consensus control of multi-agent nonlinear robot systems with saturation and external bounded disturbances. Accordingly, a new TSM control method is proposed for multi-agent robot systems, which solves the finite-time leader–follower consensus control design for networked systems in the presence of disturbance and control input constraint. The rest of this paper is set as follows. In Section 2, problem formulation is stated. In Section 3, some simulation results are used to demonstrate the effectiveness of the proposed method. Finally, the conclusion is drawn in Section 4.

2. Leader–follower consensus control formulation for a multi-agent robot system by using of terminal sliding-mode method

In this section, the structure of the terminal sliding-mode method is provided for leader–follower consensus control of the multi-agent robot system. We consider a class of multiple mechanical nonlinear systems (1) $\begin{array}{r}{T}_i{\ddot{q}}_i+C_i\left(q_i,{\dot{q}}_i\right){\dot{q}}_i+N_i\left(q_i\right)+D_i={\tau }_i,\end{array}$(1) where $q_i\in R^m$, $i=1.\dots .n$ is the state of the $i$th system, ${\tau }_i\in R^m$ is the saturated control input vector, $T_i\subset R^{m\times m}$ is an inertia matrix, $C_i\left(q_i,{\dot{q}}_i\right)$ is the centripetal and Coriolis matrix, $N_i\left(q_i\right)$ denotes the friction terms and $D_i$ is disturbance. Denote $v_i={\dot{q}}_i$. System (1) can be written as $\begin{array}{rl}{\dot{q}}_i& =v_i\end{array}$ (2) $\begin{array}{rl}{\dot{v}}_i& =f_i\left(q_i,v_i\right)+g_i{u}_i+{\delta }_i+{\vartheta }_i,\end{array}$(2) where $v_i\in R^m$ denotes the velocity. $\begin{array}{rl}{f}_i\left(q_i,v_i\right)& =-T_i^{-1}\left(C_i\left(q_i,v_i\right)v_i+N_i\left(q_i\right)\right)\end{array}$ $\begin{array}{rl}{\vartheta }_i& =-T_i^{-1}{D}_i\end{array}$ (3) $\begin{array}{rl}{g}_i& =-T_i^{-1}\end{array}$(3)

Defined that the upper bound of input control is ${\tau }_{imax}$, which is positive, ${\delta }_i=u_i-{\tau }_i$, and the saturation function $sat\left(u_i\right)$ is expressed as follows: (4) $\begin{array}{r}{u}_i=\left\{\begin{array}{cc}{\tau }_{imax}& u_i>{\tau }_{imax}\\ u_i& |u_i|\le {\tau }_{imax}\\ -{\tau }_{imax}& u_i<-{\tau }_{imax}\end{array}\right.\end{array}$(4) From the description above, it is known that ${\delta }_i$ is the error caused by input saturation, which is the most important parameter to solve the control input saturation problem. As adaptive method has omnipotent ability of approximation, so use it to approximate ${\delta }_i$ here.

For the problem of leader–follower consensus control in multi-agent systems, two state error measures are considered for each follower agent, that is, absolute and relative state errors. The absolute error is the state error of an individual follower agent with respect to the reference trajectory (the state of the leader agent). The absolute state errors of the $i$th follower agent are defined by $\begin{array}{rl}{e}_{qi}& =q_i-q_0\end{array}$ (5) $\begin{array}{rl}{e}_{vi}& =v_i-{\dot{q}}_0\end{array}$(5) The leader agent trajectory $q_0$ and its derivatives are considered in a ${\mathrm{\Omega }}_0$ compact set defined by ${\mathrm{\Omega }}_0=\left\{\left(q_0,{\dot{q}}_0,{\ddot{q}}_0\right)\left|{q_0}^2+{{\dot{q}}_0}^2+{{\ddot{q}}_0}^2\le c_1\right.\right\}$, and $c_1$ is a positive constant.

The dynamic equations for the absolute errors $e_{qi}$ and $e_{vi}$ can be obtained using (2) as $\begin{array}{rl}{\dot{e}}_{qi}& =e_{vi}\end{array}$ (6) $\begin{array}{rl}{\dot{e}}_{vi}& =-{\ddot{q}}_0+f_i\left(q_i,v_i\right)+g_i{u}_i+{\delta }_i+{\vartheta }_i\end{array}$(6) Which can be re-expressed in the compact form as $\begin{array}{rl}{\dot{e}}_q& =e_v,\end{array}$ (7) $\begin{array}{rl}{\dot{e}}_v& =-Q_0+F+Gu+\delta +\vartheta ,\end{array}$(7) where $\begin{array}{rl}{e}_q& =(e_{q1}^T,e_{q2}^T,\dots ,e_{qn}^T{)}^T\in R^{mn}\end{array}$ $\begin{array}{rl}{e}_v& =(e_{v1}^T,e_{v2}^T,\dots ,e_{vn}^T{)}^T\in R^{mn}\end{array}$ $\begin{array}{rl}F& =(f_1^T,f_2^T,\dots ,f_n^T{)}^T\in R^{mn}\end{array}$ $\begin{array}{rl}{Q}_0& ={\left({\ddot{q}}_0^T,{\ddot{q}}_0^T,\dots ,{\ddot{q}}_0^T\right)}^T\in R^{mn}\end{array}$ $\begin{array}{rl}u& =(u_1^T,u_2^T,\dots ,u_n^T{)}^T\in R^{mn}\end{array}$ $\begin{array}{rl}\vartheta & =({\vartheta }_1^T,{\vartheta }_2^T,\dots ,{\vartheta }_n^T{)}^T\in R^{mn}\end{array}$ $\begin{array}{rl}\delta & =({\delta }_1^T,{\delta }_2^T,\dots ,{\delta }_n^T{)}^T\in R^{mn}\end{array}$ (8) $\begin{array}{rl}G& =diag\left\{g_1,g_2,\dots ,g_n\right\}\in R^{\left(mn\right)\times \left(mn\right)}\end{array}$(8)

The relative error is the state error of an individual follower agent with respect to the other follower agent in the multi-agent system. The relative state errors between the $i\left(i=1,2,\dots ,n\right)$th and $j\left(j=1,2,\dots ,n\right)$th follower agents are defined as $\begin{array}{rl}{r}_{qij}& =q_i-q_j\end{array}$ (9) $\begin{array}{rl}{r}_{vij}& =v_i-v_j\end{array}$(9)

Because the common desired trajectory $q_0$ is available to only a subset of the group members and each agent in the group has access to only the information of its neighbour agents, the $i\left(i=1,2,\dots ,n\right)$th agent may not obtain the absolute state errors and all relative state errors. Considering these facts and using the weighted adjacency matrices $A$ and $B$, we define lumped state errors ${\alpha }_{qi}\in R^m$ and ${\alpha }_{vi}\in R^m$ including absolute and relative state errors as $\begin{array}{rl}{\alpha }_{qi}& =\sum _{j=1}^n{a}_{ij}{r}_{qij}+b_i{e}_{qi}\end{array}$ (10) $\begin{array}{rl}{\alpha }_{vi}& =\sum _{j=1}^n{a}_{ij}{r}_{vij}+b_i{e}_{vi}\end{array}$(10) Respectively, where $a_{ij}$ is the element of the weighted adjacency matrix $A$. The lumped state errors ${\alpha }_{qi}\in R^m$ and ${\alpha }_{vi}\in R^m$ are the sum of the absolute and relative state errors and only depend on the information of the neighbour agents of the $i$th agent. The controller for each agent is developed based on the lumped state errors ${\alpha }_{qi}\in R^m$ and ${\alpha }_{vi}\in R^m$.

In order to facilitate the subsequent theoretical analysis, the lumped state errors ${\alpha }_{qi}\in R^m$ and ${\alpha }_{vi}\in R^m$ can be re-expressed in terms of the absolute state errors $e_{qi}$ and $e_{vi}$ by some simple algebra transformation as following: $\begin{array}{rl}{\alpha }_{qi}& =\sum _{j=1}^n{a}_{ij}{r}_{qij}+b_i{e}_{qi}=\sum _{j=1}^n{a}_{ij}\left(e_{qi}-e_{qj}\right)+b_i{e}_{qi}\\ & =\sum _{j=1}^n{l}_{ij}{e}_{qj}+b_i{e}_{qi},\end{array}$ (11) $\begin{array}{rl}{\alpha }_{vi}& =\sum _{j=1}^n{a}_{ij}{r}_{vij}+b_i{e}_{vi}=\sum _{j=1}^n{a}_{ij}\left(e_{vi}-e_{vj}\right)+b_i{e}_{vi}\\ & =\sum _{j=1}^n{l}_{ij}{e}_{vj}+b_i{e}_{vi},\end{array}$(11) where $l_{ij}$ is the element of the graph Laplacian matrix $L$.

Define $\begin{array}{rl}{\alpha }_q& =({\alpha }_{q1}^T,{\alpha }_{q2}^T,\dots ,{\alpha }_{qn}^T{)}^T\in R^{mn}\end{array}$ (12) $\begin{array}{rl}{\alpha }_v& =({\alpha }_{v1}^T,{\alpha }_{v2}^T,\dots ,{\alpha }_{vn}^T{)}^T\in R^{mn}\end{array}$(12) And then the lumped state errors (12) can be written in terms of the aforementioned quantities as follows: $\begin{array}{rl}{\alpha }_q& =M_1{e}_q,\end{array}$ (13) $\begin{array}{rl}{\alpha }_v& =M_1{e}_v,\end{array}$(13) where $M_1=\left(L+B\right)\otimes I_m\in R^{mn}$ and $\otimes$ denotes the Kronecker product. Using (7), the dynamic equations for ${\alpha }_q$ and ${\alpha }_v$ are given by $\begin{array}{rl}{\dot{\alpha }}_q& ={\alpha }_v\end{array}$ (14) $\begin{array}{rl}{M}_2{\dot{\alpha }}_v& =-Q_0+F+Gu+\delta +\vartheta \end{array}$(14) Respectively, where $M_2=M_1^{-1}$.

The proposed fast terminal sliding manifold $s_i\in R^m\left(i=1,2,\dots ,n\right)$ is defined as (15) $\begin{array}{r}{s}_i={\alpha }_{vi}+{\sigma }_i{\alpha }_{qi},\end{array}$(15) where ${\sigma }_i$ is positive constant. The first time derivative of the sliding manifold (15) is given by (16) $\begin{array}{r}{\dot{s}}_i={\dot{\alpha }}_{vi}+{\sigma }_i{\alpha }_{vi}\end{array}$(16) Note that there exists no singularity problem in the preceding equation. The terminal sliding manifold given by (15) can be expressed in a compact form as (17) $\begin{array}{r}s={\alpha }_v+\sigma {\alpha }_q,\end{array}$(17) where $\begin{array}{rl}s& =(s_1^T,s_2^T,\dots ,s_n^T{)}^T\in R^{mn}\end{array}$ (18) $\begin{array}{rl}\sigma & =diag\left\{{\sigma }_1{I}_m,{\sigma }_2{I}_m,\dots ,{\sigma }_n{I}_m\right\}\in R^{\left(mn\right)\times \left(mn\right)}\end{array}$(18) Lemma 1 (An-Min et al., 2013)

If the sliding manifold $s=\overline{s}=0$ is reached, where $\overline{s}=({\overline{s}}_{11},\dots ,{\overline{s}}_{1m},\dots ,{\overline{s}}_{n1},\dots ,{\overline{s}}_{nm}{)}^T$, then the absolute state error converges to zero in finite time.

The first time derivative of the sliding manifold (17) is obtained from (16) as (19) $\begin{array}{r}\dot{s}={\dot{\alpha }}_v+\sigma {\alpha }_v\end{array}$(19) By premultiplying $M_2$ on both sides of (19) and then substituting (14) into the resulting expression, we obtain (20) $\begin{array}{r}{M}_2\dot{s}=M_2\left({\dot{\alpha }}_v+\sigma {\alpha }_v\right)=M_2\sigma {\alpha }_v-Q_0+F+Gu+\delta +\vartheta \end{array}$(20) Note that if all follower agents’ states $q_i$ and $v_i$ approach to the desired trajectories, then $e_{qi}=e_{vi}={\alpha }_{qi}={\alpha }_{vi}=0$ and hence $M_2\sigma {\alpha }_v=0$.

The control law for the $i$th follower agent in the multi-agent system is now given by (21) $\begin{array}{rl}{u}_i& =g_i^{-1}\left(-f_i\left(q_i,v_i\right)-K_i{s}_i-{\hat{\delta }}_i-{\psi }_i\right),i=1,2,\dots ,n\end{array}$(21) $\begin{array}{rl}u& =G^{-1}\left(-F-Ks-\hat{\delta }-\psi \right),\end{array}$where $K_i$ is positive definite, diagonal, and constant matrix; the robust term ${\psi }_i\in R^m$, which is determined in the succeeding equations, is used to counteract the external disturbance and the adaptive law for approximated ${\delta }_i$ is obtained from (22). (22) $\begin{array}{r}{\hat{\delta }}_i={\lambda }_i{s}_i\end{array}$(22) Substituting the control law (21) into the error dynamics (20) results in the following dynamic equation for the sliding manifold $s$ (23) $\begin{array}{rl}{M}_2\dot{s}& =M_2\sigma {\alpha }_v-Q_0-Ks+\delta -\hat{\delta }-\psi +\vartheta \\ & =\chi -Ks-\tilde{\delta }-\psi +\vartheta -Q_0,\end{array}$(23) where $\chi =M_2\sigma {\alpha }_v\in R^{mn}$ and $\begin{array}{rl}K& =diag\left\{K_1,K_2,\dots ,K_n\right\}\end{array}$ $\begin{array}{rl}\tilde{\delta }& =diag\left\{{\tilde{\delta }}_1,{\tilde{\delta }}_2,\dots ,{\tilde{\delta }}_n\right\}\end{array}$ (24) $\begin{array}{rl}\psi & =({\psi }_1^T,{\psi }_2^T,\dots ,{\psi }_n^T{)}^T\end{array}$(24)

For a sufficiently large positive constant $s_{max}$, we construct the following compact set (25) $\begin{array}{r}{\mathrm{\Omega }}_s=\left\{s|s^{T}s\le \frac{2s_{max}}{{\lambda }_{max}\left(M_2\right)}\right\},\end{array}$(25) where ${\lambda }_{max}(.)$ denotes the maximum eigenvalue of a matrix. Because the sets ${\mathrm{\Omega }}_0$ and ${\mathrm{\Omega }}_s$ are compact in $R^{3m}$ and $R^{mn}$, respectively, the variable $\chi$ has a maximum ${\chi }_M$ on the compact set ${\mathrm{\Omega }}_0\times {\mathrm{\Omega }}_s$.

Next, the robust controller ${\psi }_i$ in the control law (21) is defined as (Zeng-Guang et al., 2009), (An-Min et al., 2008) (26) $\begin{array}{r}{\psi }_{ij}\equiv {\kappa }_{i}tanh\left(\frac{m{k}_u{\kappa }_i{s}_{ij}}{ϵ}\right),k_u=0.2785,j=1,2,\dots ,m\end{array}$(26) where ${\kappa }_i$ is a positive constant satisfying ${\kappa }_i\ge {\vartheta }_{Mi}+{\ddot{x}}_0$, $ϵ$ is a positive scalar and $s_{ij}={\alpha }_{vi,j}+{\sigma }_i{\alpha }_{qi,j}$. The following inequality with respect to the robust controller ${\psi }_i$ can be easily obtained from (Zeng-Guang et al., 2009), (An-Min et al., 2008) as (27) $\begin{array}{rl}0& \le s_i^T\left({\vartheta }_i-{\ddot{q}}_0\right)-s_i^T{\psi }_i\\ & \le \sum _{j=1}^m|s_{ij}|\left({\vartheta }_{Mi}+{\ddot{q}}_0\right)-\sum _{j=1}^m{s}_{ij}{\psi }_{ij}\le ϵ\end{array}$(27)

Consider the following Lyapunov function candidate: (28) $\begin{array}{r}V=\frac{1}{2}{s}^T{M}_{2}s+\sum _{i=1}^n\frac{1}{2{\lambda }_i}{\tilde{\delta }}_i^2,\end{array}$(28) where ${\tilde{\delta }}_i={\delta }_i-{\hat{\delta }}_i$. The time derivative of the Lyapunov function (28) along (23) yields (29) $\begin{array}{rl}\dot{V}& =s^T{M}_2\dot{s}+\sum _{i=1}^n\frac{1}{{\lambda }_i}{\tilde{\delta }}_i{\tilde{\delta }}_i=s^T\chi -s^{T}Ks-s^T\psi \\ & +s^T\left(\vartheta -Q_0\right)+s^T\tilde{\delta }-\sum _{i=1}^n\frac{1}{{\lambda }_i}{\tilde{\delta }}_i\underset{i}{\hat{\delta }}\end{array}$(29)

By using (22) and (27), the following inequality (30) $\begin{array}{r}0\le s^T\left(\vartheta -Q_0\right)-s^T\psi =\sum _{i=1}^n\left(s_i^T\left({\vartheta }_i-{\ddot{q}}_0\right)-s_i^T{\psi }_i\right)\le nϵ\end{array}$(30) Can be obtained, and by using the well-known inequality (31) $\begin{array}{r}{\left(\sqrt{c_2}s-\frac{\chi }{2\sqrt{c_2}}\right)}^T\left(\sqrt{c_2}s-\frac{\chi }{2\sqrt{c_2}}\right)\ge 0\end{array}$(31)

The following inequality (32) $\begin{array}{r}{s}^T\chi \le c_2{s}^{T}s+\frac{{\chi }_M^2}{4c_2}\end{array}$(32) Can be obtained, where $c_2$ is a positive constant satisfying $c_2<{\lambda }_{min}\left(K_1\right)$ and ${\lambda }_{min}(.)$ denotes the minimum eigenvalue of a matrix.

Applying inequalities (30) and (32) to (29), $\dot{V}$ can be upper bounded by (33) $\begin{array}{r}\dot{V}\le -\left({\lambda }_{min}\left(K_1\right)-c_2\right)s^{T}s+c_3,\end{array}$(33) where $c_3=nϵ+{\chi }_M^2/4c_2$ is a positive constant. Thus, $\dot{V}$ is strictly negative outside of the following compact set ${\mathrm{\Omega }}_{s1}$ (34) $\begin{array}{r}{\mathrm{\Omega }}_{s1}=\left\{s\left(t\right)|s\left(t\right)\le \sqrt{\frac{c_3}{{\lambda }_{min}\left(K_1\right)-c_2}}\right\}\end{array}$(34) Which implies that $s$ decreases whenever $s$ is outside the compact set ${\mathrm{\Omega }}_{s1}$ and therefore, it is concluded that s is uniformly ultimately bounded.

3. Numerical results

To show the effectiveness of the presented distributed TSM control method to robust finite-time leader–follower consensus problem, the following scenarios have been done on the multi-agent system with four robots, where matrices of the robots in Equation (1) are taken as follows: $\begin{array}{rl}T& =\left[\begin{array}{cc}{t}_1& 0\\ 0& t_2\end{array}\right]\end{array}$ $\begin{array}{rl}C& =\left[\begin{array}{cc}cos\left(q_1\right)& c_1{\dot{q}}_2\\ c_2{\dot{q}}_2& sin\left(q_2\right)\end{array}\right]\end{array}$ (35) $\begin{array}{rl}N& =\left[\begin{array}{cc}{n}_1{\dot{q}}_1& 0\\ 0& n_2{\dot{q}}_2\end{array}\right]\end{array}$(35)

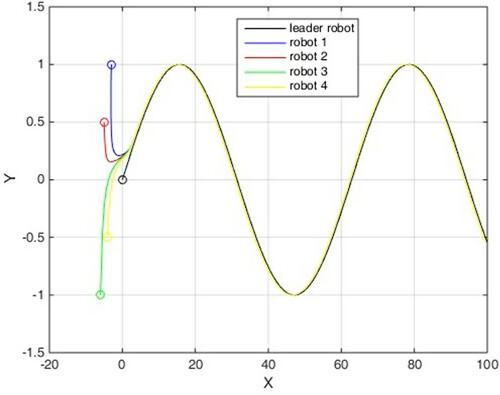
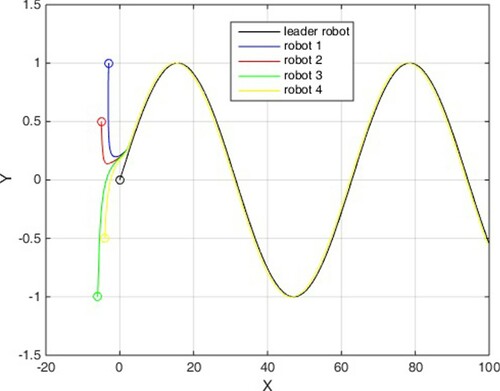
The system parameters are considered as follows: $\begin{array}{rl}{t}_1& =t_2=5\end{array}$ $\begin{array}{rl}{c}_1& =c_2=2\end{array}$ (36) $\begin{array}{rl}{n}_1& =n_2=3\end{array}$(36) The initial positions of the robots are at (−3, 1), (−5, 0.5), (−6, −1) and (−4, −0.5) respectively.

The control parameters are selected as follows: $\begin{array}{rl}A& =\left[\begin{array}{cccc}0& 1& 1& 1\\ 1& 0& 1& 1\\ 1& 1& 0& 1\\ 1& 1& 1& 0\end{array}\right]\end{array}$ $\begin{array}{rl}B& =[1,1,1,1{]}^T\end{array}$ $\begin{array}{rl}{\tau }_{imax}& =20\end{array}$ $\begin{array}{rl}K& =4I_4\end{array}$ $\begin{array}{rl}\sigma & =2I_4\end{array}$ $\begin{array}{rl}\lambda & =0.1I_4\end{array}$ $\begin{array}{rl}\kappa & =0.5I_4\end{array}$ (37) $\begin{array}{rl}\mu & =0.01,ϵ=0.01\end{array}$(37)

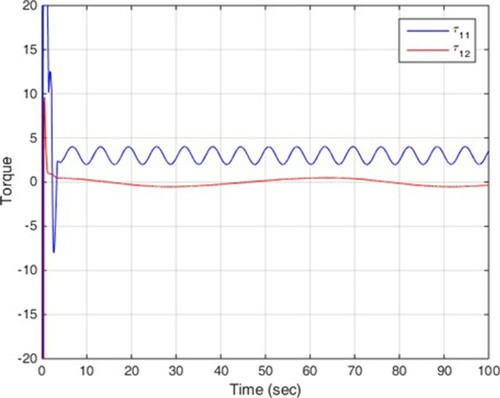
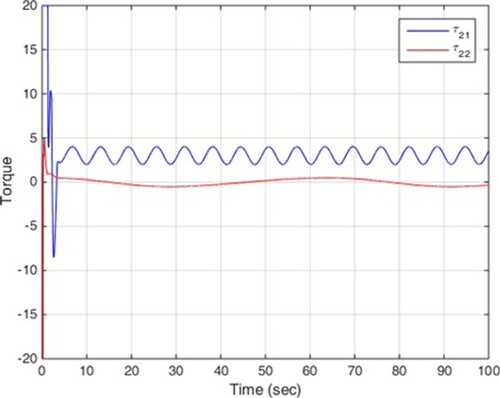
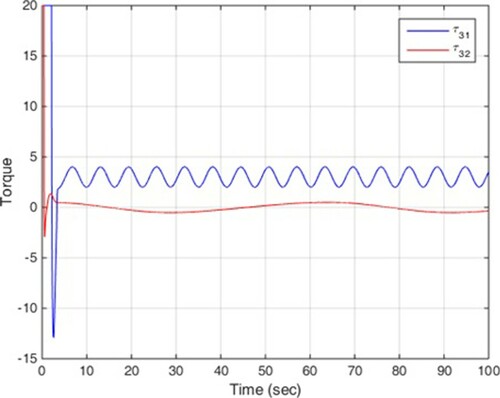
Scenario 1: without disturbance

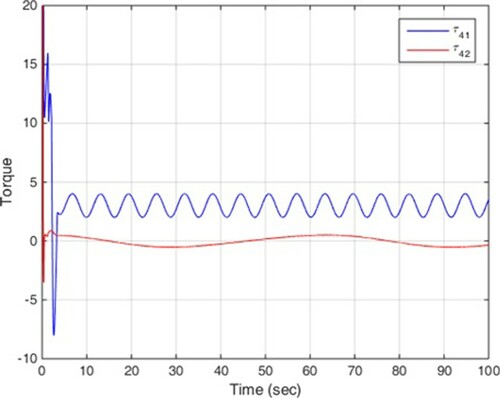
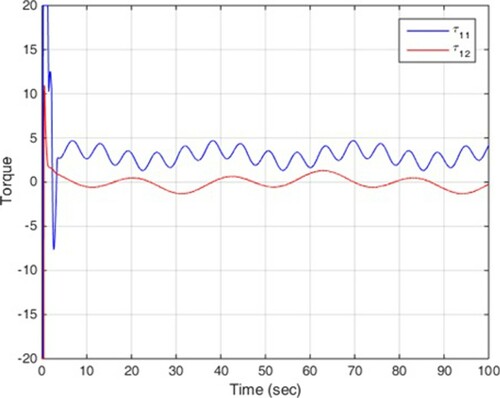
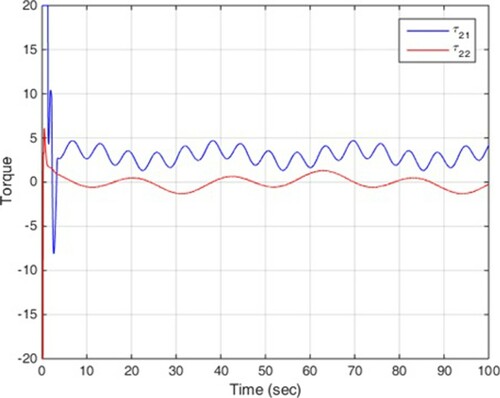
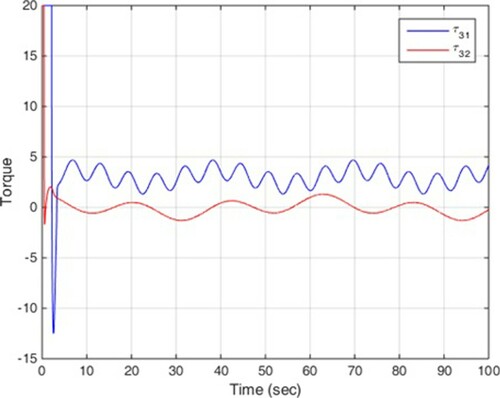
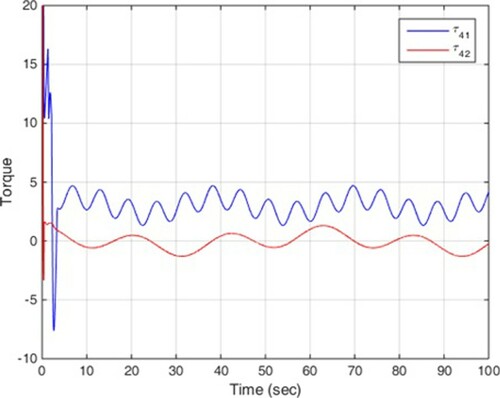
In this scenario, no disturbance is entered into multi-agent system. The simulation results are illustrated in Figures 1–5, among which, Figure 1 shows the states of four mechanical robots in leader following, and Figures 2–5 depict the control signals.

Figure 1. States of four mechanical robots in leader following.

Figure 2. Robot 1 control signals.

Figure 3. Robot 2 control signals.

Figure 4. Robot 3 control signals.

Figure 5. Robot 4 control signals.

Scenario 2: with disturbance

In this scenario, the following disturbance is entered into multi-agent system. $\begin{array}{rl}{d}_1& =0.7\text{sin}\left(0.2t\right)\end{array}$ (38) $\begin{array}{rl}{d}_2& =0.8\text{cos}\left(0.3t\right)\end{array}$(38) The simulation results are illustrated in Figures 6–10, among which, Figure 6 shows the states of four mechanical robots in leader following, and Figures 7–10 depict the control signals.

Figure 6. States of four mechanical robots in leader following.

Figure 7. Robot 1 control signals.

Figure 8. Robot 2 control signals.

Figure 9. Robot 3 control signals.

Figure 10. Robot 4 control signals.

It is clear that the proposed control can achieve the convergence of the tracking errors to zero in finite time. These two scenarios confirm the theoretical results in previous section and it is clear that disturbance does not have much effect on the efficiency of the control method.

4. Conclusion

The most important innovation of this paper is the development and analysis of finite-time leader–follower consensus control using the terminal sliding mode control method for a multi-agent robot system with control input saturation, disturbance and nonlinear effects. By using of Lyapunov theory and the terminal sliding mode control method ensure that all operating modes can be driven onto sliding surface and achieved desired leader–follower consensus in finite time even in the presence of control input constraint and external disturbances. Considering uncertainty, noise and operationalization and practical implementation of the proposed method is a good way for future studies in this field.

Disclosure statement

No potential conflict of interest was reported by the author(s).