Customized passenger path optimization for airport connections under carbon emissions restrictions

Abstract

In response to the challenge of optimizing customized passenger transport paths for airport connections while taking carbon emissions constraints into account, this paper proposes an optimization model that minimizes the total cost by addressing passenger time window constraints, determining optimal passenger transport paths, and optimizing factors like the number of drop-off stations and vehicle occupancy rates. The total cost comprises the operational expenses of customized passenger transport businesses and travel time costs per passenger. We develop an annealing genetic algorithm to solve the model and provide a case analysis. Our findings indicate that the algorithm and the model empower decision-makers to swiftly select passenger transport path schemes that minimize the total cost with their specific requirements.

KEYWORDS:

• Customized passenger transport
• path optimization
• annealing genetic algorithm
• airport connections
• carbon emissions

1. Introduction

Sustainable development has long been a concept upheld by humanity, but environmental degradation is constantly impacting the path of sustainable development in various countries. With the trend of global temperature rise, governments around the world have increasingly focussed on reducing carbon-emission in economic activities and signed the Paris Agreement in 2016, aiming to seek measures to further limit temperature increases to within 1.5${}^{\circ }$C. In the current context of advocating environmental protection, energy conservation and emission reduction are urgent, and the importance of logistics transportation in a low-carbon economy has made path planning particularly important. Therefore, research on path optimization under carbon-emission restrictions is urgently needed by enterprises.

The passenger route optimization problem is actually a demand-responsive route optimization problem, aiming at providing commuters with advanced, convenient and comfortable services. Online information platforms (such as the Internet and databases) classify passengers with similar travel needs and arrange customized services for different passenger classifications. As a new travel mode, demand-responsive transport mode plays an important role in airport connection, which can greatly improve the overall airport connection efficiency and passengers' extra time loss caused by flight delays. So, it is very important to study the optimization of customized passenger transportation routes under carbon emission restrictions.

2. Literature review

The route optimization problem has always been a hot topic of research. The essence of the customized passenger route optimization problem for airport connection is the problem in vehicle routing (VRP), which was originally formulated by Dantzig and Ramser (1959) the year 1959, and been proved by Gaery (Zhu et al., 2001) to be NP-Hard problem, and this has led to a wealth of research findings. Huber and Geiger (2017) designed an algorithm based on Variable-Neighbourhood-Search(VNS) to deal with the VRP model. Dinh et al. (2018) researched the chance-constrained VRP (CCVRP) and customized the BCP algorithm to address the VRP problem, which included random demands. And regarding the multi-depot and multi-compartment VRP, Alinaghian and Shokouhi (2018) gave a mathematical model, and designed an adaptive hybrid algorithm with NS and VNS combined. Liu et al. (2023) constructed a reliable path optimization model for multimodal transport of emergency materials with the goal of maximum reliability, and designed the Monte Carlo adaptive genetic algorithm and simulated annealing genetic algorithm. Ji et al. (2023) studied the vehicle routing problem with two-dimensional packing constraints (2L-CVRP), constructed a mixed integer linear programming model of 2L-CVRP, and proposed a branch-based pricing method to solve it. Feng and Xiao (2023) studied a class of restricted vehicle routing problem in the context of shared travel, and proposed a hybrid ant colony algorithm embedded in space-time distance to solve it.

The optimization problem of customized passenger paths for airport connection is different from the traditional VRP problem, in addition to considering the conventional time window and vehicle capacity constraints, it also considers the constraints of passengers on the train time, passenger line drop-off station and passenger load rate, plus a carbon emission limit, which makes the problem much more complex than the traditional VRP problem. At present, some scholars have studied the problem of airport transfers. For example, Ellis et al. (1974) used the polynomial Logit model (MNL) as early as 1974 to study Washington Airport, selected four connection methods such as private cars, rental cars, rental cars and large buses, and took the travel purpose, connection time and connection cost as model parameters. Yang et al. (2013) proposed an label-based accurate algorithm and set division for the hybrid integer programming model of minimum carbon emission and minimum cost in airport transfer service, and compared and analyzed the two models from five aspects. Wei et al. (2020) developed a model of programming in multi-objective and mixed integer linear (MOMILP) for demand-responsive airports, and proposed the ‘NSGA-II’ algorithm as a tool for finding the Pareto optimal solution. Lu et al. (2016) studied the routing optimization problem of flexible public transport vehicles in the case of two-way isolation, and solved it with a three-stage heuristic genetic algorithm. Wang et al. (2021) proposed a coordinated optimization method for vehicle routing and departure time that considered both inter-zone and intra-zone reservation requirements, and constructed a multi-objective coordinated optimization model to solve the problem.

In recent years, the ‘Internet +’ emerging technology has penetrated and developed into various industries, customized travel services have flourished, and route design, as a key component of customized travel service design, has garnered the interest of numerous scholars. Bakas et al. (2016) researched the scheduling methodology of demand-responsive bus systems with time windows and fixed fleet sizes. For customized bus lines, Ma et al. (2020) developed a multi-objective robust optimization model and constructed a genetic algorithm that utilizes K-means and multi-objective algorithms for optimization. Target to reduce passengers' travelling expenses to the optimal level, Chen et al. (2020) constructed a model for planning customized bus routes in multi-regional commuter operation, and designed a heuristic algorithm with two stages for it. Sun et al. (2020) designed a mixed model in integer nonlinear to optimize multi-terminal customized bus services for mixed fleets, and designed a hybrid genetic algorithm solution model combining simulated annealing and genetic algorithms. Liu and Zhang (2020) studied the location of customized passenger landing points under uncertain demand, established a random planning and opportunity constraint model, and finally verified the feasibility of the customized passenger landing point planning scheme.

The signing of the Paris Agreement in 2016 marked a major milestone in the transportation industry's efforts to reduce its carbon footprint. As a result, the ‘low-carbon’ vehicle routing issue has spurred increased interest among many researchers. The problem in ‘low-carbon’ vehicle routing was first suggested by Palmer (2007), and the vehicle path optimization model considers the relationship between vehicle speed, road conditions, and carbon emissions in vehicle routing, but without reasonable consideration of the correlation between load and fuel consumption rate. Wang et al. (2017) developed an optimization model for low-carbon and eco-friendly distribution in logistics of cold chain that can minimize the costs, and designed an algorithm in cyclic evolutionary genetic (CEGA) accordingly. Ren et al. (2020) designed an optimization for customer-oriented eco-friendly vehicle (cold chain) paths, established a model of optimization for vehicle routing in cold chain that aims to minimize carbon footprint, and created an enhanced ant colony algorithm combined with domain search to improve the global search ability. Chen et al. (2021) studied the logistics of cold chain in the front warehouse, proposed the time-based green VRP (TDG-VRP), and offered an algorithm in hybrid simulated annealing & tempering (HSATA) accordingly. Li et al. (2023) proposed a three-stage Lagrange heuristic algorithm combining mathematical planning method and heuristic algorithm to solve the routing problem of green vehicles with simultaneous pick-up and delivery.

To sum up, there are few customized passenger transport studies on airport connections in the existing studies, and the constraints considered in the existing studies on airport connections are more inclined to enterprises, with insufficient consideration of passenger needs, and few of them take carbon emission restriction into consideration. Therefore, this paper has enriched the research on passenger route optimization. Aiming at the characteristics of the optimization problem of customized passenger transport path of airport connection under carbon emission restrictions, and considering the constraints of passenger time, passenger line drop-off station and passenger load rate, this study establishes an optimization model under carbon emission restrictions to minimize the costs in operating and total travel time of customized passenger transport enterprises, and designs a heuristic algorithm according to the NP difficulty characteristics of the model, which has certain theoretical significance and practical application value, and may serve as a useful reference for decision-makers involved in customizing passenger transport for airport connections.

3. Description of the problem and modelling

3.1. Description of the problem

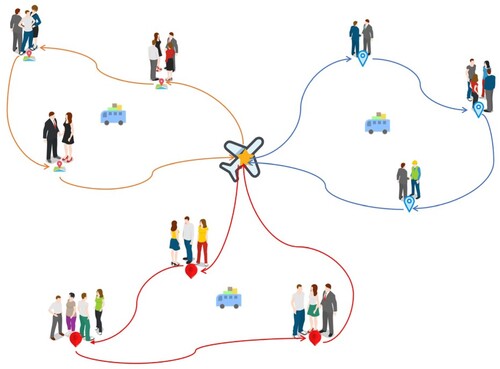
The operation mode of customized passenger transport at the airport is to pick up passengers at the airport and then send them to different destinations, as shown in Figure 1. The problem is defined as: Passengers post travel demand information on the Internet platform, including drop-off stations and drop-off time windows. According to the information provided by passengers, customized passenger transport companies make arrangements for the departure time, passengers to be transported and the order of passengers to be transported, etc., during this phase, considering the hard time window requirements and vehicle capacity constraints of passengers to reach their destinations, and seeking a passenger transport route scheme to minimize the costs under the condition of carbon footprint reductions. The questions examined in this paper only consider the closed-loop operation of vehicles leaving the airport to send passengers to their destination and back to the airport.

Figure 1. Customized passenger transport map of airport connection.

3.2. Model assumptions and variables

3.2.1. Model assumptions

1. The number of vehicles is limited, and each passenger has only one bus service.

2. All buses serving the same type, i.e. each vehicle carries the same passenger capacity.

3. Passengers can only be dropped off at the drop-off point with reservation request information.

4. When the vehicle is serviced at each drop-off point, the service time is the same for each passenger.

5. Vehicles drive at a constant speed, ignore traffic delays and road traffic is in good condition.

3.2.2. Model variables and parameters

The model variables and parameters are detailed in Table 1, where $V=\{0,1,2,\dots ,n,n+1\}$ represents the set of all nodes; 0, n + 1 represent the airport, $N=\{1,2,\dots ,n\}$ represents the drop-off station.

Table 1. Model parameters.

Decision variable
$w_{ik}$	Start service time of vehicle k to station i
$x_{ijk}$	Does vehicle k depart from station i to station j, Y: $x_{ijk}$=1; N: $x_{ijk}$=0
$y_{ik}$	Does vehicle k provide service for station i,Y: $y_{ik}$=1; N: $y_{ik}$=0
Parameter
K	Vehicle collection
V	Number collection
N	Station collection
${\mathrm{\Delta }}^{+}\left(i\right)$	Collection of arcs emitted from No.i
$Z_1$	Total travel time cost of passengers
$Z_2$	Operating costs of passenger transport enterprises
$t_p$	Unit time value
v	Average vehicle speed
$C_k$	Fixed cost of vehicle k
$f_k$	Unit fuel consumption cost of vehicle k
$d_{ij}$	Distance travelled by vehicles from station i to station j
$q_{ij}$	Passenger capacity of vehicles from station i to station j
$p_{ik}$	Number of passengers served by vehicle k at station i
$a_i$	Left TW of passengers getting off at station i
$b_i$	Right TW of passengers getting off at station i
E	Left TW of the airport
L	Right TW of the airport
$t_s$	Average service time per passenger
$Q_k$	Maximum passenger capacity of vehicle k

3.3. Objective functions and constraints

3.3.1. Objective functions

1. Passengers' overall cost on travel time

   For passengers, it is always desirable to have the lowest travel time cost, which can be expressed as: (1) $min{Z}_1=t_p\cdot \sum _{k\in K}\sum _{i\in N}\sum _{j\in N}(d_{ij}/v)\cdot x_{ijk}\cdot q_{ij}$(1)

2. Operating costs of passenger transport enterprises

   The operating costs of passenger transport enterprises are split into two types: fixed and variable costs (FC & VC). The FCs are about vehicle and about labour. Examples include vehicle depreciation, management fees and driver salaries. Variable costs mainly include fuel costs incurred by vehicle driving. The overall operational cost can be represented as follows: (2) $min{Z}_2=\sum _{k\in K}\sum _{j\in N}{C}_k\cdot x_{0jk}+\sum _{k\in K}\sum _{i\in N}\sum _{j\in N}\cdot f_k\cdot x_{ijk}\cdot d_{ij}$(2) In order to facilitate the subsequent algorithm design and solution, the linear weighting method is used for normalization, and the comprehensive optimization of the two is used as the objective function to construct an optimization model for customized passenger operation lines for airport connection, which is expressed as: (3) $minZ={\omega }_1\cdot min{Z}_1+{\omega }_2\cdot min{Z}_2$(3) In the formula, ${\omega }_1$ and ${\omega }_2$ are the weight values of the total travel time cost of passengers and the operating cost of passenger transport enterprises.

3.3.2. Constraints

1. Vehicle travel path constraints (4) $\sum _{k\in K}\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}=1\mathrm{\forall }i\in N$(4) Equation (4(4) $\sum _{k\in K}\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}=1\mathrm{\forall }i\in N$(4) ) indicates that each station is assigned to a single vehicle only, i.e. each station can only be assigned to one path.

2. Vehicle capacity constraints (5) $\sum _{i\in N}{p}_{ik}\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}\le Q_k\mathrm{\forall }k\in K$(5) Equation (5(5) $\sum _{i\in N}{p}_{ik}\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}\le Q_k\mathrm{\forall }k\in K$(5) ) imposes a constraint on the vehicle capacity, and the number of on board passengers is constrained by the maximum capacity of passenger.

3. Time window constraints (6) $\begin{array}{rl}& a_i\left(\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}\right)\le w_{ik}\le b_i\left(\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}\right)\\ & \mathrm{\forall }k\in K,\mathrm{\forall }i\in N\end{array}$(6) (7) $\begin{array}{rl}& E\le w_{ik}\le L\mathrm{\forall }k\in K,\mathrm{\forall }i\in \{0,n+1\}\end{array}$(7) Equation (6(6) $\begin{array}{rl}& a_i\left(\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}\right)\le w_{ik}\le b_i\left(\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{x}_{ijk}\right)\\ & \mathrm{\forall }k\in K,\mathrm{\forall }i\in N\end{array}$(6) ) indicates that the start of service of vehicle k to passenger i must be within the left TW & right TW of passenger i; Equation (7(7) $\begin{array}{rl}& E\le w_{ik}\le L\mathrm{\forall }k\in K,\mathrm{\forall }i\in \{0,n+1\}\end{array}$(7) ) indicates that the time of departure of the vehicle k from the airport (the time of return to the airport) must be within the left TW & right TW of the airport.

4. Carbon emission constraints (8) $\sum _{k\in K}\sum _{i\in N}\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{s}_{ij}\cdot x_{ijk}\cdot d_{ij}\le ϵ$(8) Equation (8(8) $\sum _{k\in K}\sum _{i\in N}\sum _{j\in {\mathrm{\Delta }}^{+}\left(i\right)}{s}_{ij}\cdot x_{ijk}\cdot d_{ij}\le ϵ$(8) ) indicates that the carbon emissions of the vehicle should be limited to a suitable range. Among them, ε is the carbon emission limit, and $s_{ij}$ is the bus's unit carbon emission between station i and station j.

5. Passenger time constraints in the car (9) $\sum _{i\in N}\sum _{j\in N}\frac{d_{ij}}{v}+\sum _{i\in N}{p}_{ik}\cdot t_s\le T_{max}\mathrm{\forall }k\in K$(9) Equation (9(9) $\sum _{i\in N}\sum _{j\in N}\frac{d_{ij}}{v}+\sum _{i\in N}{p}_{ik}\cdot t_s\le T_{max}\mathrm{\forall }k\in K$(9) ) indicates that with the aim of ensuring the service level of the customized passenger transportation for airport connection, the time for passengers to arrive at the drop-off station by service vehicle cannot exceed the maximum travel time. where $T_{max}$ is the maximum time of the passenger on board.

6. Line drop-off station constraints (10) $\sum _{i\in N}{y}_{ik}\le N_{max}\mathrm{\forall }k\in K$(10) Equation (10(10) $\sum _{i\in N}{y}_{ik}\le N_{max}\mathrm{\forall }k\in K$(10) ) indicates that the stops at which passengers get off the train should be limited to an acceptable range on the line. $N_{max}$ is the maximum number of drop-off stations on the line.

7. Passenger occupancy constraints (11) $\mu Q_k\le \sum _{i\in N}{p}_{ik}\cdot y_{ik}\le Q_k\mathrm{\forall }k\in K$(11) Equation (11(11) $\mu Q_k\le \sum _{i\in N}{p}_{ik}\cdot y_{ik}\le Q_k\mathrm{\forall }k\in K$(11) ) indicates that the passenger occupancy rate of all routes must meet the minimum occupancy rate of customized passenger transport connected by the airport. where μ is the minimum occupancy rate of a line.

4. Model solving

On account of the characteristics (NP-hard) of the model we built, when the number of nodes is large, it is easy to cause ‘combinatorial explosion’. Usually, problems are addressed by using intelligent algorithms (Liu et al., 2018). However, genetic algorithms have good effect, strong global search ability and wide application, so this paper uses improved genetic algorithms to solve these problems.

4.1. Coding and initial population generation

4.1.1. Encode

In this paper, an integer coding method is used to simultaneously represent airports and stations in chromosomes. When the stations' number is N while the vehicles' maximum number is K, the chromosome expression form is a random arrangement of $1\sim (N+K-1)$. Assuming the number of stations is 5, numbered 1–5, and the number of buses in the airport (numbered 0) is 3, the coding chromosome used contains a total of 7 digits, where 1–5 represents stations, and 6 and 7 represent airports. There are three types of arrangement in total.

1. As shown in Figure 2, the numbers 6 and 7 divide the chromosomes into 3 parts, that is, into 3 pathways, as follows:

   • Path No.1: 0→ 1→ 2→ 0

   • Path No.2: 0→ 3→ 4→ 0

   • Path No.3: 0→ 5→ 0

2. As shown in Figure 3, the transport scheme for the chromosome decoding is 2 paths, as below:

   • Path No.1: 0→ 1→ 2→ 3→ 0

   • Path No.2: 0→ 4→ 5→ 0

3. As shown in Figure 4, there is only 1 path after the chromosome is decoded, as follows:

   • Path No.1: 0→ 1→ 2→ 3→ 4→ 5→ 0

4.1.2. Initial population's generation

In this paper, before initializing the population, the problem requires an initial solution to be built. The steps to construct the initial solution are listed as below:

Figure 2. Chromosome code $◯1$.

Figure 3. Chromosome code $◯2$.

Figure 4. Chromosome code $◯3$.

Suppose the number of sites is n.

• Step No.1: Select the site j, $j\in \{1,2,\dots ,n\}$;

• Step No.2: Initialize the vehicles' number with $k\leftarrow 1$;

• Step No.3: Generate a traverses-site sequence $Seq\leftarrow [j,j+1,\dots ,n,1,\dots ,j-1]$;

• Step No.4: Traverse the ordinal number i and traverse until n to generate the initial solution. In traversal order, Seq traverses site $Seq\left(i\right)$, adding site $Seq\left(i\right)$ to the kth path. At the same time, when adding to the corresponding line, the vehicles' passenger capacity and the constraints of the left time window should be considered.

On the basis of the initial solution, obtain half of the initialization population, that is, assign all half of the individuals in this population to the individuals transformed from the initial solution; The remaining half of the initialization population is randomly generated. The quality of the initial population generated based on the initial solution is better than that generated randomly, which can increase the speed of searching for the optimal population, but cannot maintain the diversity of the population. Adding half of the randomly generated initial population can maintain the diversity of the population.

4.2. Fitness assessment and treatment of constraint violations

In this paper, the function of fitness is established by using the objective function's reciprocal: (12) $F=\frac{1}{Z}$(12) Constraints can't be avoided in this optimization model such as passenger capacity, windows of time, and carbon emissions, but in the evolution of algorithms, some individuals exceed these constraints. Therefore, the following methods are taken to make adjustments:

1. Calculate the amount of each constraint for an individual;

2. Determine whether the scheme shown by each individual exceeds the constraint requirements, and if it does, it is deleted with a certain probability;

3. In step (2), the corresponding individuals' number in the remaining population is randomly selected to replicate and the deleted chromosomes are replaced.

4.3. Genetic manipulation

4.3.1. Selection operation

Use binary tournaments for selection operations. Randomly select two chromosome solutions from the current population, select individuals with higher fitness values to enter the offspring population, and repeat the operation until the population size is reached.

4.3.2. Crossover operation

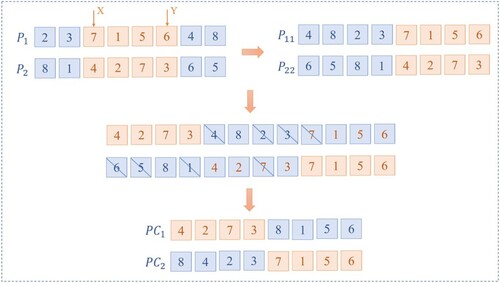
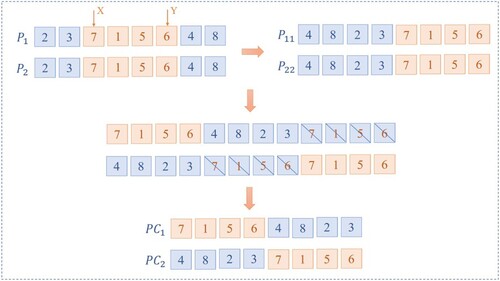
This article improves on the traditional sequential crossover. Specific practices for improved cross operation: (1) Randomly select two chromosomes $P_1$ and $P_2$ with a certain probability $P_c$, and randomly generate two intersection points X and Y; (2) Starting from the first gene after the intersection point Y, list the original sequence to obtain individuals $P_{11}$ and $P_{22}$; (3) Move the crossover segment of chromosome $P_2$ to the head of individual $P_{11}$, and move the crossover segment of chromosome $P_1$ to the tail of individual $P_{22}$; (4) Two new individuals, $P{C}_1$ and $P{C}_2$, were obtained by eliminating the same parts as the crossover fragment (see Figure 5). The biggest feature of this crossover operation is that when two chromosomes are the same, new individuals can still be generated (see Figure 6), thereby reducing the requirement for population diversity and effectively avoiding the disadvantage of traditional genetic algorithms' premature convergence.

Figure 5. Schematic diagram of cross operation for different individual improvement sequences.

4.3.3. Operation of mutation

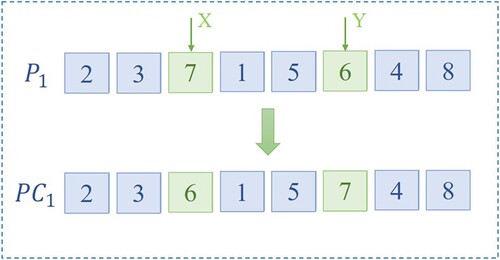
This article adopts annealing mutation operation. The individual first adopts the two point exchange mutation method, which randomly selects a chromosome $P_1$ with a certain probability $P_m$, randomly generates two mutation points X and Y, and exchanges the genes of these two mutation points to obtain a new individual $P{C}_1$, as shown in Figure 7. Then calculate the total cost of the new individual after the mutation, and the total cost of the individual before the mutation. If the total cost after mutation is lower, then the mutation is accepted, otherwise a certain annealing probability is used to determine whether the mutation has occurred. As shown in formula (13(13) $P_m=\{\begin{array}{ll}1,& C_{new}<C_{old}\\ \exp (-{\displaystyle \frac{C_{new}-C_{old}}{Temp}}),& C_{new}>C_{old}\end{array}$(13) ). (13) $P_m=\{\begin{array}{ll}1,& C_{new}<C_{old}\\ \exp (-{\displaystyle \frac{C_{new}-C_{old}}{Temp}}),& C_{new}>C_{old}\end{array}$(13) Among them, $P_m$ is the probability of accepting variation, $C_{old}$ is the total cost required before individual variation, $C_{new}$ is the total cost required after individual variation, and Temp is the annealing temperature. The annealing temperature decreases as the number of iterations of the genetic algorithm increases. The cooling method is based on literature: $Tem{p}_t=\alpha \ast T_0,0\le \alpha \le 1$.Where $\alpha =0.8$ is taken, the temperature drop is shown in formula (14(14) $Tem{p}_t=\{\begin{array}{ll}Tem{p}_0,& \mathrm{I}=1\\ 0.8\ast Tem{p}_{I-1},& I\ne 1\end{array}$(14) ) below. (14) $Tem{p}_t=\{\begin{array}{ll}Tem{p}_0,& \mathrm{I}=1\\ 0.8\ast Tem{p}_{I-1},& I\ne 1\end{array}$(14) Among them, I is the number of iterations of the genetic algorithm, and $Tem{p}_t$ is the mutation annealing temperature at the Ith iteration. $Tem{p}_0$ is the initial temperature. This article draws on the method of literature (Gu, Fu, & Liu, 2005) and sets it as the maximum fitness value of the first generation population minus the minimum fitness value, and then multiplies it by 100, as shown in formula (15(15) $Tem{p}_0=100\ast \left(max\left(C\right)-min\left(C\right)\right)$(15) ) below. (15) $Tem{p}_0=100\ast \left(max\left(C\right)-min\left(C\right)\right)$(15)

Figure 6. Schematic diagram of cross operation for the same individual improvement sequence.

Figure 7. mutation operation diagram.

4.4. Algorithm description

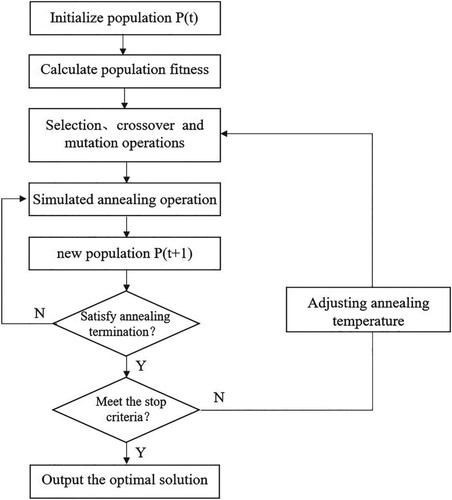
Based on the above theory, a genetic algorithm is designed for solving the optimization model in customizing passenger transport path for airport connection. Genetic algorithm (GA) is a specific algorithm that imitates the process of biological evolution, with good convergence and fast calculation speed, so genetic algorithms are commonly used to solve such problems and can achieve better results. At the same time, this article designs the Annealed Genetic Algorithm (S-GA) to address the insufficient local search ability of genetic algorithms, introducing the destruction operator and repair operator annealing mutation operation in large-scale neighbourhood search algorithms, in order to enhance the algorithm's local search ability. The algorithm process is shown in Figure 8.

Figure 8. GA solution flowchart.

5. Example analysis

5.1. Example design

Since the optimization problem of customized passenger transport routes for airport connections under carbon emission restrictions is a relatively new problem and it's impossible to find any standard test instance library, researchers have to construct test data by themselves. This paper selects the first 25 points of RC107 in the Solomon Benchmark (Solomon, 1987) instance as the drop-off stations of the airport connection route. The demand for each node in Solomon's instance was reduced by a factor of 10 to represent passengers' number disembarking for each station of the airport connection, which implies that the service time for each passenger is identical, amounting to 1 min, and the sum of alighted passengers at each station is 50. This article comprehensively draws on the parameter settings of literature (Li, 2022; Liu, 2022) to obtain the parameters required for the optimization model of customized passenger transportation routes for airport connections: the airport connection customized passenger service vehicle adopts a 9-seater (including driver) commercial vehicle, that is, the vehicles' maximum passenger capacity $Q_k$ is 8 people. The cost/unit time of passenger travel is $t_p=24\mathrm{y}\mathrm{u}\mathrm{a}\mathrm{n}/\mathrm{h}$; The vehicles' operating speed is $v=70\mathrm{k}\mathrm{m}/\mathrm{h}$; Fixed costs of the vehicle is $C_k=120\mathrm{y}\mathrm{u}\mathrm{a}\mathrm{n}/\mathrm{c}\mathrm{a}\mathrm{r}$; Estimated unit cost of fuel consumption is $f_k=1.6\mathrm{y}\mathrm{u}\mathrm{a}\mathrm{n}/\mathrm{k}\mathrm{m}$; Both cost weight values is ${\omega }_1={\omega }_2=1/2$; Unit carbon emissions is $s_{ij}=0.4\mathrm{k}\mathrm{g}/\mathrm{k}\mathrm{m}$; Carbon emission limits is $ϵ=500\mathrm{k}\mathrm{g}$; Maximum time of passengers in the car is $T_{max}=90\mathrm{m}\mathrm{i}\mathrm{n}$; The maximum number of line drop-off stations is set $N_{max}=5$; Minimum occupancy rate is $\mu =0.75$; The data of each node is shown in Table 2 (node 0 represents the airport, node $1\sim 25$ represents the drop-off station).

Table 2. Data for each node.

No.	X/km	Y/km	demands	left TW	right TW	service time/min
0	50	50	0	8:00	12:00	0
1	25	85	2	10:05	11:11	2
2	10	40	3	9:30	10:57	3
3	2	40	2	8:39	10:41	2
4	42	15	1	9:51	10:42	1
5	35	5	2	8:54	11:04	2
6	88	30	2	8:52	10:39	2
7	67	85	2	9:01	11:05	2
8	60	85	1	8:50	10:29	1
9	40	78	3	8:37	10:57	2
10	72	15	2	9:44	10:37	2
11	30	60	2	9:35	11:34	3
12	15	60	3	10:17	11:22	3
13	35	40	1	8:11	10:20	1
14	35	69	1	9:00	11:30	1
15	5	5	3	9:00	10:57	1
16	65	65	1	9:37	11:42	3
17	63	23	2	9:16	10:07	2
18	80	40	2	9:14	10:07	2
19	51	31	2	8:20	9:24	2
20	31	67	3	9:06	11:30	3
21	61	52	3	9:09	11:28	3
22	37	31	2	8:19	9:27	2
23	2	60	3	9:05	9:58	3
24	65	20	1	8:39	9:48	1
25	20	50	1	8:57	10:34	1

5.2. Result analysis

The algorithm is implemented using MATLAB R2021a programming. Assign the maximum number of iterations to 100, and the size of the population to 150. The crossover probability is 0.9, 0.8, 0.7, 0.6, 0.5, the variation probability is 0.05, 0.04, 0.03, 0.02, 0.01 for calculation, GA algorithm runs 10 times continuously under different cross-mutation probability combinations, and the results of the mean, optimal value, running time and other results are calculated as shown in Table 3.

Table 3. GA experimental data.

		Total cost/yuan
Pc	Pm	average value	optimal value	time T/s
0.9	0.01	1109.04	1070.36	49.6
0.9	0.02	1115.06	1095.59	49.3
0.9	0.03	1114.12	1087.79	49.4
0.9	0.04	1097.60	1055.44	49.2
0.9	0.05	1108.30	1024.69	49.2
0.8	0.01	1098.73	1063.50	49.0
0.8	0.02	1109.94	1053.65	48.9
0.8	0.03	1109.31	1093.63	49.2
0.8	0.04	1106.73	1057.08	49.0
0.8	0.05	1105.53	1041.89	49.0
0.7	0.01	1113.18	1083.58	48.7
0.7	0.02	1105.13	1068.38	48.6
0.7	0.03	1100.27	1044.05	48.6
0.7	0.04	1109.76	1085.20	48.7
0.7	0.05	1111.01	1052.33	48.5
0.6	0.01	1113.69	1070.34	48.3
0.6	0.02	1116.04	1085.75	48.5
0.6	0.03	1114.43	1076.83	48.4
0.6	0.04	1103.30	1058.58	48.6
0.6	0.05	1104.41	1058.86	48.4
0.5	0.01	1104.60	1046.69	48.1
0.5	0.02	1111.01	1072.08	48.2
0.5	0.03	1100.38	1053.24	48.1
0.5	0.04	1102.22	1068.79	47.9
0.5	0.05	1118.31	1034.02	48.2

5.2.1. Determination of probability combinations of GA algorithms

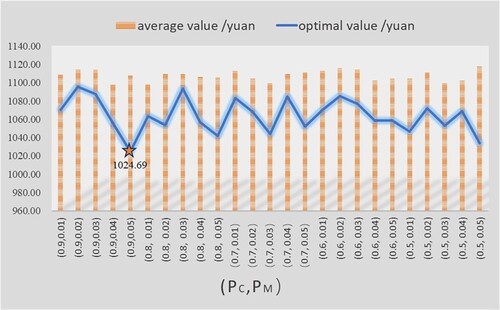
1. In terms of optimal value. From the above table, it can be concluded that the mean and optimal values of the corresponding total time cost vary with different probability combinations, as shown in Figure 9.

   Analysis shows that among the optimal solution values obtained by continuously running 10 times under different probability combinations, when $P_c=0.9$ and $P_m=0.05$, the optimal value is the lowest, with a total cost of 1024.69 yuan. Moreover, the mean value under this probability combination is not significantly different from the optimal value, indicating that the algorithm operates stably under this probability combination.

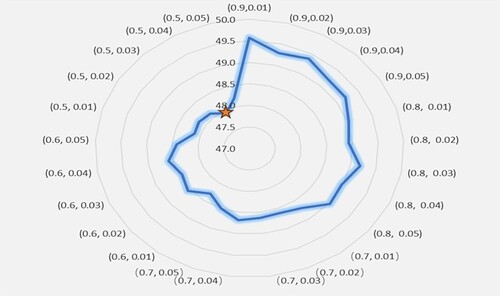
2. In terms of running time. From the above table, it can be concluded that the speed of the corresponding average running time varies with different probability combinations, as shown in Figure 10. It can be clearly seen from the radar chart that the average running time under different probability combinations is stable at less than 50 s, and the algorithm running speed is within an acceptable range. Among them, when $P_c=0.5$ and $P_m=0.04$, the GA algorithm has the shortest running time, with the shortest running time of 47.9 s.

3. In terms of pricing strategy. The objective function of this article is to have the lowest total cost, and the operating costs of the enterprise are standardized and not self-priced. Regarding autonomous pricing, it is the unit time value $t_p$ of passenger travel. So this article sets three pricing options for unit time value $t_p$: sensitivity analysis at 20 yuan/h, 24 yuan/h, and 28 yuan/h. $t_p$ is adjusted up and down according to the original 24 yuan/h to see the impact of changes in $t_p$ on the optimal value. The results indicate that if $t_p$ is too large or too small, it will increase the total cost accordingly. $t_p$ should set a reasonable pricing based on the actual situation.

5.2.2. Determination of path optimization schemes

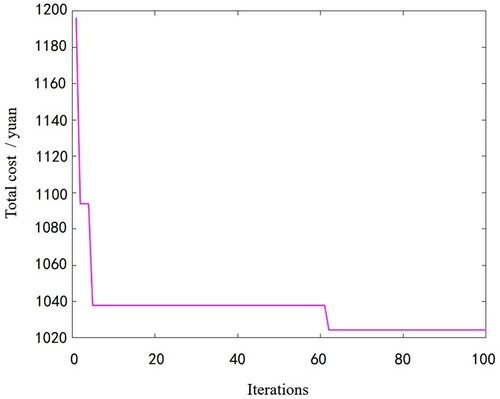
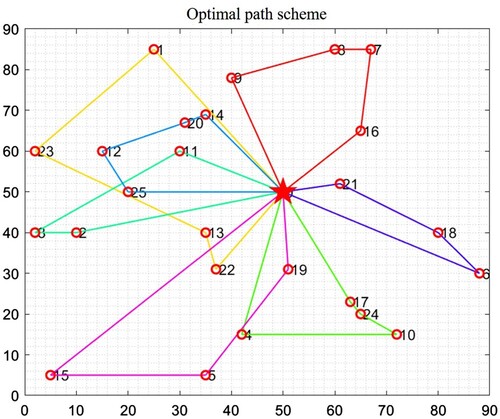
The example is tackled with an optimized genetic algorithm when crossover probability $P_c=0.9$ and mutation probability $P_m=0.05$, as shown in Figure 11. The algorithm presents a ‘ladder-like’ iterative process, indicating that it jumped out of the local optimal solution during operation, conducted a larger range of searches, and the results tended to stabilize after about 60 iterations of the algorithm. The resulting optimal path scheme is depicted in Figure 12. The data in the figure indicate that the final route scheme has 7 passenger routes. The optimal route scheme uses 7 vehicles to serve 50 passengers. The specific information of each route is shown in Table 4, and it can be found that the number of drop-off stations, passengers transported, and the load factor of vehicles on each route meet the constraints, and the total carbon emissions required by the route scheme is 278.81 kg, which meets the carbon emissions limit requirements.

Figure 9. Results under different combinations of crossover mutation probabilities.

Figure 10. Average running time under different cross-mutation probability combinations.

Figure 11. Iteration diagram.

6. Conclusion

Aiming at the optimization problem of customized passenger transport paths for airport connection with carbon emissions restrictions, this paper aims to reduce the total cost of passenger transportation as low as possible, considers the characteristics of time window constraints and passenger occupancy rate that need to be considered in the passenger transport path, and constructs an optimization model that aims to reduce the total cost of passenger transport to the bottom. The model not only considers the transportation cost of customized passenger transportation enterprises but also considers the personalized time needs of each passenger, especially adding the time constraints of passengers on the bus and the constraints of getting off the bus to meet the more detailed requirements of passengers on time to the greatest extent.

Figure 12. Path scheme roadmap.

Table 4. Seven path information statistics.

Route	Path scheme	Number of station/PCS	Number of passengers served/PCS	Attendance	Carbon emission/kg
1	0$\to$9$\to$8$\to$7$\to$16$\to$0	4	7	0.875	42.51
2	0$\to$21$\to$18$\to$6$\to$0	3	7	0.875	30.09
3	0$\to$17$\to$24$\to$10$\to$4$\to$0	4	6	0.75	32.45
4	0$\to$19$\to$5$\to$15$\to$0	3	7	0.875	49.16
5	0$\to$22$\to$13$\to$23$\to$1$\to$0	4	8	1	53.51
6	0$\to$2$\to$3$\to$11$\to$0	3	7	0.875	37.36
7	0$\to$25$\to$12$\to$20$\to$14$\to$0	4	8	1	33.73

This paper adopts an improved genetic algorithm to solve the problem. The biggest feature of the improvement is the improved sequential crossover method, which makes the crossover operation always produce new individuals, effectively avoiding ‘premature convergence’, and the algorithm has better convergence, which can effectively solve the problem and can provide decision-making reference for the airport connection customization service of relevant, customized passenger transport enterprises.

This study assumes that there is only one passenger vehicle with the same passenger capacity in customized passenger transport enterprises, and subsequent research can consider the route optimization problem of airport connection customized passenger vehicles with different passenger capacities to be more realistic and design a more efficient and accurate algorithm to solve the problem.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This research is supported by Chongqing Dr. Through Train Project [CSTB2022BSXM-JCX0099], Chongqing Social Science Planning Project [2019YBGL049; 2020QNGL43], Science Foundation of Chongqing Jiaotong University [20JDKJC-B051], Postgraduate research and innovation project of Chongqing Jiaotong University [2022S0031], Chongqing Municipal Transportation Bureau Science and Technology Project [2022-17; 2022-18], Team Building Project for Graduate Tutors in Chongqing [JDDSTD2022004].