?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
This paper discusses the encryption-decryption-based state estimation (EDBSE) issue for coupled perturbation complex networks (CPCNs) in the framework of the Kalman-type filtering scheme. A uniform distributed random variable is employed to characterize the coupled perturbation among different network units. A uniform-quantization-dependent encryption-decryption (UQDED) scheme is considered here to orchestrate the transmitted data. A novel EDBSE approach is developed such that the upper bounds of prediction error (PE) covariance (PEC) and estimation error (EE) covariance (EEC) can be derived by resolving Riccati-like difference equations and the estimation parameter (EP) is determined by minimizing the trace of the upper bound of EEC. Furthermore, a uniformly bounded condition is elaborated to evaluate the algorithm performance of EDBSE. Finally, an illustrative example is conducted to verify the validity of the introduced EDBSE method.
1. Introduction
Over the past few decades, the prosperous development of complex networks (CNs) has been witnessed, which are made up of large-scale coupled units with individual dynamics. For this reason, some complex systems in practice have been modelled and characterized by CNs, such as social networks, traffic networks, smart grids and so on. It plays a significant role to carry out the analysis and synthesis with respect to networked or dynamical systems recently, including but are not limited to synchronization (Wei et al., Citation2024; Zheng & Zhang, Citation2024), control (Ding & Sun, Citation2023; Pang et al., Citation2021, Citation2022; J. Tan et al., Citation2023; Zhu, Citation2019; Zhu & Huang, Citation2021) and state estimation (Caballero-Águila et al., Citation2020b; Feng et al., Citation2023; J. Hu et al., Citation2023; Song et al., Citation2024; H. Tan et al., Citation2024; K.-Y. Wang et al., Citation2024; L. Wang et al., Citation2022). Consequently, the design of state estimation algorithm for CNs has gained extensive research attention (C. Hu et al., Citation2023; J. Hu et al., Citation2022; F. Li et al., Citation2024; Sakthivel et al., Citation2024). For example, a Kalman-type state estimation problem was investigated in Jia et al. (Citation2023) for a kind of quantized coupled CNs with imperfect measurements and amplify-forward-relay communication, where the estimator parameter (EP) was designed under the variance-constrained index to minimize the trace of the upper bound of estimation error (EE) covariance (EEC). A distributed state estimation issue was discussed in Peng et al. (Citation2023) for a kind of CNs subject to nonlinear uncertainty. In addition, a sufficient principle regarding the stability of the upper bound of EEC was given. Although CNs have broad application prospects, they have not yet received sufficient study in the framework of Kalman-type filtering scheme, which stimulates us to carry out such an idea in this paper.
Recently, the state estimation for networked systems has appealed a great number of attention, see (Caballero-Águila et al., Citation2020a, Citation2020b, Citation2020a; Caballero-Águila & Linares-Pérez, Citation2023; García-Ligero et al., Citation2020; J. Hu et al., Citation2023; Tao et al., Citation2022) for more details. Actually, the coupled dynamic is one of the major focuses during the design of state estimation algorithm in the framework of CNs. The connection among different network units usually fluctuates due to the limited resource or changeable external environment. Consequently, a growing number of scholars have paid more attention on the state estimation for CNs with coupled dynamics. For instance, an state estimation issue was investigated in Meng et al. (Citation2023) for a class of CNs with missing packets, where an uncertain coupling was described by a parameter varying in a given interval and a sufficient criterion was presented to guarantee the pre-defined
performance. Taking the bandwidth-limited channel into account, L. Liu et al. (Citation2020) emphasized the design of a state estimation algorithm for a kind of delayed CNs, where the phenomenon of coupled delay was considered and modelled due to the limited network resource. Furthermore, the sufficient condition regarding finite-time boundedness was established by resorting to algebraic inequalities. It should be pointed out that the varying environment may be caused by network attacks besides the resource-limited situation. In this scenario, this paper aims to addressing the state estimation problem for CNs suffering from coupled perturbation induced by opponent attacks.
On another frontier, in the networked environment, data-treatment has been frequently employed to alleviate the communication burden and avoid communication constraints (H. Gao et al., Citation2023; X. Wang et al., Citation2022; Y.-A. Wang et al., Citation2023; H. Yang et al., Citation2024; J. Yang et al., Citation2022). Especially, the data-security-treatment has gradually been a focus in the dynamical analyses of networked systems (Cheng et al., Citation2023; Luo et al., Citation2023; Pang et al., Citation2022, Citation2021; Sun et al., Citation2022; Wen et al., Citation2022; Wu et al., Citation2022; Zha et al., Citation2024; Zou et al., Citation2023). Specifically, the sliding mode consensus problem under privacy preservation and disturbance was explored by J. Liu et al. (Citation2024) for a class of multi-agent systems, where an encryption–decryption strategy was proposed to enhance the data security. The secure state estimation method was proposed by Zou et al. (Citation2023) for a class of multi-rate system, where an encryption–decryption scheme was considered to defend against eavesdroppers and uniform boundedness regarding EE was given. It is worth mentioning that the employment of encryption–decryption strategy can strengthen the data security while may resulting in data distortion described by decryption error, which enhances the handling difficulty of the design of state estimation in the framework of Kalman-type filtering. For example, the set-membership filtering problems for time-varying systems subject to encryption–decryption communication protocol were tackled in Y. Gao et al. (Citation2022); J.-Y. Li et al. (Citation2023) and Ma et al. (Citation2021), where the upper bounds of decryption errors were described by resorting to uniform-type quantization scheme. It should be noted that the discussions regarding the state estimation for CNs with encryption–decryption strategy have been reported inadequately up to now, which motivates us to shorten such a gap.
Motivated by the aforementioned summary, this paper concentrates on the encryption–decryption-based state estimation (EDBSE) issue for coupled perturbation complex networks (CPCNs). The main encountered difficulties and challenges can be listed as (a) how to obtain an upper bound of EEC by resolving two coupled matrix equations in the simultaneous presence of decryption error, coupled perturbation and system noises; (b) how to determine EP in the framework of Kalman-type filtering so as to make the trace of the upper bound of EEC minimized at each instant; and (c) how to evaluate the developed estimation algorithm and give a boundedness analysis. The corresponding contributions can be summed up as (1) an attractive EDBSE method is proposed for CPCNs, where an upper bound of EEC with a recursive form involving encryption–decryption parameters and coupled perturbation information is obtained; (2) a selected EP is parameterized via optimizing variance-constrained index; and (3) a uniformly bounded condition is elaborated to evaluate the proposed estimation algorithm performance.
Notations
The notations used here are standard. For example, denotes the Euclidean norm. Matrix
means the transpose of M and
denotes the inverse operation of M. The notation P>0
signifies that P is symmetric and positive (semi-positive) definite. I and 0 denote the unit matrix and zero matrix with compatible dimensions.
2. Problem formulation and preliminaries
Consider the following CPCNs with S units (1)
(1)
(2)
(2) where
is the
-dimensional model state and
denotes the
-dimensional sensor measurement.
and Π stand for the outer coupling matrix and the inner coupling matrix, respectively.
and
are well-dimensioned known system matrices.
is a zero-mean system noise with variance
, and
is zero-mean noise from sensor measurement with variance
.
is a nonlinear function satisfying
with
and
being a known scaling matrix. The coupled perturbation is described by
with the form of
(3)
(3) where
is an external perturbation usually caused by network attacks in the unit-to-unit channel, whose element
is mutually independent regarding ϕ and uniformly distributed in
with mean 0 and variance
.
Remark 2.1
Due to the uncertain network environment, the node-to-node communication may be contaminated by malicious attacks, which is specifically manifested in the occurrence of coupled perturbation. In this paper, a uniformly distributed random variable is employed to describe the phenomenon of coupled perturbation. Obviously, if a increases, the introduced estimation algorithm accuracy will decrease, which will be confirmed by the subsequent simulation example.
To enhance the security of the transmitted data, a uniform-quantization-dependent encryption–decryption (UQDED) strategy is employed. To begin with, the encryption procedure is described by
(4)
(4) where
is an auxiliary variable and
denotes the generated codeword of encoder.
is a scaling parameter.
functions as a quantization operation characterized by
where
is the ℘-th element in
. l>0 is a scalar,
denotes quantization level,
.
The decryption output is characterized by
(5)
(5) Comparing (Equation4
(4)
(4) ) and (Equation5
(5)
(5) ) yields
. The decryption error is denoted by
. Obviously, we have
(6)
(6) which signifies that
(7)
(7)
Remark 2.2
To guarantee the security and reliability, an encryption–decryption strategy is employed in the process of data transmission, where a uniform-type quantizer is used to process data exposed in the uncertain network environment. Moreover, the decryption error can be bound by the quantization density, scaling parameter and measurement output dimension. It can be seen from (Equation7(7)
(7) ) that the decryption error is proportional to
,
and
. Actually, we can choose the smaller
and l to satisfy the high-precision requirement in practice.
Considering UQDED and coupled perturbation, the following predictor-estimator with recursive form is constructed (8)
(8)
(9)
(9) where
and
stand for the prediction and estimation of system state,
denotes the EP to be determined later.
3. Main results
We make a great effort to derive the upper bound regarding EEC and determine the EP to minimize the trace of such upper bound. First of all, the prediction error (PE) and EE
are, respectively, presented by
(10)
(10) and
(11)
(11) The following theorem introduces the covariance matrices regarding PE and EE, i.e.
and
.
Theorem 3.1
and
respectively satisfy the following recursions
(12)
(12) and
(13)
(13)
Proof.
The proof is omitted here for simplicity.
The following theorem gives the recursion with respect to the upper bound of EEC and parameterizes the EP to minimize the trace of the derived upper bound.
Theorem 3.2
For adjusted parameters ,
and
, if the following matrix equations
(14)
(14) and
(15)
(15) where
with initial condition
have solutions
and
, then
is an upper bound of
, i.e.
.
Furthermore, if the EP is parameterized by (16)
(16) then the index
can be minimized at every instant.
Proof.
According to the inequality with o>0 being an adjusted parameter,
and
being well-dimensioned matrices, yields
(17)
(17) where
is an adjusted parameter. Substitute (Equation17
(17)
(17) ) into (Equation12
(12)
(12) ) leading to
(18)
(18) Handling the nonlinearity, one has
(19)
(19) where
is a known scaling matrix defined before. In terms of the statistical characteristics of coupled perturbation, we have
(20)
(20) where
is defined in Theorem 3.1. Notice that
(21)
(21) Substitute (Equation19
(19)
(19) )–(Equation21
(21)
(21) ) into (Equation18
(18)
(18) ) yielding
(22)
(22) Subsequently, the upper bound of EEC is derived. Recall inequality
leading to
(23)
(23) and
(24)
(24) where
and
are adjusted parameters. In terms of (Equation23
(23)
(23) ) and (Equation24
(24)
(24) ), one has
(25)
(25) Note that
(26)
(26) Thus, we have
(27)
(27) Considering (Equation14
(14)
(14) )–(Equation15
(15)
(15) ), (Equation22
(22)
(22) ), (Equation27
(27)
(27) ) as well as mathematical induction, one has
.
Finally, determine the EP to minimize the trace of . Calculate
leading to
(28)
(28) Let
resulting in
(29)
(29) which can minimize the trace of
and the proof is verified completely.
Remark 3.1
Taking nonlinearity, coupled perturbation and UQDED into account simultaneously, two recursive matrix equations are concretized in (Equation14(14)
(14) ) and (Equation15
(15)
(15) ). In the framework of the Kalman-type filtering strategy, the trace of (Equation15
(15)
(15) ) is minimized by selecting the EP in (Equation16
(16)
(16) ).
4. Boundedness analysis
This section is concerned with the performance discussion of the proposed EDBSE algorithm. A uniformly bounded condition regarding is elaborated and testified in the following theorem. Before proceeding, the following assumption is presented necessarily.
Assumption 4.1
For positive scalars ,
,
,
,
,
,
,
and
, the following inequalities
hold for each θ, ρ and κ.
Theorem 4.1
Assume that . If the following condition holds
(30)
(30) with
and
, then
is said to be uniformly bounded and satisfies
for each θ.
Proof.
The minimized can be derived according to the selected EP in (Equation16
(16)
(16) ) satisfying
(31)
(31) With the help of induction, based on the initial condition
and assumption
, the conclusion
will be proved inductively. Taking the Assumption 4.1 into account, one has
(32)
(32) and
(33)
(33) Accordingly, we can obtain
In terms of the condition in (Equation30
(30)
(30) ), we can arrive at obviously
(34)
(34) To sum up, the proof of the boundedness analysis is completed.
Remark 4.1
Due to the comprehensive consideration including nonlinearity, coupled perturbation, UQDED and system noises, the constructed predictor-estimator should hold the ability to resist the uncertain factors just mentioned, thereby ensuring that the EE is limited within an acceptable range. To clarify the performance evaluation of the introduced EDBSE method, a uniformly bounded analysis is elaborated based on some reasonable parameter assumptions. In order to facilitate the clarification of the developed EDBSE algorithm, the specific implementation steps are revealed in Table .
Table 1. The EDBSE algorithm.
5. Numerical simulation
This section is devoted to carrying out a numerical simulation to demonstrate the validity of the proposed EDBSE algorithm.
Consider the CPCNs in (Equation1(1)
(1) )–(Equation3
(3)
(3) ) with 3 units. The system matrices are given by
The inner and outer coupling matrices are, respectively, given by
and
with
and
. The system state
is made up of
and
. Set the initial values of EDBSE as
,
and
. The other selected parameters satisfy
,
,
, a = 2,
, l = 1,
,
. The variances of
and
are respectively chosen as
and
. Moreover, the nonlinear function satisfies
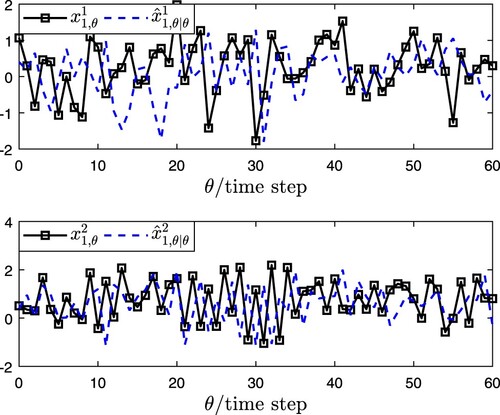
The corresponding simulation results of EDBSE method are presented in Figures . Figure denotes
and its estimation
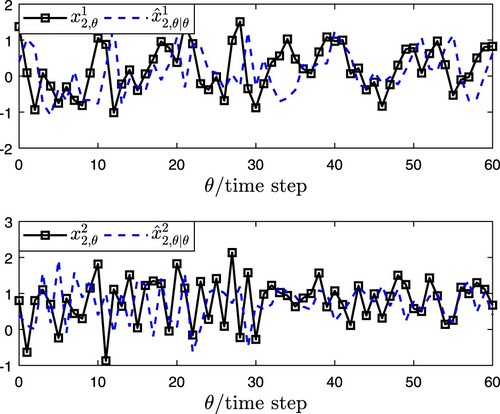
. Figure characterizes
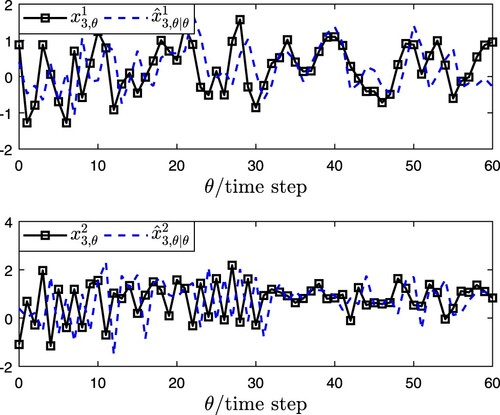
and its estimation
.
and its estimation
are plotted in Figure . From the results of Figures –, it can be seen that the developed EDBSE method can estimate the state of CPCNs effectively. The index
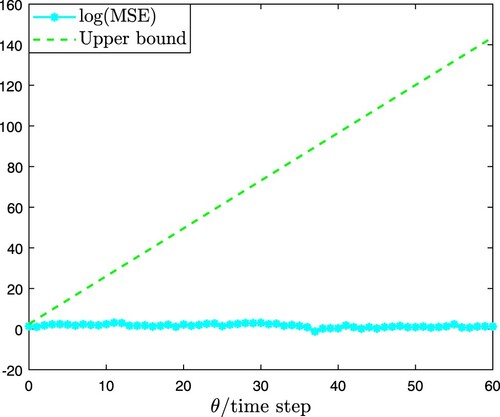
denotes the mean square error of the κ unit and MSE is the sum of
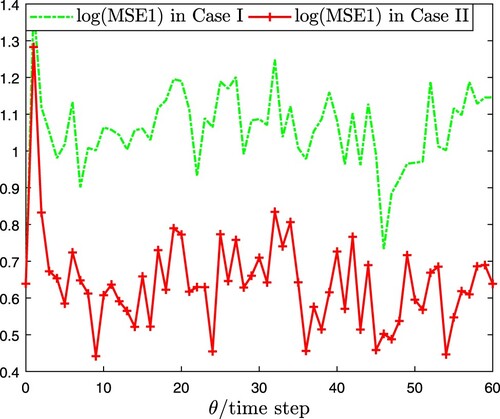
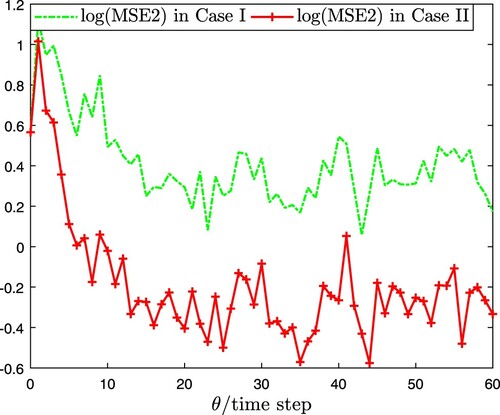
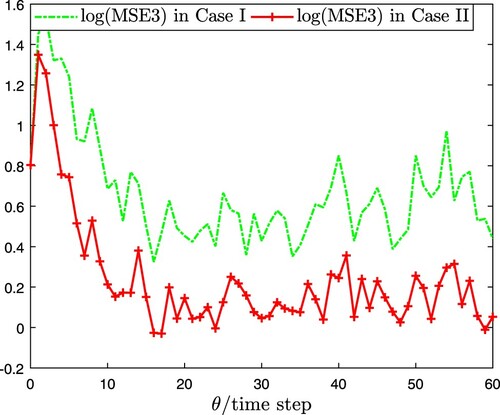
. The MSE and its upper bound are shown in Figure , which signifies that the MSE always keeps below its upper bound. To reveal the influence of coupled perturbation on the EDBSE algorithm (Case I: a = 2 and Case II: a = 0.2), comparison results regarding
are drew in Figures – respectively performed by Monte Carlo simulation with 100 iteration, i.e.
Obviously, the coupled perturbation with a larger fluctuation range can result in the reduction of estimation accuracy.
6. Conclusions
An EDBSE algorithm for CPCNs has been proposed in this paper. Firstly, a bounded nonlinearity has been described to embody the dynamical behaviour of CPCNs. Then, considering the unreliable interaction among different units, a uniform distributed random variable has been adopted to describe the phenomenon of coupled perturbation. Consequently, a UQDED strategy has been employed to pre-process data so as to enhance security and reliability. An effective EDBSE approach has been developed to guarantee the existence of the upper bound of EEC, where the EP has been designed to minimize the trace of such upper bound. Moreover, a sufficient condition has been given and testified to clarify the uniform boundedness of EE. Finally, a simulation example has been presented to verify the availability of the concerned EDBSE algorithm. The extended research directions could include the memory-based event-triggered state estimation, stochastic-communication-based state estimation and so on.
Acknowledgments
CRediT authorship contribution statement: Chaoqing Jia: Conceptualization, Methodology, Investigation, Writing-original draft, Writing-review editing, Supervision. Peixia Gao: Methodology, Writing-original draft, Writing-review
editing, Investigation, Software, Validation. Aozhan Zhou: Writing-review
editing, Software, Validation.
Disclosure statement
No potential conflict of interest was reported by the author(s).
Data availability statement
The data that support the findings of this study are available from the corresponding author, Chaoqing Jia, upon reasonable request.
Additional information
Funding
References
- Caballero-Águila, R., García-Garrido, I., & Linares-Pérez, J. (2020a). Distributed fusion estimation from measurements with correlated random parameter matrices and noise correlation. International Journal of Computer Mathematics, 97(1-2), 95–108. https://doi.org/10.1080/00207160.2018.1437264
- Caballero-Águila, R., García-Garrido, I., & Linares-Pérez, J. (2020b). Distributed fusion filtering for multi-sensor systems with correlated random transition and measurement matrices. International Journal of Computer Mathematics, 97(1-2), 263–274. https://doi.org/10.1080/00207160.2018.1554213
- Caballero-Águila, R., Hermoso-Carazo, A., & Linares-Pérez, J. (2020a). A two-phase distributed filtering algorithm for networked uncertain systems with fading measurements under deception attacks. Sensors, 20(22), 6445. https://doi.org/10.3390/s20226445
- Caballero-Águila, R., Hermoso-Carazo, A., & Linares-Pérez, J. (2020b). Networked fusion estimation with multiple uncertainties and time-correlated channel noise. Information Fusion, 54, 161–171. https://doi.org/10.1016/j.inffus.2019.07.008
- Caballero-Águila, R., & Linares-Pérez, J. (2023). Distributed fusion filtering for uncertain systems with coupled noises, random delays and packet loss prediction compensation. International Journal of Systems Science, 54(2), 371–390. https://doi.org/10.1080/00207721.2022.2122905
- Cheng, Z., Ren, H., Qin, J., & Lu, R. (2023). Security analysis for dynamic state estimation of power systems with measurement delays. IEEE Transactions on Cybernetics, 53(4), 2087–2096. https://doi.org/10.1109/TCYB.2021.3108884
- Ding, L., & Sun, W. (2023). Predefined time fuzzy adaptive control of switched fractional-order nonlinear systems with input saturation. International Journal of Network Dynamics and Intelligence, 2(4), 100019. https://doi.org/10.53941/ijndi.2023.100019
- Feng, S., Li, X., Zhang, S., Jian, Z., Duan, H., & Wang, Z. (2023). A review: State estimation based on hybrid models of Kalman filter and neural network. Systems Science & Control Engineering, 11(1), 2173682. https://doi.org/10.1080/21642583.2023.2173682
- Gao, H., Li, Y., Yu, L., & Yu, H. (2023). Collaborative-prediction-based recursive filtering for nonlinear systems with sensor saturation under duty cycle scheduling. Systems Science & Control Engineering, 11(1), 2247007. https://doi.org/10.1080/21642583.2023.2247007
- Gao, Y., Ma, L., Zhang, M., Guo, J., & Bo, Y. (2022). Distributed set-membership filtering for nonlinear time-varying systems with dynamic coding-decoding communication protocol. IEEE Systems Journal, 16(2), 2958–2967. https://doi.org/10.1109/JSYST.2021.3063357
- García-Ligero, M. J., Hermoso-Carazom, A., & Linares-Pérez, J. (2020). Covariance-based least-squares filtering algorithm under Markovian measurement delays. International Journal of Computer Mathematics, 97(1-2), 40–50. https://doi.org/10.1080/00207160.2017.1422496
- Hu, C., Ding, S., & Xie, X. (2023). Event-based distributed set-membership estimation for complex networks under deception attacks. IEEE Transactions on Automation Science and Engineering. https://doi.org/10.1109/TASE.2023.3284448
- Hu, J., Li, J., Yan, H., & Liu, H. (2023). Optimized distributed filtering for saturated systems with amplify-and-forward relays over sensor networks: A dynamic event-triggered approach. IEEE Transactions on Neural Networks and Learning Systems. https://doi.org/10.1109/TNNLS.2023.3308192
- Hu, J., Wang, C., Caballero-Águila, R., & Liu, H. (2023). Distributed optimal fusion filtering for singular systems with random transmission delays and packet dropout compensations. Communications in Nonlinear Science and Numerical Simulation, 119, 107093. https://doi.org/10.1016/j.cnsns.2023.107093
- Hu, J., Wang, Z., & Liu, G.-P. (2022). Delay compensation-based state estimation for time-varying complex networks with incomplete observations and dynamical bias. IEEE Transactions on Cybernetics, 52(11), 12071–12083. https://doi.org/10.1109/TCYB.2020.3043283
- Jia, C., Hu, J., Yi, X., Liu, H., Huang, J., & Cao, Z. (2023). Recursive state estimation for a class of quantized coupled complex networks subject to missing measurements and amplify-and-forward relay. Information Sciences, 630, 53–73. https://doi.org/10.1016/j.ins.2023.02.017
- Li, F., Cai, Y., Su, L., Shen, H., & Xu, S. (2024). H∞ state estimation for two-time-scale Markov jump complex networks under analog fading channels: A hidden-Markov-model-based method. IEEE Transactions on Circuits and Systems I: Regular Papers. https://doi.org/10.1109/TCSI.2024.3372548
- Li, J.-Y., Wang, Z., Lu, R., & Xu, Y. (2023). A component-based coding-decoding approach to set-membership filtering for time-varying systems under constrained bit rate. Automatica, 152, 110874. https://doi.org/10.1016/j.automatica.2023.110874
- Liu, J., Deng, Y., Zha, L., Xie, X., & Tian, E. (2024). Event-based privacy-preserving security consensus of multi-agent systems with encryption-decryption mechanism. International Journal of Robust and Nonlinear Control, 34(7), 4787–4801.https://doi.org/10.1002/rnc.7232
- Liu, L., Zhang, Y., Zhou, W., Ren, Y., & Li, X. (2020). Event-triggered approach for finite-time state estimation of delayed complex dynamical networks with random parameters. International Journal of Robust and Nonlinear Control, 30(14), 5693–5711. https://doi.org/10.1002/rnc.v30.14
- Luo, Y., Wang, Z., Hu, J., Dong, H., & Yue, D. (2023). Security-guaranteed fuzzy networked state estimation for 2-D systems with multiple sensor arrays subject to deception attacks. IEEE Transactions on Fuzzy Systems, 31(10), 3624–3638. https://doi.org/10.1109/TFUZZ.2023.3262609
- Ma, L., Wang, Z., Chen, Y., & Yi, X. (2021). Probability-guaranteed distributed filtering for nonlinear systems with innovation constraints over sensor networks. IEEE Transactions on Control of Network Systems Control, 8(2), 951–963. https://doi.org/10.1109/TCNS.2021.3049361
- Meng, X., Wang, Z., Wang, F., & Chen, Y. (2023). Finite-horizon H∞ state estimation for complex networks with uncertain couplings and packet losses: Handling amplify-and-forward relays. IEEE Transactions on Neural Networks and Learning Systems. https://doi.org/10.1109/TNNLS.2023.3304515
- Pang, Z.-H., Bai, C., Liu, G., Han, Q., & Zhang, X. (2021). A novel networked predictive control method for systems with random communication constraints. Journal of Systems Science and Complexity, 34(4), 1364–1378. https://doi.org/10.1007/s11424-021-0160-y
- Pang, Z.-H., Fan, L.-Z., Dong, Z., Han, Q.-L., & Liu, G.-P. (2022). False data injection attacks against partial sensor measurements of networked control systems. IEEE Transactions on Circuits and Systems II: Express Briefs, 69(1), 149–153.
- Pang, Z.-H., Fan, L.-Z., Sun, J., Liu, K., & Liu, G.-P. (2021). Detection of stealthy false data injection attacks against networked control systems via active data modification. Information Sciences, 546, 192–205. https://doi.org/10.1016/j.ins.2020.06.074
- Pang, Z.-H., Zheng, C.-B., Li, C., Liu, G.-P., & Han, Q.-L. (2022). Cloud-based time-varying formation predictive control of multi-agent systems with random communication constraints and quantized signals. IEEE Transactions on Circuits and Systems II: Express Briefs, 69(3), 1282–1286.
- Peng, H., Zeng, B., Yang, L., Xu, Y., & Lu, R. (2023). Distributed extended state estimation for complex networks with nonlinear uncertainty. IEEE Transactions on Neural Networks and Learning Systems, 34(9), 5952–5960. https://doi.org/10.1109/TNNLS.2021.3131661
- Sakthivel, N., Pallavi, S., & Kwon, O. M. (2024). H∞ state estimation for stochastic complex dynamical networks with random feedback gain variations and mixed delays. International Journal of Control. https://doi.org/10.1080/00207179.2024.2306480
- Song, W., Wang, Z., Li, Z., Wang, J., & Han, Q.-L. (2024). Nonlinear filtering with sample-based approximation under constrained communication: Progress, insights and trends. IEEE/CAA Journal of Automatica Sinica, 11(7), 1539–1556.https://doi.org/10.1109/JAS.2023.123588
- Sun, Y., Tian, X., & Wei, G. (2022). Finite-time distributed resilient state estimation subject to hybrid cyber-attacks: A new dynamic event-triggered case. International Journal of Systems Science, 53(13), 2832–2844. https://doi.org/10.1080/00207721.2022.2083256
- Tan, J., Li, Y., Xie, Q., & Wang, X. (2023). Modeling and causality analysis of human sensorimotor control system based on NVAR method. International Journal of Network Dynamics and Intelligence, 2(4), 100014. https://doi.org/10.53941/ijndi.2023.100014
- Tan, H., Shen, B., Li, Q., & Liu, H. (2024). Recursive filtering for stochastic systems with filter-and-forward successive relays. IEEE/CAA Journal of Automatica Sinica, 11(5), 1202–1212. https://doi.org/10.1109/JAS.2023.124110
- Tao, H., Tan, H., Chen, Q., Liu, H., & Hu, J. (2022). H∞ state estimation for memristive neural networks with randomly occurring DoS attacks. Systems Science & Control Engineering, 10(1), 154–165. https://doi.org/10.1080/21642583.2022.2048322
- Wang, L., Liu, S., Zhang, Y., Ding, D., & Yi, X. (2022). Non-fragile l2-l∞ state estimation for time-delayed artificial neural networks: An adaptive event-triggered approach. International Journal of Systems Science, 53(10), 2247–2259. https://doi.org/10.1080/00207721.2022.2049919
- Wang, Y.-A., Shen, B., Zou, L., & Han, Q.-L. (2023). A survey on recent advances in distributed filtering over sensor networks subject to communication constraints. International Journal of Network Dynamics and Intelligence, 2(2), 100007. https://doi.org/10.53941/ijndi0201007
- Wang, X., Sun, Y., & Ding, D. (2022). Adaptive dynamic programming for networked control systems under communication constraints: A survey of trends and techniques. International Journal of Network Dynamics and Intelligence, 1(1), 85–98. https://doi.org/10.53941/ijndi0101008
- Wang, K.-Y., Ye, D., & Zhang, T.-Y. (2024). Data-driven undetectable attack against state estimation in distributed control systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 54(5), 3134–3143. https://doi.org/10.1109/TSMC.2024.3356028
- Wei, C., Wang, X., Ren, F., & Zeng, Z. (2024). Quasi-synchronization for variable-order fractional complex dynamical networks with hybrid delay-dependent impulses. Neural Networks, 173, 106161. https://doi.org/10.1016/j.neunet.2024.106161
- Wen, P., Li, X., Hou, N., & Mu, S. (2022). Distributed recursive fault estimation with binary encoding schemes over sensor networks. Systems Science & Control Engineering, 10(1), 417–427. https://doi.org/10.1080/21642583.2022.2063203
- Wu, J., Peng, C., Yang, H., & Wang, Y. L. (2022). Recent advances in event-triggered security control of networked systems: A survey. International Journal of Systems Science, 53(12), 2624–2643. https://doi.org/10.1080/00207721.2022.2053893
- Yang, J., Ma, L., Chen, Y., & Yi, X. (2022). L2-L∞ state estimation for continuous stochastic delayed neural networks via memory event-triggering strategy. International Journal of Systems Science, 53(13), 2742–2757. https://doi.org/10.1080/00207721.2022.2055192
- Yang, H., Yan, H., Zhou, J., Zhang, Y., & Chang, Y. (2024). Neural-network-based set-membership filtering under WTOD protocols via a novel event-triggered compensation mechanism. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 54(5), 2954–2964. https://doi.org/10.1109/TSMC.2023.3348290
- Zha, L., Guo, Y., Liu, J., Xie, X., & Tian, E. (2024). Protocol-based distributed security fusion estimation for time-varying uncertain systems over sensor networks: Tackling DoS attacks. IEEE Transactions on Signal and Information Processing Over Networks, 10, 119–130. https://doi.org/10.1109/TSIPN.2024.3356789
- Zheng, Z., & Zhang, Q. (2024). Synchronization in directed nonlinear complex networks under intermittent stochastic control. Communications in Nonlinear Science and Numerical Simulation, 132, 107894. https://doi.org/10.1016/j.cnsns.2024.107894
- Zhu, Q. (2019). Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback control. IEEE Transactions on Automatic Control, 64(9), 3764–3771. https://doi.org/10.1109/TAC.9
- Zhu, Q., & Huang, T. (2021). H∞ control of stochastic networked control systems with time-varying delays: The event-triggered sampling case. International Journal of Robust and Nonlinear Control, 31(18), 9767–9781. https://doi.org/10.1002/rnc.v31.18
- Zou, L., Wang, Z., Shen, B., & Dong, H. (2023). Encryption-decryption-based state estimation with multi-rate measurements against eavesdroppers: A recursive minimum-variance approach. IEEE Transactions on Automatic Control, 68(12), 8111–8118. https://doi.org/10.1109/TAC.2023.3288624
- Zou, L., Wang, Z., Shen, B., Dong, H., & Lu, G. (2023). Encrypted finite-horizon energy-to-peak state estimation for time-varying systems under eavesdropping attacks: Tackling secrecy capacity. IEEE/CAA Journal of Automatica Sinica, 10(4), 985–996. https://doi.org/10.1109/JAS.2023.123393