Discovery of double helix of screw dislocations: a perspective

Abstract

We discuss the conversion of a pure screw dislocation into a helical (single helix) dislocation through absorption of vacancies. These helical dislocations having some edge and mostly screw character can pair up through attractive interaction to form a double helix. This attractive interaction between two helices is derived through the edge component of mixed dislocations and from the presence of vacancy jogs. Recent results on the growth of GeS [1] and PbS [3] nanowires with Eshelby twist showed large disagreements between experimental and theoretical Burgers vectors for these crystal structures, which can be resolved by introducing the double helix of screw dislocations.

IMPACT STATEMENT

Single helix and double helix of screw dislocations provide continuous growth steps for all crystalline structures. Thus, nanostructures materials can be grown without any need for catalysts. These dislocations also introduce Eshelby twist and create novel nanostructured materials with unique properties.

KEYWORDS:

• Helical screw dislocations
• double helix of screw dislocations
• Eshelby twist
• nanowire growth

1. Introduction

Screw dislocations play a critical role in crystal growth by providing continuous growth steps. This self-seeding mechanism of crystal growth can overcome the use of catalysts in the growth of nanostructures, such as nanowires, and minimize impurity contamination. The catalysts often lead to undesirable impurity contamination, where a few atoms can lead to large local concentrations and changes in properties. Recent results on the growth of GeS nanowires [1] have been interpreted invoking Eshelby twist [2] with single screw dislocations along the axes of nanowires. However, there is a large disagreement between experimental (1.75 nm) and theoretical (1.04 nm) Burgers vectors. This disagreement is similar to earlier results on the growth of PbS nanowires with Eshelby twist [3]. These discrepancies are now resolved by introducing a double helix of screw dislocations, where both single and double-helix dislocations are involved in the nanowire growth with Eshelby twist.

Screw dislocations during growth can absorb point defects such as vacancies and become helical. These helical dislocations are of mixed character with a constant angle of the helix (θ) with the screw axis and provide growth steps corresponding to the screw (bcosθ) component, where b is the Burgers vector of the dislocation. As more vacancies are absorbed, the angle and radius of the helix increase, and edge component (bsinθ) increases. A continued absorption of vacancies can result in a stack of prismatic edge dislocation loops [4].

There is an interesting aspect to the formation of helical dislocations, which involves the pairing of two helical dislocations to produce a double helix of screw dislocations. There is a repulsive interaction between two pure screw dislocations. However, helical dislocations are of the mixed character, where the edge component grows with vacancy concentration. There is an attractive interaction through the edge component. Moreover, vacancies lead to the formation of jogs, which generate additional attractive interaction between the two helical dislocations.

During crystal growth, a coaxial screw dislocation in a finite cylinder with end surfaces produces counteractive shear stresses, which produce a torque and a twist, known as Eshelby twist [2,5]. Since the Eshelby twist is inversely proportional to the square of the cylinder radius, it did not play as a significant role in large-size crystals. However, in screw-dislocation-aided growth of nanostructures, such as nanowires, Eshelby’s twist can lead to interesting helically twisted nanostructures [1,3].

We discuss the mechanism of formation of the double helix of screw dislocations, and their importance in bulk crystal growth and nanowires without involving any catalyst. Two parallel screw dislocations have a repulsive interaction and are unstable; therefore, they cannot influence the growth of nanowires. However, a pure screw dislocation can be converted into a helix or a helical dislocation through absorption of defects such as vacancies during the growth process. These mixed helical dislocations are mostly screw with a small parallel edge components, which have attractive interactions through their stress fields and jogs in both helical dislocations. This attractive interaction can lead to the formation of a double helix involving two nearly screw dislocations. These double-helix dislocations play a critical role in the growth single-crystal nanowires. Recent results on the growth of GeS (c=1.04 nm with orthorhombic crystal structure) [1] and PbS (with a = 0.594 nm, NaCl structure) [3] nanowires show that their experimental results can be interpreted satisfactorily now by invoking double-helix dislocations.

2. Results and discussions

2.1. Formation of single helix dislocation

A pure screw dislocation can acquire helicity through dislocation climb by absorbing point defects during the growth process. It should be noted that the interaction between hydrostatic stresses of vacancies and shear stresses of screw dislocations is very weak; however, local jogs and thermal stress fluctuations can introduce edge components which can interact with hydrostatic stresses of vacancies. The attractive interaction energy between two jogs (E_i) can be estimated by [4] (1) $E_{\text{i}}=\mu b^{\text{2}}{a}^{\text{2}}\text{/}\left[8\pi L\left(1-\upsilon \right)\right],$(1) where µ is the shear modulus, b is the magnitude of the Burgers vector, a is the length of the jog, L is the spacing between jogs, and υ is the Poisson’s ratio. As the edge component grows, the vacancy interaction becomes stronger and helicity grows to a critical value to balance out the increase in length of the dislocation, as discussed below.

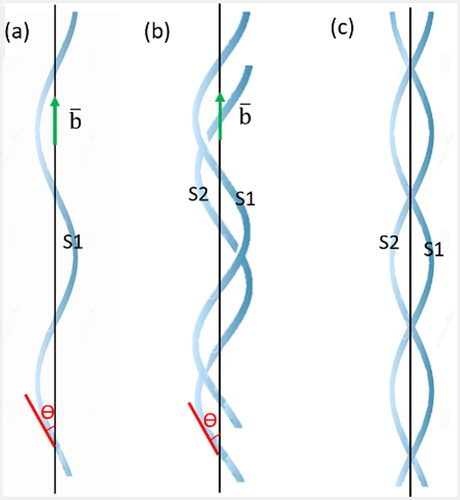
The number of vacancies absorbed per unit length N is given by (2) $N=\pi {r_{\text{h}}}^{\text{2}}b\text{/}\left(\lambda \mathrm{\Omega }\right)\text{,}$(2) where r_h is the radius of the helix, λ is the pitch of the helix, and Ω is the volume of a vacancy [4]. The helix angle θ (as shown in Figure 1(a)), which is constant along the entire length of the dislocation, is given by θ = tan⁻¹(2πr_h/λ).

Figure 1. (a) A single helical screw dislocation (n=1) at S1 with a constant helix angle Θ along the entire length of the dislocation, and the formation of a double-helix dislocation in (b) with another dislocation S2, which is shifted by a quarter of a pitch along the axis. The shift in (c) is of pitch. There is an attractive interaction between the two dislocations through the edge component and vacancy jogs, similar to hydrogen bonding between two DNA strands.

The relation between supersaturation of vacancies (c/c₀), radius, and pitch for the formation of a helix is given by [4] (3) $kT\text{ ln }\left(c\text{/}{c}_{\text{0}}\right)=2\pi \mathrm{\Omega }\tau /[b\text{{}(2\pi r_{\text{h}}{)}^{\text{2}}+{\lambda }^{\text{2}}{\text{}}}^{\text{0}\text{.5}}\text{]}$(3) where the sample is quenched from a higher concentration c to lower c₀.

Here, τ (dislocation line energy) in the helical configuration is (4) $\tau =\mu b^{\text{2}}(4\pi {)}^{-\text{1}}\left(1+\upsilon \right)(\text{1}-\upsilon {)}^{-\text{1}}\left(\text{ln }\left(\lambda /3b\right)\right)$(4) From Equation (3), we find {(2πr_h)² + λ²} to be a constant for a given supersaturation of vacancies, which implies that as r_h decreases λ must increase. Thus, for very small r_h, as expected in for the growth of nanostructures, the critical pitch length λ* is given by (5) $\left({\lambda }^{\ast }\right)=2\pi \mathrm{\Omega }\tau [bkT\text{ ln }\left(c\text{/}{c}_{\text{0}}\right){]}^{-\text{1}}$(5) If the pitch λ > λ*, the free energy of the helix decreases with increasing r_h and helix grows by absorbing vacancies and turning into the stack of vacancy loops eventually, as discussed in Figure 2. However, if λ < λ*, thermal activation and diffusion of vacancies are needed to achieve the critical value of λ*. It should be pointed out that once a helix starts to form, it is unstable with respect to radial growth. Assuming Ω ∼ b³/4 for GeS (orthorhombic) and b³ for PbS (cubic), τ = 20 eV/nm estimated from [6], supersaturation c/c₀ = 10, kT = 56 meV [1], (λ*) is estimated to be 100 nm for GeS [1], and 120 nm for PbS [3] with kT = 73 meV. From this, helix radii are estimated to be from 1 to 3 nm for helix angles varying from 5° to 10°.

Figure 2. The formation of helical screw dislocations as a result of vacancy diffusion and punching into stack of vacancy loops at S1 in MgO during high-temperature annealing. The arrow in the TEM micrograph shows imaging diffraction vector [200] with length of the marker 1000 nm.

Since vacancies at the surfaces are in a close proximity with dislocations in nanowires, these vacancies can diffuse in and cause the screw dislocation to climb and produce helicity. We have shown that screw dislocations in MgO (with NaCl structure, a = 0.42 nm) with ample supply of vacancies during high-temperature annealing result in the climb of dislocations [6–8]. In fact, the continued climb of helical dislocations can lead to a stack of vacancy dislocation loops, where loop spacing is equal to the pitch and loop radius is given by the helix radius, as shown in Figure 2. The screw dislocations at S1 lying along [110] direction have a/2[110] Burgers vector (b). Upon vacancy absorption, these screw dislocations become helical and with continued climb, they turn into stack prismatic a/2[110] dislocations loops. At S2, a/2[101] screw dislocation results in a stack of a/2[101] prismatic dislocation loops. With [200] imaging diffraction vector (g), both sets of these loops are visible as g.b = 1. The dislocations with a/2 < 011> Burgers vector are invisible with g = [200] as g.b = 0 for these dislocations in the NaCl structure of MgO. It should be noted that a large screw dislocation climb may take the dislocations out to the surface and stop helical twist. From Figure 2 (S2), pitch of the helix is determined to be 100 nm and r_h= 10 nm. This gives the helix angle of 32°, and vacancy supersaturation c/c₀ of 2.5 during annealing at 1000°C, assuming Ω ∼ b³ and τ = 20 eV/nm [6].

2.2. Formation of double helix of screw dislocations

Two parallel screw dislocations are unstable as they have repulsive interaction, where force (F) is given by F =µb²/(2πr), where r is the separation between two dislocations. In the following, we discuss the stability of two helical screw dislocations, leading to the formation of the double helix of screw dislocations. The jogs created by the absorption of vacancies in a helical dislocation interact with those in other helical dislocation. This attractive interaction is a primary source for pairing two helical dislocations and generating a double helix of screw dislocations. In addition, there is attractive interaction between two helical dislocations derived through edge components acquired through vacancy absorption. This attractive interaction force (F_A) for two parallel edge dislocations can be estimated by (6) $F_{\text{A}}=\mu b^{\text{2}}\text{si}{\text{n}}^{\text{2}}\theta \text{.}x\text{.}\left(x^{\text{2}}-y^{\text{2}}\right)/[2\pi \left(\text{1 - }\nu \right)\text{. (}{x}^{\text{2}}+y^{\text{2}}{\text{)}}^{\text{2}}\text{],}$(6) where θ is the helix angle, and x and y coordinates of second dislocation with respect to the first one. Figure 1(b) shows the formation of a double helix, where there is a relative shift by λ/4 and for the shift by λ/2, the double helix is shown in Figure 1(c). Two helical dislocations may adjust their relative positions depending upon their origin and growth conditions. It is interesting to note the similarity between single helical screw dislocation (Figure 1(a)) and single-strand ribonucleic acid (RNA), and double-helix dislocations (Figure 1(c)) and deoxyribonucleic acid (DNA) structures with two strands. The DNA is a molecule composed of two polynucleotide chains that coil around each other to form a double helix carrying genetic instructions for the development, functioning, growth and reproduction of all known organisms and many viruses. The two DNA strands are bonded by hydrogen bonds to a make double helix, analogous to vacancy jogs in helical dislocations.

2.3. Eshelby twist

A coaxial screw dislocation in a finite cylinder generates a torque at the ends, which produces a twist, known as Eshelby twist [2,5,9]. According to Eshelby’s twist model, twist per unit length (α) is given by (7) $\alpha =-nb(\pi R^{\text{2}}{)}^{-1},$(7) where b is the magnitude of the Burgers vector of screw dislocation, and R is the radius of the nanowire cylinder. It should be noted that Eshebly’s formula is not valid at the ends of the cylinder. The n = 1 case corresponds to original Eshelby’s model with a single screw dislocation. The n = 2 case was ignored so far as two parallel screw dislocations are unstable with a repulsive interaction. In this work, we show that n = 2 case is possible if two screw dislocations acquire a small edge component through absorption of vacancies and become helical.

We argue that crystal growth can occur either with a single-helix (single screw) dislocations (n=1) or a double-helix dislocations (n=2) dislocations depending upon the growth conditions and role of point defects. The growth may also combine the two growth processes, where it may start with a single screw dislocation, and a defect may initiate a second dislocation, which can be stabilized by absorption of vacancies. In the case of a helical dislocation, only the screw component (bcosθ) contributes to crystal growth, where θ is the angle of the helix which stays constant along the axis. Therefore, nb in Eshelby’s formula is replaced by nb cosθ for helical dislocations. As R increases the twist α decreases rapidly, because it is inversely proportional to the square of the cylinder radius. Therefore, Eshelby twist did not play as a significant role in large-size crystals. However, in screw-dislocation-aided growth of nanostructures, such as nanowires, Eshelby’s twist can lead to interesting helical nanostructures, particularly in two-dimensional materials [1,3].

The primary focus of this paper is on n=2 case, corresponding to two helical dislocations or the formation of the double helix of screw dislocations. We argue that crystal growth with both single screw dislocations (n=1) and double helix dislocations (n=2) can occur depending upon the growth conditions and role of defects. The growth may start with a single screw dislocation, and a defect may initiate a second dislocation, which can be stabilized by absorption of defects. Figure 1 shows the formation of single and double helical dislocations; here, helicity has been exaggerated for clarity. There is an attractive interaction for parallel mixed dislocations through the edge component and presence of jogs along the helical dislocations

Recent interesting work by Liu et al. on the growth of GeS (c=1.04 nm with orthorhombic crystal structure) nanowires showed that axial screw dislocations produced a discretized crystallographic twist along the c-axis [1]. These results in helically twisted nanowire structures were interpreted using Eshelby’s twist model [2]. However, the effective burger vector (b = 1.75 nm) was found to be fat higher than b = 1.04 nm for [0001] dislocation, expected from Eshelby’s model. Similarly, earlier work by Bierman et al. on screw-dislocation nanowire growth in PbS (with a = 0.594 nm, NaCl structure) reported effective Burgers vector (0.6 ± 0.2 nm), which is also far higher than (0.42 nm for b = a/2 < 110>) [3]. In the following, we show that the results from both experiments can be rationalized by invoking growth with single as well as double screw dislocations having helical configurations. Since only the screw component (b cos θ) of the helical dislocation takes part in the growth process, the effective Burgers vector of the double helix contributing to the growth process is 2b cos θ, which is slightly smaller than 2b. When both single and double helix dislocations participate in the growth process, we can write (8) $2\delta \mathrm{b}\cos \theta +(1-\delta )\mathrm{b}\cos \theta ={\mathrm{b}}_{\mathrm{e}}.$(8) Where δ is the fraction of double helix, (1−δ) is the fraction of single helix, θ is the angle of the helix, and b_e is experimentally observed average value of the Burgers vector. In the case GeS growth [1] with b = 1.04 nm and b_e = 1.75 nm, δ is calculated to be 71% and 69% for helix angles of 10 and 5 degrees, respectively. Similarly for PbS [3] with b = 0.42 nm and be = 0.6 nm, δ is calculated to be 45% and 43% for helix angles of 10 and 5 degrees, respectively. To explain a higher percentage of double helix in GeS than that in PbS, it is pointed out that GeS has orthorhombic (pseudo hexagonal) structure with dominant dislocations taking part in the growth process being c-dislocations. The screw dislocations can minimize greatly the energy by growing in directions [6]. On the other hand, PbS has cubic NaCl structure as in MgO, where there are no dominant Burgers vectors for screw dislocations. In fact, the growth in PbS [3] occurs along direction with mixed a/2 dislocations.

In conclusion, double-helix screw dislocations play a very important role along with single screw dislocations in the growth of bulk as well as nanostructures. A screw dislocation becomes helical by absorption of point defects during crystal growth due to the supply of vacancies from the free surfaces in close proximity in nanostructures. Two helical dislocations can lead to the formation of a double helix of dislocations and play a critical role in the growth of one-dimensional nanostructures with Eshelby’s twist for a variety of applications [10,11].

Acknowledgments

The author is pleased to acknowledge fruitful comments by Professor John Prater and technical help from two of his PhD students, Parand Riley and Pratik Joshi.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by NSF: [Grant Number NSF DMR-2016256].