Mechanical alloying: a critical review

Abstract

Mechanical alloying (MA) is a powder process that consists of repeated cold welding, fracturing, and rewelding of powder particles in a high-energy ball mill. This process is capable of synthesizing different types of non-equilibrium phases including supersaturated solid solutions, nanocrystalline materials, metallic glasses, high-entropy alloys, and several others. MA'd materials have found many applications. The present article critically reviews recent developments in emerging areas of nanostructured materials and nanocomposites, high-entropy alloys, alloys synthesized from immiscible elements, and heterostructured materials. Current challenges and future directions of research in the general area of MA are also indicated.

IMPACT STATEMENT

This paper reviews recent developments in the field of mechanical alloying, an important area of materials processing.

KEYWORDS:

• Mechanical alloying
• metallic glasses
• nanocrystalline materials and nanocomposites
• high-entropy alloys
• alloys between immiscible elements
• heterostructured materials

1. Introduction

The quest for new and improved processing methods during the last few decades has led to the discovery of new and improved materials as also to improve the existing processing methods and development of novel techniques to process and characterize these materials. Among the several techniques developed, special mention may be made of rapid solidification processing, mechanical alloying, plasma processing, physical vapor deposition, chemical vapor deposition, ion implantation, among others [1]. The new materials developed include metallic glasses, quasicrystalline materials, nanostructured materials and nanocomposites, high-entropy alloys, and others. Even though each one of these methods and materials is useful, some specific advantages have been noted for some techniques/materials. The present article will focus on the technique of mechanical alloying (MA) and the novel materials developed using MA, with special emphasis on recent developments. However, to make this article comprehensive and self-sufficient, a brief introduction will be provided followed by some developments on some of the topics investigated earlier.

2. Origins and early developments

Mechanical alloying has been defined as a process that involves repeated cold welding, fracturing and rewelding of powder particles in a high-energy ball mill. The technique of MA was developed in 1966 by John Benjamin at INCO Laboratories out of an industrial necessity. They were looking for an alloy that could be strengthened at room temperature by precipitation hardening and at elevated temperatures through dispersion hardening. Since such an alloy was not commercially available at that time, they developed the oxide dispersion strengthened (ODS) Ni-based superalloy that contained 0.5% Y₂O₃ which produced a fine dispersion of about 5-nm size precipitates dispersed in a nickel-base matrix. The Ni-matrix developed precipitation hardening and addition of Y₂O₃ resulted in dispersion strengthening. These early developments were described by Benjamin himself [2,3].

The technique of MA was originally developed to produce ODS superalloys that exhibited excellent mechanical properties at elevated temperatures. This technique was hardly known outside INCO for quite some time. However, in the middle of 1980s it was realized that milling of powder mixtures can result in the formation of supersaturated solid solutions, intermetallic phases and even amorphous alloys. Later, synthesis of quasicrystalline alloys was also reported in the mechanically alloyed Al-Cu-Fe system. The metastable effects achieved in these alloys processed by MA suggest that the technique of MA is very similar to the then more popular technique of rapid solidification processing (RSP) developed a few years earlier by Pol Duwez at CalTech [4]. Subsequently, it was realized that the types of phases produced by MA and RSP methods are very similar. An exhaustive list (current at the time of publication) of such supersaturated solid solutions, intermediate phases, amorphous alloys and quasicrystalline phases may be found in the literature [5,6].

The process of MA consists of loading the blended elemental powders, in the appropriate proportions, along with the grinding media into the milling container and milling the powder blend for the appropriate length of time. The milled powders are taken out from the container at periodic intervals and characterized using x-ray diffraction (XRD), electron microscopy, and other techniques. The milled powders are subsequently consolidated into a bulk shape to enable mechanical property evaluation. Most commonly, consolidation is carried out by spark plasma sintering (SPS), even though other methods such as vacuum hot pressing, hot isostatic pressing, and conventional sintering and microwave sintering methods are also employed.

MA is a stochastic process that involves many process variables such as type of mill, milling container, milling energy/speed, milling time, type, size, and size distribution of grinding medium, ball-to-powder weight ratio, extent of vial filling, milling atmosphere, process control agent, and temperature of milling. Thus, the researcher has at his disposal a big opportunity to obtain the desired constitution of the powder by optimizing these large number of process variables. Even though a detailed study of the effect of these variables on the constitution of the milled powders has been undertaken in conventional powder materials, detailed studies are not available on high-entropy alloys (HEAs) and other novel materials. The most investigated parameter, however, is the milling time.

Mechanically alloyed materials have found applications in many different industries. Apart from the ODS alloys, other applications include hydrogen storage alloys, supercorroding alloys, Meal Ready to Eat, paints, and solders, amongst others. A full description of the applications may be found in Refs. [5,6].

Since a very comprehensive and exhaustive review [5] and a book [6] on MA have appeared some time ago, and the fundamentals, mechanism of alloying, and other aspects including applications of mechanically alloyed products have been fully covered in them, the present review article will focus on some of the more recent results and presents a critical analysis of the present status of the MA field. The reader is advised to consult Refs. [5,6] for details of the different aspects of these earlier investigations. Some additional details of the topics which were already covered earlier will also be discussed.

However, before discussing these new topics, we will briefly review the recent interesting results obtained on some of the traditional topics.

3. Some recent results on traditional topics

As mentioned above, MA has been known to produce a variety of metastable effects including supersaturated solid solutions, intermetallics, and metallic glasses. Most of the products of MA happen to be nanostructured if they are crystalline in nature. But, since metallic glasses and nanostructured materials have their own special attributes, and are heavily researched into, we will cover these topics separately. We will now discuss about supersaturated solid solutions and some aspects of metallic glasses produced by MA.

3.1. Supersaturated solid solutions

Solid solution alloys show many desirable properties such as increase in strength and modulus, changes in density depending on the density of the solute element, and elimination of undesirable second phases. Supersaturated solid solutions could also be used as the starting materials to produce a large volume fraction of fine precipitates on annealing. Thus, this area has attracted the attention of scientists for a long time.

Supersaturated solid solutions have been produced by solid-state quenching from an elevated temperature, RSP, MA, vapor deposition, sputtering, thermal evaporation, and electrodeposition, among other techniques. It has been noted that the highest solubility extensions could be obtained starting from the vapor state (vapor deposition, sputtering, etc.) and the lowest from solid state quenching, with intermediate values by starting from the liquid state (RSP). These limits are typically decided by the respective equilibrium phase diagrams. Thermodynamic studies have been conducted to predict the solid solubility limits that could be achieved by the different techniques. However, since MA is a completely solid-state processing method, phase diagram restrictions do not apply here and consequently, solid solubility limits comparable to those achieved by RSP have been achieved by MA methods also. In fact, the solid solubility limits obtained by MA are frequently higher than those obtained by RSP methods. There have been some differences as well. Refs. [5,6] provide an exhaustive list of the solid solubility extensions achieved by MA in different alloy systems till that time.

3.2. Comparison of solid solubility limits by different methods

Table 1 summarizes some of the results of solid solubility extensions obtained in different alloy systems by different techniques. A practical difficulty in comparing these results is that the same alloy system has not been investigated by all the different methods. Thus, results are scattered. From the results presented it is reasonably clear that the solubility extensions are the highest in vapor-deposited/quenched alloys and the next highest values are obtained in MA-processed alloys. The levels of solid solubility extensions achieved are related to the extent of departure form equilibrium obtained during processing. Since departures have been estimated to be about 160 kJ/mol in vapor-processed alloys and that in MA processing is 30 kJ/mol, it is natural that vapor-processed alloys exhibit the highest solid solubility extensions [28]. Another important microstructural difference appears to be that the grain size in the milled powders is frequently of nanometer dimensions. This certainly helps in increasing the solid solubility limits. Based on many solid solubility extensions observed in several alloy systems, it was reported that the solid solubility extension was significantly higher if the equilibrium solid solubility was very small. The solid solubility extensions have also been rationalized based on Hume-Rothery rules for solid solution formation in noble metal alloy systems.

Table 1. Comparison of solid solubility limits obtained by different non-equilibrium processing methods.

		Extended solid solubility limit (at.%)
System	Maximum equilibrium solid solubility (at.%)	Value	Technique	References
Ag-Cu	14	24	MA	[7]
		100	MA	[8]
		100	RSP	[4]
Ag-Fe		40	Co-sputtering	[9]
		20	Magnetron sputtering	[10]
		25	RSP	[11]
		100	MA	[12]
Cu-Co		10	Melt spinning	[13]
		15	RSP	[11]
		88	Vapor deposition	[14]
		100	MA	[15]
Cu-Fe	11.0	20	MA	[16]
		30	MA	[16,17]
		40	Vapor deposition	[18]
		65	MA	[19]
Cu-Nb	0.1	3	MA	[20]
		10	MA	[21]
Fe-Al	45	40	MA	[22]
		50	MA	[23]
Fe-Cu	15	25	High-rate sputtering	[24]
		40	MA	[17]
		50	Thermal evaporation	[14]
Ti-Mg	0.0	3.6	MA	[25]
		30	MA	[26]
		43.4	Vapor quenching	[27]

Even though both RSP and MA are non-equilibrium processing methods, the solid solubility extensions achieved are different. The exact reasons for this difference are not very clear at present. Solid solution formation is associated with the absence of solute partition. This is relatively easy to understand in the case of RSP because of the rapid solidification rates involved during solidification. But such a situation does not exist in MA powders since they do not melt and therefore no solidification is involved. However, it is possible that segregation of solute atoms to interfaces such as grain boundaries and triple junctions in MA powders and the enhanced diffusivity due to the presence of defects could be responsible for the increased solid solubility levels in MA powders. Further work is required on this aspect.

The solid solubility limits reported in MA-processed systems are approximate values and too much accuracy cannot be assigned to them. This is because solid solubility limits are determined form the lattice parameters of supersaturated solid solutions, which are determined form XRD patterns of the milled powders. The milled powders exist in a heavily cold-worked conditions and therefore the XRD peaks are broad. The other reasons for the inaccuracies are discussed in Ref. [5].

3.3. Comparison of glass-forming ranges in MA and RSP alloys

Metallic glasses or amorphous alloys are produced by both RSP and MA methods. But the systems in which glasses are formed and the composition ranges in which they are formed appear to be quite different. Additionally, the criteria for glass-forming ability and the mechanism of formation of metallic glasses also are different in both these methods.

In the early years of research on glass formation by MA, it was argued that the powder particles melted in highly localized areas, as very high temperatures were reached due to the high rate of plastic deformation. This is due to the large amount of energy transferred to the powder particles during deformation of the powder between colliding milling balls and container wall. Subsequent quenching of this small amount of liquid by heat conduction into the less deformed, and hence cooler, interior regions of the particles resulted in the formation of the amorphous phase [29]. If this is true, the mechanism for the formation of metallic glasses is very similar in both RSP and MA methods. However, energy input calculations, temperature rise estimates, and experimental measurements suggest that the temperature rise during MA is not large enough for the powder particles to melt. It was estimated that the maximum rise in the powder temperature is only about 200 K. Thus, it was concluded that this is not the mechanism for glass formation through MA. Consequently, the composition ranges of glass formation have been reported to be significantly different in both the cases.

Table 2 compares the composition ranges of glass formation in different alloy systems by RSP and MA methods [30]. From these values, the composition ranges for glass formation by these two methods are significantly different in different alloy systems.

Table 2. Comparison of glass-forming composition ranges in different alloy systems processed by RSP and MA methods [29].

	Glass formation composition range (at.% solute)
Alloy system	By RSP	By MA
Fe83-xCrxC17	24–50 Cr	10–60 Cr
Fe83-xMoxC17	5–26 Mo	5–60 Mo
Ni-Nb	33.3–48 and 55–58 Nb	20–80 Nb
Ni-Ta	33.4–45 Ta	40–80 Ta
	30–60 Ta	20–90 Ta
	35–65 Ta	–
Ti-Cu	30–75 Cu	10–50 Cu
	35–70 Cu	10–90 Cu
Ti-Ni	20–62 Ni	10–70 Ni
	24–46 Ni	–
Zr-Co	20–52 Co	27–92 Co
Zr-Fe	20–42.5 and 88–93 Fe	10–78 Fe
Zr-Ni	20–70 Ni	27–83 Ni

Let us now look at the more recent developments in the field of MA. The new topics to be covered in this review include:

• Metallic glasses,

• Nanocrystalline alloys and nanocomposites,

• High-entropy alloys,

• Alloys between immiscible elements, and

• Heterostructured materials.

4. Metallic glasses

Metallic glasses have an interesting combination of mechanical, physical, and chemical properties. They are typically produced by rapidly solidifying their melts at high solidification rates to bypass the process of crystallization. Normally, very high solidification rates of nearly 10⁶ K/s were required to produce metallic glasses in most systems; consequently, they were produced in the form of ribbons, wires, or droplets with a cross-section/thickness of a few micrometers [31–34]. Metallic glasses have been produced in several alloy systems by RSP and some other different techniques.

It was later realized that glassy alloys could be produced in a large section thickness of the order of a few millimeters to centimeters by carefully controlling the chemical composition of the alloy. These could be produced at relatively slow solidification rates, as obtained in metal mold casting techniques. The critical solidification rate for formation of these glassy alloys, now referred to as bulk metallic glasses (BMGs), is as low as 0.1 K/s and at the most about 100 K/s. The largest diameter of a homogenous glassy alloy rod is reported to be 80 mm in a Pd_42.5Cu₃₀Ni_7.5P₂₀ alloy [35].

Based on results obtained on several different alloys systems, Inoue [36] proposed three criteria for the formation of BMGs. These are:

1. The alloy must contain at least three different components. Glass formation becomes easier with increasing number of components in the alloy.

2. A significant atomic size difference (>12%) should exist among the constituent elements in the alloy.

3. There should be negative heat of mixing among the (major) constituent elements in the alloy system.

Amongst the above, the first criterion is based on the thermodynamic and kinetic aspects of glass formation, and the second one is based on topological aspects (structure and dense packing of atoms), while the third is essential for mixing of atoms (alloying to occur) and formation of a homogeneous glassy phase. With the development of several new BMGs, some apparent exceptions have been noted in a few alloy systems [37].

The glass-forming ability (GFA) of an alloy needs to be high for glass formation to occur, and the GFA is defined in many ways. One of the most used criteria to determine GFA has been a high reduced glass transition temperature, T_rg = T_g/T_l, where T_g is the glass transition temperature and T_l is the liquidus temperature of the alloy. However, since this is an experimentally determined value (and is time-consuming to determine and difficult to measure), several other empirical criteria have been proposed to explain BMG formation in alloy systems. These criteria are based on the thermal properties of the alloys and physical characteristics of the component atoms and include the so called ΔT_x, α, β, γ, γ_m, δ, ϕ, and ω, among others. Despite this large number of parameters, the predictability of glass formation has not significantly improved [38] and it has been difficult to exactly specify which alloy compositions would produce the glassy phases.

Metallic glasses have found industrial applications based on their strength, corrosion resistance and interesting magnetic properties. The most important and industrial application among them has been to use the Fe-based metallic glassy alloys as core laminations for distribution transformers [34,37].

All the above criteria have been developed for metallic glasses processed from the molten state. The technique of MA has also been employed to produce amorphous alloys for nearly 40 years. However, there have not been any systematic investigations to study the conditions under which amorphous phases are formed by MA and the mechanism of their formation. Mostly qualitative statements have been made. To overcome this gap in the literature, systematic investigations were carried out to predict glass formation in alloy systems processed by MA.

4.1. Criterion for glass formation

Fe-based glassy alloys were synthesized by MA in alloy systems corresponding to the generic composition of Fe₄₂X₂₈Zr₁₀B₂₀ (where the subscripts represent the composition of the alloy components in atomic percentage and X = Al, Co, Ge, Mn, Ni, or Sn). Other alloying elements such as Nb and C have also been added to the above compositions in some investigations. The phase evolution during milling was monitored through X-ray diffraction (XRD) methods.

The element X in the general alloy composition Fe₄₂X₂₈Zr₁₀B₂₀ was selected based on the number of intermetallics it forms with Zr under equilibrium conditions at room temperature [39]. This number increases from 1 with Mn to 8 with Al, which provides a basis to analyze the results systematically. Further, the negative heat of formation of the intermetallics with Zr is much higher than that with either Fe or B [40]. Thus, the probability of forming an intermetallic with Zr during milling is higher than with Fe or B. Figure 1 presents the XRD patterns of the blended elemental powder mixtures of Fe₄₂Al₂₈Zr₁₀B₂₀ and Fe₄₂Co₂₈Zr₁₀B₂₀ compositions as a function of milling time. On milling the Fe₄₂Al₂₈Zr₁₀B₂₀ powder mix for 20 h, amorphization had occurred, as evidenced by the presence of a broad diffuse peak centered at the angular position corresponding to the (110)_Fe peak. On further milling (say, for 50 h), however, this diffuse peak started becoming sharp, and additional low-intensity peaks started appearing. This process, referred to here as mechanical crystallization, will be discussed later in some detail. The sequence of phase formation on milling the powders was different depending on the alloy system. It may be noted that while an amorphous phase had formed on milling the Fe₄₂Al₂₈Zr₁₀B₂₀ powder blend for 20 h, amorphization did not occur in the Fe₄₂Co₂₈Zr₁₀B₂₀ powder blend. The phase formation sequence in all the six powder blends can be summarized into three groups as follows:

1. BE powder → Intermetallics → Solid solution

   Examples: Mn- and Sn-containing systems,

2. BE powder → Solid solution

   Example: Co-containing system,

3. BE powder → Intermetallics → Amorphous phase → (Mechanical) Crystallization

   Examples: Al-, Ge-, and Ni-containing systems.

Figure 1. XRD patterns of the blended elemental powder mixtures of (a) Fe₄₂Al₂₈Zr₁₀B₂₀ and (b) Fe₄₂Co₂₈Zr₁₀B₂₀ compositions as a function of milling time. An amorphous appeared on milling the Fe₄₂Al₂₈Zr₁₀B₂₀ powder mix for 20 h, and then a crystalline phase started to form from the amorphous matrix. The Fe₄₂Co₂₈Zr₁₀B₂₀ powder mix showed only a solid solution phase even after milling for 30 h. No amorphous phase formed in this powder blend.

Please place (a) and (b) for Figures 1, 2, 5, 7, 8, 9, 10, and (a), (b), and (c) for Fig. 13.

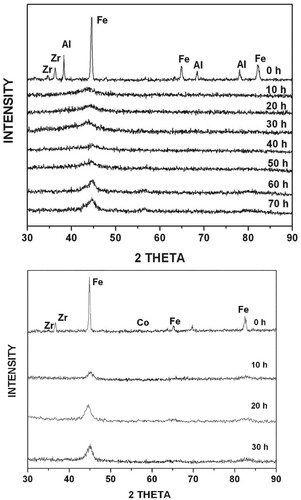
The time required for amorphization, which can be considered a measure of GFA of the alloy, is also different for different powder blends. Table 3 summarizes the results obtained, including the number of intermetalc phases present under equilibrium between X and the constituent elements (Zr, Fe, or B) in the powder bend [41]. A close examination of Table 3 clearly reveals that the ease of amorphization (i.e. GFA) increased with the number of intermetallics present in the constituent Zr-X binary phase diagrams. This is apparent from the powder blends containing Al or Ni, which amorphized in 10 or 20 h, respectively. While the quaternary Fe–Zr–Al–B mix contains eight intermetallic phases in the Zr-Al binary system, the Fe–Zr–Ni–B mix contains seven intermetallic phases between Zr and Ni. Similarly, the Ge-containing system which also amorphized in 10 h, contains five intermetallic phases between Zr and Ge. The Zr–Co, Zr–Mn, and Zr–Sn systems which did not show amorphization on milling contained five, one, and three intermetallic phases, respectively. However, when we consider the total number of intermetallic phases in the binary systems of the quaternary alloy, it can be clearly seen that systems which amorphized on milling contain $\ge$ 10 intermetallic phases in all the constituent binary phase diagrams. If the alloy system contained <10 intermetallic phases, then amorphization was not observed. Note, however, that even when the total number of intermetallics is only 10 (with the Ge-containing alloy), the time required for amorphization is only 10 h. But this is a special case because Ge is a semimetal with strong directional bonds. Thus, it becomes easier to amorphize alloys containing Ge (or other semi metals). From a critical analysis of the constituent binary phase diagrams, it also becomes clear that when the phase diagrams contain extensive solid solutions, it will be very difficult to amorphize them, e.g. Fe-Co.

Table 3. Time required for glass formation in Fe₄₂X₂₈Zr₁₀B₂₀ alloys and the number of intermetallics in the respective binary phase diagrams.

	Number of intermetallics between
Element X	X and Zr	X and Fe	X and B	Total number of intermetallics	Milling time required for amorphization (h)
Al	8	5	2	15	10
Co	5	Nil	3	8	No amorphization
Ge	5	5	Nil	10	10
Mn	1	Nil	5	6	No amorphization
Ni	7	1	4	12	20
Sn	3	2	Nil	5	No amorphization

4.2. Mechanism of amorphization

Thermodynamic principles suggest that amorphization occurs when the free energy of the hypothetical amorphous phase, ΔG_A, is less than that of the crystalline phase, ΔG_C i.e. ΔG_A < ΔG_C. A crystalline phase normally has a lower free energy than the amorphous phase. But its free energy can be increased by introducing a variety of crystal defects such as dislocations, grain boundaries, stacking faults, etc. [42]. If an intermetallic has formed, then additional energy can be introduced by disordering the crystal lattice. By this approach, it is possible to obtain a situation when ΔG_C + ΔG_D > ΔG_A, where ΔG_D is the free energy increase due to introduction of crystal defects. The magnitude of energy increase is different for different types of defects. As an example, increasing the dislocation density to 10¹⁶/m² increases the free energy by about 1 kJ/mol, while decreasing the grain size down to 1 nm increases the free energy by about 10 kJ/mol [28]. The only way a solid solution could contribute to a free energy increase in the system is by grain refinement. But this increase in energy is not sufficiently high to amorphize the system [28]. On the other hand, the presence of intermetallics in an alloy system significantly increases the energy contributing to amorphization. This is due to two important effects. First, disordering of intermetallics contributes an energy of about 15 kJ/mol of atoms to the system. For example, in strongly ordered intermetallics such as NiAl and γ-TiAl that continue to be in the ordered state till melting, the disordering energy has been estimated to be about 17.5 kJ/mol [43] Secondly, a slight change in the stoichiometry of the intermetallic increases the free energy of the system drastically. In addition, grain size reduction contributes about 5 kJ/mol. Further, disordering of intermetallics has also been shown to be possible by heavy deformation [44]. Since MA reduces the grain size to nanometer levels and disorders the usually ordered intermetallics, the energy of the milled powders is significantly raised. In fact, it is raised to a level above that of the hypothetical amorphous phase. This condition leads to a situation where formation of the amorphous phase is favored over the crystalline phase.

Phase diagram features have been used to predict glass formation by RSP and other methods as well. For example, since alloys with high T_rg values are known to be good glass formers, and alloys in the vicinity of deep eutectics exhibit high T_rg values, deep-eutectic alloy compositions have been shown to exhibit high GFA [45]. Further, elemental solids exhibiting many polymorphic phases have been shown to exhibit higher GFA than elements that do not have many polymorphs [46]. In contrast, amorphous phases are obtained mostly around equiatomic compositions by the MA methods. Also, the composition range for amorphous phase formation is much wider in alloys produced by MA than in those obtained by RSP [5,6]. Difficulty in amorphization has been observed with RSP in alloys having melting maxima, too many peritectic reactions, high-temperature eutectics and also alloys having positive heats of mixing. However, amorphization has been observed in most of these cases by MA [5,6]. Further, it was observed that it is not possible to transform very dilute alloys (with low concentration of solute atoms) to the amorphous state by MA methods [47]. On the other hand, solute contents of as low as 9 at.% were found sufficient for glass formation in Fe–Zr and Co–Zr alloy systems by RSP methods [48]. Thus, even though phase diagrams are useful guidelines in choosing alloy compositions for easy glass formation by both the methods, the features to look for appear to be quite different for the RSP and MA methods. It is just fortuitous that some alloy compositions can be amorphized by both the methods. Thus, these observations provide a simple and visual means of identifying alloy systems which are likely to become amorphous on subjecting them to milling. If the equilibrium phase diagrams show the presence of a room temperature solid solution phase over a wide composition range, then amorphization is not easy. On the other hand, if the phase diagram contains a large number of intermetallic phases, then amorphization is a possibility.

4.3. Mechanical crystallization

It was briefly mentioned in the previous section that an amorphous phase transforms into a crystalline phase on continued milling after the formation of the amorphous phase, and that this phenomenon was referred to as mechanical crystallization. This is a very unusual process and has lot of potential applications in alloy design approaches since it will be possible to produce the alloy in either a fully amorphous, amorphous + nanocrystalline composite, or a completely crystalline state with different grain sizes, depending upon the time of milling or the temperature and time of annealing of the amorphous alloy.

XRD patterns of the blended elemental powder mix of the composition Fe₄₂Ge₂₈Zr₁₀B₂₀ mechanically alloyed for 10 and 60 h are shown in Figure 2(a). One may note the significant change in the XRD patterns. While the pattern from the alloy milled for 10 h clearly shows the presence of an amorphous phase, the pattern at 60 h of milling shows the presence of a crystalline phase, superimposed over the broad and diffuse halo, characteristic of the amorphous phase. By analyzing the sharp diffraction peaks, it was possible to establish that the crystalline phase corresponds to the BCC structure with the lattice parameter a = 0.2878 nm, suggesting that this is an α-Fe solid solution containing the solute elements present in the powder blend. Primary crystallization of metallic glasses produced by RSP methods was shown to produce a crystalline solid solution phase coexisting with an amorphous phase, which has a composition different from that of the initial glassy phase [49]. Thus, formation of the α-Fe phase in our MA powder may be interpreted to be a result of primary crystallization occurring in the amorphous alloy as a result of continued milling.

Figure 2. XRD patterns of the blended elemental powder mixes milled for different times. (a) Fe₄₂Ge₂₈Zr₁₀B₂₀ powder mix mechanically alloyed for 10 and 60 h. While an amorphous phase formed on milling for 10 h, a crystalline phase (α-Fe) started appearing on continued milling up to 60 h. (b) Fe₄₂Ni₂₈Zr₁₀C₁₀B₁₀ powder blend milled for 8 and 30 h. An amorphous phase appeared on milling the powder for 8 h, while the powder mix milled for 30 h showed the additional presence of some crystalline phases due to mechanical crystallization.

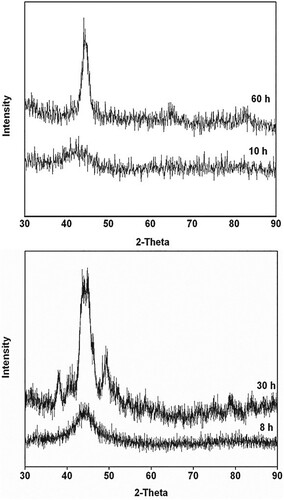
Figure 2(b) shows the XRD patterns of the Fe₄₂Ni₂₈Zr₁₀C₁₀B₁₀ powder blend milled for 8 and 30 h. Similar to Figure 2(a), the powder milled for 8 h is fully amorphous and the same powder milled for 30 h shows the presence of sharp crystalline peaks superimposed over the amorphous phase. But, the important difference between Figures 2(a and b) is that while the crystalline phase is the α-Fe solid solution in Figure 2(a), it is a mixture of crystalline phases in Figure 2(b). Thus, the sequence of phase formation in these powders during milling is that the blended elemental powder first forms intermetallic phases, then an amorphous phase, and eventually mechanical crystallization occurs resulting in the formation of crystalline phase(s).

Mechanical crystallization processes have also been observed in other alloy systems that formed the amorphous phase on MA [50–52]. In fact, it is now becoming apparent that this phenomenon of mechanical crystallization is not as rare as it was once thought to be [53]. There can be many reasons for the formation of a crystalline phase after the formation of an amorphous phase during MA. The important factors could be (a) rise in temperature to a level above that of the crystallization temperature of the amorphous alloy [5,6], (b) powder contamination due to which a stable crystalline impurity phase forms [54], (iii) phenomenon of inverse melting [55], and (iv) basic thermodynamic considerations. After critically analyzing the various issues involved, it now appears that basic thermodynamic stabilities of the different phases under the conditions of milling are responsible for mechanical crystallization. This was explained with reference to a free energy versus composition diagram.

Figure 3 is a schematic diagram showing the variation of free energy with composition for the Fe-based alloy systems investigated here. The possible (stable and metastable) constitution in this system is (a) blended elemental (BE) powder mixture, (b) α-Fe, the solid solution of all the alloying elements in Fe, (c) an amorphous phase, (d) intermetallic phases, and (e) different combinations of these phases. The stability of any phase will be determined by its relative position in the free energy plot - the lower the free energy the more stable the phase is. Since it is possible to have a large number of intermetallic phases in this multicomponent system, and since it is difficult to indicate each of them separately, for simplicity, all of them are grouped together as ‘‘Intermetallics’’.

Figure 3. Hypothetical free energy versus composition diagram to explain the mechanism of mechanical crystallization in the Fe₄₂X₂₈Zr₁₀B₂₀ system. Note that point ‘‘1’’ represents the free energy of the blended elemental powders, point ‘‘2’’ formation of the α-Fe solid solution containing all the alloying elements in Fe, point ‘‘3’’ formation of the homogeneous amorphous phase, point ‘‘4’’ a mixture of the amorphous phase with a different solute content than at ‘‘3’’ and the α-Fe solid solution, and point ‘‘5’’ is for the equilibrium situation when the solid solution and intermetallic phases coexist.

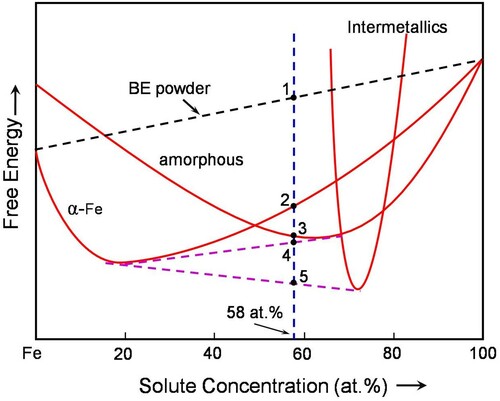
We will now consider the relative stabilities of the different competing phases in the Fe₄₂X₂₈Zr₁₀B₂₀ system. For our discussions here, we have considered all the solute elements together, which make up to 58 at%, as ‘‘solute’’. The free energy of the BE powder mixture is indicated by point ‘‘1’’, which represents the point of intersection of the composition vertical with the line joining the free energies of pure Fe and the ‘‘solute’’. On milling this powder, a solid solution phase containing all the solute elements in Fe (or a mixture of intermetallics and a solid solution, in some cases) is seen to form and its free energy is indicated by point ‘‘2’’. The solid solution forms because it has a lower free energy than the BE powder mixture. Since MA introduces a variety of crystal defects, the crystalline phases in the milled powders will contain excess energy. This energy will continue to increase with milling time and reach a value which is above that of the metastable amorphous phase. Thus, the amorphous phase gets stabilized (point ‘‘3’’). On primary crystallization of the amorphous phase, the new constitution will be a mixture of the α-Fe solid solution or intermetallics and the amorphous phase, which now has a composition different from the original amorphous phase. Further, the new solid solution phase also has a composition different from the original α-Fe phase. The free energy of the mixture of this solid solution and the amorphous phases, indicated by ‘‘point 4’’, will have a free energy lower than that of the amorphous phase. The equilibrium mixture of the α-Fe solid solution and ‘‘intermetallics’’ will have the lowest free energy of all the phase mixtures, as indicated by point ‘‘5’’ in the figure. It may be noted that the process of mechanical crystallization is unique to the MA process and can be achieved only on milling of the amorphous powder.

5. Nanocrystalline alloys and nanocomposites

Nanostructured materials are defined as those metals and alloys that have grain sizes in the range of 1–100 nm in at least one dimension. These materials have been shown to exhibit high hardness and strength, good ductility, increased diffusivity, excellent sintering characteristics, and interesting combination of electrical and magnetic properties [56–59].

It has been frequently demonstrated that mechanically alloyed materials show powder particle refinement as well as grain refinement with increasing milling time. These sizes decrease very rapidly in the early stages of milling and more gradually later. Eventually, in almost all the cases, the grain size of the mechanically alloyed materials is in the nanometer range, unless the powder becomes amorphous. The minimum grain size achieved has been reported to be a few nanometers, ranging typically from about 5–50 nm, but depending on the material and processing conditions [5]. For example, it was reported that the grain size decreases with increasing milling energy, higher ball-to-powder weight ratio, and lower temperatures. The ease with which nanostructured materials can be synthesized is one reason why MA has been extensively employed to produce nanocrystalline and nanocomposite materials [60].

5.1. Nanostructured materials

The grain size of the milled materials decreases with milling time and reaches a steady-state condition (saturation level) when a balance is established between the fracturing and cold-welding events during MA. This minimum grain size, d_min is different depending on the material and milling conditions. The value of d_min achievable by milling is determined by the competition between the plastic deformation via dislocation motion that tends to decrease the grain size, and the recovery and recrystallization behavior of the material that tends to increase the grain size. This balance gives a lower bound for the grain size of pure metals and alloys.

The d_min obtained is different for different metals and also is found to vary with the crystal structure (Figure 4). In most of the metals, the minimum grain size attained is in the nanometer dimensions. But metals with a body-centered cubic (BCC) crystal structure reach much smaller values in comparison to metals with the other crystal structures. This is related to the difficulty of extensive plastic deformation and consequent enhanced fracturing tendency during milling. It was also reported that d_min decreases with an increase in the melting temperature of the metal. As shown in Figure 4, this trend is amply clear in the case of metals with close-packed structures (face-centered cubic (FCC) and hexagonal close-packed (HCP)), but not so clear in metals with a BCC structure. Another point of interest is that the difference in grain size is much less amongst metals that have high melting temperatures; the minimum grain size is virtually constant. Thus, for the HCP metals Co, Ti, Zr, Hf, and Ru, the minimum grain size is almost the same even though the melting temperatures vary between 1495°C for Co and 2310°C for Ru.

Figure 4. Variation of minimum grain size, d_min in mechanically milled FCC, HCP, and BCC metals as a function of the melting temperature of the metal. Note that even though the FCC and HCP metals show a decrease in grain size with increasing melting temperature of the metal, such a trend is not clearly seen in BCC metals. Further, when the melting temperature is very high (say >2000K), then the grain size remains almost unchanged irrespective of the melting temperature of the metal.

It was suggested that d_min is determined by the minimum grain size that can sustain a dislocation pile-up within a grain and by the rate of recovery. Based on the dislocation pile-up model, the critical equilibrium distance between two edge dislocations in a pile-up, L_c (which could be assumed to be the crystallite or grain size in milled powders), was calculated [61] using the equation: $L_c=\frac{3G\mathit{b}}{\pi \left(1-\nu \right)H}$where G = shear modulus, b = Burgers vector, ν = Poisson’s ratio, and H = hardness of the material. According to the above equation, increased hardness results in smaller values of L_c (grain size) and an approximate linear relationship was observed between L_c and the minimum grain size obtained by milling of a number of metals. Other attempts have also been made to theoretically predict d_min on the basis of thermodynamic properties of materials [62].

A number of studies are available in the literature dealing with the synthesis, structure and properties of nanostructured materials processed by MA. Virtually, every type of material is processed by MA [63–69].

However, since not many significant things have been reported in recent years on the synthesis of nanostructured materials by MA, we will not spend much time on this aspect. But lot of exciting things have happened in the area of synthesis and characterization of nanocomposites processed by MA. We will discuss this topic now.

5.2. Nanocomposites

Composites are traditionally produced by solidification processing methods since processing is inexpensive and large tonnage quantities can also be produced. But it is not easy to disperse fine reinforcement particles in a liquid metal since agglomeration of the fine particles occurs and clusters are produced. Further, wetting of the particles is poor and consequently even the most vigorous stirring is not able to break the agglomerates. Additionally, the fine powders tend to float to the top of the melt during processing of the composites through solidification processing. Thus, solid-state processing methods such as MA are effective in dispersing fine particles (including nanoparticles) [70]. An added advantage is that since no melting is involved, even a large volume fraction of the reinforcement can be introduced.

The particle type, size, morphology, volume fraction, and distribution of reinforcing particles in the metal matrix play an important and critical role in enhancing or limiting the overall properties of the composite material. Further, the mechanical properties of the composite tend to improve with increasing volume fraction. Reinforcing the matrix with much smaller particles, in the submicron or nanometer range, is one of the key factors in producing high-performance composites, which yield improved mechanical properties. However, when incorporating smaller reinforcing particles into the metal matrix, inhomogeneous dispersion, settling of reinforcements and poor wettability in the metal matrix are inevitable and subsequent treatment by thermomechanical processes may not be effective in entirely eliminating these drawbacks. Accordingly, if the reinforcement size is very fine (of nanometer dimensions), then the volume fraction added is typically limited to about 2–3%.

Some of the specific goals sought in processing of nanocomposite materials through MA include incorporation of a high-volume fraction of ultrafine reinforcements and achievement of high ductility, and even superplasticity in some composites. It is also possible that due to the increased ductility, the fracture toughness of these composites could be higher than in their coarse-grained counterparts. In line with these goals, detailed studies were undertaken on the processing and characterization of a variety of nanocomposites via MA. We were able to achieve a very uniform distribution of the reinforcement phases in different types of matrices, including dispersion of a high volume fraction of nanometer-sized Al₂O₃ in Al [71] and SiC in Mg [72], and other composites based on aluminum [73–75], copper [76,77], magnesium [78,79], and molybdenum for high-temperature applications [80] among others.

We will now describe two representative investigations in detail. One deals with a ceramic-based intermetallic-containing nanocomposite and the other describes a novel composite containing metallic glass as the reinforcement in an Al-alloy matrix. We were able to obtain superplasticity in Ti₅Si₃+γ-TiAl composites [81,82], and will report the most recent results on the microstructure and abnormal deformation behavior of Al-metallic glass nanocomposites fabricated by MA [83,84].

5.3. Ti₅Si₃ + 40 vol.% γ-TiAl composites

Lightweight intermetallic alloys based on γ-TiAl are promising materials for high-temperature structural applications, e.g. in aircraft engines or stationary turbines [85,86]. Even though they have many desirable properties such as high specific strength and modulus both at room and elevated temperatures, and good corrosion and oxidation resistance, they suffer from inadequate room temperature ductility and insufficient creep resistance at elevated temperatures, especially between 800 and 850°C, an important requirement for elevated temperature applications of these materials. Therefore, efforts were made to develop high-temperature materials with adequate room temperature ductility for easy formability and also to increase the high-temperature strength through suitable heat treatment or alloying additions to obtain sufficient creep resistance. It was shown that the compressive strength of binary γ-TiAl alloys with nanometer-sized grains is about 2600 MPa at room temperature and that, at temperatures higher than about 500°C, the strength drops very rapidly to low values [87,88]. In fact, the strength was found to decrease at a faster rate for ultrafine-grained materials than for the coarse-grained counterparts. That is, the smaller the grain size of the specimen, the stronger and sharper is the drop in yield strength at elevated temperatures. This observation suggests that monolithic nanostructured materials may not be suitable for achieving the desired creep resistance. The Ti–Al–Si alloy system was chosen because it is a model system to study the influence of phase distribution and microstructure on the high-temperature deformation behavior of ceramic–intermetallic composites.

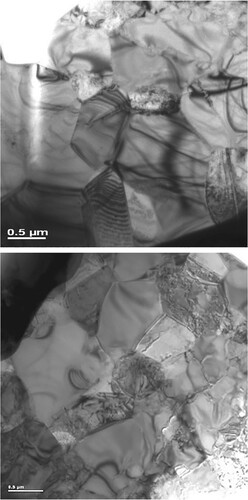
Composites of γ-TiAl and ζ-Ti₅Si₃ phases, with the volume fraction of the ζ-Ti₅Si₃ phase varying from 0 to 60 vol%, were produced by MA of the blended elemental powders. Fully dense and porosity-free compacts were produced by hot isostatic pressing, with the resulting grain size of each of the phases being about 400 nm. Figure 5 shows scanning electron micrographs of the ζ-Ti₅Si₃ + 40 vol% γ-TiAl composite showing that the two constituent phases are of sub-micron grain size and that they are very uniformly distributed throughout the microstructure. Grains with annealing twins inside them represent the γ-TiAl phase and the other grains the Ti₅Si₃ phase. Such a microstructure is expected to be conducive to superplastic deformation behavior. Both compression and tensile testing of these composite specimens were conducted at different temperatures and strain rates [82]. From the tensile stress–strain plots of the ζ-Ti₅Si₃ + 40 vol% γ-TiAl composite specimens, the following conclusions can be drawn. First, the strength decreased with increasing temperature and decreasing strain rate, both expected from normal mechanical behavior of metallic materials. Secondly, the specimens tested at 950°C and a strain rate of 4 × 10⁻⁵ s⁻¹ and 1000°C and a strain rate of 4 × 10⁻⁴ s⁻¹ exhibited large ductilities of nearly 150 and 100%, respectively (Figure 6).

Figure 5. (a) Low-magnification and (b) high-magnification scanning electron micrographs of the γ-TiAl + 60 vol% ζ-Ti₅Si₃ composite specimen. The microstructure shows that the two phases are of ultrafine grain sizes, very uniformly distributed in the microstructure, and approximately of equal proportions. Such a microstructure is conducive to observing superplastic deformation under appropriate conditions of testing.

Figure 6. Tensile engineering stress vs. strain curves for the γ-TiAl + 60 vol% ζ-Ti₅Si₃ composite alloy tested at different temperatures and strain rates. The tests were conducted in air until fracture occurred.

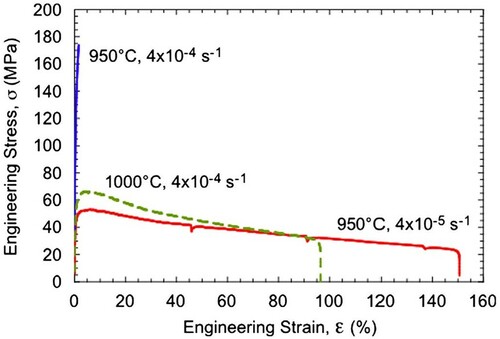
Considering that this composite is based on a ceramic material (Ti₅Si₃) this is a very high amount of deformation, suggestive of superplastic deformation. The final proof is provided by TEM investigations that confirm the continued stability of the equiaxed microstructure after tensile deformation. Even though the strain rate employed is relatively low, it is interesting that superplasticity was observed at 950°C, corresponding to about 0.5 T_m, where T_m is the melting temperature of the alloy. This should be compared with the coarse-grained γ-TiAl material which shows superplastic behavior only at temperatures about 300–400°C higher than the temperature observed in this investigation [82,89] Figure 7 shows TEM micrographs of the specimens before and after tensile testing, showing retention of the equiaxed microstructure after testing.

Figure 7. Transmission electron micrographs of the γ-TiAl + 60 vol% ζ-Ti₅Si₃ composite alloy (a) before and (b) after mechanical testing. Note that the grain size is still in the submicrometer range after testing and that there is dislocation accumulation in the γ-TiAl grains.

5.4. Al-Metallic glass composites

The most common and useful reinforcements in Al-based alloys have been ceramic materials to increase the strength and modulus of elasticity. However, a relatively new concept in developing useful nanocomposites has been to introduce metallic glass particles into an aluminum matrix. During consolidation and/or during annealing the metallic glass may crystallize and produce dispersions of nanometer dimensions. The advantage of a metallic glass reinforcement is that it improves the recyclability of the composites. It has been suggested that even though the addition of metallic glass particles as reinforcement to the Al-based matrix improves the strength of the matrix, they severely degrade the plasticity. However, refinement of the metallic glass to nanoparticles is the key factor for simultaneously obtaining both high strength and plasticity in the composites. MA has been shown to achieve uniform distribution of metallic glass nanoparticles in the Al-alloy matrix.

A Ti-based metallic glass powder with the composition Ti_55.5Cu_18.5Ni_17.5Al_8.5 was produced by MA of blended elemental powders. These powders, in the proportions of 0, 2, 6 and 8 vol.%, were mixed with gas-atomized Al-7075 powder and the mixture was again milled for different time periods. The milled powder was subsequently cold pressed into ingots at room temperature and then hot extruded at 673 K and 590 MPa pressure. Samples from the hot extruded bars were characterized for their microstructure using XRD, SEM, and TEM methods and the mechanical properties were evaluated at different temperatures in both tensile and compressive modes.

The TEM microstructure of the hot extruded Al 7075 + 8 vol.% metallic glass sample prepared from the composite powder milled for 30 h is shown in Figure 8. Since it is possible for the metallic glass particles to crystallize under heavy deformation, the mixture of glassy + partially crystallized glassy particles can be considered as a composite (metallic glass matrix composite, MGMC) and this composite acts now as a reinforcement in the Al-matrix. Figure 8(a) shows the bright-field TEM micrograph showing the presence of four different phases – (i) α-Al matrix, (ii) MgZn₂ (∼40 nm) precipitates (indicated by blue arrows), (iii) micron-sized MGMC particles, and (iv) irregular MGMC (∼100 nm) particles (indicated by yellow arrows). Figure 8(b) shows the interface between the Al matrix and the MGMC particle indicating a clean interface and that there is no interface phase present in these samples [83].

Figure 8. TEM microstructure of the hot-extruded composite from 30 h milled composite powders. (a) Bright-field TEM image. The yellow arrows indicate the presence of MGMC nanoparticles, and the blue arrows indicate the MgZn₂ precipitates. (b) The interface between the α-Al matrix and the MGMC particle, which is clean and devoid of any undesirable products.

Exceptional mechanical properties were obtained owing to the presence of bimodal distribution of metallic glass (micro- and nanoparticles) in the Al-matrix. The strength of the Al-8 vol.% metallic glass composite was as high as 1000 MPa, which is significantly high compared to the unreinforced Al-7075 alloy (297 MPa). The yield strength of these composites is much higher than many other Al-composites with other metallic glass reinforcements. Further, the experimentally determined strength values were observed to be much higher than the theoretically calculated strength levels (by the upper-bound ‘rule-of-mixtures’ model).

5.5. Abnormal deformation behavior

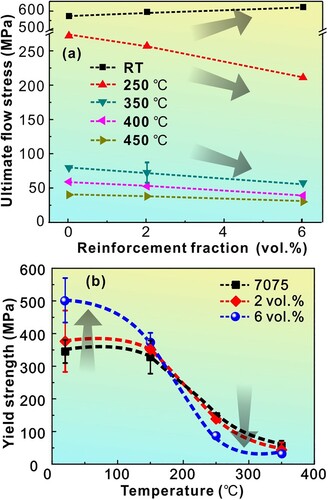
Figure 9(a) shows the variation of the ultimate tensile flow stress of the Al7075 matrix and the composites as a function of the test temperature. Note that the flow stress increased with increasing volume fraction of the reinforcement at room temperature and 150°C. But, at higher testing temperatures, the flow stress decreased almost linearly with increasing volume fraction of the metallic glass particles. Figure 9(b) presents the variation of the tensile yield strength of the composites as a function of temperature. The room temperature yield strength increased from ∼345 MPa for the Al-7075 matrix to ∼500 MPa for the composite with 6 vol% of the reinforcement. A similar trend was observed at 150°C also, even though the values are different. But, at temperatures >250°C, the composite was found to be weaker than the monolithic alloy. In fact, the rate at which the strength decreased with increasing temperature was faster in the composite than in the monolithic alloy [84]. The increased strength of the composite at room temperature is mostly due to the direct loading effect of hard metallic glass and dislocation strengthening in the matrix.

Figure 9. (a) The ultimate flow stress of the Al-7075 matrix and composites vs. volume fraction of the reinforcement at RT, 250°C, 350°C, 400°C, and 450°C. Note that while the strength increased with increasing volume fraction of the reinforcement at lower temperatures (RT and up to150°C), the strength decreased at higher temperatures. (b) Variation of the tensile yield strength of the Al-7075 matrix and composites as a function of the test temperature.

There may be many reasons for this abnormal deformation behavior of rapid reduction of the yield strength of the composites at higher temperatures in comparison to that of the matrix. These include thermal softening at higher temperatures, low viscosity of the metallic glass particles in the supercooled liquid region, damage accumulation (microcracks forming in the matrix, break-up of the matrix-reinforcement interface, cracking of the reinforcement, etc.), and overaging of the composites because of accelerated aging kinetics of the matrix in the composite. After careful consideration of the various possibilities, it was concluded that overaging of the matrix is the most probable reason for this abnormal behavior.

It is possible that the matrix in the composite is overaged at the temperature at which the test was done because of accelerated aging effects in the composite. It was reported that in age-hardenable alloys, the aging kinetics are a sensitive function of the aging temperature. For example, the time to reach peak aging in the Al 2014/ SiC_p composite ‘decreased much more with increasing temperature than it did in the unreinforced alloy’ [90]. Similar observations of accelerated aging were also reported in an A-3.5 wt.% Cu alloy with 6%, 13%, and 20% SiC particle composites [91] and others [92].

It was suggested that when a composite consisting of an age-hardenable matrix is quenched from the solutionizing temperature, the soft matrix undergoes plastic deformation due to the thermal stresses induced as a result of the CTE (coefficient of thermal expansion) mismatch between the matrix and the reinforcement. This deformation leads to the formation of heterogeneous nucleation sites for the precipitates to form due to the generation of dislocations and vacancies. Therefore, these precipitates grow and the material reaches the peak hardness value faster at higher temperatures. Since no heterogeneous nucleation sites are available in the unreinforced matrix, peak hardness will be reached much later. Even though this appears to be the most plausible explanation at the moment, a thorough study is required to provide a better understanding of the phenomenon of composite softening.

6. High-entropy alloys

Traditionally, alloys are synthesized with one (or at the most two) principal elements known as solvent and other alloying additions (solutes) are added in small quantities to achieve the desired properties like enhanced strength, high-temperature capability, corrosion and oxidation resistance, formability, and others. Conventional alloys such as stainless steels for corrosion resistance, nickel-based superalloys for high-temperature applications, and precipitation-hardened aluminum alloys for enhanced strength are classic examples of these concepts. However, a new paradigm was developed in 2004 when Cantor [93] and Yeh [94] independently published their papers on the structure of alloys containing many principal elements. Cantor’s alloys contained equal proportions of as many as sixteen components in one alloy and twenty in the other. Yeh’s alloy contained as many as 6–8 elements, all in equal proportions. Such type of alloys are now known as high-entropy alloys (HEAs). HEAs are defined as multicomponent alloys containing five or more constituents in equal or near equal proportions, with at least 5 at.% of each component [95]. HEAs have been shown to possess interesting properties such as high strength, high fracture toughness at cryogenic temperatures, enhanced thermal stability, superior oxidation and corrosion resistance.

These HEAs are also known by other names such as multicomponent alloys, multiple-principal-element alloys, multiprincipal component alloys, alloys with multiprincipal metallic elements, equiatomic multicomponent alloys, multicomponent solid solution alloys, compositionally complex alloys, and complex concentrated alloys. However, the term high-entropy alloys has come to stay even though it is now well recognized that high entropy alone is not responsible for the constitution of these alloys. Several reviews [for example, 96–102] and a couple of books [95,103] are published in this fast-growing research area.

6.1. Phase stability

The attraction of HEAs derives mainly from the fact that these alloys possess simple crystal structures in their as-cast state and some of them continue to exhibit the same crystal structure even on annealing at high temperatures without undergoing any phase transformations. This was most surprising because many binary and ternary alloys exhibit complex intermetallic phases in their equilibrium state, whereas these complex alloys with five or more elements.in equal proportions, exhibit simple structures. The occurrence of simple structures in these complex alloys was attributed to the high configurational entropy of mixing, reaching values of 1.61 R for a five-component alloy and 2.08 R for an eight-component alloy, where R is the gas constant. The configurational entropy of mixing (ΔS_config) can be calculated using the equation: $\mathrm{\Delta }{S}_{config}=-R\sum _{i=1}^n{x}_{i}ln{x}_i$where n is the number of components and x_i are their mole fractions. For alloys with equimolar ratio, the above equation reduces to: $\mathrm{\Delta }{S}_{config}=-R\text{ ln}\left(\frac{1}{n}\right)=R\text{ ln }n.$

Traditionally, multicomponent alloys with a configurational entropy of >1.5R are referred to as HEAs.

As mentioned above, HEAs exhibit simple crystal structures in their cast state. Many different criteria have been proposed to explain the structures of HEAs in terms of atomic size difference, δ, configurational entropy of mixing, ΔS_mix, enthalpy of mixing, ΔH_mix, valence electron concentration, electronegativity difference, and $\mathrm{\Omega }$, a parameter involving the melting temperature, T_m, ΔS_mix and ΔH_mix. Plots have been published delineating the phase stability regions of the different phases with the above parameters. For example, it was shown [104] that the solid solution (BCC and FCC) phases in these HEAs are stable under the following conditions:

0 < δ < 8.5,

−22 < ΔH_mix < 7 kJ/mol, and

11 < ΔS_mix < 19.5 J/(K-mol).

On the other hand, bulk metallic glasses are formed when the following conditions are satisfied:

δ > 9,

−35 < ΔH_mix < −8.5 kJ/mol, and

7 < ΔS_mix < 14 J/(K-mol).

Essentially it should be recognized that small atomic size differences reduce the lattice strain in the solid solution making it stable. Further, if the entropy of mixing is positive and large, mixing (alloying) will not occur and if it is very large and negative intermetallics get stabilized. Thus, small atomic size differences and small negative heat of mixing help in the formation and stabilization of solid solutions.

The mechanical properties of HEAs have been recently reviewed [101]. The hardness and strength of these alloys is reasonably high. The strengthening in these alloys is attributed to multiple deformation mechanisms including solid solution strengthening, order hardening, and in some cases due to the presence of precipitates and/or secondary phases. It is also becoming slowly clear that the best combination of properties for applications can be achieved not necessarily by using equimolar alloys but by modifying those compositions to non-equimolar alloys to achieve the desired properties.

6.2. Characteristics of HEAs

HEAs are characterized by four important core characteristics – (i) high entropy, (ii) severe lattice distortion, (iii) sluggish diffusion, and (iv) cocktail effects. As mentioned above, high configurational entropy (or entropy of mixing) decreases the free energy of the system according to the equation: $\mathrm{\Delta }{G}_{mix}=\mathrm{\Delta }{H}_{mix}-T\mathrm{\Delta }{S}_{mix},$where G is the Gibbs free energy, T is temperature, and H is enthalpy. The lowered energy can stabilize a phase with higher entropy, especially at higher temperatures. Simple structures such as FCC, BCC, and combinations of these are produced in majority of these HEAs. However, it is not necessary that high entropy always stabilizes these simple structures. Other phases such as intermetallics, sometimes in minor quantities, also exist along with these simple structures. It has been reported that bulk metallic glasses can also be synthesized in these alloy systems.

Since HEAs contain a number of elements of different sizes, the alloys experience lattice distortion. The strain energy associated with lattice distortion impedes dislocation movement and leads to solid solution strengthening. The occupancy of the neighboring lattice sites by different atoms not only leads to lattice distortion, but also to sluggish diffusion. This effect is also facilitated by the different diffusivities of the different constituent elements in the alloy. The sluggish diffusion effects allow structural stability and retention of high-temperature strength in these alloys. The cocktail effect suggests that the properties of the alloy are determined not only by the properties of the individual elements, but also by the interaction effects of the different elements. According to Cantor [102], ‘it is never likely that a large number of components would automatically guarantee high configurational entropy, formation of a single phase, slow diffusion, or extreme resistance to dislocation flow and fracture, leading to high strength  and toughness.’

The several reviews and books listed above discuss the processing, properties and applications of HEAs. The HEAs have been synthesized by many different processes including melting and casting, a wrought process including homogenization followed by cold/hot working and annealing, magnetron sputtering, mechanical alloying, high-pressure torsion, and others. Keeping in view the focus of this critical review, we will discuss here the structure and other attributes of mechanically alloyed HEAs.

6.3. Mechanically alloyed HEAs

Several alloy systems belonging to the HEA family have been processed by MA and other severe plastic deformation processes such as high-pressure torsion (HPT) and equal channel angular pressing (ECAP). The first synthesis of a HEA by MA is attributed to Varalakshmi et al. [105] who synthesized a nanocrystalline solid solution alloy in a six-component system.

Brief overviews of mechanically alloyed HEAs are available in the literature [106–108]. Instead of describing the results obtained on the different alloy systems, we will only highlight here some of the salient features and important results.

The results obtained on mechanically alloyed powders are mostly similar to those achieved by the casting methods, even though some differences exist between them. Similar types of phases are obtained in both cases. However, even in the mechanically alloyed cases, some differences are noted depending on the process parameters. For example, it was shown that milling of AlCoCuNiZn powder blends did not lead to complete alloying when grinding balls of 20 mm diameter and a rotation speed of 300 rpm were used to mill the powder for 50 h. But a homogeneous FCC phase was obtained when the milling speed was increased to 350 rpm and a mix of balls of different sizes were employed [109]. Energy analysis showed that the total energy transferred during milling in the second route was nearly 1.7 times higher compared to the first route, suggesting that higher energy input was required to achieve formation of the homogeneous phase. A similar result of formation of nanocrystalline Al₂NbTi₃V₂Zr was reported only when high energy ball milling was conducted [110]. Increased configurational entropy (by increasing the number of components in the alloy) does not appear to accelerate formation of homogeneous phases. On the other hand, the increased entropy resulted in reduced densification rates during consolidation due to the increased activation energies of diffusion with increasing number of elements [111]. Additionally, the phase evolution has also been shown to be different depending on the consolidation method used [112].

It has been reported that milling of powder blends for a long time (e.g. 140 h) resulted in the formation of amorphous phases. But it is not clear whether the powder blend first forms a solid solution phase, which then transforms to an amorphous phase on continued milling. This is a worthwhile line of investigation.

6.4. Phase selection rules

Hume-Rothery has pioneered predicting the crystal structure of solid solutions and intermediate phases based on the electronic structure of atoms. He used the concepts of atomic size difference, electronegativity, and valence values of the constituent elements to predict solid solubility limits and structure of intermediate phases [113]. There have been several investigations on phase formation in HEAs. Based on some of the thermodynamic parameters, the nature of the phase formed (solid solution phase, amorphous phase, etc.) in HEAs has been predicted. For example, Jiang et al. [114] suggested that solid solution phases are obtained when the conditions −7.27 kJ/mol < ΔH_mix < 4 kJ/mol and δ < 4.27% are satisfied. Further, a BCC phase is predicted when the valence electron concentration (VEC) is < 6.87 and an FCC phase when VEC > 8. A mixture of the BCC and FCC phases is predicted at intermediate VEC values. The electron-to-atom ratio (e/a) was also shown to be important in determining the nature of the solid solution phase. An FCC phase is predicted when e/a < 1.65 and a BCC phase when e/a > 2.05. A mixture of the two structures is obtained at intermediate values.

A parameter that has found widespread appeal among researchers is $\mathrm{\Omega }$ defined as: $\mathrm{\Omega }=\frac{T_m\mathrm{\Delta }{S}_{mix}}{|\mathrm{\Delta }{H}_{mix}|}$where the melting temperature of n-element alloy, T_m, is calculated using the rule of mixtures: $T_m=\sum _{i=1}^n{c}_i(T_m{)}_i$Here (T_m)_i is the melting point of the ith component of the alloy. A value of $\mathrm{\Omega }$ ≥ 1 is required to form the solid solution phase.

All the above predictions are based on experimental results obtained on the as-cast structures. It is not clear whether the above predictions (and others) are equally applicable to HEAs processed by other methods and also in the annealed condition. In other words, is the phase formed dependent on the processing method? So far, there have not been any such predictions when only the mechanically alloyed HEAs are considered. Since Hume-Rothery suggested atomic size difference and electronegativity as important parameters contributing to phase stability, an analysis was conducted whether these simple parameters could predict the correct phase formed in HEAs, both in the as-cast and mechanically alloyed states as well.

6.4. A new criterion

As mentioned earlier, Hume-Rothery rationalized the extent of solid solubility limits achieved in noble metal systems through atomic size difference (δ), electronegativity (χ), and valences of the constituent metals. He used the concept of valence electron concentration (VEC) to suggest that FCC (substitutional) solid solutions are stable up to a VEC of 1.4 and that BCC phases are stable at a VEC of 1.5. A higher VEC of 1.75 was suggested for the stability of HCP solid solutions [113].

It was later suggested by Darken and Gurry [115] that the extent of solid solubility limits (very high, high, and low) can be obtained by plotting the electronegativity difference (Δχ) against atomic size difference (Δδ). In these plots, referred to as Darken-Gurry plots, the electronegativity is plotted against the atomic size (corresponding to a coordination number of 12), and an ellipse is inscribed with an atomic size difference of ±15% and an electronegativity difference of ±0.3. Elements lying within the ellipse are expected to show high solid solubilities.

Instead of the several empirical rules suggested above to explain phase formation in HEAs, we have plotted Δχ against Δδ (as a Darken-Gurry plot) to correctly predict the phases formed in HEAs. Accordingly, Figure 10(a) shows that the correct phase is predicted in mechanically alloyed HEAs using these simple parameters.

Figure 10. Electronegativity (Δχ) vs. atomic size difference (Δδ%) (Darken-Gurry plots) for the investigated HEAs. (a) for alloys processed by MA and (b) for alloys processed by all techniques. These plots clearly outline the Δχ vs. Δδ% regions for the different phases observed (FCC, BCC, amorphous, etc.).

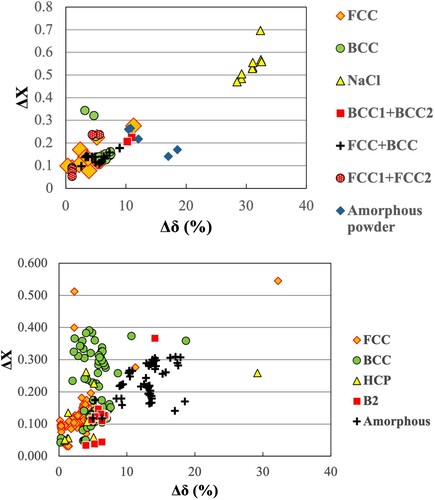
From these plots it becomes clear that FCC phases are stabilized when the atomic size difference is very small, typically less than about 6% and the electronegativity difference is <0.3. On the other hand, BCC phases are stable when both the atomic size difference and electronegativity difference are larger. On the other hand, phases with the NaCl structure are stable at still higher values of Δχ and Δδ, viz., very large atomic size difference (30–35%) and an electronegativity difference between 0.45 and 0.7. Lastly, amorphous phases are produced when the atomic size difference is large (>10%), but the electronegativity difference is between 0.1 and 0.3 [116].

It needs to be pointed out in this context that the earlier criteria were able to predict formation of the solid solution phase. But they were not able to distinguish between the FCC and BCC phases, except based on VEC. However, using our new criterion, it is possible to distinguish the formation of the FCC and BCC phases in these complex alloys based on these simple parameters. This criterion predicts the correct phase not only in mechanically processed HEAs but also in alloys processed by any technique (Figure 10(b)) [116].

6.5. High-entropy metallic glasses

From the above description, it may be noted that both high-entropy alloys (HEAs) and bulk metallic glasses (BMGs) contain a large number of components. But, BMGs are glassy in nature, while HEAs are crystalline. Additionally, many metallic glasses are formed in alloy systems, mostly with some metalloid elements present, even though metal–metal alloy systems have also been reported to form glasses. Further, these two apparently different types of materials exhibit quite different characteristics regarding their structure, processing and properties. While HEAs exhibit solid solution phases, BMGs show the amorphous/glassy structure. Further, while BMGs and metallic glasses in general, have been developed based on one principal element, HEAs contain all the constituent atoms in equal or near equal proportions.

It has been recently reported that some of the HEA compositions could be amorphized by solidification processing. Arguing that the crystallization process of the multicomponent supercooled liquid tends to be more sluggish than that of the simple alloy systems, Ma et al. synthesized the first BMG rod with equal amounts of the constituent elements and a 1.5 mm diameter rod in the Ti₂₀Zr₂₀Hf₂₀Ni₂₀Cu₂₀ system by copper mold casting [117]. Since then several tens of complex alloys, typical of HEAs, have been produced in the glassy state [37,118]. Although majority of these alloys are produced by the copper mold casting or other solidification routes, a few of them have been produced by MA methods. These include Fe₂₀Si₂₀B₂₀Al₂₀Nb₂₀ [119], Fe₂₀Si₂₀B₂₀Al₂₀Ni₂₀ [119], Fe₂₀Cr₂₀Ni₂₀Zr₂₀Si₂₀ [120], BeCoMgTi [121], BeCoMgTiZn [121], FeSiBAlNi(Co,Cu,Ag) [122], and many others [108].

In all these cases, however, it is not clear whether these amorphous phases crystallize into a simple solid solution phase on annealing the amorphous powder, ribbon or rod. It is also surprising that it was reported that the blended elemental powder mix directly transforms to the amorphous phase without going through the formation of either a solid solution or intermetallics [121]. Another point of interest is that the high entropy in these complex alloys does not appear to be neither necessary nor sufficient to produce them in the BMG state [118]. It was pointed out that high-entropy metallic glasses could be obtained only in alloys that show easy glass formability (i.e. high GFA). It is not clear if HEAs with low GFA can be produced in the glassy state.

6.6. Some important issues

Let us now highlight the specific advantages and limitations of the MA technique in processing of HEAs.

1. As mentioned earlier, mechanical alloying is capable of synthesizing a variety of metastable phases in a number of alloy systems, including supersaturated solid solutions and amorphous alloys (metallic glasses). Additionally, one of the most important attributes of MA is to refine the particle and grain sizes, the latter often down to nanometer levels, if the powder continues to be crystalline. Thus, MA is one of the most appropriate processing methods to synthesize nanocrystalline HEAs.

2. It was also noted that the HEAs processed by MA can transform to the glassy state on continued milling of the powders. Thus, it is possible to obtain both nanocrystalline and glassy HEAs, or mixtures of them, by mechanically alloying the powders for the appropriate length of time.

3. MA is a completely solid-state processing method and thus the limitations imposed by the liquid state and phase diagrams do not play any role in this processing method. This is especially true in HEAs since the alloys contain at least five elements with possibly sufficiently different melting temperatures. A situation like this could pose difficulties in the melting and casting methods and also lead to possible problems of segregation

4. Alloys with a positive heat of mixing (immiscible systems) can phase separate in the liquid and solid states and pose problems in melting and achieving homogeneity of the melt. But MA, being a completely solid state processing method, does not have any such problems since no melting is involved.

5. MA is known to extend the solid solubility limits in alloy systems in general and even in immiscible systems. Thus, the ease of obtaining a solid solution phase in HEAs is much easier when these alloys are processed by MA.

6. In some cases, alloys with the HEA composition have been produced in the amorphous state. But their transformation behavior to a simple solid solution phase has not been reported. This poses the question whether solid solution phase is the equilibrium phase in these complex alloys.

7. Contamination of the powder alloys by the milling media, milling container, and the atmosphere in which the powders are milled is of serious concern. This will interfere with the powder integrity and possibly the mechanical properties of the alloy. However, this is not of serious concern if the product made from these powders is used in less critical applications. Further, the contaminants (usually oxides, carbides, and nitrides) can be used to advantage in further strengthening of the alloy. In fact, the lightweight Al₂₀Li₂₀Mg₁₀Sc₂₀Ti₃₀ HEA developed by Koch’s group [123] was a single-phase FCC alloy. The alloy in the milled condition had a grain size of 12 nm and a high hardness of 5.8 GPa. However, when the alloy contained about 0.4 at.% N and 1.39 at.% O, (inherited from a batch of the Sc powder, which was contaminated during the process of converting the as-received pellets into powder by cryomilling) it had a grain size of 12 nm, but a high hardness of 6.1 GPa.

8. As pointed out by Vaidya et al. [108] ‘production of contamination-free alloys will (also) facilitate the reliable measurements of diffusion and in turn provides comprehensive understanding of their phase stability and mechanical behavior’.

9. One of the ways to minimize powder contamination is to mill the powder for shorter periods of time. But, in this case the steady-state condition is not reached, and consequently full alloying does not occur. However, longer milling introduces contamination. Also, in some cases, longer milling leads to amorphization of the powder, thus changing the constitution of the alloy.

10. In some cases, HEAs are synthesized by sequential alloying. First two components are milled together and then milling is continued by adding a third component and like this all the components are added and milled at the end. A downside of this method is that the powders milled in the beginning are milled for the longest time and thus there is a high possibility of this powder getting contaminated, especially if these are prone to easy contamination.

7. Immiscible alloys

When two elements with a negative heat of mixing (ΔH_mix) are combined together alloying occurs due to a reduction in the free energy of the system. On the other hand, it will be very difficult (and even impossible) to mix two or more elements that exhibit positive ΔH_mix to synthesize an alloy. In other words, the solid solubility of one element in the other is almost zero. Such alloys are normally referred to as immiscible alloys. This immiscibility can occur both in the solid and liquid states. Immiscibility in the liquid state is less common because of the high diffusivity of the component atoms in the liquid state. Immiscibility, on the other hand, is much more common in the solid state. Typical examples of the latter include Ag-Ni, Cu-Cr, Cu-Fe, Cu-W, Fe-Mg, Ti-Mg, Zr-Nb, among several others. There are also systems in which ΔH_mix is slightly positive when the constituents are miscible in the liquid state due to the entropic contribution to the free energy of mixing at high temperatures. But phase separation occurs at lower temperatures in the solid state, especially at room temperature, resulting in no or little mutual solid solubility and no intermetallic phases. Thus, it becomes necessary to ‘drive’ the elements forcibly to overcome the effects of positive ΔH_mix to get alloyed. This becomes possible only through non-equilibrium processing methods such as vapor quenching and mechanical alloying. Ma has presented an overview of alloys created between immiscible elements [124].

Several different processes have been employed to make alloys in systems with positive ΔH_mix. These include vapor quenching (sputtering, evaporation) [125,126], liquid quenching [127], laser ablation [128], mechanical alloying [129,130], and ion beam mixing [131,132]. Both amorphous phases and solid solutions have been reported to form in these alloys with a positive ΔH_mix. Amorphous phases are typically produced in some alloy systems only by vapor-quenching techniques, even though there are occasional references to formation of amorphous phases by other techniques as well. But these reports are questionable and unreliable, especially due to powder contamination, during MA. Even if amorphization occurs, it is at best partial and never complete. Solid solution phases are achieved in many alloys using MA and several other techniques. However, in keeping with the focus of this article, we will discuss the results obtained only on mechanically alloyed powders, and therefore only the solid solutions.

7.1. Limitations

Most often the results on mechanically alloyed powders are obtained using XRD techniques to determine the lattice parameters of crystalline phases and also to determine the solid solubility limits. But, as pointed out by several researchers [5,6,124], measurements of lattice parameters and estimating solid solubility limits are fraught with several difficulties. Firstly, the XRD peaks in MA powders are broad and diffuse and so accurate measurement of the peak position is difficult. Secondly, due to lattice strain and presence of stacking faults in the milled powder, the peak positions could be displaced. Thirdly, extrapolation of the trend of lattice parameter vs. solute concentration observed at lower solute contents to higher concentration levels may not always follow the same trend. The lattice parameters do not always follow the Vegard’s law due to elastic strain and magnetovolume effects [24]. These facts make lattice parameter measurements unreliable for determining solute concentrations in the solid solution phases.

7.2. Extended solid solutions

Supersaturated solid solutions have been produced in these systems through methods such as vapor quenching, ion mixing, and MA. Some of these maximum solid solubility values, in alloys produced by MA, are listed in Table 4, along with the ΔH_mix values in these systems. However, due to the fact that there are many variables in the MA process, the solid solubility values reported could be different depending on the process variables employed in the experiment.

Table 4. Solid solubility extensions achieved in systems with a positive heat of mixing processed through MA.

System	Equilibrium room temperature solid solubility (at.% solute)	Extended solid solubility limit (at.% solute)	Heat of mixing (kJ/mol) (Ref. 133)	Refs.
Ag-Cu	0.0	100	10	[8,134]
Ag-Ni	0.0	4.3	68	[129,130]
Ce-Yb	0.0	50		[135,136]
Co-Cu	0.0	100	26	[12]
Cr-Cu	0.0	20	51	[137]
Cu-Ag	0.0	100	8	[8,134]
Cu-Fe	0.3	20	50	[16]
Cu-Nb	0.1	3	9	[20]
Fe-Cu	7.2	20	53	[138–140]
Fe-W	0.0	30	0	[141]
Nb-Zr	0.0	20	15	[130]
Ni-Ag	0.0	6.6	56	[129,130]
Ti-Mg	0.0	6	59	[141]
W-Fe	2.0	50	0	[142]
Zr-Nb	0.0	52	17	[141]

It has been reported that in some systems with a positive ΔH_mix which satisfy the Hume-Rothery rules for solid solution formation (with similar crystal structures along with others) extensive solid solutions are formed, e.g. Cu–Ag [8,134] and Cu-Co [12,15]. In the Cu-Co system, the high-temperature FCC phase of Co has been found to be responsible for the complete solid solution formation. The result for the Cu–Ag system is in conformity with the result obtained by RSP methods [4,127]. But such a situation does not exist in the Ti-Mg system, even though all the Hume-Rothery rules are satisfied. Only a limited solid solubility of 3.6 at.% Mg in Ti was reported [25].

High-pressure torsion (HPT) experiments on Ni-Ag foils were conducted to investigate solid solubility extensions. No alloying was noticed between Ag and Ni even after 100 rotations of HPT [141]. Application of higher loads, e.g. 4 MN, suggested that increasing amounts of strain induced some limited mutual solid solubility of Ag in Ni and Ni in Ag. Exact values of solid solubility extension were not reported. Similarly, in the Nb-Zr system, detailed transmission electron microscopy (TEM) experiments suggested that a homogeneous solid solution formed with a grain size of <100 nm. The solid solution contained as much as 52 at.% Nb in Zr. On MA of Nb-Zr powder blends subjected to MA for 2 h of milling showed that, based on the XRD technique, the Nb-20 at.% Zr powder blend formed a homogeneous solid solution. Significant powder contamination occurred when Zr-rich Zr-Nb powder blends were subjected to MA.

7.3. Reasons for solid solubility extensions

Limited solid solutions are observed in systems which did not satisfy the Hume-Rothery rules. The values are different depending on the system and the process variables employed. Possible reasons for the extension of solid solubility limits have been explained earlier [5,6]. We will now discuss the specific reasons for solid solubility extensions in systems with a positive ΔH_mix.

In a system like Fe-Cu, FCC solid solutions are stable up to 40 at.% Fe, while the BCC solid solutions are stable up to 20 at.% Cu. Normally, a two-phase FCC + BCC mixture is expected to coexist in between these two composition extremes, but there is no two-phase region in this system processed by MA. It was reported that the two solid solutions, in the FCC + BCC region, have the same composition as the overall composition of the powder mixture. The two-phase coexistence represents an extended region of overlapping solubility for the two phases, rather than the usual two-phase region or a clear switchover at the concentration where the two phases have the same free energy. It is reported that MA could move the composition of both the phases towards the overall composition (i.e. full mixing) serving to homogenize the alloy [143,144]. This is in contrast to a normal two-phase mixture where the compositions of the two phases remain constant, beyond the solubility limits.

The external forcing action of MA at low temperatures drives the system toward composition homogenization. There is no stable or metastable equilibrium, and the common tangent construction and lever rule are not applicable in this situation. What results is a novel two-phase coexistence which is defined by a region of overlapping solubility, rather than the normal solubility gap.

A two-phase region could also form due to spinodal decomposition of a hypothetical supersaturated solid solution phase to achieve a (meta)stable equilibrium. MD atomic simulations have shown that, on quenching these materials at approximately 5 × 10¹⁰–5 × 10¹¹ K/s, the solid solution becomes inhomogeneous. These phases will exhibit compositional modulations on nanometer or even sub-nanometer level. Modulation wavelengths of 1–3 nm have been observed in the Au-Ni system [145].

Thermodynamic considerations suggest that an increased solid solubility can be obtained if the free energy of the two-phase mixture existing at that composition can be raised over that of the metastable solute-rich solid solution phase. Accordingly, increased solid solubility was obtained by premilling both the Ti and Mg powders before milling the Ti-Mg powder blend, reaching a level of 3.6 at.% Mg in Ti. The milling temperature was also changed, but this did not have much effect on changing the solid solubility limit [25]. The increase in solid solubility was attributed to the presence of titanium in the nanocrystalline state [146].

7.4. Correlation between solid solubility limit and heat of mixing

Table 4 lists the ΔH_mix values for the systems with a positive ΔH_mix [133] for which solid solubility extensions are reported by MA processing. The ΔH_mix values range from 0 to 68 kJ/mol. Similarly, the extended solid solubility level achieved is also different in different alloy systems. It is very small in some cases (6 at.% Mg in Ti) and 100% in some other systems, e.g. Cu–Ag and Co-Cu. However, by looking at the trends of solid solubility extensions and the ΔH_mix values, it is possible, to a first approximation, to relate the level of solid solubility extension to the heat of mixing in that system.

An important point to be noted is that the extent of solid solubility increase is qualitatively related to the magnitude of ΔH_mix. The heat of mixing increases in the sequence Zr-Nb < Ti-Mg < Ag-Ni and accordingly the solid solubility decreases in this sequence from 52 at.% Nb to 6 at.% Mg to 4.3 a.% Ni. In general, it is noted that the solid solubility under non-equilibrium processing conditions increases with a decrease in the value of ΔH_mix. The general trend for the alloy systems listed in Table 4 is shown in Figure 11. Thus, it is fair to conclude that it is possible to alloy immiscible metals through non-equilibrium processing methods and that it becomes more difficult to achieve alloying when the magnitude of the positive heat of mixing is large.

Figure 11. Plot showing the relationship between heat of formation and the extended solid solubility limits achieved in alloy systems with a positive heat of mixing. It may be noted qualitatively that higher solid solubility limits have been achieved in alloy systems with a low positive heat of mixing and lower solubilities in systems with a high positive heat of mixing. That is these two parameters move in opposite directions.

8. Heterostructured materials

Conventional wisdom informs us that strength and ductility of materials do not move in the same direction. The higher the strength the lower is the ductility, and high ductility is obtained only when the material is not very hard and strong. For example, 304 stainless steel shows a tensile strength of 515 MPa in the hot finished and annealed condition with a ductility of 40%. On the other hand, the same steel in the cold worked (1/4 hard) condition has a tensile strength of 860 MPa, but the ductility drops off to 10% [147]. Most metallic alloys exhibit a similar behavior. This trade-off between strength and ductility cannot be easily solved using our conventional principles and processing methods.

The three popular methods to strengthen single-phase materials – (i) solid solution strengthening, (ii) strain hardening, and (iii) reduction in grain size – increase the strength but also reduce the ductility. The problem of strengthening two-phase or multi-phase materials is more complex. In recent years, nanocrystalline materials have shown reasonably high strength and hardness along with good plasticity (due to reduction in grain size to <100 nm) [148,149] reaching superplastic tensile extensibility of as much as 5,000% [150].

It was reported that a bimodal grain size distribution is produced in copper using thermo-mechanical treatment. The microstructure contained micrometer-sized grains embedded in a matrix of nanocrystalline and ultrafine grains resulting in high strength along with large amounts of ductility [151]. A high strength of 330 MPa was achieved from the ultrafine-grained matrix and good tensile fracture strain of about 65% from the micrometer-sized grains. This should be compared with the high strength of >400 MPa in a pure nanocrystalline state, but with a ductility of <1% [152]. The inhomogeneous microstructure induced strain hardening mechanisms that stabilized the tensile deformation [151].

In recent years a new concept of heterostructured materials was developed. These materials simultaneously exhibit high strength and large amounts of ductility [153–156]. The heterostructured materials are defined as materials containing zones with dramatic strength differences. In simple terms, the microstructure is not homogeneous but consists of two different microstructural features even in a pure metal. That is the microstructure is heterogeneous. This heterogeneous microstructure is abbreviated as heterostructure. The heterostructure can activate a new mechanism of deformation – hetero-deformation induced (HDI) strengthening and HDI strain hardening to alleviate or even totally avoid the strength-ductility trade-off [153–157]. The mechanical behavior of these novel materials cannot be explained in terms of conventional material science. Therefore, researchers have been paying serious attention to an understanding of this phenomenon and the development of such materials. Zhu [158] has recently presented an elegant summary of this fast emerging field of heterostructured materials.

During the past several years, many attempts have been made to simultaneously increase the strength and ductility by modifying the microstructures of materials. These modifications include gradient structures, heterogeneous lamellar structure, harmonic structure, laminate structure, dual-phase steel, nanodomained structure, nano-twinned grains, bimodal grain size, etc. The case of bimodal grains size was discussed above [151]. A characteristic feature of all these materials is that they consist of heterogeneous zones that have significantly different mechanical and physical properties (often differing by >100%). Even though composite materials also contain different phases with widely varying physical and mechanical characteristics, many of the properties of the composites can be predicted through the rule of mixtures using the volume fraction and properties of the individual components. However, in the heterostructured materials, the measured properties appear to be way above those predicted by the rule of mixtures.

The heterostructured materials can be processed by different methods including annealing of plastically deformed materials (the microstructure is sensitive to the conditions during plastic deformation and annealing), powder metallurgy followed by thermo-mechanical processing [159], surface mechanical attrition treatment [160], accumulative roll bonding [161], among others. and these types of microstructures can be produced by several different conventional processing methods, including the commercial ones. These novel materials can be processed easily and economically using the current commercial processes and therefore these materials can be easily produced using the current industrial practices.

Figure 12 presents a schematic of the four typical heterostructures being currently extensively investigated. These include heterogeneous lamellae, laminate structure, gradient structure, and harmonic (core–shell) structure [155]. It may be noted from this figure that the heterogeneous structure can take many different forms. The underlying theme of all these microstructures is that it contains a mixture of a soft phase (of micrometer dimensions) dispersed in a hard phase (usually of nanometer dimensions). It is the interface between these two phases that is responsible for the improved properties; the interface density can be tuned by changing the volume fraction of the phases.

Figure 12. Typical heterostructures currently investigated. (a) Heterogeneous lamellar structure, (b) laminate structure, (c) gradient structure, and (d) harmonic (core-shell) structure. The smallest features in all these schematics are of nanometer dimensions, while the other features depend on the fabrication process [155].

Figure 13 presents some actual micrographs. Figure 13(a) shows the microstructure of coarse-grained equiaxed titanium and Figure 13(b) the microstructure of the same titanium sample produced by asymmetric rolling and partial recrystallization. While the coarse-grained titanium shows equiaxed grain structure, the sample produced by asymmetric rolling and partial recrystallization shows the hetero-lamellar structure. The asymmetric rolling elongated the initial equiaxed grains into a lamellar structure, which is heterogeneous with some areas having finer lamellar spacing than others. The asymmetric rolling also imparts a higher strain near the sample surface, which produces a nanostructured surface layer as well as a slight structure gradient before and after recrystallization. During the subsequent partial recrystallization the lamellae with finer structure recrystallized to form soft microcrystalline lamellae while others underwent recovery to maintain the hard ultrafine-grained structure [153]. Figure 13(c) shows a transmission electron micrograph of a copper specimen that exhibits bimodal distribution of grain sizes. This specimen was rolled at liquid nitrogen temperature to 93% cold work and then annealed at 200°C for 3 min. This treatment led to complete recrystallization followed by secondary recrystallization. The latter treatment produced about 25 vol.% of grains with sufficiently large sizes. While high strength was obtained due to the fine nanocrystalline grain sizes, pronounced strain hardening was achieved through the large grains. Thus, both sufficiently high strength and good ductility were achieved in this sample [151].

Figure 13. Actual micrographs of some heterostructured materials. (a) EBSD image of initial coarse-grained equiaxed pure titanium [153], (b) EBSD image of heterogeneous lamellar Ti after partial recrystallization [153], and (c) shows a transmission electron micrograph of a copper specimen that exhibits bimodal distribution of grain sizes. This specimen was rolled at liquid nitrogen temperature to 93% cold work and then annealed at 200°C for 3 min. This latter treatment produced about 25 vol.% of grains with sufficiently large sizes [151].

The above observations suggest that MA could be a very appropriate method to produce these heterostructured materials. In principle, one could control the grain size of the product by controlling the milling time and/or temperature. Using the same principle, one can produce a completely different grain size and then these two powders can be blended together and milled for a short time. Such processing can easily produce a bimodal grain size distribution. If the material to be processed is ductile, a lamellar structure is produced by MA processing. The lamellar thickness can be controlled by controlling the milling time. Such a material can be mixed with another nanocrystalline or ultrafine-grained grain-sized material and this mixture can again be a different type of heterostructured material. Thus, opportunities seem to be unlimited to produce a variety of heterostructured materials using the technique of MA.

9. Concluding remarks, challenges, and future directions for research

As detailed above, MA is a versatile technique capable of producing a variety of non-equilibrium (metastable) materials with interesting characteristics and properties. Some topics covered in the present article are metallic glasses, nanocrystalline materials and nanocomposites, high-entropy alloys, immiscible alloys, and heterostructured materials. All these materials, except for heterostructured materials, have been investigated for some time now and continue to be investigated through MA. Lot of information is generated and is available in the open literature. However, the area of heterostructured materials is relatively new; but some of its variants, e.g. bimodal grain sizes, have been studied in earlier years. In fact, it has been clearly shown that any new phases/alloys (e.g. extended solid solutions, quasicrystalline phases, metallic glasses, HEAs, heterostructured alloys) that have been produced by any of the novel non-equilibrium techniques can also be successfully synthesized by MA.

When dealing with mechanically alloyed materials, one of the important issues is contamination of the milled powders. While this is undesirable in most cases, it is beneficial in some cases. Powder contamination, especially with interstitial elements such as carbon, oxygen, and nitrogen, either from the atmosphere, or the original powder, or from the milling media can deteriorate the mechanical properties of the material. It is also possible that impurities are also introduced into the powder during consolidation. Thus, the level of impurities can be reduced if the milled powder can be used as-is. On the other hand, when these compounds are uniformly dispersed in the matrix, the material can be stronger and harder, although it is most likely to be brittle. Thus, any material for a specific application must be properly chosen so that these impurities do not have any adverse effect on the material properties and performance. Accordingly, if the application requires materials which will not tolerate impurities, special precautions need to be taken to minimize these impurities to below the tolerance level or even completely avoid them. This is possible and doable, but the powder becomes expensive. On the other hand, some applications such as paints, solders, coatings, etc. can use powders without consolidation and can also tolerate impurities and so these powders can be used as they are.

Another important issue is the homogeneity of the milled powder. Since the final powder is produced by milling blended elemental mixture, diffusion plays an important role to achieve homogeneity of the composition. It is noted in the literature that researchers do not always mill the powders until a steady-state condition is reached [5,6]. In such a situation, the powder exhibits variation in composition from point to point and one cannot expect the powder to be homogeneous. Even if the powder is milled to a steady-state condition, homogeneity cannot always be guaranteed because of the different diffusivities of the constituent elements involved. This non-homogeneity could also be a matter of concern in some critical cases. The problem is exacerbated in the case of HEAs, which contain many components in the alloy.

Novel materials such as metallic glasses and nanostructured materials and nanocomposites are projected to be materials of the future for many applications. The problem of homogeneity assumes even greater importance there. Therefore, it becomes necessary that researchers pay attention to these issues of powder contamination and homogeneity in these materials.

Since the technique of MA produces powders, these need to be consolidated to full density while retaining the metastable phases and without losing the desired microstructural features such as glassy nature or nanostructural features. Innovative consolidation techniques have been developed for this purpose and successfully applied.

A concern with most of these novel materials—metallic glasses, nanomaterials, HEAs, and heterostructured alloys is that niche applications for these materials are still lacking. Rapid solidification has been the preferred technique to produce metallic glasses. Such metallic glass sheets have been stacked together and bonded to produce transformer core laminations. Such Fe-based metallic glass cores have been used in distribution transformers with advantages [162,163]. Similarly, bulk metallic glasses, again produced by solidification methods, have also found many different applications [37]. But such applications for glasses produced by MA have not been realized. The major (tonnage) application of MA materials has been as oxide dispersion strengthened (ODS) superalloys for applications in the aerospace industry and for high-temperature applications [5,6]. MA powders have also found applications in small volume quantities. These include solders, hydrogen-storage materials, production of metals and alloys through reduction reactions of natural ores among many others [5,6]. It will be useful to explore more such applications for MA products.

It has also come to be realized that the MA process can be used to recycle used and discarded materials to produce value-added materials for subsequent consumption. They can be pulverized, separated, and used to mix with other powders to produce composites. The bottom line is that newer and improved materials are being continuously developed for novel applications [164].

Even though applications for MA have been relatively limited, there have been several scientific discoveries made using this technique. For example, rationale for formation of extended solid solutions and mechanisms for metallic glass formation have been satisfactorily explained, and ease of producing nanomaterials and nanocomposites has been achieved. New scientific discoveries are still being made. It has been shown that MA is a very appropriate technique to synthesize nanocomposites, hydrogen storage materials, and HEAs. But it will be most desirable if the same alloy/system is synthesized by all these different techniques and the structure, characteristics, and properties are compared.

It has been well recognized that MA is a technique that can be used when majority of the other techniques fail to synthesize a material. Thus, this is the ‘go to’ technique in many cases. This is because MA is a completely solid-state processing technique and restrictions of phase diagrams (for processing from the liquid state as in RSP methods) do not control phase selection. Thus, more concerted efforts by researchers can open many more new applications for these materials produced using this simple technique.

Disclosure statement

No potential conflict of interest was reported by the author(s).