Energy and stochasticity: the yin and yang of dislocation patterning

ABSTRACT

Dislocations form patterns that strongly influence mechanical properties. Prevailing theories are dichotomous: patterns either form by energy minimization or stochasticity during plastic flow. Using discrete dislocation dynamics simulations, it is shown that both energy and stochasticity contribute to patterns. Monte Carlo simulations reveal that short-range forces between dislocations lead to wall-like structures, while long-range forces control the wall thickness. Perturbation simulations demonstrate that persistent, low-density regions form when the network is perturbed over sufficient deformation. These findings suggest a two-stage process where stochasticity forms low-density regions, which then lead to confined walls through local energy minimization.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

Dislocation patterns govern mechanical properties of metals. Contrary to previous thinking, we demonstrate that both energy minimization and stochasticity govern the emergence and nature of dislocation patterns.

KEYWORDS:

• Dislocation
• patterning
• elastic interactions

Introduction

Dislocation lines—the primary carriers of plasticity in crystalline solids—have a tendency to self-organize into quasi-ordered patterns, often comprised of low-density cells surrounded by high density walls, as shown in Figure 1(a). These patterns are important because they strongly influence mechanical properties, such as fatigue life [1], resistance to irradiation damage [2], hydrogen embrittlement [3], and propensity for void nucleation [4,5]. While many hypotheses have been proposed to explicate these patterns [6–13], the most widely cited are the theory of low energy dislocation structures (LEDS) [10], which posits that patterns form to minimize energy, and the stochastic patterning (SP) model [9,14] in which stochastic noise drives patterning. On the other hand, recent work using continuum dislocation dynamics simulations suggests that the LEDS and SP mechanisms operate concurrently to drive patterning [6,7,15,16]. Simulations using discrete dislocations have also revealed fundamental aspects of patterning [17–19]. Despite these advances, the basic dislocation processes which give rise to patterning are not well understood. Here we show using discrete dislocation dynamics (DDD) simulations that both energy minimization and stochasticity play important roles in pattern formation; they are the yin and yang (the seemingly opposing forces that share a deep interconnection) of dislocation patterning.

Figure 1. (a) Transmission electron micrograph of cellular patterning in Ni [24] (reproduced with permission). (b) Snapshot from MC-DDD simulation of wall structure formation. (c) $4.3\mu \mathrm{m}$ thick slab extracted from a DDD tensile test simulation after 0.5% strain with a perturbation region radius $R=4.3\mu \mathrm{m}$. Colors in (b,c) represent slip systems.

We can decompose the problem of cellular pattern formation into two mechanistic questions: What gives rise to regions of low density which eventually become cells? And what stabilizes and confines the dislocation content within the high density walls? Coupled to these questions is the quandary over what controls the length scales characterizing the cells and walls. To pursue answers to these questions, we have developed DDD-based techniques and studied dislocation patterning in single crystalline, face-centered cubic (FCC) metals.

Materials and methods

DDD simulations were performed using the ParaDiS code [20] with the subcycling time integrator [21] using elastic constants for pure Cu (shear modulus of 54.6 GPa and Poisson's ratio of 0.324). To simulate wall formation, the Monte Carlo DDD (MC-DDD) approach of Deka and Sills was used [22]. Periodic boundary conditions were used in the plane of the putative wall (the x–y plane) and infinite boundary conditions in the direction orthogonal to the wall (in the z-direction) to avoid spurious image interactions that may affect wall formation. For all results in the manuscript, our cubic simulation cell is 30, 000b on each edge (results with a larger cell are shown in the Supplemental Material) and is oriented with $x:⟨111⟩,y:⟨2\overline{1}\overline{1}⟩,z:⟨01\overline{1}⟩$ axes. We model an FCC metal with $\frac{1}{2}⟨110⟩-\{111\}$ slip systems. Each MC-DDD simulation was initialized with an array of parallel edge dislocations separated by distance $L_x=6000b$ (we show in the Supplemental Material that our findings are insensitive to the initial structure). No stresses were applied. During the MC line insertion step, periodic dislocation lines which span the simulation cell were inserted randomly. If the net force toward the center of the box on the inserted dislocation line resulting from elastic interactions with all dislocations in the system is below $F_{\mathrm{tol}}$ (negative forces are attractive), then the line is accepted. Otherwise it is deleted and another attempt is made. Below we present normalized values for the MC-DDD force acceptance parameter as $F_{\mathrm{tol}}^{\ast }=F_{\mathrm{tol}}/\mu b$, where μ is the shear modulus and b is the magnitude of the Burgers vector. In MC-DDD the acceptance criterion can be designed to answer specific questions about dislocation structure formation and evolution. The criterion we used here was designed to enable studies of planar wall formation. All $\frac{1}{2}⟨110⟩$ dislocations are confined to $\{111\}$ planes, no climb motion and no cross-slip is allowed except for in a few simulations given in the Supplemental Material. Each MC-DDD simulation was run on a single CPU for up to two weeks. Wall thicknesses resulting from these simulations were quantified by determining the thickness that contains 95% of the total dislocation line length, $t_{95}$. The steady-state thickness was obtained by fitting a tanh function to the $t_{95}$ vs. MC step number data and taking $90\mathrm{\%}$ of the asymptotic value as steady-state.

For the DDD perturbation simulations of cell formation, fully periodic boundary conditions were used. The initial system was comprised of straight, periodic dislocation lines which were first relaxed under zero applied stress until a stable network formed. All $\frac{1}{2}⟨110⟩$ dislocations are confined to $\{111\}$ planes, no climb motion and no cross-slip was allowed. Then a strain rate of ${10}^3{\mathrm{s}}^{-1}$ was applied in the $⟨001⟩$ direction. To perturb the network, junction formation was suppressed by preventing node splits associated with junction formation and using a relatively large core radius of a = 600b [23], which almost entirely suppresses junction formation. To compute radial dislocation density profiles from the center of the cubic simulation cell, the simulation cell was divided into 30 spherical shells of equal thickness. The total dislocation line length inside each shell was then used to compute the density as a function of radius. Each perturbation simulation was typically run on 64 cores for 4 weeks.

Results

First we consider cell-wall formation using MC-DDD simulations. We showed previously how these MC-DDD simulations naturally lead to the formation of cell-wall-like structures—as shown in Figure 1(b)—that converge to a steady-state thickness $t_{ss}$ as long as $F_{\mathrm{tol}}^{\ast }$ is below a critical value, $F_{\mathrm{tol}}^{\mathrm{c}\ast }$ [22]. Since the interaction forces between dislocations result from following downhill gradients in elastic energy, this finding is in line with the LEDS hypothesis.

Given that MC-DDD predicts formation of stable wall structures, such as those observed in cellular patterns, we seek to determine what aspects of dislocation physics govern wall formation and control the wall thickness. While the formation of these cell-wall-like structures is insensitive to many physical phenomena (see Supplemental Material), the range of elastic interactions has a strong influence. In materials, the range and magnitude of elastic interactions are controlled by the dislocation core structure (e.g. extended versus compact) and arrangement of lines (e.g. dipolar bundles, low-angle boundaries). Here we are interested in modulating short- and long-range interactions to see how they influence wall formation. By ‘short’ and ‘long’ range interactions, we simply mean elastic interactions nearer to dislocations versus their long-range 1/r tails. To reduce the short-range interactions we increase the dislocation core radius, a, used to compute dislocation stress fields [25]. While increasing a does not alter the steady-state wall thickness, it does have a significant influence on the acceptance rate for MC line insertion, as shown in Figure 2(a). Specifically, as a is increased the acceptance rate systematically decreases, meaning it becomes more difficult for a new dislocation line to find an attractive site in the wall. In fact, if a>200b, the acceptance rate essentially goes to zero under conditions where a stable wall would form ($F_{\mathrm{tol}}^{\ast }<F_{\mathrm{tol}}^{\mathrm{c}\ast }$). This means it is not possible to find a line insertion position and geometry that satisfies the MC acceptance criterion. Thus, our simulations require short-range interactions to promote wall formation. However, it is possible that other mechanisms not considered here could still enable wall formation.

Figure 2. Results from MC-DDD simulations of wall formation. (a) MC acceptance rate for different core radii a when $F_{\mathrm{tol}}^{\ast }=-2.7\times {10}^{-3}$. (b) Wall thickness (see Methods) as a function of MC step for different f and $F_{\mathrm{tol}}$. (c) Steady state thickness as a function of acceptance force tolerance for different long-range force cut-offs f. Curves show fit to a function of the form $A+B(F_{\mathrm{tol}}^{\ast }{)}^{-3}$. Gray regions in (b) and (c) denote when the finite simulation cell size artificially influences the wall thickness.

To study the influence of long-range interactions, we investigated the effect of truncating the long-range field at different lengths. We accomplished this truncation by computing the difference between each dislocation's stress field computed with core radius a and that computed with core radius fa, where f>1. Since the long-range field of a dislocation is independent of a, this scheme smoothly truncates the long-range field at a range specified by f [26] (fa is like an outer cut-off radius). Figure 2(b) presents a set of results showing evolution of the wall thickness with three different values of f and $F_{\mathrm{tol}}$. These results indicate that as the long-range interactions are progressively removed (as f is reduced): (1) the steady-state wall thickness is decreased, (2) sensitivity of the steady-state wall thickness on $F_{\mathrm{tol}}^{\ast }$ is reduced, and (3) the critical value $F_{\mathrm{tol}}^{\mathrm{c}\ast }$ increases. To more clearly illustrate these trends, we plot the steady-state wall thickness as a function of $F_{\mathrm{tol}}^{\ast }$ for different values of f in Figure 2(c).

Collecting these results together, we see that wall formation observed in our simulations clearly analogizes with a phase transition; as $F_{\mathrm{tol}}^{\ast }$ is decreased, the dislocation ‘phase’ changes from a random, unbounded network (uncondensed phase) to a stable, confined wall with well-defined thickness (condensed phase). The critical value $F_{\mathrm{tol}}^{\mathrm{c}\ast }$ at which this transition proceeds is analogous to the boiling point. When long-range interactions are (nearly) ‘entirely’ removed, as in the case of f = 5, the transition from the uncondensed to condensed phase is sharp. However, when long-range interactions are present, this transition becomes smeared [27–29]; rather than an abrupt change in steady-state thickness, it gradually reduces to an asymptotic value as $F_{\mathrm{tol}}^{\ast }\to -\mathrm{\infty }$. As f increases and more and more long-range interactions are included in the simulations, the phase transition continues to smear. Furthermore, as f increases, $F_{\mathrm{tol}}^{\mathrm{c}\ast }$ decreases, meaning that the boiling point is depressed. Our results seem to indicate that in the asymptotic limit of purely short-range elastic interactions, $F_{\mathrm{tol}}^{\mathrm{c}\ast }\to 0$ and $t_{\mathrm{ss}}\to 0$, meaning that zero-thickness walls form under infinitesimally attractive interaction forces between the dislocations in the wall.

Our studies of short- and long-range interactions lead us to conclude that wall formation is driven by attractive short-range elastic interactions, a finding that is consistent with other DDD simulations [17,18]. Long-range interactions, on the other hand, control the thickness of the walls and the strength of the attractive interactions that are necessary for walls to form. It is typically assumed that long-range interactions are self-screened by the dislocation network, so that the typical interaction range scales with ${\rho }^{-1/2}$ [30]. Our results thus predict that the wall thickness will decrease as the dislocation density increases since long-range interactions are attenuated, which is consistent with recent detailed transmission electron microscope measurements [31].

These results elucidate fundamental aspects of wall structures, but what about the low-density cell interiors? Where do they come from and what governs their diameter? One possibility is that cells are a natural result of statistical fluctuations in the dislocation density field, as envisaged by SP. Since dislocation motion is noisy, resulting from avalanche-style slip events [32,33], the local dislocation density is constantly fluctuating. If a large enough fluctuation occurs resulting in a region of relatively low density, the dislocation network could locally destabilize leading to a persistent ‘hole’ which does not fill back in. In this view, cells form as a result of an instability in the network, similar to the recent theory of Zaiser, Groma, and colleagues [6,7,16].

To quantify the potential for such instabilities, we developed a perturbation technique within DDD that allows us to initiate cell formation. In this approach, we define a spherical perturbation region of radius R centered in our simulation cell within which junction formation is suppressed. Outside this region, junctions are still able to form as usual. The binary junction suppression is accomplished using methods discussed previously by Sills et al. [23]. In our simulations, the formation of these junctions is the primary mechanism for dislocation multiplication, so by locally suppressing their formation a region of low dislocation density develops with strain, as shown in Figure 1(c). This provides a framework for performing a perturbation analysis of dislocation networks.

We employ this perturbation technique during standard tensile test simulations. Figure 3(a) shows how the dislocation density inside of the perturbation region, ${\rho }_i$, evolves during a DDD simulation with a box size of $17\mu \mathrm{m}$, initial dislocation density of ${10}^{12}{\mathrm{m}}^{-2}$, and various values of R. When $R<3.4\mu \mathrm{m}$, we find that while the dislocation density inside the perturbation zone is lower than outside of it, the multiplication rate is nonzero. On the other hand, if $R>3.4\mu \mathrm{m}$ the multiplication rate inside the perturbation region is negative, indicating that the network in that region is unstable; see Figure 1(c) for a snapshot when $R=4.3\mu \mathrm{m}$. The resulting radial dislocation density profile is shown in Figure 3(b) at a few strain levels, showing a sigmoidal behavior. This behavior implies that there is a critical perturbation volume of order $100{\rho }^{-3/2}$, above which the dislocation network becomes locally destabilized. This critical perturbation volume is set by the strengths of the dislocation junctions in the network. As the perturbation volume increases, the arms spanning the volume increase in length until no junctions are strong enough to anchor them, driving the local multiplication rate to zero.

Figure 3. Results from DDD perturbation simulations. (a) Dislocation density inside the perturbation region as a function of strain for different R values. (b) Radial dislocation density profiles with $R=4.3\mu \mathrm{m}$ and different tensile strains, showing the development of a hole. Sigmoidal fit lines also shown. (c) Difference in dislocation density between outside and inside after removing the perturbation, showing an unstable response when ${\epsilon }_p>0.3\mathrm{\%}$.

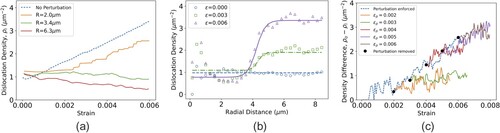
Carrying the analysis further, after some chosen amount of perturbation strain ${\epsilon }_p$ we subsequently lifted the perturbation by re-enabling junction formation, and then continued straining. This process was repeated for various levels of perturbation strain ${\epsilon }_p$ resulting in different dislocation densities outside of the perturbation region, ${\rho }_o$. The perturbation strain here is not intended to represent an applied strain level which would induce patterning, but rather a means for quantifying the stability of the dislocation network with respect to low density fluctuations. For these reasons, we cannot directly compare the perturbation strains here to experimental strains (it is not possible to do such a perturbation analysis experimentally). In Figure 3(c) we plot the difference in dislocation density between the outside and inside of the perturbation region, ${\rho }_o-{\rho }_i$, as a function of strain. The dashed curve shows the behavior while the perturbation is enforced; the density difference grows continuously with strain since the cell is always present. Other curves show what happens when the perturbation is removed. When the perturbation strain is greater than 0.3% and the perturbation is lifted, the difference in dislocation density continues to grow as if the system were still being perturbed (approximately follows the dashed curve). On the other hand, when the perturbation strain is less than 0.3% the dislocation density difference saturates, indicating that the network within the perturbation region has begun to multiply: the hole is filling back in. Additional results showing similar behavior are in the Supplemental Material. This bifurcated behavior indicates that there is a critical perturbation magnitude, above which a low density region is ‘permanently’ locked in place. These results provide strong evidence supporting the notion that dislocation networks are intrinsically unstable and will naturally form regions of low density under the action of statistical fluctuations. While the levels of strain attained here are small compared with experimental strains typically associated with patterning, the dislocation density levels in our DDD simulations are in the range where cellular patterns are observed in single crystalline FCC metals [34]. Hence, we believe that our assessment of dislocation network instability is directly relevant to experimentally observed patterning.

Discussion

The insight gained above provides a new window into the phenomenon of dislocation patterning, suggesting a two-stage process. First, regions of low density (holes) naturally form as a result of instabilities in plastic flow. After a region in the network is destabilized so that ‘free volume’ is liberated, dislocation lines within the low density zone are able to move more freely since they have more space around them. They are able to identify and move towards attractive regions on the periphery of the low density zone by cross-slipping to change their glide plane. The acceptance rates from our MC-DDD simulations indicate that finding such attractive regions becomes easier as the dislocation density increases, suggesting that attractive sites are easier to find at high densities. If attractive enough sites can be located, the periphery of the cell will condense into a stable wall structure. Recent work by Wu, Zaiser, and coauthors has further demonstrated that formation of low and high density regions ‘self replicates’ giving rise to a large-scale patterned structure which originates from a cell ‘nucleus’ [7,16]. This pictures shows how LEDS and SP mechanisms can work together to produce a cellular pattern.

While we are still far from a complete picture, the results presented herein provide unprecedented insight into the basic processes which underlie patterning obtained via discrete dislocation simulations with few assumptions and/or approximations. They reveal that dislocation networks contain several hidden length scales which are likely to influence patterns. The wall thickness is set by the elastic interactions within the network and the balance between short- and long-range stresses, and the cell size is set by the stability of the dislocation junctions which enable multiplication and govern network stability. Of course additional processes not considered here are likely to play a role. For example, many researchers have argued that cross-slip of screw dislocations is essential for patterning [8,17]. We have argued above that cross-slip enables dislocation lines in the free volume of a cell to find attractive spots on the cell's periphery. In other words, we believe that cross-slip plays an important role in ‘selecting’ the force tolerance value underlying wall formation. Although we did not consider cross-slip in our perturbation simulations, this should be pursued as future work. In future efforts, it may be possible to combine the two approaches employed here (MC-DDD and perturbation analysis) in a single simulation to construct a true cellular pattern. Overall, our results mechanistically reveal the synergistic roles played by energy minimization and stochastic flow in dislocation patterning. These insights could be used to design processing conditions yielding dislocation patterns with better properties, such as resistance to fatigue or irradiation damage.

Acknowledgments

The authors thank Dr. Péter Ispánovity, Dr. Brad Boyce, and Dr. Hojun Lim for their valuable feedback on this work.

Disclosure statement

The authors declare no competing interests.

Data availability statement

After publication, all datasets associated with this work will be published at the following Data DOI:10.5281/zenodo.6470996.

Additional information

Funding

Work at Rutgers University was supported by Sandia National Laboratories [contract # 2100008] for code and algorithm development and by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES) [award # DESC0022154] for simulation execution and analysis. This article has been authored by an employee of National Technology & Engineering Solutions of Sandia, LLC [contract no. DE-NA0003525] with the U.S. Department of Energy (DOE). The employee owns all right, title and interest in and to the article and is solely responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan https://www.energy.gov/downloads/doe-public-access-plan.