Statistical analysis of multi-criteria inventory classification models in the presence of forecast upsides

Abstract

Companies may receive forecast upsides that can undermine their ability to support customer demand on time. Therefore, it is critical to include forecast upsides when performing comparative analysis of inventory classification models. This study focuses on this subject. The study includes statistical methods and sensitivity analysis to determine the performance of which MCIC model is statistically significant with respect to inventory and customer orders fill rate. Results show that the PBB-model outperforms other models when forecast upside is present and the result is statistically significant. On the other hand, when no forecast upside is present, the R-model, which does not use descending ranking criteria, outperforms other models, and the difference is statistically significant. We also find that adding descending ranking criteria to the R-model and ZF-model does not improve their Service-Cost Performance Index.

Keywords:

• Multi-criteria Inventory classification
• service-cost performance
• descending ranking criteria
• safety stock
• orders fill rate

1. Introduction

ABC classification is a well-known method of inventory classification. This classification scheme divides the stock keeping units (SKUs) into a number of classes based on certain criteria. Inventory classification plays an important role in the management of inventory. When classifying inventory, two questions need to be addressed: (1) How many classes must be used? and (2) How do we determine the borders between these classes (Van Kampen, Akkerman, & Pieter van Donk, 2012)?

The traditional ABC classification is based on Pareto’s principle. The criterion used is annual dollar usage. This method assumes that 20% of items are responsible for 80% of the annual dollar usage (Chu, Liang, & Liao, 2008). Items are then categorized into class A, B, or C. Class A items are considered the most important, will typically contain items that account for 80% of the total annual dollar usage but only make up 20% of the total items. Class B items are considerably less important and typically contain 30% of the total items that are responsible for approximately 15% of the total annual dollar usage. The least important are class C items, which contribute the lowest total annual dollar usage but contain a large number of inventory items. They are responsible for approximately 5% of the annual dollar usage value and contain around 50% of the total number of items. Companies can afford to keep a higher stock of class B and C items than class A items, whereas class A items need to be monitored very closely (Beheshti, Grgurich, & Gilbert, 2012).

The traditional method is simple and easy to use. It is argued in the literature that other factors can also play a role in inventory classification which may include lead time, inventory cost, and obsolescence (Torabi, Hatefi, & Pay, 2012). Therefore, multi-criteria inventory classification (MCIC) has been used in recent studies in the context of inventory classification.

Multi-criteria ABC classification considers more than one factor or criterion that can impact inventory classification. Criteria used in the literature are cost, lead time, criticality, obsolescence, durability, stockability, order size requirement, commonality, substitutability, and repairability (Guvenir & Erel, 1998; Ng, 2007; Partovi & Anandarajan, 2002; Ramanathan, 2006; Torabi et al., 2012; Zhou & Fan, 2007). The literature shows that many techniques have been used to classify inventory, including matrix-based methodology, cluster analysis, analytic hierarchy process (AHP), genetic algorithm, neural networks, and optimization models.

Companies maintain different varieties of products, namely SKUs. Controlling and giving them equal attention is not easy or productive (Kabir & Akhtar Hasin, 2013). Inventory-control policies include maintaining an appropriate safety stock level, customer orders fill rate, and reorder points (Babai, Ladhari, & Lajili, 2015; Cohen & Ernst, 1988). Inventory classification can help in developing inventory control policies (Guvenir & Erel, 1998). For example, since class A consists of a smaller number of items but is responsible for a higher annual dollar usage, it is suggested to maintain a tighter inventory control, which includes regular cycle counting and better forecasting methods for class A items.

It is useful to understand the performance of MCIC models on inventory cost reduction and customer orders fill rate. The customer orders fill rate is defined as the probability of filling an entire customer order within a specified period (Song, 1998). Babai et al. (2015) presented a service-cost performance index (SCPI) analysis of four MCIC models (Ng-model, H-model, ZF-model, and R-model). They concluded that the R-model and ZF-model perform better in a combined SCPI. The reason for this is that in the Ng-model and H-model, the criteria are ranked in descending order (). And since the unit cost and higher annual dollar usage are used as the most important criteria, items having a higher unit cost and higher annual dollar usage receive a higher classification (class A or B) in the Ng-model and H-model. When the safety stock costs of all items are summed, this results in a higher total safety stock cost in these models.

We define ‘forecast upside’ as a scenario when actual demand is higher than the forecast. It is also referred to as positive forecast error or just forecast error in this study. When actual customer demand becomes higher than the forecast, it can result in inventory shortages, which will eventually impact the customer orders fill rate. Babai et al. (2015) did not consider a model comparison when forecast upside is present. They also did not include PBB-model in the comparison. Also, it is not evident how the R-model and ZF-model will perform when descending criteria ranking is included in these models, as found with the Ng-model and H-model, and whether there will be any difference in the SCPI. We also do not know if the difference in the performance of the models differs significantly. This study fills these gaps. Since this study focuses more on fulfilling orders fill rate, the study does not include the scenario of forecast downside. In the case of forecast downside, actual customer demand becomes lower than the forecast which creates inventory surplus. This poses a risk of having higher inventory cost than having lower orders fill rate. The contribution of this paper is as follows:

Comparative analysis of the SCPI of MCIC is studied in three different scenarios: (1) when forecast error is not present; (2) when forecast error is present but the same across all classes A, B, and C; and (3) when forecast error is present, but this error is different for classes A, B, and C. Hypothesis testing that assesses the significance of differences between the inventory performance of MCIC models is included. The recent PBB-model (Park, Bae, & Bae, 2014), modified R-model, and modified ZF-model are included in the comparison. The modified R-model and modified ZF-model add descending criteria ranking functionality to these models so that criteria can be ranked in descending order. Altogether, we used seven models for comparison: R-model, Ng-model, ZF-model, H-model, PBB-model, modified R-model, and modified ZF-model.

2. Literature review

In today’s world, a moderate-sized company must deal with thousands of inventory items, and inventory classification decisions may become challenging. Different methods and techniques used in the ABC classification of inventory are listed in Table 1, which is extracted from the work of Van Kampen et al. (2012) and further modified to include more recent studies. This study is focused on optimization models, which will be discussed in detail in the next section.

Table 1. Methods and techniques used in ABC classification (Van Kampen et al., 2012).

Method	Techniques	Research
Single-criteria	Traditional ABC	Canen and Galvão (1980), Chrisman (1985) , Portougal (2002), Onwubolu and Dube (2006)
Multi-criteria	Analytic hierarchy process (AHP)	Gajpal, Ganesh, and Rajendran (1994), Nan-fang and Xue (2004), Molenaers, Baets, Pintelon, and Waeyenbergh (2012), Lolli, Ishizaka, and Gamberini (2014), Munna, Rahman, and Roney (2015), Arikan and Citak (2017)
	Cluster analysis	Ernst and Cohen (1990), Canetta*, Cheikhrouhou, and Glardon (2005),
	Decision tree	Huiskonen (2001), Boylan, Syntetos, and Karakostas (2008)
	Distance modeling	Chen, Li, Kilgour, and Hipel (2008), Keshavarz Ghorabaee, Zavadskas, Olfat, and Turskis (2015)
	Genetic algorithm	Guvenir and Erel (1998)
	Graphical matrix	D’Alessandro and Baveja (2000), Ghobbar and Friend (2002), Syntetos, Boylan, and Croston (2005)
	Neural network	Partovi and Anandarajan (2002), Yu (2011), Kabir and Akhtar Hasin (2013)
	Optimization models	Ramanathan (2006), Ng (2007), Zhou and Fan (2007), Hadi-Vencheh (2010), Hatefi and Torabi (2010), Torabi et al. (2012), Park et al. (2014)

2.1. Optimization models

Recently, linear optimization models have gained attention in inventory classification. They are similar to DEA like models. In these models, criteria values for each item are converted into a scalar score. The weights for each criterion are generated by DEA like linear optimization models (Ng, 2007). Ramanathan (2006) used a weighted linear optimization (WLO) model to rank inventory. He noted that this type of optimization model has an advantage over other techniques because it gives optimal inventory scores without the user having to specify weights. In addition to the R-model, many other models have been proposed.

2.1.1. R-model

Ramanathan (2006) presented a WLO model to use in inventory classification, whereby the weight of each criterion on each item is automatically generated when the model is run. Also, after the model is run, the aggregate inventory score for each inventory item is maximized, which he termed ‘optimal inventory score.’ Based on the scores, items can be classified into classes A, B, or C. The R-model is shown below:(1)

where j = criteria, m = inventory items, N = total number of inventory items,  = weight of mth inventory items under criteria j, and  = score of mth inventory items under criteria j.

The objective function gives the optimal inventory score for the mth item. The model is repeatedly solved for each item by changing the objective function. The scores are used to classify the inventory items. The first constraint is a normalization constraint, which ensures that the weighted sum of an inventory item for all jth criteria is not greater than 1. The equation is written for all ‘n’ inventory items. The second constraint ensures that the weight of the jth criteria on the mth inventory item is not negative.

2.1.2. Ng-model

Ng (2007) presented an alternative linear optimization model and also presented a transformation technique, which ensures that results can be obtained without using a linear optimizer. He ranked the criteria in descending order in the Ng-model:(2)

where j = criteria, i = inventory items,  = weight of the ith inventory item under criteria j, and  = score of ith inventory item under criteria j.

The objective function is a maximization function. When the model is solved, the objective function maximizes the score for each inventory item. Weights are automatically generated when the model is solved. The first constraint is a normalization constraint, which ensures that summation of the weights received on the ith inventory item by criteria j is equal to 1. The second constraint is a descending ranking of the criteria, which shows that criterion 1 is more important than criterion 2, and criterion 2 is more important than criterion 3. In other words, it can be interpreted in mathematical form as follows: . The advantage of employing the Ng-model is that it lets the user identify which criterion s/he considers more important than others while ranking the inventory items. The R-model does not use this constraint.

2.1.3. ZF-model

Zhou and Fan (2007) pointed out that the R-model will always give an aggregate score of 1 to an item if it scores a higher value than other items in the certain criterion, even if it scores low in other criteria. This can assign that item an A classification. To correct this problem, the authors calculated good and bad indexes for each item using a maximization and minimization linear programming model, respectively. Then these two indexes were combined to produce a composite index. In the minimization problem, aggregate scores of the items are minimized so that each item gets a least-favorable weight for itself. The minimization model is shown below:(3)

where i = inventory items, n = criteria,  = score of ith inventory item under criteria n,  = weight of ith inventory item under criteria n, and  = least favorable aggregate score of ith inventory item.

The first constraint ensures that the weighted sum for all items based on the same set of weights must be greater than or equal to 1. The second constraint ensures that the sum of the weights on the ith item is greater than 0. The ZF-model is a WLO model. The objective function scores each inventory, which the authors termed as ‘least favorable’ or ‘bad index.’

They used the R-model for the maximization problem. The resulting scores from the model are referred to as a good index, which ensures that each item receives the most favorable weight for itself that maximizes its score when the model is solved. The model is shown below:(4)

where  = most favorable aggregate score of ith inventory item.

Furthermore, the two indexes are combined to produce a ‘composite index’ using the formula shown in Equation (5(5) ).(5)

where gI^* = maximum value of good index, gl⁻ = minimum value of bad index, bI^* = maximum value of bad index,  = minimum value of bad index,  = control parameter that is specified by user, and nI_i = composite index for an item i. The resulting composite indexes are then used to rank the inventory item to assist in inventory classification.

2.1.4. H-model

Hadi-Vencheh (2010) pointed out that the inventory score of an item from the Ng-model is independent of the weights associated with each criterion. This means that the weight of each criterion becomes irrelevant in determining the aggregate score of an item. Hadi-Vencheh (2010) extended the Ng-model and attempted to correct this issue. He used the sum of the squared weights in the normalization constraint, which converts the model into a non-linear model. The H-model is shown below:(6)

where  = relative importance weight attached to jth criteria, and  = score of ith inventory item under criteria j.

The objective function maximizes the aggregate score for each inventory item. Constraint 1 ensures that the sum of the squared values of all weights equals 1. Constraint 2 ensures that the weights are in ascending order. All weights are greater than zero.

2.1.5. PBB-model

Park et al. (2014) proposed an optimization model that gives a cross-efficiency optimal score. First, an optimal inventory score is calculated using the R-model, which the authors termed as WLO model. Then, they introduced another model to achieve the cross-efficiency optimal scores for an item evaluated by another item as shown below:(7)

where u_rk = weight given to the rth criterion of the kth item (y_rk), y_rk = score on item k under criterion r,  = optimal performance of inventory score as received from R-model, and  = optimal cross-efficiency score for item p evaluated by item k.

2.1.6. Modified R-model

In the modified R-model, we included a descending ranking criteria constraint. While solving the model, criteria with higher importance receive higher weights. All other constraints and the objective function used in the R-model remain unchanged. The modified R-model is shown below:(8)

2.1.7. Modified ZF-model

Similar to the modified R-model, we included a descending order criteria constraint in the modified ZF-model. Due to this constraint, weights are assigned to the criteria based on the importance level when the model is solved. All other constraints and the objective function used in the ZF-model remain unchanged. The modified ZF-model is shown below:(9)

3. Method

We considered the technique ‘optimization models’ in the comparative analysis in this study. Relevant studies are shown in Table 1. Formulations of the seven models were shown previously in Section 2. Our analysis of the models involves a three-step process. In the first step, each model is run for all inventory items. Criteria used are annual dollar usage, average unit cost, and lead time. Annual dollar usage is considered as the most important, whereas lead time as the least important criterion. We used Lingo optimization software to solve the models. Items are classified into classes A, B, or C. The second step involves evaluation of the SCPI for each model using the safety stock cost and overall fill rate (FRT), as was done by Babai et al. (2015). The notation and formula used are shown in the Appendix. The SCPI of each model is compared in three different categories: First: with no forecast upside. Second: with constant forecast upside across all classes, whereby forecast errors ranging from 15 to 40% are used. Third: with variable forecast error across classes A, B, and C. Forecast error for class A ranges from 20 to 45%, for class B from 25 to 50%, and for class C from 30 to 55%. To assist in the sensitivity analysis, a wide range of forecast error is used at multiple customer service levels (CSLs). We used three CSL categories:

First: Class A = 99% CSL, Class B = 95% CSL, and Class C = 90% CSL

Second: Class A = 95% CSL, Class B = 90% CSL, and Class C = 85% CSL

Third: Class A = 90% CSL, Class B = 85% CSL, and Class C = 80% CSL

The sensitivity analysis will attempt to answer the following questions: Does a model outperform other models for a wide range of forecast errors? Does more than one model outperform other models at different forecast error levels? Do the results differ at different CSLs?

To calculate the positive forecast error, or in other words, to know how much the actual demand is higher than the forecast, we can use the following formula (Hartnett & Romcke, 2000):(10)

The third step involves hypothesis testing. We constructed an ANOVA table for randomized block design where inventory performance of items under each model is considered treatment and each block refer to a certain forecast error applied on each item. The structure of the randomized block design (Bhattacharya & Johnson, 1977) is shown in Table 2; the resulting ANOVA is shown in Table 3.(11) (12) (13)

Table 2. Data structure for randomized block design with b blocks and k treatments.

	Treatments
	Ng	H	PBB	R	ZF	Modified-R	Modified-ZF	Block mean
Blocks	y11	y12	y13	y14	y15	y16	y17	y1.
15% forecast error	y21	y22	y23	y24	y25	y26	y27	y2.
20% forecast error	y31	y32	y33	y34	y35	y36	y37	y3.
25% forecast error	y41	y42	y43	y44	y45	y46	y47	y4.
30% forecast error	y51	y52	y53	y54	y55	y56	y57	y5.
35% forecast error	y61	y62	y63	y64	y65	y66	y67	y6.
40% forecast error	y71	y72	y73	y74	y75	y76	y77	y7.
Treatment means	y.1	y.2	y.3	y.4	y.5	y.6	y.7	y.

Table 3. ANOVA table for randomized block design.

Source	Sum of Squares	d.f.	Mean square	F-Ratio
Treatments	SST	k–1	MST = SST/k–1	MST/MSE
Blocks	SSB	b–1	MSB = SSB/b–1	MSB/MSE
Residual	SSE	(b–1)(k–1)	MSE = SSE/(b–1)(k–1)
Total	Total SS	bk–1

Hypothesis testing is set as follows:

H_o: No treatment difference (T₁ = T₂ = … = T_k)

VS

H₁: At least one treatment difference occurs

3.1. Illustrative example 1

We applied methods described in the previous section on two different data-sets: one including 47 inventory items used in the previous literature (Babai et al., 2015; Flores, Olson, & Dorai, 1992; Ng, 2007; Ramanathan, 2006) and the other including 10 inventory items used by Park et al. (2014). Experimental results of the first data-set of 47 items will be presented first.

We assumed a holding cost 20% of the average unit cost and a standard deviation of 2.62% of the annual forecasted demand, as used by Babai et al. (2015). We evaluated two cases: first, when forecast error is present and does not vary across classes A, B, and C; and second, when forecast error varies across classes A, B, and C.

Case 1: When forecast error is present and does not vary across classes A, B, and C

We extracted Table 4 from the work of Babai et al. (2015), modified it by adding a 15% forecast error, recalculated values for the new annual demand by using Equation (10(10) ), and determined the calculated revised (new) stock cost and overall FRT by using Equations (15(15) ) and (16(16) ). They are included in the Appendix. The analysis is shown in the shaded portion of Table 4, where CSLs of 99, 95, and 90% are used for classes A, B, and C, respectively.

Table 1 Safety stock cost and overall FRT for H-model without forecast error and at 15% forecast error (CSL is 99%, 95%, and 90% for classes A, B, and C, respectively).

Table

Table

Table 4 shows the safety stock cost and overall FRT for the H-model when there is no forecast error (non-shaded region), and also when the forecast error is 15% across all items (shaded region). When summed, the total safety stock cost for all 47 items is found to be $999.80 with no forecast error, and $1149.78 with 15% forecast error. The overall FRT with and without forecast error is calculated by Equation (16(16) ):

Overall FRT (from H-model) = 1401/1415 = 0.9904

Overall FRT (from H-model) with 15% forecast error = 1610/1627 = 0.9895

The same calculations are performed for the other six models and shown in Table 5. Table 5 includes a positive forecast error across six different forecast error levels, ranging from 15 to 40%. The given forecast error is constant across all items. For example, at 15% forecast error, all items received a 15% forecast error, regardless of which class they belong to. It can be seen that the R-model results in the lowest safety stock when there is no forecast error. This is similar to the findings of Babai et al. (2015). However, when forecast error is present, the PBB-model results in the lowest safety stock cost. These results will be discussed in detail in the next section. In order to be consistent and make the comparison simple, the values are normalized on a scale from 0 to 1 and shown in Table 6.

Table 5. Safety stock cost and FRT of various MCIC models without forecast error and when forecast error varies across classes A, B, and C.

	No forecast error		Forecast error 15%		Forecast error 20%		Forecast error 25%		Forecast error 30%		Forecast error 35%		Forecast error 40%
Model	Safety stock cost	FRT	Safety stock cost	FRT	Safety stock cost	FRT	Safety stock cost	FRT	Safety stock cost	FRT	Safety stock cost	FRT	Safety stock cost	FRT
Ng-model	1010.89	0.9913	1162.444	0.9907	1213.09	0.9905	1263.635	0.9903	1314.18	0.9901	1364.726	0.9899	1415.271	0.9897
H-model	999.79	0.9904	1149.775	0.9897	1199.765	0.9895	1249.775	0.9893	1299.745	0.9891	1349.736	0.9889	1399.726	0.9887
PBB-model	854.496	0.9787	982.671	0.9772	1025.396	0.9767	1068.121	0.9762	1110.846	0.9757	1153.57	0.9753	1196.295	0.9748
R-model	739.327	0.9843	996.83	0.9738	1040.17	0.9732	1083.511	0.9726	1126.851	0.9721	1170.192	0.9716	1213.532	0.9710
ZF-model	945.305	0.9842	1155.571	0.9842	1205.813	0.9839	1256.055	0.9835	1306.297	0.9832	1356.54	0.9829	1406.782	0.9826
ModifiedR-model	1000.758	0.9911	1150.873	0.9904	1200.911	0.9902	1250.949	0.9900	1300.987	0.9899	1351.025	0.9896	1401.063	0.9894
ModifiedZF-model	996.219	0.9897	1145.65	0.9889	1195.46	0.9887	1245.27	0.9885	1295.08	0.9883	1344.89	0.9880	1394.71	0.9878

Table 6. Summary of safety stock cost and customer orders fill rate for MCIC models at 15% forecast error.

Model	Cost	Achieved FRT	Normalized cost (A)	Normalized FRT (B)	Sum (A+B)
Ng-model	1162.4440	0.9907	0.8453	1.0000	1.8453
H-model	1149.7750	0.9897	0.8547	0.9991	1.8537
PBB-model	982.6710	0.9772	1.0000	0.9864	1.9864
R-model	996.8300	0.9738	0.9858	0.9829	1.9687
ZF-model	1155.5710	0.9842	0.8504	0.9935	1.8438
Modified R-model	1150.8730	0.9904	0.8538	0.9997	1.8536
Modified ZF-model	1145.6540	0.9889	0.8577	0.9982	1.8559

In the case of safety stock cost, a normalized value of 0 corresponds to the highest safety cost. We call this ‘x,’ and the remaining values are percentages of ‘x.’ In the case of achieved FRT, a normalized value of 1 corresponds to the highest FRT. We call this ‘y,’ and the remaining values are a percentage of ‘y.’ These two normalized values are summed for each model and are called the SCPI. This normalized scale allows the comparison of the models on a single scale. The higher the value of SCPI, the better is the model. This index makes it easier to compare the inventory performance of the models. The model that results in the highest SCPI score outperforms the other models. Table 7 presents a summary of the various forecast error levels. It can be seen that the PBB-model received the highest SCPI.

Table 7. SCPI at various forecast error levels and CSL of 99, 95, and 90%, for classes A, B, and C, respectively.

	Ng-model	H-model	PBB-model	R-model	ZF-model	Modified R-model	Modified ZF-model
No forecast error	1.7313	1.7385	1.8525	1.9929	1.7749	1.7385	1.7405
15% forecast error	1.8453	1.8537	1.9863	1.9687	1.8438	1.8535	1.8559
20% forecast error	1.8452	1.8536	1.9860	1.9683	1.8436	1.8535	1.8559
25% forecast error	1.8452	1.8536	1.9857	1.9679	1.8435	1.8535	1.8559
30% forecast error	1.8452	1.8536	1.9855	1.9676	1.8434	1.8536	1.8559
35% forecast error	1.8452	1.8536	1.9852	1.9672	1.8432	1.8535	1.8558
40% forecast error	1.8452	1.8536	1.9849	1.9669	1.8431	1.8535	1.8557

3.1.1. ANOVA and testing hypothesis for example 1 Case 1: when forecast error is present and does not vary across classes A, B, and C

The purpose of the hypothesis testing is to determine if there is a significant difference in the SCPI among the different MCIC models. Using the method explained previously in Section 3, we created an ANOVA table when forecast error is present and does not vary across classes A, B, and C, as shown in Table 8.

Table 8. ANOVA for service-cost inventory performance of MCIC models when forecast error does not vary.

	Some of squares	d.f.	Mean square	F-Ratio	F-Alpha
Treatments	SST = 0.13854	k–1 = 6	0.023089549	311341.3	F0.95(6,30) = 2.4205
Blocks	SSB = 1.78611E-06	b–1 = 5	2.97685E-07	4.014013
Residual	SSE = 2.2E-06	(b–1)(k–1) = 30	7.41615E-08
Total	0.138541303	bk–1 = 41

The hypotheses are set as follows:

H_o: No significant difference of SCPI among different MCIC methods

VS

H₁: Significant difference of SCPI among MCIC methods exists

The interpretation of these results is as follows: We reject the null hypothesis when F_ratio for treatment or MST/MSE > F_α (k–1, (b–1) (k–1)).We find that F_0.95 (6,30) = 2.4205 and F_ratio for treatment = 311341.3, we reject the null hypothesis, and we conclude that the treatment difference exists at the 95% confidence interval. In other words, the SCPI of all MCIC methods is not statistically equal. In order to find which MCIC method is significantly different, we constructed multiple t confidence intervals for pairwise comparisons of treatment means using Bonferroni’s method (Mendenhall, Sincich, & Boudreau, 2016). Bonferroni’s formula is given as:(14)

where p = number of sample (treatment) means in the experiment, g = number of pairwise comparison [g = p (p–1)/2], α = error rate, ν = number of df associated with MSE, S = , and B_ij = critical value for each treatment pair (ij).

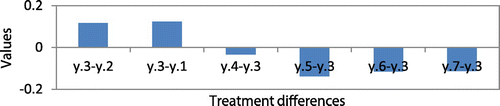
A treatment difference exists when the difference between the treatment means (y.i–y.j) is greater than B_ij. These calculations are shown in the Appendix. We find that the mean of treatment 3 significantly exceeds all other treatments. In other words, treatment 3 significantly outperforms other treatments. This is shown in Figure A1 in the Appendix.

Case 2: When forecast error is present and varies across classes A, B, and C

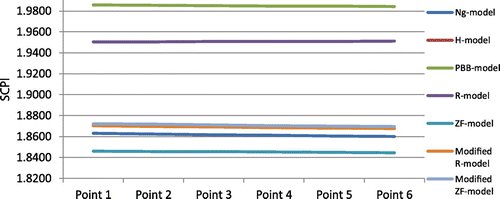
In this case, we evaluate the MCIC inventory performance when the positive forecast error is unique for classes A, B, and C but different across these classes. We can construct Table 9 for safety stock cost and overall FRT. The values are calculated with CSLs of 99, 95, and 90% for classes A, B, and C, respectively. Results are shown in Table 9 and Figure 1. Table 9 shows that the PBB-model results in the highest SCPI at all forecast error levels. A similar result is shown in Figure 1.

Table 9. Safety stock cost and overall FRT for MCIC models when forecast error varies, and CSL is 99, 95, and 90% for classes A, B, and C, respectively.

Model	A = 20%, B = 25%,			A = 25%, B = 30%,			A = 30%, B = 35%,			A = 35%, B = 40%,			A = 40%, B = 45%,			A = 45%, B = 50%,
	C = 30%			C = 35%			C = 40%			C = 45%			C = 50%			C = 55%
	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI
Ng-model	1230.689	0.9900	1.8630	1281.2340	0.9898	1.8623	1331.7800	0.9896	1.8617	1382.3260	0.9894	1.8611	1432.8710	0.9892	1.8605	1483.4170	0.9890	1.8600
H-model	1218	0.9890	1.8705	1268.6960	0.9888	1.8698	1318.6870	0.9886	1.8692	1368.6770	0.9884	1.8686	1418.6670	0.9882	1.8681	1468.6570	0.9880	1.8676
PBB-model	1062.091	0.9757	1.9856	1104.8160	0.9753	1.9853	1147.5400	0.9748	1.9850	1190.2660	0.9744	1.9848	1232.9910	0.9739	1.9845	1275.6760	0.9734	1.9842
R-model	1094.362	0.9700	1.9503	1137.7030	0.9694	1.9505	1181.0430	0.9689	1.9507	1224.3830	0.9684	1.9509	1267.7230	0.9678	1.9510	1311.0650	0.9673	1.9511
ZF-model	1242.987	0.9816	1.8460	1293.2290	0.9813	1.8457	1343.4710	0.9810	1.8455	1393.7130	0.9807	1.8452	1443.9560	0.9803	1.8449	1494.1980	0.9800	1.8447
ModifiedR-model	1211.758	0.9896	1.8704	1269.7950	0.9894	1.8694	1319.8350	0.9892	1.8691	1369.8720	0.9890	1.8685	1419.8910	0.9889	1.8681	1469.9480	0.9887	1.8675
ModifiedZF-model	1214.86	0.9881	1.8724	1264.6710	0.9879	1.8717	1314.4820	0.9877	1.8711	1364.2930	0.9874	1.8704	1414.1040	0.9872	1.8699	1463.9150	0.9870	1.8694

Figure 1. Graphical analysis of service-cost performance index (SCPI).

Point 1: A = 0.2, B = 0.25, C = 0.3; Point 2: A = 0.25, B = 0.30, C = 0.35; Point 3: A = 0.30, B = 0.35, C = 0.40; Point 4: A = 0.35, B = 0.40, C = 0.45

Point 5: A = 0.40, B = 0.45, C = 0.50; Point 6: A = 0.45, B = 0.50, C = 0.55

3.1.2. ANOVA and testing hypothesis for example 1 Case 2: when forecast error is present and varies across classes A, B, and C

The ANOVA when the forecast error is different across classes A, B, and C is shown in Table 10.

Table 10. ANOVA for service-cost performance index of MCIC models when forecast error varies across classes A, B, and C.

	Some of the squares	d.f.	Mean square	F-Ratio	F-Alpha
Treatments	SST = 0.10025073	k–1 = 6	0.016708455	60554.694	F0.95(6,30) = 2.4205
Blocks	SSB = 1.85473E-05	b–1 = 5	3.09122E-06	11.2031821
Residual	SSE = 8.2777E-06	(b–1)(k–1) = 30	2.75923E-07
Total	0.100277553	bk–1 = 41

The hypotheses are set as follows:

H_o: No significant difference of SCPI among different MCIC methods

VS

H₁: Significant difference of SCPI among MCIC methods exists

The interpretation of these results is as follows: We find that the F_ratio for treatment = 60554.694, which is greater than F_0.95 (6,30) = 2.4205, we reject the null hypothesis, and we conclude that a treatment difference exists at the 95% confidence interval at variable forecast error levels across classes A, B, and C. In other words, the SCPI of all MCIC methods is not statistically equal. We also constructed multiple t confidence intervals for pairwise comparisons of treatment means using Bonferroni’s method (Mendenhall et al., 2016). We find that the mean of treatment 3 (PBB-model) significantly exceeds that of all other treatments. This is shown in Figure A2 in the Appendix. It can be concluded that the PBB-model significantly outperforms other models.

3.2. Illustrative example 2

The data used for example 2 is from Park et al. (2014) and consists of ten inventory items. Safety stock cost and overall FRT are calculated both for Cases 1 and 2. In Case 1, forecast error does not vary across classes A, B, and C. In Case 2, forecast error varies across classes A, B, and C. Results are transformed into a SCPI. Results for Cases 1 and 2 for example 2 are shown in the Appendix (A3 and A4).

3.2.1. ANOVA and testing hypothesis for example 2 Case 1: when forecast error does not vary across classes A, B, and C

Hypothesis testing is performed in this section, and ANOVA results are shown in Table 11.

Table 11. ANOVA for service-cost performance index of MCIC models when forecast error does not vary across classes A, B, and C.

	Some of the squares	d.f.	Mean square	F-Ratio	F-Alpha
Treatments	SST = 0.076341	k–1 = 6	0.012723439	346275.1	F0.95(6,30) = 2.4205
Blocks	SSB = 2.99631E-06	b–1 = 5	4.99385E-07
Residual	SSE = 1.32E-06	(b–1)(k–1) = 30	3.67437E-08
Total	0.076344952	bk–1 = 41

The hypotheses are set as follows:

H_o: No significant difference of SCPI among different MCIC methods

VS

H₁: Significant difference of SCPI among MCIC methods exists

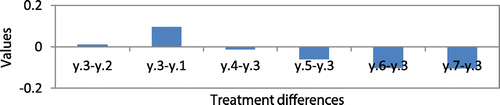
The interpretation of these results is as follows: We find that F_0.95 (6,30) = 2.4205 < F_ratio for treatments = 346275.1, we reject the null hypothesis, and we conclude that a treatment difference exists at the 95% confidence interval at non-variable forecast error levels across classes A, B, and C. This shows that the SCPI of all MCIC methods is not statistically equal. We also create multiple t confidence intervals for pairwise comparisons of treatment means. Treatment means are compared with critical values of each treatment pair (B_ij). We find that the mean of treatment 3 (PBB-model) significantly exceeds that of all other treatments. In other words, the PBB-model significantly outperforms the other models. This is shown in Figure A3 in the Appendix.

3.2.2. ANOVA and testing hypothesis for example 2 Case 2: when forecast error varies across classes A, B, and C

We performed hypothesis testing, and the ANOVA is shown in Table 12.

Table 12. ANOVA for service-cost performance index of MCIC models when forecast error varies across classes A, B, and C.

	Some of the squares	d.f.	Mean square	F-Ratio	F-Alpha
Treatments	SST = 0.057955	k–1 = 6	0.009659169	40597.6194	F (6,30) = 2.4205
Blocks	SSB = 9.86045E-06	b–1 = 5	1.64341E-06	6.9072712
Residual	SSE = 8.57E-06	(b–1)(k–1) = 30	2.37925E-07
Total	0.057973439	bk–1 = 41

The hypotheses are set as follows:

H_o: No significant difference of SCPI among different MCIC methods

VS

H₁: Significant difference of SCPI among MCIC methods exists

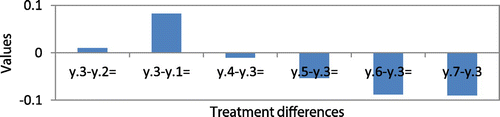
The interpretation of these results is as follows: We find that F_0.95 (6,30) = 2.4205 < F_ratio for treatments = 40597.619, we reject the null hypothesis, and we conclude that a treatment difference exists at the 95% confidence interval at variable forecast error levels across classes A, B, C. This means that the SCPI of all MCIC methods is not statistically equal. We also construct multiple t confidence intervals for pairwise comparisons of treatment means using Bonferroni’s method (Mendenhall et al., 2016). We find that the mean of treatment 3 (PBB-model) significantly exceeds that of all other treatments. In other words, the PBB-model significantly outperforms other models. This is shown in Figure A4 in the Appendix.

4. Results and discussion

In the illustrative Examples 1 and 2 presented in Section 3, we analyzed the safety stock cost and overall FRT of MCIC models at CSLs of 99, 95, and 90% for classes A, B, and C, respectively. We found that the PBB-model outperformed other models. In order to determine if the same result is true at other CSLs, we constructed Tables 13 and 14, in order to compare the results at other CSLs for both data-sets.

Table 13. Service-cost performance index for MCIC models – first data-set of 47 items.

Model	CSL 99%, 95%, 90%			CSL 95%, 90%, 85%			CSL 90%, 85%, 80%
	With no forecast error	With forecast error (constant between classes A, B, and C)	With forecast error (variable for classes A, B, and C)	With no forecast error	With forecast error (constant between classes A, B, and C)	With forecast error (variable for classes A, B, and C)	With no forecast error	With forecast error (constant between classes A, B, and C)	With forecast error (variable for classes A, B, and C)
Ng-model	1.7314	1.8453	1.8630	1.785	1.880	1.899	1.7950	1.8925	1.9116
H-model	1.7386	1.8537	1.7704	1.577	1.886	1.904	1.7989	1.8969	1.9150
PBB-model	1.8525	1.9864	1.9856	1.874	1.982	1.980	1.8712	1.9783	1.9764
R-model	1.9929	1.9687	1.9520	1.997	1.941	1.923	2.0000	1.9343	1.9155
ZF-model	1.7749	1.8438	1.8474	1.828	1.851	1.854	1.8246	1.8534	1.8559
Modified R-model	1.7386	1.8536	1.8704	1.791	1.887	1.905	1.8008	1.8989	1.9171
Modified ZF-model	1.7406	1.8559	1.8724	1.792	1.888	1.906	1.8007	1.8989	1.9164

Table 14. Service-cost performance index for MCIC models – second data-set of 10 items.

Model	CSL 99%, 95%, 90%			CSL 95%, 90%, 85%			CSL 90%, 85%, 80%
	With no forecast error	With forecast error (constant between classes A, B, and C)	With forecast error (variable for classes A, B, and C)	With no forecast error	With forecast error (constant between class A, B, and C)	With forecast error (variable for class A, B, and C)	With no forecast error	With forecast error (constant between class A, B, and C)	With forecast error (variable for class A, B, and C)
Ng-model	1.8929	1.8930	1.9052	1.918	1.918	1.930	1.9252	1.9255	1.9390
H-model	1.9775	1.9764	1.9771	1.978	1.977	1.976	1.9766	1.9760	1.9754
PBB-model	1.9894	1.9883	1.9873	1.986	1.985	1.983	1.9839	1.9828	1.9809
R-model	1.9775	1.9764	1.9768	1.978	1.977	1.976	1.9766	1.9760	1.9754
ZF-model	1.9293	1.9284	1.9347	1.939	1.944	1.944	1.9397	1.9388	1.9453
Modified R-model	1.8875	1.8874	1.9002	1.913	1.913	1.926	1.9198	1.9200	1.9344
Modified ZF-model	1.8855	1.8853	1.8980	1.905	1.904	1.918	1.9072	1.9069	1.9216

Results of both data-sets at various CSLs show that the PBB-model displays better service-cost performance both with non-variable and variable forecast error compared to other MCIC models. The lowest safety stock cost and highest overall FRT is achieved from the PBB-model when forecast error is present, and the difference is statistically significant at 95% confidence level. However, with no forecast error, the R-model results in a better SCPI in the first data-set, as was also seen by Babai et al. (2015), but in the second data-set, the R-model was second after the PBB-model. We cannot conclude that the R-model will always result in better service-cost performance when the forecast error is not present. Since Babai et al. (2015) did not include the PBB-model in their study, the effect of the PBB-model on the comparative analysis is unknown. Babai et al. (2015) claimed that models that do not use descending ranking criteria result in better service-cost performance with no forecast error. This finding does not change since the PBB-model also does not use descending ranking criteria.

According to Babai et al. (2015), the R-model outperforms other models, since it does not impose descending ranking order among criteria. To further investigate this, we included descending ranking orders between criteria both in the R-model and the ZF-model, and referred to this as the modified R-model and modified ZF-model. We found that adding descending ranking criteria does not increase the performance of the models, but rather decreases the performance. This also complements the findings of Babai et al. (2015).

Although the PBB-model does not use descending ranking criteria, it does use a different approach than the R-model. It not only uses self-evaluation, as in the case of the R-model, but it also cross-evaluates other items while giving an optimal score to an item. When the PBB-model is solved for a given inventory item, it maximizes the inventory score of that item while simultaneously minimizing the scores of other competing items. Thus, the scores of items are further refined because they go through two different evaluations. Therefore, classification of items is much more stable so it minimizes the effect of forecast error on the SCPI. This can be seen, when forecast error is present in the PBB-model, and it performs better than the other models at all forecast error levels.

This study recommends the PBB-model over other MCIC models for inventory classification. The only problem with using the PBB-model is its extensive calculations, which uses two models – one for self-evaluation and the other for peer-evaluation. Results of the first model are used in solving the second model. This increases the number of calculations and adds complexities. But in this age, a software program could be developed to facilitate the calculation of the models and make them less time-consuming.

The performance metrics used in this study are order FRT and safety stock cost in combination, for comparing the performance of models. However, when the performance metrics change, the results of the comparative analysis might change. Other models may show better performances. For example, if order FRT is the only consideration, Ng-model, modified R-model, and modified ZF-model show better performances as can be seen in Table 9 and Figure 1.

5. Conclusion

This study provides a comprehensive comparison of service-cost performance of seven MCIC models in three different scenarios: (1) when there is no forecast upside; (2) when forecast upside is present, but does not vary across classes A, B, and C; and (3) when forecast upside is present and varies across classes A, B, and C. We find that at no forecast upside, models that do not use descending ranking criteria (R-model, PBB-model, ZF-model) show a higher SCPI than models that use descending ranking criteria (Ng-model and H-model). In both Cases 2 and 3, when forecast upside is present, the PBB-model outperforms other MCIC models, and the result is statistically significant.

A service-cost performance evaluation of the MCIC models provides an understanding of how the models would behave in different forecast scenarios. When companies are not able to improve the accuracy of their forecast, they would like to use an inventory classification method that minimizes the risk of an increase in inventory cost and at the same time increases the fill rate of orders.

For future research, the performance of MCIC models could be further evaluated by changing the criteria used in the models and see if the comparative results change, that is, whether a given MCIC model would outperform with variable criteria sets. The bootstrap approach can also be employed in this regard. Also, a scenario of forecast downside can be considered in future research.

Disclosure statement

No potential conflict of interest was reported by the authors.

Appendix

The total cost of safety stock and overall FRT is given by (Babai et al., 2015) as:(15) (16)

where

N = Number of SKUs in the inventory system

C_T= Total safety stock cost for all inventory items

k_i = Safety factor for item i against the Customer Service Level (CSL)

h_i = Unit inventory holding cost of item i

D_i= Mean annual demand of item i

 = Standard deviation of annual demand for item i

L_i= Lead time of item i

Q_i= Order quantity of item i

FR_i= Fill rate of item i

FRT= Overall fill rate of the inventory system

G(x) = Loss function of the standard normal distribution ^{Figure A1Figure A2Figure A3Figure A4}

Figure A1. Comparison of treatment differences for sample data-set 1 for Case 1.

Figure A2. Comparison of treatment differences for sample data-set 1 for Case2.

Figure A3. Comparison of treatment differences for sample data-set 2 for Case1.

Figure A4. Comparison of treatment differences for sample data-set 2 for Case2.

Table A1. ANOVA for 47 items for Case 1 when forecast error is present and does not vary across classes A, B, and C.

Table A2. Comparing treatment means for 47 items for Case 1.

Table A3. Service-cost performance index of MCIC models for example 2 and Case 1: when forecast error does not vary across classes A, B, and C (CSLs of 99, 95, and 90% for classes A, B, and C, respectively).

Table

	No forecast upside			At 15% fcst error			At 20% fcst error			At 25% fcst error			At 30% fcst error			At 35% fcst error			At 40% fcst error
Models	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI
Ng-model	57.65	0.9958	1.8929	66.29	0.9956	1.8930	69.18	0.9954	1.8930	72.06	0.9953	1.8929	74.94	0.9952	1.8929	77.82	0.9951	1.8930	80.712	0.9951	1.8929
H-model	52.11	0.9854	1.9775	59.93	0.9844	1.9766	62.54	0.9841	1.9765	65.14	0.9837	1.9762	67.75	0.9834	1.9758	70.35	0.9831	1.9758	72.96	0.9827	1.9753
PBB-model	51.49	0.9854	1.9894	59.21	0.9844	1.9886	61.79	0.9840	1.9883	64.36	0.9836	1.9880	66.93	0.9833	1.9878	69.51	0.983	1.9876	72.08	0.9827	1.9873
R-model	52.11	0.9854	1.9775	59.93	0.9844	1.9766	62.54	0.9841	1.9765	65.14	0.9837	1.9762	67.75	0.9834	1.9758	70.35	0.9831	1.9758	72.96	0.9827	1.9753
ZF-model	54.84	0.9864	1.9293	63.07	0.9855	1.9285	65.81	0.9851	1.9284	68.56	0.9848	1.9280	71.3	0.9845	1.9278	74.04	0.9842	1.9277	76.78	0.984	1.9274
Modified R-model	58.02	0.9960	1.8875	66.73	0.9957	1.8873	69.63	0.9956	1.8874	72.53	0.9955	1.8874	75.43	0.9954	1.8873	78.34	0.9953	1.8873	81.24	0.9953	1.8872
Modified ZF-model	57.95	0.9930	1.8855	66.64	0.9926	1.8853	69.54	0.9924	1.8853	72.44	0.9922	1.8851	75.34	0.9921	1.8851	78.23	0.9919	1.8851	81.13	0.9918	1.8849

Table A4. Service-cost performance index of MCIC models for example 2 and Case 2: when forecast error varies across classes A, B, and C (CSLs of 99, 95, and 90% for classes A, B, and C, respectively).

Table

	A = 20%, B = 25%,			A = 25%, B = 30%,			A = 30%, B = 35%,			A = 35%, B = 40%,			A = 40%, B = 45%,			A = 45%, B = 50%,
	C = 30%			C = 35%			C = 40%			C = 45%			C = 50%			C = 55%
Models	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI	Safety stock cost	FRT	SCPI
Ng-model	70.914	0.9951	1.9061	73.79	0.995	1.9057	76.67	0.9949	1.9052	79.56	0.9949	1.9048	82.44	0.9948	1.9043	85.32	0.9956	1.9039
H-model	64.95	0.9834	1.9776	67.55	0.9831	1.9775	70.16	0.9828	1.9771	72.68	0.9825	1.9780	75.37	0.9822	1.9765	77.98	0.9844	1.9778
PBB-model	64.27	0.9831	1.9877	66.85	0.9828	1.9875	69.42	0.9825	1.9873	72	0.9823	1. 9871	74.57	0.9820	1.9869	77.14	0.9844	1.9886
R-model	64.95	0.9832	1.9774	67.55	0.9829	1.9773	70.16	0.9825	1.9768	72.76	0.9823	1.9767	75.37	0.9820	1.9763	77.98	0.9844	1.9778
ZF-model	67.89	0.9843	1.9356	70.63	0.984	1.9352	73.37	0.9837	1.9347	76.11	0.9835	1.9344	78.86	0.9832	1.9338	81.6	0.9855	1.9351
Modified R-model	71.32	0.9953	1.9011	74.22	0.9952	1.9007	77.12	0.9951	1.9002	80.02	0.9951	1.8998	82.92	0.9950	1.8993	85.82	0.9957	1.8989
ModifiedZF-model	71.23	0.9921	1.8991	74.12	0.992	1.8987	77.02	0.9918	1.8980	79.92	0.9917	1.8975	82.82	0.9916	1.8969	85.71	0.9926	1.8968