Newsvendor revisited: risk premiums of loss aversion

ABSTRACT

The classical newsvendor model in economics and decision theory treats losses and gains equally likely. However, decision makers are usually loss-averse as probable losses have more impact on humans than probable gains. This study presents a new variant of the newsvendor problem of loss-averse decision makers. The optimal order quantity is found by maximizing the expected utility of bounded functions. The implications of loss aversion on the certainty equivalents and risk premiums were also analyzed. Two case studies of exponential utility and normal demand were considered. A new elegant form of the optimal order quantity is established. The results show that when exponential loss aversion exists, the newsvendor optimal quantity serves as a lower(upper) bound on the optimal quantities. Moreover, high loss aversion entails higher RP. Similar findings hold by increasing the overage/underage costs and the demand standard deviation. Possible future extensions are demonstrated at the end of the paper.

KEYWORDS:

• Newsvendor
• loss aversion
• risk aversion
• utility
• inventory

1. Introduction

The newsvendor problem (alternatively called newsboy or single-period inventory) is a mathematical model in applied economics and operations management that is used to determine the optimal inventory. It simply pertains to how much to order of a certain product that exhibits uncertain customer demand (Kyparisis George & Koulamas, 2018; Mitra, 2018; Shen, Zhao, & Xie, 2017). In the classical newsvendor model, the product is sold to customers at a fixed price. If the product remains in stock (i.e., not sold), it will be salvaged for some other cheaper clearance price. High-order quantities result in salvage (overage cost), while low-order quantities result in lost opportunity (underage costs). The optimal order quantity is a one that minimizes the two cost components. There are wide applications of the newsvendors in single-day sales, In China for instance, the revenue of the Single Day promotions have risen rapidly from ¥0.1 billion in 2009 to ¥168.2 billion in 2017 (Cheng, Hongyan, & Thorstenson, 2018).

Newsvendor is a typical decision-making problem. Decision-making is the outcome of a process which involves an assessment of different options and then making a choice of which option to choose. The methods of decision-making involve cognitive processing. Studies on how people make decisions found that different people tend to think about decisions in a systematic way, reflecting the fact that human beings have a common set of cognitive skills, which are influential in making decisions (Hastie & Dawes, 2001).

The management of inventory is a critical factor for the success of modern business, particularly in retail industry. While profit maximization/cost minimization served as a milestone objective for a long time, the utility models are gaining more research interest nowadays. The decision makers are usually risk-averse, meaning that individuals have a positive and diminishing marginal utility for money. Risk-averse behavior of the decision makers affects their future choices and decisions, a matter which has been acknowledged by other studies in literature. It drastically influences the ordering, the pricing and other marketing decisions in business environments. Risk attitudes are described by utility functions. The ‘utility’ is an economic term referring to the total satisfaction attained from consuming goods or services. Therefore, the satisfaction of a surplus made by some trade/business is not necessarily well assessed by the expected value; rather, the utility is the rational valuation of the surplus from the perspective of the decision maker.

An underlying assumption in the classical newsvendor is that profit has the same impact as that of loss (i.e., risk-neutral decision maker). In risk neutrality, the decision maker employs the expectations of probable payoffs. For instance, a risk-neutral person would prefer an order quantity that yields an even-chance probable payoffs of (−$1000, $5000) over another order quantity that yields the payoffs ($1000, $2000) where the expected value of the first is $2000 and the second is $1500. However, most (if not all) individuals will prefer the second-order quantity due to loss aversion. This shows the failure of the Expected Value Theory and stresses on the need for a theory that explains such a behavior. This also implies that the classical newsvendor problem does not consider the resulting risk of loss. Due to loss-averse attitudes, individuals will be alert in potential losses and therefore, the optimal quantities that maximize their satisfaction are not those found by the classical problem. Risk attitudes are modeled by the utility theory; therefore, the newsvendor problem is revisited under the assumption of loss-averse decision makers in recent research (Bing-Bing, Zhi-Ping, & Tian-Hui, 2017; Meng, Tian Bai, & Zhu, 2018).

Utility theory has successfully explained the natural/cognitive behavior of decision makers. In the classical newsvendor problem, the decision maker must decide how much to order under the assumption of risk-neutral behavior. However, low percent of individuals can be found risk-neutral. Indeed, most of us tend to be loss-averse more than we do as risk-averse, (Dalalah & Alkhaledi, 2016; Liu, Song, Bing, & Cheng, 2015; Meng, Tian Bai, & Zhu, 2017).

In light of the above violations of the Expected Value Theory, this paper tackles the newsvendor problem with the utilities taken care of. The decision maker is assumed to have loss-averse attitude for more realistic decision-making behavior. This implies that the probable payoffs will be mapped into a utility function that measures the satisfaction attained. Thus, the monetary values are estimated by the utility. Our model is similar to the classical newsvendor problem in some aspects where the newsvendor can sell the products at an initial price. If the product is not sold, it will be salvage at a cheaper clearance price. However, the net wealth is evaluated by its utility, i.e., u(x), where u(x) is the utility function and x is the profit/cost incurred. The resulting nonlinear objective function that maximizes the expected utility will be analytically solved to get the optimal order quantity.

In general, the utility function should satisfy some conditions to model loss aversion. It has been emphasized by literature studies that the utility function should be convex on gains, concave on losses with upper and lower bounds; otherwise, a simple behavior as the one found in the classical Petersburg paradox cannot be explained (Pfiffelmann, 2011). The category of exponential functions (shown in Section 3) serves as a good utility choice that has asymptotic lower and upper bounds. Utilities have a significant impact on the newsvendor choices. Recently, the topic of risk attitudes has attracted more attention by the researchers in supply chain and revenue management fields (Dalalah & Alkhaledi, 2016).

Few studies have considered bounded utilities in the newsvendor problem. Consequently, this paper addresses the problem of maximizing the expected exponential utilities for a normal demand. The impact of loss aversion is analyzed to build a better insight to the problem. The extra amounts of fund the newsvendor require for undertaking the risk are also explored; the amounts reimbursed for the extra risk are known as risk premiums (RP).

This paper is organized as follows. A literature review is presented in Section 2 followed by the methodology in Section 3; here, the concepts of utility, certainty equivalents and RP are explained in Section 3.1, followed by the formulation of expected utility model in Section 3.2. Two different case studies are presented in Section 3.3. Next, the results and discussion are presented in Section 4. The managerial implications of the model are demonstrated in Section 5. Finally, the paper is concluded in Section 6.

2. Literature review

The classical newsvendor model is a common framework in operations management field. The simplest and most elementary form of the newsvendor problem is optimizing the stocking quantity where newsvendors should decide how much units to order under a stochastic future demand model. The problem tackles the maximization of the expected profits which are measured by the surplus of wealth end of the sales period. The model has served as a paradigm for many real applications that can be found in different aspects of business. The newsvendor problem can be found in inventory management, supply chain management, manufacturing sectors, scheduling, option pricing models, sports, fashion, telecom and many other areas (Subrata Dalalah, Hayajneh, & Sanajleh, 2015; Liu, Chen, & Liu, 2006; Mitra, 2018). The classical form of the newsvendor problem has been extensively studied in literature under the consideration of different conditions, such as multiple products and different pricing methods. Due to its closed form solution, the classical problem represented an elegant structure of stochastic inventory models.

Thorough surveys about the newsvendor problem can be found in the handbook of Choi (2012) which demonstrates the applications and implications of the newsvendor models in realistic context. For example, in some newsvendor problems, the demand is stimulated by sale prices; in others, the demand is driven by the inventory or by some marketing instruments. Some pricing techniques can be found in an early work of Petruzzi and Dada (1999) and a recent work of Mitra (2018). In Wang and Zhou (2011), an advertisement-sensitive demand has been considered for revenue sharing contract for an entire supply chain coordination. Sirong Luo and Sethi (2016), as an example, addressed the optimality conditions of a price-setting newsvendor problem for the additive and multiplicative demand. In the same context, Carrizosa Emilio and Olivares-Nadal, Pepa (2016) proposed an approach to explore a single-item newsvendor problem under a new setting which combines temporal dependence and tractable robust optimization when the demand is modeled as time series that follows an autoregressive process.

The newsvendor problem of a seasonal product demand has been addressed by Yossi and Pazgal (2008) with the presence of forward-looking customers. Their work falls under the concept of strategic customers who may cooperate with the seller to a certain extent. Further analysis to strategic customers has been demonstrated in Xuanming and Zhang (2008). They showed that the optimal stocking quantity can be lower than that of the classical newsvendor problem due to strategic customers. Strategic customers of risk aversion were considered by Wang and Qiying (2013). In their work, different utility functions have been employed to find the optimal stocking quantity when the customers are exposed to the seller available prices but not the quantity.

The management of the newsvendor problem from the behavioral aspects has its share in literature. The social and cognitive theories were considered in decision making as in Gino and Pisano (2008) and Bendoly, Croson, Goncalves, and Schultz (2010). Dynamic pricing of finite inventories of a heterogeneous population was also a successful approach by Su (2008). He showed that the customer population compositions may affect the optimal results. Advanced selling has been also explored in literature for the anticipated impact on profits (Cheng et al., 2018).

Different newsvendor objective functions were studied by Wang and Qiying (2013) such as maximizing the expected utility and maximizing the probability of achieving a level of profit. Prospect Theory has been successful in explaining the behavioral aspects in operations management settings, e.g., the classical newsvendor problem (Long & Nasiry, 2014) and the revenue sharing contracts (Becker-Peth & Thonemann, 2016). The first-order optimality conditions for risk-averse expectations of utility were demonstrated by Keren and Pliskin (2006), particularly for a uniform demand.

In addition to the above, Choi, Li, and Yan (2008) looked at the trade-offs of the mean variance to explore different attitudes toward risk. The conditional value at risk (CVaR) –one of the special risk metrics– has been also considered in the newsvendor problem. For instance, Gotoh and Takano (2007) tried to minimize the CVaR to find the optimal order quantity. The reader can also find additional pricing and ordering strategies that have been introduced by Chen, Xu, and Zhang (2009). Their results were compared to risk-neutral newsvendors. Wang, Fan, and Liu (2018) developed a markdown pricing model for retailers of perishable goods that not only maximize the retailer’s revenue but also maximize the aggregated consumer utility in the long run based on the integration of equity theory, commodity theory and social comparison theory

Loss aversion as another point of view of decision making is intuitively appealing and well supported in marketing, finance and organizational behavior. Indeed, most of the references listed in this article demonstrate that the decision-making behavior of managers is consistent with loss aversion as it has a substantial impact on the newsvendor decision. Loss-averse models have been slightly explored under the utility theory. Wang and Webster (2009) and Hui, Zhai, and Chen (2016) are among the first to study such a problem. Shen, Pang, and Cheng (2011) and Ma, Xue, Zhao, and Zeng (2016) considered loss aversion under a recourse option in the newsvendor problem. They studied the effect of loss aversion and the effect of uncertainties on the order quantity in both supply and demand. Loss aversion and rationality in the newsvendor problem under recourse options has been also studied in Vipin and Amit (2017).

To study the newsvendor’s risk attitude, many researchers have adopted the utility approach, such as Hui et al., 2016; Meng et al. (2018). For instance, Meng et al. (2018) employed anchoring as an approach for competitive newsvendors. They considered two demand-splitting rules for quantity competition including proportional demand allocation and demand reallocation. Loss-averse newsvendor’s problem has been solved using a robust optimization in Hui et al. (2016) which has been formerly considered in Wang and Webster (2009). Other researchers as Chen, Hao, and Li (2014) considered a loss-averse retailer in the supply chain with the option contracts to establish channel coordination. As for loss aversion with non-status quo reference point, Becker-Peth and Thonemann (2016) designed revenue sharing contracts for human retailers to coordinate the supply chain.

Theories regarding decision making generally fall into two categories: normative theories of cognition and descriptive theories of cognition. Normative theories are concerned with how we should make judgments and take decisions (Over, 2004). Theories falling into this category include formal logic, probability and decision theory. Descriptive theories set out to describe how people actually think when making decisions and how they build an empirical evidence to support their choices.

The decision making is an information-processing approach, which is concerned with how individuals choose between different options. While the utility theory has been considered in few studies in the literature, this paper presents a model to maximize the utility and presents an elegant formulation for the solution of the optimal stocking quantity. The effects of different loss-averse attitudes are analyzed under the assumption of normal demand and exponential utilities. Moreover, the resulting RP vs. the value of risk aversion, cost components and demand standard deviations are analyzed.

3. Methodology

The proposed model utilizes different methods to solve the utility newsvendor problem. The concept of utility and certainty equivalents are analytically explained which in turn lead to the estimation of RP. Strict formulation of the optimal order quantity is established, and an optimization of nonlinear utility objective function is conducted to numerically solve for the optimal quantities.

3.1. The utility, certainty equivalents and risk premiums

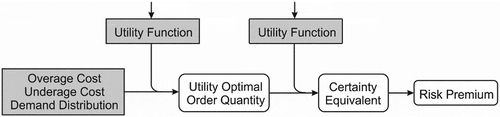
In this section, the utility theory is explained along with the certainty equivalents and RP. First, the characteristic utility function of risk and loss aversion is presented in closed forms. Later, boundedness in the utilities is explained by demonstrating Petersburg paradox. Figure 1 shows a flowchart of the research methods employed to attain the optimal order quantity. The inputs of the model are shown in shadowed boxes. The optimal order quantity is found via optimization of the resulting nonlinear objective function that exhibits a unique maximum.

Figure 1. The proposed model methodological steps.

Utility is a measure of preferences over some set of goods or services; it represents the satisfaction experienced by the consumer. Certainty equivalent (CE) is the equivalent amount of wealth of a risky project (gamble) from the perspective of the investor. Risk premium (RP) is the extra amount of money conceived by the investor for undertaking the risk. The utility is usually described by a function that maps the monetary values to their utility values, where u(x) is the utility of a quantity x. For example, consider a discrete lottery L that is denoted by the rewards and probabilities L(x₁, p₁; x₂, p₂; …; x_n, p_n). The expected utility of this lottery is given by .

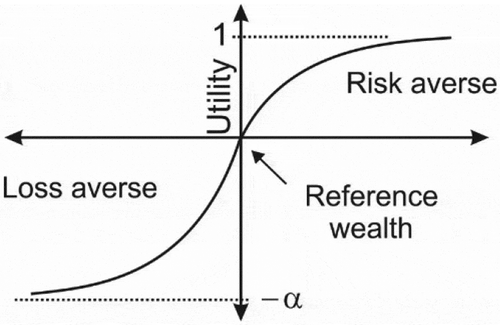
Risk aversion is described by a strictly increasing and concave function for a positive net wealth, while loss aversion is described by a strictly decreasing convex function for negative net wealth. Due to necessity for boundedness in utilities (the reader is referred to Petersburgh Paradox), the exponential utility function has become one interesting formulation that gives bounded utilities. A classical form of the exponential utility function that captures most of loss aversion features is given by:

(1)

where ν, α, , and . The coefficient of absolute risk aversion is defined as . In this study, three coefficients are considered, namely, the coefficient of risk aversion ν, and the two coefficients of loss aversion (α and λ). Higher values of ν and mean higher risk aversion and loss aversion, respectively. When ν = , and α = 1, loss aversion will have the same impact as risk aversion (i.e., the decision maker fears losses as much as he regrets gains). However, when ν > , the decision maker is more risk-averse; otherwise, he/she will be more loss-averse when α > 1 (i.e., more loss fearing). Figure 2 depicts the function of bounded utilities.

Figure 2. Risk and loss aversion of bounded utilities.

Certainty Equivalents (CEs) on the other hand are usually estimated by utility functions when the expected utility is given for a risky asset. Obviously, individuals will estimate their CEs according to their risk attitudes. Those who are risk seekers tend to overestimate the expected value, while those who are risk-averse tend to underestimate the risky asset (i.e., the newsvendor problem), particularly when loss is involved.

There is a consensus that the utilities have to be bounded to explain some decision-making behaviors. The need for bounded utilities can be demonstrated easily by Petersburg paradox. Petersburg paradox is thoroughly explained in Pfiffelmann (2011) that it is a gamble in which the player will win as much as $2ⁿ when a coin lands heads, where n refers to the nth throw at which the coin lands heads for the first time. The gamble is terminated at the first landing of heads. Clearly, the expected value of such gamble is ∞ declaring violation in the Expected Value Theory. The expected value of such lottery is found easily where EV = . Although, the expected value is infinity, yet, real experiments revealed that individuals only pay an amount as low as $3 for such a gamble. In contrast, we can easily show that the above form in Equation (1) presents limited expected utility. That is, for a reward of $2, the expected utility EU =  = EU =  =  = . Using the geometric series, it can be found that the expected utility of the above gamble equals to EU = , which is a finite quantity; hence, when , EU = 1, while when EU = 0, meaning that EU is bounded by the interval = [0, ].

The certainty equivalents can be found using the inverse of the expected utility function, Figure 3. The reason for this is owed to the assumption that both the expected utility value and CE will have the same utility from the perspective of the decision making. Therefore, the certainty equivalent of a risky asset is given by:

(2)

Figure 3. Risk attitudes illustrated, where CE refers to certainty equivalent, RP: risk premium, EV: expected value and is the inverse transform of the utility function u.

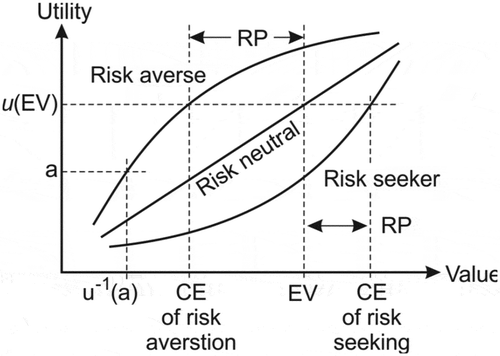
An asset’s risk premium is a form of compensation for investors who undertake extra risk compared to risk-free asset in a given investment. Risk premium is the minimum amount of money by which the expected return on a risky asset must exceed the anticipated return on a risk-free asset to induce an investor to hold the risky one. Risk premium is measured by:

(3)

where and are the risk premium, expected value and the certainty equivalent of a given setting of a risky asset i (such as the newsvendor problem). However, positive and negative risk premiums depend on the initial reference wealth. For simplicity, we consider an initial wealth of ‘0’ in our risk premium analysis. Now, for a continuous potential reward X that has the probability density function f(x), the expected utility is expressed in the form:

(4)

In the subsequent sections, the expected utility of different demand distributions is derived for the newsvendor problem followed by an optimization analysis to find the optimal order quantity.

3.2. The expected utility model of the newsvendor

In our model, the retailer (Newsvendor) faces a cost of c per unit of the product which can be sold to customers at a full price of p. Leftover units will be salvaged at a price of s, where s < c < p. As the demand is random, the retailer must determine the optimal stocking quantity to maximize his expected utility rather than maximizing the expected monetary value of his profits. No strategic planning takes place between the retailer and the customers in this setting. For a specific order quantity, if the realized demand is low, the leftover quantity will be sold at the salvage value; hence, the cost of overage is given by . On the other hand, lost opportunities may arise if large demand is realized when stocked quantities are low; hence, the cost of underage is given by . While the classical newsvendor problem results in an elegant structure, with utility maximization, the solution of the problem gets more complicated and therefore, more computational efforts are required to find the optimal stocking quantity.

In a newsvendor cost optimization model, the goal is to minimize the costs which appear as negative quantities in the loss margin of Figure 1. Let the stocking quantity be . When the demand (x) is less than in a cost newsvendor model, the retailer’s decrease in wealth is and therefore the expected utility is given by . Similarly, when the demand is greater than the order quantity , the expected drop in wealth is and the expected utility is given by . By summing the two terms, we have:

(5)

3.3. Applications of the utility theory using exponential and normal demand

3.3.1. Case I: the expected utility of the normal distribution

In this section, the expected utility is presented when the demand is normally distributed. Let the demand X~N(µ,σ), where and is the corresponding cumulative function; by considering the above utility in (1) for a positive net wealth, the expected utility can be found by the following:

(6)

which is simply expressed as:

Write the power part in the integration as:

(7)

The expected utility can then be expressed as:

(8)

However, , where ; accordingly, the expected utility reduces to the expression:

(9)

The above is the expected utility attained when the rewards are normally distributed. Therefore, the objective of an agent is to maximize the quantity . It simply states that the decision maker who is facing continuous and normally distributed rewards should seek those of higher averages and low variances. This result, which has been repeatedly reported in literature, conforms to the findings in risk management where low risk is observed in narrow reward ranges and higher gains may be attained in rewards of high mean values.

3.3.2. Case II: the exponential utility and normal demand

To proceed in this section, we now consider a loss-averse newsvendor of exponential utility and a normally distributed demand. In particular, there is a single risk-averse retailer who must determine how many units to order of some product. The demand X is random where X~N(µ,σ). Since a cost model is considered here, the second part of the utility function should be used (i.e., x < 0). Substitute both the utility and the demand distribution in (5) to get the following expression:

(10)

For simplicity, let and ; hence, the above expands to the following:

Note that, the second and fourth integration parts sum to 1; hence, we get:

(11)

Using the simplified expression in (7), we get the following:

For simplicity once again, let , , and to get the following:

(12)

By taking the constants out of the integration, the above is simplified to:

(13)

A further inspection of the above expression shows that it is nonlinear of a unique maximum as a function of . The optimal order quantity can be found by , where . Using Leibniz law of differentiation for the first part, we get:

The above is also equivalent to:

(14)

Recall that , and , and using a similar operation in (7), the power in the first expression will be =; accordingly, the expression (14) will reduce to the following form:

which also equals to:

(15)

The integration part above represents another normal distribution of the mean and a standard deviation of σ. Let be a cumulative density function of this normal distribution where:

(16)

Accordingly, we have:

(17)

For part B of the expression in (13), a similar procedure can be followed, where:

which by similar analysis of the first part will result in:

(18)

It should also be noted that the integration part above has a normal distribution with a mean of and a standard deviation of σ. Therefore, a new normal distribution is found which is given by the cumulative density function :

(19)

where:

(20)

Finally, summing the derivatives of part A and B and equating to ‘0’ results in the following optimality formula:

By solving the above, we get an elegant formulation as follows:

(21)

where , , , and both and have the same standard deviation of σ. Note that does not appear in (21); hence, it does not affect the optimal quantity when only losses are considered. An alternative formulation of the above is:

(22)

The above expression is an implicit function of . Closed form solution of is not attainable; hence, a simple solution algorithm can be implemented, such as the one presented as pseudo code in Appendix 1 or by a simple incremental search in Excel. More importantly, the two resulting cumulative distributions and have the same standard deviation of σ; however, with shifted means around µ, recall that and have opposite signs. Figure 4 depicts the two distributions, where refers to the cumulative distribution of the expected utility in the case of overstocking and refers to the cumulative distribution of utilities upon understocking.

Figure 4. The three distributions, the demand (middle), overage (right) and underage (left), all having the same standard deviation σ.

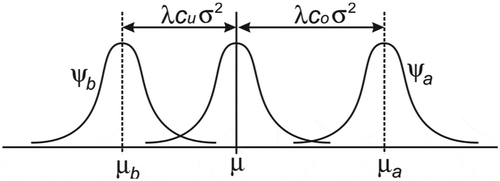
Of note, the two distributions approach the exact demand distribution when λ approaches ‘0’ (i.e., risk neutrality); indeed, a value of ‘0’ brings the model to the classical newsvendor problem, where:

(23)

We also have and for the same reason above. In this case, we know that ; hence, the solution reduces to the following where, :

(24)

The above analysis shows that when an exponential utility function is used, the optimal order quantity of the classical newsvendor will serve as an upper limit of the utility-optimal quantity if and as a lower limit if . The optimal order quantity of the classical newsvendor is denoted by either or and that of our model by ; therefore, for any positive values of , , , λ and σ we have .

4. Results and discussion

The relationship between the risk-aversion parameter λ and the optimal quantity can be depicted for any set of selected costs, demand means and standard deviations. Essentially, when α > 1, higher loss aversion (high λ) yields smaller optimal quantity than and higher quantity than with an increasing tendency to the mean (µ) as depicted in Figures 5 and 6 for the given parameters. This is also explained by the limit in (23), where the closer the decision maker to risk neutrality, the closer the optimal quantity to that of the classical newsvendor problem. Of note, the optimal quantity of our model approaches the optimal quantity of the classical newsvendor problem (200 for the case of equal overage and underage costs in Figures 5 and 6). Higher risk attitudes entail smaller optimal quantity if and high optimal quantity if .

Figure 5. Utility-optimal stocking quantity vs. the risk-aversion parameter λ. For this numerical example, , , µ = 200, σ = 30.

Figure 6. Utility-optimal order quantity vs. the loss aversion parameter λ. For this numerical example, , , µ = 200, σ = 30.

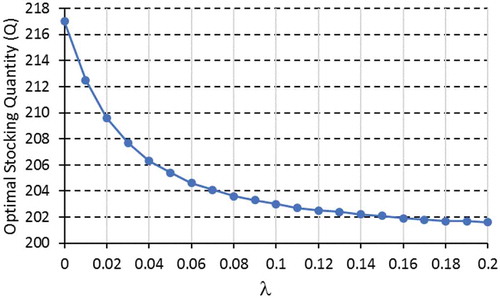
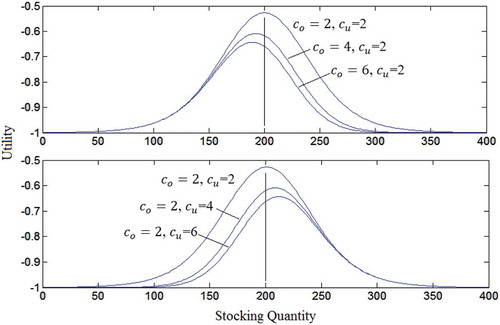
In Figure 5, a numerical example is presented to show the optimal order quantity as a function of loss-aversion parameter (λ). Clearly, when the overage cost is high compared to the underage cost, the optimal quantity will be less than the mean value (µ). Increasing the loss aversion makes the newsvendor tends to order as much as the mean value (µ). Low loss aversion means the newsvendor tends to be risk-neutral and behaves like the classical newsvendor problem. For the same values given in Figure 5, the classical newsvendor problem yields an optimal quantity of 183 which is the minimum bound of the utility-optimal quantity.

Similarly, Figure 6 shows that when the underage cost is higher than the overage cost, the newsvendor will order more than µ. For any loss aversion value (λ), the utility-optimal quantity is always less than the classical newsvendor optimal quantity (217 for this example), where low loss aversion means getting closer to the classical newsvendor.

To test the effect of underage/overage costs, Equation (21) is used for dissimilar values of cost ( and ). Figure 7 shows that high values result in low optimal quantity; on the other hand, high values mean high-order quantity as well; however, the magnitude of the decrease/increase in the optimal quantity gets smaller for higher values of the costs.

Figure 7. The expected utility for different newsvendor settings, where λ = 0.02, µ = 200, σ = 30.

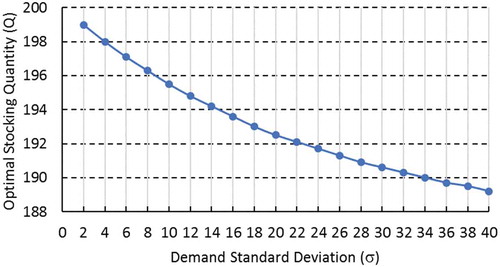
As for the standard deviation, the behavior of the optimal quantity under exponential utility is depicted in Figure 8, where high σ values result in low utility-optimal quantity. It should be noted that smaller standard deviation means that the two distributions and are getting closer to each other; hence, the optimal value will approach the mean value of µ as σ decreases.

Figure 8. Utility-optimal quantity vs. the demand standard deviation, where , , µ = 200, λ = 0.02.

4.1. Risk premiums

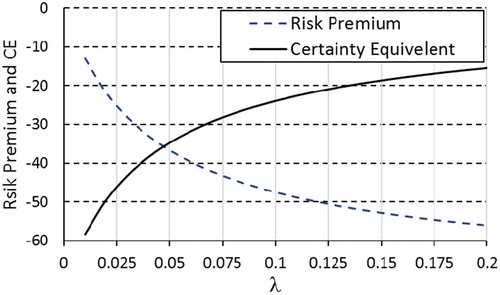
To test the effect of the loss-aversion parameter (λ) on the RP, we start with a utility model of the following parameters: , , µ = 200, σ = 30. Table 1 shows the resulting optimal stocking quantity, the optimal utility, the certainty equivalent and the RP. The certainty equivalents were found using (2) and the RP using (3). Different values of λ have been used to test the effect of loss aversion on the resulting RP. To calculate the expected costs, the same parameters above were used but for a classical newsvendor problem of a normal demand. The resulting cost of the optimal quantity for this part of the problem is 71.38, which does not depend on λ anyway. The risk premium is the difference between the expected value and the certainty equivalent as shown in Table 1.

Table 1. The absolute value of risk premiums vs. the loss-aversion parameter, where , , µ = 200, σ = 30.

	Utility model			Classical newsvendor model
λ	Utility opt. Q	Expected utility	CE	Exp. cost	|RP|
0.01	187.7	−0.4425	−58.4293	−71.3802	12.9509
0.02	190.6	−0.6291	−49.5911	−71.3802	21.7891
0.03	192.5	−0.7266	−43.2273	−71.3802	28.1529
0.04	193.9	−0.7852	−38.4512	−71.3802	32.929
0.05	194.8	−0.8237	−34.7114	−71.3802	36.6688
0.06	195.6	−0.8509	−31.719	−71.3802	39.6612
0.07	196.1	−0.8709	−29.2453	−71.3802	42.1349
0.08	196.6	−0.8863	−27.1774	−71.3802	44.2028
0.09	196.9	−0.8985	−25.4188	−71.3802	45.9614
0.1	197.2	−0.9083	−23.8923	−71.3802	47.4879
0.11	197.5	−0.9164	−22.561	−71.3802	48.8192
0.12	197.7	−0.9232	−21.3879	−71.3802	49.9923
0.13	197.8	−0.929	−20.3467	−71.3802	51.0335
0.14	198	−0.934	−19.415	−71.3802	51.9652
0.15	198.1	−0.9384	−18.5806	−71.3802	52.7996
0.16	198.3	−0.9422	−17.8173	−71.3802	53.5629
0.17	198.4	−0.9455	−17.115	−71.3802	54.2652
0.18	198.5	−0.9485	−16.4787	−71.3802	54.9015
0.19	198.5	−0.9512	−15.8949	−71.3802	55.4853
0.2	198.6	−0.9536	−15.3523	−71.3802	56.0279

The magnitude of RP increases as loss-aversion increases. Higher RP will not induce higher sales. Figure 9 shows the certainty equivalent vs. the parameter λ. The certainty equivalents (as negative values) decrease by increasing the loss-aversion parameters, while the absolute value of the RP increases indicating higher amounts to be imposed by the newsvendor for the willingness to hold the risky asset.

Figure 9. The resulting certainty equivalents and risk premiums vs. the loss-aversion parameter λ, where , , µ = 200, σ = 30 with zero reference wealth.

To test the effect of underage cost on risk premiums, another example is presented with the parameters: , µ = 200, σ = 30, λ = 0.02. In this example, different underage costs are tested which result in different CE and RP values as shown in Table 2. Figure 10 shows the resulting risk premiums. Clearly, the certainty equivalents increase as the underage cost increases. This means, the newsvendor willingness to hold this inventory problem decreases as the underage costs increase.

Figure 10. Risk premiums of utility newsvendor vs. variable underage cost, where , µ = 200, σ = 30, λ = 0.02.

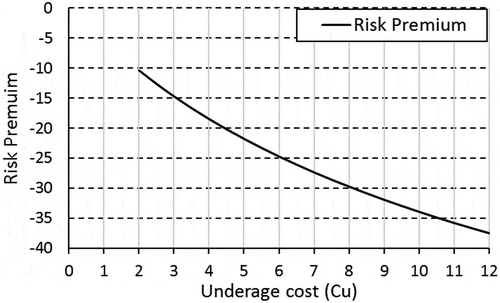
Table 2. The results of the classical newsvendor and utility models, where , µ = 200, σ = 30, λ = 0.02.

Classical newsvendor model			Utility model
cu	Optimal Q	Exp. cost	Utility opt. Q	Exp. utility	CE	|RP|
2	200.1	−47.8731	200.1	−0.5272	−37.4541	10.419
2.5	204.3	−53.3341	202.8	−0.5567	−40.6754	12.6587
3	207.7	−57.9514	204.9	−0.5786	−43.2086	14.7428
3.5	210.6	−61.9416	206.5	−0.5955	−45.2552	16.6864
4	213	−65.448	207.7	−0.609	−46.9524	18.4956
4.5	215.2	−68.5702	208.8	−0.62	−48.3792	20.191
5	217.1	−71.3802	209.6	−0.6291	−49.5911	21.7891
5.5	218.8	−73.9319	210.4	−0.6368	−50.6401	23.2918
6	220.3	−76.2664	211	−0.6433	−51.543	24.7234
6.5	221.7	−78.4161	211.5	−0.649	−52.3485	26.0676
7	223	−80.4064	212	−0.6539	−53.0514	27.355
7.5	224.2	−82.2583	212.4	−0.6583	−53.6911	28.5672
8	225.3	−83.9887	212.8	−0.6622	−54.2651	29.7236
8.5	226.4	−85.6116	213.1	−0.6656	−54.7709	30.8407
9	227.4	−87.1393	213.4	−0.6687	−55.2365	31.9028
9.5	228.3	−88.5813	213.6	−0.6715	−55.6609	32.9204
10	229.1	−89.9464	213.9	−0.674	−56.0429	33.9035
10.5	229.9	−91.242	214.1	−0.6763	−56.3969	34.8451
11	230.7	−92.4743	214.3	−0.6784	−56.7223	35.752
11.5	231.4	−93.649	214.5	−0.6804	−57.0343	36.6147
12	232.1	−94.771	214.7	−0.6822	−57.3167	37.4543

Similar patterns of certainty equivalents and risk premiums are observed upon increasing the overage cost as in Table 3 for instance, when , µ = 200, σ = 30 and λ = 0.02, the magnitude of RP will increase as shown in Figure 11.

Figure 11. Resulting risk premiums for an increasing overage cost, where , µ = 200, σ = 30, λ = 0.02.

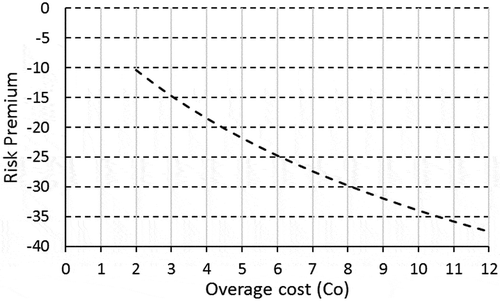
Table 3. The results of the classical newsvendor and utility models where, , µ = 200, σ = 30 and λ = 0.02.

Classical newsvendor model			Utility model
co	Optimal Q	Exp. cost	Utility opt. Q	Exp. utility	CE	|RP|
2	200.1	−47.8731	200.1	−0.5272	−37.4541	10.419
2.5	195.9	−53.3341	197.4	−0.5567	−40.6754	12.6587
3	192.5	−57.9514	195.3	−0.5786	−43.2086	14.7428
3.5	189.6	−61.9416	193.7	−0.5955	−45.2552	16.6864
4	187.2	−65.448	192.5	−0.609	−46.9524	18.4956
4.5	185	−68.5702	191.4	−0.62	−48.3792	20.191
5	183.1	−71.3802	190.6	−0.6291	−49.5911	21.7891
5.5	181.4	−73.9319	189.8	−0.6368	−50.6401	23.2918
6	179.9	−76.2664	189.2	−0.6433	−51.543	24.7234
6.5	178.5	−78.4161	188.7	−0.649	−52.3485	26.0676
7	177.2	−80.4064	188.2	−0.6539	−53.0514	27.355
7.5	176	−82.2583	187.8	−0.6583	−53.6911	28.5672
8	174.9	−83.9887	187.4	−0.6622	−54.2651	29.7236
8.5	173.8	−85.6116	187.1	−0.6656	−54.7709	30.8407
9	172.8	−87.1393	186.8	−0.6687	−55.2365	31.9028
9.5	171.9	−88.5813	186.6	−0.6715	−55.6609	32.9204
10	171.1	−89.9464	186.3	−0.674	−56.0429	33.9035
10.5	170.3	−91.242	186.1	−0.6763	−56.3969	34.8451
11	169.5	−92.4743	185.9	−0.6784	−56.7223	35.752
11.5	168.8	−93.649	185.7	−0.6804	−57.0343	36.6147
12	168.1	−94.771	185.5	−0.6822	−57.3167	37.4543

The optimal order quantity of both the classical and utility newsvendor models are shown in Figures 12 and 13 for different cost settings. Note that when the overage and underage costs are the same, both optimal quantities will be the same. Clearly, the classical newsvendor bounds the resulting optimal quantity of the utility model.

Figure 12. Resulting optimal quantity of the classical and utility newsvendors, where , µ = 200, σ = 30, λ = 0.02.

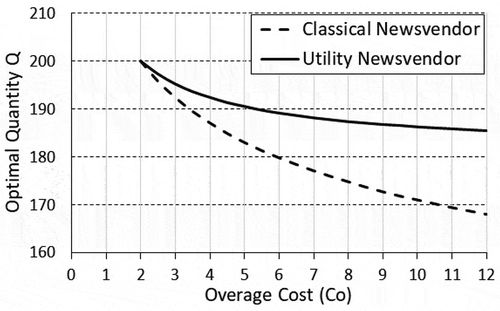
Figure 13. Resulting optimal quantity of the classical and utility newsvendors, where , µ = 200, σ = 30, λ = 0.02.

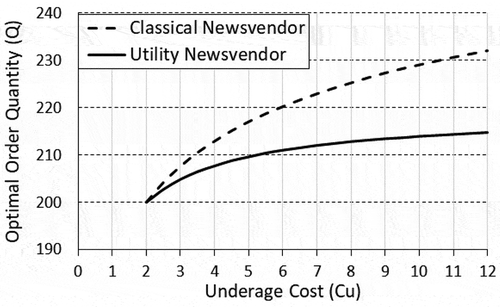
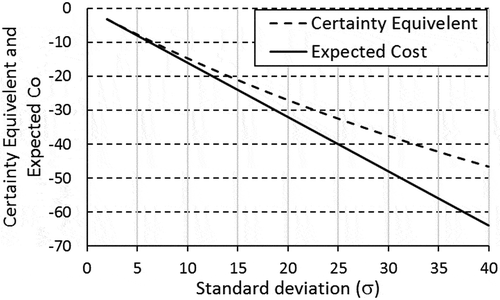
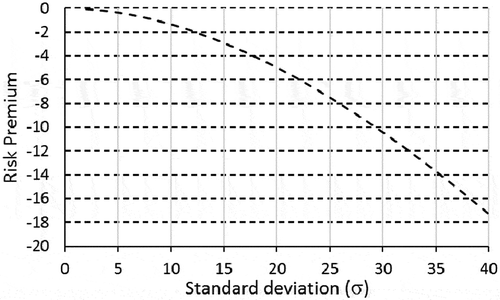
As for the effect of the demand standard deviation (σ), Table 4 shows the results for different values of σ which are also depicted in Figures 14 and 15. Clearly, the gap between the expected values and the certainty equivalents increases by increasing σ; hence, the magnitude of risk premiums gets higher.

Figure 14. Certainty equivalents and the expect cost vs. σ.

Figure 15. Risk premiums of the utility model, where , µ = 200 and λ = 0.02.

Table 4. The risk premiums (last column) for different demand standard deviations, where , µ = 200 and λ = 0.02.

	Utility model			Classical model
σ	Utility optimal. Q	Exp. utility	CE	Classical optimal. Q	Exp. cost	|RP|
2	200	−0.0606	−3.1257	200	−3.1915	0.0658
4	200	−0.1158	−6.1536	200	−6.3831	0.2295
6	200	−0.1659	−9.0701	200	−9.5746	0.5045
8	200	−0.2116	−11.8875	200	−12.7662	0.87871
10	200	−0.2534	−14.6113	200	−15.9577	1.34641
12	200	−0.2917	−17.2444	200	−19.1492	1.90482
14	200	−0.3268	−19.7856	200	−22.3408	2.55516
16	200	−0.3591	−22.2441	200	−25.5323	3.28821
18	200	−0.3889	−24.6247	200	−28.7238	4.09907
20	200	−0.4165	−26.9355	200	−31.9154	4.97986
22	200	−0.442	−29.1698	200	−35.1069	5.93708
24	200	−0.4656	−31.3305	200	−38.2985	6.96797
26	200	−0.4876	−33.4325	200	−41.49	8.05751
28	200	−0.5081	−35.474	200	−44.6815	9.20751
30	200	−0.5272	−37.4541	200	−47.8731	10.419
32	200	−0.545	−39.3729	200	−51.0646	11.6917
34	200	−0.5617	−41.2426	200	−54.2561	13.0135
36	200	−0.5773	−43.0546	200	−57.4477	14.3931
38	200	−0.592	−44.8244	200	−60.6392	15.8148
40	200	−0.6058	−46.5448	200	−63.8305	17.2857

The resulting risk premiums are shown in Figure 15 where higher σ means higher magnitude of risk premiums and hence more risk and less willingness to hold the risky asset as compared to the risk-neutral newsvendor. The parameters used for this instance are: , µ = 200 and λ = 0.02. Table 4 shows the resulting premiums of this instance. Notice that due to the similarity of the normal distribution around the mean, the optimal values remain the same regardless the standard deviation of the demand; however, higher standard deviations increase the magnitude of risk premiums.

To summarize, individuals adjust their cognitive processing during the course of solving a decision problem in an opportunistic way; therefore, the magnitude of RP will increase by either increasing the overage or increasing the underage costs when a model of exponential utility function and normal demand is taken into consideration. The magnitude of RP will also increase as loss-aversion parameters increase which will make the newsvendor see the risky assets unattractable. Similarly, higher standard deviations of the demand entail higher RP which indicate more hesitancy to hold the risky asset (i.e., the newsvendor problem).

5. Managerial implications of the utility newsvendor problem

The major concern in utility newsvendor problem is how to identify two main characteristics; those are: the demand distribution and the utility function of the decision maker. Forecasting and standard statistical techniques are indeed helpful in predicting the demand distributions using sales historical data. By fitting statistical distributions to actual past demand data, the newsvendor can identify the correct demand parameters. In our model, we assume that the decision maker has access to the underlying demand distribution. Demand censoring is out of the scope of this article as it has further implications necessitating a hybrid of forecasting, data fitting, statistical analysis, utility and optimization analysis.

As for the utility function, although there are standard forms that are available in the literature of economics and decision theory, experiments to identify the utility function still can be conducted. Typical experiments on how to fit the data to the adequate utility function can be found in many literature studies (Dalalah et al., 2016).

Other implications may be noticed when different newsvendors exhibit different utility functions. One underlying assumption here is that all newsvendors share the same utility valuation of wealth. If the newsvendors have dissimilar utilities, each should be considered as a separate case. Moreover, we build upon the current literature in our model by analyzing the newsvendors of reliable suppliers. Unreliability in the supply entails failure to satisfy the customers’ demand and hence, the optimal order quantity models will be no longer valid. Supplier capacity constraints and the variable ordering costs, on the other hand, can elevate the managerial implications of the problem.

Managers may also consider strategic commitments with customers and suppliers. Strategic decisions will change the overall point of view. Long-term contracts, commitments and strategic behavior may be preferred options for sustainable business. In contrast, the newsvendor models (the classical or the utility models) only consider a single period of no strategic commitments of the involved parties.

6. Conclusions

Loss aversion of a newsvendor problem was addressed under the assumption of bounded utility. Different demand models have been considered along with different utility functions, namely, the normal and the exponential. An elegant implicit formulation was found for the optimal order quantity. A simple numerical search algorithm was used to find the order quantity . The analysis showed that the classical newsvendor optimal quantity serves as lower/upper bound on the utility-optimal quantity when >/>. As loss aversion vanishes by decreasing the parameter λ, the utility model approaches the classical newsvendor model.

For the case of normal demand, two other normal distributions of shifted means but similar standard deviations resulted in the final optimality form. The gap between the two distributions was affected by loss aversion, where low loss aversion entails closer distributions. The two distributions would coincide with the demand distribution when loss aversion disappears. Contrarily, higher demand standard deviation would put the two distributions further apart which also entails more risk and therefore lower utility-optimal quantity. As for RP, the magnitude of RP increases as loss aversion, as well as overage and underage costs, increases. Higher demand standard deviations would also increase the magnitude of RP. Higher RP means low willingness of the newsvendor to hold the risky asset.

The formulas (21) and (22) represent a new pair of equations that would add a scientific value to the related work of the newsvendor variants under loss aversion. The presented model formulas are advantageous in finding the optimal order quantity of short-shelf life inventory when loss is an important factor in the decision-making process. The proposed newsvendor utility model is limited to a single period with stationary and well-defined stochastic demand distributions and fixed underage and overage costs. Multiperiod utility newsvendor models may be considered for future extensions. The model can be extended to the scope of pricing by relaxing the assumption of fixed prices. Moreover, pricing techniques that have been applied to the classical newsvendor model are also good candidates to start exploring further extensions.

Appendix 1

A simple search algorithm can be used to solve Equation (22). Let:

The following pseudo code presents the basic structure of the search algorithm:

Inputs: Cu,Co,λ,α,μ,σ;

Initial guess Q;

Initialize Δ to some value;

Initialize θ to small value < 1;

Initialize ε to extremely small value (i.e., stop criterion);

Loop;

if(Δ ≤ ε) then Exit loop;

F1=f(Q,Cu,Co,λ,α,μ,σ);

Q=Q+Δ;

F2= f(Q,Cu,Co,λ,α,μ,σ);

   if((F1>0 & F2<0) or (F1<0 & F2>0)) then

   Q=Q-Δ;

   Δ=Δ×θ;

   End if;

End loop;

Optimal order quantity = Q;