A numerical approach for solving problems in robotic arm movement

ABSTRACT

Mechanical robotic arm control problems are examined in the numerical solutions for the second order system with the R.Kutta algorithms. The dynamics of a robotic arm be able to designated by a set of combined non-linear equations in the formula of coriolis, centrifugal effects and gravitational torques. This investigation attempted to minimize the error of an industrial robotic arm, which improves production systems. Results of comparisons illustrate the effectiveness of the numerical integrating algorithm based on the actual joint velocities and positions with each instant of time between the exact and numerical solutions. The obtained tables of data help to analyze the variation in the velocity and position joints at different time. The numerical results obtained by R.kutta -techniques perfectly match with the exact velocities. Depending on the relative error calculated at the obtained tables of results to reach the required motion of the mechanical robot arm.

KEYWORDS:

• Mechanical robotic arm
• Numerical solutions
• Runge-Kutta algorithms
• Matlab program

1. Introduction

With the growing importance and demand of robotics in manufacturing and space uses, many investigators have been concentrated on the control and modeling aspects of robot manipulators in the latest years (Zer & Semercigil, 2008). In prior three decades, robotics finds concentrated applications in manufacturing processes to perform difficult tasks. Perfect tasks include insertion, fastening, assembly and grinding (Nandhakumar, Selladurai, Muthukumaran, & Sekar, 2010).

The expression robotic is basically defined as the paper, strategy and usage of robotic systems for industrial (ISO 8973, 1994). Robotics is usually employed to achieve hazardous, very repetitive, unsafe and unkind jobs. They have several different jobs such as arc welding, assemblage, material handling, spraying, painting, and machine load and unload function, etc. Robotic arm is planned to move material, parts, or particular devices through variable programmed motions to perform a variability of jobs (Elfasaikhany, Baylon, Salgado, & Yanez, 2011).

Several publications are obtainable on the study of constrained motion of the robotic with differential equations. These equations arrange for easy solutions not including nonlinear differential equations steering to controlled constraints (Ata & Johar, 2004; Mcclamroch, 1986; Nandhakumar et al., 2010; Nandhakumer, Selladurai, & Sekar, 2009). The operation and positioning of a robotic arm with regard to mechanical efficiency and control accurateness is depended on the special influences of manipulator gravity (Nandhakumer et al., 2009; Rubio, 2018).

Mathematical simulations of robot dynamics to calculate dynamic nonlinearity and coupling effects, every so a lot, are employed to reach maximum performance and accuracy in robotic mechanism. The strategy of a robotic control systems is very complicated due to the coupled nonlinear appearance of its dynamic. The dynamic of a robotic is able to be defined by a collection of combined nonlinear equations in the system of centrifugal effects, coriolis, and gravitational torques. The importance of these forces is based on the physical considerations of the robotic arm, the load, and the speed it involves at which the robot functions. The numerical methods are properly supported methods for answering the systems of differential equations and create the accuracy, stable, and efficiency (Auzins and Slide, 1995; Ellis & Ricker, 1994; Nandhakumar et al., 2010).

R.Kutta approaches are useful to define numerical solutions for the complications, which are showed as differential equations relating Initial Value Problems that happen in the domains of industrial by Alexander & Coyle (1990; Dekker & Verwer, 1984; Evans, 1991a; Evans & Yaakub, 1996, 1998; Hairer & Wanner, 1996; Murugesan, Dhayabaran, Amirtharaj, & Evans, 2002; Murugesan, Dhayabarin, Amirtharaj, & Evans, 2001; Murugesan, Dhayabarin, & Evans, 1999a, 1999b, 2000; Yaakub & Evans, 1999a, 1999b). The R.Kutta method had been initiated at the twentieth century. Investigations in this region are enormous and it is still active. This is because of its elasticity in the resolve of approximate solutions and its nature of extending accuracy (Sekara, Murugesha, & Murugesanb, 2004).

For a robotic with two degrees of freedom, underneath the theory of lumped equivalent masses and massless-links, the dynamics are denoted in expression systems of nonlinear equations. The motion of a robotic and inertial load had been investigated by characterizing their governing equation such as a singular system of second-order differential equations. Singular system theory has been investigating the motion of a robotic (Nandhakumar et al., 2010; Nandhakumer et al., 2009; Paraskevopoulos & Koumboulis, 1991; Paraskevopoulos, Koumboulis, & Zervas, 1995). This is the general task corresponding for a robot gripping an inertial weight.

2. Mechanical robotic arm representation

The dynamics of Robotic arm difficult was at first considered by Taha (1988), for the reason of its natural accuracy in the finding of fairly accurate solutions. Researches (Lim & Seraji, 1997; Oucheriah, 1999; Polvcarpou & Loannou, 1996; Ponalagusamy & Senthilkumar, 2009; Sekar, Murugesh, & Murugesan, 2004) have investigated the different sides of linear and nonlinear systems. The Initial Value Problems are resolved through R.K. methods which in turn being employed to calculate numerical solutions for which different difficulties, this are displayed as differential equations are examined by Evans (1991b), Hung (2000), Shampine & Gordon (1975), and Shampine & Watts (1977). Watts and Shampine have developed numerical programs for R.K fourth-order technique. R.K method of fifth-order has been developed by Butcher, J. C. (Butcher, 1964, 1987, 1990). The numerical technique of robotic mechanism has been achieved (Gopal, Murugesan, & Murugesh, 2006). The usages of nonlinear differential algebraic control systems to restrained robotic system have been studied by Huang & Tseng (Huang & Tseng, 1991).

It is worth mentioning that coupled physical characteristics and nonlinearity are included in planning a robotic dynamic performance and its control system. A collection of coupled nonlinear second-order differential equations in the formula of Centrifugal forces, gravitational torques, and Coriolis denotes the dynamic of the robotic. The meaning of the forces directly mentioned above is dependency on the two physical factors of the robotic specifically the speed and the load it transmits at the robotic operates. The design of the control system come to be more composite by increase accurateness and requirements of the user depended on the differences of the factors stated above. A full description of a robotics’ structure with accurate illustration is presented by Yaqub (Yaqub & Al-Sultan, 2012). The aim on determining the robotic dynamic equations in real-time, an effective numerical solution, is essential. The researchers (Rubio, 2018; Rubio & Garcia, 2018; Rubio et al., 2018; Taha, 1988) talk over on the dynamic of robotic arm problems, as denoted in the next formula.

(1)

where is the matrix of coupled inertia, is the matrix of centrifugal and coriolis. is the matrix of gravity, is the input torques affected at different joints. For a robotic by two degrees of freedom, through assumption lumped equivalent massless links, i.e. it indicates that point load (mass) is focused at the end links, the dynamic equations are signified below:

(2)

where

The quantities of the robotic parameters employed are z₁ and z₂ = 1 m, M₁ = 2 Kg, M₂ = 5 Kg. In the situation of problem of set point regulation, the state-run vectors are denoted below:

(3)

where and are the angles of joints 1 and 2, respectively, and are wanted. Henceforward, Equation (2) can be written in state space demonstration as,

(4)

Now, the robotic is basically a twice reversed pendulum and the lagrangin method is worked to improve the equation. It is detected that by choosing the appropriate factors, the nonlinear Equations (3) of the two robotic arm links model can be decreased to the next system of linear equation (Lim & Seraji, 1997; Oucheriah, 1999; Polvcarpou & Loannou, 1996; Ponalagusamy & Senthilkumar, 2009; Sekar et al., 2004; Taha, 1988) as

(5)

From Equation (5), one can achieve the system of second-order linear equations

Where the values of the factors concerning the joint-1 are known by,

= 0.1730, = −0.2140, = 0.00265 and the values of factors concerning the joint-2 are known by,

= 0.0438, = 0.3610, = 0.0967 and by choosing = 1 and = 1 with initial conditions,

and the corresponding exact solution is given by,

(6)

Using the achieved values, the relative error for the RK-Ode45-algorithm has been calculated using the following Equation (7) in Tables 1–4.

(7)

Table 1. Results of the mechanical robotic arm model for and Relative Error for R.K. Ode45.

Solution Number	Time second	Exact Solution	R.K. Ode15s	R.K. Ode45	R.K. ode23tb	Error
1	0.0	−1.0000	−1.0000	−1.0000	−1.0000	0
2	0.5	−0.9742	−0.9773	−0.9773	−0.9773	0.318209813
3	1.0	−0.8942	−0.9069	−0.9069	−0.9069	1.420263923
4	1.5	−0.7576	−0.7867	−0.7866	−0.7867	3.827877508
5	2.0	−0.5641	−0.6164	−0.6163	−0.6164	9.253678426

Table 2. Results of the mechanical robotic arm model for and Relative Error for R.K. Ode45.

Solution Number	Time second	Exact Solution	RK Ode15s	RK Ode45	RK ode23tb	Error
1	0.0	0.0000	0.0000	0.0000	0.0000	0.0000
2	0.5	0.1045	0.0920	0.0920	0.0920	11.96172249
3	1.0	0.2161	0.1901	0.1903	0.1902	11.93891717
4	1.5	0.3304	0.2908	0.2909	0.2909	11.95520581
5	2.0	0.4426	0.3896	0.3898	0.3897	11.92950746

Table 3. Results of the mechanical robotic arm model for and Relative Error for R.K. Ode45.

Solution Number	Time second	Exact Solution	R.K. Ode15s	R.K. Ode45	R.K. ode23tb	Error
1	0.0	−1.0000	−1.0000	−1.0000	−1.0000	0
2	0.5	−0.9986	−0.9986	−0.9986	−0.9986	0
3	1.0	−0.9945	−0.9946	−0.9946	−0.9946	0.010055304
4	1.5	−0.9881	−0.9882	−0.9882	−0.9882	0.010120433
5	2.0	−0.9793	−0.9795	−0.9795	−0.9795	0.020422751

Table 4. Results of the mechanical robotic arm model for and Relative Error for R.K. Ode45.

Solution Number	Time second	Exact Solution	R.K. Ode15s	R.K. Ode45	R.K. ode23tb	Error
1	0.0	0.0000	0.0000	0.0000	0.0000	0
2	0.5	0.0054	0.0054	0.0054	0.0054	0
3	1.0	0.0105	0.0105	0.0105	0.0105	0
4	1.5	0.0153	0.0152	0.0152	0.0152	0.653594771
5	2.0	0.0198	0.0194	0.0194	0.0194	2.02020202

3. Results and discussions

Check and endorsement of the robotic arms are one of the works that needs get longer time because many iterations are required. For the period of our investigations, several problems rise such as: incorrect calibration of the motor, wrong angle calculations, complications by the physical angles and positions measurement, and it has been burned of the servo motors because of an over load that was not estimated as showed in Yaqub & Al-Sultan (Yaqub & Al-Sultan, 2012). Precision in the solution for a robotic arm prototypically determines the control of the motivation of robotics.

Next Tables 1–4 show the results achieved by MATLAB program commands. The exact and numerical solutions of the robotic arms model problematic have been calculated time for disparate intervals by (Equation (5)). The values of , , and are designed for timeextending (0.0–2.0). It is important to stress for the robotic arms model difficult that the achieved discrete solution using the R.K.-Ode45-algorithm assurances extra perfect evaluation using R.K.-Ode15s and R.K.-Ode23tb techniques. By applying the achieved results, the joint angles and angular velocities have been measured by Equation (3) and presented in Tables 1–4. 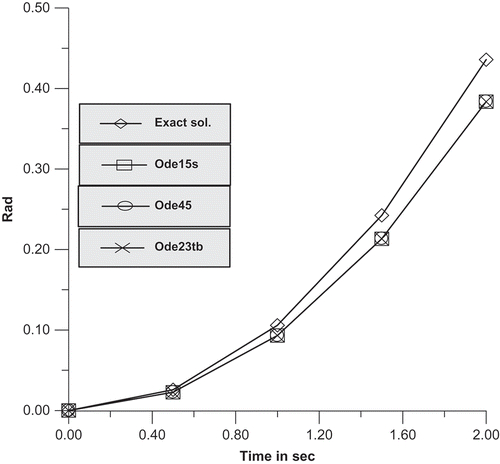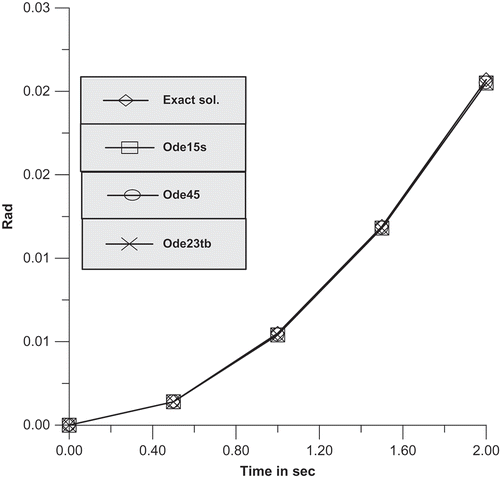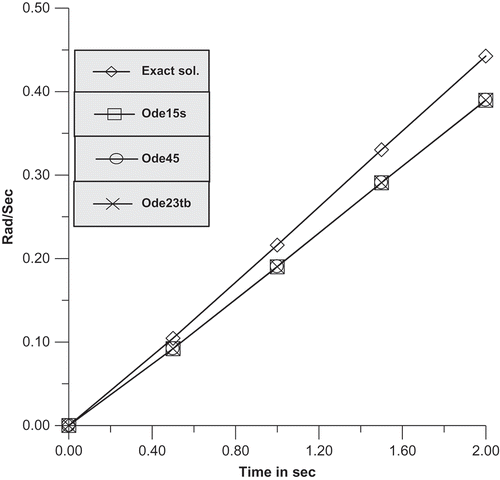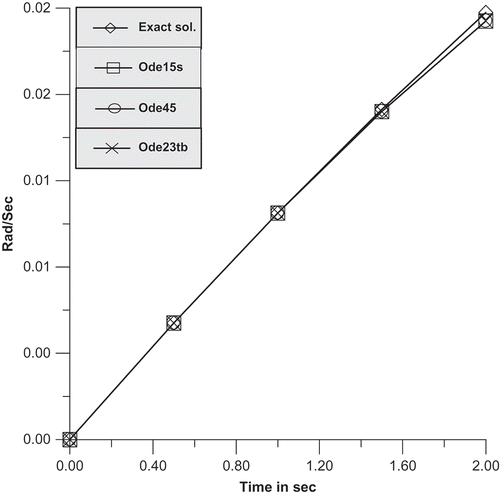The differences in the parameters are having values of unity and plotted and shown in the Figures 1–4. The position levels of the joint angles obtained under R.K.-Ode45, R.K.-Ode15s and R.K.-Ode23tb techniques are approximately 16% lower than those of the exact position level of the robotic (Figure 1). Figures 3–4 present the velocity curves of the exact and numerical solutions; the ultimate error percentage of the joint/1 is higher than of the joint-2.

Figure 1. Position q₁ at joint (1).

Figure 2. Position q₂ at joint (2).

Figure 3. Velocity on joint/1.

Figure 4. Velocity on joint/2.

From Figures 1–4 and Tables 1–4, the next observations are made:

• In the robotic arms model designed for study, the solution achieved by the R.K.-Ode45- algorithm is found to be accurate from R.K.-Ode15s and R.K.-Ode23tb techniques.

• The inaccuracy in solutions achieved by all the R.K.-techniques increases with increase in time.

• The R.K.-Ode45-method yields perfect result even whenever it is matched with R.K.-Ode15s and R.K.-Ode23tb techniques for nonlinear system.

• In Figures 1–2, it has been detected that the considered joints’ angle q₁ and q₂ are deviating along the time as compared to the exact values.

• Figures 3 and 4 show the velocity charts at joint (1 & 2).

• The velocities on joint one and two become more with the increasing in period time.

• Results of velocities achieved by R.K.-techniques perfectly match with those of the exact.

4. Conclusions

In this paper, the iterations are made to discover the superiority of the solution achieved by R.K.-Ode45-method compared with that of R.K.-Ode15s and R.K.-Ode23tb solutions for the same condition. From the tables and figures, we detect that the R.K.-Ode45-method yields less error. This R.K.-Ode45-method is extra appropriate for observing the mechanical robotic arm difficult of singular system at varying and invariant time states. The numerical solutions investigated by R.K.-Ode45-algorithm are close to the actual results of the mechanical robotic arm model difficult. This algorithm is able to be employed for all value of independent variable on a numerical processor. For this reason, the RK-Ode45-algorithm is more appropriate for studying the system of second-order IVPs.

Models accuracy has been described in the large-deflection dynamics of robotic arms that are usually highly expensive computationally to be suitable for nonlinear processes control. Efficient solution techniques and appropriate model order reduction may steer to quickly yet accurate dynamic models which will be convenient for control. Reliable feedback linearization for nonlinear processes systems will be useful in determining the control mechanism of the movement of robots are also a solve problem (Rubio, 2018). Extensive literature exists for a mechanical robotic arm model which determines the control mechanism of the movement of robots that need solutions to many challenging and untouched problems for control, planning and design (Meda-Campana, 2018; Rubio & Garcia, 2018; Salisbury, Townsend, Ebrman, & DiPietro, 1988; Spong, Hutchinson, & Vidyasagar, 2005).

Disclosure statement

No potential conflict of interest was reported by the authors.