Two strategies of two-level facility network design for autonomous ground vehicle operations

ABSTRACT

We compare two models of two-level facility location problems for network design in autonomous ground vehicle (AGV) operations. The two-level model consists of locations for charging stations (main facilities), as well as for storage locations (substations). Demand points will represent processing locations. In both formulations, demands are assigned to substations and substations are assigned to main facilities. The formulations differ in whether each connection between a facility and a substation is counted once in absolute terms, or once per demand. These represent two different views, in which transfer between a main facility and substation is carried out either in bulk, e.g. using a shuttle, or by each AGV independently. Selected experimental results are presented for geometric networks and networks consisting of uniformly distributed points on a regular mesh. These results indicate that the two formulations lead to vastly different network designs in terms of the number of facilities and connectivity.

KEYWORDS:

• Logistics networks
• facility location problems
• autonomous ground vehicles
• cyber-physical systems
• network design

1. Introduction

The rise of Industry 4.0 and the increasing importance of cyber-physical systems have motivated a number of new applications and optimisation problems in production and manufacturing (Jazdi, 2014; Lee, Bagheri, & Kao, 2015). Autonomous vehicles have emerged as one of the forces at the forefront of these developments, helping in automating various processes more efficiently (Gerla, Lee, Pau, & Lee, 2014).

More particularly, autonomous ground vehicles (AGVs) (Luettel, Himmelsbach, & Wuensche, 2012) have been driving the innovation in relation to Industry 4.0 from a number of perspectives. Architectural design is among the main aspects (Touchton, Galluzzo, Kent, & Crane, 2006), along with in-plant transport organisation (Gola & Kłosowski, 2017; Kłosowski, Gola, & Thibbotuwawa, 2018), scheduling and rescheduling in AGV operations (Bocewicz, Banaszak, Nielsen, & Muszyński, 2017), predictive control of AGVs (Falcone, Borrelli, Tseng, Asgari, & Hrovat, 2008), as well as tracking of the vehicles (Wit, Crane, & Armstrong, 2004).

In contemporary manufacturing and logistics, both AGVs and unmanned aerial vehicles (UAVs) play increasingly important roles (Lee et al., 2015). More broadly, there are a number of related applications of UAVs (Khosiawan, Khalfay, & Nielsen, 2018; Khosiawan, Park, Moon, Nilakantan, & Nielsen, 2018) that are relevant also for this study, including relay networks (De Freitas et al., 2010), navigation by evolutionary algorithms (Nikolos, Valavanis, Tsourveloudis, & Kostaras, 2003), emergency refuelling (Kladis, Economou, Tsourdos, White, & Knowles, 2008), motion planning and guidance (Goerzen, Kong, & Mettler, 2010; Golabi, Shavarani, & Izbirak, 2017), as well as routing with stochastic targets (Enright, Frazzoli, Savla, & Bullo, 2005). While a number of recent studies have been focused on UAVs, a number of these concepts are also relevant and partially transferrable and adaptable to the domain of AGVs.

In this context, interesting optimisation problems arise in the design of cyber-physical system infrastructure, which is of an increasing importance to improve efficiency of various operations (Rajkumar, Lee, Sha, & Stankovic, 2010). Such infrastructure problems often lead to specific location problems (Nasab, Tavana, & Yousefi, 2014), e.g. typically in determining charging station locations (Mehar & Senouci, 2013).

In this paper, we study two formulations of two-level facility location problems for network design in AGV operations. While one of these formulations is equivalent to a previously studied two-level facility location problem, the other formulation represents a new perspective that amalgamates the contributions of high-level transport that may correspond to a shuttle service. In addition, we present a new perspective on the problem from the point of view of an application in AGV operations.

Given a number and locations of facilities, substations and demand points, the aim is to select their locations such that an objective value based on cost and distance is minimised. In AGV operations, main facilities will represent charging hubs, substations will represent storage and parking space, and demands will represent processing locations.

In our formulations, the first one represents the problem of finding minimum network and facility cost, counting each connection between a facility and a substation just once. The second model counts each such connection per demand. The latter model is practically equivalent to what is currently known in the literature as the multilevel facility location problem (Marić, 2012). These models are interpreted in a way such that the connections between charging hubs and storage space can be interpreted as carried out in bulk, e.g. using a shuttle service, or, alternatively, with each AGV independently.

The experimental results are presented for randomly generated geometric networks. These results indicate that only this small difference in the interpretation of the problem leads to a large change in the structure of the optima. This highlights the need to consider specific properties of a real-world application in formulation used for practical modelling.

The rest of the paper is structured as follows. In Section 2, we give an overview of facility location applications within cyber-physical systems operations. Section 3 presents the two formulations of the two-level facility location problems for AGV operations. Section 4 provides selected experimental results and a brief discussion. Last but not least, Section 5 concludes and summarises this work.

2. Facility location in cyber-physical systems

Facility location problems have been widely studied in a number of applications and areas of operations research. Such applications include location problems in logistics systems for remanufacturing (Lu & Bostel, 2007), distribution system design (Klose & Drexl, 2005), aerial search optimisation (Kress & Royset, 2008), positioning of UAVs in mobile ad-hoc networks (Wang, Huo, & Alidaee, 2014) or -level facility location games (Xu & Du, 2006). Sectors and areas of interest the agricultural sector (Zangeneh, Akram, Nielsen, & Keyhani, 2015), warehouse location (Michel & Van Hentenryck, 2004) or customer service centre location (Chalupa & Nielsen, 2018a).

With hierarchical models specifically in mind, these models are among the most popular operations research problems, with a range of different applications in health care, distribution, retail, waste management, airline management or computer networks (Şahin & Süral, 2007). Notable real-world case studies include two-level facility network for sand recycling (Barros, Dekker, & Scholten, 1998), hierarchical facility location in UAV delivery systems (Shavarani, Nejad, Rismanchian, & Izbirak, 2018) or multilayer wireless ad-hoc networks (Gu, Pei, Ly, Gerla, & Hong, 2000).

Another significant perspective on facility location problems is their application in distribution planning (Aikens, 1985). With the rise of importance of such problems in supply chain network design (Melo, Nickel, & Saldanha-Da-Gama, 2009), further insights into the behaviours of location models and algorithms are tantamount for many real-world applications. One such application is the design of complex multilevel distribution networks, with central distribution centres feeding decentralised distribution centres that in turn service customers. These are known from, e.g. parcel delivery systems (Bruns, Klose, & Stähly, 2000). This is amplified by the rise of the industrial use of autonomous vehicles and cyber-physical systems in general, for which efficient operations systems are of a rapidly growing interest (Khosiawan & Nielsen, 2016). Applications related to healthcare facilities are also at the forefront (Marić, Stanimirović, & Božović, 2015).

One particular area of interest for the hierarchical variants of location problems is in determining suitable locations for charging stations (Mehar & Senouci, 2013). In Figure 1, we depict a typical scenario of AGV operations consisting two types of facilities on two levels. The high-level facilities represent charging hubs, while low-level substations represent storage space. Two-level facility location models then represent the abstraction of the problem of placing the charging hubs and the substations such that the overall costs of establishing the facilities and operations of the model are minimised.

Figure 1. An illustration of a typical two-level model of AGV operations consisting of charging hubs (facilities), parking spaces (substations) and processing locations. The problem of optimal location of these charging hubs and parking spaces translates into a two-level facility location problem.

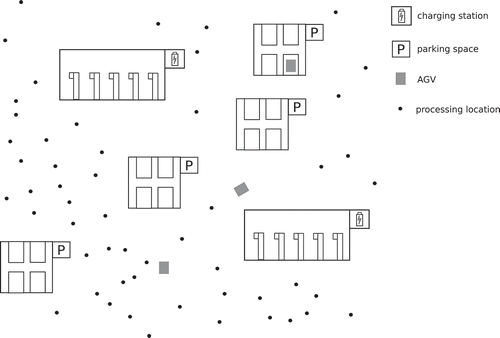
This model can then be reduced to two types of facility location problems that will be described in Section 3. One of the models is less conventional, while the other model represents a conventional multilevel facility location problem.

Regarding the algorithmic approaches, hierarchical facility location has mostly been explored in the raw form (Şahin & Süral, 2007). A 3-approximation algorithm is known for a standard general multilevel facility location problem (Aardal, Chudak, & Shmoys, 1999). Practical solving techniques for relatively large instances have been employed, such as specialised genetic algorithms using dynamic programming and caching (Marić, 2012). Specific attention has been dedicated to two-level problems, as these represent a conceptually important simplification of the multilevel perspective (Aardal, Labbé, Leung, & Queyranne, 1996; Ro & Tcha, 1984; Zhang, 2006). However, less attention has been dedicated to the interpretation of facility hierarchy, its relationship to the real-world application domain, as well as the impact of this interpretation on design of practical algorithms to solve such location problems. With many techniques available to solve facility location problems (Chalupa & Nielsen, 2017, 2018b), it is worth noting that tabu search algorithms usually stand out in terms of their performance (Al-Sultan & Al-Fawzan, 1999; Arostegui, Kadipasaoglu, & Khumawala, 2006). However, for the purpose of this paper, we will focus on the real-world interpretation of integer linear programming (ILP) based models of these problems in AGV operations and cyber-physical systems in general. One can see these problems as natural extensions of dynamic assembly line balancing problems (Becker & Scholl, 2006; Boysen, Fliedner, & Scholl, 2007; Li, Janardhanan, Tang, & Nielsen, 2016).

3. Two ILP formulations of the two-level facility location problems

In this section we present the two formulations of the two-level facility location problems for AGV operations. The formulations differ in the weight of the connections of the higher level in the objective value. While the first model counts the distance between a facility and a substation just once, the second model counts the cost each path between a facility, through a substation, to each demand. Even though in some applications, the term customer is used to denote the end points, we prefer the term demand because of the nature of our application. The second model is practically identical to the standard formulation of the multilevel facility location problem (Marić, 2012).

Figure 2 illustrates the general vision of two-level facility location problems from both geometric (on the left-hand side) and network (on the right-hand side) perspectives. The aim of these problems is to minimise the total cost of opening the facilities and substations and the total of the distances within the network. In Problem 1, each connection is counted separately, i.e. the total cost of each tree is minimised, connecting a facility, substations and the respective demands. Conversely, Problem 2 counts each path from a facility to a demand separately, counting the distances from facilities to substations once per each demand.

Problem 1: Minimum Network and Facility Cost Model. Given facility sites, substation sites and end demands, cost values and for each facility and substation, respectively, as well as distance values from facility to substation and distance values from substation to demand , the first ILP optimisation model will be the following:

(1)

s.t.

(2)

(3)

(4)

(5)

where and are binary variables representing that substation is assigned to facility and demand is assigned to substation . Variables and are also binary, indicating whether a facility or a substation is open, respectively.

Figure 2. Illustrations of the geometric interpretation (a) and the layered network interpretation (b) of the two-level facility location problems.

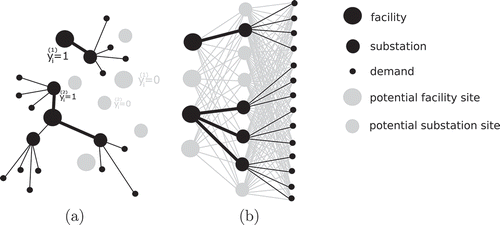
In this formulation, the first two terms represent the cost of opening the facilities and the substations, while the remaining terms represent the total distances from facilities to substations and from substations to demands. Constraint (2) ensures that an open substation is assigned to exactly one facility. Constraint (3) represents that each demand is assigned to exactly one substation. Note that (2) and (3) differ in the right-hand side, as a demand always has to be assigned, while assignment of a substation to a facility depends on whether the substation is opened. Constraints (4) and (5) then ensure that a facility or a substation is actually open and the sites chosen for the demands.

Problem 2: Shortest Path and Minimum Facility Cost Model. This formulation stems from an observation that one could introduce dummy ‘facilities’ representing pair of an actual facility and substation , effectively reducing the three layers of the facility-substation-demand network into just two layers. This gives us such dummy facilities. For the purposes of the formulation, we will assume that for a facility and substation , dummy facilities will be grouped by facilities in terms of their indices first, i.e. . This is similar to the standard multilevel facility location problem, in which each decision variable maps a candidate path in the multilevel network to a demand (Marić, 2012).

Let us have facility sites, substation sites and end demands. Let be the cost value for each facility and let the cost values for dummy facilities be and be equal to the cost of the substation corresponding to the dummy facility. Let the distance values be from facility to substation and let be the distance value from substation to demand . Then, the second ILP optimisation model will be the following:

(6)

s.t.

(7)

(8)

(9)

where are binary variables representing whether facility and substation are both simultaneously open, are binary variables representing that demand is assigned to substation and substation is assigned to facility , and is also a binary variable indicating whether facility is open.

One can notice that this formulation is somewhat similar to the formulation of the classical facility location problem. However, there are additional terms and dummy variables needed, indicating that the problem not only requires more decision variables, but is indeed somewhat more intricate than classical facility location. The first two terms in the cost function and constraints (7) and (8) are virtually equivalent to the formulation of the facility location problem obtained for dummy facilities and demands with aggregate distance values from demand to substation and from substation to the facility. The last term in the objective function represents the total cost of facilities. This needs to be treated separately, as the cost of opening a facility has to be counted exactly once, even though it may correspond to multiple values of .

Dummy variables are established for this purpose. For a facility and substation , is the variable determining whether both the facility and the substation are open. Facility is therefore open if at least one is a non-zero value, for some corresponding substation . This observation is used in constraint (9).

4. Selected results

In order to evaluate the formulations, we have performed experiments for two types of facility location instances with 25 facilities, 50 substations and 200 demands.

The first type of instances consists of geometric data points generated uniformly at random within a area with integer coordinates. Euclidean distance was used as a metric. The cost of each facility was units, while the cost of a substation was unit. This reflects the assumption that a facility will be much more expensive to open than a substation. We believe such an assumption is inherent in many real-world applications, especially if substations can be dynamically moved. This also highlights the relevance of these formulations in the context of the emerging dynamic optimisation within the Internet of Things (IoT).

The second type of instances consists of facilities, substations and demands distributed regularly on a mesh within area. All other parameters were the same, including the cost values.

We generated the corresponding Problem 1, Problem 2, and used the branch-and-cut MILP solver CBC from the COIN-OR package to solve these problems (Bonami et al., 2008; Linderoth & Lodi, 2011). The experiments were performed using a machine with an Intel Core i7-6820 CPU @ 2.70 GHz, 32 GB RAM, with Windows 10 as the operating system.

Figure 3 depicts the optimal networks obtained with respect to the objectives and constraints outlined in the two problems studied, in the uniformly random model. Network (a) represents the result obtained for Problem 1 and network (b) represents Problem 2. One can observe that network (a) exhibits a more centralised structure. This is a consequence of the fact that the connections between facilities and substations are counted just once, effectively minimising the cost of the tree corresponding to a facility. This can be highly relevant for several real-world applications, e.g. if the facility-substation connection represents a shuttle service that can serve many demands at once. In such applications, it can actually be desirable to treat the overall demand per substation at once, rather than optimising the fine-grained structure of the network.

Figure 3. An illustration of the optimal network designs for random geometric networks with 25 facility sites, 50 substation sites and 200 demands. Illustration (a) represents the optimal network design obtained for the first formulation, while illustration (b) depicts the optimal network design for the second formulation.

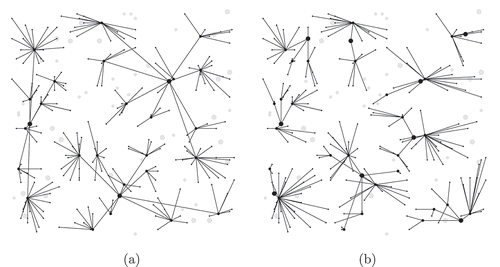
Network (b) in Figure 3 contrasts with network (a) to some extent. Even though the costs of opening the facilities and substations were the same as in Problem 1, the optimal design consists of many more facilities. Table 1 sheds more light on the structure of the networks designed, from a numerical perspective. The optimum for Problem 1 consists of only three facilities, while the optimum for Problem 2 contains as many as nine facilities. The numbers of substations are roughly similar, i.e. the difference lies in the demands served by the facilities on the higher level. It is also worth noting that the number of facilities open would likely be lower for Problem 2 if opening a facility was even more costly.

Table 1. Computational results obtained for Problem 1 and Problem 2 derived from the same geometric network with 25 facility sites, 50 sites and 200 demands.

Metric	Problem 1	Problem 2
# facilities	3	9
# substations	25	27
Average # substations per facility	8.33	3
Average # demands per substation	8	7.41
Objective value	2501.2	6872.9
Objective value	3282.7	4546.8
CPU time	11 s	830 s

Figure 4 shows the optimal network structures found for the uniformly placed candidate sites on a regular mesh. Table 2 provides the corresponding metrics, similar to the previous instances. One can see that in this configuration, the number of main facilities is similar to the random instances, while the number of substations is higher. In terms of practical problem difficulty, the time needed to find these solutions has been several times higher than in the random case.

Table 2. Computational results obtained for Problem 1 and Problem 2 derived from the same uniformly distributed sites with 25 facility sites, 50 substation sites and 200 demands.

Metric	Problem 1	Problem 2
# facilities	4	9
# substations	35	35
Average # substations per facility	8.75	3.89
Average # demands per substation	5.71	5.71
Objective value	2378.5	3048.35
objective value	5472.1	4259.59
CPU time	70 s	3892 s

Figure 4. An illustration of the optimal network designs for facilities, substations and demands distributed uniformly on a regular mesh with 25 facility sites, 50 substation sites and 200 demands. Illustration (a) represents the optimal network design obtained for the first formulation, while illustration (b) depicts the optimal network design for the second formulation.

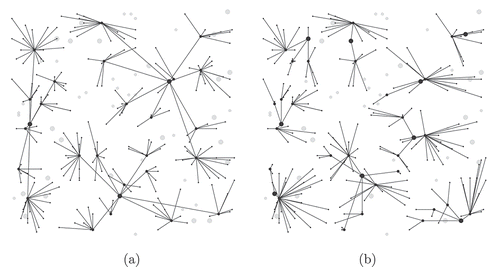
These solutions highlight the importance of details in formulations of these problems, as well as the input data distributions. These aspects may have a significant impact on the application and are inherently tied to the real-world interpretation of the problem, as well as to the interplay between the cost and distance elements of these problems.

The motivation for further extension of this work is mainly two-fold. Firstly, the dynamic optimisation aspect and dynamic relocation problems are of a high interest. Given a number of fixed facilities and current substations, one can decide whether a substation should be further opened or closed, based on the current data. Secondly, simulation of complex flows within the network and studying of its behavioural aspects may provide another interesting real-world perspective.

In terms of model complexity, these are the base two-level linear models for underlying problems that can be found in a number of scenarios in manufacturing and logistics. These can further be extended for simulation and optimisation in real-world applications. Such extensions are left for future work can include not only models with dynamic relocation, but also other future constraints such as time windows or sequence dependencies.

5. Conclusions

We compared two formulations of two-level facility location problems in network design applications for AGV operations. In these problems, one is given a number of candidate facilities, substations and demands. The aim is find the optimal locations of facilities and substations with respect to a given objective and a set of constraints.

The two formulations differ in the way they treat the distances between facilities and substations. The first formulation counts each connection between a facility and a substation just once, corresponding to applications, for which, e.g. a shuttle service is available. The second formulation is equivalent to the classical perspective on the multilevel facility location problems, treating the total cost of a path for a demand to a facility separately. Our experimental results were presented for random geometric networks, as well as networks with candidate sites distributed regularly on a mesh. These results indicate that the networks designed according to the two formulations have contrasting structures. While the first formulation leads to a lower number of facilities, the second formulation leads to a more fine-grained networks.

We believe the findings highlight the inherent link between the real-world application and the formulation of the corresponding problem. This will be of an increasing interest, especially given the possible future dynamic variants of the problem, as well as behavioural models based on simulation within such networks.

Modelling in some domains within manufacturing and logistics remains open for future studies. Further constraints include time windows and sequence dependencies. However, the models explored in this study represent the fundamentals that be used to model more complex problems in the future.

Disclosure statement

No potential conflict of interest was reported by the authors.