Protecting bridge piers with loose rock riprap

Abstract

An expression for sizing loose rock riprap placed around bridge piers is derived based on an evaluation of moments that resist and promote overturning of a single rock particle, on an elementary potential flow theory which provides models of velocities around piers of various cross-sectional shapes, and on widely accepted empirical relations and coefficients used to calculate shear stresses acting on rock riprap and the critical values of shear stress at which rock is moved. Minimum diameters of stable rock riprap given by the analytical relation for circular columns compare favorably with measured values collected in three experimental studies carried out by others. Theoretical shape factors, which are multiplied times the stable rock size needed for a circular column of the same width, were found for piers having square ends and for piers having sharp ends with interior nose angles of 60°, 90°, and 120°. A safety factor that provides a suitable margin of error needed for design is found by comparing calculated and measured rock sizes for both round-nosed and square-nosed pier experimental data. Comparison of predictions from the developed equation to those from other formula shows that the approach clearly delivers more desirable design estimates of stable riprap diameter. Notwithstanding its simplicity, the relation provides sound theoretical insights to the important parameters affecting stability of loose rock riprap used to protect bridge piers.

Keywords:

• bridge pier
• riprap
• hydraulics
• scour
• erosion
• potential flow

Introduction

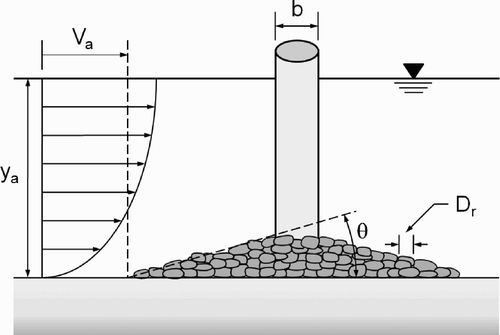
The most widely used method today for protecting bridge piers against local scour consists of placing loose stones on the surrounding streambed (Parker et al. 1998, p. 4; Lagasse et al. 2007, p. 14), as shown in Figure 1. However, the practice is far from being new. Although Ancient Romans used crib-like cofferdams to place pozzolanic concrete footings below water, their pumps were not adequate to sink foundations to any considerable depth. For this reason, they often surrounded piers with rock riprap (De Camp 1974, p. 205), making up for weaknesses by building both foundations and piers extremely large. However, as Gest (1930, p. 159) explains, this practice aggravated the danger by diminishing the waterway areas, thereby increasing water velocities during floods and the potential for erosion. As a result, the method was not always successful, as noted by the Roman architect and engineer Marcus Vitruvius Pollio (commonly known as Vitruvius) who reported that “it was not enough to dump loose rock about the foundations because the current was likely to burrow beneath and undermine the heaviest structure” (Kirby et al. 1956, p. 69).

Figure 1. Riprap mounded around two bridge piers to prevent scour.

In spite of Vitruvius’ reservations about its use, on-site studies of seven modern bridges, at which loose rock riprap had been installed as a pier scour countermeasure, led Nece (1974) to conclude that the method generally works well, with little loss or subsidence of the placed stones if the riprap is sized and installed properly. However, the technique is not without its drawbacks. In addition to Nece (1974), both Klingeman (1973) and Piésold (1991, p. 243) note that under some circumstances placement of a riprap blanket around a bridge pier promotes erosion around the edges of the armored zone, which can cause the riprap covering to fail if the channel deepens enough in the unprotected areas between piers. Chiew (2004) found if enough loose riprap was placed around a pier in degrading channels it would eventually develop into a stable protective mound as the surrounding streambed lowered and the bed shear stresses were reduced.

Based on small-scale experimental studies, Parola (1993), Chiew (1995, 1997), Chiew and Lim (2000), and Unger and Hager (2006) all describe various ways in which riprap protection at bridge piers can fail. Melville and Coleman (2000, p. 350) summarize the findings of several studies by identifying the following four pier riprap failure mechanisms:

	(1) Shear failure caused by stones not being able to resist the hydrodynamic forces imparted by the streamflow.
	(2) Winnowing failure caused by erosion of underlying soils through the porous protective layer from the effects of flow turbulence and seepage.
	(3) Edge failure caused by erosion at the periphery of the riprap apron which does not extend far enough horizontally to prevent scour and which is not capable of deploying and armoring the slopes of the resulting scour hole.
	(4) Bed-form undermining caused by dunes migrating past the protective layer and eroding beneath the edge of the apron, which, as for edge failure, is not capable of armoring the exposed slopes leading to the dune troughs.

Satisfactory filters that prevent winnowing of soils, along with rock covers of sufficient extent and thickness that armor surrounding stream beds automatically as they erode, are essential design elements needed for a successful riprap armoring system. However, here the center of interest is the size of rock needed to prevent shear failure. Based largely on potential flow theory, a rational expression is developed for calculating the representative diameter of stable loose stone placed around bridge piers. Stability is determined from the ratio of static moments resisting and promoting overturning of a single rock particle, which defines a safety factor. Flow velocities and the shear stresses they produce are found from a combination of empirical relations and theoretical solutions of two-dimensional flow fields. The resulting expression for stable rock diameter is then tested and compared with existing formulae using small-scale experimental data obtained from three previous studies carried out by others.

Experimental data

Experimental data collected in small-scale laboratory channels by Quazi and Peterson (1973), Rothwell and Bohan (1974), and Parola (1993) are used to evaluate the riprap sizing formula developed here, and to compare it with formulae developed by others. In each of the three experimental studies, protective covers of loose rock riprap were placed around cylindrical columns representing bridge piers. The laboratory channels all had rectangular cross-sections of constant shape with solid beds, and the riprap was modeled using crushed, angular gravel. All tests were carried out with gravel placed in horizontal layers that surrounded the model piers completely. Although differences in thickness and lateral extent of the riprap layers, and the duration of experiments, leads to some inconsistencies between data, the assemblage comprises a valid and useful means of testing the theoretical formulations that are developed, and for comparing results of expressions developed by others for sizing loose rock riprap to protect bridge piers.

All of the experiments were carried out using a procedure in which applied hydraulic loads were increased by small amounts until failure occurred. The hydraulic loads were varied by changing flow rates, adjusting downstream water levels, or by some combination of flow rate and water level changes. Failure (that is, riprap displacement) occurred at some applied load, which, because of the incremental increases, was always larger than the true failure load. How much larger depends on the size of the load increments. Presumably, the researchers made sure that their load increments were small so that any differences between the true and the reported failure conditions were insignificant. Information collected from experiments using cylindrical piers having circular cross sections or cross sections with semi-circular upstream and downstream ends is summarized in Table 1. Those data from experiments using square-nosed piers having rectangular cross-section are presented in Table 2. Tabulated data include the following items: pier width b, pier length ℓ, median diameter of the rock mixture D ₅₀, the approach flow depth y _a located a short distance upstream from the pier, and the depth-averaged approach flow velocity V _a.

Table 1. Experimental riprap data for round-nosed model piers aligned with approach flow.

	Median particle diameter,	Approach flow depth,	Approach flow velocity,
Data source	D 50 (mm)	y a (m)	V a (m/s)
Quazi and Petersen (1973)^a	2.58	0.073	0.271
	2.58	0.097	0.280
	2.58	0.122	0.311
	2.58	0.143	0.274
	2.58	0.183	0.276
	3.85	0.042	0.349
	3.85	0.064	0.411
	3.85	0.079	0.390
	3.85	0.091	0.427
	3.85	0.106	0.418
	3.85	0.103	0.418
	3.85	0.140	0.390
	3.85	0.152	0.451
	3.85	0.161	0.457
	3.85	0.180	0.457
	3.85	0.201	0.427
	6.77	0.064	0.450
	6.77	0.073	0.506
	6.77	0.085	0.457
	6.77	0.109	0.476
	6.77	0.134	0.540
	6.77	0.164	0.528
	6.77	0.158	0.497
	6.77	0.179	0.458
	6.77	0.192	0.576
	10.5	0.097	0.555
	10.5	0.082	0.543
	10.5	0.106	0.570
	10.5	0.122	0.625
	10.5	0.146	0.668
	10.5	0.154	0.545
	10.5	0.189	0.522
	13.6	0.116	0.707
	13.6	0.140	0.714
	13.6	0.173	0.634
	13.6	0.195	0.622
	14.4	0.097	0.570
	14.4	0.106	0.579
	14.4	0.125	0.631
	14.4	0.158	0.683
	14.4	0.167	0.695
	14.4	0.192	0.739
Parola (1993)^b	4.0	0.11	0.45
	4.0	0.24	0.46
	4.0	0.34	0.47
	6.0	0.20	0.56
	6.0	0.29	0.60
	6.0	0.10	0.48
	8.0	0.27	0.58
	8.0	0.33	0.61
	8.0	0.17	0.63
	12.0	0.31	0.78
	12.0	0.27	0.61
Notes: Values are conditions at observed failure.
^aRock specific gravity S r=2.64, pier width b=0.064 m, pier length ℓ=0.159 m, and channel width w=0.914 m for all measurements.
^b S r=2.92, b=0.114 m, ℓ=0.114 m, and w=1.829 m for all measurements.

Table 2. Experimental riprap data for square-nosed model piers aligned with approach flow.

			Median particle		Approach flow
	Pier width,	Pier length,	diameter, D 50	Approach flow	velocity, V a
Data source	b (m)	ℓ (m)	(mm)	depth, y a (m)	(m/s)
Rothwell and Bohan (1974)^a	0.472	1.052	22.0	0.381	0.580
	0.472	1.052	16.5	0.381	0.530
	0.472	1.052	12.9	0.381	0.483
Parola (1993)^b	0.114	0.254	4.0	0.13	0.36
	0.114	0.254	4.0	0.27	0.40
	0.114	0.254	4.0	0.42	0.38
	0.051	0.144	4.0	0.11	0.42
	0.051	0.144	4.0	0.25	0.44
	0.051	0.144	4.0	0.35	0.46
	0.114	0.254	4.0	0.39	0.36
	0.114	0.254	4.0	0.11	0.40
	0.114	0.254	4.0	0.26	0.42
	0.114	0.254	6.0	0.11	0.46
	0.114	0.254	6.0	0.26	0.42
	0.114	0.254	6.0	0.39	0.44
	0.114	0.254	6.0	0.39	0.41
	0.114	0.254	6.0	0.10	0.47
	0.114	0.254	6.0	0.23	0.47
	0.114	0.254	6.0	0.05	0.43
	0.114	0.254	8.0	0.22	0.49
	0.114	0.254	8.0	0.32	0.51
	0.114	0.254	8.0	0.35	0.59
	0.051	0.144	8.0	0.17	0.64
	0.051	0.144	8.0	0.23	0.73
	0.051	0.144	8.0	0.32	0.79
	0.114	0.254	8.0	0.20	0.52
	0.114	0.254	8.0	0.23	0.51
	0.114	0.254	8.0	0.21	0.52
	0.114	0.254	8.0	0.09	0.50
	0.114	0.254	8.0	0.19	0.50
	0.114	0.254	8.0	0.31	0.52
	0.114	0.254	12.0	0.26	0.62
	0.114	0.254	12.0	0.36	0.68
	0.051	0.144	12.0	0.20	0.81
	0.051	0.144	12.0	0.28	0.88
	0.114	0.254	12.0	0.39	0.74
	0.114	0.254	12.0	0.26	0.77
	0.114	0.254	12.0	0.40	0.57
	0.114	0.254	12.0	0.28	0.58
	0.114	0.254	12.0	0.38	0.78
	0.114	0.254	12.0	0.27	0.62
	0.114	0.254	12.0	0.38	0.64
Notes: Values are conditions at observed failure.
^a S r=2.65 and w=4.10 m for all measurements.
^b S r=2.92 and w=1.829 m for all measurements.

Rock particle stability

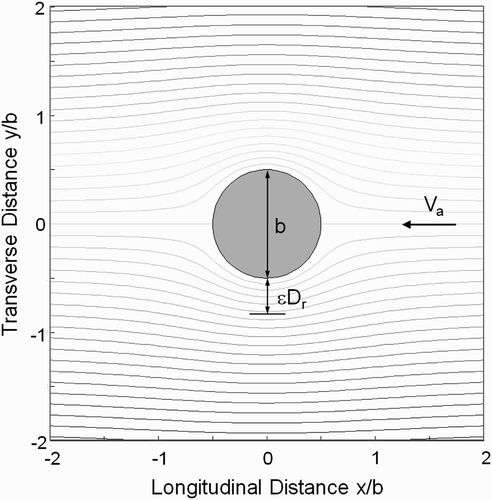
The general problem of protecting a pier with riprap and the related variables is illustrated in Figure 2. Although shown mounded around a pier, Engels (1929, p. 92–93), based on laboratory experiments carried out more than a century ago, found that rock riprap placed in a level cover layer that is flush with or below the streambed provides more reliable protection.

Figure 2. Illustration of the general pier riprap design problem.

The ratio of static moments resisting and promoting overturning of a single rock particle on the side of a riprap mound defines the stability safety factor f _s. For small longitudinal channel and water-surface slopes, Froehlich (2012, 2013) calculates f _s as follows:

where

τ*=τ/[(S _r−1)ρ gD _r], dimensionless shear stress, τ is the shear stress acting on riprap, S _r=ρ_r/ρ, rock specific gravity, ρ_r the rock mass density, and ρ the mass density of the ambient fluid (which is considered to be water), g the gravitational acceleration, D _r the representative rock riprap particle (usually D _r=D ₅₀, median intermediate diameter of rocks in a riprap mixture), θ the side-slope angle of the riprap cover, ϕ_r the rock riprap mass angle of repose, and the dimensionless critical shear stress for a horizontal bed or Shields’ parameter (Vanoni 1977, p. 96), which is approximately 0.06 for turbulent flows (Anderson 1961). The parameter β, angle of rock movement along the slope with respect to horizontal, and the parameter η_o, particle stability number for horizontal beds and small water-surface slopes, which represents the ratio of shear stress to critical shear stress on a horizontal bed multiplied by the relative difference in mass density of the riprap and the ambient fluid. For a horizontal rock riprap cover placed around a pier, θ=0° and β=90°, which reduces Equation (1) to

Derivation of Equation (1) departs from the conventional approach, which is described by Stevens and Simons (1971), Stevens et al. (1976), and Julien (1998, p. 121–126), because the buoyant force is not subtracted from the gravitational force to obtain the submerged weight of a particle, which is considered to be a de-stabilizing force. Instead, the buoyant force is treated separately, and it is split into distinct components that resist and promote overturning, similar to the conventional treatment of submerged particle weight. A consistent stability factor, which has an upper limit of S _r, results when gravitational and buoyant forces are taken into account in this manner. As a result, the upper bound of f _s increases in a logically consistent manner as ρ decreases in comparison to ρ_r (for example, if the surrounding fluid were air instead of water).

A relation for τ needed to calculate the size rock that will resist overturning moments is provided by Manning's formula (Chow 1959, p. 98), which is uncomplicated and accepted widely. Bed shear stress for flows in wide channels is then found as

where n is the Manning's roughness coefficient (which is considered to be dimensionless), and k _u the units conversion factor (1.0 for SI units, 1.486 for US Customary units), y the water depth, and V the depth-averaged velocity. An expression for n for rock riprap as a function of D _r is given by Maynord (1991) as

where k _n =0.145, a dimensionless coefficient. Combining Equations (5) and (6) provides the following relation for τ as a function of the relative roughness of the riprap, D _r/y, and V:

From Equations (3) and (7), η_o is then found as

where Fr=V/√gy, Froude number of the depth-averaged flow.

The shape and angularity of rock are also factors that affect particle stability and flow resistance. Coarse, angular rock, usually made by crushing or blasting, or from scree, is more resistant to hydrodynamic forces than round river rock. Effect of rock angularity is accounted for by specified values of the mass angle of repose ϕ_r, which is larger for angular rock than rounded rock (Simons & Sentürk 1977, p. 442). Froehlich (2011), based on data from 74 stockpiles of dumped natural and crushed rock, found that ϕ_r depends primarily on rock particle angularity and, to lesser extents, on the gradation and the median particle diameter of a stone mixture. Considering rock particle angularity alone, Froehlich (2011) shows that

Potential flow around bridge piers

Calculation of η_o by Equation (8) requires an appropriate velocity in the vicinity of a pier. Here V is estimated using theoretical expressions for two-dimensional, incompressible, inviscid, irrotational flow (that is, potential flow) about solid bodies. For some simple body shapes, such as circles, comparatively uncomplicated analytical solutions are possible. While such solutions have always been of interest as illustrative examples of potential flow, they are also of practical use because they provide theoretical insights into the principal factors that affect hydrodynamic processes. However, for completely general bodies even potential flow solutions are not easy, and one often needs to rely on numerical solutions of the governing partial differential equations.

From elementary potential flow theory (White 1994, Chapter 8) for plane flow in x−y coordinates where the effects of molecular and turbulent viscosity are neglected, a stream function ψ exists such that

where u and v are the velocities in the x and y directions, respectively. The condition of irrotationality then reduces to Laplace's equation for ψ, that is, ∇²ψ=0. Lines of constant ψ are streamlines of the flow, and the difference in the value of the function ψ between two streamlines equals the volumetric flux through the intervening space.

Circular cylinder in unbounded uniform flow

A classic problem in potential flow theory is that of steady flow around a fixed circular cylinder placed in an unbounded uniform flow having an approach velocity V _a in the positive x direction. The stream function for this case is (Milne-Thomson 1960, p. 154)

where r is the radial distance from the cylinder center, b the cylinder diameter, and δ the angular coordinate, with δ=0° corresponding to the rear stagnation point on the cylinder surface. In reality, rather complicated flow patterns exist around even a simple obstacle such as a circular column (Dargahi 1989; Graf & Yulistiyanto 1998; Unger & Hager 2007). However, when the surface boundary layer separates from the rear of a vertical cylinder in turbulent flow, creating a broad, pulsating wake, the external flow in front of and on the sides of the cylinder is not too different from the prediction given by the potential flow solution. The use of potential flow theory to model flow around a bridge pier is supported by the observations of Raudkivi and Ettema (1982), who found that when bed sediments surrounding a circular cylindrical column are large in comparison to the column diameter (that is, when D _r/b>0.125), erosion takes place mainly at the sides of the pier, where potential flow theory predicts the maximum velocity to occur.

The maximum theoretical velocity along the boundary of a circular cylinder occurs where δ=90°, and is twice the uniform flow velocity. Breusers and Raudkivi (1991) and Hoffmans and Verheij (1997, p. 125) developed relations for the size of riprap needed to protect bridge piers based on V=2×V _a. However, from Equation (11), fluid speed drops comparatively quickly along the δ=90° radius, becoming V=10/9×V _a a distance b from the cylinder surface. Recognizing that the average velocity acting over a rock placed adjacent to a pier will be less than the maximum value at the boundary of a circular cylinder given by potential flow theory, Graziano and Jones (1990) use V=1.5×V _a to size pier riprap.

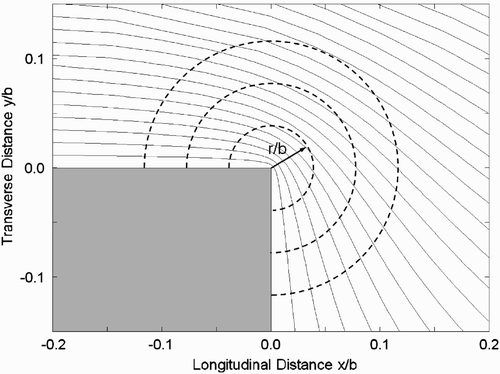
A circular cylinder in an unbounded uniform flow is used as an elementary bridge pier against which solutions for piers under other conditions and of other shapes will be compared. The potential flow stream function gives the average velocity within a distance (r−b/2) adjacent to a circular cylinder as V¯=[ψ (r)−ψ (b/2)]/(r−b/2). The maximum average velocity within a distance r=ϵ D _r adjacent to a column of circular cross-section in a uniform flow as shown in Figure 3 occurs along the δ=90° radius and is calculated as

where ϵ is some multiplier on the order of unity which needs to be determined. The value of V¯ is used to represent the depth-averaged velocity acting on a stone when calculating the particle stability number η _o .

Figure 3. Streamlines around a single unbounded circular column in a uniform flow of velocity V _a. Average velocity V¯ is calculated over a distance ϵ D _r as shown.

Combining Equations (1), (7), (8), and (12) gives, after some rearrangement, the following analytical expression for the stable value of D _r at the base of the circular pier:

where

is a factor that depends on properties of the rock (described by ϕ_r and and its placement (from the specified side-slope angle θ), and the specified degree of safety (defined by the safety factor f _s),

is a factor that accounts for the relative pier width given by the ratio b/D _r, and Fr _a=V _a/√gy _a, Froude number of the flow approaching the pier. The expression for K _b includes the sought-after rock diameter D _r, thereby making Equation (13) a transcendental formula and necessitating iterative solution.

For θ=0° (that is, for a horizontal bed), β=90°, and the factor K _r given by Equation (14) reduces to

To illustrate the influence of f _s on K _r, with k _n =0.145, , S _r=2.65 (an average value for common rock used as riprap), K _r=0.098 for f _s=1.0, and 0.175 for f _s=1.25. The relation of K _b as a function of b/ϵ D _r given by Equation (15) is graphed in Figure 4, which shows that K _b increases quickly with b/ϵ D _r. For example, with ϵ=1, as b/D _r goes from 1 to 5, K _b increases by more than a factor of two.

Figure 4. Pier factor K _b as a function of b/ϵ D _r.

Comparison of calculated and measured stable diameters at round-nosed piers

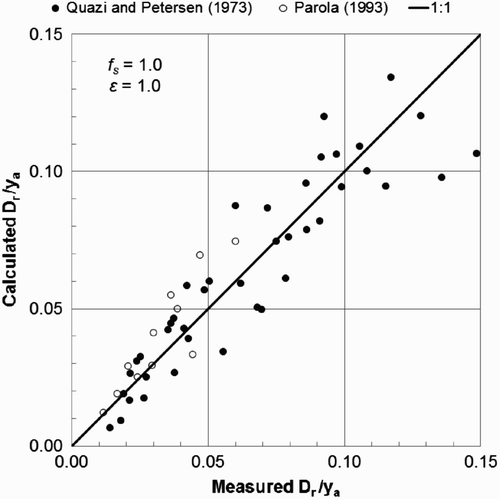
To test Equation (13) for circular cylindrical piers, calculated values of D _r/y _a are compared with measured values obtained from the assembled experimental data. Although the model pier in tests carried out by Quazi and Petersen (1973) was not circular, instead having semi-circular upstream and downstream ends and a length-to-width ratio of 2.5, flow patterns around the nose, where riprap size is critical, are close to those for circular piers as long as the pier and the flow are aligned. For this reason, these measurements are included in the comparison.

Using the widely accepted coefficients (a value that applies to low turbulence levels such as those in the experimental studies) and k _n =0.145, and setting f _s=1 and ϵ=1, values of D _r/y _a given by Equation (13) for round-nosed piers are compared with measured values in Figure 5. With f _s=1, the calculated values are intended to provide the expected value of D _r that is just stable. The root mean square error of the predicted values of D _r/y _a is 0.0264, and the coefficient of determination of the relation is 0.841. The fit is notably good with errors randomly distributed over the entire range of values, as Figure 5 shows.

Figure 5. Comparison of calculated and measured values of relative diameters of stable rock riprap placed around columns of circular cross-section in small-scale experiments.

The ability of Equation (13) to predict stable rock sizes as well as it does is not unexpected. The potential flow theory provides a reasonable approximation of the flow field around cylinders away from the boundary layer. Combining this flow solution with widely used empirical relations for critical shear stress and flow resistance that are well documented and thoroughly tested yields a good estimate of stable riprap diameter for the model pier. Although minor improvement of the predictions can be gained by adjusting the values of , k _n , and ϵ slightly, the widely accepted measures of τ_co* and k _n , are relied upon, along with a value of ϵ that can be reasoned easily.

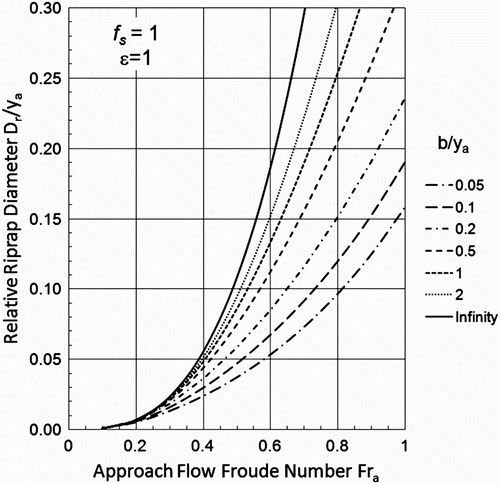
In spite of its simplicity, Equation (13) provides insights to important parameters that affect riprap stability at bridge piers. For example, the ratio of pier width to approach flow depth b/y _a in small-scale experimental studies generally can be varied within only a small range. For this reason, the influence of large and small values of the ratio on rock stability is difficult to explain based on empirical studies alone. The effect of pier width on rock diameter is shown theoretically by writing Equation (15) in terms of the ratios D _r/y _a and b/y _a as follows:

For a fixed value of V _a, Equation (17) shows that D _r increases with b, reaching a maximum for extremely wide piers where the largest average velocity acting on rock particles adjacent to the piers will approach twice the approach flow velocity. Solutions for D _r/y _a as a function of Fr _a and for a range of b/y _a given by Equation (13) with f _s=1 and ϵ=1 are shown in Figure 6. Because of the presence of the ratio D _r/y _a in Equation (17), solution of Equation (13) requires iteration, but the influence of Froude number is damped significantly when the value of b/y _a is small. The stable rock diameter approaches the value needed in uniform flow without a pier as b/y _a→0, exactly as it should.

Figure 6. Minimum relative stable riprap diameter D _r/y _a as a function of approach flow Froude number Fr _a and relative pier width b/y _a.

Supplementary potential flow solutions

Further application of potential flow solutions allows additional conditions that affect riprap stability to be taken into account. In the following sections, analytical expressions are developed that evaluate the influences of lateral velocity gradients of the approach flow and the presence of nearby piers.

Single cylinder in slight cross-flow shear

If the flow approaches a single column with a small constant vorticity or shear such that ∂ v/∂ x−∂ u/∂ y=ω, then, if v=0 everywhere, the transverse velocity gradient ∂ u/∂ y=−ω. The stream function for this situation is given by Milne-Thomson (1960, p. 184) as

With δ=90°, the potential flow model gives the maximum mean velocity within a distance ϵ D _r adjacent to a cylindrical column in a slight cross-flow shear as

where Ω=| ω | b/V _a dimensionless measure of cross-flow shear or vorticity. Combining Equations (1), (7), (8), and (19), and then rearranging as in the case of uniform flow without shear, the expression for stable D _r/y _a becomes

where

is a factor that accounts for the effect of the approach velocity cross-flow shear.

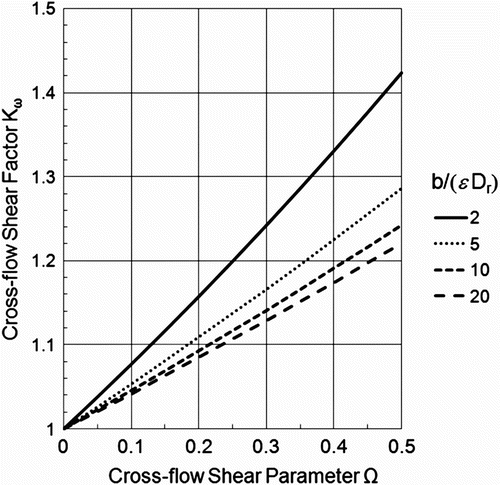
The shear flow adjustment factor K _ω is graphed as a function of Ω for several values of the ratio b/D _r in Figure 7. When the cross-flow gradient or vorticity ω=0 (that is, when the approach flow is uniform and aligned with the pier), then K _ω=1, as expected. As b increases, the effect of shear flow on riprap size increases as well, which one would reason intuitively since the maximum increase in velocity at the side of the pier would also be larger. Cross-flow shear may be particularly significant at piers located in river bends, or at bridge piers near river banks where large lateral velocity gradients are likely to be present.

Figure 7. Cross-flow shear factor K _ω as a function of cross-flow shear parameter Ω=ω b/V _a and relative pier width b/D _r.

Modern bridge hydraulic engineering design relies on inexpensive, readily available, and extremely powerful computing capabilities along with advanced software applications to evaluate complex hydraulic conditions at bridge sites. For example, the Federal Highway Administration's two-dimensional depth-averaged flow and sediment transport model FST2DH (Froehlich 2003) provides highly detailed descriptions of flow fields from which velocity gradients and vorticity can be determined easily.

Equally spaced cylinders in uniform flow

Bridges spanning large floodplains are sometimes built with many equally spaced piers formed from cylindrical column bents. If the piers are located close together, velocities near the leading columns will be greater than around a single cylinder in a uniform flow because water will need to pass through slightly smaller areas. An approximate stream function for an infinite row of circular cylinders of diameter b, spaced a distance p between centers, and aligned perpendicular to a uniform flow is given by Streeter (1948, p. 117) as

where the coordinate system origin is located at the pier center. With x=0, Equation (22) can be approximated as

from which the maximum average velocity within a distance ϵ D _r adjacent to a cylindrical column is found as follows:

The following expression for the diameter of stable rock riprap for equally spaced circular piers placed normal to a uniform approach flow is found by combining Equations (1), (7), (8), and (24):

where

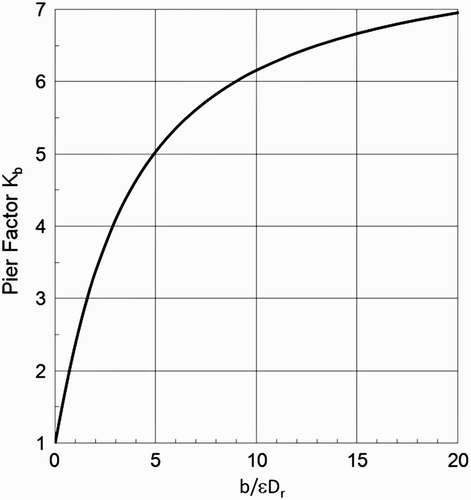
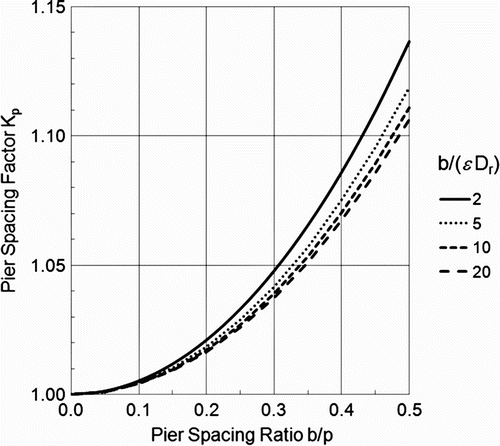
is a factor that accounts for the effect of adjacent pier proximity. The pier-spacing adjustment factor K _p is graphed in Figure 8 as a function of b/p for several values of the ratio b/ϵ D _r. When the spacing p is large in comparison to pier diameter (that is, as b/p→0) the factor K _p approaches one, as expected. However, even when piers are rather close together the influence of spacing is not particularly great. For example, if the spacing between pier centers p=2b, giving b/p=0.5 (that is, piers that are very close together), the minimum stable rock diameter increases by less than 15%.

Figure 8. Pier-spacing factor K _p as a function of the pier-spacing ratio b/p and relative pier width b/D _r.

Pier shape factors

Particle stability at cylindrical piers having cross-section shapes other than circular is the next factor to consider. Piers having rectangular cross-sections with noses that are either square (square-nosed) or pointed (sharp-nosed) are common. Because normalized rock diameters needed to create stable riprap covers given by Equation (13) depend on the cubed value of the average velocity acting over a distance ϵ D _r adjacent to a pier, adjustment coefficients that account for piers having cross-section shapes other than circles can be found as

where V¯ average velocity adjacent to a circular column given by Equation (12), and V¯ _s average velocity adjacent to cylindrical pier having a different cross-sectional shape. The more general problem of determining the two-dimensional flow pattern around an obstacle placed in a fluid initially moving with uniform velocity V _a is solved here by the method of conformal mapping.

Potential flow conformal mapping solutions

Conformal transformations that map the unit disk or half-plane onto the interior of a bounded or unbounded polygon in the complex plane, which represents the pier cross-section in the physical flow domain, are used to solve Laplace's equation for the stream function. The calculations are carried out numerically using SCPACK, a computer program developed by Trefethen (1980) that applies the Schwarz-Christoffel transformation to map the unit disk to two-dimensional regions with irregular or unbounded (but not curved or multiply connected) geometries, which may contain vertices at infinity.

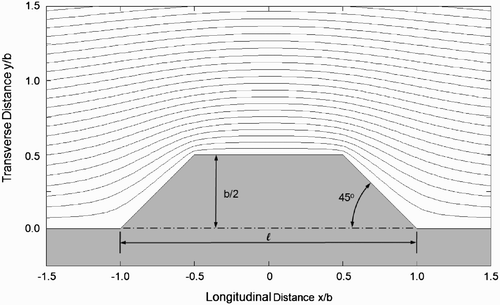
Streamlines around the upper half of an unbounded sharp-nosed pier with a 90° interior nose angle (which produces a 45° half angle) and a total pier length-to-width ratio ℓ/b=2 calculated numerically are shown in Figure 9. For all polygonal pier shapes considered, whether their front ends are square or pointed, the maximum velocities occur at their upstream corners, where the velocity goes to infinity according to the potential flow theory. To find the maximum average velocity acting over a distance ϵ D _r within the ideal flow field adjacent to a corner, stream functions were calculated at a finite number of points along circular arcs of radii r centered at the pier's corner, as shown in Figure 10. When divided by the arc radius, the difference in the maximum stream function found along an arc, that is, ψ (r)_max, and the value of ψ at the pier corner gives the maximum average velocity within a distance r adjacent to the corner.

Figure 9. Streamlines around the upper half of an unbounded sharp-nosed pier with a 90° interior nose angle and a length-to-width ratio ℓ/b=2 that is aligned with the approach flow.

Figure 10. Streamlines around the corner of an unbounded infinitely long square-nosed pier showing circular arcs centered at the upstream corner along which the maximum stream functions are found by conformal mapping solutions of the potential flow field.

Square-nosed piers

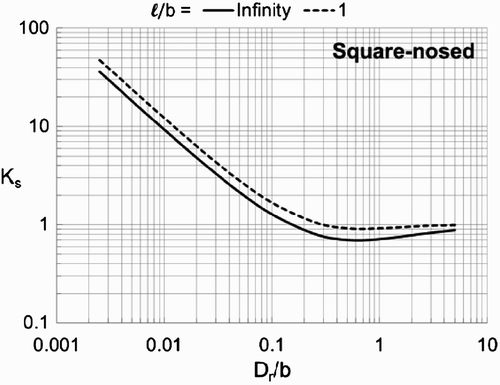
Shape factors given by Equation (27) using numerically calculated average velocities adjacent to unbounded square-nosed piers with ℓ/b=1 (that is, a square column) and infinity, both of which are aligned with a uniform approach flow, are shown in Figure 11 as a function of the normalized distance ϵ D _r/b from the corner. As ϵ D _r/b→∞, the shape factor K _s→1, just as it should since V¯ _s→V _a. Because V¯ _s→∞ at the corner as ϵ D _r→0, the factor K _s becomes much larger than unity for ϵ D _r/b<0.1. However, as ϵ D _r/b increases, the shape factors for both piers fall below unity, reaching minimums of about 0.9 for the square column and about 0.7 for the square-nosed pier of infinite length. These findings contradict the general notion that adjustment factors for square-nosed piers are constant and always greater than one (Parola 1993; Lagasse et al. 2006, p. 95–96; Lagasse et al. 2009, p. DG11.6). After considering the results of previous studies, Melville and Coleman (2000, p. 355) concluded that neither pier shape nor alignment of a pier with the approach flow are significant factors affecting riprap stability. However, pier shape and approach flow angle can both have large influences on stable particle diameter, as will be shown.

Figure 11. Theoretical shape factor K _s as a function of relative distance from the pier corner ϵ D _r/b for unbounded square-nosed piers aligned with the flow with length-to-width ratios ℓ/b of infinity and one.

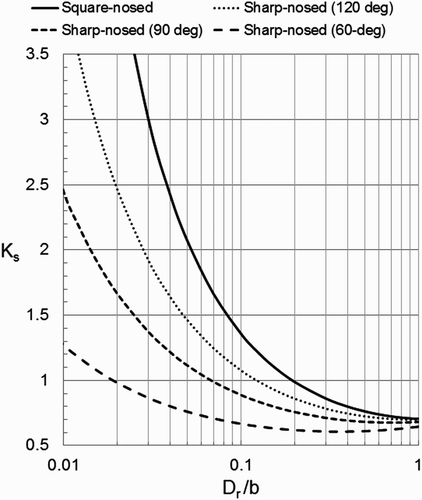
The 42 experimental measurements on stable rock sizes at square-nosed piers, three from Rothwell and Bohan (1974) and 39 from Parola (1993), are used to test the theoretical shape factor relations shown in Figure 11. Measured shape factors, which were found by dividing the measured stable particle diameter by the value of D _r given by Equation (13) for a circular column of the same width, are compared in Figure 12 with the theoretical relation for infinitely long unbounded square-nosed piers aligned with the approaching streamflow. The graphical relation provides a notably good fit to the data points, which are randomly scattered about the curve for values of K _s ranging from 0.7 to 3.

Figure 12. Theoretical relation for square-nosed pier K _s graphed with measured values from small-scale experiments.

Dependence of K _s on the ratio ϵ D _r/b as shown in Figures 11 and 12 helps explain the contradictions in views regarding the influence of pier shape on riprap stability. Because D _r/b<0.2 for most experimental studies, the need for larger sized stones at square-nosed piers is a likely conclusion. However, tests carried out with larger values of D _r/b might well lead to the finding that the influence of pier shape is negligible. Values of D _r/b>0.3 at archetype piers occur commonly.

Sharp-nosed piers

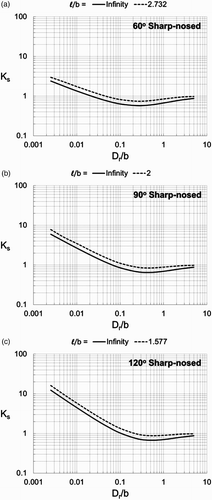
Computations similar to those that were carried out for square-nosed piers were used to produce the graphical relations shown in Figure 13 for sharp-nosed piers having interior nose angles of 60°, 90°, and 120°. The general pattern is the same as for square-nosed piers: K _s is significantly greater than one for small values of D _r/b, decreasing to a minimum that is less than one for D _r/b between 0.1 and 1, and then increasing toward unity as D _r/b approaches infinity. As clearly shown in Figure 13, K _s increases as the pier nose becomes more blunt (that is, less sharp) for a particular value of D _r/b.

Figure 13. Theoretical shape factors K _s as a function of relative distance from the pier corner ϵ D _r/b for unbounded piers having sharp ends with interior nose angles of (a) 60°, (b) 90°, and (c) 120° for length-to-width ratios ℓ/b of infinity and one.

Mathematical approximations

The theoretical K _s relation for square-nosed piers with ℓ/b=∞ shown in Figure 12 provides a notably good fit to the experimental data that are displayed in the graph. For this reason, the graphical relations established for both square-nosed and sharp-nosed piers with ℓ/b=∞ will be used to evaluate K _s for piers of all length-to-width ratios. To simplify application of the factor, the following mathematical approximations of the graphical relations for K _s have been developed:

Relations for K _s given by Equation (28) are shown in Figure 14.

Figure 14. Shape factor K _s from mathematical approximations of the theoretical graphical relations as a function of relative distance from the pier corner ϵ D _r/b for infinitely long unbounded piers aligned with a uniform flow.

Approach flow alignment

For other than circular columns, maximum velocities adjacent to piers will be larger when they are not aligned with approaching streamflow. Additionally, turbulence of the flow is likely to increase at non-aligned piers, which will increase the range of time-varying shear stresses acting on a rock particle at the pier base, thereby making it less stable. Consequently, larger riprap will be needed to protect against erosion.

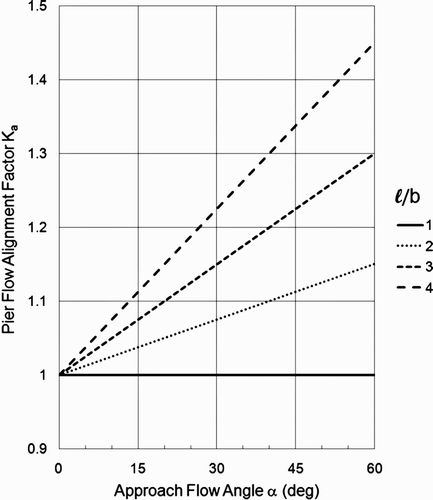
Although conformal mapping can also be used to analyze flow patterns around polygons representing non-aligned bridge piers, an adjustment factor K _α presented by Choi et al. (2002), which is based on small-scale laboratory experiments on non-aligned round-nosed piers having length-to-width (ℓ/b) ratios greater than one, is used here as an alternative. The graphical relation for K _α given by Choi et al. (2002), which represents accurately their experimental data, is matched closely by the following mathematical expression:

where α is the flow alignment angle in degrees (α=0° for flow that is aligned with the centerline axis of a pier). Values of K _α given by Equation (29) are shown in Figure 15 as a function of α and the ℓ/b ratio.

Figure 15. Pier flow alignment factor K _a given by the mathematical approximation of the graphical relation presented by Choi et al. (2002) as a function of the approach flow angle α and the pier length-to-width ratio ℓ/b.

Combined effects

The combined effects of cross-flow gradients, pier spacing, and pier shape are not evaluated here theoretically. However, since neither of the factors K _ω or K _p is likely to be considerably greater than one, errors caused by their multiplicative influence will be minimal. For this reason, the following expression is used to calculate the minimum stable rock riprap diameter at bridge piers:

where the factors K _r, K _b, K _ω, K _p, K _s, and K _α are given by Equations (14), (15), (21), (26), (28), and (29), respectively. Because expressions for the adjustment factors K _b, K _ω, K _p, and K _s include the ratio of rock diameter to pier width D _r/b, the solution for D _r/y _a given by Equation (30) requires iteration, beginning with an initial estimate of D _r.

Selection of safety factor

The formula for sizing rock riprap to protect bridge piers predicts the experimental data well using widely accepted coefficients for calculating the critical shear stress and the flow resistance of the rock. Nonetheless, an adequate safety factor f _s, which is the ratio of resisting moments to overturning moments acting on a riprap particle of diameter D _r, is needed in Equation (14) for K _r to account for uncertainty of the relation, imperfections in materials, flaws in construction, and rock cover degradation over time. Suitable safety factors depend on the accuracy of design load calculations (that is, calculated water velocities and depths, and the shear stresses that they produce on the riprap surrounding a pier), on the consequences of failure, and on the cost of over-designing the protective cover to achieve the desired factor of safety.

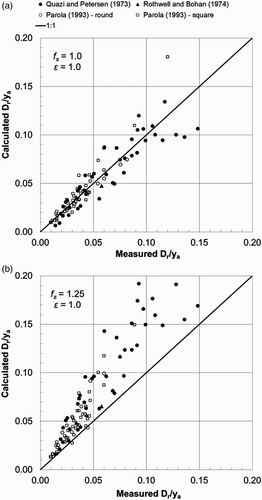
Values of D _r/y _a given by Equation (30) with f _s=1.0 and 1.25 are plotted in Figure 16 against measured values from both round-nosed and square-nosed pier experiments. The good predictive ability of Equation (30) with f _s=1.0 is shown in Figure 16(a), in which scatter about the 1:1 line is random for the entire range of D _r/y _a. With f _s=1.25, the 1:1 line in Figure 16(b) provides a clear lower bound to all except two of the measurements, which fall slightly below the line. Recalling from Equation (1) that f _s≤S _r=ρ_r/ρ, selection of an appropriate value of the safety factor depends in part on the mass densities of the riprap material and the ambient fluid. Based on the visual display of data in Figure 16, setting f _s=1.25 appears to be a good choice when applying Equation (30) to size loose rock riprap placed in water, for which specific gravity S _r ≈ 2.65. Larger safety margins are produced with f _s>1.25.

Figure 16. Comparison of calculated and measured values of relative diameters of stable rock riprap placed around both round-nosed and square-nosed piers in small-scale experiments with (a) f _s=1.0 and (b) f _s=1.25.

Comparison to other formulae

Several formulae for sizing stable rock riprap at bridge piers are summarized and compared by Melville and Coleman (2000, p. 348–356), Lagasse et al. (2006, p. 95–97), and Lagasse et al. (2007, p. 15), all of whom find that there is a wide range of predicted sizes for any given flow condition. Predictions of D _r given by a few of these formulae for round-nosed and square-nosed bridge piers aligned with approaching streamflow are compared now with estimates given by Equation (30).

Each of the expressions included in the comparison can be written in the general form

where K _r is the factor that accounts for rock properties, K _b the factor that accounts for the effect of pier width b, K _s the factor that accounts for pier shape, and κ the approach flow Froude number exponent. Details of the formulae presented by Quazi and Peterson (1973), Breusers et al. (1977), Breusers and Raudkivi (1991), Parola (1993), Chiew (1995), Yoon and Yoon (1997), and Lagasse et al. (2009) are provided in Table 3.

Table 3. Summary of existing formulae for sizing stable rock riprap used to protect round-nosed and square-nosed cylindrical column bridge piers.

For all of the pier riprap formulae included in the comparison, K _r=K/(S _r−1)^κ/2, where K dimensionless coefficient, which is different for each expression. The factor K _b=1 for most of the formulae, which implies that the calculated rock diameter has no dependance on pier width. Only Parola (1993), Chiew (1995), and Yoon and Yoon (1997) take into account pier width explicitly. The effect of pier shape is addressed only by Parola (1993) and Lagasse et al. (2009), who specify K _s for shapes other than round-nosed.

The formulae of Quazi and Petersen (1973) and Chiew (1995) predict values of D _r/y _a for critical conditions, which are compared with values given by Equation (30) with f _s=1. The remaining formulae provide design estimates that incorporate a factor of safety, which assures a stable rock size. Values of D _r/y _a given by these relations are compared with the predictions of Equation (30) with f _s=1.25.

Comparison of predictions for round-nosed piers

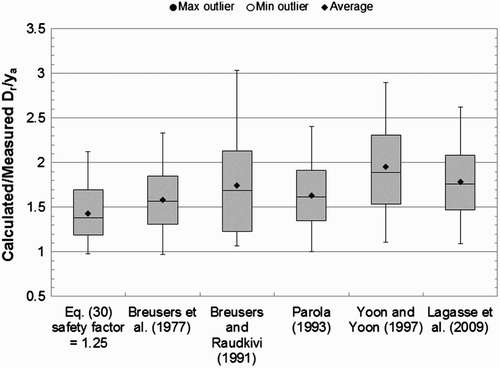
Ratios of calculated to measured critical values of D _r/y _a (that is, values of D _r/y _a that provide minimally stable rock size) for round-nosed pier data only are compared in the box-and-whisker diagrams shown in Figure 17. A box-and-whisker diagram provides a convenient way of depicting graphically the prediction error (that is, the predicted value minus the measured value) through their five-number summaries: the smallest observation (sample minimum, not including outliers), lower quartile (Q1), median (Q2), upper quartile (Q3), and largest observation (sample maximum, not including outliers). Outliers are those measurements not within 1.5×IQR of the lower and upper quartiles, where IQR=Q3−Q1=inter−quartile range. The minimum and maximum outliers are also shown in the diagram, along with the average. Spacing between different parts of the boxes helps indicate the degree of dispersion (spread) and skew (asymmetry) of the prediction errors.

Figure 17. Box-and-whisker diagrams comparing the ratios of calculated and measured expected relative diameters of stable rock riprap given by various formulae for the round-nosed pier experimental data.

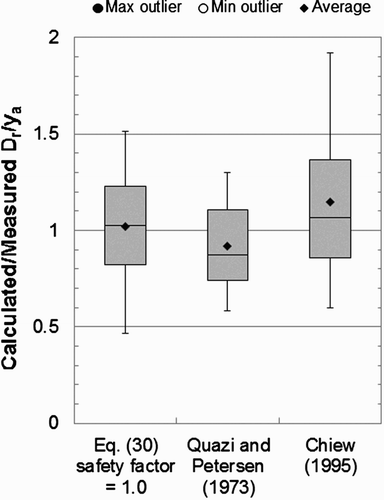
From the box-and-whisker diagrams in Figure 17, the theoretical predictions given by Equation (30) are shown to be consistently accurate (the IQR extends from about 0.8 to 1.2), with median and average values both near one, and with little skew. However, the IQR of predictions from the Quazi and Petersen (1973) formula, which is based on a multiple-regression fit to their data, is smallest. Chiew's (1995) equation generally over-predicts the critical particle size, the IQR of its estimates is the largest of the three formulae compared, and the maximum predicted value of D _r/y _a is nearly two, which is significantly larger than the maximums given by the other equations.

Formulae that provide values intended for design include those of Breusers et al. (1977), Breusers and Raudkivi (1991), Yoon and Yoon (1997), Lagasse et al. (2009), and Equation (30) with f _s=1.25. The box-and-whisker diagrams in Figure 18 show that all of the formulae predict values of D _r that are stable (that is, predict values of D _r/y _a>1), except for one measurement that Equation (30) and Bruesers et al. (1973) estimate as slightly less than one. However, it is the magnitude of the average and median values of D _r/y _a, along with the maximums and the presence of outliers, which distinguish prediction quality for design. Estimates given by Equation (30) have the smallest median and average, the narrowest IQR, and the lowest maximum value, which show that the equation consistently provides the smallest stable riprap size. For these reasons, Equation (30) clearly delivers more desirable design estimates than the other formulae.

Figure 18. Box-and-whisker diagrams comparing the ratios of calculated and measured design relative diameters of stable rock riprap given by various formulae for the round-nosed pier experimental data.

Comparison of predictions for square-nosed piers

Ratios of calculated to measured values of D _r/y _a for square-nosed pier data are compared in the box-and-whisker diagrams shown in Figure 19. Only Parola (1993) and Lagasse et al. (2009) provide K _s for square-nosed piers, which are constant values that are given in Table 3. As the theoretical evaluation for square-nosed and sharp-nosed piers has shown, K _s is not constant, possessing instead considerable variation dependent on the ratio D _r/b. For this reason, it is no surprise that the predicted median and average design values of D _r/y _a given by Equation (30) with f _s=1.25 are significantly less than design estimates given by the Parola (1993) and Lagasse et al. (2009) equations. The comparison therefore shows that Equation (30) also provides design estimates of riprap size that are both reliable and more suitable than those given by other formulae.

Figure 19. Box-and-whisker diagrams comparing the ratios of calculated and measured relative diameters of stable rock riprap given by various formulae for the square-nosed pier experimental data.

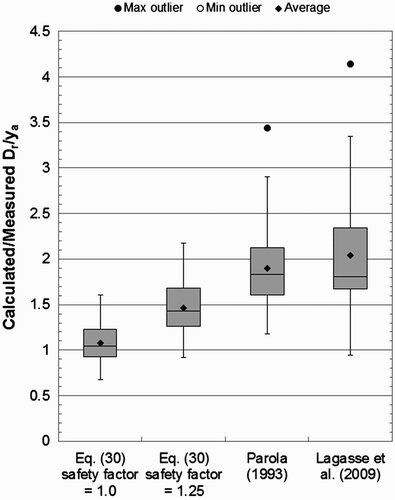
Also shown in Figure 19 is the box-and-whisker diagram of predictions given by Equation (30) with f _s=1.0. The estimates are well-balanced, with the median and average values both close to one. The D _r/y _a prediction IQR is notably small, extending from about 0.9 to 1.2.

Example application

A brief example follows that illustrates the use of the procedure developed in this paper to determine the size of stable rock riprap needed to halt scour around a 0.914 m wide, 7.315 m long, sharp-nosed bridge pier that has a 90° interior nose angle. Angular rock riprap with S _r=2.65 is to be placed in the form of a horizontal apron surrounding the pier at the current streambed level. Hydraulic analysis using the two-dimensional depth-averaged flow and sediment transport model FST2DH (Froehlich 2003) shows that for the design flood, y _a=5.58 m, V _a=3.11 m/s, and α=5°. The two-dimensional depth-averaged flow solution also shows that a slight cross-flow shear will exist for which ω=0.15. Just one pier, which is located at the center of the main channel, supports the bridge deck. A safety factor f _s=1.25 is to be used for sizing the riprap, and ϵ=1.

Because the riprap will form a horizontal surface after placement, θ=0°, giving β=0°, which allows K _r to be calculated from Equation (16) as follows:

where k _n =0.145 and . An initial estimate of the pier factor K _b from Equation (15) is made with an assumed D _r=0.3 m as follows:

Taking into account cross-flow shear obtained from the two-dimensional, depth-averaged flow numerical model used to simulate flow at the bridge, Ω=| ω | b/V _a=0.15×0.914/3.11=0.044, and from Equation (21),

Because no other piers are nearby, K _p=1. The shape factor for a 90° sharp-nosed pier is found from Equation (28) as

Finally, the flow alignment factor K _α is calculated from Equation (29) as follows:

With Fr _a=V _a/√gy _a=3.11/√9.81×5.58=0.420, the initial estimate of D _r/y _a is found from Equation (30) as

which gives D _r=0.0422×y _a=0.0422×5.58 m=0.235 m. Because the calculated value of D _r differs substantially from the initial estimate, two additional iterations were needed to obtain a final value of D _r=0.257 m, which is the minimum stable rock riprap diameter with f _s=1.25.

Summary and conclusions

An expression that provides the minimum diameter for stable loose rock riprap placed around cylindrical column bridge piers is derived based on an evaluation of moments resisting and promoting overturning of a single rock particle, on an elementary inviscid flow theory that provides models of velocities around piers of various cross-sectional shapes, and on widely accepted empirical relations and coefficients used to calculate shear stresses acting on rock riprap particles and the critical values of shear stress at which particles are moved. The theoretical formulation helps to understand the influences of pier width, cross-flow shear, pier spacing, and pier shape, which are often difficult to discover from the results of small-scale physical model experiments alone.

Stable riprap diameters calculated by the theoretical relation developed here for circular columns compare favorably with measured values collected in several experimental studies carried out by others. Because the approach taken predicts stable rock sizes remarkably well for a single cylindrical column, the analysis was extended to account for cross-flow shear, the effect of nearby piers, and both square-nosed and sharp-nosed pier shapes. However, the theoretically derived coefficients that help explain the additional effects should not be stretched to extreme conditions until experiments are carried out to confirm their use.

Theoretical shape factors, which are multiplied times the stable rock size needed for a circular column of the same width, were found for piers having square ends and for piers having sharp ends with interior nose angles of 60°, 90°, and 120° based on potential flow models of velocities. The shape factors are not constant: they approach one for a large-diameter stone, and increase in value as rocks become small in comparison to pier widths.

The theoretical shape factor relation for square-nosed piers was tested using available experimental measurements. The relation for infinitely long piers, which was found to provide a particularly good fit to the data, was adopted for practical calculation of shape factors for both square-nosed and sharp-nosed pier. Comparison of calculated and measured rock sizes for both round-nosed and square-nosed pier experiment data suggests that a safety factor f _s=1.25 provides an appropriate margin of error needed for design.

Comparison of predictions from Equation (30) to those from other formulae shows that the equation clearly delivers more desirable design estimates of the stable riprap diameter. Notwithstanding its simplicity, the relation provides sound theoretical insights to the important parameters affecting stability of loose rock riprap used to protect bridge piers.

Notes on contributor

Dr Froehlich is a consulting engineer who specializes in complex and computationally intensive analyses of water resource projects. His technical interests include flood risk management, bridge hydraulics and scour, river training works, stream channel rehabilitation, urban stormwater drainage systems, dam failures, and surface-water hydrology.

Notation

The following symbols are used in this paper:
b	=	pier width;
D r	=	representative rock riprap particle diameter, usually D 50 of the riprap mixture;
D 50	=	diameter of median particle size of a riprap mixture;
f s	=	riprap safety factor that represents the ratio of moments resisting overturning to moments promoting overturning of a single rock particle;
Fr a	=	V a/ √gy a Froude number of the flow approach- ing a bridge pier;
g	=	gravitational acceleration;
IQR	=	interquartile range;
k n	=	rock riprap flow resistance coefficient;
k u	=	Manning formula units coefficient;
K	=	pier riprap formula coefficient;
K b	=	rock riprap sizing factor that accounts for pier width;
K b1, K b2	=	rock riprap sizing factors that account for pier width in Chiew's (1995) formula;
K p	=	rock riprap sizing factor that accounts for transverse pier spacing;
K r	=	rock riprap sizing factor that accounts for rock properties slope effects;
K s	=	rock riprap sizing factor that accounts for pier shape, particularly the shape of the upstream end or nose of the pier;
K α	=	rock riprap sizing factor that accounts for pier alignment with the approach flow;
K ω	=	rock riprap sizing factor that accounts for cross-flow shear;
ℓ	=	pier length;
n	=	Manning formula roughness coefficient;
p	=	transverse pier-spacing distance;
Q1	=	lower quartile;
Q3	=	upper quartile;
r	=	radial distance;
S r	=	rock riprap specific gravity;
u	=	velocity in x direction;
v	=	velocity in y direction;
V	=	depth-averaged velocity;
V a	=	depth-averaged approach flow velocity, or uniform flow velocity;
V¯	=	average velocity over a distance ϵ D r adjacent to a bridge pier
W	=	channel width;
x	=	longitudinal coordinate;
y	=	transverse coordinate; water depth;
y a	=	approach flow depth;
z	=	complex number;
α	=	mass angle of repose of falling apron stone.
β	=	angle of particle movement along a slope with respect to horizontal;
δ	=	angular coordinate;
ϵ	=	rock diameter multiplication factor used to determine the distance adjacent to a bridge pier over which an average velocity is found;
η	=	particle stability number for general bank slope and water-surface slope conditions;
ηo	=	particle stability number for horizontal beds and small water-surface slopes;
θ	=	riprap mound side-slope angle;
κ	=	general pier riprap formula Froude number exponent;
ρ	=	water mass density;
ρr	=	rock riprap mass density;
τ	=	hydrodynamic shear stress acting on a riprap-covered surface;
τ*	=	τ/(√S r−1ρ gD r) dimensionless shear stress;
	=	Shields’ parameter (that is, dimensionless critical shear stress) for rock riprap on a horizontal bed;
ϕr	=	rock riprap mass angle of repose;
ψ	=	stream function;
ω	=	vorticity or cross-flow shear;
Ω	=	ω b/V a dimensionless measure of cross-flow shear or vorticity;