How Does Value Added Compare to Student Growth Percentiles?

Abstract

We compare teacher evaluation scores from a typical value-added model to results from the Colorado Growth Model (CGM), which 16 states currently use or plan to use as a component of their teacher performance evaluations. The CGM assigns a growth percentile to each student by comparing each student's achievement to that of other students with similar past test scores. The median (or average) growth percentile of a teacher's students provides the measure of teacher effectiveness. The CGM does not account for other student background characteristics and excludes other features included in many value-added models used by states and school districts. Using data from the District of Columbia Public Schools (DCPS), we examine changes in evaluation scores across the two methods for all teachers and for teacher subgroups. We find that use of growth percentiles in place of value added would have altered evaluation consequences for 14% of DCPS teachers. Most differences in evaluation scores based on the two methods are not related to the characteristics of students’ teachers.

• Teacher effectiveness
• Teacher evaluation
• Teacher quality

1. INTRODUCTION

1.1 Measuring Teachers’ Contributions to Student Achievement

Spurred in some cases by the federal government's Race to the Top initiative, many states and school districts have included in their performance evaluations measures of teacher effectiveness based on student achievement data. States and districts that want to measure teacher effectiveness by using test scores must choose from a menu of options that include value-added models and the Colorado Growth Model (CGM). Value added is widely used to measure the performance of teachers. For example, the District of Columbia, Chicago, Los Angeles, and Florida use value added. Several states, including Colorado, Georgia, and Massachusetts, use the CGM to measure the effectiveness of schools or teachers.^1,2

Value added provides a measure of teachers’ contributions to student achievement that accounts for factors beyond the teacher's control. The basic approach of a value-added model is to predict the standardized test score performance that each student would have obtained with the average teacher and then compare the average performance of a given teacher's students to the average of the predicted scores. The difference between the two scores—how the students actually performed with a teacher and how they would have performed with the average teacher—is attributed to the teacher as his or her value added to students’ test score performance. Value-added models typically account for student background characteristics in addition to prior test scores. Some value-added models also make additional adjustments designed to improve accuracy and fairness of the measures for used in evaluations. These adjustments include accounting for measurement error in prior test scores and empirical Bayes shrinkage to reduce the risk that teachers, particularly those with relatively few students, receive a very high or very low effectiveness measure by chance.

The CGM is a student-level model that assigns percentile ranks by comparing each student's current achievement to other students with similar past test scores. Each student growth percentile (SGP) indicates a relative rank for the student's academic growth during the school year. The median (or average) SGP of a teacher's students provides the measure of teacher effectiveness. The CGM does not account for student background characteristics such as status as an English language learner, the existence of a learning disability, or eligibility for free or reduced-price lunch (FRL).

Some policymakers view the choice between the CGM and value added as a choice between greater accuracy in measuring teacher performance and what they may perceive as more transparency (Hawaii Department of Education 2013).³ Even though the method for calculating SGPs is arguably more complex than a value-added model, states may be choosing to adopt the CGM due to its association with “simple” measures of student growth. Another advantage that some policymakers tout is that the CGM does not adjust for student background characteristics other than prior test scores, thereby avoiding setting lower expectations for students from different racial or ethnic groups. Whatever the merits of this argument, by excluding student characteristics the CGM also might unfairly disadvantage teachers with, for example, many English language learners, special education students, or FRL students. For their part, teachers tend to prefer as many control variables as possible. Policymakers may also prefer the CGM because SGPs can be computed with publicly available software that does not require extensive customization for use by a state or district. In contrast, a value-added model typically requires numerous decisions (e.g., which student characteristics to include). However, other policymakers may prefer the flexibility provided by value-added models, and although the CGM software is public, it is complex and requires trained staff to implement.

1.2 Research Questions

We compared estimates of teacher effectiveness from a value-added model to those from the CGM by examining two questions:

• How large are the changes in evaluation scores when replacing value added with SGPs?

• Are the changes related to the characteristics of teachers’ students?

To answer the questions, we used data on students and teachers in the District of Columbia Public Schools (DCPS) during the 2010–2011 school year to calculate value-added estimates and CGM measures of teacher effectiveness for the same teachers. We use the value-added model that was used by DCPS during that school year so that our results represent how evaluation scores of teachers would have changed had DCPS replaced the value-added model with the CGM.

The CGM may induce bias because it does not account for student background characteristics and because of other differences between the CGM and value-added models.⁴ Although we lack a benchmark for unbiased estimates that would allow us to test directly for bias, our analysis can suggest how large the bias might be and which teachers would most likely be affected by a change from the value-added model to the CGM. However, we cannot rule out the possibility that value-added estimates are also biased because of the sorting of teachers to students on the basis of characteristics that are not accounted for in either the value-added model or the CGM.⁵ Also, not all value-added models used for teacher evaluation share all of the features and procedures of the DCPS value-added model. Some of these features could affect the amount of bias in value-added estimates.⁶   

1.3 Earlier Literature Comparing Value-Added Models and the Colorado Growth Model

Most of the earlier literature comparing the CGM to value-added models focused on school-level rather than on teacher-level estimates (Castellano 2011; Ehlert et al. 2012; Castellano and Ho 2012, 2013). Some of the school-level studies found substantive differences between estimates based on these competing models. Ehlert et al. (2012) found that school-level CGM estimates were lower for high-poverty schools relative to a school-level value-added model. Goldhaber et al. (2012), examining teacher-level estimates for North Carolina teachers, found that, although estimates from the two models were highly correlated, teachers of more disadvantaged students tended to receive lower scores on the CGM compared to a value-added model that accounted for other student background characteristics in addition to prior test scores. Wright (2010) also examined teacher-level estimates and found that, compared to the EVAAS value-added model, the CGM produces lower scores for teachers with more students who are FRL eligible. Although the EVAAS model differs in many ways from the CGM, in at least one respect it is more similar to the CGM than most value-added models, including the value-added model we examine, because it does not account for student background characteristics.

We contribute to the existing literature in three ways. First, we provide new evidence of how a change from a value-added model to the CGM would affect teachers. To do so, we examine estimates in a context in which a value-added model is used with high-stakes consequences. Second, whereas earlier studies considered changes in the abstract, we document how changes would affect consequences for teachers in the DCPS IMPACT teacher evaluation system. Finally, by examining how evaluation scores would change for teachers of students with particular characteristics, we provide new evidence on the reasons for the pattern of changes.

1.4 Overview of Findings

The SGP estimates correlate with the value-added estimates at 0.93 in math and 0.91 in reading. Given the knifeblade nature of an evaluation system, however, even highly correlated results can cause some teachers who would be retained as a consequence of their value-added estimate to lose their jobs as a consequence of the SGP-based estimate, or vice versa. Applying the rules of the multiple-measure IMPACT evaluation system to evaluation scores that substitute SGP scores for value-added scores, we found that 14% of teachers would change from one of the four broad performance categories to another as a result of shifting from the value-added model to the CGM. Changes in these categories have important consequences for teachers, ranging from the receipt of performance pay to dismissal.

We also found that, in general, teachers of students with low pretest scores would fare better in the CGM than in a value-added model, but teachers with other types of disadvantaged students would fare worse. In contrast, previous work has found that teachers with many low pretest students received lower SGP-based estimates relative to value-added estimates.

2. IMPACT EVALUATION SYSTEM AND VALUE ADDED IN DC PUBLIC SCHOOLS

2.1 The IMPACT Teacher Evaluation System

In the 2009–2010 school year, DCPS launched IMPACT, a new teacher evaluation system. IMPACT, which placed teachers into one of four performance categories, carried significant consequences. Teachers who performed poorly—in the bottom category for one year or the second-lowest category for two consecutive years—were subject to separation; those in the top category were eligible for additional compensation. As part of its evaluation of teacher effectiveness, IMPACT incorporated value-added estimates.

For the 2010–2011 school year, individual value-added scores constituted 50% of the IMPACT score for general education DCPS teachers who taught math, reading/English language arts (ELA), or both subjects in grades 4–8. The rest of the IMPACT score was calculated by using a point-based formula that included scores from a series of structured classroom observations known as the Teaching and Learning Framework (TLF) (35%), a rating from the principal measuring the teacher's “commitment to the school community” (10%), and the school-level value-added score (5%) (District of Columbia Public Schools 2011).

Based on his or her IMPACT score, a teacher was placed into one of four performance categories that depended on strict cutoffs. Teachers in the lowest category (ineffective) were subject to separation at the end of the year. Those in the second-lowest category (minimally effective) in two consecutive years were also subject to separation. No high-stakes consequences applied to teachers in the third category (effective). Teachers in the highest category (highly effective) were eligible for additional compensation. In the 2010–2011 school year, of the teachers with value-added scores as part of their evaluation, 3% were ineffective, 28% minimally effective, 66% effective, and 3% highly effective.

To incorporate a value-added estimate into a teacher's IMPACT score, DCPS translated value-added estimates into Individual Value Added (IVA) scores based on a formula that gave each teacher a score from 1.0 to 4.0. The formula made a Fahrenheit-to-Celsius–type of translation from the original value-added estimate—measured in terms of DC Comprehensive Assessment System (CAS) test score points—to the 1.0–4.0 scale.⁷ Scores for the other components were also on a scale from 1.0 to 4.0. All components were combined with the IVA score by using weights to form a teacher's overall IMPACT score. For teachers who taught both math and reading/ELA, the two IVA scores were averaged.

2.2 The DCPS Value-Added Model

We estimated teacher value added for math and reading by using data on DCPS students and teachers during the 2010–2011 school year according to the method described in Isenberg and Hock (2011), from which the description below is taken.⁸ To calculate teacher value added, we estimated the following regression by subject: (1) $$\begin{array}{c}\hfill Y_{ig}={\lambda }_g{Y}_{i(g-1)}+{\omega }_g{Z}_{i(g-1)}+{\alpha }^{\text{'}}{X}_{1i}+{\eta }^{\text{'}}{T}_{tig}+{ϵ}_{tig},\end{array}$$(1) where Y_ig is the post-test score for student i in grade g and Y_{i(g − 1)} is the same-subject pretest for student i in grade g-1 during the previous year. The variable Z_{i(g − 1)} denotes the pretest in the opposite subject. Thus, when estimating teacher effectiveness in math, Y_ig and Y_{i(g − 1)} represent math tests, with Z_{i(g − 1)} representing reading tests and vice versa. The pretest scores capture prior inputs into student achievement, and the associated coefficients λ_g and ω_g vary by grade. The vector X_i denotes control variables for individual student background characteristics, specifically, indicators for eligibility for free lunch, eligibility for reduced-price lunch, English language learner status, special education status, and student attendance in the prior year. The coefficients on these characteristics are constrained to be the same across grades.

The vector T_tig contains one indicator variable for each teacher-grade combination. A student contributed one observation to the value-added model for each teacher to whom the student was linked. The contribution was based on a roster confirmation process that enabled teachers to indicate whether and for how long they have taught the students on their administrative rosters and to add any students not listed on their administrative rosters. Students were weighted in the regression according to their dosage, which indicates the amount of time the teacher taught the student.⁹ The vector η includes one coefficient for each teacher-grade combination. Finally, ϵ_tig is the random error term. 

The data contained information on students’ test scores and background characteristics and, importantly for the estimation of value added, enabled students to be linked to their teachers. DCPS students in grades 3 through 8 and in grade 10 took the DC CAS math and reading tests. Our analysis was based on students who were in grades 4 through 8 during the 2010–2011 school year and who had both pre- and post-test scores. To enable us to compare teachers across grades, for the value-added model, we standardized student test scores within subject, year, and grade to have a mean of zero and a common standard deviation. We excluded students who were repeating the grade; therefore, in each grade, we compared only students who completed the same tests. Isenberg and Hock (2011) provide complete details of the data used for the value-added model.

To accommodate a correction for measurement error in the pretest score, the value-added model was estimated in two regression steps. The DCPS model also includes two subsequent steps to adjust estimates for comparability across grades and to account for imprecise estimates.

1. Measurement error correction. Measurement error in the pretest scores will attenuate the estimated relationship between the pre- and post-test scores. We adjusted for measurement error by using an errors-in-variables correction (eivreg in Stata) that relies on published information on the test-retest reliability of the DC CAS. We used an errors-in-variables regression to regress the post-test score on the pretest scores, student background characteristics, and grade and teacher indicators. Because the errors-in-variables regression does not allow standard errors to be clustered by student, we obtained adjusted post-test scores, which subtract the predicted effects of the pretest scores from the post-test scores, the results of which we used to obtain the initial teacher effects in the next step.

2. Main regression. We estimated teacher effects by regressing the adjusted post-test scores from the first step on student background characteristics and teacher-grade indicators, clustering standard errors by student. In this regression, the initial teacher value-added estimates were the coefficients on the teacher indicators, with their variance given by the squared standard errors of the coefficient estimates. The coefficients on prior test scores and background characteristics are shown in Appendix Table B.1.

3. Combine teachers’ estimates across grades. We combined teachers’ estimates into a single value-added estimate when the teacher taught students in several grades. We made teachers’ estimates comparable across grades and then combined them by using a weighted average. To do so, we standardized the estimated regression coefficients within each grade so that the means and standard deviations of their distributions were the same. When combining the standardized estimates, we based the weights on the number of students taught by each teacher to reduce the influence of imprecise estimates obtained from teacher-grade combinations with few students.

4. Empirical Bayes procedure. We used an empirical Bayes procedure as outlined in Morris (1983) to account for imprecise estimates. These “shrinkage” estimates were approximately a precision-weighted average of the teacher's initial estimated effect and the overall mean of all estimated teacher effects. We calculated the standard error for each shrinkage estimate by using the formulas provided by Morris (1983). As a final step, consistent with the decision made by DCPS for IMPACT, we removed from our analysis any teachers with fewer than 15 students and recentered the shrinkage estimates to have a mean of zero.

3. COLORADO GROWTH MODEL

Damian Betebenner (2007) developed the CGM for the Colorado Department of Education (CDE). The CDE and other states and districts use the CGM to provide data on individual student academic growth as well as on school- and district-level performance (CDE 2008).¹⁰ Betebenner et al. (2011) present a rationale for using SGP measures in teachers’ evaluations that are based on multiple measures of effectiveness. The CDE allows local education agencies to use the CGM to measure teacher effectiveness (CDE 2014). Other states have already adopted the CGM to measure teacher effectiveness (Appendix Table A.1). For teachers’ evaluations, some of these states will use student growth percentiles at the school level rather than at the teacher level.

The CGM can be implemented by using a package for the R statistical software program, which its developers freely provide online with documentation. The CGM employs a different approach than a typical value-added model. In the first step, the CGM estimates an SGP for each student (Betebenner 2007). The SGP is a student's academic achievement rank in a given year, grade level, and subject relative to the achievement of other students with the same baseline score or history of scores. Thus, a student with an SGP of 50 is said to perform on the post-test as well as or better than half of the students with the same pretest score (or scores) while a student with an SGP of 90 is said to have exceeded the post-test performance of all but 10% of the students with the same pretest score. The SGPs condition only on students’ prior achievement in the same subject, and do not account for achievement in other subjects or any other student characteristics. The CGM performs the first step through a series of 100 quantile regressions conducted at each percentile of the distribution of student achievement on the post-test.

We calculated SGPs following the approach described in Betebenner (2007). The CGM estimates SGPs for each student by using quantile regression of the post-test on a flexible function of the history of same-subject pretests. The quantile regression provided estimated relationships between the pretests and the post-test for any given quantile of the regression residual. Thus, for any given history of pretest scores, the predicted values from the quantile regression traced out the conditional quantiles of the post-test score. Then, the student's actual post-test was compared to the predicted values conditional on the student's pretest history. The student was assigned the largest quantile for which the student's post-test exceeded the predicted post-test as his or her SGP.

We estimated unweighted quantile regressions separately by grade level and subject. The pretest scores were entered into the model as B-spline cubic basis functions, with knots at the 20th, 40th, 60th, and 80th percentiles. These functions allowed for the relationship between pretests and the post-test to vary across the range of pretest scores. Given the maximum of four test scores available for use in DCPS—three pretests and one post-test—the conditional quantile model can be expressed as (2) $$\begin{array}{ccc}& & Q_{Y_{ig}}\left(q|Y_{i(g-1)},Y_{i(g-2)},Y_{i(g-3)}\right)\hfill \\ & & =\sum _{m=1}^3\sum _{j=1}^3{\beta }_{gmj}\left(q\right){\varphi }_{gmj}\left(Y_{i(g-m)}\right),\hfill \end{array}$$(2) where Y_{i(g − m)} is student i's pretest m grades prior to the post-test Y_ig in grade g. The functions ϕ_gmj for j = 1–3 give the grade- and pretest-specific B-spline cubic basis functions. β_gmj(q) represent the parameters to be estimated in the quantile regression for quantile q, which together with ϕ_gmj, describe the conditional polynomial relationship between each pretest and the post-test for quantile q. The relationship is estimated for each of 100 quantiles in increments of 0.5 between the 0.5th quantile and the 99.5th quantile.

To obtain the SGP for each student, the student's post-test is compared to the array of predicted post-test scores for each of the 100 quantiles $Q_{Y_{ig}}\left(q\right)$ and assigned an SGP of q* such that q* is the largest quantile q for which the student's post-test exceeds the predicted post-test (i.e., $q^{*}=arg{max}_q\left\{Q_{Y_{ig}}\left(q\right)\right\}$ such that $Y_{ig}\ge Q_{Y_{ig}}\left(q\right)$).¹¹ We followed Betebenner (2007) and used the SGP based on the maximum number of pretests available for each student. Thus, the SGP for a student with three pretests (the maximum available for any student in our dataset) was based on the results of a quantile regression that included only students with three observed pretests. However, the SGP for a student with one observed pretest was based on a quantile regression that included all students with at least one pretest, though the regression used only information about the most recent pretest. For students with two observed pretests, the quantile regression included only students with at least two observed pretests and information on the two most recent pretests. 

The quantile regression included only pretests taken in the years immediately prior to the posttest with no gaps and only for students who progressed a single grade level per year during the period with observed pretests. We included all 2010–2011 DCPS students meeting these conditions in the quantile regression regardless of whether they were linked to teachers eligible to receive a value-added estimate. We calculated the CGM evaluation scores only for teachers who received a value-added estimate.

In the second step, the CGM attributes academic growth to teachers as measured by using the SGP. We obtained a measure of teacher effectiveness in DCPS based on the CGM by calculating the median SGP of students linked to the teacher (Colorado Department of Education 2008). Specifically, we combined SGPs into a teacher value-added measure by calculating the dosage-weighted median for all students linked to each teacher. Although most states adopting the CGM plan to use median SGPs, Arizona is using the average SGP (Appendix Table A.1). Thus, we also calculated the dosage-weighted average SGP.

4. WHY EVALUATION SCORES MIGHT CHANGE

The procedure to obtain a measure of teacher effectiveness based on the CGM differs from the procedure we used to estimate teacher value added on several dimensions. These differences could affect which teachers achieve the largest changes between the CGM and the value-added model used in DCPS. The first two factors suggest that the CGM may penalize teachers of disadvantaged students, but other factors could work in other directions. It is thus an empirical question of which effect dominates. Although we discuss these factors here to provide important context for our results, we did not attempt to distinguish the contributions of the role of these various factors in this study because the number of DCPS teachers in the single year of data available to us for this analysis is too small to convincingly do so.

First, given that the CGM does not account for student background characteristics, an evaluation system that uses the CGM as its measure of teacher effectiveness in place of a value-added model may penalize teachers who teach many disadvantaged students. Unlike the value-added model, the CGM does not include information on students’ opposite subject pretests or any student background characteristics other than same-subject pretest scores. The CGM includes additional years of pretest scores for students when these earlier scores are available, and allows for more flexibility in how current scores depend on prior scores. The additional information and flexibility may, in part, compensate for the CGM's exclusion of other observable characteristics.

Second, whereas our value-added model accounts for measurement error in the pretests by using an errors-in-variables technique (Buonaccorsi 2010) that is applied in many of the value-added models used for teacher evaluation, the CGM does not apply a similar correction. The errors-in-variables correction produces a steeper relationship between pretests and achievement than that obtained from a model with no adjustment. The result of accounting for measurement error in value-added models is a lower level of predicted achievement for a student with relatively low pretest scores, thereby raising the measured contribution of the student's teacher to his or her posttest score. Thus, the correction may help teachers of students with lower pretest scores. The CGM does not provide for a similar correction and therefore may reduce the evaluation scores of teachers of low pretest students relative to the evaluation scores they would have achieved in a value-added model, although the precise consequences of measurement error for SGP estimates are unknown.¹²

However, a third factor—the lack of teacher fixed effects—could work in the opposite direction. Given that the value-added model includes teacher fixed effects (binary indicators for each teacher-grade combination in the analysis file), the adjustment for prior achievement is based on comparisons of students with higher and lower levels of prior achievement who were taught by the same teacher. Holding teacher quality constant, the comparisons can identify the degree to which prior achievement affects current achievement. The exclusion of such fixed effects, as in the case of the CGM, means that the adjustment for prior achievement is based in part on comparisons of students with different teachers. Thus, the CGM risks confounding the structural relationship between pretest scores and achievement—one that is based on how much students learn during the year with an average teacher—with the way in which teachers are matched to students. For example, take the case of more effective teachers teaching at schools with higher-achieving students.¹³ In this example, even if students retained no knowledge from year to year such that there was no structural relationship between pretest scores and achievement, pretest scores and effective teaching would be positively correlated. Thus, the SGP for a student with a low pretest score would reflect both the lower average effectiveness of teachers of similar students and the lower predicted achievement for the student. As a result, teachers of students with low pretest scores would receive higher scores under the CGM than under the value-added model.    

A fourth factor—the lack of an empirical Bayes shrinkage technique—could push teachers of disadvantaged students to both extremes. Like many other value-added models used by states or districts, the DCPS value-added model uses empirical Bayes shrinkage to address imprecise value added-estimates (McCaffrey et al. 2003). A value-added estimate for a teacher with relatively few students will tend to be less precise because there is less information about the teacher's contribution to student achievement. Additionally, some students have harder-to-predict test scores because their characteristics are imprecisely measured or performance of students with the same characteristic is varied. For example, the level of poverty among students who are eligible for subsidized meals may vary substantially, but that variation is not directly measured by the characteristics included in the value-added model. Students who are disadvantaged will have test scores that are less precisely predicted by a value-added model, and teachers of these students will also tend to have less precise estimates (Herrmann et al. 2013).

Finally, for teachers linked to students in multiple grade levels, the CGM makes no distinction between SGPs of students in different grades when calculating the median SGPs, though it is possible that the quantile regression approach may make the multiple-grade issue less of a concern than it would be for a more typical value-added model.¹⁴ 

Table 1 Comparison levels for teachers of students with high and low levels of disadvantage

	Math		Reading
	Low	High	Low	High
Characteristic	level	level	level	level
Pretest score (same-subject)	0.72	−0.63	0.68	−0.62
English language learner	0.0%	33.0%	0.0%	25.5%
Learning disability	0.0%	20.9%	0.0%	20.7%
Eligible for free or reduced-price lunch	23.4%	96.1%	22.6%	96.2%

Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE).NOTE: The high level of disadvantage is the 90th percentile of the average student characteristic at the teacher level, and the low level is the 10th percentile. The percentiles are reversed for the pretest score. The table is based on teacher-level averages of student characteristics for the 334 math teachers and 340 reading/ELA teachers in grades 4 through 8 with value-added estimates.

Other differences in the production of CGM measures compared to measures produced by a value-added model could affect the distribution of changes. As recommended by Betebenner (2007), we calculate SGPs that account for as many as three prior same-subject test scores for each student, whereas the value-added model used one prior same-subject test score and one prior opposite-subject test score.¹⁵ Also, unlike the value-added model, the CGM does not standardize estimates by grade level, which could also affect which teachers have larger changes.¹⁶

5. METHODS AND DATA

We estimated value added and median growth percentiles for the 334 math teachers and 340 reading/ELA teachers in grades 4 through 8 who taught at least 15 eligible students during the 2010–2011 school year, the threshold used by DCPS to determine eligibility to receive a value-added estimate as part of the evaluation. We then compared the two sets of evaluation scores in four ways. First, we calculated correlations between value added and median growth percentiles for math and reading estimates. Second, we scaled both sets of scores to have a standard deviation of one and a mean of zero and calculated the average absolute difference in standard deviations of teacher value-added estimates for math and reading. Third, we transformed both sets of scores into percentile ranks and calculated percentiles of absolute changes in ranks between the two sets of scores for math and reading. Finally, we calculated the proportion of teachers who would change IMPACT effectiveness categories if value-added estimates were replaced with median growth percentiles. To do so, we converted both sets of evaluation scores into the IVA evaluation component and calculated two sets of IMPACT scores. We scaled the median growth percentiles to have the same standard deviation and mean as the value-added scores before converting to IVA so that the same conversion method could be applied to both sets of scores.¹⁷

To make comparisons of the effect of switching from value added to the CGM, we examined how teachers with “many” and “few” disadvantaged students would fare under both models. We defined a teacher as teaching many disadvantaged students by calculating the percentage of students with a given characteristic for all teachers and then finding the percentage of students that corresponded to a teacher at the 90th percentile of the distribution of teachers. Similarly, we defined a teacher as teaching few disadvantaged students at the 10th percentile. In Table 1, we present the summary statistics for the teachers in our math and reading samples. For example, math teachers with 96.1% of FRL-eligible students were at the 90th percentile of the distribution of teachers in terms of the proportion of such students in teachers’ classrooms. Teachers at the 10th percentile of the distribution had 23.4% of their students FRL-eligible. For reading/ELA teachers, the percentiles were similar. Pretest scores were measured in standard deviations of student achievement, which we adjusted to be constant across grades.

Using regression analysis, we calculated the effect of replacing value-added estimates with median growth percentiles for teachers of students with high and low levels of disadvantage. We calculated the difference between the two evaluation scores (in standard deviations of teacher value added) for each teacher and used that as the dependent variable in a teacher-level regression.¹⁸ The explanatory variables were the proportion of each teacher's students with the characteristics in Table 1. We included these characteristics individually in separate regressions and simultaneously in one regression.¹⁹ We then scaled the regression coefficients to reflect the effect of moving from the low level of disadvantage to the high level indicated in Table 1. Doing so produced a “difference-in-differences” style estimate of the difference in evaluation scores for a teacher with more disadvantaged students relative to a teacher with fewer disadvantaged students. We estimated separate regressions for math and reading.²⁰

6. RESULTS

6.1 Magnitude of Differences

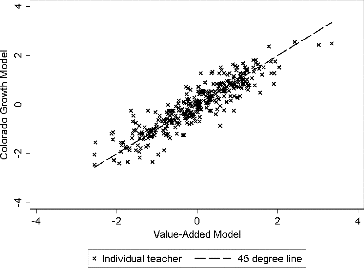
We found substantive differences between evaluation scores based on the CGM and the value-added model. The evaluation scores were correlated at 0.93 for math and 0.91 for reading (Table 2, row 1). The level of correlation might suggest a high degree of similarity, but even high correlations can obscure substantive differences in estimates for individual teachers. As seen in Figure 1, the changes are substantial for many teachers. A scatterplot for reading evaluation scores is similar (Appendix Figure C.1). We find that the average teachers’ estimates differ by 0.29 standard deviations of teacher value added in math and 0.33 standard deviations in reading (row 2).

As an alternative approach, we compared the percentile ranks of teachers under the two models and found evidence of some substantial differences. We show the magnitude of the changes by comparing percentile ranks in Table 2, rows 3 through 5. We found that the median math and reading/ELA teacher moved 6 percentiles in the distribution of effectiveness. Five percent of teachers moved at least 22 percentiles in the distribution for math and 25 percentiles in reading. However, because of the concentration of teachers around the average evaluation score, teachers who are close to the average can move a large number of percentiles in response to only a small change in evaluation scores.

Table 2 How much evaluation scores change when using median student growth percentiles in place of value added

	Math	Reading	Combined
Changes in evaluation component scores
Correlation between value added and student growth percentiles	0.93	0.91	—
Average absolute change in estimates (standard deviations of teacher value added)	0.29	0.33	—
Median absolute change in percentile rank	6	6	—
95th percentile absolute change in percentile rank	22	25	—
Percentage of teachers who change IMPACT effectiveness categories
Using 50% weight on the value-added component score	—	—	14.2
Using 35% weight on the value-added component score	—	—	8.7

Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE).NOTE: Correlation is calculated as a Pearson correlation.

Figure 1 Student growth percentile and value-added evaluation scores in math. Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE). Notes: The figure includes data for the 334 math teachers in grades 4 through 8 with value-added estimates. The two sets of evaluation scores are scaled to have a mean of zero and a standard deviation of one.

In addition to examining changes to the component scores, we also examined how replacing value-added estimates with median growth percentiles would change teacher IMPACT scores, which incorporate the other evaluation components. As a result of changes to the value-added component score, 14.2% of teachers would change IMPACT performance categories, with a different evaluation consequence as a result (second to last row of Table 2). All of these teachers who changed IMPACT performance categories transitioned to a neighboring category. We show these transitions in Appendix Table C.1. For example, of the 53 highly effective DCPS teachers, 8 transitioned to the effective category when replacing value added with SGPs.²¹ For the 2011–2012 school year, DCPS reduced the weight given to value added in the calculation of IMPACT scores from 50% to 35%. Using this lower weight, 8.7% of teachers would have changed IMPACT performance categories when replacing value-added estimates with median growth percentiles (last row of Table 2).²²

6.2 Distribution of Differences

Teachers of students with low pretest scores would earn higher evaluation scores based on the CGM relative to the value-added model, whereas teachers with more disadvantaged students in some other categories would earn lower evaluation scores. As shown in the first row of Table 3, teachers of students with low pretest scores have lower value-added results in math by −0.57 standard deviations relative to teachers of students with high pretest scores, but this difference is just −0.42 standard deviations for median growth percentiles. Consequently, teachers of students with low pretest scores would gain 0.16 standard deviations of teacher value added in math relative to teachers of students with high pretest scores when replacing value-added estimates with median growth percentiles. Similarly, teachers of students with low pretest scores would gain 0.17 standard deviations in reading (first row of Panel B of Table 3). However, teachers with more English language learners would earn lower evaluation scores under the CGM than under the value-added model—by 0.16 standard deviations in reading and 0.10 standard deviations in math. Differences for teachers with many special education students and those with many FRL-eligible students are smaller in magnitude and not statistically significant.

Table 3 How evaluation scores change for teachers of disadvantaged students when using growth percentiles in place of value added

	Difference in estimates for more disadvantaged versus advantaged classrooms (standard deviations of teacher value added)
			Change when replacing value
Measure of student disadvantage	Value added	Median SGPs	added with SGPs (difference-in-differences)
Panel A: Math
Pretest score (same subject)	−0.57	−0.42	0.16* (0.06)
English language learner	0.71	0.56	−0.16* (0.06)
Learning disability	−0.08	−0.17	−0.09 (0.09)
Eligible for free or reduced-price lunch	−0.76	−0.69	0.06 (0.06)
Panel B: Reading
Pretest score (same subject)	−0.97	−0.80	0.17* (0.08)
English language learner	0.43	0.33	−0.10* (0.05)
Learning disability	−0.34	−0.39	−0.04 (0.04)
Eligible for free or reduced-price lunch	−1.00	−0.92	0.08 (0.07)

Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE).NOTE: The reported estimates give the average difference in evaluation scores for a teacher with more disadvantaged students relative to a teacher with fewer disadvantaged students. The change when switching from a value-added model to the CGM in the last column is the difference between the estimates in the first two columns. The high level of disadvantage is the 90th percentile of the indicated characteristic; the low level is the 10th percentile. The percentiles are reversed for the pretest score. The high and low levels of disadvantage are those in Table 1. The regression results are not adjusted to account for other characteristics of students included in the value-added model. In the first two columns, a positive number indicates that a teacher with more disadvantaged students receives higher evaluation scores. In the last column, a positive number indicates that a teacher with more disadvantaged students would receive higher evaluation scores from the CGM relative to the value-added model compared to a teacher with fewer disadvantaged students. Standard errors in parentheses.*Statistically significant at the 5% level.

The results in Table 3 show how, on average, the changes are related to the listed student characteristics. They do not, however, describe the marginal change in evaluation scores associated with each characteristic, holding other characteristics constant. For example, the results do not distinguish between differences in results for two teachers with low-achieving students when only one teacher's students are also FRL-eligible. In Table 4, we report on the marginal differences.²³

The results that adjust for other covariates to obtain marginal changes show larger differences across the two models. Under the CGM, teachers of students with low pretest scores score 0.41 standard deviations better in math and 0.44 standard deviations better in reading compared to teachers of students with high pretest scores. All else equal, reading/ELA teachers who taught more students with learning disabilities would earn lower evaluation scores under the CGM than under a value-added model by 0.16 standard deviations, and those with more FRL-eligible students would earn lower evaluation scores by 0.21 standard deviations. In math, marginal differences associated with teaching special education students or FRL-eligible students were not statistically significant. For both math and reading, differences for teachers with many English language learners were similar in the cases of both adjustments and no adjustments.

Teachers of students with low pretest scores would generally benefit from a change to the CGM if the levels of other student characteristics in their classes were the same as those among teachers of students with high pretest scores (Table 4). Given, however, that teachers with low pretest scores tended to have more disadvantaged classrooms as measured by other characteristics, the unadjusted results for pretest scores were far more modest (Table 3).²⁴ If the overlap in categories were perfect, then accounting for student background characteristics in a value-added model would be unnecessary if the model already accounted for pretest scores. The overlap in categories of disadvantage are far from perfect, however, which is one reason for the extent of the differences we found between measures of teacher effectiveness from the CGM compared to the value-added model.

Table 4 How evaluation scores change for teachers of disadvantaged students when using growth percentiles in place of value added, adjusting for other student characteristics

	Difference in estimates for more disadvantaged versus advantaged classrooms when replacing value added with SGPs (standard deviations of teacher value added)
Measure of student disadvantage	Math	Reading
Pretest score (same subject)	0.41* (0.13)	0.44* (0.18)
English language learner	−0.15* (0.06)	−0.10* (0.05)
Learning disability	−0.12 (0.08)	−0.16* (0.05)
Eligible for free or reduced-price lunch	−0.03 (0.10)	−0.21* (0.11)

Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE).NOTE: The reported estimates give the average difference in evaluation scores for a teacher with more disadvantaged students relative to a teacher with fewer disadvantaged students when switching from a value-added model to the CGM. The high level of disadvantage is the 90th percentile of the indicated characteristic; the low level is the 10th percentile. The percentiles are reversed for the pretest score. The high and low levels of disadvantage are those in Table 1. The regression results are adjusted to account for other characteristics of students included in the value-added model. A positive number indicates that a teacher with more disadvantaged students would receive higher evaluation scores from the CGM relative to the value-added model compared to a teacher with fewer disadvantaged students. Standard errors in parenthesis.*Statistically significant at the 5% level.

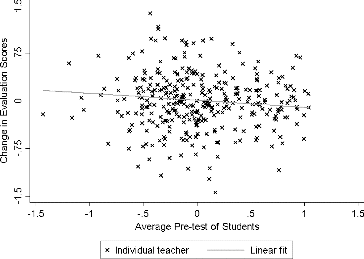
Even though some of the relationships reported in Tables 3 and 4 were statistically significant, the characteristics of teachers’ students cannot explain most changes between estimates generated from the value-added model and the CGM. For example, the R-squared is 0.03 for the regression of changes on average pretest scores. The limited role of pretest scores in explaining changes is also evident in Figure 2. For this figure, we converted teacher evaluation estimates from both the value-added model and the CGM to the number of standard deviations from the mean estimate, and then subtracted the value-added measure from the CGM measure. Figure 2 plots changes in math evaluation scores from replacing value-added estimates with median growth percentiles against the average achievement of teachers’ students on the math pretest. Positive changes on the vertical axis indicate higher scores in the CGM relative to the value-added model. The trend line is based on the relationship in Table 3, row 4. Even though the trend is statistically significant, most changes are substantially above or below the trend. (The same plot for reading is in Appendix Figure C.2.) Even with all characteristics of teachers’ students included simultaneously to explain the changes, the R-squared increases only to 0.10. Thus, teachers may be more likely to change effectiveness categories if they teach students with certain characteristics, but most changes are unrelated to these characteristics.

Figure 2 Change in math evaluation scores when using student growth percentiles in place of value added, by average achievement of teachers’ students. Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE). Notes: The figure includes data for the 334 math teachers in grades 4 through 8 with value-added estimates. The change is reported in standard deviations of teacher value added. A positive change indicates that the teacher would receive higher evaluation scores from the CGM relative to the value-added model.

7. DISCUSSION

7.1. Interpretation of Findings

Two main findings from this study are consistent with previous research. First, we found evidence of substantial differences between measures of teacher effectiveness based on the CGM compared to a value-added model. These differences would have resulted in 14% of teachers receiving different consequences under the DCPS evaluation system. Second, even though some changes were related to the background characteristics of teachers’ students, most teachers’ evaluation scores changed for other reasons. The exclusion of students’ background characteristics from the CGM may be the most visible difference between the two approaches, but it is not the only reason that the two sets of evaluation scores differ. Although we cannot pinpoint these other reasons with our current dataset that includes only one year of evaluation scores, they could include the absence of measurement error correction in the CGM, the absence of shrinkage in the CGM, the use of teacher fixed effects in the value-added model, differences in how the two approaches compare results for teachers of students in different grades, and/or other differences between the two approaches.

Our findings that the CGM provides a relative benefit to teachers with lower-achieving students (but not for other measures of student disadvantage) stands in contrast to the findings of Goldhaber et al. (2012) and Wright (2010). However, our data from one year and one district are not sufficient to identify specific reasons for these different findings. In addition to differences in the value-added models used for these analyses—for example, Wright (2010) did not include student background characteristics besides pretest scores, and Goldhaber et al. (2012) did not account for measurement error in pretest scores—other factors could affect the results, such as differences in the degree to which effective teachers are sorted to schools with more disadvantaged students in each study district. Furthermore, although statistically significant, it is possible that the differences between our results and previous research are a result of statistical noise and would not be replicated using a different cohort of teachers in DCPS. Additional investigation using data from multiple districts and larger sample of teachers could shed light on the reasons for the differences in our results from previous research.

7.2 Consequences for Use in Evaluation

Aside from differences in outcomes for teachers with different types of students, use of the CGM in place of a value-added model may have different consequences in a policy environment.

First, some policymakers appear to believe that the CGM is more transparent to teachers than a value-added model, but the CGM's transparency may be more perceived than real. The SGP as a measure of student academic growth is appealing because it combines the key feature of a value-added model—accounting for a student's level of performance at baseline—with percentiles, a familiar metric for reporting test scores. However, percentiles of test score levels may be familiar to many teachers, but percentiles of test score growth are unlikely to be familiar to many teachers. Thus, CGM results have to be carefully communicated to teachers. Another potential benefit of the CGM in terms of transparency is its perceived simplicity, which is in part a function of not accounting for student background characteristics other than same-subject pretest scores. A third benefit is that adopting the CGM allows districts to sidestep a potentially charged discussion of which student characteristics to account for. A value-added model typically accounts for several background characteristics and prior achievement in multiple subjects. Finally, it is not clear whether the method of quantile regression used to calculate SGPs has any transparency benefit relative to a value-added model.

Second, as teachers come to understand the metric by which they are evaluated, they will likely respond to a different set of incentives under the CGM compared to a value-added model. One difference is that a value-added model implicitly depends on the mean performance of a teacher's students, but the CGM depends on students’ median performance. On the one hand, the median is robust to outliers; thus, for example, a stray unmotivated student who randomly fills in the bubbles on the test does not harm teachers. However, given that only the student at the median student growth percentile would matter for a teacher's CGM-based evaluation score, the teacher would have no incentive to attend to struggling students and the highest performing students because their student growth percentiles do not affect the median growth percentile for a teacher. Of course, an easy alternative would call for adapting the CGM by using the average growth percentile of a teacher's students rather than the median growth percentile, as Arizona is doing. Using historical DCPS data, we verified that the two approaches yield highly correlated results and produce similar results (Appendix Tables C.2 and C.3).²⁵ However, the results may diverge in practice if the median were used and incentivized teachers to change their behavior accordingly. 

A second incentive problem, less easily rectified, is that teachers may seek to avoid teaching at schools whose students have background characteristics associated with lower SGPs.²⁶ Adapting the CGM to account for student characteristics might eliminate these incentives, but it might also eliminate the CGM's perceived transparency benefits.

8. CONCLUSION

We found evidence of substantial differences between measures of teacher effectiveness based on the CGM compared to a value-added model. We quantified the magnitude of the change by substituting CGM-based teacher evaluation scores for value-added estimates for DCPS teachers in the 2010–2011 school year. This would have resulted in 14% of teachers receiving different consequences under the DCPS evaluation system. The consequences ranged from receiving performance pay to dismissal. Even though some changes were related to the background characteristics of teachers’ students, most teachers’ evaluation scores changed for other reasons. In sum, it is likely to make a difference for a sizable share of teachers whether a state or district chooses to evaluate its teachers by using a value-added model or the CGM.

Our findings do not conclusively indicate bias in the CGM, but we found that reliance on the CGM in place of a value-added model would have depressed the evaluation scores for teachers with more English language learners and raised scores for teachers with more low-achieving students based on one year of teacher-student linked data from DCPS. Although the CGM may offer some advantages relative to the value-added models used by states and districts—invariance to test score scales and more flexibility in the adjustments for pretest scores, for example—it is also a flawed measure of teacher effectiveness because it excludes important features of value-added models that are widely thought to reduce bias. Its design also raises concerns about teacher incentives associated with the avoidance of teaching assignments that involve certain types of students (such as special education students) or the tendency to devote attention to students who are more likely to influence performance outcomes based on the CGM—those students for whom a teacher expects to see growth near the median growth percentile. States or school districts considering the adoption of the CGM for teacher evaluation systems should consider whether these concerns can be resolved and whether the potential validity and incentive benefits of a value-added model can offset any perceived loss in transparency.

Additional information

Notes on contributors

Elias Walsh

Elias Walsh is Researcher, Mathematica Policy Research, Madison, WI (E-mail: [email protected]). Eric Isenberg is Senior Researcher, Mathematica Policy Research, 111 East Wacker Drive, Suite 920, Chicago, 60601, IL (E-mail: [email protected]).

Eric Isenberg

Elias Walsh is Researcher, Mathematica Policy Research, Madison, WI (E-mail: [email protected]). Eric Isenberg is Senior Researcher, Mathematica Policy Research, 111 East Wacker Drive, Suite 920, Chicago, 60601, IL (E-mail: [email protected]).

Notes

In Appendix Table A.1, we provide a complete list of states that use or plan to use the CGM in teacher evaluation systems.

We use the term “Colorado Growth Model,” the original name for this methodology, which was developed for the Colorado Department of Education. As its use has spread, some states refer to this model by replacing “Colorado” with their own states’ name or just call it the “growth model.” It is also known as the student growth percentile, or SGP, model.

The Hawaii Department of Education document states that “while theoretically possible to account for other factors that can impact growth or performance, doing so would make the model impossible to interpret in a reasonable manner. The Hawaii Growth Model's purpose is to provide an easy to understand, transparent, and credible growth metric.”

For this discussion of bias, we have assumed that evaluation scores based on the two models are both intended to measure the same dimension of teacher effectiveness.

However, growing evidence suggests that some value-added models provide measures of teacher effectiveness with small bias (Kane and Staiger 2008; Kane et al. 2013; Chetty et al. 2014).

In addition to features designed to reduce bias, the empirical Bayes shrinkage procedure induces some bias in teachers’ value-added estimates to reduce the risk that teachers, particularly those with relatively few students, will receive a very high or very low effectiveness measure by chance. Instead of producing unbiased estimates, shrinkage seeks to minimize the mean squared error of the value-added estimates.

The translation method used in the analysis differs slightly from the one used by DCPS in the 2010–2011 school year. It is more similar to the method used in the 2011–2012 to 2013–2014 school years.

Although the value-added model used by DCPS has since incorporated several changes, our analysis is based on the value-added model used during the 2010–2011 school year.

To estimate the effectiveness of teachers who share students, we used a technique called the full roster method, which attributed equal credit to teachers of shared students. Following this method, each student contributed one observation to the value-added model for each teacher to whom he or she was linked, with students weighted according to the dosage they contributed (Hock and Isenberg 2012).

The District of Columbia Public Charter School Board used the CGM as a component of its school performance reports (Office of the State Superintendent of the District of Columbia Public Schools 2011).

We use version 7.0 of the Student Growth Percentile package for R statistical software (Betebenner 2007) to implement the quantile regression and obtain SGPs.

The CGM estimates a flexible relationship between pretest scores and achievement, which could contribute to the magnitude of this difference because the relationship between pretests and achievement is typically flatter for high- and low-scoring students than for students in the middle of the distribution of pretest scores. However, the effect that measurement error in pre- and post-tests has on SGP estimates is not well understood, in part because the CGM uses quantile regression. Thus, the direction and magnitude of potential bias in the CGM from measurement error is unknown.

Recent work has found that, on average, disadvantaged students may be less likely to be taught by the most effective teachers, though the differences are small and depend on the districts or grade levels studied (Glazerman and Max 2011; Isenberg et al. 2013, Mansfield 2012; Sass et al. 2012).

The SGP estimates do not depend on the scale of the assessment (Briggs and Betebenner 2009).

As a sensitivity test, we also compared evaluation scores based on the CGM by using only a single year of prior same-subject test scores. Results were similar to those from the CGM that used three pretests (Appendix Table C.3).

Although the student-level SGPs have similar levels of dispersion across grades because they do not depend on the scale of the assessments, the amount of dispersion in median or average SGPs at the teacher level can vary across grades. As is the case for the value-added estimates, differences in the amount of dispersion can arise if the test better measures the contributions of teachers or if there is more dispersion in teacher effectiveness in some grades.

We used a conversion method that differs from the method used by DCPS in the 2010–2011 school year. Under our method, the mean value-added estimate was mapped to 2.5; the scores were spread out such that the lowest-scoring 10% of teachers would receive a score of 1.0 and the highest-scoring 10% of teachers would receive an estimate of 4.0 if the estimates had a normal distribution.

We calculated standard errors robust to heteroscedasticity. We weighted observations based on the number of students contributing to the teacher's value-added estimate.

In the regression that included all characteristics simultaneously, we also included the average prior attendance and the average opposite-subject pretest score of teachers’ students because the value-added model also accounted for these characteristics.

The linear regression specification will not properly measure the full effect of replacing value added with median growth percentiles if not shrinking or other differences in the two approaches push teachers of disadvantaged students into both extremes. To address this concern, we also examined whether teachers of disadvantaged students were more likely to have evaluation scores in either or both extremes. We do not report results of this analysis because our sample of teachers was not large enough to make the findings informative.

Transitions were somewhat more likely for less effective teachers. Whereas minimally effective and ineffective teachers represent 35 percent of all DCPS teachers, they represent 42 percent of transitions. However, this difference was not statistically significant.

Changes resulting from replacing value added with average student growth percentiles were slightly smaller (Appendix Table C.2).

This analysis is possible because there is substantial variation in prior achievement within each measure of student disadvantage. Of the pairwise correlations between these characteristics, only the correlation between pretests and special education status exceeds 0.3.

The results in Tables 3 and 4 are consistent with positive correlations between the categories of student disadvantage.

Castellano and Ho (2012) compared mean and median SGP results for schools and found a root mean squared error of four percentiles.

Similarly, teachers may seek to avoid teaching students with high pretest scores if teaching such students is associated with lower evaluation scores, as in our results from DCPS. This incentive is possible even though teachers of students with high pretest scores receive higher evaluation scores on average under both approaches, because the value-added model (if unbiased) provides estimates of teacher effectiveness that do not depend on school or classroom assignments. However, the avoidance of such assignments may require more information about the consequences of using the CGM to measure teacher effectiveness than is likely available to most teachers.

²⁷The value-added model we estimated also accounts for a prior opposite-subject test score.

APPENDIX A

WHERE THE COLORADO GROWTH MODEL IS USED

Table A.1 States using student growth percentiles in teacher evaluations

State	Level of aggregation	First school year for evaluations
Arizona	Teacher	2013–2014
Arkansas	Teacher	2014–2015
Colorado	Local decision	2013–2014
Georgia	Teacher	2012–2013
Hawaii	Teacher	2014–2015
Indiana	Teacher	2012–2013
Kentucky	Teacher	2014–2015
Massachusetts	Teacher	2013–2014 (some schools started in 2011–2012)
Mississippi	Teacher	2014–2015
New Hampshire	Grades within schools	2013–2014
New Jersey	Teacher	2013–2014
Rhode Island	Teacher	2014–2015
Virginia	Local decision	2012–2013
Washington	Teacher	2016–2017
West Virginia	School	2013–2014
Wyoming	Local decision	2015–2016

Source: State education agency websites.NOTE: The first school year for evaluations is a no-stakes pilot year for some states. Arizona uses average SGPs in evaluations, whereas all other states use or plan to use median SGPs. The three states marked as “local decision” allow local education agencies to decide the level of aggregation.

APPENDIX B

RELATIONSHIPS BETWEEN STUDENT CHARACTERISTICS AND ACHIEVEMENT FROM THE VALUE-ADDED MODEL

We present the estimated relationships between student characteristics and achievement from the math and reading value-added models Table B.1.

Table B.1 Relationships between student characteristics and achievement from the value-added model, by subject

Characteristic	Math	Reading
English language learner	0.47 (0.36)	−0.47 (0.35)
Specific learning disability	−1.13 (0.39)	−3.16 (0.37)
Other learning disability	−1.63 (0.47)	−2.29 (0.42)
Eligible for free lunch	−1.25 (0.23)	−1.28 (0.21)
Eligible for reduced-price lunch	−0.94 (0.39)	−0.85 (0.36)
Fraction of the prior year student attended school	7.07 (2.23)	0.66 (1.83)
Pretest score (same-subject)	0.65 (0.02)	0.62 (0.02)
Pretest score (opposite-subject)	0.15 (0.03)	0.14 (0.02)

Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE).NOTE: Standard errors are in parentheses. Coefficients and standard errors are reported in units scaled to correspond to the scale of the DC CAS assessments. A standard deviation of student achievement in these units is 17.7 points in math and 16.1 points in reading. The reported coefficient estimates of pretest scores represent averages of the coefficients estimated separately for each grade. The associated standard errors similarly represent averages across grades. These numbers are presented for descriptive purposes only.

APPENDIX C

ADDITIONAL RESULTS

Teachers moved by at most one effectiveness category when replacing value added with median SGPs, and less effective teachers were somewhat more likely to change categories. Whereas minimally effective and ineffective teachers represent 35% of all DCPS teachers, they represent 42% of transitions. However, this difference was not statistically significant. We describe how teachers transitioned between effectiveness categories in Table C.1.

 

 

Table C.1 Number of teachers by IMPACT effectiveness rating and effectiveness rating based on median student growth percentiles

	IMPACT effectiveness rating (based on value added)
Effectiveness rating
based on median
student growth	Highly		Minimally
percentiles	effective	Effective	effective	Ineffective
Highly effective	45	10	0	0
Effective	8	220	18	0
Minimally effective	0	21	117	7
Ineffective	0	0	3	22

Source: Mathematica calculations based on DCPS data.NOTE: The method of converting value-added estimates to IVA scores used in the analysis differs slightly from the one used by DCPS in the 2010–2011 school year. It is more similar to the method used in the school years 2011–2012 to 2013–2014. Because some districts are considering using average SGPs instead of median SGPs, we also examined differences between the value-added estimates and average SGPs. The changes in evaluation scores when replacing value-added estimates with average SGPs are smaller than those when using median SGPs (Table C.2.). With one exception, the changes are also less related to measures of student disadvantage with using average SGPs; teachers of students with more learning disabled students receive lower evaluation scores when replacing value added with average SGPs (Panel A of Table C.3). In another sensitivity analysis, we estimated a version of the CGM that—as in the value-added model we estimated—accounts for only one prior same-subject test score.²⁷ We found no substantial change in the results; the correlation in estimates of teacher effectiveness across models was 0.99 for both math and reading. We also compared results from the one-prior-test-score CGM to the value-added model and found that they were similar to the comparison of the three-prior-test-score CGM to the value-added model (Panel B of Table C.3). Finally, we presented some of our main results only for math. In Figures C.1 and C.2, we present results for reading. The results for reading are similar to the results for math.

Table C.2 How much evaluation scores change when using average student growth percentiles in place of value added

	Math	Reading	Combined
Changes in Evaluation Component Scores
Correlation between value added and student growth percentiles	0.96	0.95	—
Average absolute change in estimates (standard deviations of teacher value added)	0.21	0.23	—
Median absolute change in percentile rank	4	5	—
95th percentile absolute change in percentile rank	16	19	—
Percentage of Teachers Who Change IMPACT Effectiveness Categories
Using 50% weight on the value-added component score	—	—	11.5
Using 35% weight on the value-added component score	—	—	6.8

Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE).NOTE: Correlation is calculated as a Pearson correlation.

Table C.3 How evaluation scores change for teachers of disadvantaged students when using alternative growth percentile measures in place of value added

	Difference in estimates for more disadvantaged versus advantaged classrooms when replacing value added with SGPs (standard deviations of teacher value added)
Measure of student disadvantage	Math	Reading
Panel A: Average student growth percentile, accounting for up to three prior test scores
Pretest score (same-subject)	0.07 (0.05)	0.12 (0.07)
English language learner	−0.11* (0.05)	−0.06 (0.04)
Learning disability	−0.14* (0.06)	−0.09* (0.03)
Eligible for free or reduced-price lunch	−0.03 (0.05)	0.03 (0.06)
Panel B: Median student growth percentile, accounting for one prior test score
Pretest score (same subject)	0.23* (0.06)	0.17* (0.07)
English language learner	−0.12* (0.06)	−0.10* (0.05)
Learning disability	−0.07 (0.09)	−0.04 (0.04)
Eligible for free or reduced-price lunch	0.12 (0.06)	0.08 (0.06)

Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE).NOTE: The reported estimates give the average difference in evaluation scores for a teacher with more disadvantaged students relative to a teacher with fewer disadvantaged students when switching from a value-added model to the CGM. The high level of disadvantage is the 90th percentile of the indicated characteristic; the low level is the 10th percentile. The percentiles are reversed for the pretest score. The high and low levels of disadvantage are those in Table 1. These regression results are not adjusted to account for other characteristics of students included in the value-added model. A positive number indicates that a teacher with more disadvantaged students would receive higher evaluation scores from the CGM relative to the value-added model compared to a teacher with fewer disadvantaged students. Standard errors in parentheses.*Statistically significant at the 5% level.

Figure 1 Student growth percentile and value-added evaluation scores in reading. Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE). Notes: The figure includes data for the 340 reading/ELA teachers in grades 4 through 8 with value-added estimates. The two sets of evaluation scores are scaled to have a mean of zero and a standard deviation of one.

Figure 2 Change in reading evaluation scores when using student growth percentiles in place of value added, by average achievement of teachers’ students. Source: Administrative data from DCPS and the Office of the State Superintendent of Education of the District of Columbia (OSSE). Notes: The figure includes data for the 340 reading/ELA teachers in grades 4 through 8 with value-added estimates. The change is reported in standard deviations of teacher value added. A positive change indicates that the teacher would receive higher evaluation scores from the CGM relative to the value-added model.