On the Distribution of Worker Productivity: The Case of Teacher Effectiveness and Student Achievement

ABSTRACT

It is common to assume that worker productivity is normally distributed, but this assumption is rarely, if ever, tested. We estimate the distribution of worker productivity, where individual productivity is measured with error, using the productivity of teachers as an example. We employ a nonparametric density estimator that explicitly accounts for measurement error using data from the Tennessee STAR experiment, and longitudinal data from North Carolina and Washington. Statistical tests show that the productivity distribution of teachers is not Gaussian, but the differences from the normal distribution tend to be small. Our findings confirm the existing empirical evidence that the differences in the effects of individual teachers on student achievement are large and the assumption that the differences in the upper and lower tails of the teacher performance distribution are far larger than in the middle of the distribution. Specifically, a 10 percentile point movement for teachers at the top (90th) or bottom (10th) deciles of the distribution is estimated to move student achievement by 8–17 student percentile ranks, as compared to a change of 2–7 student percentile ranks for a 10 percentile change in teacher productivity in the middle of the distribution.

KEYWORDS:

• Education
• Measurement error
• Multivariate analysis
• Non-Gaussian distribution
• Probability density
• Robust procedures
• Teacher productivity

1. Introduction

By how much does the productivity of one worker within an occupation vary from the productivity of another worker? We answer this question for teachers, estimating the distribution of worker productivity in the form of a probability density. Teacher productivity, as measured by student outcomes, has been widely studied, and it is well established that the difference between high-productivity and low-productivity teachers is quite large, with long-term implications for student achievement and labor market outcomes. This observation has led to policy proposals that intervene at varying points in the probability distribution of teacher productivity. Most school systems invest significant resources in professional development, a strategy used to try to improve the productivity of all teachers, but more recently policy initiatives have focused on the tails of the distribution: significant raises for the best performing teachers and dismissal for the worst performing teachers. The efficacy of such policies depends, in part, on the shape of the distribution of teacher productivity. We estimate a complete productivity distribution using a nonparametric estimator that corrects for measurement error and focus on the extent to which the shape of the distribution differs from the widely held assumption of normality.

There is surprisingly little academic focus on the shape of the distribution of worker productivity. This is perhaps not surprising given that most jobs produce multiple outputs so a focus on only one or two would only capture a slice of employee production. Only a few studies outside of education estimate densities of employee productivity. A notable example is Mas and Moretti (2009), which offers a kernel density estimate for productivity of supermarket cashiers. Mas and Moretti find productivity to be very roughly bell-shaped. (See also, Bandiera et al. 2009 and Paarsch and Shearer 1999.) Density estimates are now quite common in the teacher effects literature (e.g., Boyd et al. 2008; Kane et al. 2008; Goldhaber and Hansen 2013), but these studies do not carefully examine the tails of the distribution and all make the assumption that the productivity distribution is Gaussian.

There areseveral benefits to focusing on public school teachers in examining the distribution of worker productivity. First, education is a major industry with K-12 education expenditures in the United States comprising approximately 4% of GDP. Teachers comprise the single largest college-educated profession—there are over three million public school teachers—and they play a vital role in the creation of future human capital.¹ Second, while the productivity of a worker always depends on available capital and elements of team production, teachers are more isolated from other factors of production than are many other professionals so estimating an unconditional productivity distribution is meaningful.²

The distribution of teacher productivity is also immediately relevant in today's education policy environment. Traditionally, education policies have been applied broadly across the productivity spectrum; focusing on rewards for seniority or credentials and the provision of in-service training (professional development). But while it is still not the norm in public schools, a number of states and local systems have recently implemented policies tying teacher evaluations to consequential personnel decisions, some of these involve dismissing the very worst performing teachers and rewarding the most effective; policies focused on the tails of the productivity distribution.³

Assuming that productivity is normally distributed, it is reasonable to infer that policies shifting the distribution of effectiveness in the tails of the distribution will have far larger effects on student achievement than would policies that shift the effectiveness of the average teacher. Traditionally, research on teacher effects has reported estimates of these effects based on the assumption that the distribution of productivity is normal.⁴ A number of studies make the assumption of normality in the context of exploring the implications for students of increases in the quality of teachers by changing the mix of people in the teaching profession through firing, layoffs, or non-tenuring teachers, or through retention bonuses.⁵ Chetty et al. (2014b), for instance, considered the implications of Hanushek's (2009) hypothetical that teachers in the bottom 5% of the value-added distribution be dismissed (with the assumption that they could be replaced by teachers of average quality). Based on their findings on the impacts of teacher quality on adult earnings, they present a back-of-the-envelope calculation that substituting an average teacher for a bottom 5% teacher would increase the present value of average lifetime earnings of a student by $14,500. (The average class size in Chetty et. al. was 28.2, so the total net present value of the replacement is estimated to be $407,000.) This, along with other simulations in the published literature, assumes that teacher quality follows a Gaussian distribution.⁶

The assumption of normality is convenient—most policy questions can then be settled by just knowing the standard deviation of teacher productivity measured in units of student outcomes. While it is fairly standard to assume that most social psychological variables are normally distributed in the population (often by construction), as Mayer (1960) notes, “…there is little reason to assume that ability is in fact normally distributed” (p. 189). We are only aware of one paper (Pereda-Fernández 2016) that investigates the potential that the distribution of teacher effects is nonnormal. This work relies on estimating higher-order moments of residuals to detect departures from normality and finds that the distribution of teacher effects is slightly skewed and platykurtic (i.e., it has fatter tails).⁷

Our interest in the shape of the productivity distribution calls for use of a nonparametric density estimate so that the shape of the distribution is determined empirically rather than by assumption. We present a formal statistical test for normality. Normality is very strongly rejected, but the rejection largely reflects the large samples and the power of the test. While the distribution of teacher productivity could be heavily skewed or multi-modal, etc., in fact, the distribution looks much like a bell curve—just not a bell curve that is Gaussian (nor t-); the difference is in the tails rather than in the overall shape.

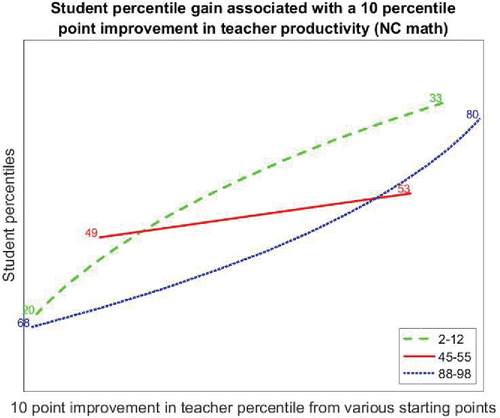
Consistent with the broader literature, we find that the difference in terms of student achievement between effective and ineffective teachers is quite large. When we focus on what happens at different points in the productivity distribution, asking the question “what happens when you replace a teacher with a given productivity with a teacher who performs at a level 10 percentile points higher in the teacher productivity distribution,” our estimates illustrate the differential impact that teachers at the extremes have on student achievement from those in the middle of the distribution. Figure 1 offers a visual summary of our key findings illustrated with math scores from North Carolina. The plot links teacher percentiles on the horizontal axis to student percentiles on the vertical axis. The lines show the effect of movement across the tails versus movement in the center of the distribution—the former lines being much steeper. An improvement of teacher effectiveness at the bottom (moving from the 2nd to the 12th percentile) or top (moving from the 88th to the 98th percentile) tends to be associated with a change in student achievement of about 13 student percentiles, versus a comparably sized change in teacher productivity near the median of the distribution (moving from the 45th to 55th decile), which is generally associated with a change in student achievement of about four student percentiles.

Figure 1.  Student gain associated with improvement in teacher productivity.

A second methodological issue that arises in estimating teacher productivity is that the estimates of individual productivity include measurement error, which is ignored by standard nonparametric techniques. To oversimplify slightly, point estimates of value added for an individual teacher are least-squares regression coefficients on teacher indicator variables in what can be thought of as an educational production function. The point estimate for the jth teacher, ${\widehat{\delta }}_j$, consists of the true level of productivity, δ_j, plus an approximately normally distributed sampling error, ν_j, with standard deviation ${\sigma }_{{\nu }_j}$. The observed dispersion of estimated productivity, ${\widehat{\sigma }}_{\widehat{\delta }}$, overstates the true dispersion, σ_δ, precisely because the observed dispersion includes the sampling error (Rockoff 2004). When parametric estimates are made, it is therefore commonplace in the teacher effectiveness literature to use empirical Bayes shrinkage (Aaronson et al. 2007) methods to account for sampling error. This shrinkage process, however, assumes normality and generally shrinks all estimates by an equal proportion without distinction between the length of the tails versus the center of the distribution (Guarino et al. 2015; Mehta 2015). Since we care about getting the shape right, we employ a recent method from the statistics literature, Delaigle and Meister (2008a, 2008b) that is intended precisely to give a nonparametric density estimate when the observed data points are subject to heteroscedastic error.

We conduct our empirical analysis on three separate datasets: the widely used data from the Tennessee STAR experiment, and longitudinal data from North Carolina and Washington State. We carry out the analysis across multiple sites in order to assess the extent to which our findings generalize across experimental and nonexperimental settings, different educational contexts and grades. While there are some differences in the estimates, for example, larger estimated teacher effects in earlier grades, the findings are remarkably robust across datasets in showing differential marginal productivity in the tails of the distribution.

2. Methodological Approach to Density Estimation

Density estimation is a two-step process in which we first estimate individual teacher effects and then generate a nonparametric density estimate from the individual teacher estimates.⁸ We observe i = 1, …, n students assigned to j = 1, …, J teachers in subject s, and we let I_{(i, t) ∈ j} be an indicator variable for whether student i is assigned to teacher j at time t. If A_{i, s, t} is an outcome measure of interest, for example, a test score, then we can write (1) $$\begin{array}{ccc}\hfill A_{i,s,t}& =& \sum _{p=1}^3{\lambda }_p{A}_{i,s,t-1}^p+{\delta }_1{I}_{\left(i,t\right)\in 1}+\cdots +{\delta }_J{I}_{\left(i,t\right)\in J}+X_{i,t}\beta +{\epsilon }_{i,t},\hfill \end{array}$$(1) where X is a set of student covariates, A^p_{i, s, t − 1} is a cubic polynomial of lagged test scores in one or more subjects, and ϵ is a random error.

Some researchers also add a school fixed effect to Equation (1(1) $$\begin{array}{ccc}\hfill A_{i,s,t}& =& \sum _{p=1}^3{\lambda }_p{A}_{i,s,t-1}^p+{\delta }_1{I}_{\left(i,t\right)\in 1}+\cdots +{\delta }_J{I}_{\left(i,t\right)\in J}+X_{i,t}\beta +{\epsilon }_{i,t},\hfill \end{array}$$(1) ), hence measuring the impact of teacher effectiveness within school. But this attributes any mean differences in the quality of teachers who are employed in different schools to the school effect as opposed to teachers, which is potentially problematic if schools are able to hire teachers of differing average abilities.⁹ This may be particularly important when investigating the tails of the distribution given that schools have quite different applicant pools (e.g., Gross et al. 2010). For this reason, and because recent research suggests that teacher productivity is transferable across schools (Xu et al. 2012; Glazerman et al. 2013; Chetty et al. 2014b), our preferred specification omits school fixed effects. However, our findings are quite similar if we instead include school effects.¹⁰

The estimates ${\widehat{\delta }}_j$ can be regarded as the true δ_j plus sampling error. The central goal in the article is to determine the underlying random density of the ${\delta }_j\text{"}s$, which we do with a nonparametric estimator. Since ${\widehat{\delta }}_j$ is simply a regression coefficient, under reasonable assumptions, the sampling error is approximately normal. The methodological problem is that the dispersion of the observed ${\widehat{\delta }}_j$, which includes sampling error v_j, exaggerates the dispersion of δ_j, ${\widehat{\sigma }}_{\widehat{\delta }}^2\approx {\sigma }_{\delta }^2+\frac{1}{J}{\sum }_{j=1}^J{\sigma }_{{\nu }_j}^2$.¹¹ Since ${\widehat{\sigma }}_{\widehat{\delta }}^2$ and ${\sigma }_{{\nu }_j}^2$ are estimable, it is possible to back out an estimate of σ²_δ. This “backing out” is essentially what empirical Bayes estimators do.¹²

If the errors in Equation (1(1) $$\begin{array}{ccc}\hfill A_{i,s,t}& =& \sum _{p=1}^3{\lambda }_p{A}_{i,s,t-1}^p+{\delta }_1{I}_{\left(i,t\right)\in 1}+\cdots +{\delta }_J{I}_{\left(i,t\right)\in J}+X_{i,t}\beta +{\epsilon }_{i,t},\hfill \end{array}$$(1) ) are homoscedastic, then the error variance estimated from the standard errors on the regression coefficients on the teacher dummy variables will be—roughly—inversely proportional to the square root of the number of students of teacher j, $\sqrt{n_j}$, and therefore heteroscedastic. Novice teachers are generally lower performers than are more experienced teachers (Kane and Staiger 2002; Rockoff 2004), and n_j is typically smaller for novice teachers in the North Carolina and Washington datasets. Thus, δ and ${\sigma }_{{\nu }_j}^2$ may not be independent. In particular, failing to account for measurement error may cause a particular problem in estimating the shape of the lower tail of the distribution.

The second reason that sampling error can vary is that some classes are more heterogeneous than others. Suppose that the error variance, ${\sigma }_{{\epsilon }_i}^2$, varies across students. The variance of ${\widehat{\delta }}_j$ will be roughly proportional to ${\sum }_{i\in j}{\sigma }_{{\epsilon }_i}^2/n_j$. We use White robust standard errors to accommodate possible heteroskedasticity, despite the fact that n_j is sometimes smaller than is desirable from the point of view of consistency arguments.

Given a point estimate and standard error for each teacher, we take advantage of recent advances in the statistics literature and use the algorithm for nonparametric density estimation in the presence of measurement error described in Delaigle and Meister (2008a,b).¹³ This method is designed precisely to compute a nonparametric density estimate from data that include heteroskedastic errors. Standard nonparametric kernel density estimates calculate empirical densities by counting up the fraction of data points near a given x-ordinate while down-weighting the points further from the ordinate. The D–M algorithm increases the down-weighting for observations with larger measurement error. As with standard kernel density estimates, the D–M algorithm computes a discrete approximation, f(x_l), to the density at a specified set of grid points. We use L = 200 grid points x_l uniformly distributed on $\left[min\left({\widehat{\delta }}_j\right),max\left({\widehat{\delta }}_j\right)\right]$, where f(•) is rescaled so that ${\sum }_{l=1}^{L}f\left(x_l\right)\times \Delta x=1$, and where Δx is the distance between grid points.

Smoothed densities are themselves statistical estimates. There may be concern about the accuracy of the location of percentiles in the tails of the distribution precisely because relatively few observations fall in the tail. We adopt the following bootstrap strategy to compute confidence intervals. We resample the data with replacement 1000 times to produce 1000 estimates of $\left({\widehat{\delta }}_j,{\widehat{\sigma }}_{{\delta }_j}\right)$, holding the bandwidth constant at the bandwidth used for the original sample.¹⁴ We apply the Delaigle and Meister deconvolution estimator to each resample. For each bootstrap sample, we compute the impact of a one standard deviation improvement in teacher quality and report the 5th and 95th percentiles of the bootstrap sample as confidence intervals.

In order to test the distributions for normality we use a modified Kolmogorov–Smirnov (KS) statistic. For each D-M smoothed density we compute sample mean and variance $m={\sum }_{i=1}^n{\sum }_{l=1}^L{x}_{l}f\left(x_l\right)\Delta x$, $v={\sum }_{i=1}^n{\sum }_{l=1}^L{\left(x_l-m\right)}^{2}f\left(x_l\right)\Delta x$. We then compute the KS statistic as ${D=\max }_l|F\left(x_l\right)-\Phi \left(x_l;m,v\right)|$, where F(x_l) is the cumulative distribution function and Φ(•) is the normal cdf with mean m and variance v. To obtain critical values under the null of normality, we generate 2000 Monte Carlo draws of artificial data drawn from N(m, v) of length equal to the number of teachers in the real sample and apply the D–M smoother to each artificial sample. We then tabulate the Monte Carlo values of D to find critical values for the real sample. As we report below, the null of normality is rejected because of the thickness of the tails of the distribution.

We associate each teacher percentile with adjusted student gains. To calculate the adjusted student gains, we subtract the products of the test score variables (lagged math and reading scores, with squared and cubed terms) and their associated coefficients from the value-added model defined in Equation (1(1) $$\begin{array}{ccc}\hfill A_{i,s,t}& =& \sum _{p=1}^3{\lambda }_p{A}_{i,s,t-1}^p+{\delta }_1{I}_{\left(i,t\right)\in 1}+\cdots +{\delta }_J{I}_{\left(i,t\right)\in J}+X_{i,t}\beta +{\epsilon }_{i,t},\hfill \end{array}$$(1) ) from the current-year test score: (2) $$\mathrm{Adjusted}\mathrm{Gai}{\mathrm{n}}_{i,s}=A_{i,s,t}-\sum _{p=1}^3{\lambda }_p{A}_{i,s,t-1}^p$$(2)

3. Data

Each of the three datasets we employ has advantages and disadvantages. The advantage of the STAR data is that there is random assignment of students to classrooms and teachers within schools, eliminating a potential source of bias in the estimation of teacher effectiveness (Rothstein 2010). STAR, however, includes a relatively small sample of teachers and students in early grades only, each teacher is observed only once, and the findings may not be generalizable (Hanushek 1999).

The advantage of using data from North Carolina and Washington is that each state database includes a large, longitudinal sample of teachers and students, a rich set of covariates on students, multiple classroom observations on individual teachers, and the data are more current than STAR. The disadvantage of the observational data from these states is that, unlike the STAR experiment, students in North Carolina and Washington are not randomly assigned to teachers. Given this, it is necessary to estimate value-added models to obtain teacher effect estimates, and there is the usual risk that covariate adjustments fail to account for aspects of the process that leads to student-teacher matches that may be correlated with student achievement.¹⁵

The value-added models that we estimate include prior-year math and reading standardized test scores, free/reduced price lunch status, special education/learning disability status, gender, race/ethnicity, and grade indicators as predictors for all sites; however, specific variable definitions are not completely consistent across sites. For North Carolina and Washington, we also include limited English proficiency and for North Carolina we also include parental education.

3.1. Tennessee STAR Data

The Tennessee STAR experiment was primarily designed to answer questions about the efficacy of reduction in class size.^16,17 The experiment followed a single cohort from kindergarten through third grade. Students were randomly assigned within schools to “regular” classes of approximately 24 students, “small” classes of approximately 16 students, or “regular-with-aide” classes of approximately 24 students. For a variety of reasons, the randomization was imperfect (Hanushek 1999), but has still been judged to be useful for studying teacher and class effects.¹⁸ Teachers in STAR are only observed once so class and teacher effects are not separately identified. Test scores in STAR are designed to be vertically aligned. We take original test scores and standardize by subtracting the mean and dividing by the standard deviation for each grade-year.

3.2. North Carolina and Washington Data

Both the North Carolina and Washington datasets have been used widely for investigating teacher policy issues.¹⁹ The administrative data in North Carolina are from the North Carolina Department of Public Instruction, and are compiled and managed by Duke University's North Carolina Education Research Data Center. The data from Washington are from the Office of the Superintendent of Public Instruction. In each state, the data include information on student achievement on standardized tests in math and reading that are administered as part of each state's accountability system, and, importantly for our purposes, in each state teachers and students can be linked together, enabling the estimation of teachers' value added.²⁰ We normalize student achievement growth within grade and year, as with the STAR data. The data also include information about student demographics (e.g., free/reduced price lunch status, race/ethnicity, etc.) that are used in the estimation of the value-added models described above.

We use data for teachers and students from school years 1995–1996 through 2004–2005 in North Carolina and 2006–2007 through 2012–2013 in Washington. In each state, we only include students who have valid math or reading pre- and post-test scores. We also restrict our analytic samples to elementary schools (grades 3–5 in North Carolina and 4–6 in Washington), and in ways designed to ensure that the person identified as the proctor of an exam is in fact a student's classroom teacher. Specifically, we restrict the data to self-contained, non-specialty classes, and only include teachers who are assigned to reasonable class sizes, and we only include those student–teacher matches in which the person identified as the proctor has credentials and school and classroom assignments that are consistent with their teaching the specified grade and class for which they proctored the exam.²¹

3.3. Sample Statistics

The above restrictions result in samples of 13,586 student–year observations (6591 unique students) and 793 teacher observations in STAR (teachers in STAR are only observed once); 1,791,228 student–year observations and 87,604 teacher–year observations (24,707 unique teachers) in North Carolina; and 771,190 student–year observations and 35,518 teacher–year (11,826 unique teachers) observations in Washington.

Table 1 reports sample statistics for select variables by site at the student–year level, with and without the sample restrictions described above. Across all three sites the restricted sample of students is somewhat more advantaged as measured by free/reduced price lunch status and student achievement. This is not surprising given that low income and low achieving students are more likely to be mobile and therefore less likely to have both a base year and follow-up test score, a requirement to be in the sample.

Table 1. Descriptive statistics of student characteristics, by site.

	STAR		NC		WA
	Unrestricted	Restricted	Unrestricted	Restricted	Unrestricted	Restricted
Standardized Math Score	0.000	0.091	0.000	0.057	0.000	0.004
	(1.00)	(1.004)	(1.00)	(0.978)	(1.00)	(0.999)
Standardized Reading Score	0.000	0.105	0.000	0.045	0.000	0.005
	(1.00)	(1.002)	(1.00)	(0.978)	(1.00)	(0.997)
Lagged Math Score	0.000	0.160	0.000	0.045	0.000	0.004
	(1.00)	(0.952)	(1.00)	(0.978)	(1.00)	(0.997)
Lagged Reading Score	0.000	0.151	0.000	0.040	0.000	0.001
	(1.00)	(0.963)	(1.00)	(0.983)	(1.00)	(1.00)
Free/Reduced Price Lunch	0.511	0.450	0.469	0.443	0.446	0.449
	(0.500)	(0.498)	(0.499)	(0.497)	(0.497)	(0.497)
Special Ed/Learning Disability	0.124	0.159	0.075	0.067	0.137	0.126
	(0.33)	(0.366)	(0.264)	(0.249)	(0.344)	(0.332)
White	0.621	0.701	0.600	0.625	0.631	0.628
	(0.485)	(0.458)	(0.49)	(0.484)	(0.483)	(0.483)
Minority	0.368	0.299	0.400	0.375	0.328	0.326
	(0.482)	(0.458)	(0.49)	(0.484)	(0.470)	(0.469)
Female	0.470	0.491	0.488	0.497	0.488	0.492
	(0.499)	(0.500)	(0.500)	(0.500)	(0.500)	(0.500)
N (teachers)	1,016	857	48,914	24,747	16,886	11,826
N (teacher–years)	1,016	857	145,935	87,604	77,261	35,544
N (students)	11,601	6288	1,262,070	906,667	800,319	503,490
N (student–years)	34,803	12,265	3,019,821	1,791,228	1,598,657	771,406

NOTE: Standard deviations in parentheses. Students are only included in restricted sample if they have a current and prior-year test score. Teachers are only included in the restricted sample if they are coded as a regular classroom elementary teacher and have at least 10 valid students.

4. Results

While we are primarily interested in the shape of the productivity distribution, a few intermediate results warrant mention. Supplemental Table A-2 shows selected coefficient estimates from the models used to derive teacher value added. The estimated coefficients across the different sites are quite consistent. The coefficient estimates on prior test scores in the same subject are typically in the range of 0.50–0.70, but, consistent with prior literature (e.g., Goldhaber et al. 2013a, 2013b; Johnson et al. 2015), cross-subject tests also predict gains in both math and reading. And, again consistent with prior literature (e.g., Rivkin et al. 2005; Boyd et al. 2006; Goldhaber 2006, 2007; Clotfelter et al. 2008, 2010), students eligible for free or reduced price lunch have test scores that are lower by 7–12% of a standard deviation, special education students and those who are identified as having specific learning disabilities also perform more poorly as do African–American students.

As signaled above, we find that the distribution of teacher productivity is non-Gaussian. In this vein, Table 2 reports both estimates of kurtosis and the results of a formal test for normality. D–M estimates of kurtosis are around four for math and four-and-a-half to five for reading. (The D–M correction for measurement error leads to slightly higher kurtosis estimates.) In order to help think about the level of leptokurtosis reported in Table 2, kurtosis equal to 4 corresponds to a t- distribution with 10 degrees of freedom and kurtosis equal to 5 corresponds to 7 degrees of freedom.

Table 2. Characteristics of teacher effectiveness distribution.

Panel A. Math	STAR	NC	WA
Effect sizes
Unadjusted	0.47	0.22	0.23
EB Adjusted	0.44	0.21	0.22
D-M Adjusted	0.46	0.21	0.22
Skewness (unadjusted)	0.07	0.03	0.27
Skewness (D-M adjusted)	0.10	−0.04	0.34
Kurtosis (unadjusted)	4.30	3.71	4.04
Kurtosis (D-M adjusted)	4.46	3.98	4.41
Modified KS p-value	0.001	0.000	0.000
N	857	24747	11826
Panel B. Reading
Effect sizes
Unadjusted	0.41	0.16	0.20
EB Adjusted	0.38	0.14	0.18
D-M Adjusted	0.40	0.14	0.18
Skewness (unadjusted)	−0.28	−0.15	0.07
Skewness (D-M adjusted)	−0.31	−0.54	0.11
Kurtosis (unadjusted)	5.05	4.35	3.96
Kurtosis (D-M adjusted)	5.56	5.66	4.57
Modified KS p-value	0.000	0.000	0.000
N	844	24747	11826

NOTE: Effect sizes represent the effect of a one standard deviation change in teacher effectiveness on student achievement.

Normality would permit a simple description of the productivity distribution, but the Kolmogorov–Smirnov test, reported in Table 2, strongly rejects a normal distribution for each site in our study. Contingent on the degree to which the productivity distribution diverges from normality, this could have important policy implications. There is, for instance, work suggesting that policy interventions that focus on the tails of the teacher productivity distribution could have dramatic impacts on student test achievement and later life outcomes (e.g., Chetty et al. 2014b; Hanushek 2009), but the assumption of normality may lead to an under- or overstatement of the importance of very effective or ineffective teachers.

It is traditional to use a one standard deviation change in teacher effectiveness as the definition of an “effect size.” Even though we find that the standard deviation is not a sufficient statistic to describe the teacher effectiveness distribution, we show standard deviations in Table 2. For each site, we report both unadjusted estimates of a one standard deviation change in teacher quality, as well as estimates of the effect sizes that are adjusted for estimation error using the Delaigle and Meister approach and empirical Bayes shrunken estimates.²² The estimated impacts on student achievement are comparable to those previously estimated in these sites (Nye et al. 2004; Rothstein 2010; Goldhaber et al. 2013a). And, also consistent with prior research (e.g., Kane and Staiger 2012; Lefgren and Sims 2012; Goldhaber et al. 2013b), there is a higher variance in the distribution of teacher quality in math relative to reading.

As is apparent from the table, the approach taken to adjust for measurement error—Delaigle and Meister (DM) or empirical Bayes (EB)—makes only a small difference in the estimated impact of a one standard deviation change in teacher quality. The estimated effects in North Carolina and Washington shrink more noticeably under each adjustment type when they are based on only a year's worth of matched teacher student data (reported in Table A-1 in the online supplemental material), as would be expected given that the signal-to-noise ratio is lower with only a year's worth of data (McCaffrey et al. 2009; Goldhaber and Hansen 2013).²³

One striking finding is that the estimated teacher effects are far larger in the STAR data than in either of the other states.^24,25 One^{Table 3}possible explanation is that this reflects the fact that the STAR teacher effects are 1-year teacher-classroom effects (teachers are observed for a single year and class only), and these will be subject to greater measurement error. This, however, does not appear to be the explanation: the 1-year estimates from North Carolina and Washington (see Table A-1 in the online supplemental material) are slightly larger but not anywhere near the magnitude of the STAR findings. Another possibility is that STAR creates heterogeneously sized classrooms by design, and this will suggest greater classroom–teacher effects as a consequence of the purposeful assignment of teachers to different sized classes (Pereda-Fernández 2016).²⁶ As a check, we estimate teacher effects using a two-stage process in which we control for class size—first regressing student achievement on student covariates and class size and then using the residuals to estimate teacher effects. The estimated impacts are essentially unchanged.

It is also possible that there is differential-less selection of students into classrooms in STAR than in the state samples. If there are compensating matches between teacher effectiveness and unobserved student academic ability in the sense that the more effective teachers tend to be matched with students who are likely to struggle and vice versa, then the teacher effect estimates in the state samples (but not STAR where students are randomly assigned to classes) would understate the true impact of teachers. Unfortunately we cannot directly test for this possibility, but it seems quite unlikely as most academic evidence suggests that more advantaged students tend to be assigned to more effective and qualified teachers (e.g., Kalogrides and Loeb 2013; Goldhaber et al. 2015).

Another plausible explanation is that the larger STAR effects are due to the fact that they are based on achievement in earlier grades. Teachers may appear to have larger estimated effects on students in early grades due to growth in the accumulation of knowledge over time and what is tested as student's progress through school (Cascio and Staiger 2012). Lipsey et al. (2012), for instance, report that the mean achievement gains for students, across seven nationally normed, longitudinally scaled achievement tests, shrinks substantially as students advance from one grade to the next.²⁷ For instance, the mean growth in math and reading test achievement between first and second grade is approximately a full standard deviation, whereas the mean growth between 5th and 6th grade is about a third of a standard deviation in reading and 40% of a standard deviation in math. Consequently, the effects of changes in teacher quality in Table 2, translated into months of student learning, do not appear very different in STAR from the two other sites once teacher effects are translated into typical months of student learning.²⁸

We turn now to our primary results on productivity. Table 3 provides point estimates of the distribution of productivity accounting for heteroskedastic error in Panel A (comparable results for the single year estimates are available upon request). Each row identifies the percentiles of adjusted student achievement gains for a teacher at a given point in the distribution of teacher productivity, where the teacher percentile represents a position in the DM-based estimated distribution and the student percentiles are from the distribution of student value added. The teacher and student distributions are commensurable in the sense that both are mappings from test score measures to percentiles. We match teacher and student percentiles by reverse mapping the teacher percentile to a test score measure and then mapping that test score measure to the corresponding student percentile. Our findings are generally not all that different from what would be expected from a normal distribution (the corresponding percentiles for a normal distribution are reported in the angle brackets in the table).

Table 3. Teacher productivity percentiles versus student achievement gains percentiles, with 95% confidence intervals.

	STAR		NC		WA
Percentile	Math	Reading	Math	Reading	Math	Reading
2	8.3	8.4	19.9	24.1	20.9	24.9
	(6.1,10.6)	(3.5,12.8)	(19.5,20.4)	(23.7,24.7)	(20.1,21.7)	(24,25.7)
	⟨8.4⟩	⟨9.6⟩	⟨21.9⟩	⟨27.7⟩	⟨20.2⟩	⟨25.2⟩
5	14	16.8	26.1	30.1	26.4	30
	(11.9,16.3)	(14.1,19.4)	(25.7,26.5)	(29.7,30.5)	(25.8,27.1)	(29.4,30.6)
	⟨13.2⟩	⟨14.9⟩	⟨26.8⟩	⟨31.2⟩	⟨25.5⟩	⟨29.5⟩
12	23.4	25.3	33.5	36	33.4	35.6
	(21,25.5)	(23.2,27.7)	(33.1,33.8)	(35.7,36.2)	(33,33.8)	(35.2,35.9)
	⟨21.8⟩	⟨23.2⟩	⟨33.3⟩	⟨35.5⟩	⟨32.4⟩	⟨34.8⟩
15	26.2	28.2	35.6	37.5	35.4	37.1
	(24.2,28.5)	(26,30.4)	(35.3,35.9)	(37.3,37.8)	(34.9,35.8)	(36.7,37.4)
	⟨24.9⟩	⟨26.1⟩	⟨35.3⟩	⟨36.9⟩	⟨34.5⟩	⟨36.4⟩
45	47.5	47.6	49.1	46.7	48.4	46.8
	(45.6,49.5)	(45.8,49.5)	(48.9,49.4)	(46.5,46.8)	(48,48.7)	(46.5,47)
	⟨48.7⟩	⟨47.8⟩	⟨49.4⟩	⟨46.2⟩	⟨49.4⟩	⟨47.4⟩
50	50.7	50.4	51	47.9	50.2	48.1
	(48.7,52.9)	(48.6,52.5)	(50.7,51.3)	(47.7,48.1)	(49.9,50.5)	(47.8,48.4)
	⟨52.5⟩	⟨51.1⟩	⟨51.4⟩	⟨47.6⟩	⟨51.4⟩	⟨49⟩
55	54.2	53.5	52.8	49	52	49.4
	(51.9,56.1)	(51.5,55.3)	(52.6,53.1)	(48.9,49.2)	(51.7,52.3)	(49.1,49.7)
	⟨56.1⟩	⟨54.5⟩	⟨53.4⟩	⟨48.9⟩	⟨53.5⟩	⟨50.5⟩
85	75.9	71.7	65.9	56.9	65.7	60
	(74,77.3)	(70.1,73.4)	(65.5,66.2)	(56.7,57.2)	(65.3,66.2)	(59.6,60.4)
	⟨77.9⟩	⟨74.4⟩	⟨67.3⟩	⟨58.7⟩	⟨67.4⟩	⟨61.2⟩
88	78.2	74	67.8	58.1	67.8	61.6
	(76.6,79.8)	(72.4,75.9)	(67.5,68.2)	(57.8,58.4)	(67.4,68.3)	(61.3,62.1)
	⟨80.5⟩	⟨77⟩	⟨69.3⟩	⟨60.1⟩	⟨69.3⟩	⟨62.8⟩
95	86.5	82.4	74.3	62.3	75.5	67.4
	(84.4,88.7)	(79.9,85.2)	(73.9,74.8)	(61.9,62.8)	(74.8,76.1)	(66.8,68)
	⟨87.7⟩	⟨84.3⟩	⟨75.4⟩	⟨65⟩	⟨75.3⟩	⟨67.8⟩
98	93.3	89.5	80	66.2	81.7	72.9
	(91,94.9)	(86.3,91.8)	(79.4,80.6)	(65.4,67.1)	(80.9,82.4)	(72,73.8)
	⟨91.6⟩	⟨89⟩	⟨80.1⟩	⟨69⟩	⟨79.8⟩	⟨71.8⟩

NOTE: Rows give the percentile of student achievement measured by value added for the indicated point in the teacher productivity distribution. For example, a teacher at the 2nd percentile of productivity on student achievement in math in the STAR data has a mean student outcome at the 8.3rd percentile of student gains. 95% confidence intervals appear in parentheses and corresponding percentiles for a normal distribution in angle brackets.

As is common in estimates of teacher effects, the distribution shows considerable dispersion. As examples, if a school district were able to hire a 98th percentile teacher to replace a median teacher, this would move student achievement from a low estimate of 18 percentile points according to the North Carolina reading results (48th to 66th student percentiles) to a high of 42 percentile points according to the STAR math results (51st to 93rd percentiles). These are all large substantive effects.

Figure 1 provided visual evidence that differences in marginal effectiveness in the lower and upper tails are far larger than in the middle of the distribution, using North Carolina math scores. Table 4 restates^{Table 5}the evidence numerically, showing the difference in the point estimates given in Table 2 and adding confidence intervals for the differences. A 10 percentile movement across the teacher productivity distribution has two-and-a-half to three-and-a-half times the effect on output, as measured by student test percentiles, in the tails of the distribution as does the same movement in the middle of the distribution. We give 95% confidence intervals from the bootstrap described above (in Section 2) in parentheses. The confidence intervals suggest that the estimated effects of movements in different parts of the distribution are estimated with reasonable precision. The numbers given in angle brackets show what the estimated effects would be if the productivity distributions were normal with means and standard deviations shown in Table 4. Importantly, while we reject normality, the nonparametric distributions we estimate do not depart appreciably from normality across all sites and both subjects.

Table 4. Effect of 10 percentile movement across the productivity distribution.

	STAR		NC		WA
Percentiles	Math	Reading	Math	Reading	Math	Reading
2–12	15	16.9	13.5	11.8	12.5	10.6
	(12.6,17.5)	(12.8,21.8)	(13,14)	(11.4,12.3)	(11.7,13.2)	(9.9,11.4)
	⟨13.4⟩	⟨13.5⟩	⟨11.4⟩	⟨7.9⟩	⟨12.2⟩	⟨9.6⟩
45–55	6.7	5.9	3.7	2.4	3.6	2.7
	(6.1,7.4)	(5.2,6.5)	(3.6,3.8)	(2.3,2.5)	(3.4,3.8)	(2.5,2.8)
	⟨7.3⟩	⟨6.7⟩	⟨4.0⟩	⟨2.7⟩	⟨4.1⟩	⟨3.1⟩
88–98	15	15.5	12.2	8.1	13.8	11.3
	(12.9,16.8)	(12.5,18)	(11.6,12.8)	(7.3,8.9)	(13,14.6)	(10.3,12.1)
	⟨11.1⟩	⟨12.0⟩	⟨10.9⟩	⟨8.9⟩	⟨10.5⟩	⟨9.1⟩

NOTE: 95% confidence intervals in parentheses; corresponding effect for a normal distribution in angle brackets.

5. Policy Implications and Conclusions

The standard assumption of policy analysts is that the distribution of employee productivity is normal. Prior to our study, this assumption has not been empirically verified. As we show, the distribution of teacher effectiveness departs from the Gaussian, but not significantly, suggesting that the assumption of normality in estimating the implications of productivity initiatives that target different points in the distribution is reasonably well evaluated by assuming the distribution to be Gaussian. And, consistent with existing literature, we find that teachers can have a very large effect on student outcomes.

The fact that the estimated effects of teacher quality are not uniform across the productivity distribution has important implications for teacher policy. For instance, some new teacher policy initiatives focus on selective recruitment and retention (e.g., Dee and Wyckoff 2013). But this type of targeted intervention targeting the tails of the productivity distribution is far rarer than the productivity initiative – professional development – training that targets teachers regardless of estimates of their performance. Moreover, professional development is a ubiquitous and costly strategy. A recent report (TNTP 2015) estimates that professional development activities cost an average of $18,000 per teacher, but do not lead to systemic improvement in teacher effectiveness, a finding that reflects the broader literature.²⁹ Our findings reinforce the notion that experimentation in influencing the tails of the distribution might be a fruitful approach to upgrade the overall quality of the teacher workforce.

Chetty et al. (2014b), for instance, considered the implications of Hanushek's (2009) hypothetical that teachers in the bottom 5% of the value-added distribution be dismissed (with the assumption that they could be replaced by teachers of average quality). Based on their findings on the impacts of teacher quality on adult earnings, they present a back-of-the-envelope calculation that substituting an average teacher for a bottom 5% teacher would increase the present value of average lifetime earnings of a student by $14,500. (The average class size in Chetty et al. was 28.2, so the total net present value of the replacement is estimated to be $407,000). Yet this, along with the other simulations, assumes that teacher quality follows a Gaussian distribution.³⁰ As we report above, the distribution of teacher effectiveness we estimate is roughly bell-shaped, but departs notably from the Gaussian in the tails. Consistent with this picture we find that policies that change the placement of teachers across a wide swatch of the distribution are reasonably well evaluated by assuming the distribution to be Gaussian, but that movements within the tails are in some cases quite different.

Chetty et al. reached their conclusion about the value of replacing a bottom 5% teacher based on the following calculation. A one standard deviation change in teacher effectiveness is associated with a 1.34% change in the net present value (NPV) of lifetime earnings, where NPV is estimated to be $522,000 2010 dollars. The authors then ask what would happen if the bottom five percent of teachers were replaced with the median teacher. Since the average person in the bottom five percent of a Gaussian is 2.06 standard deviations below the mean, Chetty et al. calculated the gain to be 2.06 × 0.0134 × <ent > $ </ent > 522, 000 = < ent > $ </ent > 14, 500. We present the analogous calculation for each of our six data sets in the bottom of Table 5, empirically determining the average number of standard deviations from the mean for an average bottom five percent teacher. Not surprisingly given our findings that the assumption of a Gaussian distribution is a close approximation to the distribution we calculate, the Chetty et al.-type simulation is also pretty consistent. With three of the distributions, the values of replacement are larger than the values calculated from the Gaussian, but smaller for the other three, but the differences are all within 10% of what would have been found with the assumption of a normal distribution.

Table 5. Value of replacing teachers across the productivity distribution.

		STAR		NC		WA
		Math	Reading	Math	Reading	Math	Reading
Replacing teacher at the 2nd percentile with a teacher at the 12th percentile	DM	$7,076	$9,638	$6,622	$7,369	$6,390	$6,343
	Gaussian	$6,141	$6,141	$6,141	$6,141	$6,141	$6,141
Replacing teacher from the bottom 5% with an average teacher	DM	$14,844	$15,891	$14,014	$14,713	$13,623	$13,773
	Gaussian	$14,500	$14,500	$14,500	$14,500	$14,500	$14,500

NOTE: Based on calculation from Chetty et al. (2014) and assuming .878 standard deviation change from 2nd to 12th percentile with a Gaussian distribution.

While replacing teachers under the fifth percentile with average teachers has been proposed it has rarely been implemented.³¹ To see the difference in a policy focused in the tails, we do the same calculation simulating the effect of replacing a teacher at the 2nd percentile of the distribution with a teacher at the 12th percentile. The results are reported in the upper part of Table 5. The importance of looking carefully at the tails demonstrates in two ways. First, the gain from this 10 percentile move is roughly half of the entire gain from swapping the bottom five percent for median teachers. Thus, improving the effectiveness of the very worst teachers might be a valuable strategy—if there is a cost effective way to do so. Second, the differences between the nonparametric and Gaussian estimates are much larger here—so using an appropriate nonparametric estimator really matters. Depending on the dataset, we find the differences to range from 57% for STAR reading to 3% for WA reading.

The above simulation demonstrates that the effectiveness of investments in changing teacher quality at the tails of the distribution is likely to be far larger than in the middle. Yet while there are policy initiatives focused on the tails, the great majority of investment in teachers is focused on improving the average quality of the teacher workforce through professional development; this despite the fact that both experimental (Garet 2008: Glazerman et al. 2010) and nonexperimental (TNTP 2015; Yoon 2007) estimates suggest that efforts focused on improving the performance of in-service teachers yield little or mixed impacts on student achievement.

It is important to recognize that while the productivity of the teacher workforce is itself a critically important societal issue, the findings we report on the productivity of teachers may not generalize to other sectors of the economy. In particular, there are at least two reasons to be cautious. The first is that teaching is a multifaceted and relatively complex job (Lanier 1997). The second is that while there is growing interest in the use of teacher evaluations for personnel policies and incentives in education, most teachers have very high job security, especially after being tenured (McGuinn 2010), and are compensated based on a salary schedule, not based on performance measures. It is unclear how these differences between the public school teacher labor market and the broader labor market might affect the distribution of marginal productivity for different types of workers. Nevertheless, our findings are important as they suggest we need more research on marginal productivity as the efficacy of different types of investments in developing and maintaining a high-quality workforce depend on the returns to their focus on different points in the quality distribution.

Acknowledgments

We are grateful to Aurore Delaigle for the code for density estimation with measurement error, to Joe Walch for research assistance, and to Shelly Lundberg, James Cowan, Cory Koedel, Nick Huntington-Klein and the UCSB Econometrics Working Group for helpful comments.

Supplementary materials

Supplementary materials contain estimates of underlying regressions for teacher effects as well as robustness checks. The supplemental data can be accessed on the publisher's website.

Additional information

Funding

We acknowledge support from the Center for Scientific Computing from the CNSI, MRL: an NSF MRSEC (DMR-1121053) and NSF CNS-0960316, and the National Center for the Analysis of Longitudinal Data in Education Research (CALDER), funded through Grant R305C120008 to the American Institutes for Research from the Institute of Education Sciences, U.S. Department of Education.

Notes

2 This is likely to be particularly true at the elementary level (our focus), where team production is minimal because most teachers are responsible for the instruction of a classroom of students throughout the majority of the day. Jackson and Bruegmann (2009) found, at the elementary level, that increases in the value added of a given teacher's peers in a school has a small spillover impact on the achievement of students in that teacher's classroom. But the magnitude of this spillover effect is relatively small when compared to the overall magnitude of teachers' individual contributions to student learning. Additionally, evidence on the portability of the effectiveness across contexts (grades and schools) also suggests limited team production (Bacher-Hicks et al. 2014; Chetty et al. 2014a).

3 High-stakes uses of output-based measures of teacher productivity have been spurred by such federal initiatives as the Race to the Top and Teacher Incentive Fund grant competitions. For simulation evidence on how influencing the composition of the teacher workforce might affect its overall productivity, see Hanushek (2009), Goldhaber and Hansen (2010), Chetty et al. (2014b), and Rothstein (2014); see Goldhaber (2015) on why such simulations could result in misleading estimates of the effects of workforce composition policies.

4 In a review of the effects of teacher effectiveness, Hanushek and Rivkin (2010) suggested that the effect of a one standard deviation change in teacher effectiveness, based on models that include school fixed effects (so are within school estimates), are in the range of 0.11–0.15% of a standard deviation of student achievement. Estimates that do not include school effects and therefore assign differences in schools to teachers, tend to be larger, in the neighborhood of 0.20–30% of a standard deviation (Aaronson et al. 2007; Goldhaber and Theobald 2013; Kane and Staiger 2008). The estimates we describe below are consistent with this range, with the exception of Tennessee where the estimated effects are somewhat larger.

5 See, for instance: Chetty et al. (2014b), Hanushek (2009), and Rothstein (2015) on teacher dismissals; Goldhaber and Hansen (2013) and McCaffrey et al. (2009) on selective tenuring; Boyd et al. (2010) and Goldhaber and Theobald (2013) on layoffs; and Chetty et al. (2014b) and Rothstein (2015) on selective retention bonuses.

6 See Equation (14) and Online Appendix D of the Chetty et al. (2014) study for details about the simulation; and particularly p. 2672, where Chetty et al. said “Under the assumption that [value added] is normally distributed.

7 Pereda-Fernández (2016) differed substantively from our approach in that the author uses test score levels rather than the value-added approach that we follow and limits the sample to kindergarten. The paper also offers a novel approach to measuring spillover effects, an issue that we do not address.

8 Teacher effects can be estimated on a yearly basis, but then cannot be distinguished from classroom effects. As we discuss below, we estimate both teacher effects using multiple years of teacher (as many as are available for each teacher) data and yearly teacher–classroom effects. Given the increase in the precision of the estimates, our preferred specification is one that includes multiple years of teacher data, but our findings are qualitatively similar if instead we use teacher–classroom–year effects.

9 It is also possible, with panel data, to identify school level effects based on teachers who move from one school to another, but this form of identification also relies on strong assumptions, such as teachers being equally effective in different school contexts.

10 The Tennessee STAR data only includes 1 year of data so the only way to estimate specifications that include a school effect for this dataset is to exclude a hold out teacher for each school. Another alternative is to estimate teacher effects in two stages, first regressing student achievement on student covariates and class size and then using the residuals to estimate teacher effects. The correlation in the Tennessee data between the one-stage and two-stage teacher effects is very high, over 0.97.

11 This requires δ_j and ν_j to be uncorrelated, which should be the case from a regression. However, the two need not be independent. In fact, higher moments are likely correlated for reasons offered below.

12 Empirical Bayes (EB) methods (e.g., Aaronson et al. 2007) impose parametric assumptions—in practice they impose normal distributions, which is precisely what we wish to avoid. Note too that shrinking estimates and then using a nonparametric density estimate is not appropriate because shrinkage reduces mean square error but does not eliminate measurement error. In addition, there is some evidence that this practice leads to biased estimates of teacher effectiveness (Demming 2014; Guarino et al. 2015).

13 We use the plug-in bandwidth estimator suggested by Delaigle and Gijbels (2002, 2004). The code implementation, due to Aurore Delaigle, is available at http://www.ms.unimelb.edu.au/∼aurored/links.html#Code. For further exposition, see also Meister (2009), p. 92ff. See also Delaigle, Hall, and Meister (2008) for related work.

14 Hall and Kang (2001) examined a closely related smoother bootstrap and suggest that holding the bandwidth constant is appropriate.

15 There is some disagreement in the field about the extent to which this adjustment approach results in unbiased teacher effect estimates. See, for instance, Amrein-Beardsley (2014), Chetty et al. (2014a), Goldhaber and Chaplin (2015), Kane and Staiger (2008), Kane et al. (2013), and Rothstein (2009, 2010, 2014).

16 For examples of studies using the STAR data, see, for instance: Chetty et al. (2011); Finn et al. (2007); Folger (1989); Krueger (1999); Word et al. (1990).

17 Krueger (1999) gives some indirect estimates connecting improvements in the Stanford Achievement Tests to later earnings. Chetty et. al. (2011) linked kindergarten test scores to young adult earnings.

18 Krueger (1999), for instance, wrote, “The implementation of the STAR experiment was not flawless, but my reanalysis suggests that the flaws in the experiment did not jeopardize its main results.”

19 For instance, see, in the case of North Carolina, Clotfelter et al. (2009, 2010), Goldhaber and Hansen (2013), Rothstein (2010). And, in the case of Washington, Goldhaber, and Theobald (2013), Goldhaber et al. (2013a,c), and Krieg (2006).

20 The North Carolina data do not explicitly match students to their classroom teachers, it identifies the person administering the class's end-of-grade tests. At the elementary level, the majority of those administering the test are likely the classroom teacher; however, as we describe below, we also take several precautionary measures to reduce the possibility of inaccurately matching non-teacher proctors to students. In Washington, the proctor of the state assessment was used as the teacher–student link for 2006–2007 through 2008–2009. The “proctor” variable was not intended to be a link between students and their classroom teachers so this link may not accurately identify those classroom teachers. However, the state's new Comprehensive Education Data and Research System (CEDARS) contains a unique course ID that allows direct matching of students and teachers since 2009–2010.

21 In keeping with common practice in the literature, we require at least ten students to be in the teacher's class each year. We set a maximum class size of 29 students in North Carolina because that is the maximum allowed by state law, but allow a more lenient maximum class size of 33 in Washington State because maximum class sizes are negotiated at the district level in Washington. The maximum observed class size under STAR is 24 students. These restrictions make little difference in our samples, only 8% of classrooms are dropped due to this restriction in the STAR dataset and 1% in North Carolina and Washington.

22 Following Aaronson et al. (2007), we estimate the variance of ν_j with the mean of the standard errors across all fixed effects. We use heteroskedasticity-robust standard errors of the fixed effects.

23 Note that the STAR teacher effects are based on a single year so there is no analog to the single versus multi-year effect estimates that can be derived from the North Carolina and Washington datasets.

24 This is consistent with other research estimating the variance of teacher effects using the STAR data (Hanushek and Rivken 2010; Nye et al. 2004).

25 It is interesting to compare STAR effect sizes here to those in Pereda-Fernández (2016), despite the differences in the sample and the use of value added. We estimated a math effect size of 0.46. As an example (Table 3 column (4)), Pereda–Fernández estimates a direct effect of 0.156 and a social multiplier of 2.2 (both with large standard errors) which would give a point estimate of 0.34—fairly close to what we find.

26 About 28% of class sizes in the analytic sample are less than 18 students in STAR as compared to 20% in North Carolina and 10% in Washington.

27 Whereas the within grade variance in test performance tends to rise as students advance from one grade to the next.

28 We convert to months of schooling by dividing the effect sizes by the average grade and subject gains for the grades in each site (from Table 5 of Lipsey et al. 2012) to obtain an equivalent proportion of a school year, and then multiply this number by 9, assuming that most school years are 9 months. The effect sizes in STAR translate into a difference of about 5.5 months, whereas they translate into 3.9 months in North Carolina and 5.1 months in Washington.

29 Both experimental (e.g., Garet 2008; Glazerman et al. 2010) and nonexperimental estimates (e.g., Yoon 2007) suggest that efforts focused on improving the performance of in-service teachers yield little or mixed impacts on student achievement.

30 See Equation (14) and Online Appendix D of the Chetty et al. (2014) study for details about the simulation; and particularly p. 2672, where Chetty et al. said “Under the assumption that [value added] is normally distributed.”

31 Washington DC's recent teacher accountability policies under IMPACT may come closest to mimicking the Chetty et al. thought experiment (see Dee and Wyckoff 2013).