Value-Added and Student Growth Percentile Models: What Drives Differences in Estimated Classroom Effects?

ABSTRACT

This study shows value-added models (VAM) and student growth percentile (SGP) models fundamentally disagree regarding estimated teacher effectiveness when the classroom distribution of test scores conditional on prior achievement is skewed (i.e., when a teacher serves a disproportionate number of high- or low-growth students). While conceptually similar, the two models differ in estimation method which can lead to sizable differences in estimated teacher effects. Moreover, the magnitude of conditional skewness needed to drive VAM and SGP models apart often by three and up to 6 deciles is within the ranges observed in actual data. The same teacher may appear weak using one model and strong with the other. Using a simulation, I evaluate the relationship under controllable conditions. I then verify that the results persist in observed student–teacher data from North Carolina.

KEYWORDS:

• Evaluation
• SGP
• Student growth
• Teacher effectiveness
• VAM

1. Introduction

This study identifies how two leading models used for teacher effectiveness measurement, value-added models (VAM) and student growth percentile (SGP) models, compare to each other and shows why they differ. Variations of both models are currently in use across the United States and a growing body of work has provided direct comparisons of their reliability and validity. I expand this work by showing that skewness in the distribution of test scores in a classroom (conditional on prior achievement) is a significant factor driving these differences and can cause estimated teacher effects to differ between models often by three and up to 6 deciles. As such, a particular teacher can appear in the bottom third according to one model while appearing in the top third in the other.

Student test scores are often used to evaluate teachers (Staiger and Rockoff 2010). In 2015, the Center on Great Teachers and Leaders at American Institutes for Research published a survey of all 50 states and Washington, D.C. (here considered a state) regarding education policies and practices. They report VAMs are in use in 15 states and SGP models are in use in 19 states (Figure 1). Two of the most notable implementations are the Tennessee Value Added Assessment System (TVAAS) in Tennessee and an SGP model in Colorado (sometimes called the Colorado Model). Further, these models are increasingly being used in human resource decisions and almost always used in conjunction with other measures of the teacher’s performance (typically accounting for 15%–50% of the evaluation).

Figure 1. Mandate states with model type.

Overall, 39 states mandate student growth measures be included in some capacity in teacher evaluation (the remaining 12 recommend usage). With respect to human resource decisions such as tenure and retention, 41 states specifically mandate or recommend student growth measures (Figure 1). Although VAM and SGP models are the most common, some states either made no recommendation or specify an alternative model, and no states mandate or recommend more than one.

Researchers and practitioners in education have long sought improvements in teacher quality as a means of improving student outcomes (Hanushek and Rivkin 2010; Staiger and Rockoff 2010). Teacher performance pay and other incentives based on student-outcome metrics have been explored at length, but have been met with considerable criticism (Goldhaber et al. 2008). In particular, nonrandom student assignment to classrooms can create validity issues for these metrics (Rothstein 2010; Paufler and Amrein-Beardsley 2014; Loeb, Soland, and Fox 2014). Given the possible benefits and potential problems associated with using student growth measures to assess teacher performance, a more complete understanding of the data and methodological requirements for using student achievement data as a measure of teacher effectiveness is necessary.

A number of studies have compared VAM and SGP models based on their ability to provide stable teacher effectiveness estimates from year to year and across varying empirical specifications (Tekwe et al. 2004; Wright 2010; Goldschmidt, Choi, and Beaudoin 2012; Ehlert et al. 2013). Other studies show that VAM and SGP models can differ substantially when examining teachers in the tails of the effectiveness distribution (Goldhaber, Walch, and Gabele 2014) and in the presence of nonrandom assignment (Guarino et al. 2015).

Castellano and Ho (2015) showed that VAM and SGP models disagree because VAM models minimize squared error and SGP models minimize absolute error, and due to differences in the type of regression used. VAMs typically use OLS and the classroom mean as a measure of teacher performance while SGP models use quantile regression and the classroom median. Further, differences in the aggregation function (means or median) used are more important in driving differences between the two than differences in the type of regression (Castellano and Ho 2015). Like Castellano and Ho (2015), I show there are large differences driven by the aggregation function (which are fundamentally driven by skewness) using different data and methods. I extend these findings by using both simulated and actual student–teacher data to show the factor driving the disagreement about a particular classroom between VAM and SGP models is skewness in the within-class distribution of current-year test scores conditional on prior-year test scores, or more simply, conditional skewness. Nontechnically, this type of within-classroom conditional skewness could be described as a teacher serving or creating a few very high- or very low-growth students.

1.1. Within-Classroom Conditional Skewness

The distribution of interest in this study is the distribution of observed current-year student test scores A_{i, t, j}, conditional on their past observed achievement A_{i, t − 1, k} (where i indicates individual students, t indicates exam year, and j and k indicate particular classrooms). This is the relationship generating residuals (e_{i, t, j}) from a standard OLS model with fixed effects for each classroom: (1) $$A_{i,t,j}=\sum _{n=1}^N{\alpha }_i{A}_{i,t-n,k}+{\beta }_j{I}_j+e_{i,t,j}.$$(1)

The purpose of estimating this regression is to examine the skewness in the distribution of e_{i, t, j}, for each classroom gives us “within-classroom conditional skewness.” Some classrooms will have approximately equal proportions of positive residuals (students that performed better than expected) and negative residuals (students that performed worse than expected). This will yield within-classroom conditional skewness = 0. Some classrooms will have a larger proportion of positive residuals or negative residuals. This will yield negative or positive within-classroom conditional skewness.

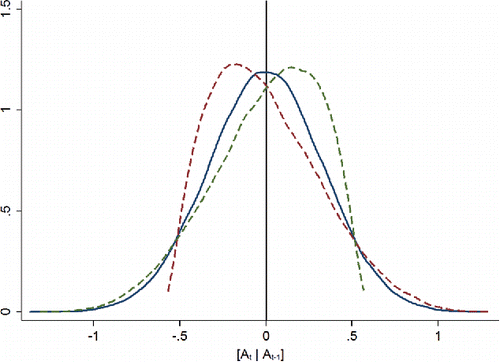
Graphically, this could appear as in Figure 2. All three plots (each representing a distribution of classroom-specific residuals, e_{i, t, j}, current test scores, A_{i, t, j}, conditional on past test scores, A_{i, t − 1, k}, centered on zero) have identical means with differing degrees of skewness (positive, zero, and negative) and thus different medians. The following analysis shows VAM and SGP models will differ in their assessment of these three types of classrooms (despite no difference in mean achievement) and quantifies the size of this effect.

Figure 2. Hypothetical skewed versus unskewed conditional distribution of test scores.

I use differences in the decile placement of a particular classroom across models to quantify the size of the differences that can be driven by within-classroom conditional skewness. I show that real-world within-classroom conditional skewness exists with sufficient magnitude to drive differences often of 3 and up to 6 deciles between the estimated effectiveness of a particular teacher produced by VAM and SGP models. A 4-decile disagreement means a particular teacher could be ranked in the 70th percentile according to one model and the 30th percentile according to the other. (Large decile differences could appear simply due to little variation in estimated teacher effects. Summary statistics below will show this is not the case for the data used here.)

2. Methods

Both VAM and SGP models are capable of a large degree of complexity (Betebenner 2009; Wright 2010; Goldhaber, Walch, and Gabele 2014). However, for comparison purposes, the models examined herein have been simplified to their most basic levels. Regressors are limited to prior test scores and, for the VAM, teacher fixed effects. (I estimated a more complex covariate adjusted model that is closer to what might be used in real-world applications and found no change to the overall inference.)

The term “value-added model” (VAM) typically refers to a broad class of linear models that use either fixed or random effects to identify a specific classroom’s contribution to the academic performance of students conditional on the students’ previous performance (see Meyer 1997; Ballou, Sanders, and Wright 2004; Hanushek and Rivkin 2010). A simple VAM using teacher fixed effects is described by (2) $$A_{i,t,j}=\sum _{n=1}^N{\alpha }_i{A}_{i,t-n,k}+{\beta }_j{I}_j+e_{i,t,j.}$$(2) Here, A_{i, t, j} denotes the performance of an individual student, i, in year t, and classroom j, and A_{i, t − n, k} denotes that same student’s performance on the test from N previous years (and subsumes all prior inputs to the student’s education). In this case, β_j denotes the effect of being in classroom j, and I_j represents an indicator variable for classroom j, while e_{i, t, j} denotes a student-specific error term. It is the estimate of β_j that is attributed to the teacher using a VAM approach.

In a student growth percentile (SGP) model, each student’s growth percentile is calculated by estimating the distribution of student test scores in a given year conditioned on prior test scores using quantile regression (Koenker and Bassett 1978; Koenker and Hallock 2001; Betebenner 2009). Quantile regression can be estimated for any number of quantiles (the extreme being a single quantile regression line, which might be used to estimate the conditional medians—as opposed to the conditional means of OLS). It is typical, when using SGP models, to use 99 quantile regression lines. To calculate a student’s growth percentile, their actual score is compared to the fitted values from all 99 quantile regressions; the percentile corresponding to the regression line that best fits the student’s actual score is the student’s growth percentile (Wright 2010). To identify a specific classroom effect, students’ growth percentiles are aggregated to the classroom (or school or district) level using the median for that group (unlike a VAM which uses fixed effects to identify mean classroom effects (while using the mean instead of median is possible in SGP, it has not typically been done as using a mean treats the percentiles as cardinal rather than ordinal)).

To understand how SGP models work and why one would expect different estimates of teacher effects compared to VAMs, I provide a brief description of relevant aspects of quantile regression. Conditional on covariate (or set of covariates) x, the τth quantile function is given by (3) $$Q_y(\tau \mid x)=\text{argmin}\sum {\rho }_{\tau }(y_i-x_i^{\text{'}}\beta ).$$(3) Here, ρ becomes the absolute value function when τ = 0.5. By changing τ, a single QR analysis could yield many regression lines fitting any quantile desired. I estimated 99 regression lines as is consistent with SGP models in practice. While it is common to estimate the conditional quantile functions as linear combinations of cubic B-spline functions to smooth SGP estimates (Betebenner 2009; Wright 2010), here I use a linear specification to facilitate direct comparison to the VAM. I explore the inclusion of spline estimation in Section 5.1.

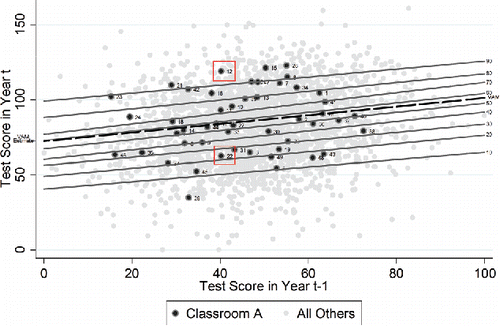
Figure 3 provides a visual explanation of the calculations of—and differences between—VAM and SGP models. Figure 3 contains 1000 simulated students with test scores from periods t and t − 1 plotted. Students have been divided into 20 classrooms and students from a particular classroom, “Classroom A,” have been bolded as larger, darker points and have been assigned a number. (These data have been created to facilitate this visualization. They are not the data used in the subsequent analysis.)

Figure 3. VAM and SGP model comparison.

A standard OLS regression line passes through the () coordinate for the entire sample with a slope that minimizes the squared error terms. The VAM adds in a fixed effect for each classroom. The fixed effect is represented by shifting the regression line up or down such that the new line maintains the same slope but passes instead through the () point for that particular classroom. The VAM estimate of classroom effects is the amount by which the line is shifted up or down; when the intercept term is suppressed, the VAM estimate can be equivalently viewed as the classroom-specific y-intercept. This is labeled “VAM Estimate” in Figure 3 and is a function of the average period t score conditional on period t − 1 scores for that particular classroom (Classroom A).

Although the main analysis uses 99 quantile regressions for the SGP model, Figure 3 shows only 9 lines for visual clarity, which represent the 10th–90th quantiles (by 10s). Where an OLS regression line represents means conditional on the x-variable(s), each quantile regression line represents a specific quantile conditional on the x-variable(s). These are seen in Figure 3, labeled 10–90.

For the main analysis, the SGPs were calculated using the statistical software, Stata. Quantiles 0.01 to 0.99 by 0.01 are modeled, the student’s observed score is compared to each expected quantile. The quantile with the smallest difference between expected and observed is assigned to that student. Visually, one can see how this is done in Figure 3. To calculate the SGP estimate of classroom effects, each individual student in the classroom is assigned the quantile of the regression line that falls closest to their actual point. For instance, student “22” (shown in Figure 3 within a red box) received a score of approximately 40 in period t − 1 and a score of approximately 60 in period t. This puts student “22” closest to the 20th percentile regression line, and she is assigned a 20 (or 0.2). The interpretation here is that while student “22” improved her score, she did not improve as much as 80% of the other students who had also initially scored a 40. Similarly, student “12” (also shown within a red box), falls closest to the 90th percentile regression line, and is assigned a 90 (or 0.9). This same calculation is done for all students in Classroom A. The SGP estimate of classroom performance is the median of these values. For Classroom A, the median student percentile is 50, so Classroom A would receive an estimated classroom performance of 50 (or 0.5).

For both VAM and SGP models, the estimated effects of Classroom A would then be viewed in the context of the estimated effects for all other classrooms. When ranked against the VAM-estimated classroom effects of other classrooms, Classroom A appears in the 70th percentile. That is, the bold VAM line lies above all but 15 of the 50 analogous lines estimated for other classrooms (not pictured). When ranked against the SGP-estimated classroom effects of other classrooms, Classroom A appears in the 50th percentile. The same data are used to calculate these two estimates, yet they differ due to the use of different empirical methods.

The visual explanation highlights that there are two fundamental differences between VAM and SGP models: the distribution being summarized, and the statistic used to summarize the distribution. VAM estimates conditional means (often relying on OLS and classroom fixed effects) to identify the effect of being in a particular classroom for the mean student. SGP models estimate conditional quantiles (often relying on quantile regression) to identify each student’s growth percentile based on prior scores. These percentiles are then summarized at the median for each classroom.

For VAM, the distributions being summarized are the actual current-year test scores conditional on prior-year test scores because the regression line represents the expected or estimated current-year test score conditional on prior performance. Thus, the (squared) deviations from the regression line are also conditional on prior-year scores. The same idea applies to SGP models and deviations from quantile regression lines. While differences in the summarized distribution are real and nonnegligible, the larger difference between these two models is in the aggregation function used to summarize the respective distributions (Castellano and Ho 2015). I show that conditional skewness in the distributions being summarized by each model causes the two to disagree about the estimated effectiveness ranking of a particular classroom. I also show that the amount of conditional skewness that occurs in the real world can cause disagreements as large as 6 deciles in actual classrooms.

3. Data

When examining models of classroom performance, criticism often arises regarding the nonrandom assignment of students to classrooms (Rothstein 2010; Paufler and Amrein-Beardsley 2014; Loeb, Soland, and Fox 2014). Some schools disproportionately serve high or low performing students and, within schools, some teachers are disproportionately assigned high or low performing students. For this reason, I employ simulated data absent any sort of selection bias. I then apply the same analysis to observed data from North Carolina schools. As an extension, I also explore simulated data with nonrandom student assignment to classrooms.

To create the simulated dataset, 1000 simulated classrooms are created. Students are assigned to these classrooms randomly in a way that matches the observed average class size. Test scores for each student, i, in years 1 and 2 are a function of a student contribution (S¹_i and S²_i, respectively) and a classroom, j, contribution. (It has become common practice to refer to this as a “teacher effect” or “teacher effectiveness,” although it is more accurate to think of it as a “classroom effect” as it estimates the common effect for all students in the same classroom.) The classroom contributions in years 1 and 2, respectively, are C¹_j and C²_j, such that: (4) $${\text{Score}}_{i,1}=S_i^1+C_j^1$$(4) (5) $${\text{Score}}_{i,2}=S_i^2+C_j^2.$$(5)

The above equations are parameterized to closely match the observed data. Table 1 shows the summary statistics for the observed North Carolina data (described below) and simulated data. The top section of Table 1 shows summary statistics at the individual student-level test scores, and the second section shows summary statistics at the classroom level. Note that columns 1 (observed North Carolina data) and 2 (simulated) match very closely in all aspects except the correlation of student scores from Year 1 to Year 2 and the correlation of the classroom average score from Year 1 to Year 2. The smaller intertemporal correlations in the simulated data are largely a function of the random assignment. When students are not randomly assigned to classrooms (described in Section 5.2), the correlation of classroom average score and the variance of classroom average scores rise.

Table 1. Observed and simulated data summary statistics.

	(1)	(2)
	Observed (NC)	Simulated
1. Individual students
Mean(score1)	344.73	344.62
Var(score1)	86.79	85.88
Mean(score2)	351.03	350.86
Var(score2)	84.53	85.66
Corr(score1, score2)	0.82	0.62
2. Classroom average
Var(score1)	24.01	24.49
Var(score2)	24.93	27.13
Corr(score1, score2)	0.88	0.71
3. Absolute conditional skewness
Mean	0.444	0.385
SD	0.366	0.309
4. VAM estimated effects
Mean	75.85	137.84
SD	2.48	5.01
Min	58.28	122.45
Max	92.50	151.49
5. SGP estimated effects
Mean	50.34	49.54
SD	17.20	23.23
Min	4.50	2
Max	97	98

Section 3 of Table 1 describes the distribution of conditional skewness in the datasets, and Sections 4 and 5 show the variation in estimated VAM and SGP effects, respectively.

To avoid the real-world problem of nonrandom assignment of students to classrooms, in the simulated data, student assignment to classrooms is completely independent from both student contribution (S¹_i and S²_i) and classroom contribution (C¹_j and C²_j). Even though students are randomly assigned to classrooms, a portion of the classrooms still end up with student variation such that the classroom distribution of test scores is skewed conditional on past scores. It is likely that, in practice, students are assigned nonrandomly to classrooms with some classrooms intentionally receiving a skewed classroom distribution of student variation. If this assignment and resulting conditional skewness is associated with underlying teacher ability, it may bias the estimation of classroom effects (Rothstein 2010). This bias is avoided here in the simulated data.

The observed student–teacher data come from school administrative files from North Carolina maintained by the North Carolina Education Research Data Center (NCERDC) at Duke University and include years 2008–2012. These data allow for the linking of student records regarding test scores and demographics to teachers, and offer the ability to track particular teachers over time. These data have been used extensively in prior research on related topics, largely because of the ability to link teachers and students (Clotfelter, Ladd, and Vigdor 2006; Goldhaber, Walch, and Gabele 2014). I restrict my sample to 4th grade math teachers linked to 4th grade end-of-grade math exams because these students are most likely to have a well-defined general or math-specific teacher.

Math teachers are identified using the state course code associated with their course. A teacher is identified as a math teacher if they teach a math course or if they teach math during a block course (e.g., a multi-subject course such as Social Studies/Math/Science). A teacher is identified as a general teacher if they teach an all-day self-contained class. A student’s general teacher is designated as a math teacher in this study if no specific math teacher exists. Classrooms with fewer than 5 and greater than 30 students are dropped. North Carolina does not specify a hard cap on 4th grade classrooms, but the LEA average may not exceed 26 (Zinth 2009). Yet it is uncommon for a class to exceed 30 students or fall below 5, so classes outside this range are dropped to examine “typical” classrooms. Students missing math scores are dropped as well.

4. Findings

The estimated classroom effects produced by each model are not on the same scale and so cannot be directly compared. To be consistent with methods used in prior work (Goldschmidt, Choi, and Beaudoin 2012), I sort the estimated effects into deciles. This method allows me to view how each model ranks a classroom compared to the rest of the sample, as well as to compare a specific classroom across models. It is the latter comparison with which this study concerns itself. To make comparisons, I use the Decile Difference, defined as: | VAM Decile_j - SGP Decile_j|. Decile Difference masks some information due to the discrete nature of splitting the estimates into deciles. Thus, I also use a continuous measure of model agreement by examining the correlations between the estimated teacher effects across models. This methodology has also been used in prior work (Tekwe et al. 2004; Goldschmidt, Choi, and Beaudoin 2012; Ehlert et al. 2013; Goldhaber, Walch, and Gabele 2014).

Because VAM uses mean and SGP uses median to draw inference about a classroom, I show that the existence of conditional skewness in the summarized distributions can cause the two models to disagree. As a baseline, Table 2 shows how standard VAM and SGP models compare in the simulated and North Carolina data. Columns 1 and 2 show, for the North Carolina data, the two models agree perfectly (decile difference = 0) 43.3% of the time, are within one decile of each other 81.1% of the time. The simulated data show a similar pattern but the models differ less often, agreeing perfectly 61.5% and within one decile 97.7% of the time (Table 2, columns 3 and 4).

Table 2. VAM-SGP decile difference: Simulated and North Carolina data.

	North Carolina		Simulated
Dec. diff.	Freq.	Percent	Freq.	Percent
0	8149	43.3	615	61.5
1	7668	40.8	362	36.2
2	2365	12.6	23	2.3
3	539	2.9
4	90	0.5
5	9	0.1
6	1	0.1
Total	18,821	100	1000	100

As seen in Table 2, standard VAM and SGP models can disagree with nontrivial frequency by 3 deciles. A large portion of the disagreement can be eliminated by forcing the two models to use the same aggregation function (means or medians). I show this by comparing a standard VAM to an SGP model that summarizes the student percentiles at the classroom mean (instead of the usual median), and comparing a standard SGP model to a VAM that summarizes the classroom scores at the median rather than mean. The median VAM is calculated by estimating a 50th percentile regression model of current scores on past scores and classroom fixed effects. Canay (2011) noted that conditional quantiles (used in QR) violate the requirement of standard fixed effects models that expectations are linear operators. This can lead to biased estimates and is not an appropriate way to evaluate teachers. It is included in this comparison for completeness and symmetry.

The first two columns of Table 3 repeat from Table 2 to remind the reader how the two standard models compare using the simulated data. The last four columns show that the VAM and SGP models that are modified to both use means (or both use medians) agree exactly in terms of decile placement in 89.6% (84.2%) of cases. The modified models agree within 1 decile 100% (99.6%) of the time. Using correlations instead of decile difference continues to show this pattern. When comparing the models that use the same aggregation function, the correlations rise from 0.976 to approximately 0.99. This shows that a large amount of the disagreement between VAM and SGP models comes from using different measures of central tendency to summarize classroom performance.

Table 3. Model agreement comparisons of VAM and SGP models; simulated data.

			Both use mean		Both use median
	Standard VAM/SGP		VAM / Mean SGP		SGP / Med. VAM
Dec. diff.	Freq.	Percent	Freq.	Percent	Freq.	Percent
0	615	61.5	896	89.6	842	84.2
1	362	36.2	104	10.4	154	15.4
2	23	2.3			4	0.4
Total	1000	100	1000	100	1000	100
Correlation	0.976		0.995		0.989
	Standard VAM/SGP correlations by absolute skewness
	Tercile			Corr. equality
	1	2	3	χ^2	Prob > χ^2
	0.982	0.977	0.971	9.52	0.025

Because means and medians are equal in the absence of skewness, it is conditional skewness in the classroom distribution of scores that is driving much of the disagreement between these two models. (Means and medians can also differ in the presence of outliers in one tail (a form of skewness) but the bounded nature of the test scores limits the effect of such outliers.) To explore this, the bottom portion of Table 3 shows the correlation between the standard models by (absolute) conditional skewness tercile. Tercile 1 contains classrooms that exhibit very little conditional skewness and the correlation is relatively high at 0.982. Tercile 3 contains classrooms that exhibit very high conditional skewness and the correlation is lower at 0.971. A chi-squared test for the joint equality of the correlations across conditional skewness terciles rejects the null hypothesis of equality, providing evidence that conditional skewness causes much of the disagreement between the two models.

Using simulated data allows me to examine the relationship free of student-selection. However, because the simulated data are free from many real-world sources of variation (despite matching the North Carolina data on observable moments), they provide only a limited view of the scope of this issue. To be relevant for policy discussions, I investigate whether the insights obtained in the simulated data persist in the real-world.

Using student–teacher data from North Carolina, Table 4 again shows VAM and SGP models that use the same aggregation function agree far more often than the standard models. Models that both use means (or both use medians) agree within one decile in 98.7% (96.9%) of cases (compared to 84.1% with the standard models). Correlations show the same relationship. The standard VAM/SGP correlation is 0.936. (This is comparable to the Spearman rank correlation found in Goldhaber, Walch, and Gabele (2014) of 0.94.) The correlation then grows to 0.985 and 0.978 for comparisons where both models use means or medians, respectively.

Table 4. Model agreement comparisons of VAM and SGP models; North Carolina.

			Both use mean		Both use median
	Standard VAM/SGP		VAM / Mean SGP		SGP / Med. VAM
Dec. diff.	Freq.	Percent	Freq.	Percent	Freq.	Percent
0	8149	43.3	12,815	68.1	12,410	65.9
1	7668	40.8	5763	30.6	5841	31.0
2	2365	12.6	232	1.2	509	2.7
3	539	2.9	11	0.1	55	0.3
4	90	0.5			6	0.1
5	9	0.1
6	1	0.1
Total	18,821	100	18,821	100	18,821	100
Corr.	0.936		0.985		0.978
	Standard VAM/SGP correlations by absolute skewness
	Tercile			Corr. equality
	1	2	3	χ^2	Prob > χ^2
	0.958	0.941	0.912	23.5	0.0000

Just as in the simulated data, the bottom of the table shows that it is conditional skewness that drives estimates of classroom effectiveness apart. The correlation between VAM and SGP models for low-skewness classrooms (Tercile 1) is greater than the correlation for high-skewness classrooms (Tercile 3), 0.958 compared to 0.912. A chi-squared test for the joint equality of the correlations across conditional skewness terciles rejects the null hypothesis of equality, again providing strong evidence that conditional skewness causes much of the disagreement between the two models.

Tables 3 (for simulated data) and 4 (for North Carolina Data) provide strong evidence that classroom conditional skewness is a driving force behind model disagreement. They do not, however, show how much of the disagreement is caused by conditional skewness. In particular, can conditional skewness of magnitudes observed in actual classrooms cause meaningful differences between the models?

To isolate the differences caused by conditional skewness alone, I hold the summarized distribution constant and allow the method of aggregation to vary. These results are reported in Table 5. Although it looks similar to Tables 3 and 4, it provides a different comparison. That is, a standard VAM (which uses classroom means) is compared to a VAM using classroom medians, and the standard SGP model (which uses classroom medians) is compared to an SGP model using classroom means. As such, all disagreements are caused by conditional skewness alone. Table 5 shows that conditional skewness is capable of causing VAM and SGP estimates to occasionally diverge by as many as 4 deciles and causing 9%–12% of classes to differ by at least 3 deciles.

Table 5. Degree of disagreement due to skewness; North Carolina.

	mean versus med		mean versus med
	VAM		SGP
Dec. diff.	Freq.	Percent	Freq.	Percent
1	9160	48.7	9329	49.6
2	7341	39.0	7764	41.2
3	1902	10.1	1555	8.3
4	358	1.9	166	0.9
5	55	0.3	7	0.1
6	5	0.1
Total	18,821	100	18,821	100

A 3-decile disagreement could cause a classroom to appear in the top quarter of the effectiveness distribution according to one model and the bottom half of the distribution according to the other. Because states and districts often choose only one of these models to use in their evaluation schemes, knowing when different models will disagree may be of particular importance.

5. Extensions

The above analysis is purposefully simplified to make the fundamental differences between VAM and SGP models clear. However, the data and models are capable of incorporating more complexity. I explore three extensions here: (1) B-spline estimation of the SGP model (a common estimation method in practical applications); (2) nonrandom assignment in the simulated data; and (3) a comparison of estimated versus known teacher effects in the simulated data.

5.1. B-Spline Estimation

In the treatment above, the SGP model was estimated linearly. This was done to minimize the difference between VAM and SGP models to focus on the fundamental underlying differences. However, in practical applications of SGP models, nonlinear estimation in the form of B-splines is often used. To verify the results discussed above are not a function of this simplification, I reestimate the results from Table 3 replacing the linear SGP model with an SGP model estimated with cubic B-splines with three internal knots. This nonlinear estimation serves primarily to model the tails of the distribution better. Table 6 shows that the results are largely unchanged from the linear specification used in Table 4. This suggests the findings are robust to practical applications.

Table 6. Model agreement comparisons of VAM and SGP spline models; North Carolina.

			Both use mean		Both use median
	Standard VAM/SGP		VAM / Mean SGP		SGP / Med. VAM
Dec. diff.	Freq.	Percent	Freq.	Percent	Freq.	Percent
0	7869	41.75	11797	62.59	9577	50.76
1	7541	40.06	6593	35.10	7831	41.63
2	2607	13.88	417	2.24	1306	7.04
3	658	3.52	14	0.19	98	0.53
4	129	0.69			8	0.12
5	17	0.18
Total	18,821	100	18,821	100	18,821	100
Corr.	0.917		0.973		0.956
	Standard VAM/SGP correlations by absolute skewness
	Tercile			Corr. equality
	1	2	3	χ^2	Prob > χ^2
	0.949	0.934	0.905	18.25	0.0001

5.2. Nonrandom Assignment in Simulated Data

The primary reason for incorporating simulated data into the analysis is to examine the model differences in the absence of nonrandom student-classroom assignment. This helps to understand the underlying differences. However, it is well-documented that students are often not randomly assigned to classrooms (Jacob and Lefgren 2007; Rothstein 2010). The differences in model disagreement frequency between the simulated and North Carolina Data suggest that nonrandom assignment may be playing a role in how these models compare to each other. To examine how nonrandom assignment can affect the amount of conditional skewness, I created a second simulated dataset wherein the top half of students from year 1 were randomly assigned to the top half of teachers from year 1, and the same with the bottom half. This showed no change to the amount of conditional skewness created.

This does not necessarily mean nonrandom assignment does not drive conditional skewness and differences between the two models. Nonrandom assignment is likely based on many factors, with prior performance being only a piece of the matching that occurs. It is likely that students and teachers are matched on a set of unobservable compatibility characteristics for which prior performance may be a crude proxy.

5.3. Estimated Versus Known Teacher Effects in Simulated Data

The purpose of this study is to show when, why, and how VAM and SGP models will differ from each other. The question of which model is “best” in an absolute sense remains up for debate. Other studies have attempted to answer this question examining things like model stability over time and correlation with other measures of teacher effectiveness (Tekwe et al. 2004; Wright 2010; Goldschmidt, Choi, and Beaudoin 2012; Ehlert et al. 2013).

It is natural to ask how well the VAM and SGP models used in this study are able to estimate the actual (known) classroom effects ranking created in the simulated data; and it is tempting to view this exercise as a test of model validity. However, given it is based on simulated data, it really serves only to identify which model most closely mimics the data-generating process of the simulated data (Berk 2010).

Table 7 shows that the VAM recovers the actual classroom effects in the simulated data (D_j from Equation (5(5) $${\text{Score}}_{i,2}=S_i^2+C_j^2.$$(5) )) marginally better than the linear or spline SGP models, while the SGP models perform almost identically to each other. This is hardly surprising as the VAM is an additive model and the simulated data are generated additively (Student variation, S_i, plus classroom variation, C_j). Given there are many complexities in the real-world that cannot be captured in simulated data, this comparison is far from conclusive. It could, however, serve as a starting point for further research.

Table 7. Estimated versus actual effects; simulated data.

	VAM/Actual		SGP (linear) / Actual		SGP (spline) / Actual
Dec. diff.	Freq.	Percent	Freq.	Percent	Freq.	Percent
0	526	52.6	434	43.4	437	43.7
1	399	39.9	450	45	451	45.1
2	70	7	95	9.5	92	9.2
3	5	0.5	20	2	19	1.9
4			1	0.1	1	0.1
Total	1000	100	1000	100	1000	100
Correlation	0.967		0.945		0.945

6. Conclusion and Future Work

While a number of studies have documented that differences exist between different VAM and SGP models, and Castellano and Ho (2015) showed these differences are largely caused by differences in the aggregation function used to attribute student performance to a particular teacher, this is the first study to identify and explore conditional skewness as the underlying factor that drives model differences and the first to quantify the practical magnitudes of these differences. While VAM and SGP models differ in their methodology, ultimately they provide very similar estimates of classroom effectiveness for many classrooms. However, I find evidence that the main characteristic of the data that causes the two models to diverge is classroom skewness in current-year test scores conditional on prior year scores (conditional skewness). I further show that conditional skewness of magnitudes observed in the actual student–teacher data can drive large differences between the models on the order of 1 to 6 deciles, a meaningful finding when one considers these models are being used to inform compensation, retention, and tenure decisions.

While disagreements of such magnitudes may be troubling, conditional skewness is observable a posteriori. It is possible to adjust one’s interpretation of the effectiveness estimate linked to a particular teacher if it is known that their classroom was particularly skewed that year. This article does not claim to identify which model is correct or better, but rather identifies where and by how much the two models disagree and suggests this be carefully considered when using these models to make personnel and other weighty decisions. If the classroom exhibits positive conditional skewness, the VAM estimate (all else equal) provides an inflated estimate compared to the SGP estimate and vice versa.

Supplemental Material

Supplemental data for this article can be accessed on the publisher's website.

Acknowledgments

The author thanks Karen Conway, Robert Mohr, Damian Betebenner, Suzanne Graham, Andrew Houtenville, and Gene Sprechini for their continuing support of this project. The author also thanks participants at the UNH economics seminar, the Lycoming College Faculty Research Forum, and participants at the Eastern Economic Conference for their helpful comments, and the North Carolina Education Research Data Center for providing the data.