Fuzzy bi-criteria scheduling on parallel machines involving weighted flow time and maximum tardiness

Abstract

This paper considers a bi-criteria scheduling on parallel machines in fuzzy environment which optimizes the weighted flow time and maximum tardiness. The fuzziness, vagueness or uncertainty in processing time of jobs is represented by triangular fuzzy membership function. The bi-criteria problem with weighted flow time and maximum tardiness as primary and secondary criteria, respectively, for any number of parallel machines is NP-hard. So, a heuristic algorithm is proposed to find the optimal sequence of jobs processing on parallel machines so as to minimize the secondary criterion of maximum tardiness without violating the primary criterion of weighted flow time. A numerical illustration is also given in support of the algorithm proposed.

Keywords:

• fuzzy processing time
• average high ranking
• maximum tardiness
• weighted flow time
• due date
• weighted shortest processing time

Public Interest Statement

In this bi-objective parallel machine scheduling problem a system of n-independent jobs are to be processed on any of the available m-identical parallel machines. The processing times of jobs are considered to be uncertain or vague in nature due to the presence of some external sources. Fuzzy set theory is used to handle the uncertainty involved. The delay in processing of jobs is called tardiness or lateness and the delayed job is called tardy job. The flow time of a job is the total time it spends in the system i.e. sum of waiting times and processing times. In case when the jobs have different degree of importance, indicated by the weight of the job, the total weighted flow time is the simplest measure of the quality of service received by the jobs. Therefore, the paper seeks to highlight optimization of maximum tardiness and minimum weighted flow time of jobs.

1. Introduction

Scheduling is concerned with the optimal allocation of scare resources with objective of optimizing one or several criteria’s (Baker, 1974). Scheduling of jobs has been a fruitful area of research for many decades, in which order of processing of jobs is decided. If the jobs are scheduled properly, it not only saves time but also increases the efficiency of the system. The classical parallel machine scheduling problem includes the scheduling of n- independent jobs say {1, 2, …, n}, on a set of m-identical parallel machines say {1, 2, …, m}. Every job is considered with a deterministic processing time p_i, a release date r_i, and a due date d_i while optimizing the objective function as number of tardy jobs, maximum tardiness, weighted flow time, maximum completion time, etc. However, due to the sources of uncertainty and complex nature of the problems in real-time situations, it is quite erratic to set them as precise values. Some researchers work on the concept of probability distribution to model parallel machine problem that is usually predicted from chronological data. But, whenever production data are unreliable or presented in vague way, stochastic models may not be the best choice. Fuzzy set theory may provide an alternative approach for dealing with the vagueness. Zadeh (1965) was first to introduce fuzzy sets as a mathematical way of representing impreciseness or vagueness in everyday life. Fuzzy set theory has numerous applications in various fields such as engineering, medicine, manufacturing, and others. In real-life situations, the processing times of jobs are not always exact due to incomplete knowledge or uncertain environment which implies the existence of various external sources and types of uncertainty. Fuzzy set theory can be used to handle uncertainty inherent in actual scheduling problems.

On single machine bi-criteria, Smith (1956) was the first to consider minimization of weighted completion time subject to minimal value of T_max. The other literature on single machine bi-criteria includes (Chand & Schneeberger, 1986; Gupta, Hariri, & Potts, 1999). Su, Chen, and Chen (2012) dealt with scheduling on parallel machines to minimize the maximum tardiness. For parallel-machine scheduling problems concerning bi-criterion, Parkash (1997) studied the bi-criteria scheduling problems on parallel machines and analyzed that the bi-criteria function is NP-hard. Sarin and Hariharan (2000) proposed a heuristic for a two-machine case with objective as minimizing number of tardy jobs under the constraint of minimizing maximum tardiness. A review of scheduling on parallel machines was given by Mokotoff (2001). Gupta, Ruiztorres, and Webster (2003) considered the scheduling of jobs on identical parallel machines for minimizing maximum tardiness with optimal flow time. In his paper, the type of scheduling problems is presented as: Identical parallel machines; Uniform parallel machines and unrelated parallel machines. Optimizing dual performance measures on parallel machines in fuzzy environment is fairly an open area of research. A survey of literature has revealed little work reported on the bi-criteria scheduling problems on parallel machine in fuzzy environment. Jha, Indumati, Singh, and Gupta (2011) formulated a fuzzy bi-criterion release time problem related to cost minimization and reliability maximization objectives under budgetary constraint. Sunita and Singh (2010a, 2010b) studied the optimization of various characteristics on parallel machines in fuzzy environment. Gupta, Gupta, Sharma, and Aggarwal (2012) developed an algorithm for the bi-objective problem which optimizes the number of tardy jobs without violating the value of T_max with uncertain processing time. Sharma, Gupta, and Seema (2013) developed an algorithm to schedule jobs on parallel identical machines so as to minimize the secondary criteria of weighted flow time without violating the primary criteria of maximum tardiness in fuzzy environment. Sharma, Gupta, and Seema (2012) studied the bi-objective problem with total tardiness and number of tardy jobs as primary and secondary criteria, respectively, for any number of parallel machines in fuzzy environment.

The two approaches can be involved for bi-criteria problems: both the criteria’s are optimized simultaneously by using suitable weights for the criteria’s. Second, the criteria’s are optimized sequentially by first optimizing the primary criterion and then the secondary criterion subject to the value obtained for the primary criterion. In the present paper, we study the bi-objective scheduling on parallel machines in which the problem is divided into two steps: in the primary step, the weighted flow time of jobs is calculated and in the secondary step, the maximum tardiness is minimized with bi-objective function as T_max/WFT. The concept of fuzziness in processing time of jobs is introduced as in real-life situations the processing time of jobs may vary due to the lack of complete knowledge and the decision-making process gets more complicated with increment in the number of constraints.

The rest of the paper is organized as follows: In Section 2, problem is formulated. Section 3 describes the basics of fuzzy set theory. Section 4 deals with various theorems for optimizing the bi-criteria problem. Section 5 describes the algorithm proposed to find the optimal sequence for bi-criteria problem T_max/WFT. In Section 6, numerical illustrations are given to support the proposed algorithm. The paper is concluded in Section 7 followed by the references.

2. Problem formulation

The following notations have been used throughout the present paper.

i	=	designate the ith job, i = 1, 2, 3, …, n
di	=	due date of the ith job
Ci	=	completion time of the ith job
wi	=	weightage of the ith job
Ti	=	tardiness of the ith job = max (Ci − di, 0)
Tmax	=	maximum tardiness
n	=	total number of jobs to be scheduled
m	=	total number of parallel machines
WFT(S)	=	weighted flow time of jobs for sequence S

The following assumptions are taken into consideration for developing bi-criteria algorithm on parallel machines.

1. The jobs are available at time zero.

2. No pre-emption of jobs is allowed.

3. The machines are identical in all respects.

4. The machines are available all the time.

5. The jobs are independent of each other.

6. Each machine can process at most one job at a time.

Before formulating the bi-criteria problem, the mathematical formulation for the single criterion’s are represented first. These are:

2.1. Criterion: weighted flow time

The weighted flow time is the weighted version of flow time. The formulation to minimize the WFT is as follows:$$\text{Minimize}\text{WFT}(S)=\sum _{i=1}^n{w}_i{C}_i$$

Subject to the condition that all weights for jobs are non-negative,

Here, S is the given sequence and WFT(S) is the corresponding objective function of weighted flow time.

2.2. Criterion: maximum tardiness

Tardiness is given by T_i = max (C_i − d_i, 0), where C_i and d_i are the completion time and due date of the ith job, respectively. Maximum tardiness is given by T_max = max(T_i).

The formulation is as follows:$$\begin{array}{c}\text{Minimize}Z=T_{max},\hfill \\ \text{Subject}\text{to}\text{constraint}:T_{max}\ge C_i-d_i\forall i\hfill \end{array}$$

along with the non-negativity constraints.

The formulation of the bi-criteria problems is similar to that of single criteria problems but with some additional constraints requiring that the optimal value of the primary objective function is not violated. Here, the problem is divided into two steps: one is primary in which weighted flow time of jobs is minimized and in secondary step, the maximum tardiness of jobs is minimized under the objective function value of primary criterion.

3. Basic fuzzy set theory

A fuzzy set $\stackrel{\sim }{A}$ defined on the universal set of real numbers R, is said to be a fuzzy number if its membership function has the following characteristics:

1. ${\mathit{\mu }}_{\stackrel{\sim }{A}}:R\to [0,1]$ is continuous.

2. ${\mathit{\mu }}_{\stackrel{\sim }{A}}=0$ for all x ∈ (−∞, a₁) ∪ (a₃, ∞).

3. ${\mathit{\mu }}_{\stackrel{\sim }{A}}$ is strictly increasing on [a₁, a₂] and strictly decreasing on [a₂, a₃].

4. ${\mathit{\mu }}_{\stackrel{\sim }{A}}=1$ for x = a₂.

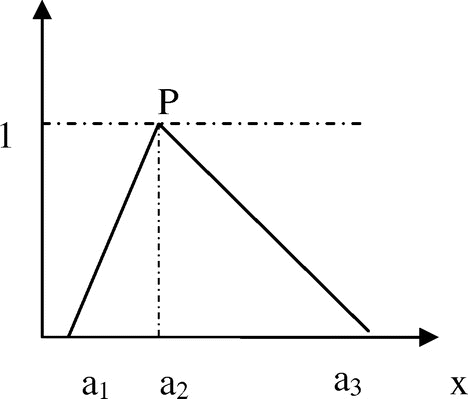
3.1. Triangular fuzzy number

Triangular fuzzy number (TFN) is a fuzzy number represented with three points as $\stackrel{\sim }{A}=(a_1,a_2,a_3)$, where a₁ and a₃ denote the lower and upper limits of support of a fuzzy set $\stackrel{\sim }{A}$. The membership value of the x denoted by ${\mathit{\mu }}_{\stackrel{\sim }{A}}(x),x\in R^{+}$, can be calculated according to the following formula (Figure 1).$$\begin{array}{c}{\mathit{\mu }}_{\stackrel{\sim }{A}}(x)=\left\{\begin{array}{cc}0;\hfill & x\le a_1\\ \frac{x-a_1}{a_2-a_1};\hfill & a_1<x<a_2\\ \frac{a_3-x}{a_3-a_2};\hfill & a_2<x<a_3\\ 0;\hfill & x\ge a_3\end{array}\right.\hfill \end{array}$$

Figure 1. Triangular fuzzy number.

3.2. Average high ranking

The system characteristics are described by membership function; it preserves the fuzziness of input information. However, the designer would prefer one crisp value for one of the system characteristics rather than fuzzy set. In order to overcome this problem, we defuzzify the fuzzy values of system characteristic by using the Yager’s (1981) formula. If $\stackrel{\sim }{A}=(a_1,a_2,a_3)$, then its crisp value is defined as:(1) $$\text{crisp}(\tilde{A})=h(\tilde{A})=\frac{3a_2+a_3-a_1}{3}$$(1)

3.3. Fuzzy arithmetic operations

If ${\tilde{A}}_1=(m_{A_1},{\mathit{\alpha }}_{A_1},{\mathit{\beta }}_{A_1})$ and ${\tilde{A}}_2=(m_{A_2},{\mathit{\alpha }}_{A_2},{\mathit{\beta }}_{A_2})$ be the two TFNs, then

1. ${\tilde{A}}_1+{\tilde{A}}_2=(m_{A_1},{\mathit{\alpha }}_{A_1},{\mathit{\beta }}_{A_1})+(m_{A_2},{\mathit{\alpha }}_{A_2},{\mathit{\beta }}_{A_2})=(m_{A_1}+m_{A_2},{\mathit{\alpha }}_{A_1}+{\mathit{\alpha }}_{A_2},{\mathit{\beta }}_{A_1}+{\mathit{\beta }}_{A_1})$.

2. ${\tilde{A}}_1-{\tilde{A}}_2=(m_{A_1},{\mathit{\alpha }}_{A_1},{\mathit{\beta }}_{A_1})-(m_{A_2},{\mathit{\alpha }}_{A_2},{\mathit{\beta }}_{A_2})=(m_{A_1}-m_{A_2},{\mathit{\alpha }}_{A_1}-{\mathit{\alpha }}_{A_2},{\mathit{\beta }}_{A_1}-{\mathit{\beta }}_{A_2})$, if the following condition is satisfied $DP\left(\stackrel{\sim }{A_1}\right)\ge DP\left(\stackrel{\sim }{A_2}\right)$, where $DP(\stackrel{\sim }{A_1})=\frac{{\mathit{\beta }}_{A_1}-m_{A_1}}{2}$ and $DP(\stackrel{\sim }{A_2})=\frac{{\mathit{\beta }}_{A_2}-m_{A_2}}{2}$. Here, DP denotes difference point of a TFN.

3. Otherwise; ${\tilde{A}}_1-{\tilde{A}}_2=(m_{A_1},{\mathit{\alpha }}_{A_1},{\mathit{\beta }}_{A_1})-(m_{A_2},{\mathit{\alpha }}_{A_2},{\mathit{\beta }}_{A_2})=(m_{A_1}-{\mathit{\beta }}_{A_2},{\mathit{\alpha }}_{A_1}-{\mathit{\alpha }}_{A_2},{\mathit{\beta }}_{A_1}-m_{A_2})$.

4. $k{\tilde{A}}_1=k(m_{A_1},{\mathit{\alpha }}_{A_1},{\mathit{\beta }}_{A_1})=(k{m}_{A_1},k{\mathit{\alpha }}_{A_1},k{\mathit{\beta }}_{A_1})$; if k > 0.

5. $k{\tilde{A}}_1=k(m_{A_1},{\mathit{\alpha }}_{A_1},{\mathit{\beta }}_{A_1})=(k{\mathit{\beta }}_{A_1},k{\mathit{\alpha }}_{A_1},k{m}_{A_1})$; if k < 0.

4. Theorems

The following theorems have been established to optimize the bi-criteria scheduling on parallel machines involving weighted flow time and maximum tardiness.

4.1. Theorem

A sequence S of jobs following weighted smallest processing time (WSPT) rule, in which the jobs are placed to the earliest available location on the machines in WSPT order, minimizes the weighted flow time.

Proof

Let if possible sequence S obtained by using the WSPT rule, i.e. by arranging the jobs in the decreasing order of their weights; break the ties (if any) arbitrary is not optimal. Let there exist a better sequence of jobs S′ (say) in which ith and jth adjacent jobs are interchanged.

Let C_i(S) and C_j(S) be the completion times of ith and jth job, respectively, in schedule S, respectively. Similarly, let C_i(S′) and C_j(S′) be the completion times of ith and jth job, respectively, in schedule S′.

For sequence S: We have$$C_i(S)=t_a+1,C_j(S)=t_a+2$$

For sequence S′: We have$$C_i(S^{\prime })=t_a+2,C_j(S^{\prime })=t_a+1$$

Next, the weighted flow time for the sequence S of jobs is(2) $$\text{WFT}(S)=w_i\times C_i(S)+w_j\times C_j(S)=w_i\times (t_a+1)+w_j\times (t_a+2)=w_i{t}_a+w_i+w_j{t}_a+2w_j=(w_i+w_j)t_a+w_i+2w_j$$(2)

Similarly, the weighted flow time for the sequence S′ jobs is(3) $$\text{WFT}(S^{\prime })=w_i\times C_i(S^{\prime })+w_j\times C_j(S^{\prime })=w_i\times (t_a+2)+w_j\times (t_a+1)=w_i{t}_a+2w_i+w_j{t}_a+w_j=(w_i+w_j)t_a+2w_i+w_j$$(3)

Since, the ith and jth jobs are placed by WSPT rule. Therefore, we have w_i ≥ w_j.

Hence, from results (2) and (3), we have

WFT(S′) ≥ WFT(S), i.e. weighted flow time for the sequence S′ is more as compared to the sequence S.

Hence, the sequence S following the WSPT rule minimizes the weighted flow time.

4.2. Theorem

A sequence S of jobs following early due date (EDD) order is an optimal sequence with maximum tardiness (T_max).

Proof

Let if possible sequence S following EDD is not an optimal sequence. Let there exist a better sequence of jobs S′ (say) i.e. a late job in S is early in S′. Let S′ be the schedule in which ith and jth adjacent jobs are interchanged, i.e.

$$S=1-2-3-4-\dots -i-j-\dots -n$$$$S^{\prime }=1-2-3-4-\dots -j-i-\dots -n$$

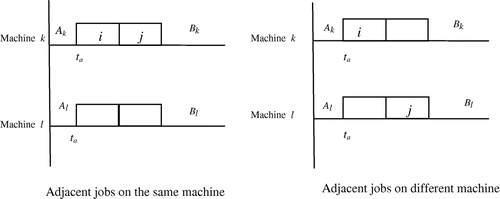
The ith and jth jobs are adjacent on parallel machines if they are placed on adjacent positions as shown in Figure 2. Further, an adjacent pair of jobs may be located on the same machine, say k, or on different machines, say k and l. The jobs appearing on the machines before an adjacent pair are designated by A and those appearing after the pair are designated by B with an appropriate subscript for the corresponding machine. Let t_a be the completion time of the job before ith job on a machine.

Figure 2. Adjacent jobs on parallel machines.

In schedule S: Irrespective of the fact that the ith and jth adjacent jobs are on same machine or on different machines, we have$$T_i=max\left\{t_a+1-d_i,0\right\},T_j=max\left\{t_a+2-d_j,0\right\}$$

In schedule S′: We have$$T_i^{\prime }=max\left\{t_a+2-d_i,0\right\},T_j^{\prime }=max\left\{t_a+1-d_j,0\right\}$$

Since, d_i ≤ d_j, we have $T_i\le T_i^{\prime }$ and $T_j\le T_j^{\prime }$.

Therefore, $max\left\{T_i^{\prime },T_j^{\prime }\right\}\ge max\left\{T_i,T_j\right\}$.

This implies that the sequence S is better.

Hence, sequence S of jobs following EDD order is the optimal sequence for T_max.

4.3. Theorem

If all the jobs have distinct weights, then no improvement can be made to the values of any secondary criterion of maximum tardiness.

Proof

Let S be the schedule obtained by arranging the jobs by WSPT order. Let C_i be the completion time of ith job and C_j be the completion time of jth job. Let S_i and S_j be the corresponding secondary criterion values. When ith and jth jobs are switched, let S′ be the schedule so obtained.

If C_i < C_j then, $C_i^{\prime }=C_j$ and $C_i=C_j^{\prime }$. Hence, $w_i{C}_i+w_j{C}_j<w_i{C}_i^{\prime }+w_j{C}_j^{\prime }$, which is a violation to primary criterion as all the other jobs contribute the same. Therefore, it implies that no improvement to the value of secondary criterion can be made with any possible exchange of jobs. The only possibility left is to rearrange the jobs having the same weights so that the value of a secondary criterion can be improved.

4.4. Theorem

If the problem of single criteria, maximum tardiness is NP-hard, the scheduling problem on parallel machines optimizing the bi-objective function maximum tardiness/WFT will also be NP-hard.

Proof

We shall prove the result by the method of contradiction:

Let if possible the bi-objective function maximum tardiness/WFT is not NP-hard. Therefore, there must exist a polynomial algorithm which can solve the problem of optimizing the bi-objective function maximum tardiness/WFT on parallel processing machines.

This implies that single criteria of maximum tardiness can be optimized in polynomial time, i.e. maximum tardiness is not NP-hard. This is a contradiction, as maximum tardiness is NP-hard.

Hence, the scheduling problem optimizing the bi-objective function maximum tardiness/WFT on parallel processing machines will also be NP-hard.

5. Algorithm

The following algorithm is proposed to find the optimal sequence for bi-criteria problem T_max/WFT:

Step 1: Find average high ranking (AHR) of the fuzzy processing time of various jobs on different machines.

Step 2: Arrange all the jobs in weighted shortest processing time (WSPT) order.

Step 3: If all the jobs have distinct weights then go to Step 5.

Step 4: If all the jobs do not have distinct weights then arrange all the jobs with same weights in EDD order. Break the tie if any arbitrarily. Note the improvement in T_max subject to the primary set of constraints.

Step 5: Assign the jobs one by one to the earliest available machine. This optimizes the objective T_max/WFT.

6. Numerical illustration

The following numerical illustrations are given to test the efficiency of algorithm proposed to optimize the bi-criteria T_max/WFT on parallel machines in fuzzy environment.

Consider an example of jobs with processing time in fuzzy environment, due date and with jobs weightage (being distinct) on three parallel machines in a flow shop. The objective is to obtain a sequence of the jobs processing optimizing the bi-criteria taken as T_max/WFT (Table 1).

Table 1. Jobs with fuzzy processing time

Jobs	1	2	3	4	5
Processing time (in fuzzy environment)	(9, 10, 11)	(16, 17, 18)	(9, 10, 11)	(6, 7, 8)	(11, 12, 13)
Due date (di)	13	19	18	11	15
Weightage (wi)	3	4	2	5	1

Solution: The AHR of processing time of given jobs as per the Step 1 using Equation 1 is as follows: (Table 2)

Table 2. Jobs with AHR of processing time

Jobs	1	2	3	4	5
AHR of processing time	32/3	53/3	32/3	23/3	38/3
Due date (di)	13	19	18	11	15
Weightage (wi)	3	4	2	5	1

On arranging the jobs as per Step 2 in WSPT order on the parallel available machines M₁, M₂, and M₃, the order of jobs becomes 4–2–1 –3–5. The in–out i.e. the flow of jobs on machines for WSPT order is as in Table 3.

Table 3. In–out of jobs following WSPT order

Jobs	4	2	1	3	5
M1	0–23/3			23/3–55/3
M2		0–53/3
M3			0–32/3		32/3–70/3
Due date (di)	11	19	13	18	15
Weightage (wi)	5	4	3	2	1
Tardiness (Ti)				1/3	25/3

Therefore, T_max = 25/3 units and weighted flow time, $\text{WFT}={\sum }_{i=1}^n{w}_i{C}_i=5\times \frac{23}{3}+4\times \frac{53}{3}+3\times \frac{32}{3}+2\times \frac{55}{3}+1\times \frac{70}{3}=201\text{units}$.

As per the Step 3, all the jobs have distinct weights; therefore, assigning the jobs to the available machines optimizes secondary criteria of T_max. Hence, the optimal sequence which optimizes the objective T_max/WFT is 4–2–1–3–5 with WFT = 201 units and minimum T_max = 25/3.

Consider another example of jobs with processing time in fuzzy environment, due date and with jobs weightage (being not distinct) on three parallel machines in a flow shop is given. The objective is to obtain sequence of the jobs processing optimizing the bi-criteria taken as T_max/WFT (Table 4).

Table 4. Jobs with fuzzy processing time

Jobs	1	2	3	4	5	6	7
Processing time (in fuzzy environment)	(7, 8, 9)	(6, 7, 8)	(10, 11, 12)	(8, 9, 10)	(6, 7, 8)	(11, 12, 13)	(8, 9, 10)
Due date (di)	12	18	19	16	10	13	15
Weightage (wi)	5	3	3	2	1	4	2

Solution: The AHR of processing time of given jobs as per Step 1 using Equation 1 is as follows: (Table 5)

Table 5. Jobs with AHR of processing time

Jobs	1	2	3	4	5	6	7
AHR of processing time	26/3	23/3	35/3	29/3	23/3	38/3	29/3
Due date (di)	12	18	19	16	10	13	15
Weightage (wi)	5	3	3	2	1	4	2

On arranging the jobs as per Step 2 in WSPT order on the parallel available machines M₁, M₂, and M₃, the order of jobs becomes1–6–2–3–4–7–5. The in–out flow of jobs on machines is as in Table 6.

Table 6. In–out of jobs in WSPT order

Jobs	1	6	2	3	4	7	5
M1	0–26/3				26/3–55/3		55/3–78/3
M2		0–38/3				38/3–67/3
M3			0–23/3	23/3–58/3
Due date (di)	12	18	19	16	10	13	15
Weightage (wi)	5	4	3	3	2	2	1
Tardiness (Ti)				10/3	25/3	28/3	11

Therefore, maximum tardiness, T_max = 11 units and $\text{WFT}={\sum }_{i=1}^n{w}_i{C}_i=5\times \frac{26}{3}+4\times \frac{38}{3}+3\times \frac{23}{3}+3\times \frac{58}{3}+2\times \frac{55}{3}+2\times \frac{67}{3}+1\times \frac{78}{3}=282.3\text{units}$.

Since the weights corresponding to jobs are not distinct, therefore, as per the Step 3 of algorithm we optimize T_max with given WFT. Following this we arrange the jobs 2 and 3 with same weightage as 3 in EDD order. Also, arrange the jobs 4 and 7 with same weightage as 2 in EDD order. Since the job 3 has EDD than the job 2, therefore, the job 3 will come before the job 2 in EDD order. The jobs 4 and 7 are already in EDD order. Following this we have the in–out of jobs as in Table 7.

Table 7. In–out of jobs following EDD order

Jobs	1	6	3	2	4	7	5
M1	0–26/3			26/3–49/3			49/3–72/3
M2		0–38/3				38/3–67/3
M3			0–35/3		35/3–64/3
Weightage (wi)	5	4	3	3	2	2	1
Due date (di)	12	18	16	19	10	13	15
Tardiness (Ti)	–	–	–	–	34/3	28/3	27/3

Therefore, maximum tardiness, T_max = 34/3 units and WFT = ${\sum }_{i=1}^n{w}_{i}C=5\times \frac{26}{3}+4\times \frac{38}{3}+3\times \frac{35}{3}+3\times \frac{49}{3}+2\times \frac{64}{3}+2\times \frac{67}{3}+1\times \frac{72}{3}=288\text{units}$ which violates the primary criterion of WFT having value 288 units. Therefore, reject the sequence1–6–3–2–4–7–5. Hence, the optimal sequence of jobs processing is 1–6–2–3–4–7–5 with minimum WFT as 282.3 units and minimum T_max as 11 units.

7. Conclusion

In this paper, an algorithm to optimize the bi-criteria scheduling problem involving maximum tardiness and weighted flow time on parallel machines in fuzzy environment is considered. The concept of fuzzy processing time is introduced in processing of jobs, as in many real-life situations the processing time of jobs may vary due to the lack of complete knowledge, uncertainty, and vagueness. The study may further be extended by introducing the concepts of non-availability constraints, machines processing the jobs with different speeds, and also by considering trapezoidal fuzzy membership functions to represent the fuzziness in processing time.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Sameer Sharma

The group of authors involved in this critically researched paper consists in Deepak Gupta, Sameer Sharma, and Kewal Krishan Nailwal. The team under the competent supervision of Deepak Gupta works in the area of scheduling problems. Some research work on optimizing scheduling problems in industry with various parameters along with the linkage models has been contributed. This paper particularly optimizes a fuzzy bi-criteria problem involving weighted flow time and tardiness. This paper will go in a long way to solve the problems faced in production management where a quality service means product is to be processed with minimum weighted flow time and meeting customer’s required due date or satisfaction of the customer. Besides this, a fuzzy environment of the problem brings the problem closer to real-life application area as fuzzy theory tackles well with vagueness and uncertainty in processing times of jobs.