Dynamics of asymmetric intraguild predation with time lags in reproduction and maturation

Abstract

A three dimensional (3D) stage-structured predator–prey model is proposed and analyzed to study the effect of intraguild predation with harvesting of the adult species. Time lags in reproduction and maturation of the organism are introduced in the system and conditions for local asymptotic stability of steady states of delay differential forms of the ODE model are derived. The length of the delay preserving the stability is also estimated. Moreover, it is shown that the system undergoes a Hopf bifurcation when the time lags cross certain critical values. The stability and direction of the Hopf bifurcations are determined by applying the normal form method and the center manifold theory. Computer simulations have been carried out to illustrate various analytical results.

Keywords:

• IGP
• reproduction delay
• maturation delay
• Hopf bifurcation

Public Interest Statement

Organisms go through multiple life stages as they proceed from birth to death. Cannibalism has become a prevalent feature of stage-structured populations in both aquatic and terrestrial food webs. Two fishes,Parrotfish and Pterois Volitans in coral reef ecosystem, are considered for the study of interactions within and among the stage-structured populations. With the proliferation of Pterois Volitans, there is a reduction in the density of herbivorous reef-fish. The reduction in herbivory in coral reefs can lead to a change of community structure of coral reefs for which corals decline with the proliferation of seaweeds. In this paper it is observed that cannibalism of Pterois Volitans population ensures the release of predation pressure on Parrotfish population. With the proliferation of Pterois Volitans, the system becomes oscillatory. Harvesting of adult Pterois Volitans helps in stabilizing the system.

1. Introduction

Many organisms go through multiple life stages as they proceed from birth to death. A stage-structured model of population growth consists of juvenile and adult organisms where the juveniles have no reproductive ability (Wang & Chen, 1997). Field observations by Rudolf (2007) suggest that cannibalism is a prevalent feature of stage-structured populations in both aquatic and terrestrial food webs. In this type of ecological interaction, two species of the same trophic level interact as predator and prey, known as intraguild predation (IGP). As stated by Polis, Myers, and Holt (1989), IGP can be classified as symmetrical or asymmetrical. Symmetric IGP occurs when there is mutual predation between two species, whereas in asymmetrical interaction, one species consistently preys upon the other (Zhang, Chen & Neumann, 2000). Stage structure with cannibalism is an asymmetric IGP (Rudolf, 2008).

Two fishes, Parrotfish and Pterois Volitans are considered for the study of interactions within and among the stage-structured populations. As observed by Morris et al. (2009), Pterois Volitans are one of the top levels of the food web in many coral reef environments. They are known to feed mostly on small fishes, which include juveniles of their own species. Apart from preying on Parrotfish, adult Pterois Volitans exhibits a distinct cannibalistic attitude towards its juvenile species. As observed by Goreau and Hayes (1994), Hare and Whitfield (2003), and Albins and Hixon (2008), the proliferation of predatory Pterois Volitans reduces the population density of herbivorous Parrotfish by changing the community structure of coral reefs for which corals decline with an increase in abundance of seaweeds. According to NOAA (National Oceanic and Atmospheric Administration), commercial harvesting of adult Pterois Volitans is required to reduce the numbers of Pterois Volitans to mitigate their impact on coral reef ecosystems (Morris & Whitfield, 2009).

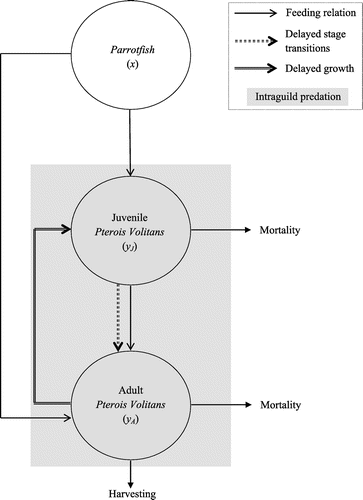
The role of time delay on ecosystem models has been investigated by Jiao, Yang, Cai and Chen (2009), and Dhar and Jatav (2013). Motivated by their works, we have studied a stage-structured system (Bhattacharyya & Pal, 2013) with Parrotfish at the first trophic level, and juvenile and adult Pterois volitans at the second and third trophic level, respectively. The model is based on the assumption that juvenile Pterois volitans can neither predate nor reproduce and the reproduction of adult Pterois volitans is mediated by some discrete time lag. The model used in this paper is a direct extension of the stage-structured model studied in (Bhattacharyya & Pal, 2013) with adult Pterois Volitans as IG-predator, juvenile Pterois Volitans as IG-prey, and Parrotfish as their common resource under the assumption that juveniles can predate, but do not reproduce. In the model, the IG-predator and IG-prey compete for Parrotfish, while the IG-predator exhibits asymmetric IGP. We assume that the reproduction of IG-predator is not instantaneous, but is be mediated by some discrete time delay required for egg deposition, embryo development, and hatching (Martin & Ruan, 2001). Further, we incorporate a discrete time lag, known as stage delay required by the IG-prey to become adult (Gourley & Kuang, 2004). The IG-predator is harvested to control its growth. We examine the effects of discrete time lags in reproduction and maturation of Pterois volitans on the dynamics of the IG-system. A schematic diagram of the system is given in Figure 1.

Figure 1. Schematic diagram of the intraguild system with delays.

Stability analysis of the systems are performed. We have estimated the delays for which the system preserves its stability around the positive steady state. We show that when the parameters representing reproduction and maturation time delay pass through some critical value, the interior equilibrium loses its stability and a Hopf bifurcation occurs. Numerical simulations under a default set of parameter values have been performed to support our analytical findings.

2. The basic model

We take a stage-structured model where Parrotfish is growing on the system with concentration $x(t)$ at time $t$. The organisms, juvenile and adult Pterois Volitans, are introduced in the system with concentrations $y_J(t)$ and $y_A(t)$, respectively, at time $t$. It is assumed that adult Pterois Volitans is cannibalistic and the juveniles have no reproductive ability—an exhibition of asymmetric IGP. The parameter ${\mathit{\tau }}_1$ represents the delay in reproduction and ${\mathit{\tau }}_2$ represents the delay in maturation of Pterois Volitans. Adult Pterois Volitans is harvested to control its growth.

We make the following assumptions in formulating the mathematical model:

(H1)	In absence of Pterois Volitans, the growth equation of Parrotfish follows logistic growth with intrinsic growth rate $r$ and carrying capacity $K$.
(H2)	The per capita feeding rate of juvenile Pterois Volitans is assumed to follow Holling II functional response. Adult Pterois Volitans feed on Parrotfish and juvenile Pterois Volitans; accordingly the per capita feeding rate of adult Pterois Volitans follows a generalized form of Holling II functional response as a function of the concentrations of Parrotfish and juvenile Pterois Volitans.
(H3)	The mortality rates of juvenile and adult Pterois Volitans are $d_1$ and $d_2$, respectively. The rate of maturation of juvenile Pterois Volitans is proportional to the concentration of the juvenile population with proportionality constant $\mathit{\mu }$.
(H4)	Adult Pterois Volitans ($y_A$) prey on Parrotfish ($x$) with uptake rate $\frac{m_{1}x{y}_A}{a_1+x+b_1{y}_J}$ which leads to the delayed growth of new juveniles ($y_J$) with growth rate $\frac{e_1{m}_{1}x(t-{\mathit{\tau }}_1)y_A(t-{\mathit{\tau }}_1)}{a_1+x(t-{\mathit{\tau }}_1)+b_1{y}_J(t-{\mathit{\tau }}_1)}$.
(H5)	Also, adult Pterois Volitans ($y_A$) exhibit cannibalism on juveniles ($y_J$) with $\frac{m_2{y}_J{y}_A}{a_2+x+b_2{y}_J}$ as uptake rate leading to the delayed growth of new juveniles ($y_J$) with growth rate $\frac{e_2{m}_2{y}_J(t-{\mathit{\tau }}_1)y_A(t-{\mathit{\tau }}_1)}{a_2+x(t-{\mathit{\tau }}_1)+b_2{y}_J(t-\mathit{\tau })}$. Thus, $m_2\left(\frac{y_J{y}_A}{a_2+x+b_2{y}_J}-\frac{e_2{y}_J(t-{\mathit{\tau }}_1)y_A(t-{\mathit{\tau }}_1)}{a_2+x(t-{\mathit{\tau }}_1)+b_2{y}_J(t-{\mathit{\tau }}_1)}\right)$ represents the reduction in growth rate of juvenile Pterois Volitans due to cannibalism.

The basic equations with all of the parameters are:(1) $$\begin{array}{cc}\hfill \frac{dx}{dt}& =rx\left(1-\frac{x}{K}\right)-\frac{mx{y}_J}{a+x}-\frac{m_{1}x{y}_A}{a_1+x+b_1{y}_J}\hfill \\ \hfill \frac{d{y}_J}{dt}& =\frac{e_1{m}_{1}x(t-{\mathit{\tau }}_1)y_A(t-{\mathit{\tau }}_1)}{a_1+x(t-{\mathit{\tau }}_1)+b_1{y}_J(t-{\mathit{\tau }}_1)}+\frac{e_2{m}_2{y}_J(t-{\mathit{\tau }}_1)y_A(t-{\mathit{\tau }}_1)}{a_2+x(t-{\mathit{\tau }}_1)+b_2{y}_J(t-{\mathit{\tau }}_1)}-\frac{m_2{y}_J{y}_A}{a_2+x+b_2{y}_J}-d_1{y}_J-\mathit{\mu }{y}_J(t-{\mathit{\tau }}_2)\hfill \\ \hfill \frac{d{y}_A}{dt}& =\mathit{\mu }{y}_J(t-{\mathit{\tau }}_2)-\left(d_2+h\right)y_A\hfill \end{array}$$(1)

with the initial conditions $x(t)={\mathit{\varphi }}_1(t)\ge 0,y_J(t)={\mathit{\varphi }}_2(t)\ge 0,y_A(t)={\mathit{\varphi }}_3(t)\ge 0,-\mathit{\tau }\le t\le 0,{\mathit{\varphi }}_i(0)>0,(i=1,2,3)$, where $\mathit{\tau }=max\{{\mathit{\tau }}_1,{\mathit{\tau }}_2\},\mathrm{\Phi }=({\mathit{\varphi }}_1,{\mathit{\varphi }}_2,{\mathit{\varphi }}_3)\in C([-\mathit{\tau },0],R_{+0}^3),$ the Banach space of continuous functions, mapping the interval $[-\mathit{\tau },0]$ into $R_{+0}^3$, where we define $R_{+0}^3=\{(x,y_J,y_A):x,y_J,y_A\ge 0\}$.

Here $\frac{1}{\mathit{\mu }}$ represents the total time spent by Pterois Volitans in its juvenile stage and $h$ is the harvesting rate of adult Pterois Volitans. Also $m,m_i$ are the maximum growth rates, $a,a_i$ are the half saturation constants, which are the concentrations of resource at which the growth rate of the organism is half maximal, $x+b_i{y}_J$ are the interference of Parrotfish and juvenile Pterois Volitans on the per capita growth rate of adult Pterois Volitans, and $e_i$ are growth efficiencies ($i=1,2$); all of these are positive quantities.

For $0\le t\le min\{{\mathit{\tau }}_1,{\mathit{\tau }}_2\}$, we have$$\begin{array}{cc}\hfill \frac{dx}{dt}& =rx(t)\left\{1-\frac{x(t)}{K}\right\}-\frac{mx(t)y_J(t)}{a+x(t)}-\frac{m_{1}x(t)y_A(t)}{a_1+x(t)+b_1{y}_J(t)}\hfill \\ \hfill \frac{d{y}_J}{dt}& =\frac{e_1{m}_1{\mathit{\varphi }}_1(t-{\mathit{\tau }}_1){\mathit{\varphi }}_3(t-{\mathit{\tau }}_1)}{a_1+{\mathit{\varphi }}_1(t-{\mathit{\tau }}_1)+b_1{\mathit{\varphi }}_2(t-{\mathit{\tau }}_1)}+\frac{e_2{m}_2{\mathit{\varphi }}_2(t-{\mathit{\tau }}_1){\mathit{\varphi }}_3(t-{\mathit{\tau }}_1)}{a_2+{\mathit{\varphi }}_1(t-{\mathit{\tau }}_1)+b_2{\mathit{\varphi }}_2(t-{\mathit{\tau }}_1)}-\frac{m_2{y}_J(t)y_A(t)}{a_2+x(t)+b_2{y}_J(t)}-d_1{y}_J(t)-\mathit{\mu }{\mathit{\varphi }}_2(t-{\mathit{\tau }}_2)\hfill \\ \hfill \frac{d{y}_A}{dt}& =\mathit{\mu }{\mathit{\varphi }}_2(t-{\mathit{\tau }}_2)-\left(d_2+h\right)y_A(t)\hfill \end{array}$$

Therefore, for $0\le t\le min\{{\mathit{\tau }}_1,{\mathit{\tau }}_2\}$, $\frac{d{y}_A}{dt}>0$ implies ${\mathit{\varphi }}_2(t-{\mathit{\tau }}_2)>\frac{1}{\mathit{\mu }}(d_2+h)y_A(t)$ and $\frac{d{y}_J}{dt}>0$ implies ${\mathit{\varphi }}_3(t-{\mathit{\tau }}_1)>\frac{1}{l_1}\left[\left\{\frac{m_2{y}_J(t)}{a_2+x(t)+b_2{y}_J(t)}+d_2+h\right\}{y}_A(t)+d_1{y}_J(t)\right]=l(t,t-{\mathit{\tau }}_1)$, where $l_1=\frac{e_1{m}_1{\mathit{\varphi }}_1(t-{\mathit{\tau }}_1)}{a_1+{\mathit{\varphi }}_1(t-{\mathit{\tau }}_1)+b_1{\mathit{\varphi }}_2(t-{\mathit{\tau }}_1)}+\frac{e_2{m}_2(d_2+h)y_A(t)}{\mathit{\mu }\{a_2+{\mathit{\varphi }}_1(t-{\mathit{\tau }}_1)\}+b_2(d_2+h)y_A(t)}$.

Thus, the system is well posed in $-\mathit{\tau }\le s\le 0$ if $0<x(s)={\mathit{\varphi }}_1(s)$, ${\mathit{\varphi }}_2(s)>\frac{1}{\mathit{\mu }}(d_2+h)y_A(s+{\mathit{\tau }}_2)$, and ${\mathit{\varphi }}_3(s)>l(s+{\mathit{\tau }}_1)$.

3. Invariance and boundedness of the System

Obviously, the right-hand sides of the equations in system $(1)$ are continuous nonnegative smooth functions on $R_{+}^3=\left\{(x,y_J,y_A):x,y_J,y_A\ge 0\right\}$. Indeed they are Lipschitzian on $R_{+}^3$ and so the solution of the system $(1)$ exists and is unique. Therefore, it is possible of Theorem $3.1.$ to prove that the interior of the positive octant of $R^3$ is an invariant region.

Theorem 3.1

For large values of $t$, all the solutions of the system $(1)$ enter into the set

$\left\{(x,y_J,y_A)\in {\mathbf{R}}^3:x(t)+y_J(t)+y_A(t)<\frac{rK+K_0}{d_0}\right\}$, where $K_0=(e_1{m}_1+e_2{m}_2){\mathit{\varphi }}_3(\mathit{\theta }),d_0=min\{r,d_1,d_2\}$, and $\mathit{\theta }\in (-\mathit{\tau },0]$.

4. Qualitative analysis of the system without delay

In this section, we restrict ourselves to analyze the model in the absence of delay. Thus, only the interaction parts of the model system are taken into account. In the absence of delay, the system $(1)$ reduces to(2) $$\begin{array}{ccc}\hfill \frac{dx}{dt}=rx\left(1-\frac{x}{K}\right)-\frac{mx{y}_J}{a+x}-\frac{m_{1}x{y}_A}{a_1+x+b_1{y}_J}& \equiv \hfill & \hfill F^1\\ \hfill \frac{d{y}_J}{dt}=\frac{e_1{m}_{1}x{y}_A}{a_1+x+b_1{y}_J}-\frac{(1-e_2)m_2{y}_J{y}_A}{a_2+x+b_2{y}_J}-(\mathit{\mu }+d_1)y_J& \equiv \hfill & \hfill F^2\\ \hfill \frac{d{y}_A}{dt}=\mathit{\mu }{y}_J-(d_2+h)y_A& \equiv \hfill & \hfill F^3\end{array}$$(2)

where $x(0)\ge 0,y_J(0)\ge 0$, and $y_A(0)\ge 0.$

The system will be permanent if there exist $u_{1_i},M_i\in (0,\infty )$ such that $u_{1_i}\le li{m}_{t\to \infty }{u}_i(t)\le M_i$, for each organism $u_i(t)$ in the system (Hofbauer & Sigmund, 1989). Permanence represents convergence on an interior attractor from any positive initial conditions and so it can be regarded as a strong form of coexistence (Ruan, 1993). From a biological point of view, permanence of a system ensures the survival of all the organisms in the long run.

Since $x(t)+y_J(t)+y_A(t)<\frac{rK+K_0}{d_0}$ as $t\to \infty$ it follows that there exist positive numbers $M_1,M_2$ with $M_1+M_2<\frac{rK}{D_0}$ such that $y_J(t)\le M_1$ and $y_A(t)\le M_2$ for large values of $t$.

The following lemma rules out the possibility of extinction of any organism in the system under suitable conditions.

Lemma 4.1

If there exist finite positive real numbers $x_1,y_{J_1},y_{A_1}$ with $x_1=K\left(1-\frac{m_1{M}_1}{a_{1}r}-\frac{m_2{M}_2}{a_{2}r}\right)$, $y_{A_1}>\frac{a_1+K+b_1{M}_1}{e_1{m}_1{x}_1}\left\{\frac{(1-e_2)m_2{M}_1{M}_2}{a_2}+(d_1+\mathit{\mu })M_1\right\}$, and $r>\frac{m_1{a}_2{M}_1+m_2{a}_1{M}_2}{a_1{a}_2}$, then for large values of $t$ each solution of $(2)$ enters in the compact set $\left\{(x,y_J,y_A):x_1\le x(t)\le K,y_{J_1}\le y_J(t)\le M_1,and{y}_{A_1}\le y_A(t)\le M_2\right\}$ and remains in it finally.

The system $(2)$ possesses the following equilibria:

(i)	organism-free equilibrium $E_0=(0,0,0)$, which always exists;
(ii)	Pterois Volitans-free equilibrium $E_1=(K,0,0)$, which always exists;
(iii)	the interior equilibrium $E^{\ast }=(x^{\ast },y_J^{\ast },y_A^{\ast })$, where $x^{\ast }$ satisfies the equation $\frac{e_1{m}_{1}xf(x)}{a_1+x+b_1\mathit{\alpha }f(x)}-\frac{(1-e_2)m_2\mathit{\alpha }{f}^2(x)}{a_2+x+b_2\mathit{\alpha }f(x)}-(\mathit{\mu }+d_1)\mathit{\alpha }f(x)=0$, with $y_A^{\ast }=f(x^{\ast })=\frac{-{\mathit{\alpha }}_0+\sqrt{{\mathit{\alpha }}_0^2+4rm{b}_1{\mathit{\alpha }}^{2}K(K-x^{\ast })(a+x^{\ast })(a_1+x^{\ast })}}{2m{b}_1{\mathit{\alpha }}^{2}K}$, $y_J^{\ast }=\mathit{\alpha }f(x^{\ast }),\mathit{\alpha }=\frac{1}{\mathit{\mu }}(d_2+h)$, and ${\mathit{\alpha }}_0=Km\mathit{\alpha }(a_1+x^{\ast })+(a+x^{\ast })\{m_{1}K-r(K-x^{\ast })b_1\mathit{\alpha }\}$. If $r>\frac{m_1{a}_2{M}_1+m_2{a}_1{M}_2}{a_1{a}_2}$, then $E^{\ast }$ exists.

We analyze the stability of system $(2)$ using eigenvalue analysis of the Jacobian matrix evaluated at the appropriate equilibrium. The detailed calculations are given in Appendix.

Lemma 4.2

The critical point $E_0$ of the system $(2)$ is always unstable.

Thus, under no circumstances the system $(2)$ collapses.

The characteristic equation of the system $(2)$ at $E_1=(K,0,0)$ is

$(\mathit{\lambda }+r)\left\{{\mathit{\lambda }}^2+\mathit{\lambda }\left(\mathit{\mu }+d_1+d_2+h\right)+(\mathit{\mu }+d_1)\left(d_2+h\right)-\frac{e_1{m}_1\mathit{\mu }K}{a_1+K}\right\}=0$, with one eigenvalue $-r$ and the remaining two eigenvalues will have negative real parts if $(\mathit{\mu }+d_1)(d_2+h)>\frac{e_1{m}_1\mathit{\mu }K}{a_1+K}$.

Lemma 4.3

The critical point $E_1$ of the system $(2)$ is locally asymptotically stable if $h>\frac{e_1{m}_1\mathit{\mu }K}{(a_1+K)(\mathit{\mu }+d_1)}-d_2$.

Thus, with high harvesting rate of adult Pterois Volitans, the system stabilizes at $E_1$.

The characteristic equation of the system $(2)$ at $E^{\ast }$ is ${\mathit{\lambda }}^3+A{\mathit{\lambda }}^2+B\mathit{\lambda }+C=0$ where $A=d_2+h-F_{{x|}_{E^{\ast }}}^1-F_{y_{{J|}_{E^{\ast }}}}^2$, $B=F_{{x|}_{E^{\ast }}}^1{F}_{y_{{J|}_{E^{\ast }}}}^2-F_{y_{{J|}_{E^{\ast }}}}^1{F}_{{x|}_{E^{\ast }}}^2-\mathit{\mu }{F}_{y_{{A|}_{E^{\ast }}}}^2-(d_2+h)(F_{{x|}_{E^{\ast }}}^1+F_{y_{{J|}_{E^{\ast }}}}^2)$ and $C=\mathit{\mu }(F_{{x|}_{E^{\ast }}}^1{F}_{y_{{A|}_{E^{\ast }}}}^2-F_{{x|}_{E^{\ast }}}^2{F}_{y_{{A|}_{E^{\ast }}}}^1)+(d_2+h)(F_{{x|}_{E^{\ast }}}^1{F}_{y_{{J|}_{E^{\ast }}}}^2-F_{y_{{J|}_{E^{\ast }}}}^1{F}_{{x|}_{E^{\ast }}}^2)$.

Lemma 4.4

The critical point $E^{\ast }$ of the system $(2)$ is locally asymptotically stable if $h>h^{\ast }$ and $\mathit{\eta }>0$, where $h^{\ast }=\frac{m{x}^{\ast }{y}_J^{\ast }}{{(a+x^{\ast })}^2}+\frac{m_1{x}^{\ast }{y}_A^{\ast }}{{(a_1+x^{\ast }+b_1{y}_J^{\ast })}^2}+\frac{e_1{m}_1{b}_1{x}^{\ast }{y}_A^{\ast }}{{(a_1+x^{\ast }+b_1{y}_J^{\ast })}^2}-\frac{m_2(1-e_2)(a_2+x^{\ast })y_A^{\ast }}{{(a_2+x^{\ast }+b_2{y}_J^{\ast })}^2}-\frac{r{x}^{\ast }}{K}-d_1-d_2-\mathit{\mu }$ and $\mathit{\eta }=AB-C$.

Thus, harvesting of adult Pterois Volitans plays a critical role on the stability of the system $(2)$ at the interior equilibrium.

Lemma 4.5

The system $(2)$ undergoes a Hopf bifurcation at $h=h_{cr}$ iff

(i)	$A(h_{cr})>0$, $B(h_{cr})>0$, $C(h_{cr})>0$,
(ii)	$f_1(h_{cr})=f_2(h_{cr}),$
(iii)	${\left\{M(h)K(h)+N(h)L(h)\right\}}_{h_{cr}}\ne 0,$

where $f_1(h)=A(h)B(h),f_2(h)=C(h)$, $K(h)=3{\mathit{\beta }}_1^2(h)-3{\mathit{\beta }}_2^2(h)+2A(h){\mathit{\beta }}_1(h)+B(h)$, $L(h)=6{\mathit{\beta }}_1(h){\mathit{\beta }}_2(h)+2A(h){\mathit{\beta }}_2(h)$, $M(h)=C^{{}^{\prime }}(h)+\left\{{\mathit{\beta }}_1^2(h)-{\mathit{\beta }}_2(h)\right\}{A}^{{}^{\prime }}(h)+{\mathit{\beta }}_1{B}^{{}^{\prime }}(h)$, $N(h)=2{\mathit{\beta }}_1(h){\mathit{\beta }}_2(h)A^{{}^{\prime }}(h)+{\mathit{\beta }}_2(h)B^{{}^{\prime }}(h)$; ${\mathit{\beta }}_1(h)$ and ${\mathit{\beta }}_2(h)$ are real and imaginary parts, Respectively, of a pair of eigenvalues in $h\in (h_{cr}-\mathit{ϵ},h_{cr}+\mathit{ϵ})$.

The condition $(iii)$ is equivalent to $\frac{dg(h)}{dh}{|}_{(h=h_{cr})}\ne 0,$ where $g(h)=f_1(h)-f_2(h).$

Thus, using numerical methods, condition $(ii)$ can be verified by showing that the curves $y=f_1(h)$ and $y=f_2(h)$ intersect at $h=h_{cr}$, whereas the condition $(iii)$ can be verified by showing that the tangent to the curve $y=g(h)$ at $h=h_{cr}$ is not parallel to the $h$ axis (Siekmann, Malchow & Venturino, 2008).

5. Qualitative analysis of the system with delays

In this section, we analyze the stability of the delayed systems at different equilibria and existence of local Hopf bifurcations.

The characteristic equation of the system $(1)$ at $E_0$ is $(r-\mathit{\lambda })(d_1+\mathit{\mu }{e}^{-\mathit{\lambda }{\mathit{\tau }}_2}+\mathit{\lambda })(d_2+h+\mathit{\lambda })=0$.

Since $r>0$, it follows that the critical point $E_0$ of the systen $(1)$ is always unstable.

The characteristic equation of the system $(1)$ at $E_1$ is $D_{E_1}(\mathit{\lambda },{\mathit{\tau }}_1,{\mathit{\tau }}_2)={\mathit{\lambda }}^3+A_{E_1}{\mathit{\lambda }}^2+B_{E_1}\mathit{\lambda }+C_{E_1}+e^{-\mathit{\lambda }{\mathit{\tau }}_2}({\overline{A}}_{E_1}{\mathit{\lambda }}^2+{\overline{B}}_{E_1}\mathit{\lambda }+{\overline{C}}_{E_1})+(\mathit{\lambda }-r){\widehat{A}}_{E_1}{e}^{-\mathit{\lambda }({\mathit{\tau }}_1+{\mathit{\tau }}_2)}=0$, where $A_{E_1}=d_1+d_2+h+r,B_{E_1}=r(d_1+d_2+h)+d_1(d_2+h),C_{E_1}=r{d}_1(d_2+h),{\overline{A}}_{E_1}=\mathit{\mu },{\overline{B}}_{E_1}=\mathit{\mu }(r+d_2+h),{\overline{C}}_{E_1}=\mathit{\mu }r(d_2+h)$, and ${\widehat{A}}_{E_1}=-\frac{\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}$.

The Jacobian of the system $(1)$ at $E^{\ast }$ is$$\begin{array}{c}\hfill \left(\begin{array}{ccc}{F}_{{x|}_{E^{\ast }}}^1& F_{y_J{|}_{E^{\ast }}}^1& F_{y_A{|}_{E^{\ast }}}^1\\ P_{11}{e}^{-\mathit{\lambda }{\mathit{\tau }}_1}+Q_{11}& P_{12}{e}^{-\mathit{\lambda }{\mathit{\tau }}_1}-\mathit{\mu }{e}^{-\mathit{\lambda }{\mathit{\tau }}_2}+Q_{12}+\mathit{\mu }& P_{13}{e}^{-\mathit{\lambda }{\mathit{\tau }}_1}+Q_{13}\\ 0& \mathit{\mu }{e}^{-\mathit{\lambda }{\mathit{\tau }}_2}& -d_2-h\end{array}\right)\end{array}$$

where $P_{11}=F_{{x|}_{E^{\ast }}}^2-\frac{m_2{y}_J^{\ast }{y}_A^{\ast }}{{(a_2+x^{\ast }+b_2{y}_J^{\ast })}^2},Q_{11}=\frac{m_2{y}_J^{\ast }{y}_A^{\ast }}{{(a_2+x^{\ast }+b_2{y}_J^{\ast })}^2},P_{12}=\mathit{\mu }+d_1+F_{y_J{|}_{E^{\ast }}}^2+\frac{m_2(a_2+x^{\ast })y_A^{\ast }}{{(a_2+x^{\ast }+b_2{y}_J^{\ast })}^2},Q_{12}=-\mathit{\mu }-d_1-\frac{m_2(a_2+x^{\ast })y_A^{\ast }}{{(a_2+x^{\ast }+b_2{y}_J^{\ast })}^2},P_{13}=F_{y_A{|}_{E^{\ast }}}^2+\frac{m_2{y}_J^{\ast }}{a_2+x^{\ast }+b_2{y}_J^{\ast }},and{Q}_{13}=-\frac{m_2{y}_J^{\ast }}{a_2+x^{\ast }+b_2{y}_J^{\ast }}$ so that $P_{11}+Q_{11}=F_{{x|}_{E^{\ast }}}^2,P_{12}+Q_{12}=F_{y_J{|}_{E^{\ast }}}^2$, and $P_{13}+Q_{13}=F_{y_A{|}_{E^{\ast }}}^2$.

The characteristic equation of the system $(1)$ at $E^{\ast }$ is $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,{\mathit{\tau }}_2)={\mathit{\lambda }}^3+A_{E^{\ast }}{\mathit{\lambda }}^2+B_{E^{\ast }}\mathit{\lambda }+C_{E^{\ast }}+e^{-\mathit{\lambda }{\mathit{\tau }}_1}({\overline{A}}_{E^{\ast }}{\mathit{\lambda }}^2+{\overline{B}}_{E^{\ast }}\mathit{\lambda }+{\overline{C}}_{E^{\ast }})+e^{-\mathit{\lambda }{\mathit{\tau }}_2}({\widehat{A}}_{E^{\ast }}{\mathit{\lambda }}^2+{\widehat{B}}_{E^{\ast }}\mathit{\lambda }+{\widehat{C}}_{E^{\ast }})+e^{-\mathit{\lambda }({\mathit{\tau }}_1+{\mathit{\tau }}_2)}({\tilde{A}}_{E^{\ast }}\mathit{\lambda }+{\tilde{B}}_{E^{\ast }})=0$, where

$A_{E^{\ast }}=d_2+h-F_{{x|}_{E^{\ast }}}^1-Q_{22}$, ${\overline{A}}_{E^{\ast }}=-P_{12}$, ${\widehat{A}}_{E^{\ast }}=\mathit{\mu }$, ${\tilde{A}}_{E^{\ast }}=\mathit{\mu }{P}_{13}$, $B_{E^{\ast }}=(Q_{12}+\mathit{\mu }-d_2-h)F_{{x|}_{E^{\ast }}}^1-(d_2+h)\left(\mathit{\mu }+Q_{12}\right)-Q_{11}{F}_{y_J{|}_{E^{\ast }}}^1$, ${\overline{B}}_{E^{\ast }}=\left(F_{{x|}_{E^{\ast }}}^1-d_2+h\right)P_{12}-P_{11}{F}_{y_J{|}_{E^{\ast }}}^1$, ${\widehat{B}}_{E^{\ast }}=\mathit{\mu }\left(d_2+h-F_{{x|}_{E^{\ast }}}^1-Q_{13}\right)$, ${\tilde{B}}_{E^{\ast }}=\mathit{\mu }\left(P_{13}{F}_{{x|}_{E^{\ast }}}^1-P_{11}{F}_{y_A{|}_{E^{\ast }}}^1\right)$, $C_{E^{\ast }}=(d_2+h)\left\{\left(\mathit{\mu }+Q_{12}\right)F_{{x|}_{E^{\ast }}}^1-Q_{11}{F}_{y_J{|}_{E^{\ast }}}^1\right\}$, ${\overline{C}}_{E^{\ast }}=(d_2+h)\left(P_{12}{F}_{{x|}_{E^{\ast }}}^1-P_{11}{F}_{y_J{|}_{E^{\ast }}}^1\right)$, and ${\widehat{C}}_{E^{\ast }}=\mathit{\mu }\left\{\left(Q_{13}-d_2-h\right)F_{{x|}_{E^{\ast }}}^1-Q_{11}{F}_{y_A{|}_{E^{\ast }}}^1\right\}$.

In order to investigate the distribution of roots of the characteristic equations, we use the following Lemma by Ruan and Wei (2003).

Lemma 5.1

For the transcendental equation $P\left(\mathit{\lambda },e^{-\mathit{\lambda }{\mathit{\tau }}_1},\dots ,e^{-\mathit{\lambda }{\mathit{\tau }}_m}\right)={\mathit{\lambda }}^n+p_1^{(0)}{\mathit{\lambda }}^{n-1}+\cdots +p_{n-1}^{(0)}\mathit{\lambda }+p_n^{(0)}+\left[p_1^{(1)}{\mathit{\lambda }}^{n-1}+\cdots +p_{n-1}^{(1)}\mathit{\lambda }+p_n^{(1)}\right]e^{-\mathit{\lambda }{\mathit{\tau }}_1}+\cdots +\left[p_1^{(m)}{\mathit{\lambda }}^{n-1}+\cdots +p_{n-1}^{(m)}\mathit{\lambda }+p_n^{(m)}\right]e^{-\mathit{\lambda }{\mathit{\tau }}_m}=0$, as $\left({\mathit{\tau }}_1,{\mathit{\tau }}_2,\dots ,{\mathit{\tau }}_m\right)$ vary, the sum of orders of the zeros of $P\left(\mathit{\lambda },e^{-\mathit{\lambda }{\mathit{\tau }}_1},e^{-\mathit{\lambda }{\mathit{\tau }}_2},\dots ,e^{-\mathit{\lambda }{\mathit{\tau }}_m}\right)$ in the open right half-plane can change, and only a zero appears on or crosses the imaginary axis.

5.1. System with reproduction time delay only $({\mathit{\tau }}_1>0,{\mathit{\tau }}_2=0)$

We now consider the case in which reproduction of the adult species is not instantaneous, but mediated by some discrete time lag ${\mathit{\tau }}_1$.

In the absence of maturation time delay, the system $(1)$ reduces to(3) $$\begin{array}{cc}\hfill \frac{dx}{dt}& =rx\left(1-\frac{x}{K}\right)-\frac{mx{y}_J}{a+x}-\frac{m_{1}x{y}_A}{a_1+x+b_1{y}_J}\hfill \\ \hfill \frac{d{y}_J}{dt}& =\frac{e_1{m}_{1}x(t-{\mathit{\tau }}_1)y_A(t-{\mathit{\tau }}_1)}{a_1+x(t-{\mathit{\tau }}_1)+b_1{y}_J(t-{\mathit{\tau }}_1)}+\frac{e_2{m}_2{y}_J(t-{\mathit{\tau }}_1)y_A(t-{\mathit{\tau }}_1)}{a_2+x(t-{\mathit{\tau }}_1)+b_2{y}_J(t-{\mathit{\tau }}_1)}-\left(d_1+\mathit{\mu }+\frac{m_2{y}_A}{a_2+x+b_2{y}_J}\right)y_J\hfill \\ \hfill \frac{d{y}_A}{dt}& =\mathit{\mu }{y}_J-\left(d_2+h\right)y_A\hfill \end{array}$$(3)

The characteristic equation of the system $(3)$ at $E_1$ is $D_{E_1}(\mathit{\lambda },{\mathit{\tau }}_1,0)={\mathit{\lambda }}^3+A_1{\mathit{\lambda }}^2+B_1\mathit{\lambda }+C_1-e^{-\mathit{\lambda }{\mathit{\tau }}_1}(A_2\mathit{\lambda }+B_2)=0$ where $A_1=A_{E_1}+{\overline{A}}_{E_1},B_1=B_{E_1}+{\overline{B}}_{E_1},C_1=C_{E_1}+{\overline{C}}_{E_1},A_2={\widehat{A}}_{E_1}$, and $B_2=-r{\widehat{A}}_{E_1}$.

Lemma 5.1.1

If ${\mathit{\tau }}_1$ is small, stability of the system $(2)$ at $E_1$ implies the stability of system $(3)$ at $E_1$.

Proof

Let the system $(2)$ is locally asymptotically stable at $E_1$. Then $h>\frac{e_1{m}_1\mathit{\mu }K}{(a_1+K)(d_1+\mathit{\mu })}-d_2$ holds. If ${\mathit{\tau }}_1$ is small, we can write $e^{-\mathit{\lambda }{\mathit{\tau }}_1}=1-\mathit{\lambda }{\mathit{\tau }}_1$.

In this case, the characteristic equation of the system $(3)$ at $E_1$ becomes $(\mathit{\lambda }+r)\left[{\mathit{\lambda }}^2+\mathit{\lambda }\left(d_1+d_2+\mathit{\mu }+h+\frac{{\mathit{\tau }}_1\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}\right)+(d_1+\mathit{\mu })(d_2+h)-\frac{\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}\right]=0$.

Since $(d_1+\mathit{\mu })(d_2+h)>\frac{\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}$, all the roots of this equation have negative real parts, and so the stability of the system without delay at $E_1$ implies the stability of system $(3)$ at $E_1$. $\square$

Lemma 5.1.2

A sufficient condition for the system $(3)$ to be locally asymptotically stable at $E_1$ is $Q_1>0,Q_3>\frac{Q_2^2}{4Q_1}$ and $h>\frac{e_1{m}_1\mathit{\mu }K}{(a_1+K)(d_1+\mathit{\mu })}-d_2$, where $Q_1=A_1^2-2B_1,Q_2=B_1^2+2A_1{C}_1-A_2^2$, and $Q_3=C_1^2-B_2^2.$

Proof

The system $(3)$ is locally asymptotically stable at $E_1$ for all ${\mathit{\tau }}_1\ge 0$ if the following conditions given by Gopalsamy (1992) and Beretta and Kuang (2002) hold:

(a)	the real parts of all the roots of $D_{E_1}(\mathit{\lambda },0,0)=0$ are negative,
(b)	for all real $\mathit{\omega }$ and any ${\mathit{\tau }}_1\ge 0$, $D_{E_1}(i\mathit{\omega },{\mathit{\tau }}_1,0)\ne 0$ where $i=\sqrt{-1}$.

$D_{E_1}(i\mathit{\omega },{\mathit{\tau }}_1,0)=0\Rightarrow -A_1{\mathit{\omega }}^2+C_1=B_{2}cos\mathit{\omega }{\mathit{\tau }}_1+\mathit{\omega }{A}_{2}sin\mathit{\omega }{\mathit{\tau }}_1$ and $-{\mathit{\omega }}^3+B_1\mathit{\omega }=\mathit{\omega }{A}_{2}cos\mathit{\omega }{\mathit{\tau }}_1-B_{2}sin\mathit{\omega }{\mathit{\tau }}_1$. Now, ${(-{\mathit{\omega }}^3+B_1\mathit{\omega })}^2+{(-A_1{\mathit{\omega }}^2+C_1)}^2={\mathit{\omega }}^2{A}_2^2+{\mathit{\omega }}^2{B}_2^2$ gives ${\mathit{\omega }}^6+Q_1{\mathit{\omega }}^4+Q_2{\mathit{\omega }}^2+Q_3=0$, where $Q_1=A_1^2-2B_1,Q_2=B_1^2+2A_1{C}_1-A_2^2$, and $Q_3=C_1^2-B_2^2.$

Sufficient conditions for the nonexistence of $\mathit{\omega }\in \mathbf{R}$ satisfying $D_{E_1}(i\mathit{\omega },{\mathit{\tau }}_1,0)=0$ can be written as:

${\mathit{\omega }}^6+Q_1{\mathit{\omega }}^4+Q_2{\mathit{\omega }}^2+Q_3>0\Rightarrow {\mathit{\omega }}^6+Q_1{\left({\mathit{\omega }}^2+\frac{Q_2}{2Q_1}\right)}^2+Q_3-\frac{Q_2^2}{4Q_1}>0$.

Thus, for all real $\mathit{\omega }$ and for any ${\mathit{\tau }}_1\ge 0,D_{E_1}(i\mathit{\omega },{\mathit{\tau }}_1,0)\ne 0$ if $Q_1>0$ and $Q_3>\frac{Q_2^2}{4Q_1}.$

Also, the real parts of all the roots of $D_{E_1}(\mathit{\lambda },0,0)=0$ are negative if $h>\frac{e_1{m}_1\mathit{\mu }K}{(a_1+K)(d_1+\mathit{\mu })}-d_2$.

Therefore, the statement of lemma $(5.1.2)$ holds.$\square$

The characteristic equation of the system $(3)$ at $E^{\ast }$ is

$D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)={\mathit{\lambda }}^3+A_{11}{\mathit{\lambda }}^2+B_{11}\mathit{\lambda }+C_{11}+e^{-\mathit{\lambda }{\mathit{\tau }}_1}(A_{12}{\mathit{\lambda }}^2+B_{12}\mathit{\lambda }+C_{12})=0$, where $A_{11}=A_{E^{\ast }}+{\widehat{A}}_{E^{\ast }},A_{12}={\overline{A}}_{E^{\ast }},B_{11}=B_{E^{\ast }}+{\widehat{B}}_{E^{\ast }},B_{12}={\overline{B}}_{E^{\ast }}+{\tilde{A}}_{E^{\ast }},C_{11}=C_{E^{\ast }}+{\widehat{C}}_{E^{\ast }}$, and $C_{12}={\overline{C}}_{E^{\ast }}+{\tilde{B}}_{E^{\ast }}.$

Lemma 5.1.3

If ${\mathit{\tau }}_1$ is small, stability of the system $(2)$ at $E^{\ast }$ implies the stability of system $(3)$ at $E^{\ast }$.

Proof

Let the system $(2)$ is locally asymptotically stable at $E^{\ast }$. Then we have $A>0,C>0$ and $AB>C$.

For small ${\mathit{\tau }}_1$, we can write $e^{-\mathit{\lambda }{\mathit{\tau }}_1}=1-\mathit{\lambda }{\mathit{\tau }}_1$ and so the characteristic equation of $(3)$ at $E^{\ast }$ becomes

${\mathit{\lambda }}^3\left(1+{\mathit{\tau }}_1{P}_{12}\right)+{\mathit{\lambda }}^2{A}_{21}+\mathit{\lambda }{A}_{22}+C=0$, where $A_{21}=A+\mathit{\mu }{\mathit{\tau }}_1{P}_{13}+{\mathit{\tau }}_1{P}_{12}(d_2+h-F_{{x|}_{E^{\ast }}}^1)+{\mathit{\tau }}_1{P}_{11}{F}_{y_J{|}_{E^{\ast }}}^1$

and $A_{22}=B-\mathit{\mu }{\mathit{\tau }}_1{P}_{13}{F}_{{x|}_{E^{\ast }}}^1-{\mathit{\tau }}_1(d_2+h)(P_{12}{F}_{{x|}_{E^{\ast }}}^1-P_{11}{F}_{y_J{|}_{E^{\ast }}}^1)+\mathit{\mu }{\mathit{\tau }}_1{F}_{y_A{|}_{E^{\ast }}}^1$.

Now, $A>0\Rightarrow d_2+h-F_{{x|}_{E^{\ast }}}^1>0$ and so $A_{21}>0$.

Also, for $AB>C$, we have $A_{21}{A}_{22}>A_{23}+{\mathit{\tau }}_{1}A\{\mathit{\mu }{P}_{11}{F}_{y_A{|}_{E^{\ast }}}^1-(d_2+h)(P_{12}{F}_{{x|}_{E^{\ast }}}^1-P_{11}{F}_{y_J{|}_{E^{\ast }}}^1)-\mathit{\mu }{P}_{13}{F}_{{x|}_{E^{\ast }}}^1\}+{\mathit{\tau }}_{1}B\{\mathit{\mu }{P}_{13}+P_{12}(d_2+h-F_{{x|}_{E^{\ast }}}^1)+P_{11}{F}_{y_J{|}_{E^{\ast }}}^1\}+O({\mathit{\tau }}_1^2)$ and so for small ${\mathit{\tau }}_1>0$, we have $A_{21}{A}_{22}>C$.

Therefore, for small ${\mathit{\tau }}_1>0$, the stability of the system without delay at $E^{\ast }$ implies the stability of system $(3)$ at $E^{\ast }$. $\square$

Lemma 5.1.4

If the system $(2)$ is stable at $E^{\ast }$ and if there exists a ${\mathit{\tau }}_1$ in $0\le {\mathit{\tau }}_1\le {\overline{\mathit{\tau }}}_1$ such that $A_{\mathit{\theta }}{\mathit{\tau }}^2+B_{\mathit{\theta }}\mathit{\tau }+C_{\mathit{\theta }}>0$ holds, then ${\overline{\mathit{\tau }}}_1$ is the maximum value $($length of delay$)$ for which the system $(3)$ is locally asymptotically stable at $E^{\ast }$, where $A_{\mathit{\theta }}{\mathit{\tau }}^2+B_{\mathit{\theta }}\mathit{\tau }+C_{\mathit{\theta }}>0,A_{\mathit{\theta }}=\frac{1}{2}{\overline{v}}_1^2|B_{12}|,B_{\mathit{\theta }}=|C_{12}|,C_{\mathit{\theta }}={\overline{v}}_1|A_{12}|+B_{11}-{\overline{v}}_1^2,{\overline{v}}_1=\frac{-|B_{12}|+\sqrt{B_{12}^2+4(A_{11}+|A_{12}|)(C_{11}-|C_{12}|)}}{2(A_{11}+|A_{12}|)}$, and ${\overline{\mathit{\tau }}}_1=\frac{-B_{\mathit{\theta }}+\sqrt{B_{\mathit{\theta }}^2-4A_{\mathit{\theta }}{C}_{\mathit{\theta }}}}{2A_{\mathit{\theta }}}$.

Proof

Let $u(t),v_J(t),and{v}_A(t)$ be the respective linearized variables of the model.

Then system $(3)$ can be expressed as(4) $$\begin{array}{cc}\hfill \frac{du}{dt}& =a_{11}u(t)+a_{12}{v}_J(t)+a_{13}{v}_A(t)\hfill \\ \hfill \frac{d{v}_J}{dt}& =a_{21}u(t)+a_{22}{v}_J(t)+a_{23}{v}_A(t)+a_{24}u(t-{\mathit{\tau }}_1)+a_{25}{v}_J(t-{\mathit{\tau }}_1)+a_{26}{v}_A(t-{\mathit{\tau }}_1)\hfill \\ \hfill \frac{d{v}_A}{dt}& =a_{31}{v}_J(t)+a_{32}{v}_A(t)\hfill \end{array}$$(4)

where $a_{11}=F_{{x|}_{E^{\ast }}}^1,a_{12}=F_{y_{{J|}_{E^{\ast }}}}^1,a_{13}=F_{y_{{A|}_{E^{\ast }}}}^1,a_{21}=-Q_{11},a_{23}=Q_{13},a_{24}=F_{{x|}_{E^{\ast }}}^2-Q_{11},a_{25}=F_{y_J{|}_{E^{\ast }}}^2-Q_{12},a_{26}=F_{y_A{|}_{E^{\ast }}}^2+Q_{13},and{a}_{31}=\mathit{\mu },a_{32}=-d_2-h$.

Taking the Laplace transformation of system $(4)$, we have(5) $$\begin{array}{cc}\hfill (s-a_{11})\overline{u}(s)& =a_{12}{\overline{v}}_J(s)+a_{13}{\overline{v}}_A(s)+u(0)\hfill \\ \hfill (s-a_{22}){\overline{v}}_J(s)& =a_{21}\overline{u}(s)+a_{23}{\overline{v}}_A(s)+e^{-s{\mathit{\tau }}_1}\{a_{24}\left(\overline{u}(s)+k_1\right)+a_{25}\left({\overline{v}}_J(s)+k_2\right)+a_{26}\left({\overline{v}}_A(s)+k_3\right)\}+v_J(0)\hfill \\ \hfill (s-a_{32}){\overline{v}}_A(s)& =a_{31}{\overline{v}}_J(s)+v_A(0)\hfill \end{array}$$(5)

where $k_1={\int }_{-{\mathit{\tau }}_1}^0{e}^{-st}u(t)dt,k_2={\int }_{-{\mathit{\tau }}_1}^0{e}^{-st}{v}_J(t)dt$ and $k_3={\int }_{-{\mathit{\tau }}_1}^0{e}^{-st}{v}_A(t)dt.$

The inverse Laplace transform of $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ will have terms which exponentially increase with time if $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ have a pole with positive real parts. Since $E^{\ast }$ needs to be locally asymptotically stable, it is necessary and sufficient that all poles of $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ have negative real parts. We shall employ the Nyquist criterion, which states that if $s$ is the arc length of a curve encircling the right half-plane, the curve $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ will encircle the origin a number of times equal to the difference between the number of poles and the number of zeroes of $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ in the right half-plane.

Let $\overline{F}(s)=s^3+A_{11}{s}^2+B_{11}s+C_{11}+e^{-s{\mathit{\tau }}_1}(A_{12}{s}^2+B_{12}s+C_{12})=0$. Also, let ${\overline{v}}_0$ be the smallest positive root of $Re\{\overline{F}(iv)\}=0.$

Then $E^{\ast }$ is locally asymptotically stable if $-A_{11}{\overline{v}}_0^2+C_{11}=A_{12}{\overline{v}}_0^{2}cos{\overline{v}}_0{\mathit{\tau }}_1-C_{12}cos{\overline{v}}_0{\mathit{\tau }}_1-B_{12}{\overline{v}}_{0}sin{\overline{v}}_0{\mathit{\tau }}_1$

and $-{\overline{v}}_0^3+B_{11}{\overline{v}}_0>-B_{12}{\overline{v}}_{0}cos{\overline{v}}_0{\mathit{\tau }}_1-A_{12}{\overline{v}}_0^{2}sin{\overline{v}}_0{\mathit{\tau }}_1+C_{12}sin{\overline{v}}_0{\mathit{\tau }}_1$.

Also, $-A_{11}{v}^2+C_{11}\le |A_{12}|v^2+v|B_{12}|+|C_{12}|.$

Therefore, the positive solution ${\overline{v}}_1$ of $(A_{11}+|A_{12}|)v^2+v|B_{12}|-(C_{11}-|C_{12}|)=0$ is always greater than or equal to ${\overline{v}}_0$.

We obtain ${\overline{v}}_1=\frac{-|B_{12}|+\sqrt{B_{12}^2+4(A_{11}+|A_{12}|)(C_{11}-|C_{12}|)}}{2(A_{11}+|A_{12}|)}\ge {\overline{v}}_0,$ where ${\overline{v}}_1$ is independent of ${\mathit{\tau }}_1$.

Also, $-{\overline{v}}_1^3+{\overline{v}}_1{B}_{11}>-{\overline{v}}_1{B}_{12}cos{\overline{v}}_1{\mathit{\tau }}_1-{\overline{v}}_1^2{A}_{12}sin{\overline{v}}_1{\mathit{\tau }}_1+C_{12}sin{\overline{v}}_1{\mathit{\tau }}_1\Rightarrow -{\overline{v}}_1^2+B_{11}>-|B_{12}|\left(1+\frac{1}{2}{\mathit{\tau }}^2{\overline{v}}_1^2\right)-|C_{12}|\mathit{\tau }-|A_{12}|{\overline{v}}_1\Rightarrow A_{\mathit{\theta }}{\mathit{\tau }}^2+B_{\mathit{\theta }}\mathit{\tau }+C_{\mathit{\theta }}>0$ where $A_{\mathit{\theta }}=\frac{1}{2}{\overline{v}}_1^2|B_{12}|,B_{\mathit{\theta }}=|C_{12}|$ and $C_{\mathit{\theta }}={\overline{v}}_1|A_{12}|+B_{11}-{\overline{v}}_1^2.$

Therefore, ${\overline{\mathit{\tau }}}_1=\frac{-B_{\mathit{\theta }}+\sqrt{B_{\mathit{\theta }}^2-4A_{\mathit{\theta }}{C}_{\mathit{\theta }}}}{2A_{\mathit{\theta }}}$ is an estimate for the length of delay for which the stability of the system at $E^{\ast }$ is preserved. $\square$

We know that $i\mathit{\omega }$$(\mathit{\omega }>0)$ is a root of $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)=0$ if and only if

$-A_{11}{\mathit{\omega }}^2+C_{11}=(A_{12}{\mathit{\omega }}^2-C_{12})cos\mathit{\omega }{\mathit{\tau }}_1-\mathit{\omega }{B}_{12}sin\mathit{\omega }{\mathit{\tau }}_1$ and ${\mathit{\omega }}^3-\mathit{\omega }{B}_{11}=\mathit{\omega }{B}_{12}cos\mathit{\omega }{\mathit{\tau }}_1+(A_{12}{\mathit{\omega }}^2-C_{12})sin\mathit{\omega }{\mathit{\tau }}_1$.

Eliminating ${\mathit{\tau }}_1$, we obtain ${\mathit{\omega }}^6+H_1{\mathit{\omega }}^4+H_2{\mathit{\omega }}^2+H_3=0$, where $H_1=A_{11}^2-2B_{11}-A_{12}^2,H_2=B_{11}^2-2A_{11}{C}_{11}+2A_{12}{C}_{12}-B_{12}^2$, and $H_3=C_{11}^2-C_{12}^2.$

Let $z={\mathit{\omega }}^2$ and $F(z)=z^3+H_1{z}^2+H_{2}z+H_3$. Then ${\mathit{\omega }}^6+H_1{\mathit{\omega }}^4+H_2{\mathit{\omega }}^2+H_3=0$ takes the form $F(z)=0$.

Lemma 5.1.5

Suppose that the conditions of Lemma $4.4$ are satisfied. Then the following results hold:

(i)	If $H_3\ge 0$ and $H_1^2\le 3H_2$, then the system $(3)$ is locally asymptotically stable at $E^{\ast }$ for all ${\mathit{\tau }}_1>0$.
(ii)	If $(a)$$H_3<0$ or $(b)$$H_3\ge 0,H_1^2>3H_2,z_1^{\ast }=\frac{-H_1+\sqrt{H_1^2-3H_2}}{3}$ and $F(z_1^{\ast })\le 0$ hold, then the system $(3)$ is locally asymptotically stable at $E^{\ast }$ for all ${\mathit{\tau }}_1\in \left[0,{\mathit{\tau }}_{1_0}\right)$, where ${\mathit{\tau }}_{1_0}=min\left\{{\mathit{\tau }}_{1_0}^1,{\mathit{\tau }}_{1_0}^2,{\mathit{\tau }}_{1_0}^3\right\}$ and ${\mathit{\tau }}_{1_0}^k=\frac{1}{{\mathit{\omega }}_k}{tan}^{-1}\left[\frac{{\mathit{\omega }}_k\{A_{12}{\mathit{\omega }}_k^4+{\mathit{\omega }}_k^2(A_{11}{B}_{12}-A_{12}{B}_{11}-C_{12})+B_{11}{C}_{12}-B_{12}{C}_{11}\}}{{\mathit{\omega }}_k^4(B_{12}-A_{11}{A}_{12})+{\mathit{\omega }}_k^2(A_{11}{C}_{12}+A_{12}{C}_{11}-B_{11}{B}_{12})-C_{11}{C}_{12}}\right]$, $(k=1,2,3)$.
(iii)	If conditions in $(ii)$ hold and $F^{\prime }(z_1^{\ast })\ne 0$, then the system $(3)$ undergoes a Hopf bifurcation $E^{\ast }$ when ${\mathit{\tau }}_1$ crosses ${\mathit{\tau }}_{1_0}^k$, $(k=1,2,3)$.

Proof

If the conditions of Lemma $4.4$ hold, then the roots of, $D_{E^{\ast }}(\mathit{\lambda },0,0)=0$ have negative real parts.

Let $\mathit{\lambda }({\mathit{\tau }}_1)=\mathit{\alpha }({\mathit{\tau }}_1)+i\mathit{\omega }({\mathit{\tau }}_1)$ be a root of $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)=0$. For ease of notation, we denote $\mathit{\alpha }({\mathit{\tau }}_1)=\mathit{\alpha }$ and $\mathit{\omega }({\mathit{\tau }}_1)=\mathit{\omega }$. Now, $\mathit{\alpha }=0$ and $\mathit{\omega }\ne 0$ gives $F(z)=0$, where $z={\mathit{\omega }}^2$.

(i)	If $H_3\ge 0$ and $H_1^2\le 3H_2$, then $F(0)\ge 0$ and $F^{\prime }(z)>0$ for all $z$ and so $F(z)=0$ has no positive root. Thus, all the roots of $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)=0$ have negative real parts for all ${\mathit{\tau }}_1>0$. Therefore, if $H_3\ge 0$ and $H_1^2\le 3H_2$ hold, the system $(3)$ is locally asymptotically stable at $E^{\ast }$ for all ${\mathit{\tau }}_1>0$.
(ii)	If $(a)$$H_3<0$, then as $F(0)<0$ and ${lim}_{z\to \infty }F(z)=+\infty$, it follows that $F(z)=0$ has at least one positive root. If $(b)$$H_3\ge 0$ and $H_1^2>3H_2$, then $F^{\prime }(z)=0$ has the two roots, $z_1^{\ast }=\frac{-H_1+\sqrt{H_1^2-3H_2}}{3}$ and $z_2^{\ast }=\frac{-H_1-\sqrt{H_1^2-3H_2}}{3}$. Since $F^{″}(z_1^{\ast })>0$ and $F^{″}(z_2^{\ast })<0$, it follows that $F(z_1^{\ast })$ and $F(z_2^{\ast })$ are local minimum and local maximum of $F(z)$. As $F(0)\ge 0$ and ${lim}_{z\to \infty }F(z)=+\infty$, it follows that $F(z)=0$ has a positive root if $F(z_1^{\ast })\le 0$. Conversely, let $F(z)=0$ has a positive root. If $F(z_1^{\ast })>0$, then as $F(0)\ge 0$, it follows that $F(z)>0$ for all $z>0$, a contradiction. Therefore, if $H_3\ge 0$ and $H_1^2>3H_2$, it follows that $F(z)=0$ has positive roots if and only if $z_1^{\ast }=\frac{-H_1+\sqrt{H_1^2-3H_2}}{3}$ and $F(z_1^{\ast })\le 0$. Let either $(a)$ or $(b)$ hold. Without any loss of generality, we assume that equation $F(z)=0$ has three positive roots, say, $z_1,z_2$, and $z_3$. Consequently, ${\mathit{\omega }}^6+H_1{\mathit{\omega }}^4+H_2{\mathit{\omega }}^2+H_3=0$ has three positive roots ${\mathit{\omega }}_1=\sqrt{z_1},{\mathit{\omega }}_2=\sqrt{z_2}$, and ${\mathit{\omega }}_3=\sqrt{z_3}$. This gives, ${\mathit{\tau }}_{1_n}^k=\frac{1}{b_k}{tan}^{-1}\left[\frac{{\mathit{\omega }}_k\{A_{12}{\mathit{\omega }}_{+}^4+{\mathit{\omega }}_k^2(A_{11}{B}_{12}-A_{12}{B}_{11}-C_{12})+B_{11}{C}_{12}-B_{12}{C}_{11}\}}{{\mathit{\omega }}_k^4(B_{12}-A_{11}{A}_{12})+{\mathit{\omega }}_k^2(A_{11}{C}_{12}+A_{12}{C}_{11}-B_{11}{B}_{12})-C_{11}{C}_{12}}\right]+\frac{n\mathit{\pi }}{{\mathit{\omega }}_k},k=1,2,3;n=0,1,2,\dots$ Then $\pm i{\mathit{\omega }}_k$ are a pair of purely imaginary roots of $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)=0$ with ${\mathit{\tau }}_1={\mathit{\tau }}_{1_n}^k$, $k=1,2,3;n=0,1,2,\dots$ The smallest ${\mathit{\tau }}_{1_n}^k$ is given by $n=0$ and we take it as ${\mathit{\tau }}_{1_0}^k$. Let ${\mathit{\tau }}_{1_0}=min\left\{{\mathit{\tau }}_{1_0}^1,{\mathit{\tau }}_{1_0}^2,{\mathit{\tau }}_{1_0}^3\right\}$. Therefore, if either $(a)$ or $(b)$ is satisfied, all the roots of $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)=0$ have negative real parts for all ${\mathit{\tau }}_1\in \left[0,{\mathit{\tau }}_{1_0}\right)$ and consequently, the system $(3)$ is locally asymptotically stable at $E^{\ast }$ for all ${\mathit{\tau }}_1\in \left[0,{\mathit{\tau }}_{1_0}\right)$.
(iii)	Let either $(a)$ or $(b)$ hold. We are interested to know the change of stability at $E^{\ast }$ which will occur at ${\mathit{\tau }}_1={\mathit{\tau }}_{1_0}^k$ for which $\mathit{\alpha }({\mathit{\tau }}_{1_0}^k)=0$ and $\mathit{\omega }({\mathit{\tau }}_{1_0}^k)\ne 0$. Since $\mathit{\lambda }({\mathit{\tau }}_1)$ is a root of $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)=0$ near ${\mathit{\tau }}_{1_0}^k$, there exists $\mathit{ϵ}>0$ such that $\mathit{\lambda }({\mathit{\tau }}_1)$ is continuously differentiable at ${\mathit{\tau }}_1\in ({\mathit{\tau }}_{1_0}^k-\mathit{ϵ},{\mathit{\tau }}_{1_0}^k+\mathit{ϵ})$.

Differentiating $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,0)=0$ with respect to ${\mathit{\tau }}_1$ and using $e^{-\mathit{\lambda }{\mathit{\tau }}_1}=-\frac{{\mathit{\lambda }}^3+A_{11}{\mathit{\lambda }}^2+B_{11}\mathit{\lambda }+C_{11}}{A_{12}{\mathit{\lambda }}^2+B_{12}\mathit{\lambda }+C_{12}}$ we obtain ${\left(\frac{d\mathit{\lambda }}{d{\mathit{\tau }}_1}\right)}^{-1}=-\frac{3{\mathit{\lambda }}^2+2A_{11}\mathit{\lambda }+B_{11}}{\mathit{\lambda }({\mathit{\lambda }}^3+A_{11}{\mathit{\lambda }}^2+B_{11}\mathit{\lambda }+C_{11})}+\frac{2A_{12}\mathit{\lambda }+B_{12}}{\mathit{\lambda }(A_{12}{\mathit{\lambda }}^2+B_{12}\mathit{\lambda }+C_{12})}-\frac{{\mathit{\tau }}_1}{\mathit{\lambda }}$.

Thus, $sign{\left\{\frac{d(Re\mathit{\lambda })}{d{\mathit{\tau }}_1}\right\}}_{\mathit{\lambda }=i{\mathit{\omega }}_k}=sign\left\{\frac{3{\mathit{\omega }}_k^4+2{\mathit{\omega }}_k^2{H}_1+H_2}{{(A_{12}{\mathit{\omega }}_k^2-C_{12})}^2+{\mathit{\omega }}_k^2{B}_{12}^2}\right\}=sign\left\{\frac{F^{\prime }(z_k)}{{(A_{12}{\mathit{\omega }}_k^2-C_{12})}^2+{\mathit{\omega }}_k^2{B}_{12}^2}\right\}$.

Therefore, if $F^{\prime }(z_k)\ne 0$ holds, then ${\left[\frac{d(Re\mathit{\lambda })}{d{\mathit{\tau }}_1}\right]}_{{\mathit{\tau }}_1={\mathit{\tau }}_{1_0}^k,\mathit{\lambda }=i{\mathit{\omega }}_k}\ne 0$ and so the system $(3)$ undergoes a Hopf bifurcation at ${\mathit{\tau }}_{1_0}^k$.$\square$

5.2. System with only maturation time delay $({\mathit{\tau }}_1=0,{\mathit{\tau }}_2>0)$

Now we consider the case in which the maturity time from juvenile to adult is mediated by a discrete time lag ${\mathit{\tau }}_2$, while the reproduction process is instantaneous.

In the absence of reproduction time delay, the system $(1)$ reduces to(6) $$\begin{array}{cc}\hfill \frac{dx}{dt}& =rx\left(1-\frac{x}{K}\right)-\frac{mx{y}_J}{a+x}-\frac{m_{1}x{y}_A}{a_1+x+b_1{y}_J}\hfill \\ \hfill \frac{d{y}_J}{dt}& =\left\{\frac{e_1{m}_{1}x}{a_1+x+b_1{y}_J}-\frac{(1-e_2)m_2{y}_J}{a_2+x+b_2{y}_J}\right\}{y}_A-d_1{y}_J-\mathit{\mu }{y}_J(t-{\mathit{\tau }}_2)\hfill \\ \hfill \frac{d{y}_A}{dt}& =\mathit{\mu }{y}_J(t-{\mathit{\tau }}_2)-\left(d_2+h\right)y_A\hfill \end{array}$$(6)

The characteristic equation of the system $(5)$ at $E_0$ is

$D_{E_0}(\mathit{\lambda },0,{\mathit{\tau }}_2)={\mathit{\lambda }}^3+{\mathit{\lambda }}^2(d_1+d_2+h-r)+\mathit{\lambda }\{d_1(d_2+h)-r(d_1+d_2+h)\}-r{d}_1(d_2+h)$

$+\mathit{\mu }{e}^{-\mathit{\lambda }{\mathit{\tau }}_2}\{{\mathit{\lambda }}^2+\mathit{\lambda }(d_2+h-r)-r(d_2+h)\}=0$.

Lemma 5.2.1

If $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$ and ${\mathit{\tau }}_2$ is small, $E_0$ is always a saddle point of the system $(5)$.

Proof

For small values of ${\mathit{\tau }}_2$ we have $e^{-\mathit{\lambda }{\mathit{\tau }}_2}=1-\mathit{\lambda }{\mathit{\tau }}_2$.

In this case, the characteristic equation of the system $(5)$ at $E_0$ becomes

${\mathit{\lambda }}^3(1-\mathit{\mu }{\mathit{\tau }}_2)+{\mathit{\lambda }}^2\{d_1+d_2+h+\mathit{\mu }-r-\mathit{\mu }{\mathit{\tau }}_2(d_2+h-r)\}-\mathit{\lambda }\{r(d_1+d_2+h)+\mathit{\mu }(d_2+h-r)+(r\mathit{\mu }{\mathit{\tau }}_2-d_1)(d_2+h)\}-r(d_1+\mathit{\mu })(d_2+h)=0$

Since $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$ and $r>0$, it follows that at least one eigenvalue of the characteristic equation will always have positive real part and consequently, $E_0$ is always a saddle point of the system $(5)$.$\square$

The characteristic equation of the system $(5)$ at $E_1$ is

$D_{E_1}(\mathit{\lambda },0,{\mathit{\tau }}_2)={\mathit{\lambda }}^3+{\widehat{A}}_1{\mathit{\lambda }}^2+{\widehat{B}}_1\mathit{\lambda }+{\widehat{C}}_1+e^{-\mathit{\lambda }{\mathit{\tau }}_2}({\widehat{A}}_2{\mathit{\lambda }}^2+{\widehat{B}}_2\mathit{\lambda }+{\widehat{C}}_2)=0$ where ${\widehat{A}}_1=r+d_1+d_2+h,{\widehat{B}}_1=d_1(d_2+h)+r(d_1+d_2+h),{\widehat{C}}_1=r{d}_1(d_2+h),{\widehat{A}}_2=\mathit{\mu },{\widehat{B}}_2=\mathit{\mu }\left(r+d_2+h-\frac{e_1{m}_{1}K}{a_1+K}\right)$, and ${\widehat{C}}_2=\mathit{\mu }r(d_2+h)-\frac{r\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}$.

Lemma 5.2.2

If ${\mathit{\tau }}_2$ is small and $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$, the stability of the system $(2)$ at $E_1$ implies the stability of system $(5)$ at $E_1$.

Proof

Let the system $(2)$ be locally asymptotically stable at $E_1$. Then we have $h>\frac{e_1{m}_1\mathit{\mu }K}{(a_1+K)(d_1+\mathit{\mu })}-d_2$.

If ${\mathit{\tau }}_1$ is small, we can write $e^{-\mathit{\lambda }{\mathit{\tau }}_2}=1-\mathit{\lambda }{\mathit{\tau }}_2$. Then, the characteristic equation of the system $(5)$ at $E_1$ is

$(\mathit{\lambda }+r)\left[{\mathit{\lambda }}^2(1-\mathit{\mu }{\mathit{\tau }}_2)+\mathit{\lambda }\left\{d_1+d_2+\mathit{\mu }+h-\mathit{\mu }{\mathit{\tau }}_2(d_2+h)+\frac{{\mathit{\tau }}_2\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}\right\}+(d_1+\mathit{\mu })(d_2+h)-\frac{\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}\right]=0$.

Since $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$ is small, $d_1+d_2+\mathit{\mu }+h-\mathit{\mu }{\mathit{\tau }}_2(d_2+h)+\frac{{\mathit{\tau }}_2\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}=d_1+\mathit{\mu }+(1-\mathit{\mu }{\mathit{\tau }}_2)(d_2+h)+\frac{{\mathit{\tau }}_2\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}>0$ and so, the stability of the system $(2)$ at $E_1$ implies the stability of system $(5)$ at $E_1$.$\square$

Lemma 5.2.3

A sufficient condition for the system $(5)$ to be locally asymptotically stable at $E_1$ is ${\widehat{Q}}_1>0,{\widehat{Q}}_3>\frac{{\widehat{Q}}_2^2}{4{\widehat{Q}}_1}$, and $h>\frac{e_1{m}_1\mathit{\mu }K}{(a_1+K)(d_1+\mathit{\mu })}-d_2$, where ${\widehat{Q}}_1={\widehat{A}}_1^2-2{\widehat{B}}_1-{\widehat{A}}_2^2,{\widehat{Q}}_2={\widehat{B}}_1^2-2{\widehat{A}}_1{\widehat{C}}_1+2{\widehat{A}}_2{\widehat{C}}_2-{\widehat{B}}_2^2$, and ${\widehat{Q}}_3={\widehat{C}}_1^2-{\widehat{C}}_2^2.$

Proof

$D_{E_1}(i\mathit{\omega },0,{\mathit{\tau }}_2)=0$ implies $-{\mathit{\omega }}^2{\widehat{A}}_1+{\widehat{C}}_1=({\mathit{\omega }}^2{\widehat{A}}_2-{\widehat{C}}_2)cos\mathit{\omega }{\mathit{\tau }}_2-\mathit{\omega }{\widehat{B}}_{2}sin\mathit{\omega }{\mathit{\tau }}_2$ and

${\mathit{\omega }}^3-\mathit{\omega }{\widehat{B}}_1=({\mathit{\omega }}^2{\widehat{A}}_2-{\widehat{C}}_2)sin\mathit{\omega }{\mathit{\tau }}_2+\mathit{\omega }{\widehat{B}}_{2}cos\mathit{\omega }{\mathit{\tau }}_2$. This gives ${\mathit{\omega }}^6+{\widehat{Q}}_1{\mathit{\omega }}^4+{\widehat{Q}}_2{\mathit{\omega }}^2+{\widehat{Q}}_3=0$, where ${\widehat{Q}}_1={\widehat{A}}_1^2-2{\widehat{B}}_1-{\widehat{A}}_2^2,{\widehat{Q}}_2={\widehat{B}}_1^2-2{\widehat{A}}_1{\widehat{C}}_1+2{\widehat{A}}_2{\widehat{C}}_2-{\widehat{B}}_2^2$, and ${\widehat{Q}}_3={\widehat{C}}_1^2-{\widehat{C}}_2^2.$

Sufficient conditions for the nonexistence of $\mathit{\omega }\in \mathbf{R}$ satisfying $D_{E_1}(i\mathit{\omega },0,{\mathit{\tau }}_2)=0$ can be written as:

${\mathit{\omega }}^6+{\widehat{Q}}_1{\mathit{\omega }}^4+{\widehat{Q}}_2{\mathit{\omega }}^2+{\widehat{Q}}_3>0\Rightarrow {\mathit{\omega }}^6+{\widehat{Q}}_1{\left({\mathit{\omega }}^2+\frac{{\widehat{Q}}_2}{2{\widehat{Q}}_1}\right)}^2+{\widehat{Q}}_3-\frac{{\widehat{Q}}_2^2}{4{\widehat{Q}}_1}>0$.

Thus, for all real $\mathit{\omega }$ and for any ${\mathit{\tau }}_2\ge 0,D_{E_1}(i\mathit{\omega },0,{\mathit{\tau }}_2)\ne 0$ if ${\widehat{Q}}_1>0$, and ${\widehat{Q}}_3>\frac{{\widehat{Q}}_2^2}{4{\widehat{Q}}_1}.$

Also, the real parts of all the roots of $D_{E_1}(\mathit{\lambda },0,0)=0$ are negative if $h>\frac{e_1{m}_1\mathit{\mu }K}{(a_1+K)(d_1+\mathit{\mu })}-d_2$.

Therefore, the statement of lemma $(5.2.3)$ holds.$\square$

The characteristic equation of the system $(5)$ at $E^{\ast }$ is

$D_{E^{\ast }}(\mathit{\lambda },0,{\mathit{\tau }}_2)={\mathit{\lambda }}^3+{\widehat{A}}_{11}{\mathit{\lambda }}^2+{\widehat{B}}_{11}\mathit{\lambda }+{\widehat{C}}_{11}+e^{-\mathit{\lambda }{\mathit{\tau }}_2}({\widehat{A}}_{12}{\mathit{\lambda }}^2+{\widehat{B}}_{12}\mathit{\lambda }+{\widehat{C}}_{12})=0$, where

${\widehat{A}}_{11}=A_{E^{\ast }}+{\overline{A}}_{E^{\ast }},{\widehat{A}}_{12}={\widehat{A}}_{E^{\ast }},{\widehat{B}}_{11}=B_{E^{\ast }}+{\overline{B}}_{E^{\ast }},{\widehat{B}}_{12}={\tilde{A}}_{E^{\ast }}+{\widehat{B}}_{E^{\ast }},{\widehat{C}}_{11}=C_{E^{\ast }}+{\overline{C}}_{E^{\ast }}$, and ${\widehat{C}}_{12}={\tilde{B}}_{E^{\ast }}+{\widehat{C}}_{E^{\ast }}.$

Lemma 5.2.4

If ${\mathit{\tau }}_2$ is small, stability of the system $(2)$ at $E^{\ast }$ implies the stability of system $(5)$ at $E^{\ast }$.

Proof

Let the system $(2)$ be locally asymptotically stable at $E^{\ast }$. Then we have $A>0,C>0$, and $AB>C$.

For small ${\mathit{\tau }}_2$, we can write $e^{-\mathit{\lambda }{\mathit{\tau }}_2}=1-\mathit{\lambda }{\mathit{\tau }}_2$ and so the characteristic equation of $(5)$ at $E^{\ast }$ becomes ${\mathit{\lambda }}^3(1-\mathit{\mu }{\mathit{\tau }}_2)+{\mathit{\lambda }}^2{\widehat{A}}_{21}+\mathit{\lambda }{\widehat{A}}_{22}+{\widehat{A}}_{23}=0$, where ${\widehat{A}}_{21}=A+\mathit{\mu }{\mathit{\tau }}_2(d_2+h+\mathit{\mu }{F}_{y_{{A|}_{E^{\ast }}}}^2-F_{{x|}_{E^{\ast }}}^1)$, ${\widehat{A}}_{22}=B+\mathit{\mu }{\mathit{\tau }}_2\{(d_2+h)F_{{x|}_{E^{\ast }}}^1+F_{y_{{A|}_{E^{\ast }}}}^1{F}_{{x|}_{E^{\ast }}}^2-F_{{x|}_{E^{\ast }}}^1{F}_{y_{{A|}_{E^{\ast }}}}^2\}$, and ${\widehat{A}}_{23}=C.$

Now, $A>0\Rightarrow d_2+h-F_{{x|}_{E^{\ast }}}^1>0$ and so ${\widehat{A}}_{21}>0$ (since ${\mathit{\tau }}_2>0$ is small); $C>0\Rightarrow A_{23}>0$.

Also, if $AB>C$, then for small ${\mathit{\tau }}_2>0$, we have ${\widehat{A}}_{21}{\widehat{A}}_{22}>{\widehat{A}}_{23}$.

Thus, for small ${\mathit{\tau }}_2>0$, the stability of the system $(2)$ at $E^{\ast }$ implies the stability of system $(5)$ at $E^{\ast }$. $\square$

Lemma 5.2.5

If the system $(2)$ is stable at $E^{\ast }$ and if there exists a ${\mathit{\tau }}_2$ in $0\le {\mathit{\tau }}_2\le {\overline{\mathit{\tau }}}_2$ such that ${\overline{A}}_{\mathit{\theta }}{\mathit{\tau }}^2+{\overline{B}}_{\mathit{\theta }}\mathit{\tau }+{\overline{C}}_{\mathit{\theta }}>0$ holds, then ${\overline{\mathit{\tau }}}_2$ is the maximum value (length of delay) for which the system $(5)$ is locally asymptotically stable at $E^{\ast }$, where ${\overline{A}}_{\mathit{\theta }}{\mathit{\tau }}^2+{\overline{B}}_{\mathit{\theta }}\mathit{\tau }+{\overline{C}}_{\mathit{\theta }}>0,{\overline{A}}_{\mathit{\theta }}=\frac{1}{2}{\overline{v}}_1^2|B_{12}|,{\overline{B}}_{\mathit{\theta }}=|C_{12}|,{\overline{C}}_{\mathit{\theta }}={\overline{v}}_1|A_{12}|+B_{11}-{\overline{v}}_1^2,{\overline{v}}_2=\frac{-|B_{12}|+\sqrt{B_{12}^2+4(A_{11}+|A_{12}|)(C_{11}-|C_{12}|)}}{2(A_{11}+|A_{12}|)}$, and ${\overline{\mathit{\tau }}}_2=\frac{-{\overline{B}}_{\mathit{\theta }}+\sqrt{{\overline{B}}_{\mathit{\theta }}^2-4{\overline{A}}_{\mathit{\theta }}{\overline{C}}_{\mathit{\theta }}}}{2{\overline{A}}_{\mathit{\theta }}}$.

Proof

Then system $(5)$ can be expressed as(7) $$\begin{array}{cc}\hfill \frac{du}{dt}& ={\overline{a}}_{11}u(t)+{\overline{a}}_{12}{v}_J(t)+{\overline{a}}_{13}{v}_A(t)\hfill \\ \hfill \frac{d{v}_J}{dt}& ={\overline{a}}_{21}u(t)+{\overline{a}}_{22}{v}_J(t)+{\overline{a}}_{23}{v}_A(t)+{\overline{a}}_{24}{v}_J(t-{\mathit{\tau }}_2)\hfill \\ \hfill \frac{d{v}_A}{dt}& ={\overline{a}}_{31}{v}_J(t-{\mathit{\tau }}_2)+{\overline{a}}_{32}{v}_A(t)\hfill \end{array}$$(7)

where $a_{11}=F_{{x|}_{E^{\ast }}}^1,a_{12}=F_{y_{{J|}_{E^{\ast }}}}^1,a_{13}=F_{y_{{A|}_{E^{\ast }}}}^1,a_{21}=F_{{x|}_{E^{\ast }}}^2,a_{22}=F_{y_{{J|}_{E^{\ast }}}}^2+\mathit{\mu },a_{23}=F_{y_{{A|}_{E^{\ast }}}}^2,a_{24}=-\mathit{\mu },a_{31}=\mathit{\mu }$, and $a_{32}=-d_2-h$.

Taking the Laplace transformation of system $(6)$, we have$$\begin{array}{cc}\hfill (s-{\overline{a}}_{11})\overline{u}(s)& ={\overline{a}}_{12}{\overline{v}}_J(s)+{\overline{a}}_{13}{\overline{v}}_A(s)+u(0)\hfill \\ \hfill (s-{\overline{a}}_{22}){\overline{v}}_J(s)& ={\overline{a}}_{21}\overline{u}(s)+{\overline{a}}_{23}{\overline{v}}_A(s)+a_{24}{e}^{-s{\mathit{\tau }}_2}\left({\overline{v}}_J(s)+k\right)+v_J(0)\hfill \\ \hfill (s-{\overline{a}}_{32}){\overline{v}}_A(s)& ={\overline{a}}_{31}{e}^{-s{\mathit{\tau }}_2}\left({\overline{v}}_J(s)+k\right)+v_A(0)\hfill \end{array}$$

where $k={\int }_{-{\mathit{\tau }}_2}^0{e}^{-st}{v}_J(t)dt.$

We shall employ the Nyquist criterion, which states that if $s$ is the arc length of a curve encircling the right half-plane, the curves $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ will encircle the origin a number of times equal to the difference between the number of poles and the number of zeroes of $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ in the right half-plane.

Let ${\overline{F}}_1(s)=s^3+{\widehat{A}}_{11}{s}^2+{\widehat{B}}_{11}s+{\widehat{C}}_{11}+e^{-s{\mathit{\tau }}_2}({\widehat{A}}_{12}{s}^2+{\widehat{B}}_{12}s+{\widehat{C}}_{12})=0$. Also, let ${\widehat{v}}_0$ be the smallest positive root of $Re\{{\overline{F}}_1(iv)\}=0.$

Then $E^{\ast }$ is locally asymptotically stable if

$-{\widehat{A}}_{11}{\widehat{v}}_0^2+{\widehat{C}}_{11}={\widehat{A}}_{12}{\widehat{v}}_0^{2}cos{\widehat{v}}_0{\mathit{\tau }}_2-{\widehat{C}}_{12}cos{\widehat{v}}_0{\mathit{\tau }}_2-{\widehat{B}}_{12}{\widehat{v}}_{0}sin{\widehat{v}}_0{\mathit{\tau }}_2$ and

$-{\widehat{v}}_0^3+{\widehat{B}}_{11}{\widehat{v}}_0>-{\widehat{B}}_{12}{\widehat{v}}_{0}cos{\widehat{v}}_0{\mathit{\tau }}_2-{\widehat{A}}_{12}{\widehat{v}}_0^{2}sin{\widehat{v}}_0{\mathit{\tau }}_2+{\widehat{C}}_{12}sin{\widehat{v}}_0{\mathit{\tau }}_2$.

Now, $-{\widehat{A}}_{11}{v}^2+{\widehat{C}}_{11}\le |{\widehat{A}}_{12}|v^2+v|{\widehat{B}}_{12}|+|{\widehat{C}}_{12}|.$

Therefore, the positive solution ${\overline{v}}_2$ of $({\widehat{A}}_{11}+|{\widehat{A}}_{12}|)v^2+v|{\widehat{B}}_{12}|-({\widehat{C}}_{11}-|{\widehat{C}}_{12}|)=0$ is always greater than or equal to ${\widehat{v}}_0$. We obtain ${\overline{v}}_2=\frac{-|{\widehat{B}}_{12}|+\sqrt{{\widehat{B}}_{12}^2+4({\widehat{A}}_{11}+|{\widehat{A}}_{12}|)({\widehat{C}}_{11}-|{\widehat{C}}_{12}|)}}{2({\widehat{A}}_{11}+|{\widehat{A}}_{12}|)}\ge {\widehat{v}}_0,$ where ${\overline{v}}_2$ is independent of ${\mathit{\tau }}_2$.

Also, $-{\overline{v}}_2^3+{\overline{v}}_2{\widehat{B}}_{11}>-{\overline{v}}_2{\widehat{B}}_{12}cos{\overline{v}}_2{\mathit{\tau }}_2-{\overline{v}}_2^2{\widehat{A}}_{12}sin{\overline{v}}_2{\mathit{\tau }}_2+{\widehat{C}}_{12}sin{\overline{v}}_2{\mathit{\tau }}_2$

$\Rightarrow -{\overline{v}}_2^2+{\widehat{B}}_{11}>-|{\widehat{B}}_{12}|\left(1+\frac{1}{2}{\mathit{\tau }}_2^2{\overline{v}}_2^2\right)-|{\widehat{C}}_{12}|{\mathit{\tau }}_2-|{\widehat{A}}_{12}|{\overline{v}}_2\Rightarrow {\overline{A}}_{\mathit{\theta }}{\mathit{\tau }}_2^2+{\overline{B}}_{\mathit{\theta }}{\mathit{\tau }}_2+{\overline{C}}_{\mathit{\theta }}>0$ where ${\overline{A}}_{\mathit{\theta }}=\frac{1}{2}{\overline{v}}_2^2|{\widehat{B}}_{12}|,{\overline{B}}_{\mathit{\theta }}=|{\widehat{C}}_{12}|$, and ${\overline{C}}_{\mathit{\theta }}={\overline{v}}_2|{\widehat{A}}_{12}|+{\widehat{B}}_{11}-{\overline{v}}_2^2.$

Therefore, ${\overline{\mathit{\tau }}}_2=\frac{-{\overline{B}}_{\mathit{\theta }}+\sqrt{{\overline{B}}_{\mathit{\theta }}^2-4{\overline{A}}_{\mathit{\theta }}{\overline{C}}_{\mathit{\theta }}}}{2{\overline{A}}_{\mathit{\theta }}}$ is an estimate for the length of delay for which the stability of the system at $E^{\ast }$ is preserved.$\square$

We know that $i\mathit{\omega }$$(\mathit{\omega }>0)$ is a root of $D_{E^{\ast }}(\mathit{\lambda },0,{\mathit{\tau }}_2)=0$ if and only if

$-{\widehat{A}}_{11}{\mathit{\omega }}^2+{\widehat{C}}_{11}=({\widehat{A}}_{12}{\mathit{\omega }}^2-{\widehat{C}}_{12})cos\mathit{\omega }{\mathit{\tau }}_2-\mathit{\omega }{\widehat{B}}_{12}sin\mathit{\omega }{\mathit{\tau }}_2$ and ${\mathit{\omega }}^3-\mathit{\omega }{\widehat{B}}_{11}=\mathit{\omega }{\widehat{B}}_{12}cos\mathit{\omega }{\mathit{\tau }}_2+({\widehat{A}}_{12}{\mathit{\omega }}^2-{\widehat{C}}_{12})sin\mathit{\omega }{\mathit{\tau }}_2$.

Eliminating ${\mathit{\tau }}_2$, we obtain ${\mathit{\omega }}^6+{\widehat{H}}_1{\mathit{\omega }}^4+{\widehat{H}}_2{\mathit{\omega }}^2+{\widehat{H}}_3=0$, where ${\widehat{H}}_1={\widehat{A}}_{11}^2-2{\widehat{B}}_{11}-{\widehat{A}}_{12}^2,{\widehat{H}}_2={\widehat{B}}_{11}^2-2{\widehat{A}}_{11}{\widehat{C}}_{11}+2{\widehat{A}}_{12}{\widehat{C}}_{12}-{\widehat{B}}_{12}^2$, and ${\widehat{H}}_3={\widehat{C}}_{11}^2-{\widehat{C}}_{12}^2.$

Let $z={\mathit{\omega }}^2$ and $G(z)=z^3+{\widehat{H}}_1{z}^2+{\widehat{H}}_{2}z+{\widehat{H}}_3$. Then ${\mathit{\omega }}^6+{\widehat{H}}_1{\mathit{\omega }}^4+{\widehat{H}}_2{\mathit{\omega }}^2+{\widehat{H}}_3=0$ takes the form $G(z)=0$. Then similar to Lemma $5.1.5$ we get the following result

Lemma 5.2.6

Suppose that the conditions of Lemma $4.4$ are satisfied. Then the following results hold:

(i)	If ${\widehat{H}}_3\ge 0$ and ${\widehat{H}}_1^2\le 3{\widehat{H}}_2$, then the system $(5)$ is locally asymptotically stable at $E^{\ast }$ for all ${\mathit{\tau }}_2>0$.
(ii)	If $(a)$${\widehat{H}}_3<0$ or $(b)$${\widehat{H}}_3\ge 0,{\widehat{H}}_1^2>3{\widehat{H}}_2,{\widehat{z}}_1^{\ast }=\frac{-{\widehat{H}}_1+\sqrt{{\widehat{H}}_1^2-3{\widehat{H}}_2}}{3}$ and $G({\widehat{z}}_1^{\ast })\le 0$ hold, then the system $(5)$ is locally asymptotically stable at $E^{\ast }$ for all ${\mathit{\tau }}_2\in \left[0,{\mathit{\tau }}_{2_0}\right)$, where ${\mathit{\tau }}_{2_0}=min\left\{{\mathit{\tau }}_{2_0}^1,{\mathit{\tau }}_{2_0}^2,{\mathit{\tau }}_{2_0}^3\right\}$, ${\widehat{z}}_k={\widehat{\mathit{\omega }}}_k^2$ are positive roots of $G(z)=0$, and ${\mathit{\tau }}_{2_0}^k=\frac{1}{{\widehat{\mathit{\omega }}}_k}{tan}^{-1}\left[\frac{{\widehat{\mathit{\omega }}}_k\{{\widehat{A}}_{12}{\widehat{\mathit{\omega }}}_k^4+{\widehat{\mathit{\omega }}}_k^2({\widehat{A}}_{11}{\widehat{B}}_{12}-{\widehat{A}}_{12}{\widehat{B}}_{11}-{\widehat{C}}_{12})+{\widehat{B}}_{11}{\widehat{C}}_{12}-{\widehat{B}}_{12}{\widehat{C}}_{11}\}}{{\widehat{\mathit{\omega }}}_k^4({\widehat{B}}_{12}-{\widehat{A}}_{11}{\widehat{A}}_{12})+{\widehat{\mathit{\omega }}}_k^2({\widehat{A}}_{11}{\widehat{C}}_{12}+{\widehat{A}}_{12}{\widehat{C}}_{11}-{\widehat{B}}_{11}{\widehat{B}}_{12})-{\widehat{C}}_{11}{\widehat{C}}_{12}}\right]$, $(k=1,2,3)$.
(iii)	If conditions in $(ii)$ hold and $G^{\prime }(z_1^{\ast })\ne 0$, then the system $(5)$ undergoes a Hopf bifurcation $E^{\ast }$ when ${\mathit{\tau }}_2$ crosses ${\mathit{\tau }}_{2_0}^k$, $(k=1,2,3)$.

5.3. System with both delays $({\mathit{\tau }}_1,{\mathit{\tau }}_2>0)$

The characteristic equation of the system $(1)$ at $E_0$ is independent of ${\mathit{\tau }}_1$ and is identical to the characteristic equation of the system $(5)$ at $E_0$. Therefore, for all ${\mathit{\tau }}_1>0$ and for small ${\mathit{\tau }}_2$ satisfying $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$, the critical point $E_0$ is always a saddle point of the system $(1)$.

Lemma 5.3.1

For small ${\mathit{\tau }}_1,{\mathit{\tau }}_2$ satisfying $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$, the stability of the system $(2)$ at $E_1$ implies the stability of system $(1)$ at $E_1$.

Proof

Let the system $(2)$ be locally asymptotically stable at $E_1$.

Then we have $d_1+d_2+\mathit{\mu }+h>\frac{e_1{m}_{1}K}{a_1+K}$ and $(d_2+h)\left(d_1+\mathit{\mu }-\frac{e_1{m}_{1}K}{a_1+K}\right)>\frac{\mathit{\mu }{e}_2{m}_{2}K}{a_2+K}$.

If ${\mathit{\tau }}_1,{\mathit{\tau }}_2$ are small, we can write $e^{-\mathit{\lambda }{\mathit{\tau }}_1}=1-\mathit{\lambda }{\mathit{\tau }}_1$ and $e^{-\mathit{\lambda }{\mathit{\tau }}_2}=1-\mathit{\lambda }{\mathit{\tau }}_2$.

The characteristic equation of the system $(1)$ at $E_1$ becomes

$(\mathit{\lambda }+r)\left[{\mathit{\lambda }}^2(1-\mathit{\mu }{\mathit{\tau }}_2)+\mathit{\lambda }\left\{d_1+d_2+\mathit{\mu }+h-{\mathit{\tau }}_1\mathit{\mu }(d_2+h)+\frac{({\mathit{\tau }}_1+{\mathit{\tau }}_2)\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}\right\}+(d_1+\mathit{\mu })(d_2+h)-\frac{\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}\right]$.

Since $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$, $d_1+d_2+\mathit{\mu }+h-{\mathit{\tau }}_1\mathit{\mu }(d_2+h)+\frac{({\mathit{\tau }}_1+{\mathit{\tau }}_2)\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}=d_1+\mathit{\mu }+(1-\mathit{\mu }{\mathit{\tau }}_2)(d_2+h)+\frac{({\mathit{\tau }}_1+{\mathit{\tau }}_2)\mathit{\mu }{e}_1{m}_{1}K}{a_1+K}>0$ and so, the stability of the system without delay at $E_1$ implies the stability of system $(1)$ at $E_1$. $\square$

Lemma 5.3.2

For small ${\mathit{\tau }}_1,{\mathit{\tau }}_2$ satisfying $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$, stability of the system $(2)$ at $E^{\ast }$ implies the stability of system $(1)$ at $E^{\ast }$.

Proof

Let the system $(2)$ be locally asymptotically stable at $E^{\ast }$. Then we have $A>0,C>0$, and $AB>C$.

For small ${\mathit{\tau }}_1,{\mathit{\tau }}_2$, we can write $e^{-\mathit{\lambda }{\mathit{\tau }}_1}=1-\mathit{\lambda }{\mathit{\tau }}_1$ and $e^{-\mathit{\lambda }{\mathit{\tau }}_2}=1-\mathit{\lambda }{\mathit{\tau }}_2$ and so the characteristic equation of $(1)$ at $E^{\ast }$ becomes ${\mathit{\lambda }}^3(1+{\mathit{\tau }}_1{P}_{12}-\mathit{\mu }{\mathit{\tau }}_2)+{\mathit{\lambda }}^2{A}^{\ast }+\mathit{\lambda }{B}^{\ast }+C=0$, where

$A^{\ast }=A+(d_2+h-F_{{x|}_{E^{\ast }}}^1)({\mathit{\tau }}_1{P}_{12}-\mathit{\mu }{\mathit{\tau }}_2)+{\mathit{\tau }}_1(P_{11}{F}_{y_J{|}_{E^{\ast }}}^1+\mathit{\mu }{P}_{13})+{\mathit{\tau }}_2\mathit{\mu }{F}_{y_A{|}_{E^{\ast }}}^2$,

$B^{\ast }=B+{\mathit{\tau }}_1\{(d_2+h)(P_{12}{F}_{{x|}_{E^{\ast }}}^1-P_{11}{F}_{y_J{|}_{E^{\ast }}}^1)+\mathit{\mu }{P}_{11}{F}_{y_A{|}_{E^{\ast }}}^1-P_{13}{F}_{{x|}_{E^{\ast }}}^1\}+{\mathit{\tau }}_2\{(d_2+h)F_{{x|}_{E^{\ast }}}^1+\mathit{\mu }$ and $Q_{11}{F}_{y_A{|}_{E^{\ast }}}^1+\mathit{\mu }(F_{{x|}_{E^{\ast }}}^2{F}_{y_A{|}_{E^{\ast }}}^1-F_{{x|}_{E^{\ast }}}^1{F}_{y_A{|}_{E^{\ast }}}^2)\}.$

Now, $A>0\Rightarrow d_2+h-F_{{x|}_{E^{\ast }}}^1>0$ and so $A^{\ast }>0$ (since ${\mathit{\tau }}_1$ and $0<{\mathit{\tau }}_2<\frac{1}{\mathit{\mu }}$ are small).

Also, if $AB>C$, then for small ${\mathit{\tau }}_1,{\mathit{\tau }}_2>0$, we have $A^{\ast }{B}^{\ast }>C$.

Thus, for small ${\mathit{\tau }}_1,{\mathit{\tau }}_2$, the stability of the system $(2)$ at $E^{\ast }$ implies the stability of system $(1)$ at $E^{\ast }$. $\square$

Lemma 5.3.3

If the system $(2)$ is stable at $E^{\ast }$ and if there exists ${\mathit{\tau }}_i$ in $0\le {\mathit{\tau }}_i\le {{\mathit{\tau }}^{\ast }}_i$ such that ${A^{\ast }}_{{\mathit{\theta }}_i}{\mathit{\tau }}^2+{B^{\ast }}_{{\mathit{\theta }}_i}\mathit{\tau }+{C^{\ast }}_{{\mathit{\theta }}_i}>0$ holds, then ${{\mathit{\tau }}^{\ast }}_i$ is the maximum value (length of delay) for which the system $(1)$ is locally asymptotically stable at $E^{\ast }$, where ${A^{\ast }}_{{\mathit{\theta }}_1}=\frac{1}{2}|{\overline{B}}_{E^{\ast }}|{\overline{v}}^{\ast 2},{A^{\ast }}_{{\mathit{\theta }}_2}=\frac{1}{2}|{\widehat{B}}_{E^{\ast }}|{\overline{v}}^{\ast 2},B_{{\mathit{\theta }}_1}^{\ast }=|{\overline{C}}_{E^{\ast }}|,B_{{\mathit{\theta }}_2}^{\ast }=|{\widehat{C}}_{E^{\ast }}|$, $C_{{\mathit{\theta }}_1}^{\ast }=C_{{\mathit{\theta }}_2}^{\ast }=\frac{{\mathrm{\Gamma }}_1}{2},{\overline{v}}^{\ast }=\frac{-|B^{\ast }|+\sqrt{B^{\ast 2}+4A^{\ast }{C}^{\ast }}}{2A^{\ast }}\ge v^{\ast }$, and ${{\mathit{\tau }}^{\ast }}_i=\frac{-{B^{\ast }}_{{\mathit{\theta }}_i}+\sqrt{{B^{\ast 2}}_{{\mathit{\theta }}_i}-4{A^{\ast }}_{{\mathit{\theta }}_i}{C^{\ast }}_{{\mathit{\theta }}_i}}}{2{A^{\ast }}_{{\mathit{\theta }}_i}},(i=1,2)$.

Proof

Let $u(t),v_J(t),and{v}_A(t)$ be the respective linearized variables of the model. Then system $(1)$ can be expressed as(8) $$\begin{array}{cc}\hfill \frac{du}{dt}& =a_{11}^{\ast }u(t)+a_{12}^{\ast }{v}_J(t)+a_{13}^{\ast }{v}_A(t)\hfill \\ \hfill \frac{d{v}_J}{dt}& =a_{21}^{\ast }u(t)+a_{22}^{\ast }{v}_J(t)+a_{23}^{\ast }{v}_A(t)+a_{24}^{\ast }u(t-{\mathit{\tau }}_1)+a_{25}^{\ast }{v}_J(t-{\mathit{\tau }}_1)+a_{26}^{\ast }{v}_J(t-{\mathit{\tau }}_2)+a_{27}^{\ast }{v}_A(t-{\mathit{\tau }}_1)\hfill \\ \hfill \frac{d{v}_A}{dt}& =a_{31}^{\ast }{v}_J(t-{\mathit{\tau }}_2)+a_{32}^{\ast }{v}_A(t)\hfill \end{array}$$(8)

where $a_{11}^{\ast }=F_{{x|}_{E^{\ast }}}^1,a_{12}^{\ast }=F_{y_{{J|}_{E^{\ast }}}}^1,a_{13}^{\ast }=F_{y_{{A|}_{E^{\ast }}}}^1,a_{21}^{\ast }=Q_{11},a_{22}^{\ast }=\mathit{\mu }+Q_{12},a_{23}^{\ast }=Q_{13},a_{24}^{\ast }=F_{{x|}_{E^{\ast }}}^2-Q_{11},a_{25}^{\ast }=P_{12},a_{26}^{\ast }=-\mathit{\mu },a_{27}^{\ast }=F_{y_A{|}_{E^{\ast }}}^2-Q_{13},a_{31}^{\ast }=\mathit{\mu },and{a}_{32}^{\ast }=-d_2-h$.

Taking the Laplace transformation of system $(7)$, we have$$\begin{array}{cc}\hfill & (s-a_{11}^{\ast })\overline{u}(s)=a_{12}^{\ast }{\overline{v}}_J(s)+a_{13}^{\ast }{\overline{v}}_A(s)+u(0)\hfill \\ \hfill & (s-a_{22}^{\ast }){\overline{v}}_J(s)=a_{21}^{\ast }\overline{u}(s)+a_{23}^{\ast }{\overline{v}}_A(s)+e^{-s{\mathit{\tau }}_1}\{a_{24}^{\ast }\left(\overline{u}(s)+k_1\right)+a_{25}^{\ast }\left({\overline{v}}_J(s)+k_2\right)\hfill \\ \hfill & +a_{27}^{\ast }\left({\overline{v}}_A(s)+k_3\right)\}+a_{26}^{\ast }{e}^{-s{\mathit{\tau }}_2}\left({\overline{v}}_J(s)+k\right)+v_J(0)\hfill \\ \hfill & (s-a_{32}^{\ast }){\overline{v}}_A(s)=a_{31}^{\ast }{e}^{-s{\mathit{\tau }}_2}\left({\overline{v}}_J(s)+k\right)+v_A(0)\hfill \end{array}$$

We shall employ the Nyquist criterion, which states that if $s$ is the arc length of a curve encircling the right half-plane, the curves $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ will encircle the origin a number of times equal to the difference between the number of poles and the number of zeroes of $\overline{u}(s),\overline{v_J}(s)$, and $\overline{v_A}(s)$ in the right half-plane.

Let $F^{\ast }(s)=s^3+A_{E^{\ast }}{s}^2+B_{E^{\ast }}s+C_{E^{\ast }}+e^{-s{\mathit{\tau }}_1}({\overline{A}}_{E^{\ast }}{s}^2+{\overline{B}}_{E^{\ast }}s+{\overline{C}}_{E^{\ast }})+e^{-s{\mathit{\tau }}_2}({\widehat{A}}_{E^{\ast }}{s}^2+{\widehat{B}}_{E^{\ast }}s+{\widehat{C}}_{E^{\ast }})+e^{-s({\mathit{\tau }}_1+{\mathit{\tau }}_2)}({\tilde{A}}_{E^{\ast }}s+{\tilde{B}}_{E^{\ast }})$. Also, let $v^{\ast }$ be the smallest positive root of $Re\{F^{\ast }(iv)\}=0.$

Then $E^{\ast }$ is locally asymptotically stable if $-v^{\ast 2}{A}_{E^{\ast }}+C_{E^{\ast }}+({\overline{C}}_{E^{\ast }}-{\overline{A}}_{E^{\ast }}{v}^{\ast 2})cos{v}^{\ast }{\mathit{\tau }}_1+v^{\ast }{\overline{B}}_{E^{\ast }}sin{v}^{\ast }{\mathit{\tau }}_1+({\widehat{C}}_{E^{\ast }}-{\widehat{A}}_{E^{\ast }}{v}^{\ast 2})cos{v}^{\ast }{\mathit{\tau }}_2+v^{\ast }{\widehat{B}}_{E^{\ast }}sin{v}^{\ast }{\mathit{\tau }}_2+{\tilde{B}}_{E^{\ast }}cos({\mathit{\tau }}_1+{\mathit{\tau }}_2)v^{\ast }+v^{\ast }{\tilde{A}}_{E^{\ast }}sin({\mathit{\tau }}_1+{\mathit{\tau }}_2)v^{\ast }=0$ and

$-v^{\ast 3}+v^{\ast }{B}_{E^{\ast }}+v^{\ast }{\overline{B}}_{E^{\ast }}cos{v}^{\ast }{\mathit{\tau }}_1+({\overline{A}}_{E^{\ast }}{v}^{\ast 2}-{\overline{C}}_{E^{\ast }})sin{v}^{\ast }{\mathit{\tau }}_1+v^{\ast }{\widehat{B}}_{E^{\ast }}cos{v}^{\ast }{\mathit{\tau }}_2+({\widehat{A}}_{E^{\ast }}{v}^{\ast 2}-{\widehat{C}}_{E^{\ast }})sin{v}^{\ast }{\mathit{\tau }}_2+v^{\ast }{\tilde{A}}_{E^{\ast }}cos({\mathit{\tau }}_1+{\mathit{\tau }}_2)v^{\ast }-{\tilde{B}}_{E^{\ast }}sin({\mathit{\tau }}_1+{\mathit{\tau }}_2)v^{\ast }>0$.

Now, $v^2(A_{E^{\ast }}-|{\overline{A}}_{E^{\ast }}|-|{\widehat{A}}_{E^{\ast }}|)\le v(|{\overline{B}}_{E^{\ast }}|+|{\widehat{B}}_{E^{\ast }}|+|{\tilde{A}}_{E^{\ast }}|)+(C_{E^{\ast }}+|{\overline{C}}_{E^{\ast }}|+|{\widehat{C}}_{E^{\ast }}|+|{\tilde{B}}_{E^{\ast }}|).$

Therefore, the positive solution ${\overline{v}}^{\ast }$ of ${\overline{A}}^{\ast }{v}^2-v{\overline{B}}^{\ast }-{\overline{C}}^{\ast }=0$ is always greater than or equal to $v^{\ast }$, where

$A^{\ast }=A_{E^{\ast }}-|{\overline{A}}_{E^{\ast }}|-|{\widehat{A}}_{E^{\ast }}|,B^{\ast }=|{\overline{B}}_{E^{\ast }}|+|{\widehat{B}}_{E^{\ast }}|+{\tilde{A}}_{E^{\ast }}|$, and $C^{\ast }=C_{E^{\ast }}+|{\overline{C}}_{E^{\ast }}|+|{\widehat{C}}_{E^{\ast }}|+|{\tilde{B}}_{E^{\ast }}|$.

We obtain ${\overline{v}}^{\ast }=\frac{-|B^{\ast }|+\sqrt{B^{\ast 2}+4A^{\ast }{C}^{\ast }}}{2A^{\ast }}\ge v^{\ast },$ where ${\overline{v}}^{\ast }$ is independent of ${\mathit{\tau }}_1,{\mathit{\tau }}_2$.

Also, $-{\overline{v}}^{\ast 3}+{\overline{v}}^{\ast }{B}_{E^{\ast }}+{\overline{v}}^{\ast }{\overline{B}}_{E^{\ast }}cos{\overline{v}}^{\ast }{\mathit{\tau }}_1+({\overline{A}}_{E^{\ast }}{\overline{v}}^{\ast 2}-{\overline{C}}_{E^{\ast }})sin{\overline{v}}^{\ast }{\mathit{\tau }}_1+{\overline{v}}^{\ast }{\widehat{B}}_{E^{\ast }}cos{\overline{v}}^{\ast }{\mathit{\tau }}_2+({\widehat{A}}_{E^{\ast }}{\overline{v}}^{\ast 2}-{\widehat{C}}_{E^{\ast }})sin{\overline{v}}^{\ast }{\mathit{\tau }}_2+{\overline{v}}^{\ast }{\tilde{A}}_{E^{\ast }}cos({\mathit{\tau }}_1+{\mathit{\tau }}_2){\overline{v}}^{\ast }-{\tilde{B}}_{E^{\ast }}sin({\mathit{\tau }}_1+{\mathit{\tau }}_2){\overline{v}}^{\ast }>0\Rightarrow {\mathit{\tau }}_1^2\left(\frac{1}{2}|{\overline{B}}_{E^{\ast }}|{\overline{v}}^{\ast 2}\right)+{\mathit{\tau }}_1|{\overline{C}}_{E^{\ast }}|+\frac{{\mathrm{\Gamma }}_1}{2}+{\mathit{\tau }}_2^2\left(\frac{1}{2}|{\widehat{B}}_{E^{\ast }}|{\overline{v}}^{\ast 2}\right)+{\mathit{\tau }}_2|{\widehat{C}}_{E^{\ast }}|+\frac{{\mathrm{\Gamma }}_1}{2}>0$ where ${\mathrm{\Gamma }}_1=B_{E^{\ast }}-{\overline{v}}^{\ast 2}+{\overline{v}}^{\ast }(|{\overline{A}}_{E^{\ast }}|+|{\widehat{A}}_{E^{\ast }}|)+({\mathit{\tau }}_1+{\mathit{\tau }}_2)|{\tilde{B}}_{E^{\ast }}|+|{\tilde{A}}_{E^{\ast }}|+|{\overline{B}}_{E^{\ast }}|+|{\widehat{B}}_{E^{\ast }}|$.

This implies ${\mathit{\tau }}_i^2{A}_{{\mathit{\theta }}_i}^{\ast }+B_{{\mathit{\theta }}_i}^{\ast }+C_{{\mathit{\theta }}_i}^{\ast }>0(i=1,2)$ where ${A^{\ast }}_{{\mathit{\theta }}_1}=\frac{1}{2}|{\overline{B}}_{E^{\ast }}|{\overline{v}}^{\ast 2},{A^{\ast }}_{{\mathit{\theta }}_2}=\frac{1}{2}|{\widehat{B}}_{E^{\ast }}|{\overline{v}}^{\ast 2},B_{{\mathit{\theta }}_1}^{\ast }=|{\overline{C}}_{E^{\ast }}|,B_{{\mathit{\theta }}_2}^{\ast }=|{\widehat{C}}_{E^{\ast }}|$, and $C_{{\mathit{\theta }}_1}^{\ast }=C_{{\mathit{\theta }}_2}^{\ast }=\frac{{\mathrm{\Gamma }}_1}{2}.$

Therefore, ${{\mathit{\tau }}^{\ast }}_i=\frac{-{B^{\ast }}_{{\mathit{\theta }}_i}+\sqrt{{B^{\ast 2}}_{{\mathit{\theta }}_i}-4{A^{\ast }}_{{\mathit{\theta }}_i}{C^{\ast }}_{{\mathit{\theta }}_i}}}{2{A^{\ast }}_{{\mathit{\theta }}_i}}$ are estimates for the length of delays for which the stability of the system at $E^{\ast }$ is preserved $(i=1,2)$. $\square$

Now, we consider $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,{\mathit{\tau }}_2)=0$ in its stable interval and regard ${\mathit{\tau }}_1$ as a parameter.

Without any loss of generality, we assume that Lemma $4.4$ and $5.2.6(ii)$ hold.

Then the system $(5)$ is stable for all ${\mathit{\tau }}_2\in [0,{\mathit{\tau }}_{2_0})$.

Let $i\mathit{\omega }(\mathit{\omega }>0)$ be a root of $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,{\mathit{\tau }}_2)=0$. Then, $-{\mathit{\omega }}^2{A}_{E^{\ast }}+C_{E^{\ast }}+\left({\widehat{C}}_{E^{\ast }}-{\widehat{A}}_{E^{\ast }}{\mathit{\omega }}^2\right)cos\mathit{\omega }{\mathit{\tau }}_2+\mathit{\omega }{\widehat{B}}_{E^{\ast }}sin\mathit{\omega }{\mathit{\tau }}_2=\left({\tilde{B}}_{E^{\ast }}sin\mathit{\omega }{\mathit{\tau }}_2-\mathit{\omega }{\tilde{A}}_{E^{\ast }}cos\mathit{\omega }{\mathit{\tau }}_2-\mathit{\omega }{\overline{B}}_{E^{\ast }}\right)sin\mathit{\omega }{\mathit{\tau }}_1-\left(\mathit{\omega }{\tilde{A}}_{E^{\ast }}sin\mathit{\omega }{\mathit{\tau }}_2-{\tilde{B}}_{E^{\ast }}cos\mathit{\omega }{\mathit{\tau }}_2+{\overline{A}}_{E^{\ast }}{\mathit{\omega }}^2-{\overline{C}}_{E^{\ast }}\right)cos{\mathit{\tau }}_1$ and $-{\mathit{\omega }}^3+\mathit{\omega }{B}_{E^{\ast }}+\mathit{\omega }{\overline{B}}_{E^{\ast }}cos\mathit{\omega }{\mathit{\tau }}_2+\left({\widehat{A}}_{E^{\ast }}{\mathit{\omega }}^2-{\widehat{C}}_{E^{\ast }}\right)sin\mathit{\omega }{\mathit{\tau }}_2=\left(\mathit{\omega }{\tilde{A}}_{E^{\ast }}sin\mathit{\omega }{\mathit{\tau }}_2+{\tilde{B}}_{E^{\ast }}cos\mathit{\omega }{\mathit{\tau }}_2-{\overline{A}}_{E^{\ast }}{\mathit{\omega }}^2+{\overline{C}}_{E^{\ast }}\right)sin\mathit{\omega }{\mathit{\tau }}_1+\left({\tilde{B}}_{E^{\ast }}sin\mathit{\omega }{\mathit{\tau }}_2-\mathit{\omega }{\tilde{A}}_{E^{\ast }}cos\mathit{\omega }{\mathit{\tau }}_2-\mathit{\omega }{\overline{B}}_{E^{\ast }}\right)cos\mathit{\omega }{\mathit{\tau }}_1$.

Squaring and adding these equations we get ${\mathit{\omega }}^6+k_1{\mathit{\omega }}^5+k_2{\mathit{\omega }}^4+k_3{\mathit{\omega }}^3+k_4{\mathit{\omega }}^2+k_5\mathit{\omega }+k_6=0$, where

$k_1=-2{\widehat{A}}_{E^{\ast }}sin\mathit{\omega }{\mathit{\tau }}_2$,

$k_2=A_{E^{\ast }}^2-{\overline{A}}_{E^{\ast }}^2+{\widehat{A}}_{E^{\ast }}^2-2B_{E^{\ast }}+2\left(A_{E^{\ast }}{\widehat{A}}_{E^{\ast }}+{\overline{A}}_{E^{\ast }}{\tilde{B}}_{E^{\ast }}-{\widehat{B}}_{E^{\ast }}\right)cos\mathit{\omega }{\mathit{\tau }}_2$,

$k_3=2\left({\widehat{C}}_{E^{\ast }}+{\overline{A}}_{E^{\ast }}{\tilde{A}}_{E^{\ast }}+{\widehat{A}}_{E^{\ast }}{B}_{E^{\ast }}-A_{E^{\ast }}{\widehat{B}}_{E^{\ast }}\right)sin\mathit{\omega }{\mathit{\tau }}_2$,

$k_4=B_{E^{\ast }}^2+{\overline{B}}_{E^{\ast }}^2-{\widehat{B}}_{E^{\ast }}^2-{\tilde{A}}_{E^{\ast }}^2-2A_{E^{\ast }}{C}_{E^{\ast }}+2{\overline{A}}_{E^{\ast }}{\overline{C}}_{E^{\ast }}-2{\widehat{A}}_{E^{\ast }}{\widehat{C}}_{E^{\ast }}$

$+2\left(B_{E^{\ast }}{\overline{B}}_{E^{\ast }}-2A_{E^{\ast }}{\widehat{C}}_{E^{\ast }}-{\widehat{A}}_{E^{\ast }}{C}_{E^{\ast }}-{\tilde{A}}_{E^{\ast }}{\overline{B}}_{E^{\ast }}\right)cos\mathit{\omega }{\mathit{\tau }}_2$,

$k_5=2\left(C_{E^{\ast }}{\widehat{B}}_{E^{\ast }}-B_{E^{\ast }}{\widehat{C}}_{E^{\ast }}-{\tilde{A}}_{E^{\ast }}{\overline{C}}_{E^{\ast }}+{\overline{B}}_{E^{\ast }}{\tilde{B}}_{E^{\ast }}\right)sin\mathit{\omega }{\mathit{\tau }}_2$ and

$k_6=C_{E^{\ast }}^2-{\overline{C}}_{E^{\ast }}^2+{\widehat{C}}_{E^{\ast }}^2-{\tilde{B}}_{E^{\ast }}^2+2C_{E^{\ast }}{\widehat{C}}_{E^{\ast }}-2{\tilde{B}}_{E^{\ast }}{\overline{C}}_{E^{\ast }}cos\mathit{\omega }{\mathit{\tau }}_2$.

Let $H(\mathit{\omega })={\mathit{\omega }}^6+k_1{\mathit{\omega }}^5+k_2{\mathit{\omega }}^4+k_3{\mathit{\omega }}^3+k_4{\mathit{\omega }}^2+k_5\mathit{\omega }+k_6$.

If $k_6<0$, then $H(0)<0$ and as ${lim}_{\mathit{\omega }\to \infty }G(\mathit{\omega })=\infty$ it follows that $H(\mathit{\omega })=0$ has finite positive roots, say, ${\mathit{\omega }}_1,{\mathit{\omega }}_2,\dots ,{\mathit{\omega }}_m$.

For every fixed ${\mathit{\omega }}_i,i=1,2,\dots ,m$, there exists a sequence $\{{\mathit{\tau }}_{1_i}^j:j=1,2,3,\dots \}$ such that $H(\mathit{\omega })=0$ holds.

Let ${\mathit{\tau }}_1^{\ast }=min\{{\mathit{\tau }}_{1_i}^j:i=1,2,\dots ,m;j=1,2,3,\dots \}.$

When ${\mathit{\tau }}_1={\mathit{\tau }}_1^{\ast }$, the equation $D_{E^{\ast }}(\mathit{\lambda },{\mathit{\tau }}_1,{\mathit{\tau }}_2)=0$ has a pair of purely imaginary roots $\pm i{\mathit{\omega }}^{\ast }$ for ${\mathit{\tau }}_2\in [0,{\mathit{\tau }}_{2_0}^{+})$.

We assume that $\mathit{\zeta }={\left[\frac{d(Re\mathit{\lambda })}{d{\mathit{\tau }}_1}\right]}_{\mathit{\lambda }=i{\mathit{\omega }}^{\ast }}\ne 0$.

By the general Hopf bifurcation theorem for functional differential equations, we get the following result:

Lemma 5.3.4

For the system $(1)$, assume that Lemma $4.4$ and $5.2.6$$(ii)$ are satisfied for all ${\mathit{\tau }}_2\in [0,{\mathit{\tau }}_{2_0})$. Then, if $k_6<0$ and $\mathit{\zeta }\ne 0$ hold, $E^{\ast }$ is locally asymptotically stable when ${\mathit{\tau }}_1\in [0,{\mathit{\tau }}_1^{\ast })$ and the system $(1)$ undergoes a Hopf bifurcation at $E^{\ast }$ as ${\mathit{\tau }}_1$ crosses ${\mathit{\tau }}_1^{\ast }$.

5.4. Direction and stability of the Hopf bifurcation

In this section, we shall study the bifurcation properties using techniques from normal form and center manifold theory by Hassard, Kazarinoff, and Wan (1981). Throughout this section, we assume that system $(1)$ undergoes Hopf bifurcation at the positive equilibrium $E^{\ast }$ for ${\mathit{\tau }}_1={\mathit{\tau }}_1^{\ast }$, and $\pm i{\mathit{\omega }}^{\ast }$ are the corresponding roots of $D(\mathit{\lambda },{\mathit{\tau }}_1,{\mathit{\tau }}_2)=0$ at $E^{\ast }$.

Without any loss of generality, we assume that ${\mathit{\tau }}_2^{\ast }<{\mathit{\tau }}_1^{\ast }$, where ${\mathit{\tau }}_2^{\ast }\in [0,{\mathit{\tau }}_{2_0})$.

Also, let $u_1(t)=x({\mathit{\tau }}_{1}t)-x^{\ast },u_2(t)=y_J({\mathit{\tau }}_{1}t)-y_J^{\ast },u_3(t)=y_A({\mathit{\tau }}_{1}t)-y_A^{\ast }$, and ${\mathit{\tau }}_1={\mathit{\tau }}_1^{\ast }+{\mathit{\mu }}_1$, where ${\mathit{\mu }}_1\in R$.

Then the system $(1)$ is transformed into a functional differential equation in $C^1=C^1([-1,0],R^2)$ as $\dot{u}=L_{{\mathit{\mu }}_1}(u_t)+F({\mathit{\mu }}_1,u_t)$, where $u(t)={(u_1,u_2,u_3)}^T\in R^3$, $u_t(\mathit{\theta })=u(t+\mathit{\theta })$, for $\mathit{\theta }\in [-1,0]$, and $L_{{\mathit{\mu }}_1}:C^1\to R,F:R\times C^1\to R$ are given by $L_{{\mathit{\mu }}_1}(\mathit{\varphi })={\mathit{\tau }}_1{M}_1\mathit{\varphi }(0)+{\mathit{\tau }}_1{M}_2\mathit{\varphi }(-1)+{\mathit{\tau }}_1{M}_3\mathit{\varphi }\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right)$ and(9) $$\begin{array}{c}\hfill F({\mathit{\mu }}_1,\mathit{\varphi })={\mathit{\tau }}_1\left(\begin{array}{c}{\displaystyle \sum _{i+j+k\ge 2}\frac{1}{i!j!k!}{f}_{ijk}^{(1)}{\mathit{\varphi }}_1^i(0){\mathit{\varphi }}_2^j(0){\mathit{\varphi }}_3^k(0)}\\ {\displaystyle \sum _{i+j+k+l+m+r+s\ge 2}\frac{1}{i!j!k!l!m!r!s!}{f}_{ijklmrs}^{(2)}{\mathit{\varphi }}_1^i(0){\mathit{\varphi }}_1^j(-1){\mathit{\varphi }}_2^k(0){\mathit{\varphi }}_2^l(-1){\mathit{\varphi }}_2^m\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right){\mathit{\varphi }}_3^r(0){\mathit{\varphi }}_3^s(-1)}\\ {\displaystyle \sum _{i+j\ge 2}\frac{1}{i!j!}{f}_{ij}^{(3)}{\mathit{\varphi }}_2^i\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right){\mathit{\varphi }}_3^j(0)}\end{array}\right)\end{array}$$(9)

where(10) $$\begin{array}{c}\hfill M_1=\left(\begin{array}{ccc}{a}_{11}^{\ast }& a_{12}^{\ast }& a_{13}^{\ast }\\ a_{21}^{\ast }& a_{22}^{\ast }& a_{23}^{\ast }\\ 0& 0& a_{32}^{\ast }\end{array}\right),M_2=\left(\begin{array}{ccc}0& 0& 0\\ a_{24}^{\ast }& a_{25}^{\ast }& a_{27}^{\ast }\\ 0& 0& 0\end{array}\right),M_3=\left(\begin{array}{ccc}0& 0& 0\\ 0& a_{26}^{\ast }& 0\\ 0& a_{31}^{\ast }& 0\end{array}\right),\end{array}$$(10) $f_{ijk}^{(1)}\equiv \frac{{\mathit{\partial }}^{i+j+k}{f}^{(1)}}{\mathit{\partial }{\mathit{\varphi }}_1^i\mathit{\partial }{\mathit{\varphi }}_2^j\mathit{\partial }{\mathit{\varphi }}_3^k},f_{ijklmrs}^{(2)}\equiv \frac{{\mathit{\partial }}^{i+j+k+l+m+r+s}{f}^{(2)}}{\mathit{\partial }{\mathit{\varphi }}_1^i\mathit{\partial }{\mathit{\varphi }}_1^j\mathit{\partial }{\mathit{\varphi }}_2^k\mathit{\partial }{\mathit{\varphi }}_2^l\mathit{\partial }{\mathit{\varphi }}_2^m\mathit{\partial }{\mathit{\varphi }}_3^r\mathit{\partial }{\mathit{\varphi }}_3^s},f_{ij}^{(3)}\equiv \frac{{\mathit{\partial }}^{i+j}{f}^{(3)}}{\mathit{\partial }{\mathit{\varphi }}_2^i\mathit{\partial }{\mathit{\varphi }}_3^j}$ and $\mathit{\varphi }={({\mathit{\varphi }}_1,{\mathit{\varphi }}_2,{\mathit{\varphi }}_3)}^T$.

By Riesz representation theorem, there exists a matrix whose components are bounded variation functions $\mathit{\eta }(\mathit{\theta },{\mathit{\mu }}_1)$, $\mathit{\theta }\in [-1,0]$ such that $L_{{\mathit{\mu }}_1}(\mathit{\varphi })={\int }_{-1}^{0}d\mathit{\eta }(\mathit{\theta },{\mathit{\mu }}_1)\mathit{\varphi }(\mathit{\theta }),$ for $\mathit{\varphi }\in C$.

In fact, we can choose$$\mathit{\eta }(\mathit{\theta },{\mathit{\mu }}_1)=\left\{\begin{array}{cc}{\mathit{\tau }}_1(M_1+M_2+M_3),\hfill & \mathit{\theta }=0\hfill \\ {\mathit{\tau }}_1(M_2+M_3),\hfill & \mathit{\theta }\in \left[-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1},0\right)\hfill \\ {\mathit{\tau }}_1{M}_3,\hfill & \mathit{\theta }\in \left(-1,-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1}\right)\hfill \\ 0,\hfill & \mathit{\theta }=-1.\hfill \end{array}\right.$$

For $\mathit{\varphi }\in C^1([-1,0],R^2)$, define$$M({\mathit{\mu }}_1)\mathit{\varphi }=\left\{\begin{array}{cc}\frac{d\mathit{\varphi }(\mathit{\theta })}{d\mathit{\theta }},\hfill & -1\le \mathit{\theta }<0\hfill \\ {\int }_{-1}^{0}d\mathit{\eta }(s,{\mathit{\mu }}_1)\mathit{\varphi }(s),\hfill & \mathit{\theta }=0\hfill \end{array}\right.$$

and$$R({\mathit{\mu }}_1)\mathit{\varphi }=\left\{\begin{array}{cc}0,\hfill & -1\le \mathit{\theta }<0\hfill \\ F({\mathit{\mu }}_1,\mathit{\varphi }),\hfill & \mathit{\theta }=0\hfill \end{array}\right.$$

Then system $(1)$ is equivalent to $\dot{u}=M({\mathit{\mu }}_1)u_t+R({\mathit{\mu }}_1)u_t$

For $\mathit{\psi }\in C^1([0,1],{(R^2)}^{\ast })$, define$$M^{\ast }\mathit{\psi }(s)=\left\{\begin{array}{cc}-\frac{d\mathit{\psi }(s)}{ds},\hfill & s\in (0,1]\hfill \\ {\int }_1^{0}d{\mathit{\eta }}^T(t,0)\mathit{\psi }(-t),\hfill & s=0\hfill \end{array}\right.$$

and a bilinear inner product $<\mathit{\psi }(s),\mathit{\varphi }(\mathit{\theta })>=\overline{\mathit{\psi }}(0)\mathit{\varphi }(0)-{\int }_1^0{\int }_{\mathit{\xi }=0}^{\mathit{\theta }}\overline{\mathit{\psi }}(\mathit{\xi }-\mathit{\theta })d\mathit{\eta }(\mathit{\theta })\mathit{\varphi }(\mathit{\xi })d\mathit{\xi }$, where $\mathit{\eta }(\mathit{\theta })=\mathit{\eta }(\mathit{\theta },0)$. Then $M=M(0)$ and $M^{\ast }$ are adjoint operators. Now, $\pm {\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }$ are eigenvalues of $M(0)$ and therefore they are also eigenvalues of $M^{\ast }$.

Let $q(\mathit{\theta })={(1,{\mathit{\rho }}_1,{\mathit{\rho }}_2)}^T{e}^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}$ be an eigenvector of $M(0)$ corresponding to the eigenvalue $i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }$ and $q^{\ast }(s)=\mathit{\sigma }(1,{\mathit{\rho }}_1^{\ast },{\mathit{\rho }}_2^{\ast })e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }s}$ be an eigenvector of $M^{\ast }$ corresponding to the eigenvalue $-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }$.

Then, $M(0)q(\mathit{\theta })=i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }q(\mathit{\theta })$ gives ${\mathit{\rho }}_1=\frac{a_{11}^{\ast }{a}_{32}^{\ast }-{\mathit{\omega }}^{\ast 2}-i{\mathit{\omega }}^{\ast }(a_{32}^{\ast }+a_{11}^{\ast })}{a_{13}^{\ast }(i{\mathit{\omega }}^{\ast }+a_{31}^{\ast }-a_{32}^{\ast })}$ and ${\mathit{\rho }}_2=\frac{a_{31}^{\ast }(i{\mathit{\omega }}^{\ast }-a_{11}^{\ast })}{a_{13}^{\ast }(i{\mathit{\omega }}^{\ast }+a_{31}^{\ast }-a_{32}^{\ast })}$

Also, $M^{\ast }{q}^{\ast }(s)=-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }{q}^{\ast }(s)$ gives ${\mathit{\rho }}_1^{\ast }=-\frac{i{\mathit{\omega }}^{\ast }+a_{11}^{\ast }}{a_{21}^{\ast }+a_{24}^{\ast }}$ and ${\mathit{\rho }}_2^{\ast }=\frac{a_{11}^{\ast }(a_{23}^{\ast }+a_{27}^{\ast })-a_{13}^{\ast }(a_{21}^{\ast }+a_{24}^{\ast })+i{\mathit{\omega }}^{\ast }(a_{23}^{\ast }+a_{27}^{\ast })}{(a_{21}^{\ast }+a_{24}^{\ast })(i{\mathit{\omega }}^{\ast }+a_{32}^{\ast })}$.

We have $1=<q^{\ast }(s),q(\mathit{\theta })>={\overline{q}}^{\ast }(0)q(0)-{\int }_{-1}^0{\int }_{\mathit{\xi }=0}^{\mathit{\theta }}\overline{q^{\ast }}(\mathit{\xi }-\mathit{\theta })d\mathit{\eta }(\mathit{\theta })q(\mathit{\xi })d\mathit{\xi }=\overline{\mathit{\sigma }}(1+\mathit{\rho }{\overline{\mathit{\rho }}}^{\ast }+{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_2^{\ast })-\overline{\mathit{\sigma }}{\int }_{-1}^0\mathit{\theta }(1,{\overline{{\mathit{\rho }}_1}}^{\ast },{\overline{\mathit{\rho }}}_2^{\ast })e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}d\mathit{\eta }(\mathit{\theta }){(1,{\mathit{\rho }}_1,{\mathit{\rho }}_2)}^T=\overline{\mathit{\sigma }}\left\{1+{\mathit{\rho }}_1{\overline{\mathit{\rho }}}_1^{\ast }+{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_2^{\ast }+{\mathit{\rho }}_1{\mathit{\tau }}_1^{\ast }{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}({\overline{\mathit{\rho }}}_1^{\ast }{a}_{26}^{\ast }+{\overline{\mathit{\rho }}}_2^{\ast }{a}_{31}^{\ast })+{\mathit{\rho }}_1{\mathit{\tau }}_2^{\ast }{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}(a_{24}^{\ast }+{\mathit{\rho }}_1{a}_{25}^{\ast }+{\mathit{\rho }}_2{a}_{27}^{\ast })\right\}$.

This gives, $\overline{\mathit{\sigma }}={\left\{1+{\mathit{\rho }}_1{\overline{\mathit{\rho }}}_1^{\ast }+{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_2^{\ast }+{\mathit{\rho }}_1{\mathit{\tau }}_1^{\ast }{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}({\overline{\mathit{\rho }}}_1^{\ast }{a}_{26}^{\ast }+{\overline{\mathit{\rho }}}_2^{\ast }{a}_{31}^{\ast })+{\mathit{\rho }}_1{\mathit{\tau }}_2^{\ast }{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}(a_{24}^{\ast }+{\mathit{\rho }}_1{a}_{25}^{\ast }+{\mathit{\rho }}_2{a}_{27}^{\ast })\right\}}^{-1}.$

Furthermore, $<q^{\ast }(s),\overline{q}(\mathit{\theta })>=0$.

Next, we study the stability of bifurcating periodic solutions. The bifurcating periodic solutions $z(t,{\mathit{\mu }}_1(\mathit{ϵ}))$ has amplitude $O(\mathit{ϵ})$ and nonzero Floquet exponent $\mathit{\beta }(\mathit{ϵ})$ with $\mathit{\beta }(0)=0$. Under our hypothesis, ${\mathit{\mu }}_{1}and\mathit{\beta }$ are given by ${\mathit{\mu }}_1={\mathit{\mu }}_2{\mathit{ϵ}}^2+{\mathit{\mu }}_4{\mathit{ϵ}}^4+\cdots$, and $\mathit{\beta }={\mathit{\beta }}_2{\mathit{ϵ}}^2+{\mathit{\beta }}_4{\mathit{ϵ}}^4+\cdots$.

The sign of ${\mathit{\mu }}_2$ indicates the direction of bifurcation, while that ${\mathit{\beta }}_2$ determines the stability of $z(t,{\mathit{\mu }}_1(\mathit{ϵ}))$. $z(t,{\mathit{\mu }}_1(\mathit{ϵ}))$ is stable if ${\mathit{\beta }}_2<0$ and unstable if ${\mathit{\beta }}_2>0$. To derive the coefficients in these expansions, we first construct the coordinates to describe a center manifold ${\mathrm{\Omega }}_0$ near ${\mathit{\mu }}_1=0$, which is a local invariant, attracting a two dimensional (2D) manifold.

Let $z(t)=<q^{\ast },u_t>$ and $W(t,\mathit{\theta })=u_t-2Re[z(t)q(\mathit{\theta })]$.

On the manifold ${\mathrm{\Omega }}_0$ we have $W(t,\mathit{\theta })=W(z(t),\overline{z}(t),\mathit{\theta })$, where

$W(z(t),\overline{z}(t),\mathit{\theta })=W_{20}(\mathit{\theta })\frac{z^2}{2}+W_{11}(\mathit{\theta })z\overline{z}+W_{02}(\mathit{\theta })\frac{{\overline{z}}^2}{2}+W_{30}(\mathit{\theta })\frac{z^3}{6}+\cdots$

In fact, $z$ and $\overline{z}$ are local coordinates of center manifold ${\mathrm{\Omega }}_0$ in the direction of $q$ and $q^{\ast }$, respectively. The existence of center manifold ${\mathrm{\Omega }}_0$ enables us to reduce $\dot{u}(t)=M({\mathit{\mu }}_1)u_t+R({\mathit{\mu }}_1)u_t$ in a single complex variable on ${\mathrm{\Omega }}_0$. For the solutions $u_t\in {\mathrm{\Omega }}_0$, since ${\mathit{\mu }}_1=0$, we have $\dot{z}(t)=i{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }z+{\overline{q}}^{\ast }(0)F_0(z,\overline{z})$, where $F_0(z,\overline{z})=F(0,W(t,0)+2Re[z(t)q(0)])$.

Therefore, $\dot{z}(t)=i{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }z+g(z,\overline{z})$, where $g(z,\overline{z})=g_{20}\frac{z^2}{2}+g_{11}z\overline{z}+g_{02}\frac{{\overline{z}}^2}{2}+g_{21}\frac{z^2\overline{z}}{2}+\cdots$

Now, $u_t(\mathit{\theta })=W(z,\overline{z},\mathit{\theta })+2Re[z(t)q(\mathit{\theta })]$ gives $u_t(\mathit{\theta })=W_{20}(\mathit{\theta })\frac{z^2}{2}+W_{11}(\mathit{\theta })z\overline{z}+W_{02}(\mathit{\theta })\frac{{\overline{z}}^2}{2}+W_{30}(\mathit{\theta })\frac{z^3}{6}+{(1,{\mathit{\rho }}_1,{\mathit{\rho }}_2)}^T{e}^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}z+{(1,{\overline{\mathit{\rho }}}_1,{\overline{\mathit{\rho }}}_2)}^T{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\overline{z}$. This gives,

$\frac{1}{2\overline{\mathit{\sigma }}}{g}_{20}=\frac{{\overline{\mathit{\rho }}}_1^{\ast }}{2}\left(f_{2000000}^{(2)}+f_{0200000}^{(2)}{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}+{\mathit{\rho }}_1^2{f}_{0020000}^{(2)}+{\mathit{\rho }}_1^2{f}_{0002000}^{(2)}{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}+{\mathit{\rho }}_1^2{f}_{0000200}^{(2)}{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}+\cdots \right)$

$+\frac{1}{2}{f}_{200}^{(1)}+{\mathit{\rho }}_1{f}_{110}^{(1)}+{\mathit{\rho }}_2{f}_{101}^{(1)}+{\mathit{\rho }}_1{\mathit{\rho }}_2{f}_{011}^{(1)}+{\mathit{\rho }}_1{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_2^{\ast }{f}_{11}^{(3)}{e}^{-{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}$,

$\frac{1}{\overline{\mathit{\sigma }}}{g}_{11}=f_{200}^{(1)}+{\mathit{\rho }}_1+{\overline{\mathit{\rho }}}_1{f}_{110}^{(1)}+({\mathit{\rho }}_2+{\overline{\mathit{\rho }}}_2)f_{101}^{(1)}+({\mathit{\rho }}_1{\overline{\mathit{\rho }}}_2+{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_1)f_{011}^{(1)}+{\overline{\mathit{\rho }}}_2^{\ast }\left({\mathit{\rho }}_1{\overline{\mathit{\rho }}}_2{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}+{\overline{\mathit{\rho }}}_1{\mathit{\rho }}_2{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}\right)f_{11}^{(3)}$

$+{\overline{\mathit{\rho }}}_1^{\ast }\left\{f_{2000000}^{(2)}+f_{0200000}^{(2)}+{\mathit{\rho }}_1{\overline{\mathit{\rho }}}_1\left(f_{0020000}^{(2)}+f_{0002000}^{(2)}+f_{0000200}^{(2)}\right)+\cdots \right\}$,

$\frac{1}{2\overline{\mathit{\sigma }}}{g}_{02}=\frac{{\overline{\mathit{\rho }}}_1^{\ast }}{2}\left(f_{2000000}^{(2)}+f_{0200000}^{(2)}{e}^{2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}+{\overline{\mathit{\rho }}}_1{f}_{0020000}^{(2)}+{\overline{\mathit{\rho }}}_1^2{f}_{0002000}^{(2)}{e}^{2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}+{\overline{\mathit{\rho }}}_1^2{f}_{0000200}^{(2)}{e}^{2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}+\cdots \right)$

$+\frac{1}{2}{f}_{200}^{(1)}+{\overline{\mathit{\rho }}}_1{f}_{110}^{(1)}+{\overline{\mathit{\rho }}}_2{f}_{101}^{(1)}+{\overline{\mathit{\rho }}}_1{\overline{\mathit{\rho }}}_2\left(f_{011}^{(1)}+{\overline{\mathit{\rho }}}_2^{\ast }{f}_{11}^{(3)}{e}^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}\right)$,

$\frac{1}{2\overline{\mathit{\sigma }}}{g}_{21}=f_{200}^{(1)}\left(W_{11}^{(1)}(0)+W_{20}^{(1)}(0)\right)$

$+f_{110}^{(1)}\left(W_{11}^{(2)}(0)+\frac{1}{2}{W}_{20}^{(2)}(-1)+{\mathit{\rho }}_1{W}_{11}^{(1)}(0)+\frac{{\overline{\mathit{\rho }}}_1}{2}{W}_{20}^{(1)}(0)\right)$

$+f_{101}^{(1)}\left(W_{11}^{(3)}(0)+\frac{1}{2}{W}_{20}^{(3)}(0)+{\mathit{\rho }}_2{W}_{11}^{(1)}(0)+\frac{{\overline{\mathit{\rho }}}_2}{2}{W}_{20}^{(1)}(0)\right)+f_{011}^{(1)}\left({\mathit{\rho }}_1{W}_{11}^{(3)}(0)+\frac{{\overline{\mathit{\rho }}}_1}{2}{W}_{20}^{(3)}(0)+\frac{{\overline{\mathit{\rho }}}_2}{2}{W}_{20}^{(2)}(0)+{\mathit{\rho }}_2{W}_{11}^{(2)}(0)\right)+\frac{1}{2}{f}_{300}^{(1)}+\frac{1}{2}({\overline{\mathit{\rho }}}_1+2{\mathit{\rho }}_1)f_{210}^{(1)}+\frac{1}{2}({\overline{\mathit{\rho }}}_2+2{\mathit{\rho }}_2)f_{201}^{(1)}+({\mathit{\rho }}_1{\overline{\mathit{\rho }}}_2+{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_1+{\mathit{\rho }}_1{\mathit{\rho }}_2)f_{111}^{(1)}+{\overline{\mathit{\rho }}}_1^{\ast }{f}_{2000000}^{(2)}\left(W_{20}^{(1)}(0)+2W_{11}^{(1)}(0)\right)+{\overline{\mathit{\rho }}}_2^{\ast }{f}_{11}^{(3)}\left({\mathit{\rho }}_1{W}_{11}^{(3)}(0)e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}+\frac{{\overline{\mathit{\rho }}}_1}{2}{W}_{20}^{(3)}(0)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}+\frac{{\overline{\mathit{\rho }}}_2}{2}{W}_{20}^{(2)}\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right)+{\mathit{\rho }}_2{W}_{11}^{(2)}\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right)\right)+{\overline{\mathit{\rho }}}_1^{\ast }{f}_{0200000}^{(2)}\left(W_{20}^{(1)}(-1)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}+2W_{11}^{(1)}(-1)e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right)+{\overline{\mathit{\rho }}}_1^{\ast }{f}_{0020000}^{(2)}\left({\overline{\mathit{\rho }}}_1{W}_{20}^{(2)}(0)+2{\mathit{\rho }}_1{W}_{11}^{(2)}(0)\right)+{\overline{\mathit{\rho }}}_1^{\ast }{f}_{0002000}^{(2)}\left({\overline{\mathit{\rho }}}_1{W}_{20}^{(2)}(-1)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}+2{\mathit{\rho }}_1{W}_{11}^{(2)}(-1)\right)+{\overline{\mathit{\rho }}}_1^{\ast }{f}_{0000200}^{(2)}\left({\overline{\mathit{\rho }}}_1{W}_{20}^{(2)}\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}+2{\mathit{\rho }}_1{W}_{11}^{(2)}\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right)e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}\right)+\cdots$

Since there are $W_{20}(\mathit{\theta })$ and $W_{11}(\mathit{\theta })$ in $g_{21}$ we need to compute them.

We have $\dot{W}={\dot{u}}_t-\dot{z}q-\dot{\overline{z}}\overline{q}=M({\mathit{\mu }}_1)u_t+R({\mathit{\mu }}_1)u_t-\left[i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }z+{\overline{q}}^{\ast }(0)F(z,\overline{z})\right]q-\left[-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\overline{z}+q^{\ast }(0)\overline{F}(z,\overline{z})\right]\overline{q}=MW-2Re[{\overline{q}}^{\ast }(0)F(z,\overline{z})q(\mathit{\theta })]+R({\mathit{\mu }}_1)u_t$ and so$$\dot{W}=\left\{\begin{array}{cc}MW-2Re[{\overline{q}}^{\ast }F(z,\overline{z})q(\mathit{\theta })],\hfill & -1\le \mathit{\theta }<0\hfill \\ MW-2Re[{\overline{q}}^{\ast }F(z,\overline{z})q(\mathit{\theta })]+F,\hfill & \mathit{\theta }=0.\hfill \end{array}\right.$$

Let $\dot{W}=MW+H(z,\overline{z},\mathit{\theta })$, where $H(z,\overline{z},\mathit{\theta })=H_{20}(\mathit{\theta })\frac{z^2}{2}+H_{11}(\mathit{\theta })z\overline{z}+H_{02}\frac{{\overline{z}}^2}{2}+\cdots$

Differentiating $W(z,\overline{z},\mathit{\theta })$ with respect to $t$ we get $\dot{W}=W_z\dot{z}+W_{\overline{z}}\dot{\overline{z}}$.

Also, we have $\dot{z}(t)=i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }z+g(z,\overline{z})$.

Therefore, $\dot{W}=\left(W_{20}z+W_{11}\overline{z}+\cdots \right)(i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }z+g(z,\overline{z}))+\left(W_{11}z+W_{02}\overline{z}+\cdots \right)(-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }z+\overline{g}(z,\overline{z}))$.

Also, $\dot{W}=(M{W}_{20}+H_{20})\frac{z^2}{2}+(M{W}_{11}+H_{11})z\overline{z}+(M{W}_{02}+H_{02})\frac{{\overline{z}}^2}{2}+\cdots$

Comparing the coefficients we get $H_{20}(\mathit{\theta })=(2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }{I}_2-M)W_{20}(\mathit{\theta })$ and $M{W}_{11}=-H_{11}(\mathit{\theta })$.

Now, $H(z,\overline{z},\mathit{\theta })=-2Re[{\overline{q}}^{\ast }(0)F(z,\overline{z})q(\mathit{\theta })]+R({\mathit{\mu }}_1)u_t=-g(z,\overline{z})q(\mathit{\theta })-\overline{g}(z,\overline{z})\overline{q}(\mathit{\theta })+R({\mathit{\mu }}_1)u_t$

$=-\left(\frac{1}{2}{g}_{20}{z}^2+g_{11}z\overline{z}+\frac{1}{2}{g}_{02}{\overline{z}}^2+\cdots \right)q(\mathit{\theta })-\left(\frac{1}{2}{\overline{g}}_{20}{\overline{z}}^2+{\overline{g}}_{11}z\overline{z}+\frac{1}{2}{\overline{g}}_{02}{z}^2+\cdots \right)\overline{q}(\mathit{\theta })+R({\mathit{\mu }}_1)u_t$ gives$$H_{20}(\mathit{\theta })=\left\{\begin{array}{cc}-g_{20}q(\mathit{\theta })-{\overline{g}}_{02}\overline{q}(\mathit{\theta }),\hfill & -1\le \mathit{\theta }<0\hfill \\ -g_{20}q(0)-{\overline{g}}_{02}\overline{q}(0)+{\mathit{\tau }}_1^{\ast }{\left(f_{11},\frac{1}{2\overline{\mathit{\sigma }}}{g}_{20}-f_{11}-f_{12},f_{12}\right)}^T,\hfill & \mathit{\theta }=0\hfill \end{array}\right.$$

and$$H_{11}(\mathit{\theta })=\left\{\begin{array}{cc}-g_{11}q(\mathit{\theta })-{\overline{g}}_{11}\overline{q}(\mathit{\theta }),\hfill & -1\le \mathit{\theta }<0\hfill \\ -g_{11}q(0)-{\overline{g}}_{11}\overline{q}(0)+{\mathit{\tau }}_1^{\ast }{\left(f_{21},\frac{1}{\overline{\mathit{\sigma }}}{g}_{11}-f_{21}-f_{22},f_{22}\right)}^T,\hfill & \mathit{\theta }=0\hfill \end{array}\right.$$

where $f_{11}=\frac{1}{2}{f}_{200}^{(1)}+{\mathit{\rho }}_1{f}_{110}^{(1)}+{\mathit{\rho }}_2{f}_{101}^{(1)}+{\mathit{\rho }}_1{\mathit{\rho }}_2{f}_{011}^{(1)}$, $f_{12}={\mathit{\rho }}_1{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_2^{\ast }{f}_{11}^{(3)}{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}$, $f_{21}=f_{200}^{(1)}+({\mathit{\rho }}_1+{\overline{\mathit{\rho }}}_1)f_{101}^{(1)}+({\mathit{\rho }}_1{\overline{\mathit{\rho }}}_2+{\mathit{\rho }}_2{\overline{\mathit{\rho }}}_1)f_{011}^{(1)}$, and $f_{22}=\left({\mathit{\rho }}_1{\overline{\mathit{\rho }}}_2{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}+{\mathit{\tau }}_2{\overline{\mathit{\rho }}}_1{e}^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}\right)f_{11}^{(3)}$.

Now, $M{W}_{20}(\mathit{\theta })=2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }{W}_{20}(\mathit{\theta })-H_{20}$ implies ${\dot{W}}_{20}(\mathit{\theta })=2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }{W}_{20}(\mathit{\theta })+g_{20}q(\mathit{\theta })+{\overline{g}}_{02}\overline{q}(\mathit{\theta })$.

This gives $W_{20}(\mathit{\theta })=\frac{i{g}_{20}}{{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}q(0)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+\frac{i{\overline{g}}_{02}}{3{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\overline{q}(0)e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+E_1{e}^{2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}$, where $E_1\in R^2$ is a constant vector. Also, $M{W}_{11}(\mathit{\theta })=-H_{11}(\mathit{\theta })$ implies ${\dot{W}}_{11}(\mathit{\theta })=g_{11}q(\mathit{\theta })+{\overline{g}}_{11}\overline{q}(\mathit{\theta })$.

This gives $W_{11}(\mathit{\theta })=-\frac{i{g}_{11}}{{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}q(0)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+\frac{i{\overline{g}}_{11}}{{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\overline{q}(0)e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+E_2$, where $E_2\in R^2$ is a constant vector. $E_1$ and $E_2$ can be determined by setting $\mathit{\theta }=0$ in $H(z,\overline{z},\mathit{\theta })$.

Since $W_{20}(\mathit{\theta })$ and $W_{11}(\mathit{\theta })$ are continuous in $[-1,0]$, we have $W_{20}(0)=\frac{i{g}_{20}}{{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}q(0)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+\frac{i{\overline{g}}_{02}}{3{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\overline{q}(0)e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+E_1$ and $\mathit{\varphi }(t)W_{11}(0)=-\frac{i{g}_{11}}{{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}q(0)e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+\frac{i{\overline{g}}_{11}}{{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\overline{q}(0)e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }\mathit{\theta }}+E_2$.

Next we focus on the computation of $E_i,(i=1,2)$.

${\int }_{-1}^{0}d\mathit{\eta }(t)W_{20}(t)={\mathit{\tau }}_1^{\ast }{M}_1{W}_{20}(0)+{\mathit{\tau }}_1^{\ast }{M}_2{W}_{20}\left(-\frac{{\mathit{\tau }}_2^{\ast }}{{\mathit{\tau }}_1^{\ast }}\right)+{\mathit{\tau }}_1^{\ast }{M}_3{W}_{20}(-1)=2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }{W}_{20}(0)-H_{20}(0)$ gives(11) $$\begin{array}{c}\hfill E_1={\left(\begin{array}{ccc}{a}_{11}^{\ast }-2i{\mathit{\omega }}^{\ast }& a_{12}^{\ast }& a_{13}^{\ast }\\ a_{21}^{\ast }+a_{24}^{\ast }{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2}& a_{22}^{\ast }-2i{\mathit{\omega }}^{\ast }+a_{25}^{\ast }{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2}+a_{26}^{\ast }{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1}& a_{23}^{\ast }+a_{27}^{\ast }{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2}\\ 0& a_{31}^{\ast }{e}^{-2i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1}& a_{32}^{\ast }-2i{\mathit{\omega }}^{\ast }\end{array}\right)}^{-1}\left(\begin{array}{c}{e}_{11}\\ e_{12}\\ e_{13}\end{array}\right)\end{array}$$(11) where $e_{11}=\frac{-i{g}_{20}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left(a_{11}^{\ast }-i{\mathit{\omega }}^{\ast }+{\mathit{\rho }}_1{a}_{12}^{\ast }+{\mathit{\rho }}_2{a}_{13}^{\ast }\right)-\frac{i{\overline{g}}_{02}}{3{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left(a_{11}^{\ast }-i{\mathit{\omega }}^{\ast }+{\overline{\mathit{\rho }}}_1{a}_{12}^{\ast }+{\overline{\mathit{\rho }}}_2{a}_{13}^{\ast }\right)-{\mathit{\tau }}_1^{\ast }{f}_{11}$, $e_{12}=\frac{-i{g}_{20}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{a_{21}^{\ast }+{\mathit{\rho }}_1(a_{22}^{\ast }-i{\mathit{\omega }}^{\ast })+{\mathit{\rho }}_2{a}_{23}^{\ast }+e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}(a_{24}^{\ast }+{\mathit{\rho }}_1{a}_{25}^{\ast }+{\mathit{\rho }}_2{a}_{27}^{\ast })+{\mathit{\rho }}_1{a}_{26}{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right\}-\frac{i{\overline{g}}_{02}}{3{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{a_{21}^{\ast }+{\overline{\mathit{\rho }}}_1(a_{22}^{\ast }-i{\mathit{\omega }}^{\ast })+{\overline{\mathit{\rho }}}_2{a}_{23}^{\ast }+e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}(a_{24}^{\ast }+{\overline{\mathit{\rho }}}_1{a}_{25}^{\ast }+{\overline{\mathit{\rho }}}_2{a}_{27})+{\overline{\mathit{\rho }}}_1{a}_{26}^{\ast }{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right\}-{\mathit{\tau }}_1^{\ast }\left(\frac{1}{2\overline{\mathit{\sigma }}}{g}_{20}-f_{11}-f_{12}\right)$,

and $e_{13}=\frac{-i{g}_{20}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{{\mathit{\rho }}_2(a_{32}^{\ast }-i{\mathit{\omega }}^{\ast })+{\mathit{\rho }}_1{a}_{31}^{\ast }{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right\}-\frac{i{\overline{g}}_{02}\overline{\mathit{\rho }}}{3{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{{\overline{\mathit{\rho }}}_2(a_{32}^{\ast }-i{\mathit{\omega }}^{\ast })+{\overline{\mathit{\rho }}}_1{a}_{31}^{\ast }{e}^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right\}-{\mathit{\tau }}_1^{\ast }{f}_{12}$.

Again, $M{W}_{11}(0)=-H_{11}(0)$ gives(12) $$\begin{array}{c}\hfill E_2={\left(\begin{array}{ccc}{a}_{11}^{\ast }& a_{12}^{\ast }& a_{13}^{\ast }\\ a_{21}^{\ast }+a_{24}^{\ast }& a_{22}^{\ast }+a_{25}^{\ast }+a_{26}^{\ast }& a_{23}^{\ast }+a_{27}^{\ast }\\ 0& a_{31}^{\ast }& a_{32}^{\ast }\end{array}\right)}^{-1}\left(\begin{array}{c}{e}_{21}\\ e_{22}\\ e_{23}\end{array}\right)\end{array}$$(12) where $e_{11}=\frac{i{g}_{11}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left(a_{11}^{\ast }-i{\mathit{\omega }}^{\ast }+{\mathit{\rho }}_1{a}_{12}^{\ast }+{\mathit{\rho }}_2{a}_{13}^{\ast }\right)-\frac{i{\overline{g}}_{11}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left(a_{11}^{\ast }-i{\mathit{\omega }}^{\ast }+{\overline{\mathit{\rho }}}_1{a}_{12}^{\ast }+{\overline{\mathit{\rho }}}_2{a}_{13}^{\ast }\right)-{\mathit{\tau }}_1^{\ast }{f}_{21}$,

$e_{22}=\frac{i{g}_{11}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{a_{21}^{\ast }+{\mathit{\rho }}_1(a_{22}^{\ast }-i{\mathit{\omega }}^{\ast })+{\mathit{\rho }}_2{a}_{23}^{\ast }+e^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}(a_{24}^{\ast }+{\mathit{\rho }}_1{a}_{25}^{\ast }+{\mathit{\rho }}_2{a}_{27}^{\ast })+a_{26}{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right\}-\frac{i{\overline{g}}_{11}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{a_{21}^{\ast }+{\overline{\mathit{\rho }}}_1(a_{22}^{\ast }-i{\mathit{\omega }}^{\ast })+{\overline{\mathit{\rho }}}_2{a}_{23}^{\ast }+e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_2^{\ast }}(a_{24}^{\ast }+{\overline{\mathit{\rho }}}_1{a}_{25}^{\ast }+{\overline{\mathit{\rho }}}_2{a}_{27})+e^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}{a}_{26}^{\ast }\right\}-{\mathit{\tau }}_1^{\ast }\left(\frac{1}{\overline{\mathit{\sigma }}}{g}_{11}-f_{21}-f_{22}\right)$ and

$e_{23}=\frac{i{g}_{11}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{{\mathit{\rho }}_2(a_{32}^{\ast }-i{\mathit{\omega }}^{\ast })+{\mathit{\rho }}_1{a}_{31}^{\ast }{e}^{-i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right\}-\frac{i{\overline{g}}_{11}\overline{\mathit{\rho }}}{{\mathit{\tau }}_1^{\ast }{\mathit{\omega }}^{\ast }}\left\{{\overline{\mathit{\rho }}}_2(a_{32}^{\ast }-i{\mathit{\omega }}^{\ast })+{\overline{\mathit{\rho }}}_1{a}_{31}^{\ast }{e}^{i{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\right\}-{\mathit{\tau }}_1^{\ast }{f}_{22}$.

Thus, we can determine $W_{20}(\mathit{\theta })$ and $W_{11}(\mathit{\theta })$. Furthermore, $g_{21}$ can be expressed by the parameters and delays. Then, we can obtain the expression of $C_1(0)=\frac{i}{2{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}\left(g_{20}{g}_{11}-2{|g_{11}|}^2-\frac{|g_{02}{|}^2}{3}\right)+\frac{g_{21}}{2},{\mathit{\mu }}_2=-\frac{Re(C_1(0)}{Re({\mathit{\lambda }}^{\prime }({\mathit{\tau }}_1^{\ast }))},{\mathit{\beta }}_2=2Re(C_1(0))$, and $T_2=-\frac{Im(C_1(0))+{\mathit{\mu }}_{2}Im({\mathit{\lambda }}^{\prime }({\mathit{\tau }}_1^{\ast }))}{{\mathit{\omega }}^{\ast }{\mathit{\tau }}_1^{\ast }}$ which determine the nature of bifurcating periodic solutions in the center manifold at the critical value.

6. Numerical simulations

In this section, we investigate numerically the effect of the various parameters on the qualitative behavior of the system using parameter values given in Table 1 throughout, unless otherwise stated. Under the set of parameter values as given in Table 1, the systems $(1)$, $(2)$, $(3)$, and $(5)$ are locally asymptotically stable at $E^{\ast }$.

Table 1. Set of parameter values used in numerical analysis.

Parameters	Description of parameters	Value
$r$	Intrinsic growth rate of Parrotfish	6
$K$	Carrying capacity	2.5
$m$	Maximal growth rate of juvenile Pterois Volitans on Parrotfish	1
$m_1$	Maximal growth rate of adult Pterois Volitans on Parrotfish	3
$m_2$	Maximal growth rate of adults on juveniles	5
$a$	Half saturation constant for uptake of Parrotfish by juvenile Pterois Volitans	1
$a_1$	Half saturation constant for uptake of Parrotfish by adult Pterois Volitans	1
$a_2$	Half saturation constant for uptake of juveniles by adults	2
$b_1,b_2$	Interference of Parrotfish and juveniles on the growth of adults	0.5
$d_1$	Mortality rate of juvenile Pterois Volitans	0.4
$d_2$	Mortality rate of adult Pterois Volitans	0.3
$e_1$	Growth efficiency of Pterois Volitans on Parrotfish	0.6
$e_2$	Growth efficiency of Pterois Volitans due to cannibalism	0.5
$1/mu$	Total time spent by Pterois Volitans in its juvenile stage	0.1
$h$	Harvesting rate of adult Pterois Volitans	0.36
${\mathit{\tau }}_1$	Reproduction delay of adult Pterois Volitans	0.5
${\mathit{\tau }}_2$	Maturation delay of juvenile Pterois Volitans	0.1

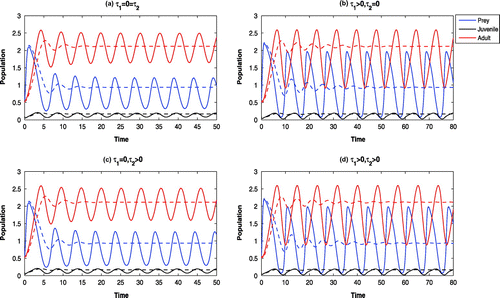
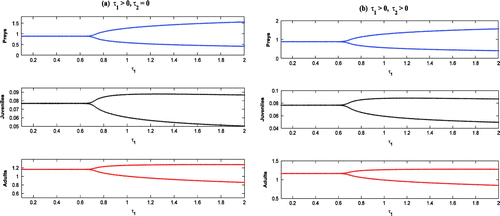
Figure 2. Phase-plane diagrams of the systems for $K=0.2$ other parameter values in Table 1. All the systems are LAS at $E_1$.

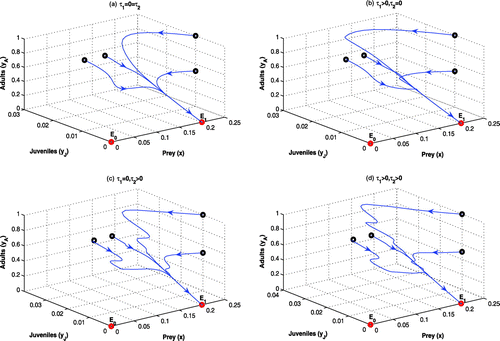
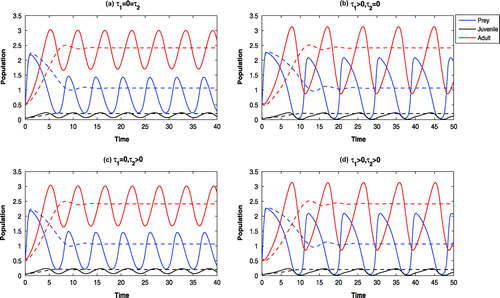
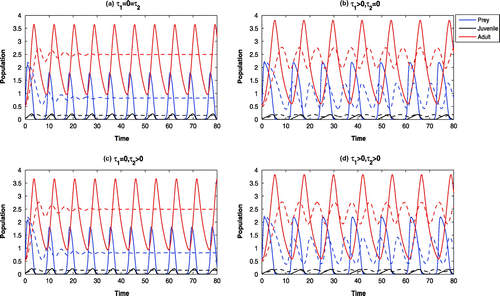
Figure 3. Time evolution of the populations for $K=2.7$ other parameter values in Table 1. The systems $(2)$ and $(5)$ are LAS at $E^{\ast }$, whereas, the systems $(1)$ and $(3)$ are oscillatory around $E^{\ast }$ (solid). For $K=2.7$ and $h=0.6$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

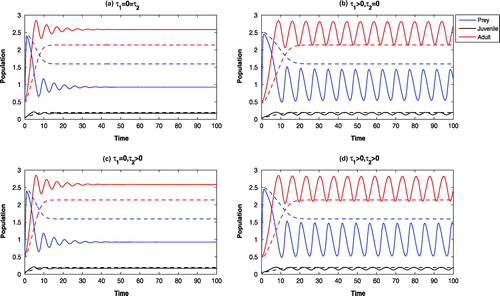
Figure 4. Time evolution of the populations for $K=3$ and other parameter values in Table 1. All the systems are oscillatory around $E^{\ast }$ (solid). For $K=3$ and $h=0.75$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

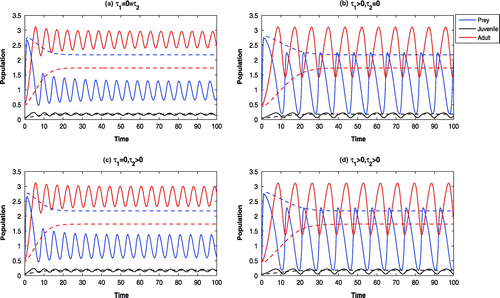
Figure 5. Time evolution of the populations for $r=1.5$ and other parameter values in Table 1. All the systems are oscillatory around $E^{\ast }$ (solid). For $r=1.5$ and $h=0.5$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

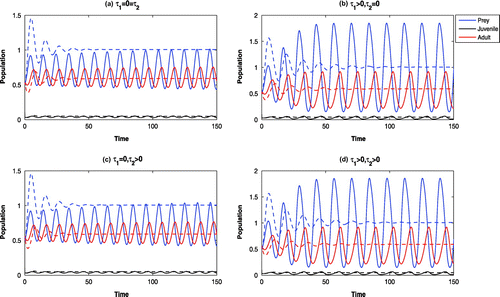
Figure 6. Time evolution of the populations for $r=3.5$ and parameter values in Table 1. The systems $(2)$ and $(5)$ are LAS at $E^{\ast }$, whereas, the systems $(1)$ and $(3)$ are oscillatory around $E^{\ast }$ (solid). For $r=3.5$ and $h=0.45$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

We carried out numerical simulations and interpret the resulting figures by varying the parameter(s) under investigation, keeping all other parameters fixed.

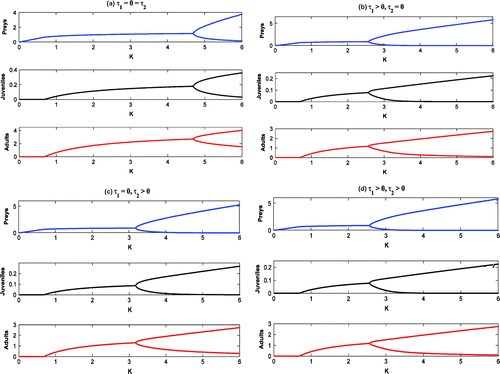
6.1. The effect of varying the carrying capacity ($K$)

With low carrying capacity of Parrotfish (viz., $K=0.2$), the juvenile and adult Pterois Volitans cannot survive and all the systems become stable at $E_1$ (cf. Figure 2). By increasing the value of $K$ (viz., $K=2.7$), the system without delay and the system with maturation time delay only are stable at $E^{\ast }$, whereas, the systems with reproduction delay only and with both delays are oscillatory around $E^{\ast }$ (cf. Figure 3 (solid)).

With high carrying capacity of Parrotfish (viz., $K=3$), all the systems are oscillatory around $E^{\ast }$ (cf. Figure 4 (solid)).

6.2. The effect of varying the intrinsic growth rate ($r$)

With low intrinsic growth rate of Parrotfish (viz., $r=1.5$), all the systems are oscillatory around $E^{\ast }$ (cf. Figure 5 (solid)). By increasing the value of $r$ (viz., $r=3.5$), the system without delay and the system with maturation time delay only are stable at $E^{\ast }$, whereas, the systems with reproduction delay only and with both delays are oscillatory around $E^{\ast }$ (cf. Figure 6 (solid)).

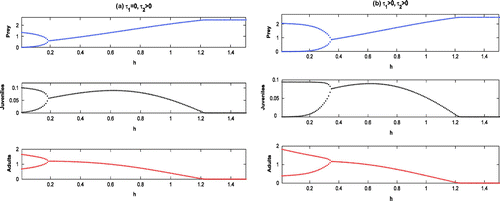
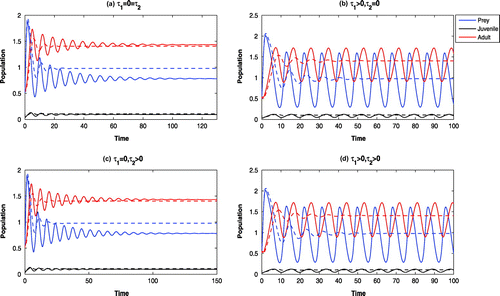
6.3. The effects of invasion

With high invasiveness of adult Pterois Volitans, the maximal growth rate of adult Pterois Volitans on Parrotfish becomes high. It is observed that, for $m_1=3.2$ the system without delay and the system with maturation time delay only are stable at $E^{\ast }$, whereas, the systems with reproduction delay only and with both delays are oscillatory around $E^{\ast }$ (cf. Figure 7 (solid)).

Figure 7. Time evolution of the populations for $m_1=3.2$ and other parameter values in Table 1. The systems $(2)$ and $(5)$ are LAS at $E^{\ast }$, whereas, the systems $(1)$ and $(3)$ are oscillatory around $E^{\ast }$ (solid). For $m_1=3.2$ and $h=0.42$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

With high growth rate of the adult Pterois Volitans (viz., $m_1=3.5$), all the systems become oscillatory around $E^{\ast }$ (cf. Figure 8 (solid)).

Figure 8. Time evolution of the populations for $m_1=3.5$ and other parameter values in Table 1. All the systems are oscillatory around $E^{\ast }$ (solid). For $m_1=3.5$ and $h=0.5$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

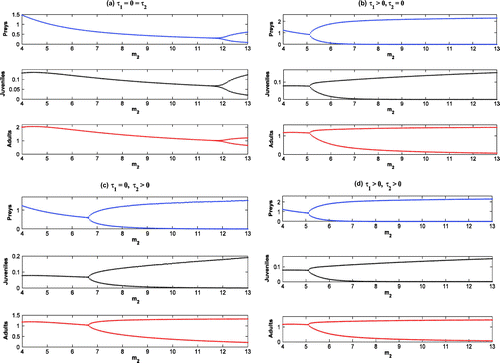
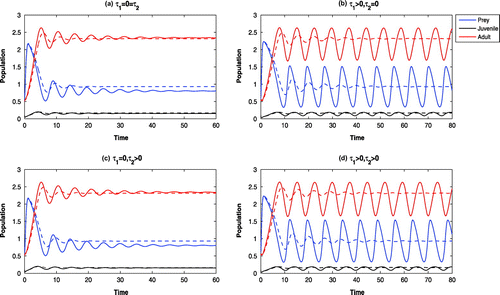
6.4. The effects of cannibalism

The rate of cannibalism is dependent on the maximal growth rate of adult maximal growth rate of on its juveniles. In absence of cannibalism (viz., $m_2=0$), all the systems become oscillatory around $E^{\ast }$ (cf. Figure 9 (solid)). Increasing the value of $m_2$ (viz. $m_2=3$), the systems $(2)$ and $(5)$ are LAS at $E^{\ast }$, whereas, the systems $(1)$ and $(3)$ are oscillatory around $E^{\ast }$ (cf. Figure 10 (solid)). Further increase of $m_2$ stabilizes the systems at $E^{\ast }$.

Figure 9. Time evolution of the populations for $m_2=0$ and other parameter values in Table 1. All the systems are oscillatory around $E^{\ast }$ (solid). For $m_2=0$ and $h=0.55$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

Figure 10. Time evolution of the populations for $m_2=3$ and other parameter values in Table 1. The systems $(2)$ and $(5)$ are LAS at $E^{\ast }$, whereas, the systems $(1)$ and $(3)$ are oscillatory around $E^{\ast }$ (solid). For $m_2=3$ and $h=0.45$, other parameter values in Table 1, all the systems are LAS at $E^{\ast }$ (dotted).

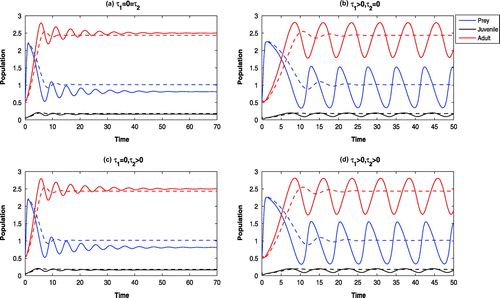
6.5. The effects of harvesting:

In absence of harvesting of adult Pterois Volitans the systems are oscillatory around $E^{\ast }$ (cf. Figure 11 (solid)). By increasing the harvesting rate (viz., $h=0.15$), the system without delay becomes stable at $E^{\ast }$ and the systems with delay are oscillatory around $E^{\ast }$ (cf. Figure 11 (dotted)). Further increase of harvesting (viz. $h=0.36$) stabilizes all the systems at $E^{\ast }$. With high rate of harvesting, juvenile as well as adult Pterois Volitans are eliminated from the system. Further, we observe the following effects:

(a)	The systems are oscillatory around $E^{\ast }$ with high carrying capacity (viz., $K=3$). In this case, increase of the rate of harvesting of adult Pterois Volitans (viz., $h=0.75$) stabilizes all the systems at $E^{\ast }$ (cf. Figure 4 (dotted)).
(b)	With low intrinsic growth rate of Parrotfish (viz., $r=1.5$), all the systems become oscillatory around $E^{\ast }$. By increasing the rate of harvesting of adult Pterois Volitans (viz., $h=0.5$), the systems stabilize at $E^{\ast }$ (cf. Figure 5 (dotted)).
(c)	With high invasiveness of the adult Pterois Volitans (viz., $m_1=3.5$), all the systems are oscillatory around $E^{\ast }$. By increasing the harvesting rate of adult Pterois Volitans (viz., $h=0.5$), the systems stabilize at $E^{\ast }$ (cf. Figure 8 (dotted)).
(d)	In absence of cannibalism of Pterois Volitans (viz., $m_2=0$), all the systems are oscillatory around $E^{\ast }$. By increasing the harvesting rate (viz., $h=0.55$), the systems stabilize at $E^{\ast }$ (cf. Figure 9 (dotted)).

Figure 11. Time evolution of the populations for $h=0$ and other parameter values in Table 1. The systems are oscillatory around $E^{\ast }$ (solid). For $h=0.15$ and other parameter values in Table 1, the systems $(2)$ and $(5)$ are LAS at $E^{\ast }$, whereas, the systems $(1)$ and $(3)$ are oscillatory around $E^{\ast }$ (dotted).

6.6. Hopf bifurcation

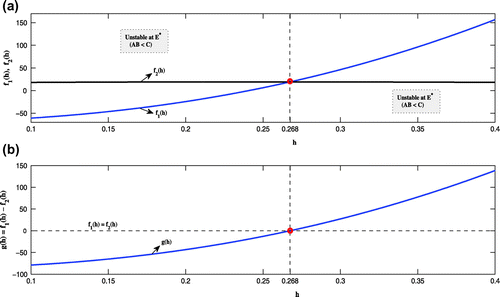
We observe that in absence of harvesting of adult Pterois Volitans, other parameter values as in Table 1, the system (2) is oscillatory around $E^{\ast }$ (Figure 11 (solid)). Increasing the maximal rate of harvesting, the system $(2)$ becomes locally asymptotically stable at $E^{\ast }$ (Figure 11 (dotted)). We therefore consider $h$ as a bifurcation parameter. From Figure 12(a) it is observed that $f_1(h)$ and $f_2(h)$ intersect at $h=0.268$, indicating that the system $(2)$ changes its stability when the parameter $h$ crosses the threshold $h_{cr}=0.268$. More specifically, for $h>h_{cr}$ we see that $f_1(h)>f_2(h)$, satisfying the condition of stability at $E^{\ast }$ as as given in Lemma $4.4$. Also, for $h<h_{cr}$ we see that $f_1(h)<f_2(h)$ and so the system $(2)$ is unstable at $E^{\ast }$. Moreover, we observe that the tangent to $g(h)$ at $h_{cr}=0.268$ is not parallel to the $h$ axis (Figure 12(b)), satisfying the condition $\frac{dg}{dh}{|}_{(h=0.268)}\ne 0$ (Lemma $4.5(iii)$). Thus the system $(2)$ undergoes a subcritical Hopf bifurcation when the parameter $h$ is increased through $h_{cr}=0.268$.

The bifurcation thresholds of the systems $(1),(2),(3)$, and $(5)$, for different parameter values, are given in Table 2.

Table 2. Hopf bifurcation thresholds.

Parameter	System (1)	System (2)	System (3)	System (5)	Referred figure
K	4.7	2.6	3.2	2.6	Figure 13
$m_2$	12	5.1	6.7	5.1	Figure 14
h	0.268	0.35	0.26	0.35	Figures 12 and 16
${\mathit{\tau }}_1$	–	–	0.7	0.65	Figure 15

Figure 12. $(a)$ The relative position of $f_1(h),f_2(h)$ showing that the system $(2)$ satisfies Lemma $4.5(ii)$ when the two curves intersect at the $h=0.268$. $(b)$ The tangent to the curve $g(h)=f_1(h)-f_2(h)$ at $h=0.268$ is not parallel to the $h$ axis, satisfying Lemma $4.5(iii)$

Figure 13. Bifurcation diagrams with $K$ as bifurcation parameter.

Figure 14. Bifurcation diagrams with $m_2$ as bifurcation parameter.

Figure 15. Bifurcation diagrams with ${\mathit{\tau }}_1$ as bifurcation parameter.

Figure 16. Bifurcation diagrams with $h$ as bifurcation parameter.

7. Discussion

We have considered an intraguild system in which adult Pterois Volitans exhibit cannibalism toward juveniles of its species and are subjected to harvesting. The main objective of this paper is to study the dynamic behavior of the system in the presence of discrete time lags in reproduction and maturation of Pterois Volitans. Experimental observations by Murray et al. (2013) reveal that Holling II functional response is quite accurate in predicting the observed functional response of fishes. This prompts us to use Holling II response function in our model. Based upon the observations of Castillo-Chavez et al. (2002) it is reasonable to assume that the mortality and maturity rates of fishes are proportional to the number of fishes present in our system. We have shown that solutions of the system are bounded in the long run. We have obtained conditions for permanence and the stability of the system at the coexistence equilibrium. It is observed that if the maximal harvesting rate of adult Pterois Volitans exceeds a certain threshold, the system stabilizes at the coexistence equilibrium through a subcritical Hopf bifurcation. Also, we have established that the systems remain locally asymptotically stable and all solutions approach $E^{\ast }$ whenever the magnitude of the delays lies below some threshold values. In order to find the expression for these threshold values, we have obtained the estimated length of stability preserving delays. The stability as well as the direction of bifurcation is obtained by applying the algorithm due to Hassard, Kazarinoff, and Wan (1981) that depends on the centre manifold theorem. From numerical simulation it is observed that in the absence of cannibalism and with low harvesting rate of adult Pterois Volitans, the IG-systems become oscillatory around the interior equilibrium. In this case, increase of cannibalism up to a certain threshold stabilizes the system at the interior equilibrium, justifying the observations of Bosch, Roos, and Gabriel (1988) that decrease of predator density due to cannibalism releases prey from predation pressure by inducing stability. Also, with high rate of cannibalism of adult Pterois Volitans, the coexisting populations show oscillatory dynamics. This supports the observations from previous modeling analyses by Diekmann et al. (1986), Hastings (1987), and Magnússon (1999) that high cannibalism level can have destabilizing effects leading to oscillations. The IG-systems become oscillatory around the interior equilibrium with low intrinsic growth rate of Parrotfish in absence of harvesting of adult Pterois volitans, a phenomenon which has not been observed in the previous studies by Dhar and Jatav (2013), Bhattacharyya and Pal (2013), and deserve further investigation. If the reproduction time delay is high, the system with both time lags becomes oscillatory around the positive equilibrium. Also, high rate of invasion of adult Pterois Volitans on Parrotfish induces oscillations around the positive equilibrium, leading to dynamic instability. This represents the phenomenon of ecological imbalance due to the presence of the invasive Pterois Volitans in a coral reef ecosystem, justifying the observations of Albins and Hixon (2008) that high predation rates of adult Pterois Volitans are detrimental to coral reef ecosystems. The dynamic instability can be controlled by increasing the maximal harvesting rate of adult Pterois Volitans. This too justifies that harvesting of these species is beneficial for coral reef ecosystem as observed by Morris, Shertzer and Rice (2011).

Throughout the article an attempt is made to search for a suitable way to control the growth of Parrotfish and Pterois Volitans and maintain stable coexistence of all the species. From analytical and numerical observations, it is seen that increase of the harvesting of adult Pterois Volitans induces stability of the system. Moreover, we observe that harvesting at higher rates are necessary to obtain stability of the systems with delay than that of the system without delay.

Acknowledgements

The authors would like to thank the referees very much for their valuable comments and suggestions.

Additional information

Funding

The research is supported by Science and Engineering Research Board, Government of India, Grant No. SR/S4/MS:863/13.

Notes on contributors

Joydeb Bhattacharyya

Our research group is headed by Dr Samares Pal and includes Dr Joydeb Bhattacharyya as a post-doctoral researcher. Research in the group addresses a wide range of questions broadly concerning the dynamics of coral-reef ecosystems under natural and anthropogenic stress. The main emphasis of our work includes mathematical modeling of coral reef ecosystems affected by seaweed allelopathy-induced coral diseases, overfishing of herbivores and invasion of predatory Pterois Volitans. The research reported in this paper will help in studying the catastrophic regime shifts in coral-reefs under the proliferation of predatory Pterois Volitans and the subsequent loss in herbivory.

Appendix 1

Proof of boundedness of the system (Theorem 3.1)

Let $\left(x(t),y_J(t),y_A(t)\right)$ be a solution of the system $(1)$ satisfying the initial conditions.

Then, corresponding to $\mathit{ϵ}>0$, there exists $T_1>0$ such that $x(t)\le K+\mathit{ϵ}$, for all $t\ge T_1$.

Let $\mathrm{\Sigma }(t)=x(t)+y_J(t)+y_A(t)$

Then for all $t\ge T_1$ we get, $\frac{d}{dt}(\mathrm{\Sigma }(t))+d_0\mathrm{\Sigma }(t)\le r(K+\mathit{ϵ})+(e_1{m}_1+e_2{m}_2){\mathit{\varphi }}_3(\mathit{\theta })$, where $d_0=min\{r,d_1,d_2\}$.

Let $K_0=(e_1{m}_1+e_2{m}_2){\mathit{\varphi }}_3(\mathit{\theta })$, where $\mathit{\theta }\in (-\mathit{\tau },0]$.

Let $u(t)$ be the solution of $\frac{du}{dt}+u{D}_0=rK,$ satisfying $u(0)=\mathrm{\Sigma }(0)$.

Then $u(t)=\frac{r(K+\mathit{ϵ})+K_0}{d_0}+\left(\mathrm{\Sigma }(0)-\frac{r(K+\mathit{ϵ})+K_0}{d_0}\right)e^{-t{d}_0}\to \frac{rK+K_0}{d_0}$ as $t\to \infty .$

By comparison, it follows that ${lim\; sup}_{t\to \infty }[x(t)+y_J(t)+y_A(t)]\le \frac{rK+K_0}{d_0},$ proving the theorem.

Proof of Theorem 4.1

Since ${lim\; sup}_{t\to \infty }[x(t)+y_J(t)+y_A(t)]\le \frac{rK+K_0}{d_0},$ it follows that ${lim\; sup}_{t\to \infty }[y_J(t)+y_A(t)]<\frac{rK+K_0}{d_0}$.

Therefore, there exists $T_1>0$ such that $y_J(t)\le M_1$ and $y_A(t)\le M_2$, for all $t\ge T_1$ where $M_1,M_2$ are finite positive constants with $M_1+M_2<\frac{rK+K_0}{d_0}$.

For all $t\ge T_1$, we have $\frac{dx}{dt}\ge x(t)\left[r\left(1-\frac{x(t)}{K}\right)-\frac{m_1{M}_1}{a_1}-\frac{m_2{M}_2}{a_2}\right].$

This implies, $\frac{dx}{dt}{|}_{{}_{x_1}}\ge 0$ for all $t\ge T_1$, where $x_1=\frac{K(r{a}_1{a}_2-m_1{a}_2{M}_1-m_2{a}_1{M}_2)}{a_1{a}_{2}r}>0$ and $r>\frac{m_1{a}_2{M}_1+m_2{a}_1{M}_2}{a_1{a}_2}$.

Also, $x\le K$ as $t\to \infty$. Therefore, there exists $T_2>0$ such that $x(t)\le K$ for all $t\ge T_2$.

Therefore, for all $t\ge max\{T_1,T_2\},$$x_1\le x(t)\le K$.

Again, for all $t\ge max\{T_1,T_2\}$, $\frac{d{y}_J}{dt}\ge \frac{e_1{m}_1{x}_1{y}_A(t)}{a_1+K+b_1{M}_1}-\frac{(1-e_2)m_2{M}_1{M}_2}{a_2}-(\mathit{\mu }+d_1)M_1>0$ if

$y_A(t)>\frac{a_1+K+b_1{M}_1}{e_1{m}_1{x}_1}\left\{\frac{(1-e_2)m_2{M}_1{M}_2}{a_2}+(\mathit{\mu }+d_1)M_1\right\}$.

Let there exists $y_{A_1}>0$ such that $\frac{a_1+K+b_1{M}_1}{e_1{m}_1{x}_1}\left\{\frac{(1-e_2)m_2{M}_1{M}_2}{a_2}+(\mathit{\mu }+d_1)M_1\right\}<y_{A_1}<M_2$.

Then $\frac{d{y}_J}{dt}>0$ for $y_A(t)\ge y_{A_1}>0$ and $t>max\{T_1,T_2\}$ and so in this case there exists $T_3>0$ and $0<y_{J_1}<M_1$ such that $y_J(t)\ge y_{J_1}$ for all $t\ge T_3$.

Therefore, for all $t\ge T_3$, if $y_{A_1}\le y_A(t)\le M_2$, then $y_{J_1}\le y_J(t)\le M_1$.

Let $T=max\{T_1,T_2,T_3\}$. Then for all $t\ge T$, there exists finite positive real numbers $x_1,y_{J_1},y_{A_1}$ with $x_1=\frac{K(r{a}_1{a}_2-m_1{a}_2{M}_1-m_2{a}_1{M}_2)}{a_1{a}_{2}r},y_{A_1}(t)>\frac{a_1+K+b_1{M}_1}{e_1{m}_1{x}_1}\left\{\frac{(1-e_2)m_2{M}_1{M}_2}{a_2}+(\mathit{\mu }+d_1)M_1\right\}$ and $r>\frac{m_1{a}_2{M}_1+m_2{a}_1{M}_2}{a_1{a}_2}$ such that $x_1\le x(t)\le K,y_{J_1}\le y_J(t)\le M_1,y_{A_1}\le y_A(t)\le M_2$.

Proof of Lemma (4.4)

The characteristic equation of the system $(2)$ at $E^{\ast }$ is ${\mathit{\lambda }}^3+A{\mathit{\lambda }}^2+B\mathit{\lambda }+C=0$, where

$A=d_2+h-F_{{x|}_{E^{\ast }}}^1-F_{y_{{J|}_{E^{\ast }}}}^2$, $B=F_{{x|}_{E^{\ast }}}^1{F}_{y_{{J|}_{E^{\ast }}}}^2-F_{y_{{J|}_{E^{\ast }}}}^1{F}_{{x|}_{E^{\ast }}}^2-\mathit{\mu }{F}_{y_{{A|}_{E^{\ast }}}}^2-(d_2+h)(F_{{x|}_{E^{\ast }}}^1+F_{y_{{J|}_{E^{\ast }}}}^2)$ and $C=\mathit{\mu }(F_{{x|}_{E^{\ast }}}^1{F}_{y_{{A|}_{E^{\ast }}}}^2-F_{{x|}_{E^{\ast }}}^2{F}_{y_{{A|}_{E^{\ast }}}}^1)+(d_2+h)(F_{{x|}_{E^{\ast }}}^1{F}_{y_{{J|}_{E^{\ast }}}}^2-F_{y_{{J|}_{E^{\ast }}}}^1{F}_{{x|}_{E^{\ast }}}^2)$.

Now, $A>0$ if $h>\frac{m{x}^{\ast }{y}_J^{\ast }}{{(a+x^{\ast })}^2}+\frac{m_1{x}^{\ast }{y}_A^{\ast }}{{(a_1+x^{\ast }+b_1{y}_J^{\ast })}^2}-\frac{e_1{m}_1{b}_1{x}^{\ast }{y}_A^{\ast }}{{(a_1+x^{\ast }+b_1{y}_J^{\ast })}^2}-\frac{(1-e_2)m_2(a_2+x^{\ast })y_A^{\ast }}{{(a_2+x^{\ast }+b_2{y}_J^{\ast })}^2}-\mathit{\mu }-d_1-d_2-\frac{r{x}^{\ast }}{K}=h^{\ast }$, (say)

and $\mathit{\eta }=AB-C$.

Therefore, by the Routh–Hurwitz criterion of stability, the system $(2)$ is stable at $E^{\ast }$ if $\mathit{\eta }>0$ and $h>h^{\ast }$.

Proof of Lemma (4.5)

The characteristic equation of the variational matrix at $E^{\ast }$ is ${\mathit{\lambda }}^3+A{\mathit{\lambda }}^2+B\mathit{\lambda }+C=0$, where

The necessary and sufficient conditions for Hopf bifurcation to occur at $h=h_{cr}$ are that

$(i)$$h_{cr}>h^{\ast }$ and $C(h_{cr})>0$,

$(ii)$$f_1(h_{cr})=f_2(h_{cr}),$

$(iii)$$Re{\left[\frac{d{\mathit{\lambda }}_j(h)}{dh}\right]}_{h_{cr}}\ne 0,j=1,2,3.$

where $f_1(h)=A(h)B(h),f_2(h)=C(h)$.

For $h=h_{cr}$, the characteristic equation becomes $(\mathit{\lambda }+A)({\mathit{\lambda }}^2+B)=0\Rightarrow \mathit{\lambda }=-A,\pm i\sqrt{B}$.

For $h\in (h_{cr}-\mathit{ϵ},h_{cr}+\mathit{ϵ}),$ the roots are in general of the form:

${\mathit{\lambda }}_1(h)={\mathit{\beta }}_1(h)+i{\mathit{\beta }}_2(h),{\mathit{\lambda }}_2(h)={\mathit{\beta }}_1(h)-i{\mathit{\beta }}_2(h)$, and ${\mathit{\lambda }}_3(h)=-A(h).$

Therefore, $\frac{d}{dh}\left({\mathit{\lambda }}^3+A{\mathit{\lambda }}^2+B\mathit{\lambda }+C\right)=0$ gives $(K+iL)\frac{d\mathit{\lambda }}{dh}+(M+iN)=0$, where

$K(h)=3{\mathit{\beta }}_1^2(h)-3{\mathit{\beta }}_2^2(h)+2A(h){\mathit{\beta }}_1(h)+B(h)$

$L(h)=6{\mathit{\beta }}_1(h){\mathit{\beta }}_2(h)+2A(h){\mathit{\beta }}_2(h)$

$M(h)=C^{{}^{\prime }}(h)+\left\{{\mathit{\beta }}_1^2(h)-{\mathit{\beta }}_2(h)\right\}{A}^{{}^{\prime }}(h)+{\mathit{\beta }}_1{B}^{{}^{\prime }}(h)$

$N(h)=2{\mathit{\beta }}_1(h){\mathit{\beta }}_2(h)A^{{}^{\prime }}(h)+{\mathit{\beta }}_2(h)B^{{}^{\prime }}(h).$

Therefore, $\frac{d\mathit{\lambda }}{dh}=-\frac{\{M(h)K(h)+N(h)L(h)\}+i\{N(h)K(h)-M(h)L(h)\}}{K^2(h)+L^2(h)}$

If ${\left\{M(h)K(h)+N(h)L(h)\right\}}_{h_{cr}}\ne 0$, then $Re{\left[\frac{d{\mathit{\lambda }}_j}{dh}\right]}_{h=h_{cr}}\ne 0$.

Therefore, if

$(i)$$h_{cr}>h^{\ast }$ and $C(h_{cr})>0$,

$(ii)$$f_1(h_{cr})=f_2(h_{cr}),$

$(iii)$${\left\{M(h)K(h)+N(h)L(h)\right\}}_{h_{cr}}\ne 0$

all hold, then a Hopf bifurcation occurs at $h=h_{cr}$ and also it is nondegenerate.