Dynamics of the interaction of plankton and planktivorous fish with delay

Abstract

This paper is devoted to the study of a plankton–fish ecosystem model. The model represents the interaction between phytoplankton, zooplankton, and fish with Holling II functional response consisting of carrying capacity and constant intrinsic growth rate of phytoplankton. It is observed that if the carrying capacity of phytoplankton population crosses a certain critical value, the system enters into Hopf bifurcation. We have introduced discrete time delay due to gestation in the functional response term involved with the growth equation of planktivorous fish. We have studied the effect of time delay on the stability behavior. In addition, we have obtained an estimate for the length of time delay to preserve the stability of the model system. Existence of Hopf bifurcating small amplitude periodic solutions is derived by considering time delay as a bifurcation parameter. It is observed that constant intrinsic growth rate of phytoplankton and mortality rate of planktivorous fish play an important role in changing one steady state to another steady state and oscillatory behavior of the system. Computer simulations illustrate the results.

Keywords:

• plankton
• fish
• stability
• equilibria
• delay

AMS Subject Classifications:

• 92D40
• 92D25

Public Interest Statement

Economically important fish species have long been regarded in isolation from each other and their habitat. In order to comprehensively assess the impacts of fisheries, the entire habitat must be considered. Only then will a sustainable and economic fishery system be possible. Predation by fish determines the abundance of herbivorous zooplankton which in turn regulates the level of phytoplankton. Also, changes in the abundance of planktivorous fish do affect both the phytoplankton and zooplankton. The relationship between phytoplankton, zooplankton, and fish culture is of paramount importance in determining the water quality, on one hand, and the natural productivity and the fish production, on the other. It is observed that constant intrinsic growth rate of phytoplankton and mortality rate of planktivorous fish play an important role in changing one steady state to another steady state and oscillatory behavior of the system.

1. Introduction

It is well known that plankton plays an integral role in marine ecosystem. Phytoplankton and zooplankton are the main two types of plankton. Many models have already been built to simulate zooplankton–phytoplankton interactions. In marine ecosystem, much attention has been paid to the effect of fish and plankton biomass. Top-down and bottom-up effects on plankton–fish dynamics have been discussed by Scheffer (1991) and Pal and Chatterjee (2012). The authors have discussed that at high fish densities, zooplankton is controlled by fish predation and algal biomass is light or nutrient limited, whereas at low fish densities, zooplankton is food limited and phytoplankton density is controlled by zooplankton grazing. Scheffer, Rinaldi, and Kuznetsov (2000) have discussed about isocline analysis and simulations to show how an increase in fish predation may affect plankton dynamics in the model and to explain which type of bifurcations may arise. Role of gestation delay in a plankton–fish model under stochastic fluctuations has been discussed by Mukhopadhyay and Bhattacharyya (2008). Realistic patterns of patchiness in plankton–fish dynamics have been studied by Upadhyay, Kumari, and Rai (2009). The authors also studied both one-dimensional and two-dimensional reaction–diffusion model of nutrient–phytoplankton–zooplankton–fish interaction. As studied by Biktashev, Brindley, and Horwood (2003), the food source for fish larvae depends on the zooplankton dynamics, which in turn is coupled to larval populations through the zooplankton mortality term. A conceptual mathematical model of fish and zooplankton populations inhabiting the lakes Naroch and Myastro has been developed and studied by Medvinsky et al. (2009).

In general, delay differential equations exhibit much more complicated dynamics than ordinary differential equations since a time delay can cause destabilization of equilibria and can induce various oscillations and periodic solutions. As observed by Bischi (1992), the effects of the time delay involved nutrient recycling on resilience, that is, the rate at which a system returns to a stable steady state following a perturbation. The researchers have suggested that characterizing a system by oscillatory behavior, an increase in the distributed time delay, can have a stabilizing effect. But it has been found that the introduction of time delays is a destabilizing process, in the sense that increasing the time delay could cause a stable equilibrium to become unstable and/or cause the populations to fluctuate (Cushing, 1977; Freedman & Rao, 1983). Chemostat-type models incorporating discrete delays have been investigated by Freedman, So, and Waltman (1989). Also, delayed models in population biology have been discussed in Gopalsamy (1984), Kuang (1993), Khare, Misra, Singh, and Dhar (2011) and Liu, Beretta, and Breda (2010). A discrete time delay term to the model of Beretta, Bischi, and Solimano (1991) was introduced in Ruan (1995). This discrete time delay term may be considered as delay due to gestation. The author also allowed the washout rates for nutrient and plankton to be different. Recently, effect of delay on nutrient cycling in phytoplankton–zooplankton interaction model has been studied by Das and Ray (2008). Rehim and Imran (2012) have induced a discrete time delay to both the consume response function and distribution of toxic substance terms in phytoplankton–zooplankton model. They have found out a range of gestation delays which initially impart stability, then induce instability and ultimately lead to periodic behavior. Due to gestation of prey, a discrete time delay toxin producing phytoplankton–zooplankton system shows rich dynamic behavior including chaos and limit cycles (Singh & Gakkhar, 2012). In particular, Gazi and Bandyopadhyay (2006) have introduced discrete time delay due to recycling of dead organic matters and gestation of nutrients to the growth equations of various trophic levels. They have studied the effect of time delay on the stability behavior and obtained an estimate for the length of time delay to preserve the stability of the model system. Effects of time delay on a harvested predator–prey model have discussed in Gazi and Bandyopadhyay (2008), Maity, Patra, and Samanta (2007) and Yongzhen, Min, and Changguo (2011).

Here, an open system is considered with three interacting components consisting of phytoplankton (P), zooplankton (Z), and planktivorous fish (F). In this paper, a plankton–fish interaction model is described. The stability of equilibrium point is described. We have derived the conditions for instability of the system around the interior equilibrium and Hopf bifurcation in presence of delay and non-delay models. Direction of Hopf bifurcation is discussed. Numerical simulations under a set of parameter values have been performed to support our analytical results.

2. The mathematical model

Let $P(t)$ be the concentration of the phytoplankton at time t with carrying capacity K and constant intrinsic growth rate r. Let $Z(t)$ be the concentration zooplankton biomass and $F(t)$ be the concentration of planktivorous fish biomass present at any instant of time t.

Let ${\mathit{\alpha }}_1$ be the maximal zooplankton ingestion rate and ${\mathit{\alpha }}_2$ maximal zooplankton conversion rate for the growth of zooplankton, respectively (${\mathit{\alpha }}_2\le {\mathit{\alpha }}_1$). Let ${\mathit{\gamma }}_1$ be the maximal planktivorous fish ingestion rate and ${\mathit{\gamma }}_2$$({\mathit{\gamma }}_2\le {\mathit{\gamma }}_1)$ be the maximal planktivorous fish conversion rate due to grazing of herbivorous zooplankton. Further, ${\mathit{\mu }}_1$, ${\mathit{\mu }}_2$ , ${\mathit{\mu }}_3$ denote the mortality rates of the phytoplankton, zooplankton, and planktivorous fish biomass, respectively. We choose Holling type II functional form to describe the grazing phenomena with $K_1$ and $K_2$ as half saturation constant.

The basic equations with all of the parameters are:(1) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\frac{dP}{dt}& =rP(1-\frac{P}{K})-\frac{{\mathit{\alpha }}_{1}PZ}{K_1+P}-{\mathit{\mu }}_{1}P\equiv J_1(P,Z,F)\\ \frac{dZ}{dt}& =\frac{{\mathit{\alpha }}_{2}PZ}{K_1+P}-\frac{{\mathit{\gamma }}_{1}ZF}{K_2+Z}-{\mathit{\mu }}_{2}Z\equiv J_2(P,Z,F)\\ \frac{dF}{dt}& =\frac{{\mathit{\gamma }}_{2}ZF}{K_2+Z}-{\mathit{\mu }}_{3}F\equiv J_3(P,Z,F).\end{array}\right\}\end{array}$$(1)

Set $X={(P,Z,F)}^T\in {{\mathbf{R}}_{+}}^3$ and $J(X)={\left[J_1(X),J_2(X),J_3(X)\right]}^T$, with $J:{{\mathbf{R}}_{+}}^3\to {\mathbf{R}}^3$. The system (Equation 1) can be written in compact form as $\dot{X}=J(X)$. Its Jacobian is(2) $$\begin{array}{c}\hfill V=\left[\begin{array}{ccc}r-\frac{2rP}{K}-\frac{{\mathit{\alpha }}_1{K}_{1}Z}{{(K_1+P)}^2}-{\mathit{\mu }}_1& -\frac{{\mathit{\alpha }}_{1}P}{K_1+P}& 0\\ \frac{{\mathit{\alpha }}_2{K}_{1}Z}{{(K_1+P)}^2}& \frac{{\mathit{\alpha }}_{2}P}{K_1+P}-\frac{{\mathit{\gamma }}_1{K}_{2}F}{{(K_2+Z)}^2}-{\mathit{\mu }}_2& -\frac{{\mathit{\gamma }}_{1}Z}{K_2+Z}\\ 0& \frac{{\mathit{\gamma }}_2{K}_{2}F}{{(K_2+Z)}^2}& \frac{{\mathit{\gamma }}_{2}Z}{K_2+Z}-{\mathit{\mu }}_3\end{array}\right].\end{array}$$(2)

3. Some preliminary results

3.1. Positive invariance

The system (Equation 1) is not homogeneous. However, it is easy to check that whenever choosing $X(0)\in {{\mathbf{R}}_{+}}^3$ with $X_i=0$, for $i=1,2,3$, then $J_i(X){\mid }_{X_i=0}\ge 0$. This ensures that the solution remains within the positive orthant, ensuring the biological well posedness of the system.

3.2. Boundedness of the system

Theorem 1

All the solutions of (Equation 1) are ultimately bounded.

Proof

We define a function$$w=P+Z+F.$$

We have $\frac{dP}{dt}\le rP(1-\frac{r}{K})$ which gives $P\le \frac{c_{1}K}{c_1+e^{-rt}}\to K$ as $t\to \infty$, where $c_1$ is constant.

For the large value of t, we get $\frac{dw}{dt}\le rP-D_{0}w$, where $D_0=min\{{\mathit{\mu }}_1,{\mathit{\mu }}_2,{\mathit{\mu }}_3\}$.

Let $x(t)$ be the solution of $\frac{dx}{dt}+x{D}_0=rK$, satisfying $x(0)=w(0)$.

Then, $x(t)=\frac{rK}{D_0}+(w(0)-\frac{rK}{D_0})e^{-D_{0}t}\to \frac{rK}{D_0}$ as $t\to \infty$. By comparison, it follows that lim ${sup}_{t\to \infty }[P(t)+Z(t)+F(t)]\le \frac{rK}{D_0}$, proving the theorem.

3.3. Equilibria

The system (Equation 1) possesses the following four equilibria: the plankton free equilibrium $E_0=(0,0,0)$, the zooplankton free equilibrium $E_{01}=\left(\frac{K(r-{\mathit{\mu }}_1)}{r},0,0\right)$, the planktivorous fish free equilibrium $E_1=(P_1,Z_1,0)$, and possibly the coexistence of the three populations $E^{\ast }=(P^{\ast },Z^{\ast },F^{\ast })$.

3.3.1. Plankton free equilibrium

$E_0(0,0,0)$ is always feasible; the Jacobian (Equation 2) evaluated at this equilibrium has the eigenvalues $-{\mathit{\mu }}_2<0$, $-{\mathit{\mu }}_3<0$ and $r-{\mathit{\mu }}_1>0$. Clearly, $E_0$ is always unstable.

3.3.2. Zooplankton free equilibrium

At $E_{01}$, the Jacobian (Equation 2) factorizes to give three explicit eigenvalues $-(r-{\mathit{\mu }}_1)<0$, $-{\mathit{\mu }}_3<0$ and ${\mathit{\mu }}_2(R_0-1)$, where $R_0$ is defined below. Thus, $E_{01}$ is locally asymptotically stable if and only if(3) $$\begin{array}{c}\hfill R_0=\frac{{\mathit{\alpha }}_{2}K(r-{\mathit{\mu }}_1)}{{\mathit{\mu }}_2[r(K_1+K)-K{\mathit{\mu }}_1]}<1,\end{array}$$(3)

3.3.3. Planktivorous fish free equilibrium

At $E_1$, the population levels are$$P_1=\frac{{\mathit{\mu }}_2{K}_1}{{\mathit{\alpha }}_2-{\mathit{\mu }}_2},Z_1=\frac{{\mathit{\alpha }}_2{K}_1[K({\mathit{\alpha }}_2-{\mathit{\mu }}_2)(r-{\mathit{\mu }}_1)-r{\mathit{\mu }}_2{K}_1]}{{\mathit{\alpha }}_{1}K{({\mathit{\alpha }}_2-{\mathit{\mu }}_2)}^2}.$$

This equilibrium is feasible if it is satisfying(4) $$\begin{array}{c}\hfill {\mathit{\alpha }}_2>{\mathit{\mu }}_2,K>\frac{r{\mathit{\mu }}_2{K}_1}{({\mathit{\alpha }}_2-{\mathit{\mu }}_2)(r-{\mathit{\mu }}_1)}.\end{array}$$(4)

At $E_1$, the Jacobian (Equation 2) factorizes to give one explicit eigenvalue ${\mathit{\gamma }}_2{Z}_1{(K_2+Z_1)}^{-1}-{\mathit{\mu }}_3$ and the quadratic ${\mathit{\lambda }}^2+\left(\frac{r{P}_1}{K}-\frac{P_1{\mathit{\alpha }}_1{Z}_1}{{(K_1+P_1)}^2}\right)\mathit{\lambda }+\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2{K}_1{P}_1{Z}_1}{{(K_1+P_1)}^3}=0$. The Routh–Hurwitz conditions for the latter are easily seen to hold, but only when (Equation 4) is satisfied. Thus, stability of $E_1$ is then ensured by(5) $$\begin{array}{c}\hfill R_1=\frac{{\mathit{\alpha }}_2{K}_1[K({\mathit{\alpha }}_2-{\mathit{\mu }}_2)(r-{\mathit{\mu }}_1)-r{K}_1{\mathit{\mu }}_2]({\mathit{\gamma }}_2-{\mathit{\mu }}_3)}{{\mathit{\mu }}_3{K}_2{({\mathit{\alpha }}_2-{\mathit{\mu }}_2)}^2}<1.\end{array}$$(5)

3.3.4. The coexistence equilibrium

The coexistence equilibrium $E^{\ast }=(P^{\ast },Z^{\ast },F^{\ast })$ cannot be found explicitly since $Z^{\ast }=\frac{{\mathit{\mu }}_3{K}_2}{{\mathit{\gamma }}_2-{\mathit{\mu }}_3}$, $F^{\ast }=\frac{[({\mathit{\alpha }}_2-{\mathit{\mu }}_2)P^{\ast }-{\mathit{\mu }}_2{K}_1]K_2{\mathit{\gamma }}_2}{{\mathit{\gamma }}_1({\mathit{\gamma }}_2-{\mathit{\mu }}_3)(K_1+P^{\ast })}$ and $P^{\ast }=\frac{-B+\sqrt{B^2+4AC}}{2A}$, where $A=r({\mathit{\gamma }}_2-{\mathit{\mu }}_3)$, $B=-[(K-K_1)r-K{\mathit{\mu }}_1]({\mathit{\gamma }}_2-{\mathit{\mu }}_3)$, $C=-K[(r-{\mathit{\mu }}_1)K_1-{\mathit{\alpha }}_1{\mathit{\mu }}_3{K}_2]$.

Thus, the condition for the existence of the interior equilibrium point $E^{\ast }(P^{\ast },Z^{\ast },F^{\ast })$ is given by, $P^{\ast }>0,Z^{\ast }>0,F^{\ast }>0$. For feasibility, we certainly need$$\begin{array}{c}\hfill {\mathit{\gamma }}_2>{\mathit{\mu }}_3\text{and}0<r<min\left\{\frac{K{\mathit{\mu }}_1}{K-K_1},\frac{{\mathit{\alpha }}_1{\mathit{\mu }}_3{K}_2+{\mathit{\mu }}_1{K}_1}{K_1}\right\}.\end{array}$$Stability analysis of the positive interior equilibrium of the system (Equation 1)

The variational matrix of system (Equation 1) around the positive equilibrium $E^{\ast }=(P^{\ast },Z^{\ast },F^{\ast })$ is$$V^{\ast }=\left[\begin{array}{ccc}{n}_{11}& n_{12}& 0\\ n_{21}& n_{22}& n_{23}\\ 0& n_{32}& 0\end{array}\right],$$

where $n_{11}=\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^2}-\frac{r{P}^{\ast }}{K},n_{12}=-\frac{{\mathit{\alpha }}_1{P}^{\ast }}{K_1+P^{\ast }}<0$, $n_{21}=\frac{K_1{\mathit{\alpha }}_2{Z}^{\ast }}{{(K_1+P^{\ast })}^2}>0$, $n_{22}=\frac{{\mathit{\gamma }}_1{Z}^{\ast }{F}^{\ast }}{{(K_2+Z^{\ast })}^2}>0$, $n_{23}=-\frac{{\mathit{\gamma }}_1{Z}^{\ast }}{K_2+Z^{\ast }}<0$, $n_{32}=\frac{K_2{\mathit{\gamma }}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^2}>0$.

The characteristic equation is $Q^3+A_1{Q}^2+A_{2}Q+A_3=0$,

where $A_1=-(n_{11}+n_{22})$, $A_2=n_{11}{n}_{22}-n_{12}{n}_{21}-n_{32}{n}_{23}$, $A_3=n_{11}{n}_{32}{n}_{23}$.

• Case1: If $n_{11}>0$, it implies that $A_3<0$. Thus, $E^{\ast }$ is unstable.

• Case2: If $n_{11}<0$, it implies that $A_3>0$.

Here, $A_1>0$, if $\frac{r{P}^{\ast }}{K}>\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^2}+\frac{{\mathit{\gamma }}_1{Z}^{\ast }{F}^{\ast }}{{(K_2+Z)}^2}$.

Also, $A_2>0$ if $-n_{12}{n}_{21}-n_{32}{n}_{23}>-n_{11}{n}_{22}$ where $n_{23}{n}_{32}<0$, $n_{12}{n}_{21}<0$ and $n_{11}{n}_{22}$ is negative. So, $A_1{A}_2-A_3>0$ if $A_1{A}_2>A_3$. Therefore, according the Routh–Hurwitz criteria, all roots of the above cubic equation have negative real parts satisfying $A_1>0,A_3>0$, and $A_1{A}_2-A_3>0$. Then, the system becomes locally asymptotically stable around $E^{\ast }$. Thus, depending upon system parameters, the system may exhibit stable or unstable behavior in this case.

Table 1. The table representing thresholds and stability of steady states

Thresholds ($R_0,R_1$)	$E_0(0,0,0)$	$E_{01}\left(\frac{K(r-{\mathit{\mu }}_1)}{K},0,0\right)$	$E_1(P_1,Z_1,0)$	$E^{\ast }(P^{\ast },Z^{\ast },F^{\ast })$
$R_0<1$	Unstable	Asymptotically stable	Not feasible	Not feasible
$R_0>1,R_1<1$	Unstable	Unstable	Asymptotically stable	Not feasible
$R_1>1$	Unstable	Unstable	Unstable	Asymptotically stable

The analytical results are summarized in Table 1.

3.4. Hopf bifurcation at coexistence

Theorem 2

When the carrying capacity K crosses a critical value, say $K^{\ast }$, the system (Equation 1) enters into a Hopf bifurcation around the positive equilibrium, which induces oscillations of the populations.

Proof

The necessary and sufficient conditions for the existence of the Hopf bifurcation for $K=K^{\ast }$, if it exists, are (i) $A_i(K^{\ast })>0$, $i=1,2,3$ (ii) $A_1(K^{\ast })A_2(K^{\ast })-A_3(K^{\ast })=0$ and (iii) $A_1^{\prime }(K^{\ast })A_2(K^{\ast })+A_1(K^{\ast })A_2^{\prime }(K^{\ast })-A_3^{\prime }(K^{\ast })\ne 0$. The transversality condition, the third (iii), is obtained observing that the eigenvalues of the characteristic equation, of the form ${\mathit{\chi }}_i=u_i+\mathbf{i}{v}_i$, must satisfy the transversality condition ${\left.\frac{d{u}_i}{dK}\right|}_{K=K^{\ast }}\ne 0$.

We will now verify the Hopf bifurcation condition (iii); putting $\mathit{\chi }=u+\mathbf{i}v$ in the characteristic equation, we get(6) $$\begin{array}{c}\hfill {(u+\mathbf{i}v)}^3+A_1{(u+\mathbf{i}v)}^2+A_2(u+\mathbf{i}v)+A_3=0,\end{array}$$(6)

On separating the real and imaginary parts and eliminating $v$, we get(7) $$\begin{array}{c}\hfill 8u^3+8A_1{u}^2+2u(A_1^2+A_2)+A_1{A}_2-A_3=0.\end{array}$$(7)

It is clear from the above that $u(K^{\ast })=0$ if $A_1(K^{\ast })A_2(K^{\ast })-A_3(K^{\ast })=0$. Further, at $K=K^{\ast }$, $u(K^{\ast })$ is the only root since the discriminate $8u^2+8A_{1}u+2(A_1^2+A_2)=0$ if  $64A_1^2-64(A_1^2+A_2)<0$.

Further, differentiating (Equation 7) with respect to K, we have $24u^2\frac{du}{dK}+16A_{1}u\frac{du}{dK}+2(A_1^2+A_2)\frac{du}{dK}+2u[2A_1\frac{d{A}_1}{dK}+\frac{d{A}_2}{dK}]+\frac{dS}{dK}=0$, where $S=A_1{A}_2-A_3$.

At $K=K^{\ast }$, we have $u(K^{\ast })=0$, so that above equation becomes ${\left[\frac{du}{dK}\right]}_{K=K^{\ast }}=\frac{-\frac{dS}{dK}}{2(A_1^2+A_2)}\ne 0$, providing the third condition (iii).

This ensures that the above system has a Hopf bifurcation around the positive interior equilibrium $E^{\ast }$.

Next, we perform detailed analysis of the bifurcation solutions to study the nature of Hopf bifurcation. We start by rewriting system (Equation 1) in the form $\dot{X}=MX+\mathbf{F}(X)+O{\Vert X\Vert }^4$ where $X=\left(\begin{array}{c}p\\ z\\ f\end{array}\right)$ : $p=P-P^{\ast }$, $z=Z-Z^{\ast }$, $f=F-F^{\ast }$ and $M=V^{\ast }$.

Here, $\mathbf{F}=\left[\begin{array}{c}{F}_1\\ F_2\\ F_3\end{array}\right]$,

where $F_1=-\frac{{\mathit{\alpha }}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^3}{p}^3+\frac{{\mathit{\alpha }}_1{K}_1}{{(K_1+P^{\ast })}^3}{p}^{2}z+\left(\frac{{\mathit{\alpha }}_1{K}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^3}-\frac{r}{K}\right)p^2-\frac{{\mathit{\alpha }}_1{K}_1}{{(K_1+P^{\ast })}^2}pz$, $F_2=\frac{{\mathit{\alpha }}_2{Z}^{\ast }}{{(K_1+P^{\ast })}^3}{p}^3-\frac{{\mathit{\gamma }}_1{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{z}^3-\frac{{\mathit{\alpha }}_2{K}_1}{{(K_1+P^{\ast })}^3}{p}^{2}z+\frac{{\mathit{\gamma }}_1{K}_2}{{(K_2+Z^{\ast })}^3}{z}^{2}f-\frac{{\mathit{\alpha }}_2{K}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^3}{p}^2+\frac{{\mathit{\gamma }}_1{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{z}^2+\frac{{\mathit{\alpha }}_2{K}_1}{{(K_1+P^{\ast })}^2}pz-\frac{{\mathit{\gamma }}_1{K}_2}{{(K_2+Z^{\ast })}^2}zf$, $F_3=\frac{{\mathit{\gamma }}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{z}^3-\frac{{\mathit{\gamma }}_2{K}_2}{{(K_2+Z^{\ast })}^3}{z}^{2}f-\frac{{\mathit{\gamma }}_2{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{z}^2+\frac{{\mathit{\gamma }}_2{K}_2}{{(K_2+Z^{\ast })}^2}zf$.

Now, let the normalized eigenvectors of M and $M^T$ corresponding to the eigenvalues $\mathbf{i}\mathit{\omega }$ and $-\mathbf{i}\mathit{\omega }$ be q and p, respectively, where $\mathbf{q}=\frac{1}{|\mathbf{q}|}\left[\begin{array}{c}-\frac{n_{12}}{n_{11}-\mathbf{i}\mathit{\omega }}\\ 1\\ \frac{n_{32}}{\mathbf{i}\mathit{\omega }}\end{array}\right]$, $\mathbf{p}=\frac{1}{|\mathbf{p}|}\left[\begin{array}{c}\frac{-n_{21}}{n_{11}+\mathbf{i}\mathit{\omega }}\\ 1\\ -\frac{n_{23}}{\mathbf{i}\mathit{\omega }}\end{array}\right]$. Let us define the following multi-linear functions for the three vectors $x=(x_1,x_2,x_3)\in R^3$, $y=(y_1,y_2,y_3)\in R^3$, and $w=(w_1,w_2,w_3)\in R^3$.$$B_i(x,y)=\sum _{j,k=1}^3{[\frac{{\mathit{\delta }}^2{F}_i}{\mathit{\delta }{\mathit{\xi }}_j\mathit{\delta }{\mathit{\xi }}_k}]}_{\mathit{\xi }=0}{x}_j{y}_k$$$$C_i(x,y,w)=\sum _{j,k,l=1}^3{[\frac{{\mathit{\delta }}^3{F}_i}{\mathit{\delta }{\mathit{\xi }}_j\mathit{\delta }{\mathit{\xi }}_k\mathit{\delta }{\mathit{\xi }}_l}]}_{\mathit{\xi }=0}{x}_j{y}_k{w}_l.$$

where $B(x,y)=\left[\begin{array}{c}2\left(\frac{{\mathit{\alpha }}_1{K}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^3}-\frac{r}{K}\right)x_1{y}_1-\frac{{\mathit{\alpha }}_1{K}_1}{{(K_1+P^{\ast })}^2}{x}_1{y}_2\\ -\frac{2{\mathit{\alpha }}_2{K}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^3}{x}_1{y}_1+\frac{2{\mathit{\gamma }}_1{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{x}_2{y}_2+\frac{{\mathit{\alpha }}_2{K}_1}{{(K_1+P^{\ast })}^2}{x}_1{y}_2-\frac{{\mathit{\gamma }}_1{K}_2}{{(K_2+Z^{\ast })}^2}{x}_2{y}_3\\ -\frac{2{\mathit{\gamma }}_2{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{x}_2{y}_2+\frac{{\mathit{\gamma }}_2{K}_2}{{(K_2+Z^{\ast })}^2}{x}_2{y}_3\end{array}\right]$,$$C(x,y,w)=\left[\begin{array}{c}-\frac{6{\mathit{\alpha }}_1{Z}_1^{\ast }}{{(K_1+P^{\ast })}^3}{x}_1{y}_1{w}_1+\frac{2{\mathit{\alpha }}_1{K}_1}{{(K_1+P^{\ast })}^3}{x}_1{y}_1{w}_2\\ \frac{6{\mathit{\alpha }}_2{Z}^{\ast }}{{(K_1+P^{\ast })}^3}{x}_1{y}_1{w}_1-\frac{6{\mathit{\gamma }}_1{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{x}_2{y}_2{w}_2-\frac{2{\mathit{\alpha }}_2{K}_1}{{(K_1+P^{\ast })}^3}{x}_1{y}_1{w}_2+\frac{2{\mathit{\gamma }}_1{K}_2}{{(K_2+Z^{\ast })}^3}{x}_2{y}_2{w}_3\\ \frac{6{\mathit{\gamma }}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}{x}_2{y}_2{w}_2-\frac{2{\mathit{\gamma }}_2{K}_2}{{(K_2+Z^{\ast })}^3}{x}_2{y}_2{w}_3\end{array}\right].$$

With these, $\mathbf{F}(X)$ will be of the form $\mathbf{F}(X)=\frac{1}{2}B(X,X)+\frac{1}{2}C(X,X,X)$.

Solving the corresponding linear system, we get$$M^{-1}B(\mathbf{q},\overline{\mathbf{q}})=\left[\begin{array}{c}{s}_1\\ s_2\\ s_3\end{array}\right],$$

where$$\begin{array}{cc}\hfill s_1& =-\frac{1}{n_{11}{n}_{32}{n}_{23}}\left[-n_{23}{n}_{32}\left[2\left(\frac{{\mathit{\alpha }}_1{K}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^3}-\frac{r}{K}\right)\frac{n_{12}^2}{n_{11}^2+{\mathit{\omega }}^2}+\frac{{\mathit{\alpha }}_1{K}_1}{{(K_1+P^{\ast })}^2}\frac{n_{12}(n_{11}+\mathbf{i}\mathit{\omega })}{n_{11}^2+{\mathit{\omega }}^2}\right]+n_{12}{n}_{23}\left(\frac{{\mathit{\gamma }}_2{K}_2}{{(K_2+Z^{\ast })}^2}\frac{\mathbf{i}{n}_{32}}{\mathit{\omega }}-\frac{2{\mathit{\gamma }}_2{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}\right)\right],\hfill \\ \hfill s_2& =-\frac{1}{n_{11}{n}_{32}{n}_{23}}\left[-n_{11}{n}_{23}\left(\frac{{\mathit{\gamma }}_2{K}_2}{{(K_2+Z^{\ast })}^2}\frac{\mathbf{i}{n}_{32}}{\mathit{\omega }}-\frac{2{\mathit{\gamma }}_2{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}\right)\right],\hfill \\ \hfill s_3& =-\frac{1}{n_{11}{n}_{32}{n}_{23}}[n_{21}{n}_{32}[2\left(\frac{{\mathit{\alpha }}_1{K}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^3}-\frac{r}{K}\right)\frac{n_{12}^2}{n_{11}^2+{\mathit{\omega }}^2}+\frac{{\mathit{\alpha }}_1{K}_1}{{(K_1+P^{\ast })}^2}\frac{n_{12}(n_{11}+\mathbf{i}\mathit{\omega })}{n_{11}^2+{\mathit{\omega }}^2}]-n_{11}{n}_{32}[\frac{-2{\mathit{\gamma }}_1{K}_1{Z}^{\ast }}{{(K_1{P}^{\ast })}^3}\frac{n_{12}^2}{n_{11}^2+{\mathit{\omega }}^2}+\frac{2{\mathit{\gamma }}_1{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}-\frac{{\mathit{\alpha }}_2{K}_1}{{(K_1+P^{\ast })}^2}\frac{n_{12}(n_{11}+\mathbf{i}\mathit{\omega })}{n_{11}^2+{\mathit{\omega }}^2}-\frac{{\mathit{\gamma }}_1{K}_2}{{(K_2+Z^{\ast })}^2}\frac{\mathbf{i}{n}_{32}}{\mathit{\omega }}]+(n_{11}{n}_{22}-n_{12}{n}_{21})\left(\frac{{\mathit{\gamma }}_2{K}_2}{{(K_2+Z^{\ast })}^2}\frac{\mathbf{i}{n}_{32}}{\mathit{\omega }}-\frac{2{\mathit{\gamma }}_2{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^3}\right)].\hfill \end{array}$$

Again,$$\begin{array}{c}\hfill {(2i\mathit{\omega }{I}_3-M)}^{-1}=\frac{1}{|2\mathbf{i}\mathit{\omega }{I}_3-M|}\left(\begin{array}{ccc}-4{\mathit{\omega }}^2-2n_{22}\mathbf{i}\mathit{\omega }-n_{23}{n}_{32}& 2\mathbf{i}\mathit{\omega }{n}_{12}& n_{12}{n}_{23}\\ 2\mathbf{i}\mathit{\omega }{n}_{21}& -4{\mathit{\omega }}^2-2n_{11}\mathbf{i}\mathit{\omega }& 2n_{23}\mathbf{i}\mathit{\omega }-n_{11}{n}_{23}\\ n_{21}{n}_{32}& n_{32}(2\mathbf{i}\mathit{\omega }-n_{11})& \mathbf{E}\end{array}\right),\end{array}$$

where $\mathbf{E}=(2\mathbf{i}\mathit{\omega }-n_{11})(2\mathbf{i}\mathit{\omega }-n_{12})-n_{12}{n}_{21}$.

Therefore,$$\begin{array}{c}\hfill {(2\mathbf{i}\mathit{\omega }{I}_3-M)}^{-1}\left[\begin{array}{c}{b}_{11}{q}_1^2+b_{12}{q}_1{q}_2\\ b_{21}{q}_1^2+b_{22}{q}_2^2+b_{23}{q}_1{q}_2+b_{24}{q}_2{q}_3\\ b_{31}{q}_2{q}_3+b_{32}{q}_2^2\end{array}\right]\\ \hfill =\frac{1}{|2\mathbf{i}\mathit{\omega }{I}_3-M|}\left[\begin{array}{c}(-4{\mathit{\omega }}^2-2n_{22}\mathbf{i}\mathit{\omega }-n_{23}{n}_{32}){\mathit{\tau }}_1+2\mathbf{i}\mathit{\omega }{n}_{12}{\mathit{\tau }}_2+n_{12}{n}_{23}{\mathit{\tau }}_3\\ 2\mathbf{i}\mathit{\omega }{n}_{21}{\mathit{\tau }}_1-(4{\mathit{\omega }}^2+2n_{11}\mathbf{i}\mathit{\omega }){\mathit{\tau }}_2+(2n_{23}\mathbf{i}\mathit{\omega }-n_{11}{n}_{23}){\mathit{\tau }}_3\\ n_{21}{n}_{32}{\mathit{\tau }}_1+n_{32}(2\mathbf{i}\mathit{\omega }-n_{11}){\mathit{\tau }}_2+\mathbf{E}{\mathit{\tau }}_3\end{array}\right],\end{array}$$

where ${\mathit{\tau }}_1=b_{11}{q}_1^2+b_{12}{q}_1{q}_2$; ${\mathit{\tau }}_2=b_{21}{q}_1^2+b_{22}{q}_2^2+b_{23}{q}_1{q}_2+b_{24}{q}_2{q}_3$; ${\mathit{\tau }}_3=b_{31}{q}_2{q}_3+b_{32}{q}_2^2$.

Using the invariant expression for the first lyapunov coefficient $l_1(0)$, we get the first lyapunov coefficients as Mukhopadhyay and Bhattacharyya (2011). $l_1(0)=\frac{1}{2\mathit{\omega }}Re[<\mathbf{p},\mathbf{c}(\mathbf{q},\mathbf{q},\overline{\mathbf{q}})-2<\mathbf{p},B(\mathbf{q},M^{-1},B(\mathbf{q},\overline{\mathbf{q}})))>+<\mathbf{p},B(\overline{\mathbf{q}},{(2\mathbf{i}\mathit{\omega }I-M)}^{-1}B(\mathbf{q},\mathbf{q}))>]$.

Now, if $l_1(0)<0$, the Hopf bifurcation will be of supercritical nature and there will be emergence of stable limit cycles.

4. The mathematical model with time delay

We have already discussed the usefulness of time delay in realistic modeling of ecosystems. Here, we consider the following modification of the model (Equation 1) incorporating discrete time delay in it. In this paper, we have introduced a discrete time delay term to the above model; this term may be considered as delay due to gestation. Here, $\mathit{\tau }$ is the discrete time delay.(8) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{dP}{dt}& =rP(1-\frac{P}{K})-\frac{{\mathit{\alpha }}_{1}PZ}{K_1+P}-{\mathit{\mu }}_{1}P\hfill \\ \hfill \frac{dZ}{dt}& =\frac{{\mathit{\alpha }}_{2}PZ}{K_1+P}-\frac{{\mathit{\gamma }}_{1}ZF}{K_2+Z}-{\mathit{\mu }}_{2}Z\hfill \\ \hfill \frac{dF}{dt}& =\frac{{\mathit{\gamma }}_{2}Z(t-\mathit{\tau })F(t-\mathit{\tau })}{K_2+Z(t-\mathit{\tau })}-{\mathit{\mu }}_{3}F\hfill \end{array}\right\}.\end{array}$$(8)

The system (Equation 8) has to be analyzed with the following initial conditions,(9) $$\begin{array}{c}\hfill P(0)>0,Z(0)>0,F(0)>0,t\in [-\mathit{\tau },0].\end{array}$$(9)

4.1. Qualitative analysis of the model with time delay

 $$\overline{V}=\left[\begin{array}{ccc}r-\frac{2r\overline{P}}{K}-\frac{{\mathit{\alpha }}_1{K}_1\overline{Z}}{{(K_1+\overline{P})}^2}-{\mathit{\mu }}_1& -\frac{{\mathit{\alpha }}_1\overline{P}}{K_1+\overline{P}}& 0\\ \frac{{\mathit{\alpha }}_2{K}_1\overline{Z}}{{(K_1+\overline{P})}^2}& \frac{{\mathit{\alpha }}_2\overline{P}}{K_1+\overline{P}}-\frac{{\mathit{\gamma }}_1{K}_2\overline{F}}{{(K_2+\overline{Z})}^2}-{\mathit{\mu }}_2& -\frac{{\mathit{\gamma }}_1\overline{Z}}{K_2+\overline{Z}}\\ 0& \frac{{\mathit{\gamma }}_2{K}_2\overline{F}}{{(K_2+\overline{Z})}^2}{e}^{-\mathit{\lambda }\mathit{\tau }}& \frac{{\mathit{\gamma }}_2\overline{Z}}{K_2+Z}{e}^{-\mathit{\lambda }\mathit{\tau }}-{\mathit{\mu }}_3\end{array}\right].$$

Remark 1

The characteristic equation for the variational matrix $V_0$ about the plankton free steady states $E_0$ and $E_{01}$ remains the same as obtained for the non-delayed system (Equation 8). Thus, in our model system, the delay has no effect on the stability nature of the system about $E_0$ and $E_{01}$.

To find conditions for the other local asymptotic stability of system (Equation 8), we use the following theorem from Gopalsamy (1992).

Theorem 3

If $D_E(\mathit{\lambda },\mathit{\tau })=0$ denotes the characteristic equation, then a set of necessary and sufficient conditions for the equilibrium to be asymptotically stable for all $\mathit{\tau }\ge 0$ are

(i)	The real parts of all the roots of $D_E(\mathit{\lambda },0)=0$ are negative.
(ii)	For all real $\mathit{\omega }$ and any $\mathit{\tau }\ge 0$, $D_E(\mathbf{i}\mathit{\omega },\mathit{\tau })\ne 0$, where $\mathbf{i}=\sqrt{-1}$.

The characteristic equation for the variational matrix $V_1$ about $E_1$ takes the following form(10) $$\begin{array}{c}\hfill D_{E_1}(\mathit{\lambda },\mathit{\tau })={\mathit{\lambda }}^3+l{\mathit{\lambda }}^2+m\mathit{\lambda }+n-e^{-\mathit{\lambda }\mathit{\tau }}(f{\mathit{\lambda }}^2+g\mathit{\lambda }+h)=0,\end{array}$$(10)

where $l=\frac{r{P}_1}{K}-\frac{{\mathit{\alpha }}_1{P}_1{Z}_1}{{(K_1+P_1)}^2}+{\mathit{\mu }}_3$, $m=\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2{K}_1{P}_1{Z}_1}{{(K_1+P_1)}^3}+{\mathit{\mu }}_3(\frac{r{P}_1}{K}-\frac{{\mathit{\alpha }}_1{P}_1{Z}_1}{{(K_1+P_1)}^2})$, $n=\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2{\mathit{\mu }}_3{K}_1{P}_1{Z}_1}{{(K_1+P_1)}^3}$, $f=\frac{{\mathit{\gamma }}_2{Z}_1}{K_2+Z_1}$, $g=\frac{{\mathit{\gamma }}_2{Z}_1}{K_2+Z_1}(\frac{r{P}_1}{K}-\frac{{\mathit{\alpha }}_1{P}_1{Z}_1}{{(K_1+P_1)}^2})$, $h=\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2{\mathit{\gamma }}_2{K}_1{P}_1{Z}_1^2}{{(K_1+P_1)}^3(K_2+Z_1)}$.

Here, $D_{E_1}(\mathit{\lambda },0)=0$ has roots with negative real parts, provided system (Equation 8) is locally asymptotically stable about equilibrium $E_1$ (for the condition, see Section 3.3.3).

For $\mathit{\omega }=0$, $D_{E_1}(0,\mathit{\tau })=n-h\ne 0$.

Now, for $\mathit{\omega }\ne 0$,

$D_{E_1}(\mathbf{i}\mathit{\omega },\mathit{\tau })=-\mathbf{i}{\mathit{\omega }}^3-l{\mathit{\omega }}^2+m\mathbf{i}\mathit{\omega }+n-e^{-\mathbf{i}\mathit{\omega }\mathit{\tau }}(-f{\mathit{\omega }}^2+g\mathbf{i}\mathit{\omega }+h)$.

Let $D_{E_1}(\mathbf{i}\mathit{\omega },\mathit{\tau })$=0 and separating the real and imaginary parts, we get $-l{\mathit{\omega }}^2+n=-f{\mathit{\omega }}^{2}cos\mathit{\omega }\mathit{\tau }+hcos\mathit{\omega }\mathit{\tau }+g\mathit{\omega }cos\mathit{\omega }\mathit{\tau }$,

$-{\mathit{\omega }}^3+m\mathit{\omega }=f{\mathit{\omega }}^{2}sin\mathit{\omega }\mathit{\tau }-hsin\mathit{\omega }\mathit{\tau }+g\mathit{\omega }cos\mathit{\omega }\mathit{\tau }$.

Squaring and adding the above two equations, we get

${\mathit{\omega }}^6++A_{11}{\mathit{\omega }}^4+A_{22}{\mathit{\omega }}^2+A_{33}=0$, where $A_{11}=l^2-f^2-2m$, $A_{22}=m^2-2ln+2fh-g^2$, $A_{33}=n^2-h^2$.

Sufficient conditions for the non-existence of a real number $\mathit{\omega }$ satisfying $D_{E_1}(\mathbf{i}\mathit{\omega },\mathit{\tau })=0$ can be written as ${\mathit{\omega }}^6+A_{11}{\mathit{\omega }}^4+A_{22}{\mathit{\omega }}^2+A_{33}>0$,

which can be transformed to ${\mathit{\omega }}^6+A_{11}{\left[{\mathit{\omega }}^2+\frac{A_{22}}{2A_{11}}\right]}^2+A_{33}-\frac{A_{22}^2}{4A_{11}}>0$.

Therefore, a sufficient condition for $E_1$ to be stable is (i) $A_{11}>0$ and (ii) $A_{33}>\frac{A_{22}^2}{4A_{11}}$.

4.2. Estimation of the length of delay to preserve stability at $E_1$

In this section, we assume that in the absence of delays, $E_1$ is locally asymptotically stable. Let $u_1(t),v_1(t),\text{and}{w}_1(t)$ be the respective linearized variables of this model. The system (Equation 8) becomes(11) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{d{u}_1}{dt}& =\widehat{A_1}{u}_1(t)+\widehat{A_2}{v}_1(t)\hfill \\ \hfill \frac{d{v}_1}{dt}& =\widehat{B_1}{u}_1(t)+\widehat{B_2}{w}_1(t)\hfill \\ \hfill \frac{d{w}_1}{dt}& =\widehat{C_1}{w}_1(t)+\widehat{C_2}{w}_1(t-\mathit{\tau })\hfill \end{array}\right\},\end{array}$$(11)

where $\widehat{A_1}=\frac{{\mathit{\alpha }}_1{P}_1{Z}_1}{{(K_1+P_1)}^2}-\frac{r{P}_1}{K}$, $\widehat{A_2}=-\frac{{\mathit{\alpha }}_1{P}_1}{K_1+P_1}$, $\widehat{B_1}=\frac{{\mathit{\alpha }}_2{K}_1{Z}_1}{{(K_1+P_1)}^2}$, $\widehat{B_2}=-\frac{{\mathit{\gamma }}_1{Z}_1}{K_2+Z_1}$, $\widehat{C_1}=-{\mathit{\mu }}_3$, $\widehat{C_2}=\frac{{\mathit{\gamma }}_2{Z}_1}{K_2+Z_1}$.

Let ${\widehat{u}}_1(L)$, ${\widehat{v}}_1(L)$, and ${\widehat{w}}_1(L)$ be the Laplace transform of $u_1(t)$, $v_1(t)$, and $w_1(t)$, respectively. Taking the Laplace transformation of system (Equation 11), we have$$\begin{array}{c}\hfill (L-\widehat{A_1}){\widehat{u}}_1(L)=\widehat{A_2}{\widehat{v}}_1(L)+u_1(0)\\ \hfill L{\widehat{v}}_1(L)=\widehat{B_1}{\widehat{u}}_1(L)+\widehat{B_2}{\widehat{w}}_1(L)+v_1(0)\\ \hfill (L-\widehat{C_1}){\widehat{w}}_1(L)=\widehat{C_2}{M}_1(L)e^{-L\mathit{\tau }}+\widehat{C_2}{e}^{-L\mathit{\tau }}{\widehat{w}}_1(L),\end{array}$$

where $M_1(L)={\int }_{-\mathit{\tau }}^0{e}^{-Lt}{w}_1(t)dt$.

The inverse Laplace transform of ${\widehat{u}}_1(L)$, ${\widehat{v}}_1(L)$, and ${\widehat{w}}_1(L)$ will have terms which exponentially increase with time, if ${\widehat{u}}_1(L)$, ${\widehat{v}}_1(L)$, and ${\widehat{w}}_1(L)$ have pole with positive real parts. Since $E_1$ needs to be locally asymptotically stable, it is necessary and sufficient that all poles of ${\widehat{u}}_1(L)$, ${\widehat{v}}_1(L)$, and ${\widehat{w}}_1(L)$ have negative real parts. We shall employ the Nyquist criterion which states that if $L$ is the arc length of a curve encircling the right half-plane, the curve of ${\widehat{u}}_1(L)$, ${\widehat{v}}_1(L)$, and ${\widehat{w}}_1(L)$ will encircle the origin a number of times equal to the difference between the number of poles and the number of zeroes of ${\widehat{u}}_1(L)$, ${\widehat{v}}_1(L)$, and ${\widehat{w}}_1(L)$ in the right half-plane.

Let $G(L)=L^3+l{L}^2+mL+n-e^{-L\mathit{\tau }}(f{L}^2+gL+h)$ from (Equation 10). Then, $E_1$ is locally asymptotically stable if(12) $$\begin{array}{c}\hfill ReG(\mathbf{i}{v}_2)=0,\end{array}$$(12) (13) $$\begin{array}{c}\hfill ImG(\mathbf{i}{v}_2)>0,\end{array}$$(13)

where $v_2$ is the smallest positive root of Equation 12 (Freedman, Erbe, & Rao, 1986).

Now, (Equation 12) and (Equation 13) become$$-l{v}_2^2+n=-f{v}_2^{2}cos{v}_2\mathit{\tau }+hcos{v}_2\mathit{\tau }+g{v}_{2}sin{v}_2\mathit{\tau },-v_2^3+m{v}_2>f{v}_2^{2}sin{v}_2\mathit{\tau }-hsin{v}_2\mathit{\tau }+g{v}_{2}cos{v}_2\mathit{\tau }$$.

To get an estimation on the length of delay, we utilize the following conditions,(14) $$\begin{array}{c}\hfill -l{v}^2+n=-f{v}^{2}cosv\mathit{\tau }+hcosv\mathit{\tau }+gvsinv\mathit{\tau },\end{array}$$(14) (15) $$\begin{array}{c}\hfill -v^3+mv>f{v}^{2}sinv\mathit{\tau }-hsinv\mathit{\tau }+gvcosv\mathit{\tau }.\end{array}$$(15)

Therefore, $E_1$ will be stable if the above inequality holds at $v=v_2$, where $v_2$ is the first positive root of Equation 14. We shall now estimate an upper bound $v_{++}$ of $v_2$, which would be independent of $\mathit{\tau }$. Then, we estimate $\mathit{\tau }$ so that (Equation 15) holds for all $0\le v\le v_{++}$, and hence in particular at $v=v_2$.

Maximizing $-f{v}^{2}cosv\mathit{\tau }+hcosv\mathit{\tau }+gvsinv\mathit{\tau }$, subject to $|sinv\mathit{\tau }|\le 1$, $|cosv\mathit{\tau }|\le 1$, we obtain(16) $$\begin{array}{c}\hfill -l{v}^2+n\le f{v}^2+h+gv.\end{array}$$(16)

Thus, the unique positive solution of  $(f+l)v^2+gv-(n-h)=0$ is denoted by $v_{++}$. Hence, if $v_{++}=\frac{-g+\sqrt{g^2+4(f+l)(n-h)}}{2(f+l)}$, then from (Equation 16) we have $v_2\le v_{++}$ which ensures that $v_{++}$ is independent of $\mathit{\tau }$. Then, we estimate $\mathit{\tau }$ so that (Equation 15) holds for all values $0\le v\le v_{++}$; now, rearranging (Equation 15) by $|sinv\mathit{\tau }|\le \mathit{\tau }v$ and $|1-cosv\mathit{\tau }|\le \frac{1}{2}{\mathit{\tau }}^2{v}^2$, we have(17) $$\begin{array}{c}\hfill \frac{g}{2}{\mathit{\tau }}^2{v}^2+(h-f{v}^2)\mathit{\tau }+(m-g-v^2)>0.\end{array}$$(17)

Thus, (Equation 15) will be satisfied if $A_{{\mathit{\theta }}_1}{\mathit{\tau }}^2+B_{{\mathit{\theta }}_1}\mathit{\tau }+C_{{\mathit{\theta }}_1}>0$, where $A_{{\mathit{\theta }}_1}=\frac{g}{2}{v}_{++}^2$, $B_{{\mathit{\theta }}_1}=h-f{v}_{++}^2$, $C_{{\mathit{\theta }}_1}=m-g-v_{++}^2$.

Then, the Nyquist criterion holds for $0\le \mathit{\tau }\le {\mathit{\tau }}_1$, where ${\mathit{\tau }}_1=\frac{1}{2A_{{\mathit{\theta }}_1}}(-B_{{\mathit{\theta }}_1}+\sqrt{B_{{\mathit{\theta }}_1}^2+4A_{{\mathit{\theta }}_1}{C}_{{\mathit{\theta }}_1}})$ and ${\mathit{\tau }}_1$ gives an estimate for the length of delay for which stability is preserved.

Theorem 4

If there exist $\mathit{\tau }$ in $0\le \mathit{\tau }\le {\mathit{\tau }}_1$ such that $A_{\mathit{\theta }}{\mathit{\tau }}^2+B_{\mathit{\theta }}\mathit{\tau }+C_{\mathit{\theta }}>0$, then ${\mathit{\tau }}_1$ is the maximum value (length of delay) of $\mathit{\tau }$ for which $E_1$ is asymptotically stable.

4.3. Qualitative analysis of the model at $E^{\ast }$ with gestation time delay ($\mathit{\tau }\ne 0$)

The characteristic equation for the variational matrix $V^{\ast }$ about $E^{\ast }$ takes the following form:(18) $$\begin{array}{c}\hfill D_E{}^{\ast }({\mathit{\lambda }}_1,\mathit{\tau })={\mathit{\lambda }}_1^3+\overline{l}{\mathit{\lambda }}_1^2+\overline{m}{\mathit{\lambda }}_1+\overline{n}-e^{-{\mathit{\lambda }}_1\mathit{\tau }}(\overline{f}{\mathit{\lambda }}_1^2+\overline{g}{\mathit{\lambda }}_1+\overline{h})=0,\\ \hfill \text{where}\overline{l}=\frac{r{P}^{\ast }}{K}-\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^2}-\frac{{\mathit{\gamma }}_1{Z}^{\ast }{F}^{\ast }}{{(K_2+Z^{\ast })}^2}+{\mathit{\mu }}_3,\\ \hfill \overline{m}=\left(\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_2+Z^{\ast })}^2}-\frac{r{P}^{\ast }}{K}\right)\left(\frac{{\mathit{\gamma }}_1{Z}^{\ast }{F}^{\ast }}{{(K_2+Z^{\ast })}^2}-{\mathit{\mu }}_3\right)+\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2{K}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^3}-\frac{{\mathit{\gamma }}_1{\mathit{\mu }}_3{Z}^{\ast }{F}^{\ast }}{{(K_2+Z^{\ast })}^3},\\ \hfill \overline{n}=\left(\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^2}-\frac{r{P}^{\ast }}{K}\right)\frac{{\mathit{\gamma }}_1{\mathit{\mu }}_3{Z}^{\ast }{F}^{\ast }}{{(K_2+Z^{\ast })}^3}+\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2{K}_1{\mathit{\mu }}_3{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^3},\\ \hfill \overline{f}=\frac{{\mathit{\gamma }}_2{Z}^{\ast }}{K_2+Z^{\ast }},\overline{g}=(\frac{r{P}^{\ast }}{K}-\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^2})\frac{{\mathit{\gamma }}_2{Z}^{\ast }}{K_2+Z^{\ast }}-\frac{{\mathit{\gamma }}_1{\mathit{\gamma }}_2{Z}^{\ast 2}{F}^{\ast }}{{(K_2+Z^{\ast })}^3}-\frac{{\mathit{\gamma }}_1{\mathit{\gamma }}_2{K}_2{Z}^{\ast }{F}^{\ast }}{{(K_2+Z\ast )}^3},\\ \hfill \overline{h}=\left(\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^2}-\frac{r{P}^{\ast }}{K}\right)\left(\frac{{\mathit{\gamma }}_1{\mathit{\gamma }}_2{Z}^{\ast 2}{F}^{\ast }}{{(K_2+Z^{\ast })}^3}+\frac{{\mathit{\gamma }}_1{\mathit{\gamma }}_2{K}_2{Z}^{\ast }{F}^{\ast }}{{(K_2+Z^{\ast })}^3}\right)-\frac{{\mathit{\alpha }}_1{\mathit{\alpha }}_2{\mathit{\gamma }}_2{K}_1{P}^{\ast }{Z}^{\ast 2}}{{(K_1+P^{\ast })}^3(K_2+Z^{\ast })}.\end{array}$$(18)

Now, $D_E{}^{\ast }(\mathbf{i}\overline{\mathit{\omega }},\mathit{\tau })=-\mathbf{i}{\overline{\mathit{\omega }}}^3-\overline{l}{\overline{\mathit{\omega }}}^2+\overline{m}\mathbf{i}\overline{\mathit{\omega }}+\overline{n}-e^{-\overline{\mathit{\omega }}\mathit{\lambda }\mathit{\tau }}(-\overline{f}{\overline{\mathit{\omega }}}^2+\overline{g}\mathbf{i}\overline{\mathit{\omega }}+\overline{h})(\text{Using Theorem}3)$.

Let $D_E{}^{\ast }(\mathbf{i}\overline{\mathit{\omega }},\mathit{\tau })=0$ and separating the real and imaginary parts, we get$$-\overline{l}{\overline{\mathit{\omega }}}^2+\overline{n}=-\overline{f}{\overline{\mathit{\omega }}}^{2}cos\overline{\mathit{\omega }}\mathit{\tau }+\overline{h}cos\overline{\mathit{\omega }}\mathit{\tau }+\overline{g}\overline{\mathit{\omega }}sin\overline{\mathit{\omega }}\mathit{\tau },$$$$-{\overline{\mathit{\omega }}}^3+\overline{m}\overline{\mathit{\omega }}=\overline{f}{\overline{\mathit{\omega }}}^{2}sin\overline{\mathit{\omega }}\mathit{\tau }-\overline{h}sin\overline{\mathit{\omega }}\mathit{\tau }+\overline{g}\overline{\mathit{\omega }}cos\overline{\mathit{\omega }}\mathit{\tau }.$$

Squaring and adding the above two equations, we get$${\overline{\mathit{\omega }}}^6+\overline{Q_1}{\overline{\mathit{\omega }}}^4+\overline{Q_2}{\overline{\mathit{\omega }}}^2+\overline{Q_3}=0,$$

where$$\begin{array}{cc}\hfill \overline{Q_1}& ={\overline{l}}^2-{\overline{f}}^2-2\overline{m},\hfill \\ \hfill \overline{Q_2}& ={\overline{m}}^2-2\overline{l}\overline{n}+2\overline{f}\overline{h}-{\overline{g}}^2,\hfill \\ \hfill \overline{Q_3}& ={\overline{n}}^2-{\overline{h}}^2.\hfill \end{array}$$

The sufficient conditions for the non-existence of a real number $\mathit{\omega }$ satisfying $D_E\ast =0$ can be written as ${\overline{\mathit{\omega }}}^6+\overline{Q_1}{\overline{\mathit{\omega }}}^4+\overline{Q_2}{\overline{\mathit{\omega }}}^2+\overline{Q_3}>0$, which can be transformed to$${\overline{\mathit{\omega }}}^6+\overline{Q_1}{\left[{\overline{\mathit{\omega }}}^2+\frac{\overline{Q_2}}{2\overline{Q_1}}\right]}^2+\overline{Q_3}-\frac{{\overline{Q_2}}^2}{4\overline{Q_1}}>0.$$

Therefore, a sufficient condition for $E^{\ast }$ to be stable is (a) $\overline{Q_1}>0$  and (b) $\overline{Q_3}>\frac{{\overline{Q_2}}^2}{4\overline{Q_1}}$.

4.4. Estimation of the length of delay to preserve stability at $E^{\ast }$

In this section, we assume that in the absence of delays, $E^{\ast }$ is locally asymptotically stable. Let $u(t),v(t),\text{and}w(t)$ be the respective linearized variables of this model. The system (Equation 8) becomes(19) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \frac{du}{dt}& =\overline{A_1}u(t)+\overline{A_2}v(t),\hfill \\ \hfill \frac{dv}{dt}& =\overline{B_1}u(t)+\overline{B_2}v(t)+\overline{B_3}w(t),\hfill \\ \hfill \frac{dw}{dt}& =\overline{C_1}v(t-\mathit{\tau })+\overline{C_2}w(t)+\overline{C_3}w(t-\mathit{\tau })\hfill \end{array}\right\},\end{array}$$(19)

where $\overline{A_1}=\frac{{\mathit{\alpha }}_1{P}^{\ast }{Z}^{\ast }}{{(K_1+P^{\ast })}^2}-\frac{r{P}^{\ast }}{K}$, $\overline{A_2}=-\frac{{\mathit{\alpha }}_1{P}^{\ast }}{K_1+P^{\ast }}$, $\overline{B_1}=\frac{{\mathit{\alpha }}_2{K}_1{Z}^{\ast }}{{(K_1+P^{\ast })}^2}$, $\overline{B_2}=\frac{{\mathit{\gamma }}_1{Z}^{\ast }{F}^{\ast }}{K_2+Z^{\ast }}$, $\overline{B_3}=-\frac{{\mathit{\gamma }}_1{Z}^{\ast }}{K_2+Z^{\ast }}$, $\overline{C_1}=\frac{{\mathit{\gamma }}_2{K}_2{F}^{\ast }}{{(K_2+Z^{\ast })}^2}$, $\overline{C_2}=-{\mathit{\mu }}_3$, $\overline{C_3}=\frac{{\mathit{\gamma }}_2{Z}^{\ast }}{K_2+Z^{\ast }}$.

Let $\overline{u}(L)$, $\overline{v}(L)$, and $\overline{w}(L)$ be the Laplace transform of $u(t)$, $v(t)$, and $w(t)$, respectively. Taking the Laplace transformation of system (Equation 19), we have$$\begin{array}{cc}& (L-\overline{A_1})\overline{u}(L)=\overline{A_2}\overline{v}(L)+u(0),\hfill \\ \hfill & (L-\overline{B_2})\overline{v}(L)=\overline{B_1}\overline{u}(L)+\overline{B_3}\overline{w}(L)+v(0),\hfill \\ \hfill & (L-\overline{C_2})\overline{w}(L)=\overline{C_1}{e}^{-L\mathit{\tau }}{K}_1+\overline{C_1}{e}^{-L\mathit{\tau }}\overline{v}(L)+\overline{C_3}{e}^{-L\mathit{\tau }}{K}_2+\overline{C_3}{e}^{-L\mathit{\tau }}\overline{w}(L)+w(0),\hfill \\ \hfill \end{array}$$

where $K_1(L)={\int }_{-\mathit{\tau }}^0{e}^{-Lt}v(t)dt$, $K_2(L)={\int }_{-\mathit{\tau }}^0{e}^{-Lt}w(t)dt$ .

Let $\overline{F}(L)=L^3+\overline{l}{L}^2+\overline{m}L+\overline{n}-e^{-L\mathit{\tau }}(\overline{f}{L}^2+\overline{g}L+\overline{h})$.

Then, $E^{\ast }$ is locally asymptotically stable if $Re\overline{F}(i{\overline{v}}_0)=0$ and $Im\overline{F}(i{\overline{v}}_0)>0$ i.e.$$\begin{array}{cc}\hfill -\overline{l}{\overline{v}}_0^2+\overline{n}& =-\overline{f}{\overline{v}}_0^{2}cos{\overline{v}}_0\mathit{\tau }+\overline{h}cos{\overline{v}}_0\mathit{\tau }+\overline{g}{\overline{v}}_{0}sin{\overline{v}}_0\mathit{\tau },\hfill \\ \hfill & -{\overline{v}}_0^3+\overline{m}{\overline{v}}_0>\overline{f}{\overline{v}}_0^{2}sin{\overline{v}}_0\mathit{\tau }-\overline{h}sin{\overline{v}}_0\mathit{\tau }+\overline{g}{\overline{v}}_{0}cos{\overline{v}}_0\mathit{\tau },\hfill \end{array}$$

where ${\overline{v}}_0$ be the smallest positive root of $Re(i{\overline{v}}_0)=0$.

To get an estimation on the length of delay, we use the following conditions,(20) $$\begin{array}{c}\hfill -\overline{l}{v}^2+\overline{n}=-\overline{f}{v}^{2}cosv\mathit{\tau }+\overline{h}cosv\mathit{\tau }+\overline{g}vsinv\mathit{\tau },\end{array}$$(20) (21) $$\begin{array}{c}\hfill -v^3+\overline{m}v>\overline{f}{v}^{2}sinv\mathit{\tau }-\overline{h}sinv\mathit{\tau }+\overline{g}vcosv\mathit{\tau }.\end{array}$$(21)

Therefore, $E^{\ast }$ will be stable if above inequality holds at $v={\overline{v}}_0$, where ${\overline{v}}_0$ is the first positive root of Equation 20. We shall now estimate an upper bound $v_{+}$ of $v_0$, which would be independent of $\mathit{\tau }$. Then, we estimate $\mathit{\tau }$ so that (Equation 21) holds for all $0\le v\le v_{+}$, and hence in particular at $\overline{v}=v_0$.

Maximizing $-\overline{f}{v}^{2}cosv\mathit{\tau }+\overline{h}cosv\mathit{\tau }+\overline{g}vsinv\mathit{\tau }$, subject to $|sinv\mathit{\tau }|\le 1$, $|cosv\mathit{\tau }|\le 1$, we obtain(22) $$\begin{array}{c}\hfill -\overline{l}{v}^2+\overline{n}\le \overline{f}{v}^2+\overline{h}+\overline{g}v.\end{array}$$(22)

Thus, the unique positive solution of  $(\overline{f}+\overline{l})v^2+\overline{g}v-(\overline{n}-\overline{h})=0$ is denoted by $v_{+}$. Hence, if $v_{+}=\frac{-\overline{g}+\sqrt{{\overline{g}}^2+4(\overline{f}+\overline{l})(\overline{n}-\overline{h})}}{2(\overline{f}+\overline{l})}$, then from above equation we have $v_0\le v_{+}$ which indicates that $v_{+}$ is independent of $\mathit{\tau }$. Then, we estimate $\mathit{\tau }$ so that (Equation 21) holds for all values $0\le v\le v_{+}$; now, rearranging (Equation 21) by $|sinv\mathit{\tau }|\le \mathit{\tau }v$ and $|1-cosv\mathit{\tau }|\le \frac{1}{2}{\mathit{\tau }}^2{v}^2$, we have(23) $$\begin{array}{c}\hfill \frac{\overline{g}}{2}{\mathit{\tau }}^2{v}^2+(\overline{h}-\overline{f}{v}^2)\mathit{\tau }+(\overline{m}-\overline{g}-{\overline{v}}^2)>0.\end{array}$$(23)

Thus, Equation 21 will be satisfied if$$A_{\mathit{\theta }}{\mathit{\tau }}^2+B_{\mathit{\theta }}\mathit{\tau }+C_{\mathit{\theta }}>0,\text{where}{A}_{\mathit{\theta }}=\frac{\overline{g}}{2}{v}_{+}^2,B_{\mathit{\theta }}=\overline{h}-\overline{f}{v}_{+}^2,C_{\mathit{\theta }}=\overline{m}-\overline{g}-v_{+}^2.$$

Then, the Nyquist criterion holds for $0\le \mathit{\tau }\le {\mathit{\tau }}_{+}$, where ${\mathit{\tau }}_{+}=\frac{1}{2A_{\mathit{\theta }}}(-B_{\mathit{\theta }}+\sqrt{B_{\mathit{\theta }}^2+4A_{\mathit{\theta }}{C}_{\mathit{\theta }}})$ and ${\mathit{\tau }}_{+}$ gives an estimate for the length of delay for which stability is preserved. Thus, we are now in a position to state the following theorem.

Theorem 5

If there exist $\mathit{\tau }$ in $0\le \mathit{\tau }\le {\mathit{\tau }}_{+}$ such that $A_{\mathit{\theta }}{\mathit{\tau }}^2+B_{\mathit{\theta }}\mathit{\tau }+C_{\mathit{\theta }}>0$, then ${\mathit{\tau }}_{+}$ is the maximum value (length of delay) of $\mathit{\tau }$ for which $E^{\ast }$ is asymptotically stable.

5. Bifurcation analysis in the presence of discrete delay

Let us consider $\mathit{\tau }\ne 0$  and assume ${\mathit{\lambda }}_1=\mathit{\mu }+\mathbf{i}\mathit{\nu }$ in Equation 18. Then, separating the real and imaginary parts, we get a system of transcendental equations as(24) $$\begin{array}{cc}& {\mathit{\mu }}^3-3\mathit{\mu }{\mathit{\nu }}^2-\overline{l}({\mathit{\mu }}^2-{\mathit{\nu }}^2)+\overline{m}\mathit{\mu }+\overline{n}\hfill \\ \hfill & =\overline{f}({\mathit{\mu }}^2-{\mathit{\nu }}^2)cos\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}+2\overline{f\mathit{\nu }\mathit{\mu }}sin\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}+\overline{g}\mathit{\mu }cos\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}+\overline{h}cos\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}+\overline{g}\mathit{\nu }sin\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }},\hfill \end{array}$$(24) (25) $$\begin{array}{cc}& -{\mathit{\nu }}^3+3{\mathit{\mu }}^2\mathit{\nu }+2\overline{l}\mathit{\mu }\mathit{\nu }+\overline{m}\mathit{\nu }\hfill \\ \hfill & =-\overline{f}({\mathit{\mu }}^2-{\mathit{\nu }}^2)sin\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}+2\overline{f}\mathit{\nu }\mathit{\mu }cos\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}-\overline{g}\mathit{\mu }sin\mathit{\nu }\mathit{\tau }-\overline{h}sin\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}+\overline{g}\mathit{\nu }cos\mathit{\nu }\mathit{\tau }{e}^{-\mathit{\mu }\mathit{\tau }}.\hfill \end{array}$$(25)

Let us consider ${\mathit{\lambda }}_1$, and hence $\mathit{\mu }$ and $\mathit{\nu }$ are functions of $\mathit{\tau }$. We want to know the change of stability of $E^{\ast }$ which will occur at the values of $\mathit{\tau }=\widehat{\mathit{\tau }}$ for $\mathit{\mu }$ = 0 and $\mathit{\nu }\ne 0$.

Then, the above two equations become(26) $$\begin{array}{c}\hfill \left.\begin{array}{cc}-\overline{l}{\mathit{\nu }}^2+\overline{n}& =-\overline{f}{\mathit{\nu }}^{2}cos\mathit{\nu }\widehat{\mathit{\tau }}+\overline{h}cos\mathit{\nu }\widehat{\mathit{\tau }}+\overline{g}\mathit{\nu }sin\mathit{\nu }\widehat{\mathit{\tau }}\\ -{\mathit{\nu }}^3+\overline{m}\mathit{\nu }& =\overline{f}{\mathit{\nu }}^{2}sin\mathit{\nu }\widehat{\mathit{\tau }}-\overline{h}sin\mathit{\nu }\widehat{\mathit{\tau }}+\overline{g}\mathit{\nu }cos\mathit{\nu }\widehat{\mathit{\tau }},\end{array}\right\}\end{array}$$(26)

Now, eliminating $\widehat{\mathit{\tau }}$, we have(27) $$\begin{array}{c}\hfill {\mathit{\nu }}^6+({\overline{l}}^2-{\overline{f}}^2-2\overline{m}){\mathit{\nu }}^4+({\overline{m}}^2-2\overline{l}\overline{n}+2\overline{f}\overline{h}-{\overline{g}}^2){\mathit{\nu }}^2+{\overline{n}}^2-{\overline{h}}^2=0.\end{array}$$(27)

From (Equation 26), we get ${\widehat{\mathit{\tau }}}_n=\frac{1}{\widehat{\mathit{\nu }}}ta{n}^{-1}\{\frac{\widehat{\mathit{\nu }}(\overline{f}\widehat{{\mathit{\nu }}^4}-\overline{f}\overline{m}\widehat{{\mathit{\nu }}^2}-\overline{h}\widehat{{\mathit{\nu }}^2}-\overline{l}\overline{g}\widehat{{\mathit{\nu }}^2}-\overline{h}\overline{m}-\overline{n}\overline{g})}{\overline{g}\widehat{{\mathit{\nu }}^4}-\overline{g}\overline{m}\widehat{{\mathit{\nu }}^2}+\overline{f}\overline{n}\widehat{{\mathit{\nu }}^2}-\overline{h}\overline{l}\widehat{{\mathit{\nu }}^2}+\overline{f}\overline{l}\widehat{{\mathit{\nu }}^4}-\overline{h}\overline{n}}\}+\frac{n\mathit{\pi }}{\widehat{\mathit{\nu }}}$. The smallest $\widehat{{\mathit{\tau }}_n}$ is given by $n=0$ and we take it as ${\widehat{\mathit{\tau }}}_n=\frac{1}{\widehat{\mathit{\nu }}}ta{n}^{-1}\{\frac{\widehat{\mathit{\nu }}(\overline{f}\widehat{{\mathit{\nu }}^4}-\overline{f}\overline{m}\widehat{{\mathit{\nu }}^2}-\overline{h}\widehat{{\mathit{\nu }}^2}-\overline{l}\overline{g}\widehat{{\mathit{\nu }}^2}-\overline{h}\overline{m}-\overline{n}\overline{g})}{\overline{g}\widehat{{\mathit{\nu }}^4}-\overline{g}\overline{m}\widehat{{\mathit{\nu }}^2}+\overline{f}\overline{n}\widehat{{\mathit{\nu }}^2}-\overline{h}\overline{l}\widehat{{\mathit{\nu }}^2}+\overline{f}\overline{l}\widehat{{\mathit{\nu }}^4}-\overline{h}\overline{n}}\}$. In order to establish the Hopf bifurcation at $\mathit{\tau }=\widehat{\mathit{\tau }}$, we need to show that $\frac{d\mathit{\mu }}{d\mathit{\tau }}\ne 0$ at $\mathit{\tau }=\widehat{\mathit{\tau }}$. We differentiate Equations 24 and 25 with respect to $\mathit{\tau }$ and setting $\mathit{\tau }=\widehat{\mathit{\tau }}$, $\mathit{\mu }=0$ and $\mathit{\nu }=\widehat{\mathit{\nu }}$, we get(28) $$\begin{array}{c}\hfill \left.\begin{array}{c}{L}_1\frac{d\mathit{\mu }}{d\mathit{\tau }}(\widehat{\mathit{\tau }})+M_1\frac{d\mathit{\nu }}{d\mathit{\tau }}(\widehat{\mathit{\tau }})=X_1\\ -M_1\frac{d\mathit{\mu }}{d\mathit{\tau }}(\widehat{\mathit{\tau }})+L_1\frac{d\mathit{\nu }}{d\mathit{\tau }}(\widehat{\mathit{\tau }})=Y_1\end{array}\right\},\end{array}$$(28)

where$$\begin{array}{cc}\hfill L_1& =-3{\widehat{\mathit{\nu }}}^2+\overline{m}-\overline{g}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-2\overline{f}\widehat{\mathit{\nu }}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}+\widehat{\mathit{\tau }}(\overline{h}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}+\overline{g}\widehat{\mathit{\nu }}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-\overline{f}{\widehat{\mathit{\nu }}}^{2}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}),\hfill \\ \hfill M_1& =-2\overline{l}\widehat{\mathit{\nu }}+2\overline{f}\widehat{\mathit{\nu }}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-\overline{g}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}+\widehat{\mathit{\tau }}(\overline{h}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-\overline{g}\widehat{\mathit{\nu }}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-\overline{f}{\widehat{\mathit{\nu }}}^{2}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}),\hfill \\ \hfill X_1& =\overline{f}{\widehat{\mathit{\nu }}}^{3}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-\overline{h}\widehat{\mathit{\nu }}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}+\overline{g}{\widehat{\mathit{\nu }}}^{2}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }},\hfill \\ \hfill Y_1& =\overline{f}{\widehat{\mathit{\nu }}}^{3}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-\overline{h}\widehat{\mathit{\nu }}cos\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}-\overline{g}{\widehat{\mathit{\nu }}}^{2}sin\widehat{\mathit{\nu }}\widehat{\mathit{\tau }}.\hfill \end{array}$$

Solving (Equation 28),

we get $\frac{d\mathit{\mu }}{d\mathit{\tau }}(\widehat{\mathit{\tau }})=\frac{L_1{X}_1-M_1{Y}_1}{L_1^2+M_1^2}$,

where $\frac{d\mathit{\mu }}{d\mathit{\tau }}(\widehat{\mathit{\tau }})$ has the same sign as that of $L_1{X}_1-M_1{Y}_1$.

Substituting the values of $L_1,M_1,X_1,\text{and}{Y}_1$ and using (Equation 26), we get$$L_1{X}_1-M_1{Y}_1={\widehat{\mathit{\nu }}}^2[3{\widehat{\mathit{\nu }}}^4+2({\overline{l}}^2-{\overline{f}}^2-2\overline{m}){\widehat{\mathit{\nu }}}^2+({\overline{m}}^2-2\overline{l}\overline{n}+2\overline{f}\overline{h}-{\overline{g}}^2)].$$

Let $H(z)=z^3+B_1{z}^2+B_{2}Zz+B_3$, where $B_1={\overline{l}}^2-{\overline{f}}^2-2\overline{m}$,  $B_2={\overline{m}}^2-2\overline{l}\overline{n}+2\overline{f}\overline{h}-{\overline{g}}^2$, $B_3=({\overline{n}}^2-{\overline{h}}^2)$ which is left side of (Equation 27) with ${\widehat{\mathit{\nu }}}^2=z$. Then, $H({\widehat{\mathit{\nu }}}^2)=0$ and we note that(29) $$\begin{array}{c}\hfill \frac{d\mathit{\mu }}{d\mathit{\tau }}(\widehat{\mathit{\tau }})=\frac{{\widehat{\mathit{\nu }}}^2}{L_1^2+M_1^2}\frac{dH}{dz}({\widehat{\mathit{\nu }}}^2).\end{array}$$(29)

Hence, we can describe the criteria for the preservation of stability (instability) geometrically as follows:

(1)	If the polynomial $H(z)$ has no positive roots, there is no change of stability.
(2)	If $H(z)$is decreasing (increasing) at all its positives roots, stability (instability) is preserved.

We note the following facts:

(i)	For the existence of $\widehat{\mathit{\nu }}$, $H(z)$ must have at least one positive real root.
(ii)	Since $H(z)$ is cubic in z , $$li{m}_{z\to \infty }H(z)=\infty .$$
(iii)	If $H(z)$ has a unique positive root, then it must increase at that point to satisfy (ii).
(iv)	If H(z) has two or three distinct positive real roots, then it must decrease at one root and increase at other; hence, (ii) is not satisfied.
(v)	If $B_3<0$, then $H(z)$ has only one root.
(vi)	If $B_1>0$, $B_3>0$, and $B_2<0$, then (i) will be satisfied.

Now, if $B_1>0$, $B_3>0$, and $B_2<0$, then the minimum of $H(z)$ will exist at $z_{min}=\frac{-B_1+\sqrt{B_1^2-3B_2}}{3}$

and (i) will be satisfied if $H(z_{min})>0$, i.e.(30) $$\begin{array}{c}\hfill 2B_1^3-9B_1{B}_2+27B_3>2{(B_1^2-3B_2)}^{3/2},\end{array}$$(30)

or $2B_1(B_1^2-3B_2)+27B_3-3B_1{B}_2>2{(B_1^2-3B_2)}^{3/2}$.

Since $27B_3-3B_1{B}_2>27B_3$ (since $B_1>0$, $B_3>0$, and $B_2<0$), and $B_1^2-3B_2>B_1^2$, hence $2B_1(B_1^2-3B_2)+27B_3-3B_1{B}_2>27B_3+2B_1^3$.

Thus, for Equation 30 to hold, it is sufficient that $27B_3+2B_1^3>2{(B_1^2-3B_2)}^{3/2}$$\Rightarrow$$B_2>\frac{1}{3}\left[B_1^2-{\left(\frac{27B_3+2B_1^3}{2}\right)}^{2/3}\right]$.

Table 2. A set of parametric values

Parameter	Definition	Value
r	Constant intrinsic growth rate for phytoplankton	1.2
K	Carrying capacity for phytoplankton	0.5
${\mathit{\alpha }}_1$	Maximal zooplankton ingestion rate	2
${\mathit{\alpha }}_2$	Maximal zooplankton conversion rate	1.5
${\mathit{\gamma }}_1$	Maximal planktivorous fish ingestion rate	1
${\mathit{\gamma }}_2$	Maximal planktivorous fish conversion rate	0.8
${\mathit{\mu }}_1$	Mortality rate of the phytoplankton	0.04
${\mathit{\mu }}_2$	Mortality rate of the zooplankton	0.06
${\mathit{\mu }}_3$	Mortality rate of the planktivorous fish	0.08
$K_1$	Half saturation constant for phytoplankton	0.8
$K_2$	Half saturation constant for zooplankton	0.9

Now, we can state the following theorem.

Theorem 6

If $B_1>0$, $B_3>0$, and relation (Equation 30) hold, then the stable positive equilibrium $E^{\ast }$ remains stable for all $\mathit{\tau }>0$.

6. Numerical simulations

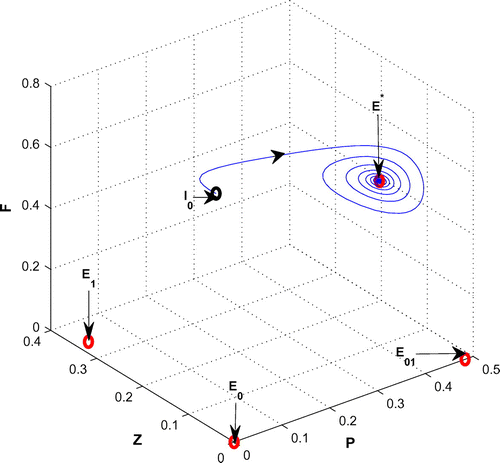
In this section, we focus our attention on the occurrence and termination of the fluctuating plankton population. We begin with a parameter set (see Table 2, Chatterjee & Pal, 2011) for which the existence condition of the coexistence equilibrium point $E^{\ast }$ is satisfied and the coexistence equilibrium point $E^{\ast }=(0.40,0.10,0.54)$ is locally asymptotically stable in the form of a stable focus with eigenvalues $-0.8003,-0.0129\pm \mathbf{i}0.2064$ (cf. Figure 1).

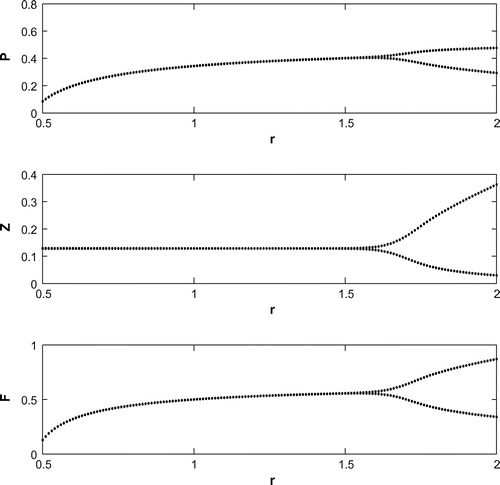
6.1. Effect of $\mathit{r}$

We have observed that the system shows oscillatory behavior around the positive interior equilibrium $E^{\ast }$ for increasing the value of $r=1.6$ with eigenvalues $-1.2305,0.0013\pm \mathbf{i}0.0.2057$ (cf. Figure 2). Decreasing the value of r from 1.2 to 0.3 with the same set of parametric values in Table 2, the system shifts to planktivorous fish free equilibrium $E_1=(0.0250,0.0766,0)$ in the form of a stable focus with eigenvalues $-0.0173,-0.0026\pm \mathbf{i}0.1188$ (cf. Figure 3). Figure 4(a–c) depicts the different steady-state behaviors of phytoplankton, zooplankton, and planktivorous fish in the system (Equation 1) for the parameter r. Here, we see a Hopf bifurcation point at $r_c^0$=1.583292 (denoted by a red star (H)) with first Lyapunov coefficient being –0.2999282. Clearly, the first Lyapunov coefficient is negative. This means that a stable limit cycle bifurcates from the equilibrium, when it loses stability.

Figure 1. The equilibrium point $E^{\ast }$ is stable for the parametric values as given in Table 2.

Figure 2. The figure depicts oscillatory behavior around the positive interior equilibrium point $E^{\ast }$ of system (Equation 1) for increasing r, from 1.2 to 1.6 with other parametric values as given in Table 2.

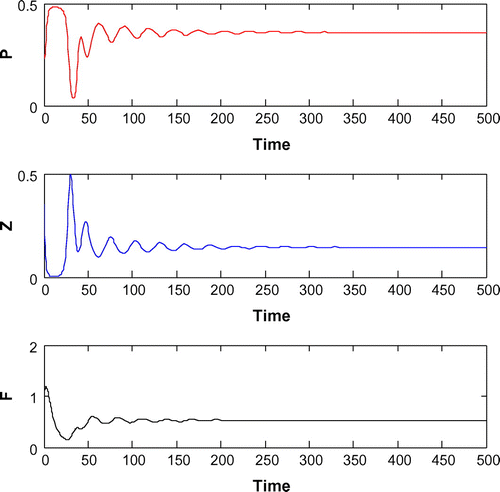
6.2. Effects of $\mathit{K}$

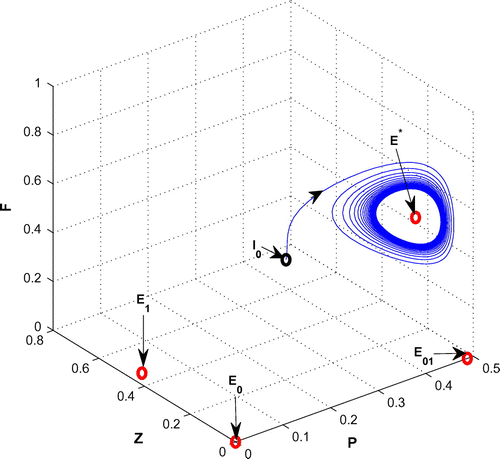
For K = 0.8, leaving all other parameters unaltered, the system exhibits oscillation around the positive interior equilibrium $E^{\ast }$ with eigenvalues $-0.8599,0.0069\pm \mathbf{i}0.2370$ (cf. Figure 5). Figure 6(a–c) depicts the different steady-state behaviors of phytoplankton, zooplankton, and planktivorous fish in the system (Equation 1) for the parameter K. Here, we see a Hopf bifurcation point at $K^{\ast }$=0.711977 (denoted by a red star (H)) with first Lyapunov coefficient being –0.3651997. Clearly, the first Lyapunov coefficient is negative. This means that a stable limit cycle bifurcates from the equilibrium, when it loses stability.

Figure 3. The figure depicts stable behavior around the planktivorous fish free equilibrium point $E_1$ of system (Equation 1) for decreasing r, from 1.2 to 0.3 with other parametric values as given in Table 2.

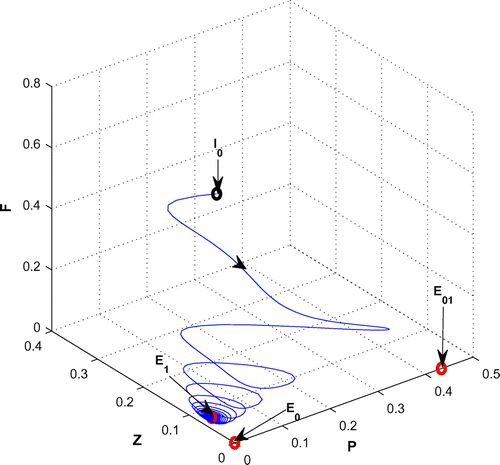
Figure 4. (a) The figure depicts different steady-state behaviors of phytoplankton for the effect of r. (b) The figure depicts different steady-state behaviors of zooplankton for the effect of r with other parametric values as given in Table 2. (c) The figure depicts different steady-state behaviors of planktivorous fish for the effect of r with other parametric values as given in Table 2.

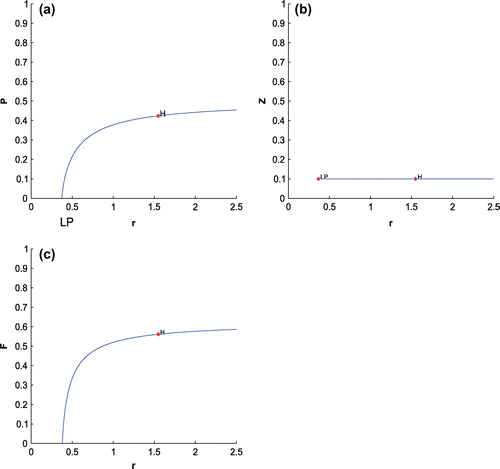
Figure 5. The figure depicts oscillatory behavior around the positive interior equilibrium point $E^{\ast }$ of system (Equation 1) for increasing K, from 0.5 to 0.8 with other parametric values as given in Table 2.

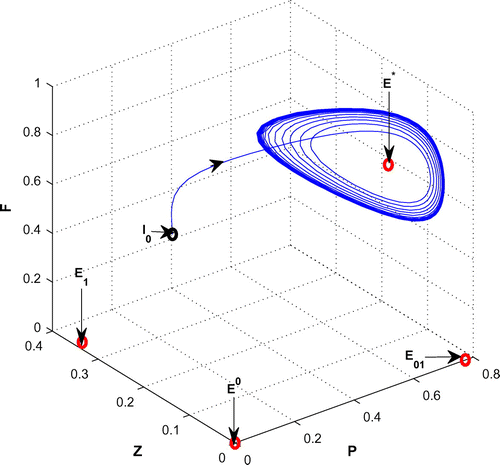
Figure 6. (a) The figure depicts different steady-state behaviors of phytoplankton for the effect of K. (b) The figure depicts different steady-state behaviors of zooplankton for the effect of K with other parametric values as given in Table 2. (c) The figure depicts different steady-state behaviors of planktivorous fish for the effect of K with other parametric values as given in Table 2.

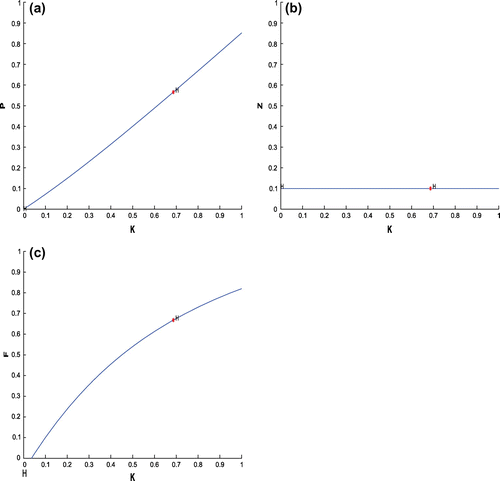
Figure 7. The figure depicts oscillatory behavior around the positive interior equilibrium point $E^{\ast }$ of system (Equation 1) for decreasing ${\mathit{\mu }}_3$, from 0.08 to 0.02 with same set of parametric values as use in Table 2.

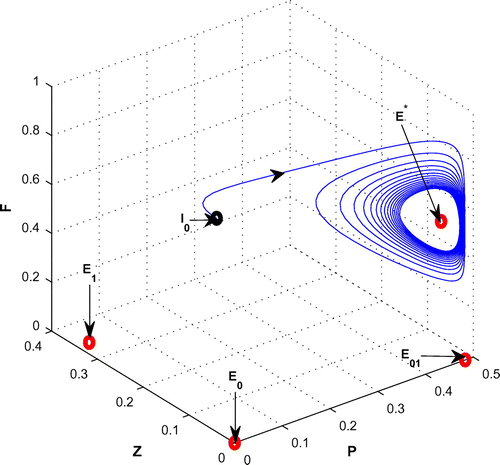
Figure 8. The figure depicts stable behavior around the planktivorous fish free equilibrium point $E_1$ of system (Equation 1) for increasing ${\mathit{\mu }}_3$, from 0.08 to 0.3 with same set of parametric values as use in Table 2.

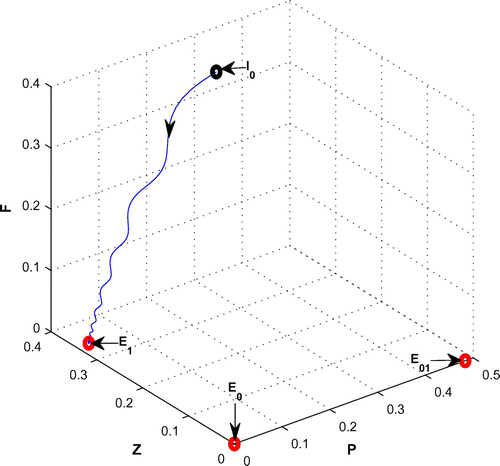
Figure 9. The figure depicts asymptotically stable behavior at positive interior equilibrium point $E^{\ast }$ of system (Equation 1) for r = 1.6 and ${\mathit{\mu }}_3=0.12$ with other parametric values as given in Table 2 ( Blue solid line). The trajectory (Black dotted line) shows stable behavior around the planktivorous fish free equilibrium point $E_1$ of system (Equation 1) for r = 1.6 and ${\mathit{\mu }}_3=.3$ with other parametric values as given in Table 2.

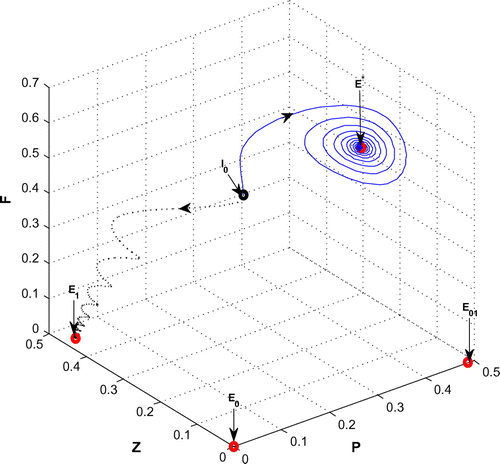
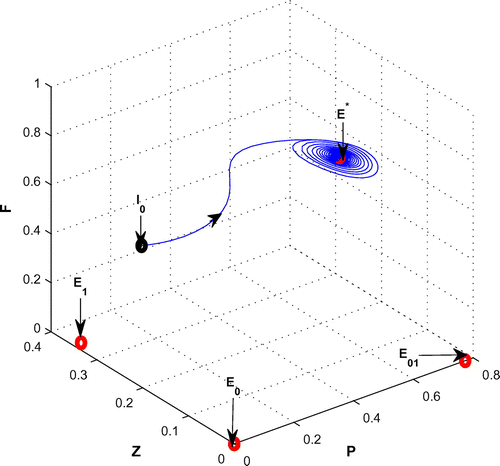
Figure 10. The figure depicts stable behavior around the positive interior equilibrium point $E^{\ast }$ of system (Equation 1) for $K=0.8$ and ${\mathit{\mu }}_3=0.12$ with other parametric values as given in Table 2.

Figure 11. The figures depict oscillatory behavior of phytoplankton, Zooplankton, and planktivorous fish population for $\mathit{\tau }=1$ with same set of other parametric values as given in Table 2.

Figure 12. The coexistence equilibrium is locally asymptotically stable for $\mathit{\tau }=1$ and $r=1$.

Figure 13. The coexistence equilibrium is locally asymptotically stable for $\mathit{\tau }=1$ and $K=0.35$.

Figure 14. The coexistence equilibrium is locally asymptotically stable for $\mathit{\tau }=1$ and ${\mathit{\mu }}_3=0.11$.

Figure 15. The bifurcation diagram of all the populations with K as the bifurcation parameter.

Figure 16. The bifurcation diagram of all the populations with r as the bifurcation parameter.

Figure 17. The K–r two parameters bifurcation diagram.

Figure 18. The $K-{\mathit{\mu }}_3$ two parameters bifurcation diagram.

Figure 19. The $r-{\mathit{\mu }}_3$ two parameters bifurcation diagram.

Figure 20. The bifurcation diagram for $\mathit{\tau }$ with all parametric values as given in Table 2.

6.3. Effects of ${\mathit{\mu }}_3$

Keeping the other parameters fixed and decreasing the value of ${\mathit{\mu }}_3$ from 0.08 to 0.02, the system exhibits oscillatory behaviors around the positive interior equilibrium $E^{\ast }$ with eigenvalues $-1.0833,0.0002\pm \mathbf{i}0.1084$ (cf. Figure 7). But the system shifts to planktivorous fish free equilibrium $E_1=(0.0250,0.3437,0)$ with eigenvalues $-0.0289,-0.0080\pm \mathbf{i}0.2516$, when ${\mathit{\mu }}_3$ increase from 0.08 to 0.3 with the same set of parametric values as in Table 2 (cf. Figure 8).

6.4. Combined effect of $\mathit{r}$ and ${\mathit{\mu }}_3$

It has already been shown that the system depicts oscillatory behavior around the positive interior equilibrium $E^{\ast }$ for $r=1.6$. If the mortality rate of planktivorous fish ${\mathit{\mu }}_3$ in increased from 0.08 to 0.12, the system becomes asymptotically stable at positive interior equilibrium $E^{\ast }=(0.3868,0.1588,0.5591)$ in the form of a stable focus with eigenvalues $-1.0114,-0.0107\pm \mathbf{i}0.2431$ (cf. Figure 9). But if the mortality rate of planktivorous fish ${\mathit{\mu }}_3$ is increased from 0.12 to 0.3, the system shifts to planktivorous fish free equilibrium $E_1=(0.025,0.4625,0)$ with eigenvalues $-0.0284,-0.0104\pm \mathbf{i}0.2918$ (cf. Figure 9).

6.5. Combined effect of K and ${\mathit{\mu }}_3$

It has already been shown that the system depicts oscillatory behavior around the positive interior equilibrium $E^{\ast }$ for $K=0.8$ (cf. Figure 5). But the system shifts to asymptotically stable behavior at $E^{\ast }=(0.5960,0.1590,0.7282)$ in the form of a stable focus with eigenvalues $-0.6461,-0.0065\pm \mathbf{i}0.2876$ for increasing the value of ${\mathit{\mu }}_3$ from 0.08 to 0.12 (cf. Figure 10).

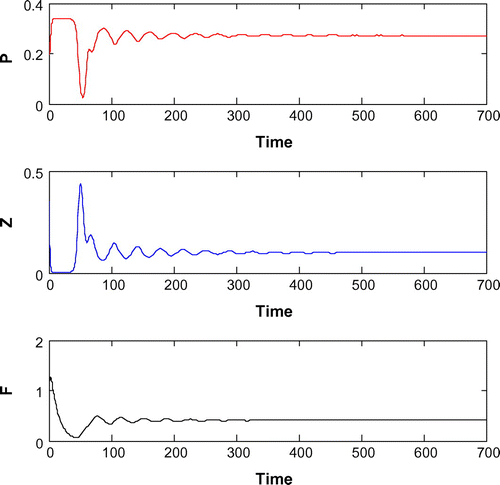
6.6. Effects of $\mathit{\tau }$

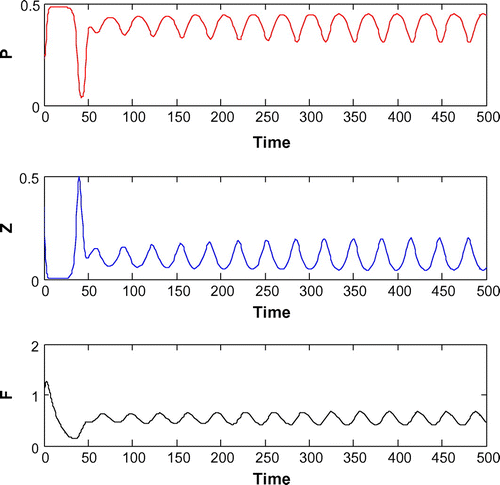
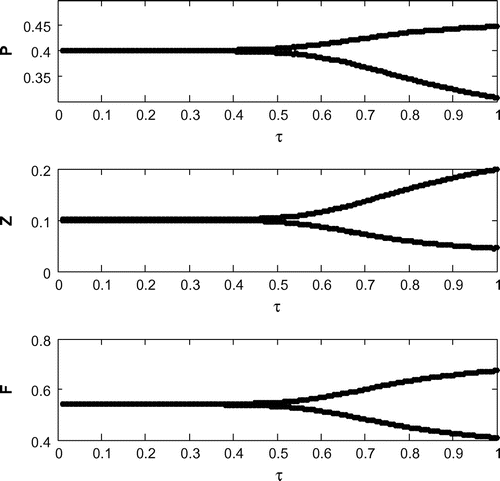
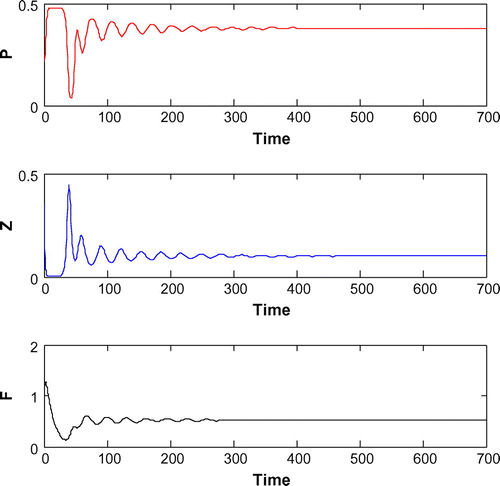
Now, we are to introduce gestation delay, $\mathit{\tau }$, in system (Equation 1). Keeping the other parameters fixed and increasing the value of the delay parameter $\mathit{\tau }$ from 0 to 1, we observe that the solution of system (Equation 8) changes from stable behavior to oscillatory behavior around the positive interior equilibrium $E^{\ast }$ (cf. Figure 11) for same set of parametric values as in Figure 1. We see that decreasing the value of r from 1.2 to 1, the system shifts to stable behavior around the positive interior equilibrium (cf. Figure 12). Similar cases happen when decreasing the carrying capacity and increasing mortality rate of planktivorous fish from 0.5 to 0.35 and 0.08 to 0.11, respectively, (cf. Figure 13 and cf. Figure 14) for same set of parametric values as in Figure 11.

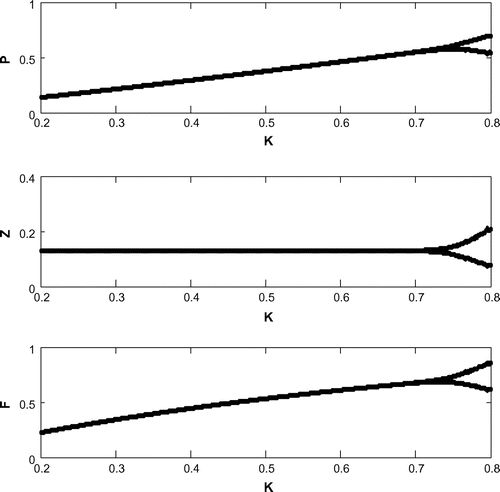
6.7. Hopf bifurcation

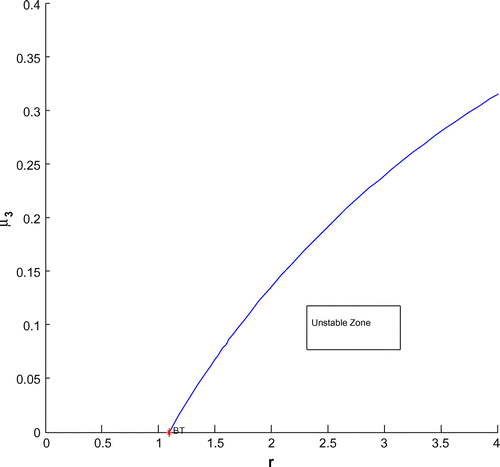
For a clear understanding of the dynamical changes due to change in constant nutrient input, K, a bifurcation diagram is plotted with this parameter as the bifurcation parameter with other three species (cf. Figure 15). We have also plotted another single parameter bifurcation diagram for r (cf. Figure 16).

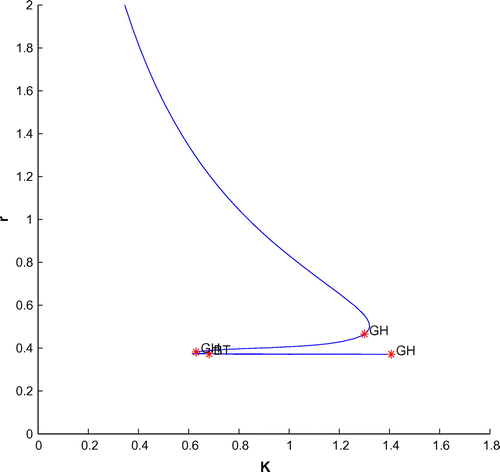
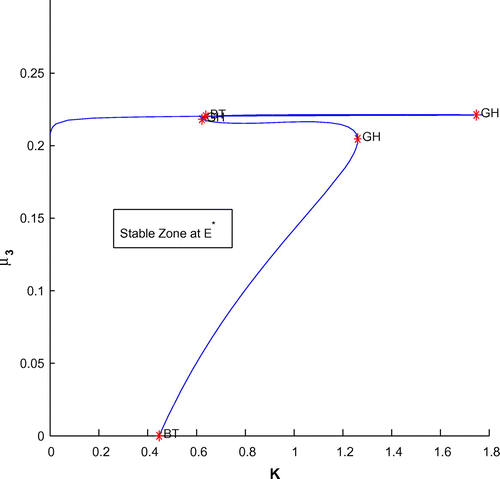
Now, we have plotted a two parameters bifurcation diagrams, K–r, $K-{\mathit{\mu }}_3$ and $r-{\mathit{\mu }}_3$ (cf. Figures 17–19). Here, we see a generalized Hopf (GH) point, where the first Lyapunov coefficient ($l_1$) vanishes but the second lyapounov coefficient is non-zero. The bifurcation point separates branches of sub and supercritical Andronov–Hopf bifurcations in the parameter plain. The Bogdanov–Takens (BT) point is the common point for the limit point curve and the curve corresponding to equilibria. Actually, at BT point, the system has an equilibrium with a double zero eigenvalues. For nearby parameter values, the system has two equilibria (a saddle and a non-saddle) which collide and disappear via a saddle-node bifurcation. The non-saddle equilibrium undergoes an Andronov–Hopf bifurcation, generating a limit cycle. Finally, a bifurcation diagram is plotted with $\mathit{\tau }$ as the bifurcation parameter with other three species (cf. Figure 20).

7. Discussion

A phytoplankton–zooplankton–fish interaction model is considered with nutrient uptake functions. Firstly, the model is studied analytically and the threshold conditions for the existence and stability of various steady states are worked out (see Table 1). It is observed that for constant intrinsic growth rate r, there is a chance for the population to fluctuate. But further increase in the value of constant intrinsic growth rate r may lead to extinction of planktivorous fish population.

It is observed that the system shifts to oscillatory behavior in presence of high value of carrying capacity. We have also observed that there is a chance of extension of planktivorous fish population for high value of mortality rate of planktivorous fish. Our study indicates that low value of mortality rate of planktivorous fish may lead to oscillatory behavior around the positive interior equilibrium.

Next, we have established that the system remains locally asymptotically stable and all solutions approach toward $E^{\ast }$ in presence of discrete delay whenever its magnitude lies below some threshold condition. Further, we have also observed the maximum value (length of delay) of $\mathit{\tau }$ (i.e. ${\mathit{\tau }}_{+}$) for which a locally asymptotically stable interior equilibrium $E^{\ast }$ will remain asymptotically stable, where ${\mathit{\tau }}_{+}=\frac{1}{2A_{\mathit{\theta }}}(-B_{\mathit{\theta }}+\sqrt{B_{\mathit{\theta }}^2+4A_{\mathit{\theta }}{C}_{\mathit{\theta }}})$ (see Theorem 5). Moreover, we analyzed conditions for bifurcation of the positive interior equilibrium. We observed that a positive interior equilibrium remains stable if $B_1>0$ and $B_3>0$ for all $\mathit{\tau }>0$ (see Theorem 6). Further, numerical simulations demonstrate the following conclusions:

(a)	The system exhibits dynamic instability due to higher gestation delay.
(b)	Low levels of constant intrinsic growth rate r induce stability around the positive interior equilibrium in presence of gestation delay.
(c)	Low levels of carrying capacity of phytoplankton K help the system (Equation 8) to approach stability at $E^{\ast }$ in presence of gestation delay.
(d)	High value of mortality rate of planktivorous fish prevents instability behavior in presence of gestation delay.

Throughout the article of this model (analytically and numerically), an attempt has been made to search for a suitable way to control the system and maintain a stable coexistence between all the species. It has been observed that to control the fracturing population and to maintain stability around the coexistence equilibrium, we have to balance the rate of carrying capacity of phytoplankton, mortality rate of planktivorous fish population, and constant intrinsic growth rate.

Acknowledgements

The authors would like to thank the referees very much for their valuable comments and suggestions.

Additional information

Funding

The research is partially supported by University Grants Commission, New Delhi [grant number MRP-MAJ-MATH-2013-609].

Notes on contributors

Samares Pal

Our research group is headed by Samares Pal and includes Anal Chatterjee as a post-doctoral researcher. Research in the group addresses a wide range of questions broadly concerning the dynamics of plankton ecosystems under environmental conditions. The main emphasis of our work includes mathematical modeling of marine ecosystems affected by fish induced, overfishing of zooplankton. The research reported in this paper will help in studying the interspecies between phytoplankton and zooplankton in presence of fish and the subsequent changes the stability behavior.

Notes

Corresponding author: Samares Pal, Department of Mathematics, University of Kalyani, Kalyani 741235, India. E-mail: [email protected].