Dynamics of the equation in the complex plane

Abstract

We investigate the dynamics of the second-order rational difference equation in the title with complex parameters and arbitrary complex initial conditions. Very little is known about rational difference equation in the complex domain. The solutions of such equation exhibit many rich and complicated asymptotic characters. Analysis of the local stability of the equilibria and periodicity of solutions has been carried out. We further exhibit several interesting characteristics of the solutions of this equation, using computations, which do not arise when we consider the same equation with positive real parameters and initial conditions. We pose several open problems and conjectures of paramount importance regarding boundedness and global asymptotic convergence. It is our belief that the analysis done here is generic in nature and can be helpful in the study of other difference equations in the complex domain.

Keywords:

• difference equation
• local asymptotic stability
• periodicity
• boundedness
• orbit plot

AMS Subject Classifications:

• 39A10
• 39A11

Public Interest Statement

Dynamics of non-linear difference equation is a contemporary area of mathematical research. Very little is known so far about these equations in the complex domain. They demonstrate rich and complicated dynamics. In this paper, we investigate the behavior of the solution sequences of a second-order rational difference equation. We assume the parameters to be complex valued and the initial values to be arbitrary complex numbers such that the equation exists. We have attempted to capture some of the interesting features of this equation both by theoretical analysis and by computations. Further, we have compared the dynamics in the complex domain with that of positive real domain which was studied earlier. Based on many computer observations and fundamental analysis we have also posed several open problems and conjectures. This paper is one of the preliminary attempts to study the dynamics of such rational systems in the complex domain.

1. Introduction and preliminaries

Consider the difference equation(1) $$\begin{array}{c}\hfill z_{n+1}=\frac{\mathit{\alpha }+\mathit{\beta }{z}_n}{A+z_{n-1}},n=0,1,\dots \end{array}$$(1)

where the parameters $\mathit{\alpha },\mathit{\beta }$ and A are complex numbers, and the initial conditions $z_{-1}$ and $z_0$ are arbitrary complex numbers. Since we are interested in studying a non-linear equation in the complex domain, without loss of generality we have assumed the coefficient of the $z_{n-1}$ term in the denominator to be one.

When the parameters and initial conditions are non-negative real numbers, Equation (1) was investigated in Kulenović and Ladas (2001) and Kocic and Ladas (1993) where the global asymptotic stability of the positive equilibrium was proved for certain ranges of the parameters (see Chatterjee, 2013 for more general results).

The set of initial conditions $z_{-1},z_0\in \mathbb{C}$ for which the solution of Equation (1) is well defined for all $n\ge 0$ is called the good set of initial conditions or the domain of definition. It is the compliment of the forbidden set of Equation (1) for which the solution is not well defined for some $n\ge 0$. See Grove, Kostrov, and Schultz (2009) for the definition and further work on obtaining the forbidden set for the first-order Riccati difference equation. However, for the second- and higher order rational difference equations, the lack of an explicit form for the solutions, makes it very challenging to obtain the good set. For Equation (1), we pose the following open problem of paramount importance and difficulty.

Open Problem 1.1

Determine the good set of initial conditions for Equation (1).

Our goal is to investigate the character of the solutions of Equation (1) when the parameters are real or complex and the initial conditions are arbitrary complex numbers in the domain of definition. For the rest of the sequel we assume that the initial conditions are from the good set.

To avoid degenerate cases, we assume $|\mathit{\alpha }|+|\mathit{\beta }|\ne 0$. For the remainder of this paper, we also assume $A\ne 0$. Then, with a change of variables $p=\frac{\mathit{\alpha }}{A^2}$ and $q=\frac{\mathit{\beta }}{A}$, without loss of generality Equation (1) reduces to the equation(2) $$\begin{array}{c}\hfill z_{n+1}=\frac{p+q{z}_n}{1+z_{n-1}},n=0,1,\dots \end{array}$$(2)

where the parameters p and q are complex numbers.

We now present some preliminary material which will be useful in our investigation of Equation (2).

Let $f:J^{\mathcal{K}+1}\to J$ be a continuous function, where $\mathcal{K}$ is a non-negative integer and J is an interval of complex numbers. Consider the difference equation(3) $$\begin{array}{c}\hfill y_{n+1}=f(y_n,y_{n-1},\dots ,y_{n-\mathcal{K}}),n=0,1,\dots \end{array}$$(3)

with initial conditions $y_{-\mathcal{K}},y_{-\mathcal{K}+1},\dots ,y_0\in J.$

We say that $\overline{y}$ is an equilibrium point of Equation (3) if$$f(\overline{y},\overline{y},\dots ,\overline{y})=\overline{y}.$$

We now impose the further restriction that the function $f(u_0,u_1,\dots ,u_{\mathcal{K}})$ be continuously differentiable.

The linearized equation of Equation (3) about the equilibrium $\overline{y}$ is the linear difference equation(4) $$\begin{array}{c}\hfill z_{n+1}=a_0{z}_n+a_1{z}_{n-1}+\cdots +a_{\mathcal{K}}{z}_{n-\mathcal{K}},n=0,1,\dots \end{array}$$(4)

where for each $i=0,1,\dots ,\mathcal{K}$$$a_i=\frac{\mathit{\partial }f}{\mathit{\partial }{u}_i}(\overline{y},\overline{y},\dots ,\overline{y}).$$

The characteristic equation of Equation (4) is the equation(5) $$\begin{array}{c}\hfill {\mathit{\lambda }}^{\mathcal{K}+1}-a_0{\mathit{\lambda }}^{\mathcal{K}}-a_1{\mathit{\lambda }}^{\mathcal{K}-1}-\cdots -a_{\mathcal{K}-1}\mathit{\lambda }-a_{\mathcal{K}}=0.\end{array}$$(5)

The following result, called the Linearized Stability Theorem, is useful in determining the local stability character of the equilibrium $\overline{y}$ of Equation (3).

Theorem A

(The Linearized Stability Theorem) The following statements are true:

(1)	If every root of Equation (5) has modulus less than one, then the equilibrium $\overline{y}$ of Equation (3) is locally asymptotically stable.
(2)	If at least one of the roots of Equation (5) has modulus greater than one, then the equilibrium $\overline{y}$ of Equation (3) is unstable.

The equilibrium solution $\overline{y}$ of Equation (3) is called hyperbolic if no root of Equation (5) has modulus equal to one. If there exists a root of Equation (5) with modulus equal to one, then $\overline{y}$ is called non-hyperbolic.

The equilibrium point $\overline{y}$ of Equation (3) is called a sink if every root of Equation (5) has modulus greater than one.

The equilibrium point $\overline{y}$ of Equation (3) is called a saddle point equilibrium if it is hyperbolic, and if in addition, there exists a root of Equation (5) with modulus less than one and another root of Equation (5) with modulus greater than one. In particular, if $\overline{y}$ is a saddle point equilibrium of Equation (3), then $\overline{y}$ is unstable.

The equilibrium point $\overline{y}$ of Equation (3) is called a repeller if every root of Equation (5) has absolute value less than one.

The following theorem is useful in determining when all roots of a polynomial equation of degree two have modulus less than one. It will provide necessary and sufficient conditions for local asymptotic stability of the equilibria.

Theorem B

A necessary and sufficient condition that all roots of the quadratic equation with real coefficients$${\mathit{\lambda }}^2+a_1\mathit{\lambda }+a_0=0$$

lie in the open disk $|\mathit{\lambda }|<1$ is$$|a_1|<a_0+1<2.$$

2. Local stability of the equilibrium

In this section, we investigate the local stability character of the equilibria of Equation (2). Here, we assume p and q to be non-negative real numbers. When the parameters are complex, the analysis is beyond the scope of this article and we leave it as an open problem.

The equilibrium points of Equation (2) are the solutions of the equation$$\overline{z}=\frac{p+q\overline{z}}{1+\overline{z}}.$$

Equation (2) has two equilibria points$${\overline{z}}_{1,2}=\frac{q-1\pm \sqrt{{(q-1)}^2+4p}}{2}.$$

The linearized equation of Equation (2) with respect to the equilibrium ${\overline{z}}_1$ is$$Y_{n+1}-\frac{q}{1+{\overline{z}}_1}{Y}_n+\frac{{\overline{z}}_1}{1+{\overline{z}}_1}{Y}_{n-1}=0,n=0,1,\dots ,$$

with associated characteristic equation$${\mathit{\lambda }}^2-\frac{q}{1+{\overline{z}}_1}\mathit{\lambda }+\frac{{\overline{z}}_1}{1+{\overline{z}}_1}=0.$$

The following lemma gives the local asymptotic stability of the equilibrium ${\overline{z}}_1$.

Lemma 2.1

The equilibrium ${\overline{z}}_1=\frac{q-1+\sqrt{{(q-1)}^2+4p}}{2}$ of Equation (2) is locally asymptotically stable for all values of the parameters.

Proof

From Theorem B we obtain the necessary and sufficient condition for all roots of the characteristic equation to lie within the open unit disk to be$$\left|\frac{q}{1+{\overline{z}}_1}\right|<1+\frac{{\overline{z}}_1}{1+{\overline{z}}_1}<2.$$

Note that ${\overline{z}}_1$ is positive and also ${\overline{z}}_1>\frac{q-1}{2}$. Thus, the above condition is satisfied for all values of the positive real parameters p and q. The proof is complete. $\square$

The linearized equation of Equation (2) with respect to the equilibrium ${\overline{z}}_2$ is$$Y_{n+1}-\frac{q}{1+{\overline{z}}_2}{Y}_n+\frac{{\overline{z}}_2}{1+{\overline{z}}_2}{Y}_{n-1}=0,n=0,1,\dots ,$$

with associated characteristic equation$${\mathit{\lambda }}^2-\frac{q}{1+{\overline{z}}_2}\mathit{\lambda }+\frac{{\overline{z}}_2}{1+{\overline{z}}_2}=0.$$

The following lemma gives the necessary and sufficient condition for the local asymptotic stability of the equilibrium ${\overline{z}}_2$. We assume p and q such that ${\overline{z}}_2\ne -1$ for the existence of linearized equation.

Lemma 2.2

The equilibrium ${\overline{z}}_2=\frac{q-1-\sqrt{{(q-1)}^2+4p}}{2}$ of Equation (2) is locally asymptotically stable if and only if $3q^2+2q-4p-1<0$.

Proof

From Theorem B, we obtain the necessary and sufficient condition for all roots of the characteristic equation to lie within the open unit disk to be$$\left|\frac{q}{1+{\overline{z}}_2}\right|<1+\frac{{\overline{z}}_2}{1+{\overline{z}}_2}<2.$$

Note that ${\overline{z}}_2$ is non-positive and also ${\overline{z}}_2<\frac{q-1}{2}$. The second half of the inequality is satisfied for all p and q. Thus, it is enough to show $\left|\frac{q}{1+{\overline{z}}_2}\right|<1+\frac{{\overline{z}}_2}{1+{\overline{z}}_2}.$ This simplifies to the condition$${\overline{z}}_2>-\frac{(1+q)}{2}$$

Substituting the value of ${\overline{z}}_2$ we obtain the necessary and sufficient condition to be$$3q^2+2q-4p-1<0.$$

The proof is complete. $\square$

Open Problem 2.1

When the parameters p and q are complex, find the necessary and sufficient conditions for the local asymptotic stability of the equilibrium when it exists.

3. Periodicities of solutions

In this section, we discuss the global periodicity and the existence of solutions that converge to periodic solutions of Equation (2).

A difference equation is said to be globally periodic of period t if $x_{n+t}=x_n$ for any given initial condition. The characterization of periodic rational difference equations (either with real or complex coefficients) of order k is a challenging area of current research. See Camouzis and Ladas (2008) and Kulenović and Ladas (2001) for several periodicity results of second- and third-order rational difference equations, respectively, with non-negative real coefficients and arbitrary non-negative real initial conditions.

The following result gives the necessary conditions for global periodicity of Equation (2). The proof is a direct consequence of Theorem 1 in Rubió-Massegú and Mañosa (2007) and thus we omit it.

Theorem 3.1

If Equation (2) is globally periodic of period p then $p\ne q$. Moreover setting$$\begin{array}{cc}\hfill \mathit{\lambda }& :=\frac{1+q-\mathit{\delta }}{1+q+\mathit{\delta }},\hfill \\ \hfill a& :=\frac{1-q+\mathit{\delta }}{1+q+\mathit{\delta }}\hfill \end{array}$$

where$$\mathit{\delta }:=\sqrt{{(1+q)}^2+4(p-q)}.$$

It must be satisfied that $0<|\mathit{\lambda }|<1$ (or $|\mathit{\lambda }|=1$ and Im($\mathit{\lambda }$)$\ge 0$), and it must hold one of the following four cases:

(1)	$a=1$, $\mathit{\lambda }\ne 1$, p is even and ${\mathit{\lambda }}^{\frac{p}{2}}=1$. In this case the equation is a globally periodic M$\ddot{o}$bius-generated equation of period p.
(2)	$a=\frac{3-\sqrt{5}}{2}$, $\mathit{\lambda }=-\frac{3-\sqrt{5}}{2}$. In this case, the equation is a globally periodic of period 5, and affine conjugated with the Lyness-type equation.
(3)	$\mathit{\lambda }=1,a\ne \pm 1,{(-a)}^p=1,\left|\frac{a^2-4a+1}{2a^2-2a+1}\right|\le 2$ and the zeros of polynomial $P(z)=z^2+\frac{a^2-4a+1}{2a^2-2a+1}z+\frac{a^2-2a+2}{2a^2-2a+1}$ are p-roots of the unity.
(4)	$\mathit{\lambda }=-\overline{a}\frac{1-a}{1-\overline{a}},0<\left|a\right|<1,\left|1-\frac{1}{a}\right|<2,a\notin \mathbb{R}$ and the zeros of polynomial $P_0(z)=z^2+\frac{1-\overline{a}}{\overline{a}}z+\frac{a}{\overline{a}}\frac{1-\overline{a}}{1-a}$ and $P_1(z)=z^2-(1-a)z+\frac{1-a}{1-\overline{a}}$are p-roots of the unity.

Apart from globally periodic equations, rational difference equation also exhibits the existence of periodic solutions and solutions that eventually converge to a periodic solution. See Camouzis and Ladas (2008) for many such examples of second- and third-order rational difference equations with non-negative real parameters and initial conditions. Further in the complex domain, these equations are even more richer in periodic solutions. Equation (2) has exhibited the existence of periodic solutions and convergence to periodic solutions of numerous possible periods. Some of the many periodicities observed computationally are reported in Table 1 with some of the time series plots shown in Figure 1. Note that, in all the tables the parameters and initial conditions are represented as (a, b) where a is the real part and b is the imaginary part of the complex numbers. Also note that, in all the figures henceforth the green plot designates real part, while the blue plot designates the imaginary part of the orbit.

Table 1. Periodicity of orbits of Equation (2)

p	q	$z_{-1}$	$z_0$	Period
(68, 117)	($-68,-117$)	(44, 151)	(51, 101)	2
($-159,0$)	($-192,0$)	(131, 7)	(170, 187)	3
($-141,0$)	($-6,0$)	(55, 9)	(19, 165)	4
($-207,-201$)	($-94,-95$)	(178, 5)	(98, 33)	6
($-139,0$)	($-63,0$)	(190, 6)	(88, 76)	6
(22, 156)	(22, 156)	(78, 48)	(81, 19)	7
(140, 179)	($-140,-179$)	(192, 109)	(27, 30)	8
(326, 363)	(50, 366)	(253, 39)	(111, 219)	9
($-205,-200$)	($-101,-101$)	(35, 25)	(200, 34)	12

It is interesting to note that Equation (2) with positive parameters and initial conditions has been long conjectured to have the equilibrium globally asymptotically stable for all values of parameters (see Kulenović & Ladas, 2001). Thus, in this case Equation (2) does not possess any periodic solutions.

Figure 1. Periodic orbit plot for Equation (2). Notes: Top left:Period-4, Top right: Period-6, Bottom left: Period-9 and Bottom right: Period-12). Here in each figure plot, the x-axis represents number of iterations and y-axis represents the trajectory at a given time instance.

4. Some special cases of the parameters

In this section, we observe the behavior of the solutions of Equation (2) when we consider first the two parameters p and q to be both real, in order to gain some understanding in the simplest model. Then, we consider one parameter to be real, while the other to be complex. We will generalize the result with means of computational outputs.

We first establish the local stability character of the equilibria of Equation (2) for the simplified case when the parameter p is any positive real number and $q=1$.

The equilibrium points of Equation (2) reduce to$${\overline{z}}_{1,2}=\pm \sqrt{p}$$

The linearized equation of Equation (2) with respect to the equilibrium ${\overline{z}}_1=\sqrt{p}$ is$$Y_{n+1}-\frac{1}{1+\sqrt{p}}{Y}_n+\frac{\sqrt{p}}{1+\sqrt{p}}{Y}_{n-1}=0,n=0,1,\dots ,$$

with associated characteristic equation$${\mathit{\lambda }}^2-\frac{1}{1+\sqrt{p}}\mathit{\lambda }+\frac{\sqrt{p}}{1+\sqrt{p}}=0.$$

The following lemma is a direct consequence of Theorem B and hence we omit the proof.

Lemma 4.1

The equilibrium ${\overline{z}}_1=\sqrt{p}$ of Equation (2) is locally asymptotically stable.

The linearized equation of Equation (2) with respect to the other equilibrium ${\overline{z}}_1=-\sqrt{p}$ is$$Y_{n+1}-\frac{1}{1-\sqrt{p}}{Y}_n+\frac{-\sqrt{p}}{1-\sqrt{p}}{Y}_{n-1}=0,n=0,1,\dots ,$$

with associated characteristic equation$${\mathit{\lambda }}^2-\frac{1}{1-\sqrt{p}}\mathit{\lambda }+\frac{-\sqrt{p}}{1-\sqrt{p}}=0.$$

Note that for existence of solutions in this case $p\ne 1$. The following lemma is a direct consequence of Theorem B and so the proof is omitted.

Lemma 4.2

The equilibrium ${\overline{z}}_2=-\sqrt{p}$ of Equation (2) is locally asymptotically stable for $p>1$ and unstable saddle if $p<1$.

Computationally, it is seen that for all real parameter p and $q=1$, the solutions of Equation (2) are convergent and converge to a neighborhood $Nbd(q,\mathit{ϵ})$ of q, as illustrated in Table 2 for few examples. Note that in all the tables henceforth by convergent point we mean the computational approximation, which is certainly very close to the actual convergence point of the solution sequence.

Open Problem 4.1

Show that when the parameter p is any real number and parameter $q=1$, every solution of Equation (2) is convergent. Determine the point of convergence.

Furthermore, it is observed that for all real valued p and q, the solution sequences are convergent and converge to $Nbd(q,\mathit{ϵ})$, as illustrated in Table 3 for few examples. For complex-valued p and real-valued q, it is seen that the solution sequences are convergent and converge to $(Nbd(q,\mathit{ϵ}),s)$, where s is a real number as illustrated in Table 4 for certain examples. In the case of real-valued p and complex-valued q,there exist solution sequences which are convergent and converge to $(Nbd(q,\mathit{ϵ}),s)$ where s is a real number as shown in Table 5 for certain examples. However, in this case chaos and higher order periodicities are also observed.

Table 2. $q=1$ and p is any real number

p	q	$z_{-1}$	$z_0$	Convergent point
(48, 0)	(1, 0)	(139, 273)	(479, 483)	(1.0013, $-0.1721$)
(78, 0)	(1, 0)	(486, 479)	(243, 400)	(1.0007, $-0.1607$)
(71, 0)	(1, 0)	(211, 458)	(396, 480)	(1.0007, $-0.1528$)
(328, 0)	(1, 0)	(17, 425)	(467, 340)	(1.0036, $-0.7693$)
(379, 0)	(1, 0)	(372, 196)	(328, 85)	(1.0199, $-1.9284$)
(353, 0)	(1, 0)	(15, 138)	(23, 48)	(1.0377, $-2.5502$)
(412, 0)	(1, 0)	(348, 158)	(476, 17)	(1.0335, $-2.6008$)
(219, 0)	(1, 0)	(191, 383)	(398, 93)	(1.0030 $-0.5691$)

Table 3. p and q are any real number

p	q	$z_{-1}$	$z_0$	Convergent Point
(395, 0)	(475, 0)	(65, 134)	(88, 167)	(474.84, 0.043865)
(385, 0)	(83, 0)	(173, 198)	(103, 177)	(83.551, $-1.2900$)
(294, 0)	(77, 0)	(40, 81)	(150, 165)	(78.339, $-1.3673$)
(395, 0)	(159, 0)	(107, 18)	(22, 27)	(160.44, $-0.16098$)
(340, 0)	(248, 0)	(38, 99)	(29, 11)	(248.32, $-0.12657$)
(426, 0)	(280, 0)	(186, 240)	(117, 163)	(280.42, $-0.20689$)
(440, 0)	(495, 0)	(0, 173)	(123, 198)	(494.90, 0.034494)
(41, 0)	(313, 0)	(132, 146)	(179, 197)	(312.29, 0.33242)

Table 4. p is complex number and q is real number

p	q	$z_{-1}$	$z_0$	Convergent point
(408, 182)	(63, 0)	(183, 127)	(19, 55)	(65.240, $-1.5480$)
(273, 192)	(483, 0)	(31, 195)	(192, 97)	(482.76, 0.49194)
(400, 28)	(211, 0)	(184, 159)	(192, 131)	(211.63, $-0.34183$)
(17, 170)	(467, 0)	(136, 152)	(149, 78)	(466.24, 0.61235)
(328, 34)	(353, 0)	(6, 55)	(9, 19)	(352.97, 0.10023)
(412, 139)	(158, 0)	(190, 6)	(88, 76)	(160.59, 0.75716)
(383, 159)	(93, 0)	(98, 89)	(129, 142)	(95.446, $-0.60822$)
(480, 68)	(293, 0)	(44, 151)	(51, 101)	(293.60, $-0.074866$)

Table 5. p is real number and q is any complex number

p	q	$z_{-1}$	$z_0$	Convergent Point
(293, 0)	(131, 8)	(151, 48)	(88, 138)	(132.06, 7.5582)
(179, 0)	(368, 79)	(137, 141)	(88, 3)	(367.48, 78.984)
(165, 0)	(212, 54)	(39, 165)	(86, 178)	(211.74, 53.948)
(195, 0)	(385, 79)	(162, 151)	(75, 43)	(384.50, 78.990)

Although the tables demonstrate only a few examples, we have broadly and meticulously carried out many computations for the different values of the parameters. Based on the numerous computer observations we make the following surprising remark.

Remark 4.1

It appears from orbit plots, there exist solutions of Equation (2) with parameters p and q real as well as complex and complex initial conditions, that converge to a value whose real part is within an $\mathit{ϵ}$-neighborhood, of the parameter q where $\mathit{ϵ}$ is a non-negative real number. Thus, the parameter q seems to be a determining factor of the point of convergence.

5. Dynamic features in the complex plane

When we consider Equation (2) with complex parameters and initial conditions, the equation exhibits a variety of characteristics such us global convergence, boundedness, existence of periodic solutions, convergence to periodic solutions as well as "chaos".

By extensive computations, we have observed that all solutions of Equation (2) with complex parameter values and arbitrary complex initial conditions, are bounded. Even in the region where we have observed "chaos", boundedness holds. This is in agreement with the case of positive real parameters and initial conditions where the boundedness criterion was demonstrated (see Kulenović & Ladas, 2001). However, the proof in the real case does not generalize to the complex case. Hence we pose the following conjecture on boundedness which is of significant importance.

Conjecture 5.1

Every solution of Equation (2) is bounded.

One of the important goals in the study of non-linear difference equation is to obtain the bounds on the parameters for which the equilibrium will be a global attractor. Although we conjecture that all solutions of Equation (2) are bounded, obtaining the parametric region for global asymptotic stability is still a significant challenge. Hence we pose the following open problem of paramount importance.

Open Problem 5.1

Obtain necessary and sufficient conditions in terms of the parameters p and q of Equation (2) for which the solutions will be globally asymptotically stable.

 

Table 6. Rapid convergence of solutions of Equation (2)

p	q	$z_{-1}$	$z_0$	Convergent point
(192, $-192$)	(97, $-97$)	(160, 28)	(84, 184)	($\mathbf{97.638},-\mathbf{98.144}$)
($-192,-192$)	($-97,-97$)	(160, 28)	(84, 184)	($-\mathbf{96.352},-\mathbf{95.813}$)
($-210,-191$)	($-95,-94$)	(160, 28)	(84, 184)	($-\mathbf{94.155},-\mathbf{92.705}$)
($-196,-196$)	($-92,-93$)	(160, 28)	(84, 184)	($-\mathbf{91.272},-\mathbf{91.633}$)
($-209,-203$)	($-98,-100$)	(160, 28)	(84, 184)	($-\mathbf{97.224},-\mathbf{98.704}$)
($-203,-197$)	($-98,-100$)	(160, 28)	(84, 184)	($-\mathbf{97.265},-\mathbf{98.778}$)
($-195,-204$)	($-104,-103$)	(160, 28)	(84, 184)	($-\mathbf{103.45},-\mathbf{101.89}$)
($-196,-197$)	($-96,-101$)	(160, 28)	(84, 184)	($-\mathbf{95.303},-\mathbf{99.775}$)
($-209,-198$)	($-101,-94$)	(160, 28)	(84, 184)	($-\mathbf{100.27},-\mathbf{92.745}$)

 

Table 7. Chaos

p	q	$z_{-1}$	$z_0$	Fractal dimension
($-197,-199$)	($-103,-103$)	(12, 80)	(105, 83)	1.82779
($-197,-202$)	($-93,-101$)	(160, 28)	(84, 184)	1.8905
(192, 192)	(97, 97)	(160, 28)	(84, 184)	1.89333
(153, 153)	(159, 159	(37, 98)	(89, 129)	1.86099
(142, 151)	(142, 151)	(55, 136)	(131, 32)	1.9127
($-141,0$)	(6, 0)	(55, 9)	(19, 165)	1.83609

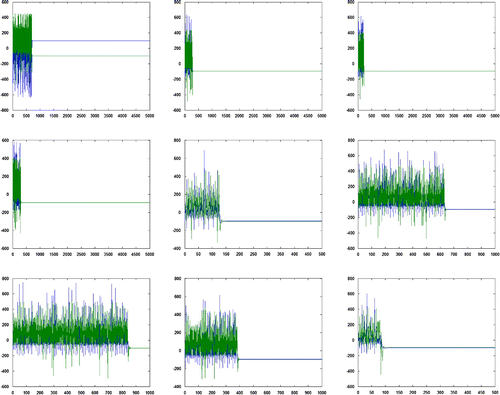
Figure 2. Rapid convergence behavior of iterates. Note: In each figure plot, the x-axis represents number of iterations and y-axis represents the trajectory at a given time instance.

One of our main goals is to compare how the dynamics of Equation (2) changes as we shift from the positive real domain to the complex domain. Although the theoretical analysis is extremely challenging, we have done extensive computations to gain some understanding. Based on these numerous simulations, we now report some observations that are essentially unique features of Equation (2) in the complex domain that were not present in the positive real domain.

5.1. Rapid convergence of iterates

There are many examples in case of p and q both complex numbers, where it is seen that the sequences are convergent to a $\mathit{ϵ}$-neighborhood $(Nbd(q,\mathit{ϵ}))$ of the parameter q all on a sudden while previous iterates are highly non-monotonous. A few examples are illustrated in Table 6 and corresponding plots of the iterates are given in Figure 2. This is a peculiar behavior observed only in the case of complex domain.

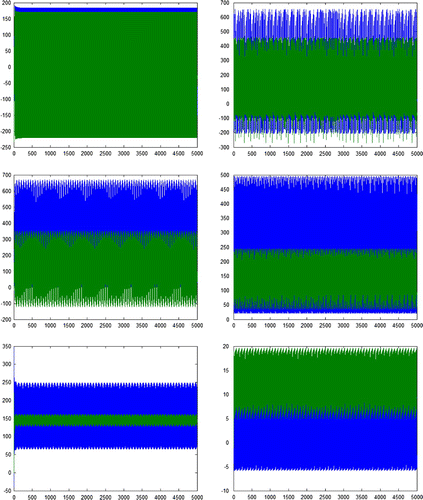
5.2. Chaos

We have observed "chaos" for several values of the parameters. Some of the examples are tabulated in Table 7 along with the computed box counting dimensions of the orbit plots. The chaotic sequence plots are given in Figure 3. Equation (2) in the positive real domain did not exhibit "chaos". In fact, it is interesting to note that, none of the 49 second-order rational difference equations with positive real parameters and initial conditions had exhibited “chaos” (see Kulenović & Ladas, 2001). This naturally leads to the following open problem.

Figure 3. Chaotic behavior of sequence. Notes: In each figure plot, the x-axis represents number of iterations and y-axis represents the trajectory at a given time instance.

Open Problem 5.2

Obtain necessary and sufficient conditions in terms of the parameters of Equation (2) for which the solution exhibits chaotic dynamics.

6. Conclusion

Non-linear difference equation in both real and complex domain is an established dynamic area of research. However, the study of rational difference equations is still in its infancy. The first-order Riccati difference equation, for which the solution could be obtained explicitly, has been studied both in the real and complex domains (see Grove, Kostrov, & Schultz, 2009; Kulenović & Ladas, 2001). Second- and third-order rational difference equations with positive real parameters and initial conditions have also been studied extensively (see Camouzis, Chatterjee, Ladas & Quinn, 2004 , 2005; Camouzis & Ladas, 2008).

When we consider the parameters and initial conditions to be complex, there is hardly anything known about rational difference equation. Our curiosity drove us to study this basic second-order rational difference equation in the complex domain. From many computer observations, we noticed as expected the richness and complexity of the dynamics. Our main purpose behind this manuscript is to probe and analyze how the dynamics changes for rational equations when we shift from positive real domain to the complex domain.

We have carried out some local stability and global periodicity analysis. We have observed computationally the different characteristics of boundedness, convergence, convergence to periodic solutions, and chaos. Each one of these characteristics of the dynamics is important in their own right and we have posed them as challenging open problems which require further theoretical investigations. Further, certain peculiar behavior of the dynamics in the complex domain has been brought forward which is in stark contrast to the positive real scenario.

The work carried out is generic in nature and can be helpful toward the study of other rational difference equations of second and higher orders. It is our belief that this work would initiate the study and understanding of rational difference equations in the complex plane.

Additional information

Funding

Esha Chatterjee’s work is supported by DST (India) [grant D.O. number SR/FTP/MS-013/2011]. Also supported in part by UGC (India).

Notes on contributors

Sk. Sarif Hassan

Sk Sarif Hassan is a visiting fellow in the International Centre for Theoretical Sciences of Tata Institute of Fundamental Research, Bengaluru, India. He has graduated from the Indian Statistical Institute, Calcutta. He is interested in Fractals, Cellular Automata, Mathematical Morphology and Discrete Dynamical Systems.

Esha Chatterjee

Esha Chatterjee is a scientist in the Department of Mathematics at Indian Institute of Science, Bengaluru, India. She has received her PhD from University of Rhode Island, USA and has been an assistant professor in Mathematics at Bryant University, USA. She works in the contemporary area of Nonlinear Difference Equations of higher orders and their applications. Her research involves the mathematical analysis of the global asymptotic stability, periodicity, boundedness character, etc of the solutions of non-linear difference equation of order more than one. She also works on difference equation models arising in the real world in various fields like biology, epidemiology, and finance among others.