Effects of two temperatures and thermal phase-lags in a thick circular plate with axisymmetric heat supply

Abstract

The present investigation is concerned with thermomechanical interactions for the dual-phase-lag in a homogeneous isotropic thick circular plate in the light of two-temperature thermoelasticity theory. The upper and lower surfaces of the thick plate are traction free and subjected to an axisymmetric heat supply. The solution is found by using Laplace and Hankel transform technique and a direct approach without the use of potential functions. The analytical expressions of displacement components, stresses, conductive temperature, temperature change and cubic dilatation are computed in transformed domain. Numerical inversion technique has been applied to obtain the results in the physical domain. Numerically simulated results are depicted graphically. The effects of thermal phase-lags and two temperatures are shown on the various components. Some particular cases are also deduced from the present investigation.

Keywords:

• two-temperature
• two phase lags
• isotropic
• thick circular plate
• Laplace transform
• Hankel transform

Public Interest Statement

The result of the problem is useful in the two-dimensional problem of dynamic response due to various thermal and mechanical sources which has various geophysical and industrial applications. The physical applications are encountered in the context of problems such as ground explosions and oil industries. This problem is also useful in the field of geo-mechanics, where the interest is in various phenomena occurring in earthquakes and measurement of displacements, stresses and temperature field due to the presence of certain sources.

1. Introduction

The use of thermal phase-lags in the heat conduction equation gives a more realistic model of thermoelastic media as it allows a delayed response to the relative heat flux vector. The result of the problem is useful in the two-dimensional problem of dynamic response due to various thermal and mechanical sources which has various geophysical and industrial applications.

Classical Fourier heat conduction law implies an infinitely fast propagation of a thermal signal which is violated in ultrafast heat conduction system due to its very small dimensions and short timescales. Catteno (1958) and Vernotte (1958) proposed a thermal wave with a single phase lag in which the temperature gradient after a certain elapsed time was given by $\mathit{q}+{\mathit{\tau }}_q\frac{\mathit{\partial }\mathit{q}}{\mathit{\partial }t}=-k\mathrm{\nabla }T$, where τ_q denotes the relaxation time required for thermal physics to take account of hyperbolic effect within the medium. Here, when τ_q > 0, the thermal wave propagates through the medium with a finite speed of $\sqrt{\frac{\mathit{\alpha }}{{\mathit{\tau }}_q}}$, where α is thermal diffusivity. When τ_q approaches zero, the thermal wave has an infinite speed and thus the single-phase-lag model reduces to the traditional Fourier model. The dual-phase-lag model of heat conduction was proposed by Tzou (1996) $\mathit{q}+{\mathit{\tau }}_q\frac{\mathit{\partial }\mathit{q}}{\mathit{\partial }t}=-k(\mathrm{\nabla }T+{\mathit{\tau }}_t\frac{\mathit{\partial }}{\mathit{\partial }t}\mathrm{\nabla }T)$, where the temperature gradient $\mathrm{\nabla }$T at a point P of the material at time t + τ_t corresponds to the heat flux vector q at the same time at the time t + τ_q. Here, $k$ is thermal conductivity of the material. The delay time ${\mathit{\tau }}_t$ is interpreted as that caused by the microstructural interactions and is called the phase-lag of temperature gradient. The other delay time τ_q interpreted as the relaxation time due to the fast transient effects of thermal inertia and is called the phase-lag of heat flux. This universal model is claimed to be able to bridge the gap between microscopic and macroscopic approaches, covering a wide range of heat transfer models. If ${\mathit{\tau }}_t=0$, Tzou (1996) refers to the model as single-phase model. Numerous efforts have been invested in the development of an explicit mathematical solution to the heat conduction equation under dual-phase-lag model. Quintanilla and Racke (2006) compared two different mathematical hyperbolic models. Kumar and Mukhopadhaya (2010a, 2010b) investigated the propagation of harmonic waves of assigned frequency by employing the thermoelasticity theory with three-phase-lags. Chou and Yang (2009) discussed two dimensional dual-phase-lag thermal behaviour in single-/multi layer structures. Zhou, Zhang, and Chen (2009) proposed an axisymmetric dual-phase-lag bioheat model for laser heating of living tissues. Kumar, Chawla, and Abbas, (2012) discussed effect of viscosity on wave propagation in anisotropic thermoelastic medium with three-phase-lag model. Ying and Yun (2015) built a fractional dual-phase-lag model and the corresponding bioheat transfer equation. Abdallah (2009) used uncoupled thermoelastic model based on dual-phase-lag to investigate the thermoelastic properties of a semi-infinite medium. Rukolaine (2014) employed dual-phase-lag models to study unphysical problems. Tripathi, Kedar, and Deshmukh (2015) discussed generalized thermoelastic diffusion problem in a thick circular plate with axisymmetric heat supply.

Chen and Gurtin (1968), Chen, Gurtin, and Williams (1968, 1969) have formulated a theory of heat conduction in deformable bodies which depends upon two distinct temperatures, the conductive temperature φ and the thermodynamical temperature T. For time independent situations, the difference between these two temperatures is proportional to the heat supply, and in absence of heat supply, the two temperatures are identical. For time dependent problems, the two temperatures are different, regardless of the presence of heat supply. The two temperatures T, $\mathit{\phi }$ and the strain are found to have representations in the form of a travelling wave plus a response, which occurs instantaneously throughout the body (Boley & Tolins, 1962). The wave propagation in the two-temperature theory of thermoelasticity was investigated by Warren and Chen (1973). Youssef (2011), constructed a new theory of generalized thermoelasticity by taking into account two-temperature generalized thermoelasticity theory for a homogeneous and isotropic body without energy dissipation. Several researchers studied various problems involving dual-phase-lags (e.g. Abbas 2015a, 2015b, 2015c; Abbas, Kumar, & Reen, 2014; Abbas & Zenkour, 2013, 2014, 2015; Atwa & Jahangir, 2014; Ezzat & Awad, 2010; Kaushal, Kumar, & Miglani, 2011; Kaushal, Sharma, & Kumar, 2010; Kumar & Mukhopadhaya, 2010a, 2010b; Kumar, Sharma, & Garg, 2014; Sharma & Marin, 2013; Youssef, 2006).

In this investigation, the thermoelastic interactions for the dual-phase-lag heat conduction in a thick circular plate are studied in the light of two-temperature thermoelasticity theory. The components of displacements, stresses, conductive temperature, temperature change and cubic dilatation are computed numerically. Numerically computed results are depicted graphically. The effect of dual-phase-lag and two-temperature are shown on the various components.

2. Basic equations

The basic equations of motion, heat conduction in a homogeneous isotropic thermoelastic solid with dual-phase-lag and two-temperature in the absence of body forces, heat sources are:(1) $$\left(\mathit{\lambda }+\mathit{\mu }\right)\mathrm{\nabla }\left(\mathrm{\nabla }·u\right)+\mathit{\mu }{\mathrm{\nabla }}^{2}u-{\mathit{\beta }}_1\mathrm{\nabla }=\mathit{\rho }\ddot{u}$$(1) (2) $$\left(1+{\mathit{\tau }}_t\frac{\mathit{\partial }}{\mathit{\partial }t}\right)K{T}_{,ii}=\left(1+{\mathit{\tau }}_q\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\tau }}_q^2\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right)[\mathit{\rho }{C}_E\dot{T}+{\mathit{\beta }}_1{T}_0{\dot{e}}_{kk}]$$(2)

$$T=(1-a{\mathrm{\nabla }}^2)\mathit{\phi }$$

and the constitutive relations are:(3) $${\mathit{\sigma }}_{ij}=2\mathit{\mu }{e}_{ij}+{\mathit{\delta }}_{ij}(\mathit{\lambda }{e}_{kk}-{\mathit{\beta }}_{1}T)$$(3) (4) $$\mathit{\rho }{T}_{0}S=\left(1+{\mathit{\tau }}_q\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\tau }}_q^2\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right)(\mathit{\rho }{C}_{E}T+{\mathit{\beta }}_1{T}_0{e}_{kk})$$(4)

where $\mathit{\lambda }$, $\mathit{\mu }$ are Lame’s constants, ρ is the density assumed to be independent of time, $u_i$ are components of displacement vector u, K is the coefficient of thermal conductivity, C_E is the specific heat at constant strain, T is the absolute temperature of the medium, ${\mathit{\sigma }}_{ij}$ and e_ij are the components of stress and strain respectively, e_kk is dilatation, S is the entropy per unit mass, β₁ = $(3\mathit{\lambda }+2\mathit{\mu }){\mathit{\alpha }}_t$, α_t is the coefficient of thermal linear expansion. τ_t, τ_q are, respectively, phase-lag of temperature gradient, the phase-lag of heat flux, a is the two-temperature parameter. In the above equations, a comma followed by suffix denotes spatial derivative and a superposed dot denotes derivative with respect to time.

3. Formulation and solution of the problem

Consider a thick circular plate of thickness 2b occupying the space D defined by 0 ≤ r ≤ ∞, − b ≤ z ≤ b. Let the plate be subjected to an axisymmetric heat supply depending on the radial and axial directions of the cylindrical coordinate system. The initial temperature in the thick plate is given by a constant temperature T₀, and the heat flux g₀F(r, z) is prescribed on the upper and lower boundary surfaces. Under these conditions, the thermoelastic quantities in a thick circular plate are required to be determined. We take a cylindrical polar coordinate system $\left(r,\mathit{\theta },z\right)$ with symmetry about z-axis. As the problem considered is plane axisymmetric, the field component $u_{\mathit{\theta }}=0$, and $u_r,u_z,T$ and C are independent of θ and restrict our analysis to the two dimensional problem with (5) $$\mathit{u}=(u_r,0,u_z)$$(5)

Equations (1) and (2) with the aid of (5) take the form:

(6) $$\left(\mathit{\lambda }+\mathit{\mu }\right)\frac{\mathit{\partial }e}{\mathit{\partial }r}+\mathit{\mu }\left({\mathrm{\nabla }}^2-\frac{1}{r^2}\right)u_r-{\mathit{\beta }}_1\frac{\mathit{\partial }T}{\mathit{\partial }r}=\mathit{\rho }\frac{{\mathit{\partial }}^2{u}_r}{\mathit{\partial }{t}^2}$$(6) (7) $$\left(\mathit{\lambda }+\mathit{\mu }\right)\frac{\mathit{\partial }e}{\mathit{\partial }z}+\mathit{\mu }{\mathrm{\nabla }}^2{u}_z-{\mathit{\beta }}_1\frac{\mathit{\partial }T}{\mathit{\partial }z}=\mathit{\rho }\frac{{\mathit{\partial }}^2{u}_z}{\mathit{\partial }{t}^2}$$(7) (8) $$\left(1+{\mathit{\tau }}_t\frac{\mathit{\partial }}{\mathit{\partial }t}\right)K{\mathrm{\nabla }}^{2}T=\left(1+{\mathit{\tau }}_q\frac{\mathit{\partial }}{\mathit{\partial }t}+\frac{{\mathit{\tau }}_q^2}{2}\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right)[\mathit{\rho }{C}_E\frac{\mathit{\partial }}{\mathit{\partial }t}(1-a{\mathrm{\nabla }}^2)\mathit{\phi }+{\mathit{\beta }}_1{T}_0\frac{\mathit{\partial }}{\mathit{\partial }t}\text{div}u]$$(8)

and constitutive relations(9) $${\mathit{\sigma }}_{rr}=2\mathit{\mu }{e}_{rr}+\mathit{\lambda }e-{\mathit{\beta }}_1(1-a{\mathrm{\nabla }}^2)\mathit{\phi }$$(9) (10) $${\mathit{\sigma }}_{\mathit{\theta }\mathit{\theta }}=2\mathit{\mu }{e}_{\mathit{\theta }\mathit{\theta }}+\mathit{\lambda }e-{\mathit{\beta }}_1(1-a{\mathrm{\nabla }}^2)\mathit{\phi }$$(10) (11) $${\mathit{\sigma }}_{zz}=2\mathit{\mu }{e}_{zz}+\mathit{\lambda }e-{\mathit{\beta }}_1\left(1-a{\mathrm{\nabla }}^2\right)\mathit{\phi }$$(11)

(12) $${\mathit{\sigma }}_{rz}=\mathit{\mu }{e}_{rz},{\mathit{\sigma }}_{r\mathit{\theta }}=0,{\mathit{\sigma }}_{z\mathit{\theta }}=0$$(12)

where $e=\frac{\mathit{\partial }{u}_r}{\mathit{\partial }r}+\frac{u_r}{r}+\frac{\mathit{\partial }{u}_z}{\mathit{\partial }z}$, $e_{rr}=\frac{\mathit{\partial }{u}_r}{\mathit{\partial }r}$, $e_{\mathit{\theta }\mathit{\theta }}=\frac{u_r}{r}$, $e_{zz}=\frac{\mathit{\partial }{u}_z}{\mathit{\partial }z}$, $e_{rz}=\frac{1}{2}\left(\frac{\mathit{\partial }{u}_r}{\mathit{\partial }z}+\frac{\mathit{\partial }{u}_z}{\mathit{\partial }r}\right)$

To facilitate the solution, the following dimensionless quantities are introduced:(13) $$\begin{array}{c}\hfill r^{\prime }=\frac{{\mathit{\omega }}_1}{c_1}r,z^{\prime }=\frac{{\mathit{\omega }}_1}{c_1}z,(u_r^{\prime },u_z^{\prime })=\frac{{\mathit{\omega }}_1}{c_1}(u_r,u_z),t^{\prime }={\mathit{\omega }}_{1}t,{\mathit{\omega }}_1=\frac{\mathit{\rho }{C}_E{c}_1^2}{K},c_1^2=\frac{\mathit{\lambda }+2\mathit{\mu }}{\mathit{\rho }}\left({\mathit{\sigma }}_{rr}^{\prime },{\mathit{\sigma }}_{\mathit{\theta }\mathit{\theta }}^{\prime },{\mathit{\sigma }}_{zz}^{\prime },{\mathit{\sigma }}_{rz}^{\prime }\right)=\frac{1}{{\mathit{\beta }}_1{T}_0}({\mathit{\sigma }}_{rr},{\mathit{\sigma }}_{\mathit{\theta }\mathit{\theta }},{\mathit{\sigma }}_{zz},{\mathit{\sigma }}_{rz}),(T^{\prime },{\mathit{\phi }}^{\prime })=\frac{{\mathit{\beta }}_1}{\mathit{\rho }{c}_1^2}(T,\mathit{\phi })({\mathit{\tau }}_q^1,{\mathit{\tau }}_t^1)={\mathit{\omega }}_1({\mathit{\tau }}_q,{\mathit{\tau }}_t)\end{array}$$(13)

in Equations (6)–(8) and after that suppressing the primes and then applying the Laplace transform defined by (14):

(14) $$\overline{f}\left(r,z,s\right)={\int }_0^{\infty }f(r,z,t)e^{-st}dt$$(14)

(15) $${\overline{f}}^{\ast }\left(\mathit{\xi },z,s\right)={\int }_0^{\infty }f\left(r,z,s\right)r{J}_n\left(r\mathit{\xi }\right)dr$$(15)

On the resulting quantities and simplifying we obtain(16) $$\left({\mathrm{\nabla }}^2-s^2\right)\overline{e}-{\mathrm{\nabla }}^2\overline{\mathit{\phi }}+{\mathit{\delta }}_1{\mathrm{\nabla }}^4\overline{\mathit{\phi }}=0$$(16) (17) $${\mathit{\tau }}_q^1{\mathit{\zeta }}_2\overline{e}+{\mathit{\tau }}_q^1{\mathit{\zeta }}_1\overline{\mathit{\phi }}-({\mathit{\tau }}_q^1{\mathit{\delta }}_1-{\mathit{\tau }}_t^{1}K){\mathrm{\nabla }}^2\overline{\mathit{\phi }}=0$$(17)

where ${\mathit{\tau }}_q^1=1+s{\mathit{\tau }}_q+\frac{s^2{\mathit{\tau }}_q^2}{2}$, ${\mathit{\tau }}_t^1=1+s{\mathit{\tau }}_t$, ${\mathit{\zeta }}_1=\frac{\mathit{\rho }{C}_E{c}_1^2}{{\mathit{\omega }}_1}$, ${\mathit{\zeta }}_2=\frac{{\mathit{\beta }}_1^2{T}_0}{\mathit{\rho }{\mathit{\omega }}_1}s$, ${\mathit{\delta }}_1=\frac{a{\mathit{\omega }}_1^2}{c_1^2}$

Eliminating $\overline{\mathit{\phi }}\text{and}\overline{e}$ from Equations (16) and (17), we obtain:(18) $$({\mathrm{\nabla }}^2-k_1^2)({\mathrm{\nabla }}^2-k_2^2)(\overline{e},\overline{\mathit{\phi }})=0$$(18)

The solutions of Equation (18) can be written in the form:

$\overline{\mathit{\phi }}={\sum }_{i=1}^3{\overline{\mathit{\phi }}}_i$, $\overline{e}={\sum }_{i=1}^3{\overline{e}}_i$ where, ${\overline{e}}_i$, and ${\overline{\mathit{\phi }}}_i$ are solutions of the following equation:(19) $$({\mathrm{\nabla }}^2-k_i^2)({\overline{e}}_i,{\overline{\mathit{\phi }}}_i)=0,i=1,2$$(19)

On taking Hankel transform of (19) defined by (15), we obtain:

(20) $$\left(D^2-{\mathit{\xi }}^2-k_i^2\right)\left({\overline{\mathit{\phi }}}_i^{*},{\overline{e}}_i^{*}\right)=0$$(20)

The solution of (20) has the form(21) $${\overline{e}}^{*}=\sum _{i=1}^2{A}_i\left(\mathit{\xi },s\right)cosh(q_{i}z)$$(21)

(22) $${\overline{\mathit{\phi }}}^{*}=\sum _{i=1}^2{d}_i{A}_i\left(\mathit{\xi },s\right)cosh(q_{i}z)$$(22)

where $q_i=\sqrt{{\mathit{\xi }}^2+k_i^2}$, $d_i=\frac{{\mathit{\tau }}_q^1{\mathit{\zeta }}_2}{{\mathit{\tau }}_q^1{\mathit{\zeta }}_1-{\mathit{\zeta }}_3{q}_i^2}$, ${\mathit{\zeta }}_3={\mathit{\tau }}_q^1{\mathit{\delta }}_1-{\mathit{\tau }}_t^{1}k$

Applying inversion of Hankel transform on (23), and (24), we get:(23) $$\overline{e}={\int }_0^{\infty }\left\{\sum _{i=1}^2{A}_i\left(\mathit{\xi },s\right)cosh\left(q_{i}z\right)\right\}\mathit{\xi }{J}_0(\mathit{\xi }r)d\mathit{\xi }$$(23) (24) $$\overline{\mathit{\phi }}={\int }_0^{\infty }\left\{\sum _{i=1}^2{d}_i{A}_i\left(\mathit{\xi },s\right)cosh\left(q_{i}z\right)\right\}\mathit{\xi }{J}_0(\mathit{\xi }r)d\mathit{\xi }$$(24)

Using (6)–(8), (13) and (23), (24), we obtain the displacement components in the transformed domain as:(25) $${\overline{u}}_r\left(r,z,s\right)=\underset{0}{\overset{\infty }{\int }}E\left(\mathit{\xi },s\right)cosh\left(qz\right)\mathit{\xi }{J}_0\left(\mathit{\xi }r\right)+\sum _{i=1}^2[(-{\mathit{\eta }}_i+{\mathit{\mu }}_i)q_i^2{\mathit{\xi }}^{2}cosh\left(q_{i}z\right)]J_1\left(\mathit{\xi }r\right)+{\mathit{\delta }}_1{\mathit{\mu }}_{i}cosh\left(q_{i}z\right)\left(\frac{{\mathit{\xi }}^3}{r}{J}_2-J_1\left({\mathit{\xi }}^4-\frac{{\mathit{\xi }}^2}{r^2}+{\mathit{\xi }}^2{q}_i^2\right)+\frac{{\mathit{\xi }}^3}{r}{J}_0\right)]d\mathit{\xi }$$(25) (26) $${\overline{u}}_z\left(r,z,s\right)={\int }_0^{\infty }G\left(\mathit{\xi },z\right)sinh\left(qz\right)\mathit{\xi }{J}_0\left(\mathit{\xi }r\right)+\sum _{i=1}^2[(-{\mathit{\eta }}_i+{\mathit{\mu }}_i)sinh\left(q_{i}z\right)\mathit{\xi }{J}_0\left(\mathit{\xi }r\right)-{\mathit{\delta }}_1{\mathit{\mu }}_{i}sinh\left(q_{i}z\right)\left(\frac{{\mathit{\xi }}^2}{r}{J}_2-J_1\left({\mathit{\xi }}^3+\frac{\mathit{\xi }}{r})+\mathit{\xi }{q}_i^2{J}_0\right)\right]$$(26)

where

$$G\left(\mathit{\xi },s\right)=\frac{{\mathit{\xi }}^{2}E(\mathit{\xi },s)}{q},q=\sqrt{{\mathit{\xi }}^2+\frac{\mathit{\rho }{c}_1^2}{\mathit{\mu }}{s}^2},{\mathit{\eta }}_i=\frac{\frac{\mathit{\lambda }+\mathit{\mu }}{\mathit{\rho }{c}_1^2}{A}_i}{\left(\frac{\mathit{\mu }{q}_i^2}{\mathit{\rho }{c}_1^2}-s^2\right)},{\mathit{\mu }}_i=\frac{d_i{A}_i}{\left(\frac{\mathit{\mu }{q}_i^2}{\mathit{\rho }{c}_1^2}-s^2\right)},{\mathit{\lambda }}^0=\frac{\mathit{\lambda }}{{\mathit{\beta }}_1{T}_0},\mathit{\zeta }=\frac{\mathit{\rho }{c}_1^2}{{\mathit{\beta }}_1{T}_0}$$

Using (6)–(8), (13), (23)–(26) we obtain the stress components and conductive temperature, temperature change T, cubic dilatation in the Laplace transform domain as:

(27) $$\overline{{\mathit{\sigma }}_{zz}}=\frac{2\mathit{\mu }}{{\mathit{\beta }}_1{T}_0}{\int }_0^{\infty }\mathit{\xi }{J}_0\left(\mathit{\xi }r\right)\left[G\left(\mathit{\xi },s\right)qcosh\left(qz\right)+(\sum _{i=1}^2\left(-{\mathit{\eta }}_i+{\mathit{\mu }}_i\right)q_i^2-\mathit{\zeta }{d}_i{A}_i+{{\mathit{\lambda }}^{0}A}_i)cosh\left(q_{i}z\right)\right]-[{\mathit{\delta }}_1\left({\mathit{\mu }}_i{q}_i-\mathit{\zeta }{B}_i\right)cosh\left(q_{i}z\right)({\mathit{\xi }}^3{J}_0\left(\mathit{\xi }r\right)-J_1\left(\mathit{\xi }r\right)\left(\frac{\mathit{\xi }-1}{r}\right)+\mathit{\xi }{q}_i^2{J}_0\left(\mathit{\xi }r\right)]d\mathit{\xi }$$(27) (28) $$\overline{{\mathit{\sigma }}_{rz}}=\frac{\mathit{\mu }}{2{\mathit{\beta }}_1{T}_0}\underset{0}{\overset{\infty }{\int }}{\mathit{\xi }}^2{J}_1\left(\mathit{\xi }r\right)\left[\{\left(\frac{q^2-{\mathit{\xi }}^2}{q}\right)E\left(\mathit{\xi },s\right)qsinh\left(qz\right)+2\sum _{i=1}^2\left({\mathit{\eta }}_i-{\mathit{\mu }}_i\right)q_{i}sinh\left(q_{i}z\right)\}+{\mathit{\delta }}_1{\mathit{\mu }}_{i}sinh\left(q_{i}z\right)\{(q_i(\frac{{\mathit{\xi }}^3}{r}{J}_2\left(\mathit{\xi }r\right))-J_1\left(\mathit{\xi }r\right)\left({\mathit{\xi }}^4+q_i^2{\mathit{\xi }}^2+\frac{4}{{\mathit{\xi }}^2{r}^2}+q_i^2\mathit{\xi }\right)+\left(\frac{2}{\mathit{\xi }r}-{\mathit{\xi }}^4-\frac{{\mathit{\xi }}^2\left(\mathit{\xi }-1\right)}{r}+q_i^2{\mathit{\xi }}^2\right)J_0\left(\mathit{\xi }r\right)\}\right]d\mathit{\xi }$$(28)

$$\overline{{\mathit{\sigma }}_{rr}}=\frac{2\mathit{\mu }}{{\mathit{\beta }}_1{T}_0}\underset{0}{\overset{\infty }{\int }}\left[-{\mathit{\xi }}^2{J}_1\left(\mathit{\xi }r\right)E\left(\mathit{\xi },s\right)cosh\left(qz\right)+(\sum _{i=1}^2\left(-{\mathit{\eta }}_i+{\mathit{\mu }}_i\right)q_i^2({\mathit{\xi }}^2{J}_1\left(\mathit{\xi }r\right)-{\mathit{\xi }}^3{J}_0\left(\mathit{\xi }r\right))+{\mathit{\delta }}_1{\mathit{\mu }}_i\{J_1\left(\mathit{\xi }r\right)(-{\mathit{\xi }}^2\left(q_i^2+{\mathit{\xi }}^2-3\right)+J_0\left(\mathit{\xi }r\right){\mathit{\xi }}^3\left(q_i^2+\frac{1}{r^2}+{\mathit{\xi }}^2\right)d\mathit{\xi }\right]+{\int }_0^{\infty }\mathit{\xi }{J}_0\left(\mathit{\xi }r\right)cosh\left(q_{i}z\right)[{\mathit{\lambda }}^{\prime }-\mathit{\zeta }{d}_i\left(1+{\mathit{\delta }}_1{q}_i^2-{\mathit{\delta }}_1\mathit{\xi }{J}_0\left(\mathit{\xi }r\right)\right)+{\mathit{\delta }}_1{J}_1\left(\mathit{\xi }r\right)\left(1-\frac{1}{r}\right)d\mathit{\xi }$$

(29) $$\overline{\mathit{\phi }}={\int }_0^{\infty }(d_1{A}_1\left(\mathit{\xi },s\right)cosh\left(q_{1}z\right)+d_2{A}_2\left(\mathit{\xi },s\right)cosh\left(q_{2}z\right))\mathit{\xi }{J}_0(\mathit{\xi }r)d\mathit{\xi }$$(29)

(30) $$\overline{T}={\int }_0^{\infty }\sum _{i=1}^2(d_i{A}_i\left(\mathit{\xi },s\right)cosh\left(q_{i}z\right)[\mathit{\xi }{J}_0\left(\mathit{\xi }r\right)\left(1+{\mathit{\delta }}_1{q}_i^2-{\mathit{\delta }}_1\mathit{\xi }\right)+J_1\left(\mathit{\xi }r\right){\mathit{\delta }}_1\mathit{\xi }\left(1-\frac{1}{r}\right)]d\mathit{\xi }$$(30)

4. Boundary conditions

We consider a cubical thermal source and normal force of unit magnitude along with vanishing of tangential stress components at the stress-free surface at $z=\pm b$. Mathematically, these can be written as:(31) $$\frac{\mathit{\partial }\mathit{\phi }}{\mathit{\partial }z}=\pm g_{0}F\left(r,z\right)$$(31) (32) $${\mathit{\sigma }}_{zz}=\mathit{\delta }\left(t\right)H\left(a-r\right)$$(32) (33) $${\mathit{\sigma }}_{rz}=0$$(33)

where

F(r, z) = z² e^−ωr, δ(t) is the Dirac delta function and H(a−r) is Heaviside function.

Applying Laplace transform and Hankel transform on both sides of the boundary conditions (31)–(33),

where $F^{\ast }\left(\mathit{\xi },z\right)=\frac{z^2\mathit{\omega }}{{({\mathit{\xi }}^2+{\mathit{\omega }}^2)}^{3/2}}$.

we obtain the values of unknown parameters as $$A_1=\frac{{\mathrm{\Delta }}_1}{\mathrm{\Delta }},A_2=\frac{{\mathrm{\Delta }}_2}{\mathrm{\Delta }},E(\mathit{\zeta },s)=\frac{{\mathrm{\Delta }}_3}{\mathrm{\Delta }}\text{where}$$$$\mathrm{\Delta }=-\frac{2\mathit{\mu }}{{\mathit{\beta }}_1{T}_0}cosh\left(qb\right)\left({\mathrm{\Delta }}_{11}{\mathrm{\Delta }}_{32}-{\mathrm{\Delta }}_{12}{\mathrm{\Delta }}_{31}\right)+sinh\left(qb\right)({\mathrm{\Delta }}_{11}{\mathrm{\Delta }}_{22}-{\mathrm{\Delta }}_{12}{\mathrm{\Delta }}_{21})$$

$${\mathrm{\Delta }}_1=g_0{\overline{F}}^{\ast }\left(\mathit{\xi },b\right)\left({\mathrm{\Delta }}_{21}{\mathrm{\Delta }}_{32}-{\mathrm{\Delta }}_{22}{\mathrm{\Delta }}_{31}\right)-\frac{a{J}_1\left(\mathit{\xi }a\right)}{\mathit{\xi }}\left({\mathrm{\Delta }}_{11}{\mathrm{\Delta }}_{32}-{\mathrm{\Delta }}_{12}{\mathrm{\Delta }}_{31}\right)$$

$${\mathrm{\Delta }}_2=-g_0{\overline{F}}^{\ast }\left(\mathit{\xi },b\right)\left(\frac{2\mathit{\mu }}{{\mathit{\beta }}_1{T}_0}cosh(qb){\mathrm{\Delta }}_{32}{-}_{D}elta22sinh(qb)\right)+\frac{a{J}_1\left(\mathit{\xi }a\right)}{\mathit{\xi }}\left(-{\mathrm{\Delta }}_{12}sinh(qb)\right)$$$${\mathrm{\Delta }}_3=g_0{\overline{F}}^{\ast }\left(\mathit{\xi },b\right)\left(\frac{2\mathit{\mu }}{{\mathit{\beta }}_1{T}_0}cosh(qb){\mathrm{\Delta }}_{31}-{\mathrm{\Delta }}_{21}sinh(qb)\right)+\frac{a{J}_1\left(\mathit{\xi }a\right)}{\mathit{\xi }}\left({\mathrm{\Delta }}_{11}sinh(qb)\right)$$

$${\mathrm{\Delta }}_{1i}=d_i{q}_{i}sinh(q_{i}b),{\mathrm{\Delta }}_{2i}=(({\mathit{\mu }}_i-{\mathit{\eta }}_i)q_i^2-{\mathit{\delta }}_1{\mathit{\mu }}_i{q}_i-\mathit{\zeta }{d}_i(1+{\mathit{\delta }}_1)+{\mathit{\lambda }}^{\ast })cosh(q_{i}b),{\mathrm{\Delta }}_{3i}=(2({\mathit{\eta }}_i-{\mathit{\mu }}_i)q_i+{\mathit{\delta }}_1{\mathit{\mu }}_i)sinh(q_{i}b)i=1,2$$

5. Inversion of double transform

Due to the complexity of the solution in the Laplace transform domain, the inverse of the Laplace transform is obtained by using the Gaver–Stehfest algorithm. Graver (1996) and Stehfest (1970a, 1970b) derived the formula given below. By this method, the inverse f(t) of Laplace transform $\overline{f}(s)$ is approximated by$$f\left(t\right)=\frac{log2}{t}\sum _{j=1}^{k}D\left(j,K\right)F\left(j\frac{log2}{t}\right)$$

with

$$D\left(j,K\right)={(-1)}^{j+M}\sum _{n=m}^{\text{min}(j,M)}\frac{n^M(2n)!}{\left(M-n\right)!n!\left(n-1\right)!\left(j-n\right)!(2n-j)!}$$

where K is an even integer, whose value depends on the word length of computer used. M = K/2, and m is an integer part of (j + 1)/2. The optimal value of K was chosen as described in Gaver–Stehfest algorithm, for the fast convergence of results with desired accuracy. The Romberg numerical integration technique (Press, Flannery, Teukolsky, & Vatterling, 1986) with variable step size was used to evaluate the results involved.

6. Particular cases

(1)	If a = 0, from Equations (25)–(30), we obtain the corresponding expressions for displacements, and stresses, conductive temperature, temperature change and cubic dilatation for thermoelastic solid without two-temperature and due to dual-phase-lag.
(2)	If τq = τt = 0, we obtain the coupled expression in thermoelasticity with two-temperature model.
(3)	τq = 0 then dual-phase-lag thermal model(DPLT) model reduce to single-phase-lag thermal model (SPLT).

7. Numerical results and discussion

The graphs have been plotted to study the effect of phase-lags and two-temperatures on the various quantities in the range 0 ≤ r ≤ 10.

The mathematical model is prepared with copper material for the purpose of numerical computation. The material constants for the problem are taken from Dhaliwal and Singh (1980).$$\mathit{\lambda }=7.76\times {10}^{10}\text{N}{\text{m}}^{-2},\mathit{\mu }=3.86\times {10}^{10}\text{N}{\text{m}}^{-2},K=386\text{J}{\text{K}}^{-1}{\text{m}}^{-1}{\text{s}}^{-1},{\mathit{\beta }}_1=5.518\times {10}^6\text{N}{\text{m}}^{-2}{\text{deg}}^{-1},\mathit{\rho }=8,954\text{kg}{\text{m}}^{-3},a=1.2\times {10}^4{\text{m}}^2/{\text{s}}^2\text{k},b=0.9\times {10}^6{\text{m}}^5/\text{kg}{\text{s}}^2,D=0.88\times {10}^{-8}\text{kg}\text{s}/{\text{m}}^3,{\mathit{\beta }}_2=61.38\times {10}^6\text{N}{\text{m}}^{-2},T_0=293\text{K},C_E=383.1\text{J}{\text{kg}}^{-1}{K}^{-1}$$

(1)	In the figures solid line corresponds to the dual-phase-lag of heat transfer with two-temperature with τq > τt, a = .07 (τq = 1.2, τt = .06)
(2)	In the figures small dashed line corresponds to the dual-phase-lag of heat transfer with two-temperature with τq < τt, a = .07 (τt = 1.2, τq = .06)
(3)	Solid line with centre symbol circle corresponds to τq > τt, a = 0
(4)	Small dashed line with centre symbol diamond corresponds to τq < τt, a = 0

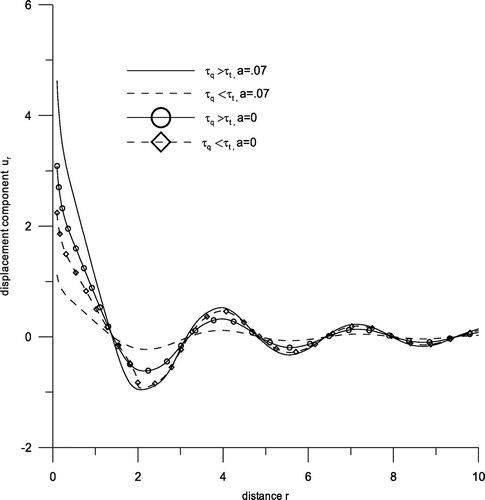
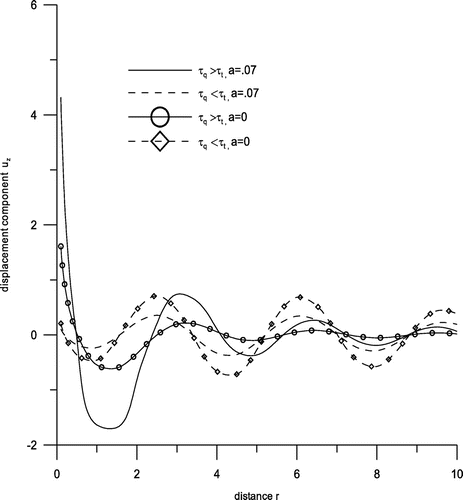
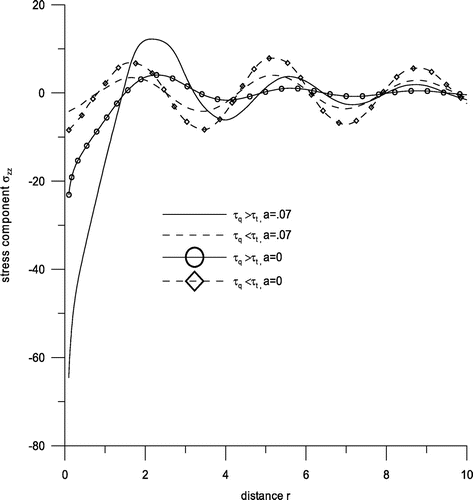
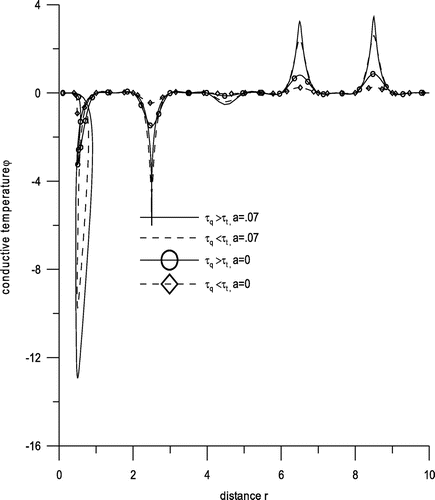
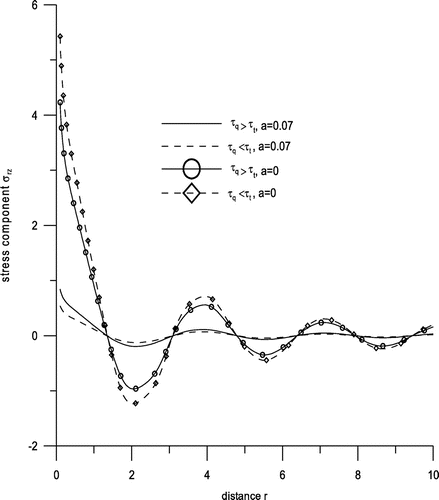
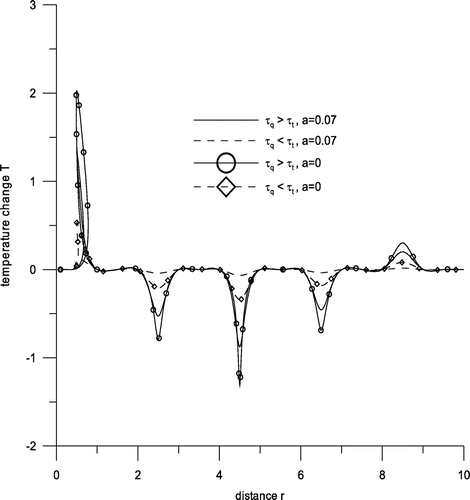
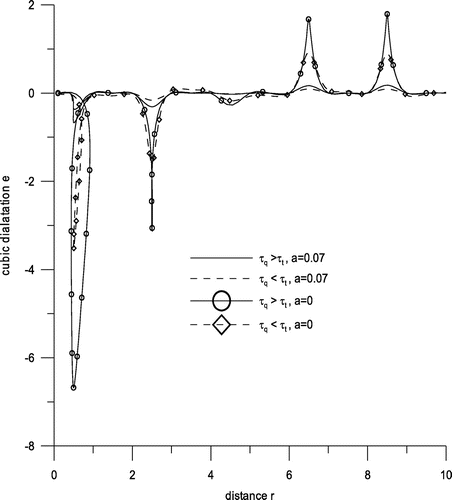
Figure 1 exhibits variations of displacement component u_r with distance r. Near the loading surface, there is a sharp decrease for the range 0 ≤ r ≤ 2 and behaviour is oscillatory in the rest for all the cases with amplitudes of oscillations decreasing as r increases. Figure 2 shows variations of displacement component u_z with distance r. Here behaviour is oscillatory for the whole range except for 0 ≤ r ≤ 1.5, as for this range, a sharp decrease is noticed. Figure 3 shows variation of stress component σ_zz with distance r. We find that there is a sharp increase for the range 0 ≤ r ≤ 3 corresponding to all the cases and similar oscillatory trend is observed afterwards. Small variations near boundary surface are observed corresponding to the case τ_q > τ_t, a = 0 for the range 3 ≤ r ≤ 10. Figure 4 gives variation of conductive temperature φ with distance r. Here, we notice that either there are sudden increases and decreases or there are small variations. Here descents are noticed at the points r = .5 and r = 2.5, whereas hikes are seen at the points r = 6.5 and r = 9. With two temperatures, there are hikes and descents while without two temperature there are small variations. Figure 5 gives variations of stress component σ_rz with distance r. It is evident from this figure that the behaviour is descending oscillatory corresponding to the case τ_q > τ_t, a = 0 and τ_q < τ_t, a = 0, i.e. without two temperatures, whereas small variations are observed corresponding to the rest. Figure 6 exhibits variations of temperature change T with displacement r. Here, there is a hike at the point r = 1 and descents at the points r = 2.5, r = 4.5, r = 6.5 and a small hike is noticed at r = 9 and small variations are observed for the remaining range except for the small neighbourhoods of these points. Maximum hikes and descents are noticed corresponding to case 3. Figure 7 shows variations of cubic dilatation e with distance r. Here we notice that corresponding to the cases 3 and 4 there are hikes and descents, whereas corresponding to cases 1 and 2 there are small variations. Figure 8 displays variations in stress component σ_rr with displacement r. Here opposite trends are noticed corresponding to the cases of without two temperature and with two temperature. As it is evident that without two temperature there is a descent at the point .5, whereas there is a hike at the same point corresponding to case of two temperature. While comparing the effect of phase lags, the trends are similar corresponding to both the cases.

Figure 1. Variation of displacement component u_r with distance r.

Figure 2. Variation of displacement component $u_z$ with distance r.

Figure 3. Variation of vertical stress component ${\mathit{\sigma }}_{zz}$ with distance r.

Figure 4. Variation of conductive temperature $\mathit{\phi }$ with distance r.

Figure 5. Variations of shear stress component ${\mathit{\sigma }}_{rz}$ with displacement r.

Figure 6. Variations of temperature change T with displacement r.

Figure 7. Variations of cubic dilatation e with displacement r.

Figure 8. Variations of radial stress component ${\mathit{\sigma }}_{rr}$ with displacement r.

8. Conclusion

From the graphs, it is evident that there is a significant impact on the deformation of various components of stresses, components of displacement, conductive temperature, temperature change and cubic dilatation in the thick circular plate while comparing the effect of thermal phase-lags and two temperatures. Amplitude of oscillation is slightly greater in case of τ_q > τ_t, a = .07 as compared with the case τ_q < τ_t, a = .07. More variations are observed in the case of without two-temperature than with two-temperature. As disturbance travels through the constituents of the medium, it suffers sudden changes resulting in an inconsistent/non uniform pattern of graphs in case of conductive temperature, temperature change, cubic dilatation. The use of thermal phase-lags in the heat conduction equation gives a more realistic model of thermoelastic media as it allows a delayed response to the relative heat flux vector. The result of the problem is useful in the two-dimensional problem of dynamic response due to various thermal and mechanical sources which has various geophysical and industrial applications.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Parveen Lata

The corresponding author Parveen Lata is an assistant professor in Mathematics, Department of Basic and Applied Sciences, Punjabi University Patiala and is pursuing the research work with collaboration of Rajneesh Kumar and Nidhi Sharma. The primary field of research is thermoelasticity and further extended to the various theories of thermoelasticity which is the most demanding area due to its wide applications in the field of aeronautics, aircrafts, geomechanics and various other fields.