Different types of Bernstein operators in inference of Gaussian graphical model

Abstract

The Gaussian graphical model (GGM) is a powerful tool to describe the relationship between the nodes via the inverse of the covariance matrix in a complex biological system. But the inference of this matrix is problematic because of its high dimension and sparsity. From previous analyses, it has been shown that the Bernstein and Szasz polynomials can improve the accuracy of the estimate if they are used in advance of the inference as a processing step of the data. Hereby in this study, we consider whether any type of the Bernstein operators such as the Bleiman Butzer Hahn, Meyer-König, and Zeller operators can be performed for the improvement of the accuracy or only the Bernstein and the Szasz polynomials can satisfy this condition. From the findings of the Monte Carlo runs, we detect that the highest accuracies in GGM can be obtained under the Bernstein and Szasz polynomials, rather than all other types of the Bernstein polynomials, from small to high-dimensional biological networks.

Keywords:

• Gaussian graphical model
• Bernstein operators
• Bleiman Butzer Hahn operators
• Meyer-König and Zeller operators
• systems biology
• bioinformatics
• statistics

Public Interest Statement

The Gaussian graphical model (GGM) is one of the well-known probabilistic modeling approaches for the complex biological systems. Briefly, this model expresses the biological interactions between components of systems, which are genes or proteins, by using the property of the conditional dependency under multivariate normally distributed data. On the other hand, the Bernstein Polynomials are one of the famous Bernstein-type of operators in the approximation theory to smoothen the data via statistical distributions within the range of [0, 1]. From previous studies, it has been shown that these polynomials are successful in getting high accuracy in inference of interactions between genes in the system when they are used as the processing step in advance of GGM. In this study, we consider all Bernstein-type of operators, as the alternatives of the Bernstein polynomials, for the pre-processing step of GGM to discard the bath effects in the original observations.

1. Introduction

The approximation theory is concerned with the study of how well given functions can be proximated by basic functions. In this theory, it is usual to apply the approximating functions in the form of linear positive operators, such as the Bernstein, Szasz–Mirakyan polynomials, the Bleiman Butzer Hahn (BBH) operator, Meyer-König and Zeller (MKZ) operator. From previous works, it is known that the Bernstein and Szasz polynomials can significantly improve the accuracy of estimates from the point of view of their inference via the Gaussian graphical model (GGM) (Purutçuoğlu & Wit, 2015). Therefore, here we investigate whether the strong alternatives of the Bernstein polynomials, i.e. the Bleiman and Hahn operator and the Meyer-König and Zeller operator, are as successful as the Bernstein polynomials and can be used alternately.

The Gaussian graphical model is a probabilistic and undirected statistical model for the complex biological networks under the normally distributed random multivariate variables whose dependency structure is represented by a graph (Dempster, 1972). In Figure 1, we represent the structure of the filtered yeast interactome (FYI) network (Han et al., 2004) as an example of realistically complex biological systems that GGM can handle with. Hereby, in GGM, we assume that the observations follow a multivariate normal distribution with a mean vector $\mathit{\mu }$ and the variance–covariance matrix $\mathrm{\Sigma }$, and the conditional independent structure of the observations can be described via a set of nodes and edges constructing an undirected network by means of the inverse of the covariance matrix, also called the precision $\mathrm{\Theta }={\mathrm{\Sigma }}^{-1}$. In $\mathrm{\Theta }$, the non-zero entries indicate the interactions between nodes, i.e. genes, and zero entries imply no interaction between the selected pair of nodes.

Figure 1. The main component of the FYI network (Han et al., 2004).

On the other hand, the Bernstein operators which cover the Bernstein and Szasz polynomials are the approximations that are based on the binomial and the Poisson distribution, respectively. But in the literature, different Bernstein-type operators are presented as well. Specifically, the Bleiman–Butzer Hahn (BBH) and the Meyer-König and Zeller (MKZ) operators which are derived from the Bernstein operators are the most well-known ones. The theoretical properties of the BBH operator (Agratini, 1996) and MKZ operator (Abel, 1995; Becker, 1977) have been studied extensively.

In biological networks, the Bernstein polynomials enable us to transform the data in a new range (Lorentz, 1953; Bernstein, 1912). Accordingly, in this study, we consider to implement the Bernstein polynomials, the BBH operator and the MKZ operator in different dimensional biological systems before estimating the model parameters of GGM.

Accordingly, in the organization of this paper, we introduce GGM and different types of operators in Section 2. In Section 3, we report our outputs based on the Monte Carlo studies. Finally, in Section 4, we summarize our results and discuss our future works.

2. Methods

2.1. Gaussian graphical model

The biological system is an expression between components of the complex biological networks and the interactions between components in this system can be probabilistically represented by the Gaussian graphical model. In this modeling approach, the nodes are indicated as $X=(X_1,\dots ,X_p)$ under the assumption that the state vector X has a multivariate Gaussian (normal) distribution via(1) $$\begin{array}{c}\hfill X\sim N(\mathit{\mu },\mathrm{\Sigma })\end{array}$$(1)

in which $\mathit{\mu }$ is a p-dimensional mean vector and $\mathrm{\Sigma }$ shows the $(p\times p)$ variance–covariance matrix for the p-dimensional normal density of the random variable X with n samples per nodes, i.e. genes. Hereby, the p-dimensional normal density of X shown in Equation (1) can be denoted by the following probability density function.(2) $$\begin{array}{c}\hfill f(X)=\frac{1}{{(2\mathit{\pi })}^{n/2}{|\mathrm{\Sigma }|}^{1/2}}exp\left[-\frac{1}{2}{\left(X-\mathit{\mu }\right)}^{\prime }{\mathrm{\Sigma }}^{-1}\left(X-\mathit{\mu }\right)\right].\end{array}$$(2)

In Equation (2), $\mathrm{\Sigma }$ is symmetric and invertible matrix, and its inverse called the precision, $\mathrm{\Theta }$, indicates the dependency structure between two nodes. Accordingly, in GGM, if there exists an edge between two nodes, i.e. ${\mathrm{\Theta }}_{ij}={\mathrm{\Theta }}_{ji}\ne 0$, these two nodes are not conditionally independent given other nodes (Whittaker, 1990). 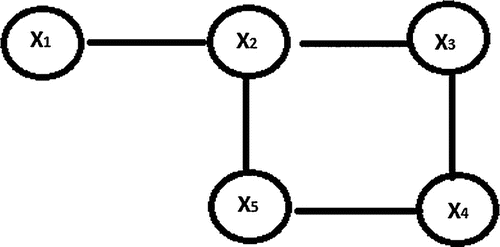In other words, the non-zero entries of the off-diagonal entries of $\mathrm{\Theta }$ imply a physical or functional interaction between the nodes (Dempster, 1972; Wermuth, 1976; Whittaker, 1990). In Figure 2, we draw a small network having five nodes in which $X_1$ is conditionally independent on $X_3$ for given $X_2$. Similarly, $X_3$ is conditionally independent on $X_5$ for given $X_2$ and $X_4$ in the same figure.

Figure 2. Simple representation of the relationship between five nodes in a system.

There are lots of techniques to estimate entries of the precision matrix in GGM. The neighborhood selection method with the lasso regression (Meinshaussen & Bühlmann, 2006) is one of the computationally efficient approaches for sparse and high-dimensional graphs. This method belongs to the class of the covariance selection approaches that is based on non-parametric calculation. In this model, given that the set of nodes and the number of nodes in the graph are denoted by $\mathrm{\Phi }$ and $\left|\mathrm{\Phi }(n)\right|$, respectively, the neighborhood of the node p in $\mathrm{\Phi }$ is the smallest subset of the node $\mathrm{\Phi }\backslash p$. Since each state of the node, i.e. gene, p, $X_p$, is defined as conditionally independent on the state of all remaining nodes, $X_{-p}$, an optimal prediction of the vector of the regression coefficient of $X_p$ in the lasso regression (Tibshirani, 1996), ${\mathit{\theta }}^p$, can be found by the following expression.(3) $$\begin{array}{c}\hfill {\mathit{\theta }}^p=arg\underset{{\mathit{\theta }}_p=0}{min}E(X_p-\sum _{k\in \mathrm{\Phi }(n)}{\mathit{\theta }}_k{X}_k{)}^2.\end{array}$$(3)

In Equation (3), $\mathrm{\Phi }$ denotes the set of nodes with n number of observations each, $E(·)$ shows the expectation of the given random variable, and ${\mathrm{\Theta }}_k^p$ stands for ${\mathrm{\Theta }}_k^p=-{\mathrm{\Sigma }}_{kp}/{\mathrm{\Sigma }}_{pp}$. Here, the best predictor for $X_p$ is detected as a linear function of variables in the set of neighbors of the node (Meinshaussen & Bühlmann, 2006).

Furthermore, the graphical lasso, also named as glasso, approach (Friedman, Hastie, & Tibshiran, 2008), is another common technique in inference of biological networks. Briefly, this method controls the type I and type II errors by detecting the probability under very low levels when the penalized likelihood expression is defined as below.(4) $$\begin{array}{c}\hfill \underset{\mathrm{\Theta }}{max}[log(\mid \mathrm{\Theta }\mid )-\text{Tr}(S\mathrm{\Theta })-\mathit{\lambda }\Vert \mathrm{\Theta }{\Vert }_1].\end{array}$$(4)

In Equation (4), $||·{||}_1$ shows the $l_1$-norm, which is the sum of the absolute value of the given element, and $\text{Tr}(·)$ presents the trace. S indicates the sample covariance matrix $S={\mathrm{\Theta }}^{-1}$. Accordingly, in inference of S in Equation (4) as an unbiased estimator of $\mathrm{\Sigma }$ in Equation (2), the sample covariance matrix is applied, i.e. $\widehat{\mathrm{\Theta }}=S$ via(5) $$\begin{array}{c}\hfill s_{ij}=\frac{1}{n}\sum _{k=1}^n(x_k^i-{\overline{x}}^{(i)})(x_k^j-{\overline{x}}^{(j)}).\end{array}$$(5)

Here, $s_{ij}$ denotes the ith row and the jth entry of S and n is the total sample size per gene as stated previously. Finally, $x_k^i$ stands for the kth sample of the ith gene and ${\overline{x}}^{(j)}$ refers to the mean term for the ith gene having totally n observations.

On the other hand, different researchers have also investigated other parametric solutions of this problem. But the main challenge under these calculations is the high dimension of genes (nodes) with respect to the observations per gene, denoted by n, i.e. $n<<p$. This inequality causes a singular covariance matrix, resulting in multiple of solutions if we perform the standard maximum likelihood technique in inference of model parameters. Hereby, in order to unravel this problem, different types of penalized methods are also suggested besides the neighborhood selection and glasso approaches as described above. These methods are based on distinct optimization approaches of the lasso regression in the estimation of $\mathrm{\Theta }$. We can also list grouped lasso (Yuan & Lin, citeyuan), elastic net method (Zou & Hastie, 2005), fused lasso (Tibshirani, Saunders, Rosset, Zhu, & Knight, 2005), adaptive lasso (Zou, 2006), coordinate-wise descent algorithm within the $l_1$-penalized lasso (Friedman, Hastie, & Tibshiran, 2007), and multivariate methods with scout algorithm (Witten & Tibshirani, witten) approaches as the other most well-known approaches used in GGM. All these methods mainly suggest similar model construction for the penalized maximum likelihood function defined for the lasso regression by either the $l_1$ norm or $l_2$-norm as the penalizing term. On the other side, recently, certain semi-parametric approaches such as the non-paranormal SKEPTIC algorithm (Liu, Han, Yuan, Lafferty, & Wasserman, 2012) and fully parametric approaches via Bayesian techniques such as the birth-death Markov chain Monte Carlo (MCMC) (Muhammadi & Wit, 2014) approach are proposed in order to estimate $\mathrm{\Theta }$ without using any optimization methods. In the literature of GGM, different types of Monte Carlo approaches have been also performed. Atay-Kayis and Massam (2005) apply Monte Carlo methods in the calculation of $\mathrm{\Theta }$ when the network graph in GGM is non-decomposable. Dobra, Lenkoski, and Rodriguez (2011) and Wang and Li (2012) introduce the reversible jump MCMC and Dauwels, Yu, Xu, and Wang (2013) implement the Monte Carlo expectation maximization method within copula GGM. Whereas among all these alternatives, the neighborhood selection approach, suggested by Meinshaussen and Bühlmann (2006), is one of the most common techniques due to its simplicity in inference. Hence, in our analyses, we prefer this method and perform it in junction with Monte Carlo simulations in order to evaluate the performance of different estimates.

2.2. Bernstein polynomials

The Bernstein polynomial was introduced by Sergey Natanovich Bernstein as a new proof of the Weierstrass approximation theorem. This polynomial privileges in the approximation theory since it applies the constructive new polynomials to prove the Weierstrass approximation instead of polynomials that are already known as mathematicians.

For the mathematical expression of these polynomials, let N be the set of positive integers for every function $f:[0,1]\to R$. Thus, the Bernstein polynomial for the nth degree is defined by(6) $$\begin{array}{c}\hfill B_n(f;t)=\sum _{k=0}^{n}f(\frac{k}{n})b_{k,n}(t),\end{array}$$(6)

where $b_{k,n}$ is called the Bernstein basis polynomial and can shown as(7) $$\begin{array}{c}\hfill b_{k,n}(t)=\left(\genfrac{}{}{0pt}{}{n}{k}\right){(1-t)}^{n-k}{t}^k\end{array}$$(7)

for $k=0,1,\dots ,n$ and $\left(\genfrac{}{}{0pt}{}{n}{k}\right)$ binomial coefficient.

If $f:[0,1]\to R$ is a continuous function, then the sequence of the Bernstein polynomials $B_n$ converges uniformly to f on [0, 1],

The Bernstein polynomial (Lorentz, 1953) has certain properties such as the positivity, symmetry, and the degree raising. The first characteristic means $b_{k:n}=b_{n-k:n}$ while $i=1,\dots ,n$. On the other hand, the second feature presents $b_{k:n}(x)>0$ and finally, the third one implies that any lower degree Bernstein polynomial is written as a linear combination of the nth Bernstein polynomials.

The generalized version of the Bernstein operator is called the Szas-Mirakyan operator and is defined as(8) $$\begin{array}{c}\hfill S_n(f;x)=e^{-nx}\sum _{k=0}^{\infty }f\left(\frac{k}{n}\right)\frac{{(nx)}^k}{k!},\end{array}$$(8)

where $x\in [0,1]$ and the function f is defined on an infinite interval $R^{+}=[0,\infty )$.

2.3. Butzer Hahn operator

Bleiman, Butzer and Hahn (BBH) operator (Bleiman, Butzer, & Hahn, 1980) which is defined by the Bernstein-type can be represented as below for the nth degree with the k basis polynomials for the value x.(9) $$\begin{array}{c}\hfill L_n(f;x)=\frac{1}{{(1+x)}^n}\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)x^{k}f(\frac{k}{n+1-k}).\end{array}$$(9)

For Equation (9), the following inequality is satisfied.(10) $$\begin{array}{c}\hfill |L_n{(f;x)|\le ||f||}_{C_B}(f\in C_B[0,\infty )).\end{array}$$(10)

Equation (10) implies that the BBH operator is linear and bounded for $x\in [0,\infty )$ when ${(1+x)}^{-n}\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)x^k=1$. Here, $C_B[0,\infty )$ is the class of the real-valued function f defined within the interval $[0,\infty )$ and for all functions of f in this interval, $lim{L}_n(f;x)=f(x)$ for each $x\in [0,\infty )$ when $n\to \infty$.

Additionally, the property of the uniform approximation of the BBH operator has been studied (Totik, 1984) when f belongs to $C[0,\infty ]$ for the continuous function on $[0,\infty )$. Also Mercer (Mercer (1989)) has independently derived the Voronovskaya-type theorem which gives an asymptotic error term for the Bernstein polynomials for the functions which are twice differentiable as follows.(11) $$\begin{array}{c}\hfill \underset{n\to \infty }{lim}n((L_n(f;x)-f(x))=\frac{x{(1+x)}^2}{2}{f}^{{}^{″}}(x)\end{array}$$(11)

for all $f\in C^2[0,\infty )$ with $f(x)=O(x)$ when $x\to \infty$, and $f^{{}^{″}}(x)$ is the second derivative of the function.

Abel (1996) has extended this study by giving the complete asymptotic expansion for the BBH operator as the following form.(12) $$\begin{array}{c}\hfill L_n(f;x)=f(x)+\sum _{k=1}^{\infty }{c}_k(f;x){(n+1)}^{-k}\end{array}$$(12) $n\to \infty$. Here, $c_k$ represents all the coefficients from $k=0$ to $k=n$.

The Szasz operator is the limiting operator of BBH (Khan, 1988) and $L_n(f;x)\ge L_{n+1}(f;x)\ge \dots f(x)$ if f is convex (Khan, Nevai, & Pinkus, 1991). $L_n(f;x)$ is convex itself if f is a non-increasing convex function.

Jayasri and Sitaraman (1993) have determined that $L_n$ is a pointwise approximation process in which the largest subclass of $C[0,\infty )$ for the Bernstein-type of operator.

Then, the following function class is introduced in the study of Hermann, Szbados, and Tandori (1991).(13) $$\begin{array}{c}\hfill \mathcal{H}=f\in C[0,\infty ]:log(|f(x)|+1)=o(x).\end{array}$$(13)

He has proved that if f belongs to $\mathcal{H}$, then for each $x>0$, the pointwise convergence is ${lim}_{n\to \infty }{L}_{n}f=f$ on $[0,\infty )$. Moreover, for some $a>0$, $f(x)=e^{ax}$, then ${lim}_{x\to \infty }{L}_n(f;x)=\infty$. Also the operator $L_n$ is arisen from the random variable with n observations, $X_n$, which has the Bernoulli distribution as below.(14) $$\begin{array}{c}\hfill P(\{X_n=k|(n-k+1)\})=\left(\genfrac{}{}{0pt}{}{n}{k}\right)p^k{q}^{n-k}\end{array}$$(14)

for the parameters $p=x/(1+x)$, $q=1/(1+x)$ and $k=0,1,\dots ,n$.

2.4. Meyer-König and Zeller operator

The operator(15) $$\begin{array}{c}\hfill M_n(f;x)=\sum _{k=0}^{\infty }f\left(\frac{k}{n+k+1}\right)m_{n+1,k}(x)\end{array}$$(15)

is known as the Meyer-König and Zeller (MKZ) operator when(16) $$\begin{array}{c}\hfill m_{n,k}(x)=\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)x^k{(1-x)}^{n+1}\end{array}$$(16)

for the nth degree and the kth basis polynomial for the value of x as stated previously.

These operators are known as the Bernstein-type of operators. Cheney and Sharma (1996) have defined this operator as a power series of the Bernstein operators.

The MKZ operator can also be obtained from the negative binomial distribution via(17) $$\begin{array}{c}\hfill M_n(f;x)={(1-x)}^{n+1}\sum _{k=0}^{\infty }\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)f\left(\frac{k}{n+k}\right)x^k.\end{array}$$(17)

3. Application

In the assessment of the polynomials’ results, we consider four different scenarios. In the first scenario, we estimate the precision matrix $\mathrm{\Theta }$ from the simulated data-sets under different kinds of the Bernstein polynomials and the Bernstein-type of operators, which are the MKZ operator and the BBH operator. For the analyses of the model, we generate 50, 100, and 500 dimensional data-sets in which each gene has 20 observations. Then, we set all the off-diagonal entries of $\mathrm{\Theta }$ to 0.9 arbitrarily and generate scale-free networks by using the huge package in the R programme language. Then, in order to evaluate whether the entry of the off-diagonal terms has any effect in inference, we change it via moderately small and small values too. Hereby, in the second and the third scenarios, the off-diagonal elements of the precision matrix set to 0.7 and 0.5, respectively, when the networks are scale-free. Finally, as the fourth plan, we change the sparsity of the system from the scale-freeness to the hubs property since the former typically indicates a high sparsity level around 90% or above and the latter implies relatively a lower sparsity level at around 80–90%. On the other hand, in our analyses, we have not controlled the performance of methods lower than these sparsities levels as the high sparsity is one of the main features of biological systems (Barabasi & Otiva, Barabasi04).

Accordingly, in all scenarios, we initially generate a data-set for the true network and keep its true path for the best model selection in further steps. Later, we transform this actual data-set via the Bernstein polynomial, the Szasz polynomial, the MKZ operator, and the BBH operator. Finally, all these non-transformed and transformed data are used to estimate the precision matrices by using the neighborhood selection (NB) method. In the application, we choose NB among alternatives due to its computational gain. For the assessment, we calculate the F-measure and the precision for each run as shown below.(18) $$\begin{array}{c}\hfill \text{Precision}=\frac{TP}{TP+FP}\text{and}\text{F-measure}=2\frac{\text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}.\end{array}$$(18)

In Equation (18), TP (true positive) indicates the number of correctly classified objects that have positive labels and FN (false negative) shows the number of misclassified objects that have negative labels and finally, Recall is calculated as $\text{Recall}=TP/(TP+FN)$.

Then, we repeat the calculation of the underlying statistics for 1000 Monte Carlo runs and their means are computed. The results are presented in Table 1.

Table 1. Comparison of the F-measure and the precision values computed with/without operators in inference of $\mathrm{\Theta }$ with 0.9 off-diagonal entries under scale-free networks

Measure	Dimension of $\mathrm{\Theta }$	No operator	Bernstein polynomial	Szasz polynomial	BBH operator	MKZ operator
F-measure	($50\times 50$)	0.0014	0.1714	0.1590	0.1132	0.1492
	($100\times 100$)	0.0001	0.0904	0.0863	0.0594	0.0812
	($500\times 500$)	0.0000	0.0171	0.0171	0.0094	0.0163
Precision	($50\times 50$)	Not Computable	0.4852	0.4789	0.3794	0.4729
	($100\times 100$)	Not Computable	0.4769	0.4749	0.4601	0.4699
	($500\times 500$)	Not Computable	0.4663	0.4682	0.4466	0.4624

Table 2. Comparison of the F-measure and the precision values computed with/without operators in inference of $\mathrm{\Theta }$ with 0.7 off-diagonal entries under scale-free networks

Measure	Dimension of $\mathrm{\Theta }$	No operator	Bernstein polynomial	Szasz polynomial	BBH operator	MKZ operator
F-measure	($50\times 50$)	Not Computable	0.0699	0.0711	0.0704	0.0712
	($100\times 100$)	Not Computable	0.0361	0.0366	0.0362	0.0368
	($500\times 500$)	Not Computable	0.0077	0.0083	0.0078	0.0080
Precision	($50\times 50$)	Not Computable	0.0403	0.0403	0.0404	0.0401
	($100\times 100$)	Not Computable	0.0201	0.0200	0.0200	0.0200
	($500\times 500$)	Not Computable	0.0040	0.0040	0.0040	0.0040

Table 3. Comparison of the F-measure and the precision values computed with/without operators in inference of $\mathrm{\Theta }$ with 0.5 off-diagonal entries under scale-free networks

Measure	Dimension of $\mathrm{\Theta }$	No operator	Bernstein polynomial	Szasz polynomial	BBH operator	MKZ operator
F-measure	($50\times 50$)	Not Computable	0.0703	0.0710	0.0702	0.0716
	($100\times 100$)	Not Computable	0.0356	0.0365	0.0362	0.0367
	($500\times 500$)	Not Computable	0.0077	0.0080	0.0077	0.0080
Precision	($50\times 50$)	Not Computable	0.0404	0.0402	0.0402	0.0403
	($100\times 100$)	Not Computable	0.0198	0.0199	0.0200	0.0199
	($500\times 500$)	Not Computable	0.0040	0.0040	0.0039	0.0040

Table 4. Comparison of the F-measure and the precision values computed with/without operators in inference of $\mathrm{\Theta }$ with 0.9 off-diagonal entries under hubs networks

Measure	Dimension of $\mathrm{\Theta }$	No operator	Bernstein polynomial	Szasz polynomial	BBH operator	MKZ operator
F-measure	($50\times 50$)	Not Computable	0.0668	0.0687	0.0677	0.0691
	($100\times 100$)	Not Computable	0.0352	0.0365	0.0358	0.0366
	($500\times 500$)	Not Computable	0.0074	0.0076	0.0075	0.0076
Precision	($50\times 50$)	Not Computable	0.0383	0.0387	0.0386	0.0387
	($100\times 100$)	Not Computable	0.0196	0.0198	0.0198	0.0198
	($500\times 500$)	Not Computable	0.0038	0.0038	0.0038	0.0038

From Table 1, it is seen that for low dimensions, the Bernstein polynomials give better results than others, in particular, the Szasz polynomials have the highest F-measure. We obtain the same results for the precision values as well. Moreover, we detect that when the dimension of the matrix increases, the F-measure and the precision value decrease. Furthermore, as shown in Tables 2 and 3, we observe similar findings in the sense the Szasz polynomials typically produce better F-measure and precision even though we decrease the correlation between genes (by off-diagonal entries 0.7 and 0.5). Whereas under these scenarios, it is found that the MKZ operator is as good as the Szasz operator in terms of the accuracy of the estimates under certain conditions. Finally when we evaluate the outputs of Tables 2–4, we see that the results of both the Szasz polynomial and the MKZ operator are very close to each other and overperform with respect to the remaining operators.

On conclusion, all these outputs imply that when the sparsity of networks decreases, all Bernstein-type of operators compute similar results and the Szasz polynomial as well as the MKZ operator are slightly better than others. On the contrary, if the sparsity level raises as mostly observed in biological networks, the operators have different accuracy values and the performance of the Bernstein polynomials, especially, the Szasz polynomial, becomes better.

4. Discussion

In this study, we have compared all well-known Bernstein-type of operators to detect which alternative produces the highest accuracy if it is applied with GGM. For this purpose, we have analyzed the Monte Carlo results of the Bernstein polynomials, BBH and MKZ operators. The results have indicated that the Bernstein polynomials have the highest accuracies if they are performed in advance of the inference of the model parameters of GGM and the MKZ operator can be another good alternative if the sparsity level of the system decreases. But for all choices of operators, we have found that these operators can improve the accuracies of estimates for different dimensional biochemical systems if they are implemented as the pre-processing step before the inference of the precision matrix. As the extension of this study, we consider other approximation methods such as the Fourier transformations in such a way that the distributional feature of the observations can be embedded to the new transformed data in order to smooth the original data-set smartly and get estimates with higher accuracy.

Acknowledgements

The authors would like to thank the anonymous referees, editors, and guest editors of this Special Issue of the journal for their valuable contributions which improve the quality of the paper.

Additional information

Funding

Vilda Purut u̧ oğlu would like to thank to SysPatho EU FP-7 Collaborative Project [project number 260429] for their support.

Notes on contributors

Vilda Purutçuoğlu

Vilda Purutçuoğlu is the associate professor in the Department of Statistics at Middle East Technical University (METU) and also affiliated faculty in the Informatics Institute, Institute of Applied Mathematics and Department of Biomedical Engineering at METU. She has completed her BSc and MSc in statistics and minor degree in economics. She received her doctorate at the Lancaster University. Purutçuoğlu’s current researches are in the field of bioinformatics, systems biology and biostatistics. She has a research group with seven doctorates and four master students who have been working on deterministic and stochastic modelings of biological networks and their inferences via Bayesian and frequentist theories. Hereby, the findings in this study are the part of the researches about the improvement of probabilistic inferences of complex networks and these findings can be helpful for eliminating batch effects in their observations before any statistical analyses.