Exact traveling wave solutions for the generalized Hirota-Satsuma couple KdV system using the exp(−φ(ξ))-expansion method

Abstract

In this research, we find the exact traveling wave solutions involving parameters of the generalized Hirota-Satsuma couple KdV system according to the exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method and when these parameters are taken to be special values we can obtain the solitary wave solutions which is derived from the exact traveling wave solutions. It is shown that the proposed method provides a more powerful mathematical tool for constructing exact traveling wave solutions for many other nonlinear evolution equations.

Keywords:

• the exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method
• the generalized Hirota-Satsuma couple KdV system
• traveling wave solutions
• solitary wave solutions

AMS Subject Classifications:

• 35A05
• 35A20
• 65K99
• 65Z05
• 76R50
• 70K70

Public Interest Statement

In this paper, we use the exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method to find the exact and solitary wave solutions of the generalized Hirota-Satsuma couple KdV system. The exact traveling wave solutions are obtained from the explicit solutions by choosing the particular value of the physical parameters. So, we can choose appropriate value of the physical parameters to obtain exact solutions we need in varied instances. There are various types of traveling wave solutions that are of particular interest in solitary wave theory.

1. Introduction

No one can deny the important role which played by the nonlinear partial differential equations in the description of many and a wide variety of phenomena not only in physical phenomena, but also in plasma, fluid mechanics, optical fibers, solid state physics, chemical kinetics, and geochemistry phenomena. So that, during the past five decades, a lot of method was discovered by a diverse group of scientists to solve the nonlinear partial differential equations. Such methods are tanh–sech method (Malfliet, 1992; Malfliet & Hereman, 1996; Wazwaz, 2004a), extended tanh method (Abdelrahman, Zahran, & Khater, 2015; El-Wakil & Abdou, 2007; Fan, 2000), sine–cosine method (Wazwaz, 2005,2004b; Yan, 1996), homogeneous balance method (Fan & Zhang, 1998; Wang, 1996), F-expansion method (Ren & Zhang, 2006; Zahran & Khater, 2014a; Zhang, Wang, Wang, & Fang, 2006), exp-function method (Aminikhad, Moosaei, & Hajipour, 2009; He & Wu, 2006), trigonometric function series method (Zhang, 2008), $(\frac{G^{{}^{\prime }}}{G})-$ expansion method (Khater, 2015; Wang, Zhang, & Li, 2008; Zahran & Khater, 2014b; Zhang, Tong, & Wang, 2008), Jacobi elliptic function method (Dai & Zhang, 2006; Fan & Zhang, 2002; Liu, Fu, Liu, & Zhao, 2001; Zahran & Khater, 2014c), The exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method (Abdelrahman, Zahran, & Khater, 2014; Islam, Nur Alam, Kazi Sazzad Hossain, Harun-Or-Roshid, & Ali Akbar, 2013; Rahman, Nur Alam, Harun-Or-Roshid, Akter, & Ali Akbar, 2014), and so on.

The objective of this article was to apply The exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method for finding the exact traveling wave solution of the generalized Hirota-Satsuma couple KdV system which play an important role in mathematical physics.

The rest of this paper is organized as follows: In Section 2, we give the description of The exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method. In Section 3, we use this method to find the exact solutions of the nonlinear evolution equations pointed out above. In Section 5, conclusions are given.

2. Description of method

Consider the following nonlinear evolution equation(2.1) $$\begin{array}{c}\hfill F(u,u_t,u_x,u_{tt},u_{xx},\dots )=0,\end{array}$$(2.1)

where F is a polynomial in u(x, t) and its partial derivatives in which the highest order derivatives and nonlinear terms are involved. In the following, we give the main steps of this method

Step 1. We use the wave transformation(2.2) $$\begin{array}{c}\hfill u(x,t)=u(\mathit{\xi }),\mathit{\xi }=x-ct,\end{array}$$(2.2)

where c is a positive constant, to reduce Equation (2.1) to the following ODE:(2.3) $$\begin{array}{c}\hfill P(u,u^{\prime },u^{″},u^{″\prime },\dots )=0,\end{array}$$(2.3)

where P is a polynomial in $u(\mathit{\xi })$ and its total derivatives, while ${}^{\prime }={\frac{d}{d\mathit{\xi }}}^{\prime }$.

Step 2. Suppose that the solution of ODE (Equation 2.3) can be expressed by a polynomial in $exp(-\mathit{\phi }(\mathit{\xi }))$ as follows(2.4) $$\begin{array}{c}\hfill u(\mathit{\xi })=\sum _{i=0}^n{a}_m{\left(exp\left(-\mathit{\phi }\left(\mathit{\xi }\right)\right)\right)}^m,\end{array}$$(2.4)

Since $a_m\left(0\le m\le n\right)$ are constants to be determined, such that $a_m\ne 0$.

The positive integer m can be determined by considering the homogenous balance between the highest order derivatives and nonlinear terms appearing in Equation (2.3). Moreover precisely, we define the degree of $u\left(\mathit{\xi }\right)$ as $D\left(u\left(\mathit{\xi }\right)\right)=m$, which gives rise to degree of other expression as follows:$$D\left(\frac{d^{q}u}{d{\mathit{\xi }}^q}\right)=n+q,D\left(u^p{\left(\frac{d^{q}u}{d{\mathit{\xi }}^q}\right)}^s\right)=np+s\left(n+q\right).$$

Therefore, we can find the value of m in Equation (2.3), where $\mathit{\phi }=\mathit{\phi }(\mathit{\xi })$ satisfies the ODE in the form(2.5) $$\begin{array}{c}\hfill {\mathit{\phi }}^{\prime }(\mathit{\xi })=exp\left(-\mathit{\phi }\left(\mathit{\xi }\right)\right)+\mathit{\mu }exp\left(\mathit{\phi }\left(\mathit{\xi }\right)\right)+\mathit{\lambda },\end{array}$$(2.5)

the solutions of ODE (Equation 2.3) are

when ${\mathit{\lambda }}^2-4\mathit{\mu }>0,\mathit{\mu }\ne 0,$(2.6) $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\xi })=ln\left(\frac{-\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}tanh\left(\frac{\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }}{2\mathit{\mu }}\right),\end{array}$$(2.6)

and(2.7) $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\xi })=ln\left(\frac{-\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}coth\left(\frac{\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }}{2\mathit{\mu }}\right),\end{array}$$(2.7)

when ${\mathit{\lambda }}^2-4\mathit{\mu }>0,\mathit{\mu }=0,$(2.8) $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\xi })=-ln\left(\frac{\mathit{\lambda }}{exp\left(\mathit{\lambda }\left(\mathit{\xi }+C_1\right)\right)-1}\right),\end{array}$$(2.8)

when ${\mathit{\lambda }}^2-4\mathit{\mu }=0,\mathit{\mu }\ne 0,\mathit{\lambda }\ne 0,$(2.9) $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\xi })=ln\left(-\frac{2\left(\mathit{\lambda }\left(\mathit{\xi }+C_1\right)+2\right)}{{\mathit{\lambda }}^2\left(\mathit{\xi }+C_1\right)}\right),\end{array}$$(2.9)

when ${\mathit{\lambda }}^2-4\mathit{\mu }=0,\mathit{\mu }=0,\mathit{\lambda }=0,$(2.10) $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\xi })=ln\left(\mathit{\xi }+C_1\right),\end{array}$$(2.10)

when ${\mathit{\lambda }}^2-4\mathit{\mu }<0,$(2.11) $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\xi })=ln\left(\frac{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}tan\left(\frac{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }}{2\mathit{\mu }}\right),\end{array}$$(2.11)

and(2.12) $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\xi })=ln\left(\frac{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}cot\left(\frac{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }}{2\mathit{\mu }}\right),\end{array}$$(2.12)

where $a_m,\dots \dots ,\mathit{\lambda },\mathit{\mu }$ are constants to be determined later.

Step 3. After we determine the index parameter m, we substitute Equation (2.4) along Equation (2.5) into Equation (2.3) and collecting all the terms of the same power $exp\left(-m\mathit{\phi }(\mathit{\xi })\right)$, $m=0,1,2,3,\dots$ and equating them to zero, we obtain a system of algebraic equations, which can be solved by Maple or Mathematica to get the values of $a_i$.

Step 4. Substituting these values and the solutions of Equation (2.5) into Equation (2.3) we obtain the exact solutions of Equation (2.3).

It is to be noted here that the construction of the exp $\left(-\mathit{\phi }\left(\mathit{\xi }\right)\right)$ is similar to the construction of the $\left(\frac{G^{\prime }}{G}\right)$-expansion. For better understanding of the duality of both methods we cite Alquran and Qawasmeh (2014), Qawasmeh and Alquran (2014a,2014b).

3. Application

Here, we will apply the exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method described in Section 2 to find the exact traveling wave solutions and the solitary wave solutions of the generalized Hirota-Satsuma couple KdV system (Yan, 2003). We consider the generalized Hirota-Satsuma couple KdV system(3.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_t=\frac{1}{4}{u}_{xxx}+3u{u}_x+3{\left(-v^2+w\right)}_x,\hfill \\ v_t=-\frac{1}{2}{v}_{xxx}-3u{v}_x,\hfill \\ w_t=-\frac{1}{2}{w}_{xxx}-3u{w}_x.\hfill \end{array}\right.\end{array}$$(3.1)

when $w=0$, Equation (3.1) reduce to be the well-known Hirota-Satsuma couple KdV equation. Using the wave transformation $u(x,t)=u(\mathit{\xi })$, $v(x,t)=v(\mathit{\xi })$, $w(x,t)=w(\mathit{\xi })$, $\mathit{\xi }=k(x-{\mathit{\lambda }}_{1}t)$ carries the partial differential Equation (3.1) into the ordinary differential equation(3.2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\lambda }}_{1}k{u}^{\prime }=\frac{1}{4}{k}^3{u}^{″\prime }+3ku{u}^{\prime }+3k{\left(-v^2+w\right)}^{\prime },\hfill \\ -{\mathit{\lambda }}_{1}k{v}^{\prime }=-\frac{1}{2}{k}^3{v}^{″\prime }-3ku{v}^{\prime },\hfill \\ -{\mathit{\lambda }}_{1}k{w}^{\prime }=-\frac{1}{2}{k}^3{w}^{″\prime }-3ku{w}^{\prime }.\hfill \end{array}\right.\end{array}$$(3.2)

Suppose we have the relations between $\left(uandv\right)$ and $\left(wandv\right)$$\Rightarrow$$\left(u=\mathit{\alpha }{v}^2+\mathit{\beta }v+\mathit{\gamma }\right)$ and $\left(w=Av+B\right)$ where $\mathit{\alpha },\mathit{\beta },\mathit{\gamma },A$, and B are arbitrary constants. Substituting this relation into second and third equations of Equation (3.2) and integrating them, we get the same equation and integrate it once again we obtain(3.3) $$\begin{array}{c}\hfill k^2{v}^{\prime 2}=-2\mathit{\alpha }{v}^4-2\mathit{\beta }{v}^3+2\left({\mathit{\lambda }}_1-3\mathit{\gamma }\right)v^2+2c_{1}v+c_2,\end{array}$$(3.3)

where $c_1$ and $c_2$ is the arbitrary constants of integration, and hence, we obtain(3.4) $$\begin{array}{cc}\hfill k^2{u}^{″}& =2\mathit{\alpha }{k}^2{v}^{\prime 2}+k^2\left(2\mathit{\alpha }v+\mathit{\beta }\right)v^{″}\hfill \\ \hfill & =2\mathit{\alpha }\left[-\mathit{\alpha }{v}^4-2\mathit{\beta }{v}^3+2\left({\mathit{\lambda }}_1-3\mathit{\gamma }\right)v^2+2c_{1}v+c_2\right]\hfill \\ \hfill & +\left(2\mathit{\alpha }v+\mathit{\beta }\right)\left[-2\mathit{\alpha }{v}^3-3\mathit{\beta }{v}^2+2\left({\mathit{\lambda }}_1-3\mathit{\gamma }\right)v+c_1\right].\hfill \end{array}$$(3.4)

So that, we have(3.5) $$\begin{array}{c}\hfill P^{″}+lP-m{P}^3=0.\end{array}$$(3.5)

where$$\begin{array}{cc}& c_1=\frac{1}{2{\mathit{\alpha }}^2\left({\mathit{\beta }}^2+2{\mathit{\lambda }}_1\mathit{\alpha }\mathit{\beta }-6\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\right)},v(\mathit{\xi })=aP(\mathit{\xi })-\frac{\mathit{\beta }}{2\mathit{\alpha }},\mathit{\alpha }=\frac{{\mathit{\beta }}^2-4}{4\left(\mathit{\gamma }-{\mathit{\lambda }}_1\right)},A=\frac{4\mathit{\beta }\left({\mathit{\lambda }}_1-\mathit{\gamma }\right)}{{\mathit{\beta }}^2-4},\hfill \\ \hfill & B=\frac{1}{6\left(-\mathit{\gamma }+{\mathit{\lambda }}_1\right){\left({\mathit{\beta }}^2-4\right)}^2}(16c_3{\mathit{\lambda }}_1{\mathit{\beta }}^2-2c_3{\mathit{\lambda }}_1{\mathit{\beta }}^4-16c_3\mathit{\gamma }{\mathit{\beta }}^2+3c_3\mathit{\gamma }{\mathit{\beta }}^4+56{\mathit{\lambda }}_1^2\mathit{\gamma }{\mathit{\beta }}^2\hfill \\ \hfill & -48{\mathit{\gamma }}^2{\mathit{\lambda }}_1{\mathit{\beta }}^2-16c_2+c_2{\mathit{\beta }}^6-12c_2{\mathit{\beta }}^4+12c_2{\mathit{\beta }}^2-16{\mathit{\gamma }}^2{\mathit{\lambda }}_1-32{\mathit{\lambda }}_1^2\mathit{\gamma }-8{\mathit{\lambda }}_1^3{\mathit{\beta }}^2+{\mathit{\beta }}^4{\mathit{\gamma }}^3\hfill \\ \hfill & -2{\mathit{\beta }}^4{\mathit{\lambda }}_1^3+32c_3\mathit{\gamma }-32c_3{\mathit{\lambda }}_1+48{\mathit{\gamma }}^3+{\mathit{\beta }}^4{\mathit{\gamma }}^2{\mathit{\lambda }}_1),\hfill \\ \hfill l& =\frac{-a}{k^2}\left(\frac{3{\mathit{\beta }}^2}{2\mathit{\alpha }}+2{\mathit{\lambda }}_1-6\mathit{\gamma }\right),m=\frac{-2\mathit{\alpha }{a}^3}{k^2}.\hfill \end{array}$$

Balancing between the highest order derivatives and nonlinear terms appearing in $P^{″}$ and $P^3$$\Rightarrow$$\left(N+2=3N\right)$$\Rightarrow$$\left(N=1\right)$. So that, by using Equation (2.4) we get the formal solution of Equation (3.5)(3.6) $$\begin{array}{c}\hfill p(\mathit{\xi })=a_0+a_{1}exp(-\mathit{\phi }(\mathit{\xi })),\end{array}$$(3.6)

substituting Equation (3.6) and its derivative into Equation (3.5) and collecting all term with the same power of $exp(-3\mathit{\phi })$, $exp(-2\mathit{\phi })$, $exp(-\mathit{\phi })$, $exp(0\mathit{\phi })$ we get:(3.7) $$\begin{array}{cc}& exp(-3\mathit{\phi }):2a_1-m{a_1}^3=0,\hfill \end{array}$$(3.7) (3.8) $$\begin{array}{cc}& exp(-2\mathit{\phi }):3a_1\mathit{\lambda }-3m{a}_0{a_1}^2=0,\hfill \end{array}$$(3.8) (3.9) $$\begin{array}{cc}& exp(-1\mathit{\phi }):2a_1\mathit{\mu }+a_1{\mathit{\lambda }}^2+l{a}_1-3m{a_0}^2{a}_1=0,\hfill \end{array}$$(3.9) (3.10) $$\begin{array}{cc}& exp(0\mathit{\phi }):a_1\mathit{\lambda }\mathit{\mu }+l{a}_0-m{a_0}^3=0.\hfill \end{array}$$(3.10)

Solving above system by using maple 16, we get:$$\begin{array}{cc}\hfill l& =\frac{{\mathit{\lambda }}^2}{2}-2\mathit{\mu },a_0=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}},a_1=\pm \sqrt{\frac{2}{m}},\text{where}(m>0).\hfill \end{array}$$

Thus the solution is(3.11) $$\begin{array}{c}\hfill p(\mathit{\xi })=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}}\pm \sqrt{\frac{2}{m}}exp(-\mathit{\phi }(\mathit{\xi })).\end{array}$$(3.11)

Let us now discuss the following cases: When ${\mathit{\lambda }}^2-4\mathit{\mu }>0,\mathit{\mu }\ne 0,$(3.12) $$\begin{array}{c}\hfill P_{(1,2)}=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}}\pm \sqrt{\frac{2}{m}}\frac{2\mathit{\mu }}{-\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}tanh\left(\frac{\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }},\end{array}$$(3.12)

and(3.13) $$\begin{array}{c}\hfill P_{(3,4)}=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}}\pm \sqrt{\frac{2}{m}}\frac{2\mathit{\mu }}{-\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}coth\left(\frac{\sqrt{{\mathit{\lambda }}^2-4\mathit{\mu }}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }}.\end{array}$$(3.13)

when ${\mathit{\lambda }}^2-4\mathit{\mu }>0,\mathit{\mu }=0,$(3.14) $$\begin{array}{c}\hfill P_{(5,6)}=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}}\pm \sqrt{\frac{2}{m}}\frac{\mathit{\lambda }}{exp\left(\mathit{\lambda }\left(\mathit{\xi }+C_1\right)\right)-1}.\end{array}$$(3.14)

when ${\mathit{\lambda }}^2-4\mathit{\mu }=0,\mathit{\mu }\ne 0,\mathit{\lambda }\ne 0$,(3.15) $$\begin{array}{c}\hfill P_{(7,8)}=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}}\mp \sqrt{\frac{2}{m}}\frac{2\left(\mathit{\lambda }\left(\mathit{\xi }+C_1\right)+2\right)}{{\mathit{\lambda }}^2\left(\mathit{\xi }+C_1\right)}).\end{array}$$(3.15)

when ${\mathit{\lambda }}^2-4\mathit{\mu }=0,\mathit{\mu }=0,\mathit{\lambda }=0$,(3.16) $$\begin{array}{c}\hfill P_{(9,10)}=\pm \sqrt{\frac{2}{m}}\frac{1}{\mathit{\xi }+C_1}.\end{array}$$(3.16)

when ${\mathit{\lambda }}^2-4\mathit{\mu }<0,$(3.17) $$\begin{array}{c}\hfill P_{(11,12)}=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}}\pm \sqrt{\frac{2}{m}}\frac{2\mathit{\mu }}{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}tan\left(\frac{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }}.\end{array}$$(3.17)

and(3.18) $$\begin{array}{c}\hfill P_{(13,14)}=\pm \frac{\mathit{\lambda }}{2}\sqrt{\frac{2}{m}}\pm \sqrt{\frac{2}{m}}\frac{2\mathit{\mu }}{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}cot\left(\frac{\sqrt{4\mathit{\mu }-{\mathit{\lambda }}^2}}{2}\left(\mathit{\xi }+C_1\right)\right)-\mathit{\lambda }}.\end{array}$$(3.18) (Note: All the obtained results have been checked with Maple 16 by putting them back into the original equation and found correct.)

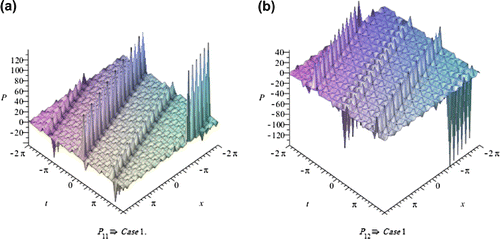
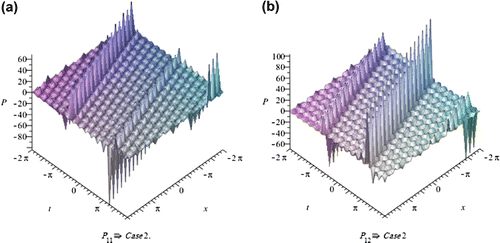
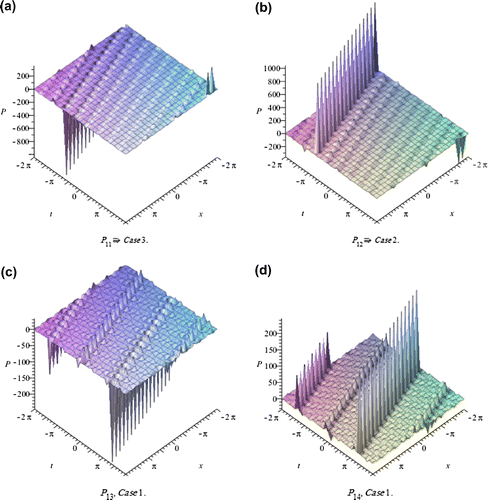
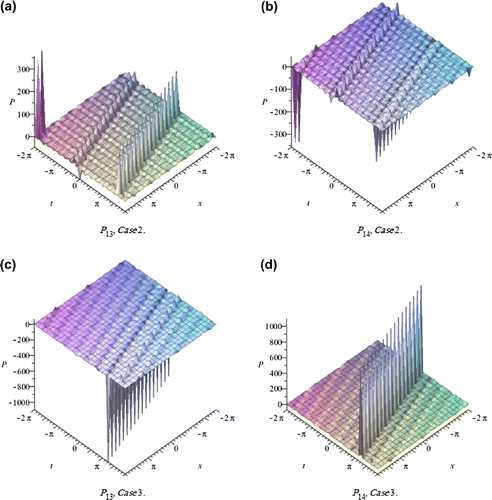
4. Physical interpretations of the solutions

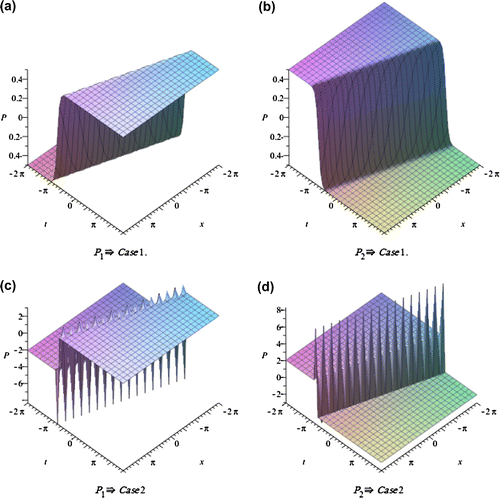
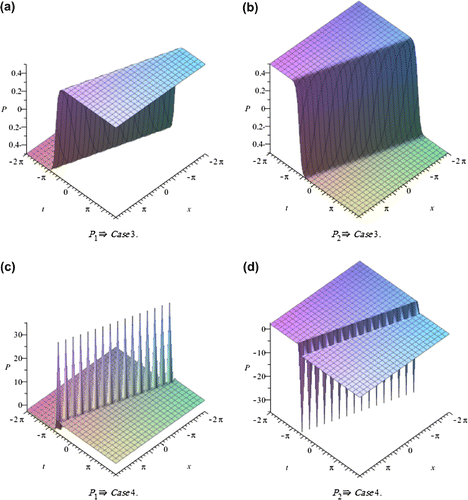
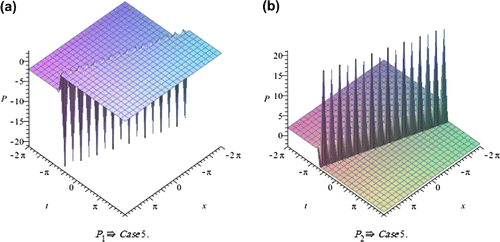
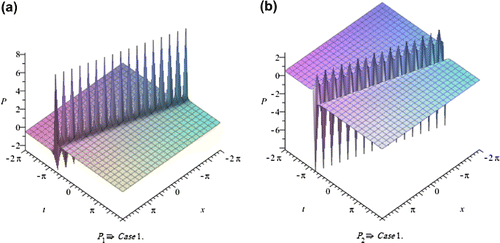
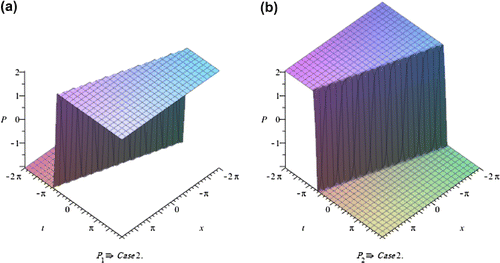
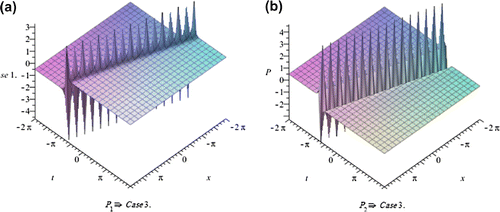
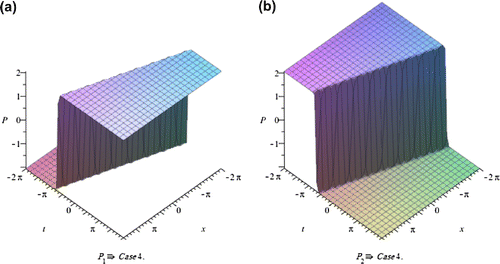
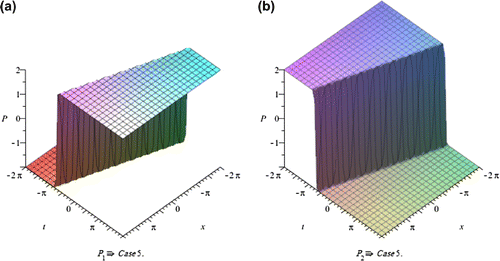
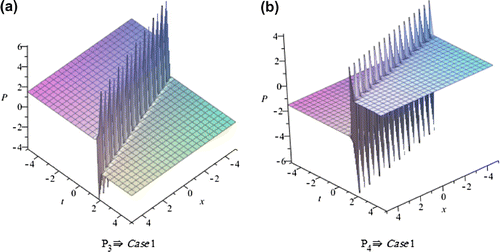
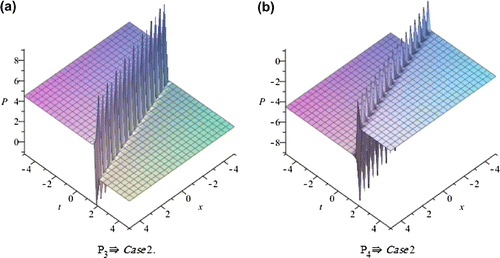
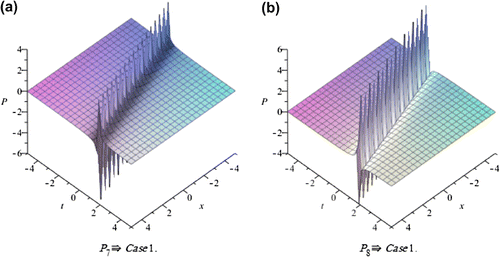
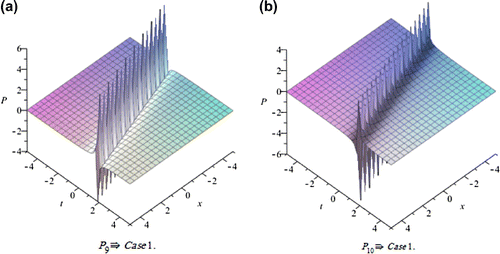
In this section, we depict the graph and signify the obtained solutions to the generalized Hirota-Satsuma couple KdV system. Now, we will discuss all possible physical significances for parameter.

Case1. when: ${\mathit{\lambda }}^2-4\mathit{\mu }>0$

(1)	$\mathit{\lambda }>0$, $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=3$, $\mathit{\mu }=2$ the solution $P_1$ and $P_2$ in Equation (3.12) represent kink shape soliton solutions.
(2)	$\mathit{\lambda }>0$, $\mathit{\mu }<0$$\Rightarrow$ For example $\mathit{\lambda }=3$, $\mathit{\mu }=-2$ the solution $P_1$ and $P_2$ in Equation (3.12) represent singular multi soliton solutions (dark and bell shaped).
(3)	$\mathit{\lambda }<0$, $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=-3$, $\mathit{\mu }=2$ the solution $P_1$ and $P_2$ in Equation (3.12) represent kink shape soliton solution.
(4)	$\mathit{\lambda }<0$, $\mathit{\mu }<0$$\Rightarrow$ For example $\mathit{\lambda }=-3$, $\mathit{\mu }=-2$ the solution $P_1$ and $P_2$ in Equation (3.12) represent singular multi soliton solutions. (bell and dark shaped).
(5)	$\mathit{\lambda }=0$, $\mathit{\mu }<0$$\Rightarrow$ For example $\mathit{\lambda }=0$, $\mathit{\mu }=-4$ the solution $P_1$ and $P_2$ in Equation (3.12) represent singular multi soliton solutions (dark and bell shaped).

 

(1)	$\mathit{\lambda }>0$, $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=3$,  $\mathit{\mu }=2$ the solution $P_1$ and $P_2$ in Equation (3.13) represent singular multi soliton solutions. (bell and dark shaped).
(2)	$\mathit{\lambda }>0$, $\mathit{\mu }<0$$\Rightarrow$ For example $\mathit{\lambda }=3$,  $\mathit{\mu }=-2$ the solution $P_1$ and $P_2$ in Equation (3.13) represent kink shape soliton solution.
(3)	$\mathit{\lambda }<0$, $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=-3$,  $\mathit{\mu }=2$ the solution $P_1$ and $P_2$ in Equation (3.13) represent singular multi soliton solutions (dark and bell shaped).
(4)	$\mathit{\lambda }<0$, $\mathit{\mu }<0$$\Rightarrow$ For example $\mathit{\lambda }=-3$,  $\mathit{\mu }=-2$ the solution $P_1$ and $P_2$ in Equation (3.13) represent kink shape soliton solution.
(5)	$\mathit{\lambda }=0$, $\mathit{\mu }<0$$\Rightarrow$ For example $\mathit{\lambda }=0$,  $\mathit{\mu }=-4$ the solution $P_1$ and $P_2$ in Equation (3.13) represent kink shape soliton solution.

Case2. when: ${\mathit{\lambda }}^2-4\mathit{\mu }>0,\mathit{\mu }=0$

(1)	$\mathit{\lambda }>0$$\Rightarrow$ For example $\mathit{\lambda }=3$ the solution $P_3$ and $P_4$ in Equation (3.12) represent singular multi soliton solutions (dark and bell shaped).
(2)	$\mathit{\lambda }<0$$\Rightarrow$ For example $\mathit{\lambda }=-3$ the solution $P_3$ and $P_4$ in Equation (3.12) represent singular multi soliton solutions (dark and bell shaped).

Case3. when: ${\mathit{\lambda }}^2-4\mathit{\mu }=0,\mathit{\mu }\ne 0,\mathit{\lambda }\ne 0$

(1)	$\mathit{\lambda }>0$,  $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=1$,  $\mathit{\mu }=0$ the solution $P_5$ and $P_6$ in Equation (3.15) represent singular kink soliton solutions.

Case4. when: ${\mathit{\lambda }}^2-4\mathit{\mu }=0,\mathit{\mu }=0,\mathit{\lambda }=0$

(1)	$\mathit{\lambda }=0$,  $\mathit{\mu }=0$$\Rightarrow$ the solution $P_7$ and $P_8$ in Equation (3.16) represent singular kink soliton solutions.

Case5. when: ${\mathit{\lambda }}^2-4\mathit{\mu }<0$

(1)	$\mathit{\lambda }>0$,  $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=2$,  $\mathit{\mu }=4$ the solution $P_1$ and $P_2$ in Equation (3.17) represent bell shape soliton and dark periodic solutions.
(2)	$\mathit{\lambda }<0$,  $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=-1$,  $\mathit{\mu }=2$ the solution $P_1$ and $P_2$ in Equation (3.17) represent singular multi soliton.
(3)	$\mathit{\lambda }=0$,  $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=0$,  $\mathit{\mu }=2$ the solution $P_1$ and $P_2$ in Equation (3.17) represent (dark and bell) periodic soliton solutions.

 

(1)	$\mathit{\lambda }>0$,  $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=2$,  $\mathit{\mu }=4$ the solution $P_{13}$ and $P_{14}$ in Equation (3.18) represent multi soliton solutions (bell and dark).
(2)	$\mathit{\lambda }<0$,  $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=-1$,  $\mathit{\mu }=2$ the solution $P_{13}$ and $P_{14}$ in Equation (3.18) represent multi soliton solutions (dark and bell).
(3)	$\mathit{\lambda }=0$,  $\mathit{\mu }>0$$\Rightarrow$ For example $\mathit{\lambda }=0$,  $\mathit{\mu }=2$ the solution $P_{13}$ and $P_{14}$ in Equation (3.18) represent multi soliton solutions (dark and bell).

Figure 1. The solitary wave solution of Equation (3.12).

Figure 2. The Solitary wave solution of Equation (3.12).

Figure 3. The Solitary wave solution of Equation (3.12).

Figure 4. The Solitary wave solution of Equation (3.13).

Figure 5. The Solitary wave solution of Equation (3.13).

Figure 6. The Solitary wave solution of Equation (3.13).

Figure 7. The Solitary wave solution of Equation (3.13).

Figure 8. The Solitary wave solution of Equation (3.13).

Figure 9. The Solitary wave solution of Equation (3.14).

Figure 10. The Solitary wave solution of Equation (3.14).

Figure 11. The Solitary wave solution of Equation (3.15).

Figure 12. The Solitary wave solution of Equation (3.16).

Figure 13. The Solitary wave solution of Equation (3.17).

Figure 14. The Solitary wave solution of Equation (3.17).

Figure 15. The Solitary wave solution of Equations (3.17 and 3.18).

Figure 16. The Solitary wave solution of Equation (3.18).

5. Conclusion

The exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method has been applied in this paper to find the exact traveling wave solutions and then the solitary wave solutions of the generalized Hirota-Satsuma couple KdV system . Let us compare between our results obtained in the present article with the well-known results obtained by other authors using different methods as follows: our results of nonlinear dynamics of the generalized Hirota-Satsuma couple KdV system are new and different from those obtained in Yan (2003), and Figures 1–16, show the solitary traveling wave solution of the generalized Hirota-Satsuma couple KdV system . We can conclude that the exp$(-\mathit{\phi }(\mathit{\xi }))$-expansion method is a very powerful and efficient technique in finding exact solutions for wide classes of nonlinear problems and can be applied to many other nonlinear evolution equations in mathematical physics. Another possible merit is that the reliability of the method and the reduction in the size of computational domain give this method a wider applicability.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Mostafa M.A. Khater

Mostafa M.A. Khater is a researcher in pure mathematics specially finding the exact and solitary wave solutions of NLPDES. He has Bsc and MSc from Zagazig University (2011) and Mansoura University(2016). He published 26 research articles in some international journals. He is a reviewer of some global journals and also editor board of Journal of Research in Applied Sciences (JRAS) and Journals of Harmonized Research.