Bayesian index to compare assumed survival functions of two hazards following exponential distributions

Abstract

In clinical studies, the period before an event occurs is frequently considered as an outcome. The general term used for this analytical method in clinical studies is “survival time analysis”. The method employs Cox regression to compare hazards between groups. In this paper, we propose an index defined in the Bayesian framework to compare hazards. This index compares the sizes of the hazards directly. Further, we propose two methods to calculate the sizes of the hazards. One is an approximate method, by which we can easily calculate the size, and the other is an exact method. In addition, we apply the proposed index to two actual clinical studies to assess its usability.

Keywords:

• Bayesian statistics
• survival time analysis
• superiority test
• one-sided test
• hypothesis test

Public Interest Statement

In clinical studies, the period before an event occurs is frequently considered as an outcome. The general term used for this analytical method in clinical studies is “survival time analysis”. The method employs Cox regression to compare hazards between groups. In this paper, we propose an index defined in the Bayesian framework to compare hazards. We apply the proposed index to two actual clinical studies to assess its usability.

1. Introduction

Events such as death and survival at the end of the studies are important outcomes in clinical studies. Survival time analysis is generally employed to compare groups when analyzing these outcomes.

It is not an exaggeration to say that in the frequentist framework, the basic methodology of survival time analysis has almost been settled (Colett, 2003; Hosmer, Lemeshow, & May, 2008). Besides, recently the method of direct comparison of hazards was proposed (Heller & Mo, 2015).

In the Bayesian framework, on the other hand, a methodology has not yet been established. In this paper, Bayes introduced the idea of inverse probability, which, following the work of Laplace and others, came to be known as Bayes’ Theorem. The Bayesian approach to statistical inference is useful for several reasons. Perhaps foremost among them is the formal manner in which Bayesian methods incorporate prior information, whether it be expert opinion or historical data. The sequential learning nature of the method, with prior knowledge being updated to yield posterior distributions, forms the basis for adaptive methods, in which models are continually updated with new information. Other advantages of the method include the ease of predictive model building and the avoidance of large-sample approximations in some cases. Furthermore, Bayesian analysis provides straightforward probabilistic statements about parameters of interest and inferential questions. The Bayesian influence can be found in a broad array of fields such as statistics, medicine, epidemiology, computer science, economics, engineering, physics, and philosophy of science. A number of papers on biomedical applications have suggested the use of Bayesian methods in healthcare evaluation (Spiegelhalter, 2004; Zhao, Feng, Chen, & Taylor, 2015), the pharmaceutical industry (Grieve, 2007; Racine, Grieve, Fluhler, & Smith, 1986), and clinical trials (Berry, 2006; Cornfield, 1976; Lee & Chu, 2012; Spiegelhalter, Freedman, & Parmar, 1993, 1994).

As mentioned above, Bayesian statistics are employed in clinical trials to evaluate outcomes, but no one has so far proposed an index for the easy interpretation of results. In Bayesian model selection, the most widely used tools are Bayes factors (BFs) (Kass & Raftery, 1995). However, these are unscaled when improper priors are used. In order to overcome this problem and approximate the underlying BFs, fractional and intrinsic BFs (Berger & Pericchi, 1996; O’Hagan, 1995) have been proposed in the literature. Thus, BFs are useful in Bayesian model selection. However, we cannot directly compare parameters of posterior distributions using BFs. Moreover, it is often difficult to interpret BFs for several reasons; one reason is that the coefficients of BFs do not have intuitive meaning.

Zaslavsky (2010, 2013) and Kawasaki and Miyaoka (2012b) were the first to propose a new type of index, called the “Bayesian index”, for the comparison of binomial proportions and to apply it to clinical trial results. These indexes can compare parameters directly, and since the results are evaluated as a probability, it is easy to understand them intuitively. In this paper, we propose the index η = P(h₁ < h₂ |${\underline{T}}_1,{\underline{T}}_2$), which is developed from the index proposed by Kawasaki and Miyaoka (2012a, 2012b), for comparison of hazards, where h_i indicates the hazard of group i, with the exponential distribution assumed for the survival function. We further assume that the prior distribution is a gamma distribution with parameters α_i and β_i. ${\underline{T}}_i$ denotes the total observation duration of group i. This index indicates the probability that the hazard of group 1 is less than that of group 2.

The remainder of the paper is organized as follows. We propose a method for the exact calculation of the index η as well as a method for an approximate calculation, with which we can easily calculate the probability of the index, in Section 2. We compare the approximate probability with the exact probability and present the results of actual clinical trials to show the utility of η in Section 3. Finally, we conclude with a brief summary in Section 4.

2. Methods

2.1. Notation

Let C_ij and Y_ij be independent. For patient number j in group i, let Y_ij be the random variable representing the time to event occurrence, C_ij be the random variable representing the time to censoring (where i = 1, 2 and j = 1, 2, …, n_i), and T_ij = min(Y_ij,C_ij) be the variable representing the observation duration. Additionally, to judge the executing or censoring event for patient number j in group i, we define the event index as$${\mathit{\delta }}_{ij}=\left\{\begin{array}{cc}1\hfill & \left(Y_{ij}\le C_{ij}\right)\hfill \\ 0\hfill & \left(Y_{ij}>C_{ij}\right)\hfill \end{array}\right.,$$

where the realized value of T_ij is t_ij. Furthermore, let the hazard function of patient number j in group i be constant as follows$$h(t_{ij})=h_i(h_i>0).$$

The probability density function and survival time function can be denoted, respectively, as$$f(t_{ij})=h_i{e}^{-h_i{t}_{ij}}\text{and}S\left(t_{ij}\right)=e^{-h_i{t}_{ij}}.$$

2.2. Posterior distribution

We give the likelihood function for group i as$$\begin{array}{cc}L\left(h_i;t_i\right)\hfill & =\prod _{j=1}^{n_i}{[h_i{e}^{-h_i{t}_{ij}}]}^{{\mathit{\delta }}_{ij}}{[e^{-h_i{t}_{ij}}]}^{1-{\mathit{\delta }}_{ij}}\hfill \\ \hfill & =h_i^{\sum _{j=1}^{n_i}{\mathit{\delta }}_{ij}}{e}^{\left(-h_i\sum _{j=1}^{n_i}{t}_{ij}\right)}\hfill \end{array}$$

Assuming gamma distributions with parameters α_i and β_i as prior distributions, and i = 1, 2, we have$$g\left(h_i\right)=\frac{{\mathit{\beta }}_i^{{\mathit{\alpha }}_i}}{\mathrm{\Gamma }({\mathit{\alpha }}_i)}{h}_i^{{\mathit{\alpha }}_i-1}{e}^{-{\mathit{\beta }}_i{h}_i}.$$

From Bayes’ Theorem, the posterior distribution for i is$$g\left(h_i|{\underline{t}}_i\right)=\frac{{({\mathit{\beta }}_i+{\sum }_{j=1}^{n_i}{t}_{ij})}^{{\mathit{\alpha }}_i+{\sum }_{j=1}^{n_i}{\mathit{\delta }}_{ij}}}{\mathrm{\Gamma }({\mathit{\alpha }}_i+\sum {\mathit{\delta }}_{ij})}{h}_i^{{\mathit{\alpha }}_i+\sum _{j=1}^{n_i}{\mathit{\delta }}_{ij}-1}{e}^{-({\mathit{\beta }}_i+\sum _{j=1}^{n_i}{t}_{ij})h_i}.$$

The posterior distribution follows a gamma distribution with parameters $a_i={\mathit{\alpha }}_i+\sum _{j=1}^{n_i}{\mathit{\delta }}_{ij}$ and $b_i={\mathit{\beta }}_i+\sum _{j=1}^{n_i}{t}_{ij}$.

2.3. Exact expression

Theorem

The exact expression for the posterior hazard of group 1 to be smaller than that of group 2 is(1) $$\mathit{\eta }=P\left(h_1<h_2|{\underline{T}}_1,{\underline{T}}_2\right)=1-\frac{1}{a_{2}Beta(a_1,a_2)}{\left(\frac{b_2}{b_1+b_2}\right)}^{a_2}{}_2{F}_1\left(a_2,1-a_1;1+a_2;\frac{b_2}{b_1+b_2}\right)=I_{\frac{b_1}{b_1+b_2}}\left(a_1,a_2\right),$$(1)

where ${}_2^{}{F}_1\left(a_1,a_2;b;x\right)$ denotes the hypergeometric series, $I_x\left(a,b\right)$ denotes the regularized incomplete beta function and Beta(a, b) denotes the beta function.

Proof

The posterior probability is given by$$g_i(h_i|{\underline{t}}_i)=\frac{b_i^{a_i}}{\mathrm{\Gamma }(a_i)}{h}_i^{a_i-1}{e}^{-b_i{h}_i}.$$

Hence, its joint probability density function is$$f_{1,2}(h_1,h_2,|{\underline{t}}_1,{\underline{t}}_2)=\frac{b_1^{a_1}{b}_2^{a_2}}{\mathrm{\Gamma }(a_1)\mathrm{\Gamma }\left(a_2\right)}{h}_1^{a_1-1}{e}^{-b_1{h}_1}{h}_2^{a_2-1}{e}^{-b_2{h}_2}.$$

From the definition, η can be given as$$\mathit{\eta }=P\left(h_1<h_2|{\underline{T}}_1,{\underline{T}}_2\right)=\frac{b_1^{a_1}{b}_2^{a_2}}{\mathrm{\Gamma }\left(a_1\right)\mathrm{\Gamma }\left(a_2\right)}\underset{0}{\overset{\infty }{\int }}\underset{0}{\overset{h_2}{\int }}{h}_1^{a_1-1}{e}^{-b_1{h}_1}{h}_2^{a_2-1}{e}^{-b_2{h}_2}d{h}_{1}d{h}_2.$$

From Theorem 1 in Kawasaki and Miyaoka (2012a),$$\mathit{\eta }=P(h_1<h_2|{\underline{T}}_1,{\underline{T}}_2)=1-\frac{1}{a_{2}Beta(a_1,a_2)}{\left(\frac{b_2}{b_1+b_2}\right)}^{a_2}{F}_1\left(a_2,1-a_1;1+a_2;\frac{b_2}{b_1+b_2}\right).$$

Furthermore, from Formulas 26.5.23 and 26.5.2 of Abramowitz and Stegun (2010), i.e.$$I_x\left(a,b\right)=\frac{1}{Beta\left(a,b\right)}·\frac{x^a}{a}·{}_2^{}{F}_1\left(a,1-b;1+a;x\right)$$

and$$I_z\left(a,b\right)=1-I_{1-z}\left(b,a\right),$$

η can be given as

$\mathit{\eta }=1-I_{\frac{b_2}{b_1+b_2}}\left(a_2,a_1\right)=I_{\frac{b_1}{b_1+b_2}}\left(a_1,a_2\right)$ □

We can calculate the exact probability by Equation (1) and using expressions containing various hypergeometric series. In this paper, we use one such expression. Kawasaki and Miyaoka (2012b) give a more detailed proof in a similar problem. For the SAS programming code used for calculating the probability of η, see Appendix 1.

2.4. Approximate expression

We can easily formulate an approximate expression using the expected value of the posterior distribution and the variance. The expected value and the variance of the difference between the posterior distributions are, respectively,$$E\left(h_{1,\text{post}}-h_{2,\text{post}}\right)=\frac{a_1}{b_1}-\frac{a_2}{b_2}\text{and}V\left(h_{1,\text{post}}-h_{2,\text{post}}\right)=\frac{a_1}{b_1^2}+\frac{a_2}{b_2^2},$$

where h_i,post denote the posterior hazard, and i = 1, 2. Therefore, we can rewrite Equation (2) as$$\mathit{\eta }=P\left(h_1<h_2|{\underline{T}}_1,{\underline{T}}_2\right)=P\left(\frac{\left(h_{1,\text{post}}-h_{2,\text{post}}\right)-E\left(h_{1,\text{post}}-h_{2,\text{post}}\right)}{\sqrt{V\left(h_{1,\text{post}}-h_{2,\text{post}}\right)}}<\frac{-E\left(h_{1,\text{post}}-h_{2,\text{post}}\right)}{\sqrt{V\left(h_{1,\text{post}}-h_{2,\text{post}}\right)}}\right)\approx P\left(Z<\frac{-E\left(h_{1,\text{post}}-h_{2,\text{post}}\right)}{\sqrt{V\left(h_{1,\text{post}}-h_{2,\text{post}}\right)}}\right)=\mathrm{\Phi }\left(\frac{-\frac{a_1}{b_1}+\frac{a_2}{b_2}}{\sqrt{\frac{a_1}{b_1^2}+\frac{a_2}{b_2^2}}}\right),$$

where Φ(·) is the cumulative distribution function of the standard normal distribution. Thus, η can easily be calculated if we know the cumulative distribution function of the standard normal distribution.

3. Results

3.1. Simulation

Our aim of simulation in Section 3.1 is to verify the condition under which the differences of the probability, indicated by the approximated method and that by the exact method, become greater. Hence, we compare the exact method and the approximation method using simulated data in this section. The simulation method is as follows. Assume the data occur randomly from the exponential distribution when the hazard ratio is between 0.40 and 1.50 in steps of 0.10, and that they occur randomly with binomial proportions when the censoring ratio is 10 or 40%. Further, let the sample sizes for the groups be either balanced or unbalanced. For the balanced cases, we set n₁ = n₂ = 10, n₁ = n₂ = 20, n₁ = n₂ = 50, or n₁ = n₂ = 100, and for the unbalanced cases, we set n₁ = 15 and n₂ = 5, or n₁ = 75 and n₂ = 25. In this simulation, we use the non-informative prior, that is, α_i = β_i = 0.001 and i = 1, 2.

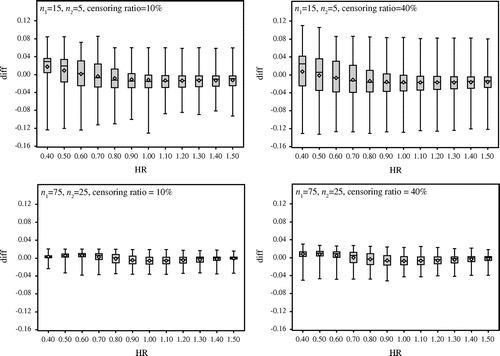
At the beginning, we verify the difference between the probability by the approximated method and that by the exact method with small sample size. Figure 1 compares the results under the censoring ratios 10 and 40% when n₁ = n₂ = 10 and n₁ = n₂ = 20. The box plots show the difference between the exact probability and the approximate probability, with the vertical axis representing the difference between the exact probability and the approximate probability, and the horizontal axis representing the hazard ratio. We make the following observations from Figure 1:

•	When the censoring ratio is 10%, the difference between the exact probability and the approximate probability is about 4% at maximum.
•	The difference is about 12% at maximum when the censoring ratio is 40% and the hazard ratio is 0.40.
•	The difference shows a variance of around 0% when the hazard ratio is 1.

Figure 1. Comparison of the results under the censoring ratios 10 and 40% when n₁ = n₂ = 10 and n₁ = n₂ = 20.

Notes: The vertical axis shows the difference between the exact probability and the approximate probability, and the horizontal axis indicates the hazard ratio.

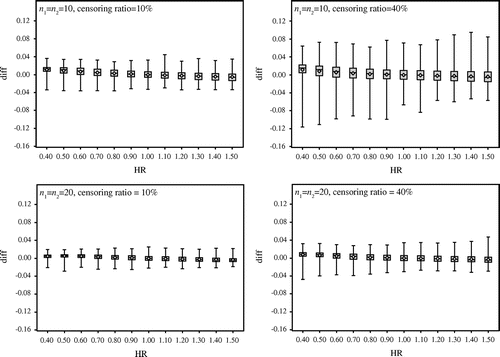
Next, we verify that with large sample size. Figure 2 compares the results under the censoring ratios 10 and 40% when n₁ = n₂ = 50 and n₁ = n₂ = 100. Figure 2 shows the following:

•	The results are not affected by censoring, and the difference between the exact probability and the approximate probability goes up to about 2.5%.
•	The interquartile range is very narrow.

Figure 2. Comparison of the results under the censoring ratios 10 and 40% when n₁ = n₂ = 50 and n₁ = n₂ = 100.

Notes: The vertical axis shows the difference between the exact probability and the approximate probability, and the horizontal axis indicates the hazard ratio.

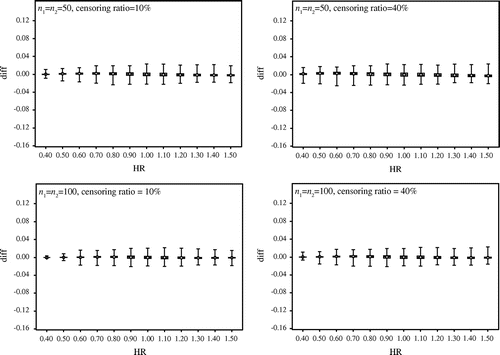
At the end, we verify that with unbalanced sample size. Figure 3 compares the results under the censoring ratios 10 and 40% for the combinations n₁ = 15, n₂ = 5 and n₁ = 75, n₂ = 25. Figure 3 shows the following:

•	Boxes are wide, and the difference between the exact probability and the approximate probability is large.
•	The difference is even larger relative to the case where both groups have the same sample size in total.

Figure 3. Comparison of the results under the censoring ratios 10 and 40% when n₁ = 15, n₂ = 5 and n₁ = 75, n₂ = 25.

Notes: The vertical axis shows the difference between the exact probability and the approximate probability, and the horizontal axis indicates the hazard ratio.

3.2. Examples

3.2.1. Chronic active hepatitis cases

In this section, we apply the proposed index to clinical trial data used in Kirk, Jain, Pocock, Thomas, and Sherlock (1980). In this trial, 44 chronic active hepatitis cases were assigned randomly to either the prednisolone group (treatment group) or the control group with no treatment (control group). From the treatment group’s 22 cases, 11 were observed and the remaining 11 were censored, and from the control group’s 22 cases, 16 were observed and the remaining 6 were censored. The most interesting outcome in the trial was the survival time of patients after the trial commenced.

The p-value was 0.0309 by the log-rank test and 0.0105 by the Wilcoxon test. This indicates a longer survival time for the treatment group at the significance level of 5%. The proposed index indicates 98.35% as the approximate probability and 99.01% as the exact probability, with the hazard of the treatment group lower than that of the control group. We assume the prior distribution to be non-informative for both groups.

3.2.2. Lung cancer data analysis

In this section, we apply the proposed index to clinical trial data used in Chen et al. (2007).

We obtained the non-small-cell lung cancer data used in Chen et al. (2007) from http://www.ncbi.nlm.nih.gov/projects/geo/ with accession number GSE4882. The data contained 672 gene profiles of 125 lung cancer patients. From among them, 38 patients died, and the remainder were censored.

The median follow-up of 101 patients was 20 months. The patients with a high-risk gene signature showed a shorter median overall survival than those with a low-risk gene signature. The p-value was 0.001 by the log-rank test; the proposed index gave 99.99% probability as calculated approximately as well as exactly. A high-risk gene signature was associated with a median relapse-free survival period of 13 months, whereas a low-risk gene signature was associated with a median relapse-free survival period of 29 months. Here, the p-value was 0.002 by the log-rank test, and the proposed index gave 99.53% as the approximate probability and 99.72% as the exact probability.

4. Discussion and conclusions

In this paper, we have proposed an index to compare the hazards defined in the Bayesian framework. Further, we have presented two probability functions: the approximation function, which provides for easy calculation, and the exact function.

Our simulation experiment shows a difference between the exact probability and the approximate probability. Specifically, when we censor more, the difference becomes larger. By contrast, we found that the difference becomes smaller with larger sample sizes; the effect of censoring too becomes less. With unbalanced sample sizes for the groups, the difference becomes larger. Thus, we recommend using the exact probability calculation for cases with small samples, unbalanced sample sizes, or numerous censorings.

We applied the proposed index to actual clinical trial data and confirmed that it shows the difference between groups very clearly. Because, we indicated it in example 1 that the hazard of the treatment group becomes lower than that of the control group with about 99% probability. Thus, as this index provides comparison of the hazards with probability, the result can be indicated within the range of 0–100%. So, the index can be very easy to understand intuitively.

Thus, the index proposed in this paper to compare hazards is easy to understand and intuitive and should be beneficial for use in research studies.

Acknowledgements

The authors also wish to thank the anonymous reviewers for their suggestions that helped to improve the manuscript.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Yohei Kawasaki

Yohei Kawasaki received the BS degree in mathematics in 2005 and the MS and PhD degrees in mathematical science from Tokyo University of Science, Japan in 2007 and 2012, respectively. He joined the Mitsubishi Tanabe Pharma Corporation, the National Center for Global Health and Medicine, Tokyo University of Science, in 2005, 2013, and 2014, respectively.

He has published over 70 research articles in reputed international journals. His research interests include the classical analysis, Bayesian analysis, Biostatistics and mathematical education. He is currently a lecturer in the Department of Drug Evaluation and Informatics, School of Pharmaceutical Sciences, University of Shizuoka, Japan.

He also is a guest researcher of National Center for Global Health and Medicine and Shizuoka General Hospital as Biostatistician.

Appendix 1

SAS programming code

The following SAS macro can be used to calculate η = P(h₁ < h₂ |${\underline{T}}_1,{\underline{T}}_2$).

The parameters are defined as follows: N1 = sample size of group 1; N2 = sample size of group 2; X1 = total survival time of group 1; X2 = total survival time of group 2; e1 = total event count for group 1; e2 = total event count for group 2; alpha1 and beta1 = hyperparameters for group 1; alpha2 and beta2 = hyperparameters for group 2.

Subject: Calculation of η = P(h₁ < h₂ |${\underline{T}}_1,{\underline{T}}_2$)

Output variables: Prob_E (Exact method) and Prob_A (Approximate method)

%MACRO PROBMK(N1=,N2=,X1=,X2=,e1=,e2=,alpha1=,beta1=,alpha2=,beta2=);

data BASE01;

/* sample sizes */

n1 = &N1; n2 = &N2;

/* all survival times */

x1 = &X1; x2 = &X2;

/* all event counts */

e1 = &e1; e2 = &e2;

XT1 = X1/N1; XT2 = X2/N2;

/* Input variables */

/* Hyperparameters */

al1 = &alpha1; be1 = &beta1;

al2 = &alpha2; be2 = &beta2;

a1 = e1 + al1; b1=(n1*XT1)+be1;

a2 = e2 + al2; b2=(n2*XT2)+be2;

run;

%let N = 1000;

/* Hypergeometric work */

data work01;

set BASE01;

o = a2; p = 1-a1;

q = 1 + a2;

u = b2/(b1 + b2);

retain K1 - K&N 1;

array K(&N);

do i = 1 to &N;

do j = 1 to i;

o1 = o + j-1;

p1 = p + j-1;

q1 = q + j-1;

K(j)=(o1*p1)/(q1);

end;

%macro kkk;

SS + %do i = 1%to %eval(&N-1);

K&i*

%end;

K&N*(u**i)/FACT(i);

%mend kkk;

%kkk

end;

F = sum(1,SS);

/* Output variables */

/* Exact */

Prob_E = 1-round(1/(a2*Beta(a1,a2))*((b2/(b1 + b2))**a2)*F,0.0001);

/* Approximate */

FFF1=((-a1/b1)+(a2/b2));

FFF2 = Sqrt(a1/b1**2 + a2/b2**2);

FFF = FFF1/FFF2;

Prob_A = round(CDF(‘Normal’,FFF),0.0001);

keep n1 n2 x1 x2 a1 b1 a2 b2 FFF1 FFF2 Prob_E Prob_A;

run;

proc print data = work01; var Prob_E Prob_A; run;

%MEND PROBMK;

* Program End;