An ecogenetic disease-affected predator–prey model

Abstract

A nonlinear ecoepidemic model of new type is introduced here, in that it contains genetically distinguishable subpopulations. Further, in the system a predator is present, that hunts these two disease-affected genotypes. Under the assumptions of the model, the disease cannot endemically survive in the predator-free environment. The healthy prey can thrive in the absence of the predators, but this is in line with previous results and does not appear to be due to the effects of the epidemics. On the other hand, the disease affects the stability of the purely demographic equilibria.

Keywords:

• predator–prey
• epidemics
• transmissible diseases
• genetic variability

AMS subject classifications:

• Primary: 92D25
• Secondary: 92D10
• 92D40

Public Interest Statement

Evolutionary adaptation in population genetics is observed in the peppered moth, Biston betularia, possessing melanic and non-melanic morphs. As a mimetic feature against predators, 200 years ago, it was light colored like trees trunks. But in the following century industrial pollution darkened the trees; the melanic moth, carbonaria, thrived instead. Parasites respond differently to host genotypes. Experiments with Plodia interpuncella and the granulosis virus, report an increased viral resistance in the virus-affected subpopulation. A predator–prey mathematical model is introduced, where the prey are genetically distinguishable and one genetic subpopulation suffers an epidemic. Specifically, the prey is Drosophila suzukii, one of its genotype being affected by nematodes; its predators are frogs, but also the commercially available Orius majusculus and Orius laevigatus . The ecosystem thrives, the predators are instrumental in disease eradication, both genotypes of the healthy prey can survive in a predator-free environment, predators elimination is unrelated to the disease presence.

1. Introduction

Mathematical ecogenetic models have recently been introduced (Venturino , 2012; Viberti & Venturino , 2014). They seem to be a particular example of what are nowadays commonly called “structured populations models,” that have been studied for quite some time, starting from the seminal work of Kostitzin in the 30s of the past century; on this, see the nice review paper (Scudo , 1976). In fact, for structured populations, now, one understands mainly populations that are not just dependent on time, but also on age, distinguishing therefore several age cohorts (Cushing , 1998). Human survival tables based on age cohorts have been in use among accountants for centuries, in order to calculate life insurance premiums. In ecology, in the simplest case of insects, for instance, these could be the larval, pupa, and adult life stages; for fishes instead, we would have eggs, larvae, immature juveniles, and adults. Structure therefore adds to the population description a new dimension, be it age, as depicted and analyzed in the classical papers (Gurtin & McCamy , 1974, 1979), and for which analytical approaches are available (Webb , 1985), or instead size, for which more sophisticated numerical methods need to be introduced (Angulo & López-Marcos , 1999). Indeed, the basic age description corresponds to a linear, or more generally nonlinear (Gurtin & Levine , 1979), wave equation, with an initial and a boundary condition at age zero, for which standard numerical schemes are available (Smith , 1985). These considerations could be extended to interacting populations (Venturino , 1984, 1987) A structure can also be superimposed on diseases: the classical Kermack–McKendrick model (Kermack & McKendrick , 1927) considers the population partitioned among susceptibles, infected, and recovered individuals. In addition, one could also include a latent period of exposed individuals in which the disease is incubating, but they are not yet able to spread it. A more general description in which all these stages are envisioned in a continuum is contained in Venturino (1985).

In the of models (Venturino , 2012; Viberti & Venturino , 2014), the main idea is to consider a population which has two identifiable genotypes, and in some way intermingles with another population. In Venturino (2012) the case of predator–prey interactions in considered. Here too, we examine a highly nonlinear system, containing a basic demographic situation of the same type as Venturino (2012), which differs however in a major feature.

In the past 20 years or so, a lot of effort in mathematical biology has been devoted to the study of ecosystems in which also epidemics spread. Thus, in addition to their demographic interactions, populations also experience transmissible diseases. The presence of the latter profoundly influences the system’s outcomes, so that a stable population configuration from the purely demographic point of view becomes instead unattainable in presence of the disease (Beltrami & Carroll , 1994; Hadeler & Freedman , 1989; Venturino , 1994). The basic demographic models can be of the predator–prey type with disease affecting the prey (Chattopadhyay & Arino , 1999; Venturino , 1995), or also the predators (Auger et al. , 2009; Venturino , 2002), but can include also e.g. competition (Saenz & Hethcote , 2006). Some of the earlier developments of this discipline are contained in Chapter 7 of Malchow, Petrovskii, and Venturino (2008). More recent contributions consider issues such as the study of equilibria (Delgado, Molina-Becerra, & Suarez , 2005) and their global stability (Zhen & Haque , 2006). Viruses in planktonic and other ecosystems have been considered in Beretta and Kuang (1998) and Singh, Chattopadhyay, and Sinha (2004), but the effect of viruses could also be favorably exploited to control the spread of pests (Bhattacharyya & Bhattacharya , 2006). More recent investigations include findings of complex dynamics (Bate & Hilker , 2013), and of chaotic behavior (Kooi, van Voorn, & Das , 2011), predation switching (Hotopp, Malchow, & Venturino , 2010), an idea taken from the purely demographic models (Khan, Balakrishnan, & Wake , 2004), applications of harvesting and control theory as measures to contain epidemics (Bairagi, Chaudhuri, & Chattopadhyay , 2009; Jana & Kar , 2013; Kar & Jana , 2013), more sophisticated models including delays (Bairagi, Sarkar, & Chattopadhyay , 2008), various functional response functions (Bairagi, Roy, & Chattopadhyay , 2007). These ecoepidemic models have also been reformulated as intraguild predations (Sieber & Hilker , 2011). A recent, rather comprehensive, review of the field is provided in Venturino (2016).

It is well known that genetic variability may influence the response to pathogens and diseases. For instance, an example of this kind of situation is provided in humans by sickle cell anemia, which affects mainly individuals belonging to a recessive blood type.

In the animal realm, the classical example of evolutionary adaptation in population genetics is provided for instance by the peppered moth Biston betularia. It is well-known that this insect has several melanic and non-melanic morphs that are genetically controlled. About 200 years ago the B. betularia was light colored and this helped against predators, mainly birds, since the trunk of the trees where they rested were mainly of light colors (Grant , 1999). In the following century, however, smoke and pollution due to the newly implanted industries in the UK rendered the trunks of dark colors, causing higher moth mortality due to predation, as they were more easily spotted. Conversely, the melanic moth, carbonaria, thrived because with its dark color it could easily hide among the trees. Rather recently, there has been a hot debate on whether this phenomenon is attributable or not to evolutionary mechanisms (Clarke , 2003; Hooper , 2002).

In Lively and Apanius (1995) it is remarked that parasites respond in different ways to various host genotypes, this being supported by some field evidence, for which parasites attack the most abundant genotype. Evidence, Lively, Craddock, and Vrijenhoek (1990) and Vrijenhoek (1993) shows that the parthenogenetic fish Poeciliopsis spp., which has a sexual and a clonal form coexisting in the population, infected by the trematode larvae Uvulifer spp., harbored more parasites than coexisting outcrossed fish. The result was the opposite in case of a highly inbred population, but later, when sexual fish were reintroduced into the initial inbred population, the clonal fish turned out to be more infected than the sexual ones (Vrijenhoek , 1993). This demonstrates that parasites can rapidly spot changes in the genotype frequency in a population.

Also, one strain of nematode that originally was able to infect four species of Drosophila, after being exposed to only one of them for a couple of years, was unable to infect one of the original species (Jaenike, 1993). Similarly, experiments with Plodia interpuncella and the granulosis virus (Read , 1991) report an increased viral resistance that was much higher in the subpopulation maintained in the presence of the virus than in the virus-free control subpopulation. This evidence indicates that host specificity may change in time due also to genetic changes.

Motivated by the fact that different genotypes may experience different responses to external interferences therefore also in animals, as mentioned above, and thus not only to predators, but also to pathogens, we consider here a hypothetical ecogenetic model, similar to some other systems already studied, that in comparison with the current literature (Venturino , 2012; Viberti & Venturino , 2014), makes a step forward, namely it introduces a disease among the genetically distinguishable population, that affects only one genotype.

Specifically, we consider two genotypes of the Drosophila suzukii, one of which is affected by nematodes, that are however not explicitly built into the model. They only partition the insects among healthy and infected classes. This fruit fly has several predators, the most common of which are the frogs. In addition, there are some that are even commercially available (Cuthbertson, Blackburn, & Audsley , 2014), such as Orius majusculus, Orius laevigatus, Atheta coriaria, Hypoaspis miles, and Anthocoris nemoralis.

The ecosystem under investigation then contains the prey, with two distinct genotypes, of which only one is subject to a disease. In addition, the predators hunt these subpopulations. Possible questions to which such a model could provide an answer is related to whether the presence of the predators is able to extinguish the disease, or whether the infection in the prey can wipe out the predators. The answers are tied to the interpretation of the actual situation at hand. For instance, we would like to get rid of the predators if they are seen as a pest; on the other hand, if the prey are a valuable resource, to eliminate the disease among them would certainly enhance their survival.

The presentation is organized as follows. In the next section, we describe mathematically the system in consideration. Section 3 studies the possible long-term behavior of the model, assessing its equilibria, and in Section 4 their stability is investigated. A final discussion of the findings concludes the paper.

2. The Model

Let X and Y be the genotypes of the prey population. We assume that one of them is prone to a disease, for which we partition its individuals in the two subpopulations of susceptibles S and infected I, so that $X=S+I$. Let Z denote the predators.

We make the standard assumptions of mathematical ecogenetic models (Venturino , 2012), without using the more sophisticated HTII response terms considered in Viberti and Venturino (2014). The two prey genotypes reproduce exponentially, a fact that is modeled via logistic terms, and produce offsprings of both genotypes with probabilities p and q, $p+q=1$.

The reproduction at rate is r, all the offsprings are born healthy, i.e. they belong to class S, in other words the disease is not vertically transmitted. The susceptibles feel the population pressure of the similar individuals and those of the other genotype, but not of the infected. Here also the infected recovering from the disease that re-enter into this class are accounted for. Its losses are due to predation and possible contagion of the disease.

The infected are recruited only via these successful contacts, are hunted and can recover. We assume the disease to be mild and also predation to occur at a fast rate, for which the disease-induced mortality can be disregarded. We also disregard the intraspecific population pressure on the infected.

The second prey genotype population Y reproduces also logistically, feeling the intraspecific population pressure, as well as the one of the other genotype. Furthermore, contacts of Y with infected constitute an additional mortality $\mathit{\mu }IY$, which we take at the same rate as the intraspecific population pressure, thus setting $\mathit{\mu }=b$. This asymmetry in the infected behavior is ascribed to the fact that they are poisonous to the predators Z, as we will see below, and in that sense they are also harmful to the genotype Y that is not their own.

The predators hunt the first genotype, independently of whether it is infected or not, and the second one Y possibly at a different rate. Their natural mortality is m, to which a mortality j due to interaction with the infected is added. Note that in describing the hunting of the predators on the infected, we separate the influences that the latter have on the predator: there is a positive effect due to the feeding, but also the contact with them might lead to the predators’ death.

The model is thus:(1) $$\begin{array}{cc}\hfill S^{\prime }& =[rp-aS](S+Y)-hSZ-\mathit{\lambda }SI+\mathit{\gamma }I\hfill \\ \hfill I^{\prime }& =I[\mathit{\lambda }S-hZ-\mathit{\gamma }]\hfill \\ \hfill Y^{\prime }& =[rq-bY](S+I+Y)-gYZ\hfill \\ \hfill Z^{\prime }& =Z[e(h(S+I)+gY)-m-jI]\hfill \end{array}$$(1)

where r is the prey reproduction rate, a and b are the intraspecific competition rates of genotypes X and Y, h and g the predators’ hunting rates on genotypes X and Y, respectively. Note that we have also implicitly assumed that it is equally likely for the predators to capture a healthy or an infected individual of genotype X. Further, $e<1$ denotes the conversion factor of captured prey into new predators, $\mathit{\lambda }$ is the disease contact rate and $\mathit{\gamma }$ represents its recovery rate.

3. Equilibria

We find the following system’s equilibria $E_k=\left(S_k,I_k,Y_k,Z_k\right)$. The origin $E_0$, the predator- and disease-free equilibria $E_1$ and the disease-free point $E_2$:$$E_1=\left(\frac{rp}{a},0,\frac{rq}{b},0\right),E_2=\left(\frac{m-eg{Y}_2}{eh},0,Y_2,\frac{H_2{Y}_2+K_2}{g^{2}eh\left(ag-hb\right)Y_2}\right),$$

where $H_2=egr(h-g)(qag+phb)-hbm(ag-hb)$, $K_2=rqm(b{h}^2-a{g}^2)$ and $Y_2$ solves(2) $$\begin{array}{c}\hfill A_2{Y}^2+A_{1}Y+A_0=0,\end{array}$$(2)

with $A_2=eg(ag-hb)$, $A_1=eghr+m(hb-ag)$, $A_0=-hrmq<0$. There are two cases, whether this quadratic (2(2) $$\begin{array}{c}\hfill A_2{Y}^2+A_{1}Y+A_0=0,\end{array}$$(2) ) has one or two nonnegative roots. In the former, by Descartes’ rule, to have a nonnegative root it is enough to impose positivity of the first coefficient, from which we have $ag>hb$. In the second case, we have instead two positive roots if $A_2<0$, $A_1>0$ and $\mathrm{\Delta }=A_1^2-4A_0{A}_2>0$. Positivity of $A_1$ is ensured by $ag<hb$, and this entails the negativity of $A_2$ and in turn the fact that the roots are real, recalling that $q<1$:$$\begin{array}{cc}\hfill \mathrm{\Delta }& ={[eghr-m(ag-hb)]}^2+4eghmrq(ag-hb)\hfill \\ \hfill & >{(eghr)}^2+m^2{(ag-hb)}^2+2eghmr(ag-bh)={[eghr+m(ag-hb)]}^2>0.\hfill \end{array}$$

We then need the nonnegativity of $Z_2$, which leads to$$Y_2{H}_2+K_2\equiv Y_2[egr(h-g)(qag+phb)-hbm(ag-hb)]+rqm(b{h}^2-a{g}^2)>0$$

in the former case, and to the opposite inequality in the latter, in view of the sign of $A_1$. Now looking once again for sufficient conditions, $K_2>0$ implies $h>g$ in the former case and then asking $H_2>0$ yields $egr(h-g)(qag+phb)>hbm(ag-hb)$. For $ag<bh$ instead, we find that requesting $K_2<0$ gives $h<g$ and then $H_2<0$ is ensured by $egr(h-g)(qag+phb)<hbm(ag-hb)$.

In summary, one equilibrium is feasible if(3) $$\begin{array}{c}\hfill Y_2\le \frac{m}{eg},ag>hb,h>g,egr(h-g)(qag+phb)>hbm(ag-hb);\end{array}$$(3)

two such points instead arise and are feasible if(4) $$\begin{array}{c}\hfill Y_2\le \frac{m}{eg},ag<hb,h<g,egr(h-g)(qag+phb)<hbm(ag-hb).\end{array}$$(4)

For the coexistence equilibrium $E_3=\left(\overline{S},\overline{I},\overline{Y},\overline{Z}\right)$, we solve the second and fourth equations of (1(1) $$\begin{array}{cc}\hfill S^{\prime }& =[rp-aS](S+Y)-hSZ-\mathit{\lambda }SI+\mathit{\gamma }I\hfill \\ \hfill I^{\prime }& =I[\mathit{\lambda }S-hZ-\mathit{\gamma }]\hfill \\ \hfill Y^{\prime }& =[rq-bY](S+I+Y)-gYZ\hfill \\ \hfill Z^{\prime }& =Z[e(h(S+I)+gY)-m-jI]\hfill \end{array}$$(1) ) for S and I, to get$$\overline{S}=\frac{hZ+\mathit{\gamma }}{\mathit{\lambda }},\overline{I}=\frac{\mathit{\lambda }(m-egY)-eh\left(hZ+\mathit{\gamma }\right)}{\mathit{\lambda }(eh-j)}.$$

Substitution into the remaining equations gives the following two conic sections(5) $$\begin{array}{cc}\hfill f(Y,Z)& =\left[\frac{e{h}^3}{\mathit{\lambda }(eh-j)}-\frac{a{h}^2}{{\mathit{\lambda }}^2}-\frac{h^2}{\mathit{\lambda }}\right]Z^2+\left[\frac{heg}{eh-j}-\frac{ah}{\mathit{\lambda }}\right]YZ+\left[rp-\frac{a\mathit{\gamma }}{\mathit{\lambda }}\right]Y\hfill \\ \hfill & +\left[\frac{rph}{\mathit{\lambda }}-\frac{2a\mathit{\gamma }h}{{\mathit{\lambda }}^2}-\frac{h\mathit{\gamma }}{\mathit{\lambda }}-\frac{hm}{eh-j}+\frac{e{h}^2\mathit{\gamma }}{\mathit{\lambda }(eh-j)}\right]Z+\frac{rp\mathit{\gamma }}{\mathit{\lambda }}-\frac{a{\mathit{\gamma }}^2}{{\mathit{\lambda }}^2}=0\hfill \end{array}$$(5) (6) $$\begin{array}{cc}\hfill g(Y,Z)& =\left[\frac{beg}{eh-j}-b\right]Y^2+\left[rq-\frac{egrq}{eh-j}-\frac{b\mathit{\gamma }}{\mathit{\lambda }}-\frac{bm}{eh-j}+\frac{ehb\mathit{\gamma }}{\mathit{\lambda }(eh-j)}\right]Y+\hfill \\ \hfill & +\left[\frac{eb{h}^2}{\mathit{\lambda }(eh-j)}-\frac{bh}{\mathit{\lambda }}-g\right]YZ+\left[\frac{rqh}{\mathit{\lambda }}-\frac{rqe{h}^2}{\mathit{\lambda }(eh-j)}\right]Z\hfill \\ \hfill & +\frac{rq\mathit{\gamma }}{\mathit{\lambda }}+\frac{rqm}{eh-j}-\frac{ehrq\mathit{\gamma }}{\mathit{\lambda }(eh-j)}=0\hfill \end{array}$$(6)

Both are conic sections of the type described by the generic equation $A{Z}^2+2HYZ+B{Y}^2+2GZ+2FY+C=0$, with, using obvious notations, $A_f\ne 0$ and $B_f=0$ for the first one and for $A_g=0$ and $B_g\ne 0$ the second one.

Now the invariants of (5(5) $$\begin{array}{cc}\hfill f(Y,Z)& =\left[\frac{e{h}^3}{\mathit{\lambda }(eh-j)}-\frac{a{h}^2}{{\mathit{\lambda }}^2}-\frac{h^2}{\mathit{\lambda }}\right]Z^2+\left[\frac{heg}{eh-j}-\frac{ah}{\mathit{\lambda }}\right]YZ+\left[rp-\frac{a\mathit{\gamma }}{\mathit{\lambda }}\right]Y\hfill \\ \hfill & +\left[\frac{rph}{\mathit{\lambda }}-\frac{2a\mathit{\gamma }h}{{\mathit{\lambda }}^2}-\frac{h\mathit{\gamma }}{\mathit{\lambda }}-\frac{hm}{eh-j}+\frac{e{h}^2\mathit{\gamma }}{\mathit{\lambda }(eh-j)}\right]Z+\frac{rp\mathit{\gamma }}{\mathit{\lambda }}-\frac{a{\mathit{\gamma }}^2}{{\mathit{\lambda }}^2}=0\hfill \end{array}$$(5) ) are$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_f& {\displaystyle =-A_f{F}_f^2-C_f{H}_f^2+2F_f{G}_f{H}_f=\frac{h^2\left(a\mathit{\gamma }-rp\mathit{\lambda }\right)}{4{\mathit{\lambda }}^2{\left(eh-j\right)}^2}\left[e^2{g}^2\mathit{\gamma }-e^{2}ghpr\right.}\hfill \\ \hfill & \left.+egjpr+ehjpr-aehm-eg\mathit{\gamma }j+eg\mathit{\lambda }m-j^{2}pr+ajm\right]\hfill \\ \hfill {\mathrm{\Pi }}_f& =-H_f^2=-{\left(\frac{heg}{2(eh-j)}-\frac{ah}{2\mathit{\lambda }}\right)}^2,\hfill \end{array}$$

so that it is a hyperbola since ${\mathrm{\Pi }}_f<0$, assuming nondegeneracy, ${\mathrm{\Gamma }}_f\ne 0$. Also (6(6) $$\begin{array}{cc}\hfill g(Y,Z)& =\left[\frac{beg}{eh-j}-b\right]Y^2+\left[rq-\frac{egrq}{eh-j}-\frac{b\mathit{\gamma }}{\mathit{\lambda }}-\frac{bm}{eh-j}+\frac{ehb\mathit{\gamma }}{\mathit{\lambda }(eh-j)}\right]Y+\hfill \\ \hfill & +\left[\frac{eb{h}^2}{\mathit{\lambda }(eh-j)}-\frac{bh}{\mathit{\lambda }}-g\right]YZ+\left[\frac{rqh}{\mathit{\lambda }}-\frac{rqe{h}^2}{\mathit{\lambda }(eh-j)}\right]Z\hfill \\ \hfill & +\frac{rq\mathit{\gamma }}{\mathit{\lambda }}+\frac{rqm}{eh-j}-\frac{ehrq\mathit{\gamma }}{\mathit{\lambda }(eh-j)}=0\hfill \end{array}$$(6) ) is a hyperbola, since$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_g& =-B_g{G}_g^2-C_g{H}_g^2+2F_g{G}_g{H}_g=\frac{rq\left(heg\mathit{\lambda }-bhj-gj\mathit{\lambda }\right)}{4{\mathit{\lambda }}^2{\left(eh-j\right)}^3}\left[e{h}^{2}jqr\right.\hfill \\ \hfill & \left.-eghjqr+eg\mathit{\gamma }hj-egh\mathit{\lambda }m-h{j}^{2}qr-g\mathit{\gamma }{j}^2+gj\mathit{\lambda }m\right]\hfill \\ \hfill {\mathrm{\Pi }}_g& =-H_g^2=-{\left(\frac{eb{h}^2}{2\mathit{\lambda }(eh-j)}-\frac{bh}{2\mathit{\lambda }}-g\right)}^2,\hfill \end{array}$$

with once again ${\mathrm{\Pi }}_g<0$ and assuming nondegeneracy, ${\mathrm{\Gamma }}_g\ne 0$.

These curves are better investigated by solving for each variable, to get:$$Y_f=-\frac{1}{2}{\displaystyle \frac{\mathit{\rho }(Z)}{\mathit{\theta }(Z)}}\equiv -\frac{1}{2}{\displaystyle \frac{A_f{Z}^2+2G_{f}Z+C_f}{H_{f}Z+F_f}},Z_g=-\frac{1}{2}{\displaystyle \frac{\mathrm{\Psi }(Y)}{\mathit{\varphi }(Y)}}\equiv -\frac{1}{2}{\displaystyle \frac{B_g{Y}^2+2F_{g}Y+C_g}{H_{g}Y+G_g}}.$$

We seek now sufficient conditions ensuring the existence of the equilibrium where all population thrive.

For $Z_g$, note that if $B_g<0$ it follows $G_g>0$, $H_g<0$. If we take also $C_g>0$, then $Z_g(0)<0$ and $\mathrm{\Psi }(Y)$ is a quadratic with one positive root in view of Descartes’ rule of signs. These roots $Y_g^{-}<0<Y_g^{+}$ always exist since ${\mathrm{\Delta }}_g>0$. This statement follows observing that $2F_g=-b{(rq)}^{-1}{C}_g-rq{b}^{-1}{B}_g$ so that easily ${\mathrm{\Delta }}_g=4F^2-4B_g{C}_g={[b{(rq)}^{-1}{C}_g-rq{b}^{-1}{B}_g]}^2>0$. Since $\mathit{\varphi }(Y)\ge 0$ whenever $Y<Y_g^{\infty }\equiv -2G_g{H}_g^{-1}$, with $Y_g^{\infty }>0$, the function $Z_g$ is positive only in between $Y_g^{+}$ and $Y_g^{\infty }$, independently of their order.

A similar analysis on $Y_f(Z)$ shows the same result. Only in the absence of more specific information on the respective hunting rates on the two genotypes, g and h, we assume both $H_f<0$ and $A_f<0$, given their asymmetry; the latter would however be a direct consequence of the former if $g\ge h$. Note also that taking $C_f>0$ we obtain $F_f>0$. The discriminant then is always positive in view of the opposite signs of the coefficients $A_f$ and $C_f$, ${\mathrm{\Delta }}_f=G^2-A_f{C}_f>0$. The function $Y_f(Z)$ then is positive only in the interval between the positive root $Z_f^{+}$ and the vertical asymptote, $Z_f^{\infty }$, independently of which one is the smallest.

Evidently since these curves are surjective on their respective half ranges, the half lines $Z\ge 0$ and $Y\ge 0$, respectively, they always meet at a feasible point. Therefore, in summary, sufficient conditions for the feasibility of the equilibrium $E_3$ are provided by the following inequalities:(7) $$\begin{array}{c}\hfill {\displaystyle \frac{eg}{eh-j}}<1,\mathit{\gamma }+\frac{m\mathit{\lambda }}{eh-j}>\frac{eh\mathit{\gamma }}{eh-j};\frac{eg}{eh-j}<\frac{a}{\mathit{\lambda }},\frac{eh}{eh-j}<\frac{a}{\mathit{\lambda }}+1,\frac{rp}{\mathit{\gamma }}>\frac{a}{\mathit{\lambda }}.\end{array}$$(7)

4. Stability

The Jacobian of (1(1) $$\begin{array}{cc}\hfill S^{\prime }& =[rp-aS](S+Y)-hSZ-\mathit{\lambda }SI+\mathit{\gamma }I\hfill \\ \hfill I^{\prime }& =I[\mathit{\lambda }S-hZ-\mathit{\gamma }]\hfill \\ \hfill Y^{\prime }& =[rq-bY](S+I+Y)-gYZ\hfill \\ \hfill Z^{\prime }& =Z[e(h(S+I)+gY)-m-jI]\hfill \end{array}$$(1) ) is(8) $$\begin{array}{c}\hfill J=\left(\begin{array}{cccc}{J}_{11}& -\mathit{\lambda }S+\mathit{\gamma }& rp-aS& -hS\\ \mathit{\lambda }I& \mathit{\lambda }S-hZ-\mathit{\gamma }& 0& -hI\\ rq-bY& rq-bY& J_{33}& -gY\\ ehZ& Z(eh-j)& egZ& J_{44}\end{array}\right)\end{array}$$(8)

with $J_{11}=rp-2aS-aY-hZ-\mathit{\lambda }I$, $J_{33}=rq-2bY-b(I+S)-gZ$ and $J_{44}=eh(S+I)+egY-m-jI$.

$E_0$ is unstable, since its eigenvalues are 0, $rp+rq$, $-m$ ,$-\mathit{\gamma }$.

The eigenvalues of the Jacobian evaluated at $E_1$ are $(ehrpb+egrqa-mab){(ab)}^{-1}$, $-r\left(aq+bp\right)a^{-1}$, $(\mathit{\lambda }rp-\mathit{\gamma }a)a^{-1}$, $-r\left(aq+bp\right)b^{-1}$, implying that this point is stable for(9) $$\begin{array}{c}\hfill mab>er(hpb+gqa),\mathit{\gamma }a>\mathit{\lambda }rp.\end{array}$$(9)

Therefore, the predators and the disease establish themselves in the ecosystem if the disease transmission rate exceeds the threshold(10) $$\begin{array}{c}\hfill {\mathit{\lambda }}^{†}=\frac{\mathit{\gamma }a}{rp}.\end{array}$$(10)

On comparing the last conditions in (9(9) $$\begin{array}{c}\hfill mab>er(hpb+gqa),\mathit{\gamma }a>\mathit{\lambda }rp.\end{array}$$(9) ) and in (7(7) $$\begin{array}{c}\hfill {\displaystyle \frac{eg}{eh-j}}<1,\mathit{\gamma }+\frac{m\mathit{\lambda }}{eh-j}>\frac{eh\mathit{\gamma }}{eh-j};\frac{eg}{eh-j}<\frac{a}{\mathit{\lambda }},\frac{eh}{eh-j}<\frac{a}{\mathit{\lambda }}+1,\frac{rp}{\mathit{\gamma }}>\frac{a}{\mathit{\lambda }}.\end{array}$$(7) ), we infer that a transcritical bifurcation leading from $E_2$ to $E_3$ might arise. The conditional is needed as (7(7) $$\begin{array}{c}\hfill {\displaystyle \frac{eg}{eh-j}}<1,\mathit{\gamma }+\frac{m\mathit{\lambda }}{eh-j}>\frac{eh\mathit{\gamma }}{eh-j};\frac{eg}{eh-j}<\frac{a}{\mathit{\lambda }},\frac{eh}{eh-j}<\frac{a}{\mathit{\lambda }}+1,\frac{rp}{\mathit{\gamma }}>\frac{a}{\mathit{\lambda }}.\end{array}$$(7) ) are only sufficient conditions for the feasibility of the coexistence equilibrium.

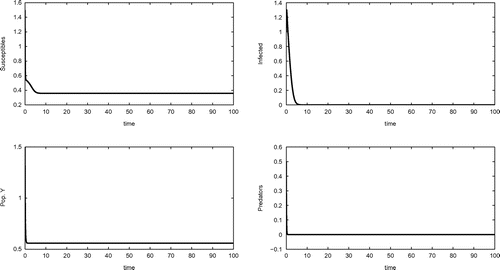
Equilibrium $E_1$, shown in Figure 1, is achieved by the following choice of system’s parameter values(11) $$\begin{array}{c}\hfill a=2.7,b=2.6,r=2.42,h=0.4,g=0.7,j=4.5,\\ \hfill m=5.5,\mathit{\lambda }=5.82,\mathit{\gamma }=3.59,p=0.4,q=0.6,e=0.95.\end{array}$$(11)

Figure 1. Equilibrium $E_1$. Parameters listed in (11(11) $$\begin{array}{c}\hfill a=2.7,b=2.6,r=2.42,h=0.4,g=0.7,j=4.5,\\ \hfill m=5.5,\mathit{\lambda }=5.82,\mathit{\gamma }=3.59,p=0.4,q=0.6,e=0.95.\end{array}$$(11) ).

4.1. The Disease-free Equilibrium $E_2$

At $E_2$ one explicit eigenvalue is available: $\mathit{\lambda }{S}_2-h{Z}_2-\mathit{\gamma }$. It gives the necessary stability condition:(12) $$\begin{array}{c}\hfill \mathit{\lambda }m<\mathit{\lambda }eg{Y}_2+eh(h{Z}_2+\mathit{\gamma }).\end{array}$$(12)

The Routh–Hurwitz conditions on the remaining minor $J^{(2)}$ of order 3 obtained deleting the second row and column of (8(8) $$\begin{array}{c}\hfill J=\left(\begin{array}{cccc}{J}_{11}& -\mathit{\lambda }S+\mathit{\gamma }& rp-aS& -hS\\ \mathit{\lambda }I& \mathit{\lambda }S-hZ-\mathit{\gamma }& 0& -hI\\ rq-bY& rq-bY& J_{33}& -gY\\ ehZ& Z(eh-j)& egZ& J_{44}\end{array}\right)\end{array}$$(8) ) give the following inequalities:$$\text{tr}(J^{(2)})<,det(J^{(2)})<0,\text{tr}(J^{(2)})M_2(J^{(2)})<det(J^{(2)}),$$

where $M_2(J^{(2)})$ represents the sum of the principal minors of order 2 of the matrix $J^{(2)}$. Now, the condition on the trace gives:$$\begin{array}{c}\hfill rp-2a{S}_2-a{Y}_2-h{Z}_2+rq-2b{Y}_2-b{S}_2-g{Z}_2<0\end{array}$$

from which using the value of $S_2$ we find$$r-{\displaystyle \frac{m}{eh}}(2a+b)-\frac{1}{h}{Y}_2[ag-bh+(g-h)(a+b)]-(g+h)Z_2<0.$$

Sufficient conditions for the above inequality are(13) $$\begin{array}{c}\hfill ehr<m(2a+b),ag>bh,g>h.\end{array}$$(13)

For the determinant, we have$$\begin{array}{cc}& e{h}^2{Z}_2{S}_2\left(rq-b{S}_2-2b{Y}_2-g{Z}_2\right)-egh{Y}_2{Z}_2\left(rp-a{S}_2\right)\hfill \\ \hfill & +e{g}^2{Y}_2{Z}_2\left(rp-2a{S}_2-a{Y}_2-h{Z}_2\right)-egh{Z}_2\left(rq-b{Y}_2\right)S_2<0\hfill \end{array}$$

which, observing that conditions (13(13) $$\begin{array}{c}\hfill ehr<m(2a+b),ag>bh,g>h.\end{array}$$(13) ) already imply negativity of the trace and therefore of the above first and third terms, is ensured by(14) $$\begin{array}{c}\hfill a{S}_2<rp,b{Y}_2<rq.\end{array}$$(14)

The last Routh–Hurwitz condition is then:$$\begin{array}{cc}& \left[\left(rp-2a{S}_2-a{Y}_2-h{Z}_2\right)+\left(rq-b{S}_2-2b{Y}_2-g{Z}_2\right)\right]\left[\left(rp-2a{S}_2-a{Y}_2\right.\right.\hfill \\ \hfill & -\left.h{Z}_2\right)\left(rq-b{S}_2-2b{Y}_2-g{Z}_2\right)+e{h}^2{Z}_2{S}_2+e{g}^2{Y}_2{Z}_2\left.-\left(rq-b{Y}_2\right)\left(rp-a{S}_2\right)\right]\hfill \\ \hfill & <e{h}^2{Z}_2{S}_2\left(rq-b{S}_2-2b{Y}_2-g{Z}_2\right)-egh{Z}_2\left(rq-b{Y}_2\right)S_2\hfill \\ \hfill & +e{g}^2{Y}_2{Z}_2\left(rp-2a{S}_2-a{Y}_2-h{Z}_2\right)-egh{Y}_2{Z}_2\left(rp-a{S}_2\right).\hfill \end{array}$$

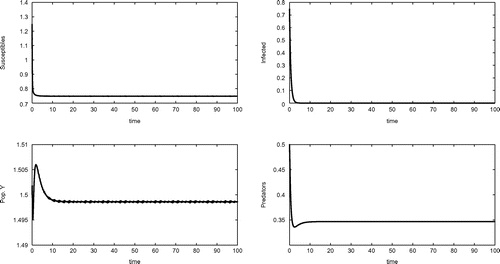
Equilibrium $E_2$, shown in Figure 2, is indeed achieved by the system, for the following set of parameter values(15) $$\begin{array}{c}\hfill a=3.1,b=2.3,r=6.4,h=2.1,g=1.7,j=3,\\ \hfill m=3.5,\mathit{\lambda }=1.8,\mathit{\gamma }=2.2,p=0.4,q=0.6,e=0.85.\end{array}$$(15)

Figure 2. Equilibrium $E_2$, for the parameters given in (15(15) $$\begin{array}{c}\hfill a=3.1,b=2.3,r=6.4,h=2.1,g=1.7,j=3,\\ \hfill m=3.5,\mathit{\lambda }=1.8,\mathit{\gamma }=2.2,p=0.4,q=0.6,e=0.85.\end{array}$$(15) ).

4.2. The Coexistence Equilibrium $E_3$

The Jacobian at this point simplifies a bit, in that $J_{22}=J_{44}=0$.

The Routh–Hurwitz conditions in this case are more involved. The condition on the trace gives here(16) $$\begin{array}{c}\hfill r-(2a+b)\overline{S}-(a+2b)\overline{Y}-(g+h)\overline{Z}-(\mathit{\lambda }+b)\overline{I}<0.\end{array}$$(16)

Denoting by $D_{ij}$ the minor of $J(E_3)$ obtained by deleting the ith row and jth column, the condition on the determinant instead provides: $-\mathit{\lambda }I{D}_{2,1}-hI{D}_{2,4}>0$ which is satisfied if we take both minors negative. This holds if we impose the following two conditions:(17) $$\begin{array}{cc}& h\overline{S}\overline{Z}\left[{\overline{J}}_{33}(eh-j)-eg(rq-b\overline{Y})\right]+g\overline{Y}\overline{Z}\left[eg(\mathit{\gamma }-\mathit{\lambda }\overline{S})-(rp-a\overline{S})(eh-j)\right]<0,\hfill \end{array}$$(17) (18) $$\begin{array}{cc}& eg\overline{Z}{\overline{J}}_{11}(rq-b\overline{Y})+eh\overline{Z}(\mathit{\gamma }-\mathit{\lambda }\overline{S}){\overline{J}}_{33}+(rp-a\overline{S})(rq-b\overline{Y})\overline{Z}(eh-j)\hfill \\ \hfill & -eh\overline{Z}(rp-a\overline{S})(rq-b\overline{Y})-(eh-j)\overline{Z}{\overline{J}}_{11}{\overline{J}}_{33}-eg\overline{Z}(\mathit{\gamma }-\mathit{\lambda }\overline{S})(rq-b\overline{Y})<0.\hfill \end{array}$$(18)

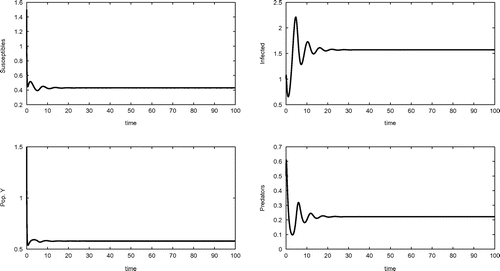
Figure 3. Coexistence equilibrium obtained for the set of parameter values (20(20) $$\begin{array}{c}\hfill a=4.7,b=3.6,r=5.42,h=2.8,g=1.7,j=1.5,\\ \hfill m=3.9,\mathit{\lambda }=2.82,\mathit{\gamma }=0.59,p=0.6,q=0.4,e=0.95.\end{array}$$(20) ).

The remaining two conditions are a much more involved. In terms of the coefficients of the monic characteristic equation ${\sum }_{k=0}^4{a}_k{\mathrm{\Lambda }}^k=0$, they are(19) $$\begin{array}{c}\hfill a_3{a}_2>a_1,a_3{a}_2{a}_1>a_1^2+a_0{a}_3^2.\end{array}$$(19)

These coefficients are, in addition to the trace $a_3$ and the determinant $a_0$ of the Jacobian, the sum of its principal minors of order 2 and 3. Explicitly:$$\begin{array}{cc}\hfill a_2& =\left|\begin{array}{cc}{J}_{11}& (\mathit{\gamma }-\mathit{\lambda }S)\\ \mathit{\lambda }I& 0\end{array}\right|+\left|\begin{array}{cc}{J}_{11}& (rp-aS)\\ (rq-bY)& J_{33}\end{array}\right|+\left|\begin{array}{cc}{J}_{11}& -hS\\ ehZ& 0\end{array}\right|\hfill \\ \hfill & +\left|\begin{array}{ccc}0& 0& \\ (rq-bY)& J_{33}\end{array}\right|+\left|\begin{array}{cc}0& -hI\\ Z(eh-j)& 0\end{array}\right|+\left|\begin{array}{cc}{J}_{33}& -gY\\ egZ& 0\end{array}\right|\hfill \\ \hfill & =hSehZ-(\mathit{\gamma }-\mathit{\lambda }S)\mathit{\lambda }I+J_{11}{J}_{33}-(rp-aS)(rq-bY)+hIZ(eh-j)+gYegZ\hfill \end{array}$$

and$$\begin{array}{cc}\hfill a_3& =-hI\left|\begin{array}{cc}(rq-bY)& J_{33}\\ Z(eh-j)& egZ\end{array}\right|+\left|\begin{array}{ccc}{J}_{11}& (rp-aS)& -hS\\ (rq-bY)& J_{33}& -gY\\ ehZ& Z(eh-j)& 0\end{array}\right|\hfill \\ \hfill & +\left|\begin{array}{ccc}{J}_{11}& (\mathit{\gamma }-\mathit{\lambda }S)& -hS\\ \mathit{\lambda }I& 0& -hI\\ ehZ& Z(eh-j)& 0\end{array}\right|-\mathit{\lambda }I\left|\begin{array}{cc}(\mathit{\gamma }-\mathit{\lambda }S)& (rp-aS)\\ (rq-bY)& J_{33}\end{array}\right|\hfill \\ \hfill & =-hI\left[(rq-bY)egZ-J_{33}Z(eh-j)\right]\hfill \\ \hfill & -eghYZ(rp-aS)-hSZ(rq-bY)(eh-j)+e{h}^{2}SZ{J}_{33}\hfill \\ \hfill & +gYZ{J}_{11}(eh-j)J_{11}hIZ(eh-j)-e{h}^{2}IZ(\mathit{\gamma }-\mathit{\lambda }S)\hfill \\ \hfill & -hS\mathit{\lambda }IZ(eh-j)-\mathit{\lambda }I\left[(\mathit{\gamma }-\mathit{\lambda }S)J_{33}-(rp-aS)(rq-bY)\right].\hfill \end{array}$$

Also the coexistence equilibrium is empirically shown to be achievable in a stable way in Figure 3 by the following choice of parameters:(20) $$\begin{array}{c}\hfill a=4.7,b=3.6,r=5.42,h=2.8,g=1.7,j=1.5,\\ \hfill m=3.9,\mathit{\lambda }=2.82,\mathit{\gamma }=0.59,p=0.6,q=0.4,e=0.95.\end{array}$$(20)

5. Conclusions

The model considered in this paper extends in a new direction the ones that have been introduced in Venturino (2012) and Viberti and Venturino (2014). Namely, we consider the fact that one of the genotypes can be subject to a disease, that however cannot affect the other one. In addition, we assume that the infected genotype has also some toxic effects for a possible specialist predator, that feeds on both genotypes.

Our findings indicate that the ecosystem in these assumptions cannot completely disappear. The model trajectories can settle toward the disease- and predator-free equilibria, toward the predator-free one, or the system can achieve coexistence of all the populations. Thus, to answer one of the questions raised in the Introduction, the disease can be eradicated, and the predators have a fundamental role in it, as the parameters related to their dynamics appear in the necessary stability condition (12(12) $$\begin{array}{c}\hfill \mathit{\lambda }m<\mathit{\lambda }eg{Y}_2+eh(h{Z}_2+\mathit{\gamma }).\end{array}$$(12) ). Both genotypes of the healthy prey can survive in an environment where the predators are absent, as it is found also in Venturino (2012). Thus, the elimination of the predators at first sight does not appear to be tied to the presence of the disease in the prey, elucidating then the statement of the Introduction. It is also interesting to note that in the assumptions of this particular ecosystem, the disease cannot endemically survive among the prey in the absence of the predators, which seems to constitute another fact in support of a negative answer to the second claim stated in the Introduction. However, at a deeper analysis, looking at the stability conditions for the equilibrium in which only the two prey genotypes thrive, (9(9) $$\begin{array}{c}\hfill mab>er(hpb+gqa),\mathit{\gamma }a>\mathit{\lambda }rp.\end{array}$$(9) ), we observe that the first one is essentially a purely demographic condition, which plays the same role of equation (11) in Venturino (2012). The second one however is new and depends on the epidemic parameters, the disease contact rate $\mathit{\lambda }$, and its recovery rate $\mathit{\gamma }$. Evidently, if in the absence of the disease the two genotypes can thrive without the predators, it is possible that in the presence instead of a particularly virulent, i.e. highly transmissible, disease, combined perhaps with a low recovery rate, or in any case if the contact rate exceeds the threshold ${\mathit{\lambda }}^{†}$, (10(10) $$\begin{array}{c}\hfill {\mathit{\lambda }}^{†}=\frac{\mathit{\gamma }a}{rp}.\end{array}$$(10) ), the system can be driven away from this equilibrium. In such case certainly the disease is introduced at an endemic level and, since the endemic predator-free equilibrium here does not exist, in addition the invasion of the predators is made possible. Furthermore, if the disease is unrecoverable, i.e. $\mathit{\gamma }=0$, the second condition in (9(9) $$\begin{array}{c}\hfill mab>er(hpb+gqa),\mathit{\gamma }a>\mathit{\lambda }rp.\end{array}$$(9) ) cannot be satisfied, implying that either the disease or the predators, or both, are always present in the system.

***As it in general occurs in ecoepidemic models, the major finding of this investigation is thus the fact that the disease deeply influences the underlying demographics of the system.

Additional information

Funding

This work has been partially supported by the project “Metodi numerici in teoria delle popolazioni” of the Dipartimento di Matematica “Giu-seppe Peano”.

Notes on contributors

Ezio Venturino

Ezio Venturino , professor of Mathematics, holds a PhD in Applied Mathematics from SUNY at Stony Brook. His research interests concern numerical analysis and mainly mathematical modeling (biological population theory, epidemiology, and socioeconomic applications). He has authored about 40 research papers in numerical analysis and 160 in mathematical modeling. He has coauthored two books for CRC and Birkhaeuser, and serves in the Editorial Board of several international Journals. This paper is part of his scientific interests in mathematical biology, in which he has contributed to found a specific research field, now called ecoepidemiolgy, dealing with interacting populations that are in addition subject to a disease. The latter can deeply influence the ecosystem behavior. Another fairly recent idea accounts for models of herd behavior and pack hunting. Sometimes a richer dynamics is discovered. More recently, he introduced models for genetically distinguishable species interactions, of which this paper is an instance.