Numerical solution of singularly perturbed problems using Haar wavelet collocation method

Abstract

In this paper, a collocation method based on Haar wavelets is proposed for the numerical solutions of singularly perturbed boundary value problems. The properties of the Haar wavelet expansions together with operational matrix of integration are utilized to convert the problems into systems of algebraic equations with unknown coefficients. To demonstrate the effectiveness and efficiency of the method various benchmark problems are implemented and the comparisons are given with other methods existing in the recent literature. The demonstrated results confirm that the proposed method is considerably efficient, accurate, simple, and computationally attractive.

Keywords:

• Haar wavelet
• operational matrix
• singularly perturbed
• boundary layer

AMS Subject Classifications:

• 42C40
• 65L10
• 65L12
• 65M70
• 65N35

Public Interest Statement

Singular perturbation problems (SPPs) have applications in various disciplines of knowledge, for instance, neurobiology, fluid mechanics, elasticity, quantum mechanics, geophysics, aerodynamics, oceanography, chemical reactor theory, convection–diffusion processes, and optimal control. It is a well-known fact that the solution of these problems exhibit multi-scale character so the usual numerical treatment of SPPs gives major computational difficulties due to the presence of boundary and interior layers and, in recent years, a large number of numerical methods have been developed to provide accurate numerical solutions. In this work, a new collocation method based on Haar wavelets is proposed for the numerical solution of singularly perturbed two-point boundary value problems. Accuracy and efficiency of the suggested method is established through comparison with the existing methods available in the open literature.

1. Introduction

Singularly perturbed problems (SPPs) arise in various branches of applied mathematics and physics such as fluid mechanics, quantum mechanics, elasticity, plasticity, semi-conductor device physics, geophysics, optimal control theory, aerodynamics, oceanography, and mathematical models of chemical reactions. Mathematically, self-adjoint SPPs are defined as(2.1) $$\begin{array}{c}\hfill \left.\begin{array}{ccc}Ly(x)\hfill & \equiv -\mathit{ϵ}{y}^{″}(x)+f(x)y(x)=g(x),\hfill & f(x)\ge 0,x\in [0,1],\hfill \\ y(0)\hfill & ={\mathit{\alpha }}_0,\hfill & y(1)={\mathit{\alpha }}_1,\hfill \end{array}\right\}\end{array}$$(2.1)

where ${\mathit{\alpha }}_0,{\mathit{\alpha }}_1$ are given constants, $\mathit{ϵ}$ is a small positive parameter such that $0<\mathit{ϵ}\ll 1$ and f(x), g(x) are sufficiently smooth functions. It is known that Problem (1.1) has a unique solution y, which in general displays boundary layers at $x=0$ and $x=1$. These type of problems are characterized by the presence of a small parameter $\mathit{ϵ}$ that multiplies the highest order derivative, and they are stiff and there exists a boundary or interior layer where the solutions change rapidly. That is, there are thin transition layers where the solution varies rapidly or jumps abruptly, while away from the layers the solution behaves regularly and varies slowly. For more details on singular perturbation problems, we refer to the monographs (Miller, O’Riordan, & Shishkin, 1996; Roos, Stynes, & Tobiska, 1996).

In recent years, the studies of SPPs problems have been tackled by many researchers but the majority of these problems cannot be solved analytically, so one would like ideally to use the numerical methods available in the open literature such as homotopy perturbation method (Chun & Sakthivel, 2010), Adomian decomposition method (Wazwaz, 2002), sinc approximation solution (Mohsen & EL-Gamel, 2008), spline collocation method (Aziz & Khan, 2002; Kadalbajoo & Arora, 2010; Kadalbajoo & Gupta, 2009; Kadalbajoo, Gupta, & Awasthi, 2008; Khan, Khan, & Aziz, 2006; Khan & Khandelwala, 2014; Kumar & Mehra, 2007; Rashidinia, Ghasemi, & Mahmoodi, 2007; Surla & Stojanovic, 1988), reproducing kernel method (Geng & Cui, 2011), finite element method (Lenferink, 2002), the finite-volume element method (Phongthanapanich & Dechaumphai, 2009), and wavelet method (Pandit & Kumar, 2014). An alternative solution is proposed in the present paper in the form of operational matrix method, which is based on Haar wavelets for the numerical solution of singularly perturbed reaction–diffusion problems.

Wavelets became an active field of research in the 1980s, with the works of researchers such as Morlet, Grossman, and Daubechies (1992) on signal processing. Starting as an alternative to Fourier analysis, their popularity soon expanded, owing mainly to the localized nature of wavelet basis in frequency and time, as well as their hierarchical structure. Wavelets have numerous applications in approximation theory and have been extensively used in the context of numerical approximation in the relevant literature during the last two decades. Different types of wavelets and approximating functions have been used in numerical solution of boundary value problems such as Daubechies, Battle–Lemarie, B-spline, Chebyshev, Legendre, and Haar wavelets. Among all the wavelet families, the Haar wavelets have gained popularity among researchers due to their useful properties such as simple applicability, orthogonality, and compact support. Compact support of the Haar wavelet basis permits straight inclusion of the different types of boundary conditions in the numeric algorithms. The basic idea of Haar wavelet method is to convert the differential equations to a system of algebraic equations by the operational matrices of integral or derivative (Chen & Hsiao, 1997; Lepik, 2008). Recently, many authors have used Haar wavelet method for solving ordinary and partial differential equations. For a historical background and an overview of wavelets in general and Haar wavelets in particular, the reader can refer to Lepik (2014).

The objective of this research is to construct a simple collocation method based on Haar wavelets for the numerical solution of singularly perturbed reaction–diffusion problems of the type (1.1) which arise in mathematical modeling of different engineering applications. The proposed method has the following advantages in comparison to the existing methods available in the open literature:

(1)	Haar wavelets collocation method (HWCM) uses simple box functions and consequently the formulation of numerical method based on these functions involves lesser manual labor.
(2)	HWCM does not require to calculate the inverse of Haar wavelet matrix.
(3)	Contrary to reproducing kernel method (RKM), HWCM performs very well for a boundary value problem defined on a very long interval.
(4)	Unlike RKM, HWCM does not require conversion of a boundary value problem into initial value problem using a procedure like shooting and hence this method eliminates the possibility of unstable solution due to missing initial condition in the case of RKM.
(5)	Contrary to RKM, the boundary value problem needs not to be reduced into a system of first-order ODE’s.
(6)	A variety of boundary conditions can be handled with equal ease.

Finally, the obtained numerical approximate results of this method are then compared with the exact solutions as well as solutions available in open literature. The numerical outcomes indicate that the proposed method yields highly accurate results.

Table 1. Maximum absolute errors for different values of N and $\mathit{ϵ}$

$\mathit{ϵ}\downarrow$	$N=16$	$N=32$	$N=64$	$N=128$
Our method
1/16	5.0862E-05	2.4680E-05	6.1100E-07	6.1100E-09
1/32	2.4680E-05	1.2244E-06	2.6471E-07	1.3139E-09
1/64	1.2244E-05	6.1100E-06	2.7082E-07	1.3161E-08
1/128	6.1100E-06	2.7082E-07	1.1038E-08	4.9550E-09
1/256	3.8149E-06	6.2121E-08	1.4415E-09	5.1021E-010
Rashidinia et al. (2007)
1/16	2.96E-06	1.18E-05d	1.15E-08	7.24E-10
1/32	1.18E-05	7.54E-07	4.67E-08	2.96E-09
1/64	4.74E-05	2.96E-06	1.86E-07	1.16E-08
1/128	1.78E-04	1.18E-05	7.46E-07	4.67E-08
1/256	7.41E-04	4.74E-05	2.98E-08	1.86E-10
Khan et al. (2014)
1/16	7.376E-05	4.938E-06	3.147E-07	1.977E-08
1/32	2.771E-04	1.947E-05	1.260E-06	7.959E-08
1/64	9.787E-04	7.448E-05	4.982E-06	3.174E-07
1/128	3.645E-03	2.773E-04	1.948E-05	1.260E-06
1/256	1.292E-02	9.787E-04	7.448E-05	4.982E-06

The organization of this paper is as follows. In Section 2, Haar wavelets and their integral are introduced. In Section 3, the Haar wavelet collocation method is presented and described for the numerical solution of the class of singularly perturbed reaction–diffusion equations. In Section 4, our method has been tested by several problems and the obtained results are compared with results of the existing methods. Finally, in Section 5, the conclusion of the study is given.

2. Haar wavelets and operational matrix of integration

Haar wavelets have been used from 1910 when they were introduced by the Hungarian mathematician Alfred Haar (Lepik, 2014). The Haar wavelet, being an odd rectangular pulse pair, is the simplest and the oldest orthonormal wavelet with compact support. The Haar wavelet family for $x\in [0,1]$ is defined as follows:(3.1) $$\begin{array}{cc}\hfill h_i(x)& =\left\{\begin{array}{ccc}& \hfill 1,& \text{for}x\in \left[\mathit{\alpha },\mathit{\beta }\right)\hfill \\ \hfill & \hfill -1,& \text{for}x\in \left[\mathit{\beta },\mathit{\gamma }\right)\hfill \\ \hfill & \hfill 0,& \text{elsewhere.}\hfill \end{array}\right.\hfill \end{array}$$(3.1)

where$$\mathit{\alpha }={\displaystyle \frac{k}{m}},\mathit{\beta }={\displaystyle \frac{k+0.5}{m}},\mathit{\gamma }={\displaystyle \frac{k+1}{m}}.$$

Here, m and k have integer values as $m=2^j,j=0,1,\cdots ,J$ and J show the resolution of the wavelet and $k=0,1,\cdots ,m-1$ is the translation parameter. Maximal level of resolution is J. The index of $h_i$ in Equation (2.1) is calculated by $i=m+k+1$. In the case with minimal values $m=1,k=0$, we have $i=2$, the maximal value of i is $2M=2^{j+1}$. We also have $i=1$ corresponding to the scaling function of Haar wavelet family, i.e. $h_1(x)=1$ in [0, 1]. For more about Haar wavelets and their applications, we refer to the monographs (Debnath & Shah, 2015; Lepik, 2014).

Figure 1. Comparison of numerical and exact solution at $N=32$ and different values of $\mathit{ϵ}$.

Figure 2. Comparison of numerical and exact solution at $N=32$ and different values of $\mathit{ϵ}$.

Figure 3. Comparison of numerical and exact solution at $N=32$ and $\mathit{ϵ}=1/5^6$.

Next, we shall establish an operational matrix for integration by means of Haar wavelets for which we follow the same notations as used in Lepik (2008) for Haar function and their integrals as follows:(3.2) $$\begin{array}{c}\hfill P_{i,1}(x)={\int }_0^x{h}_i(x)dx,P_{i,n+1}(x)={\int }_0^x{P}_{i,n}(x)dx,\text{and}{C}_{i,n}(x)={\int }_0^1{P}_{i,n}(x)dx,n=1,2,\cdots .\end{array}$$(3.2)

These integrals can be calculated analytically with the help of Equation (2.1); by doing so we get the following equations(3.3) $$\begin{array}{cc}\hfill P_{i,n}(x)& =\left\{\begin{array}{cc}0\hfill & \text{for}x\in [0,\mathit{\alpha })\hfill \\ {\displaystyle \frac{1}{n!}}{(x-\mathit{\alpha })}^n\hfill & \text{for}x\in [\mathit{\alpha },\mathit{\beta })\hfill \\ {\displaystyle \frac{1}{n!}}[{(x-\mathit{\alpha })}^n-2{(x-\mathit{\beta })}^n]\hfill & \text{for}x\in [\mathit{\beta },\mathit{\gamma })\hfill \\ {\displaystyle \frac{1}{n!}}[{(t-\mathit{\alpha })}^n-2{(t-\mathit{\beta })}^n+{(t-\mathit{\gamma })}^n],\hfill & \text{for}x\in [\mathit{\gamma },1),\hfill \end{array}\right.\hfill \end{array}$$(3.3)

where $i=2,3,\cdots$ and $n=1,2,\cdots$. Note that$$P_{1,n}(x)={\displaystyle \frac{x^n}{n!}},C_{1,n}(x)={\displaystyle \frac{1}{(n+1)!}},n=1,2,\cdots .$$

Table 2. Maximum absolute errors for different values of N and $\mathit{ϵ}$

$\mathit{ϵ}\downarrow$	$N=16$	$N=32$	$N=64$	$N=128$
Our method
1	0.32E-02	0.78E-03	0.27E-03	0.34E-04
${(1/16)}^{0.25}$	0.75E-03	0.31E-03	0.89E-04	0.18E-04
${(1/32)}^{0.5}$	0.95E-03	0.99E-04	0.31E-04	0.01E-04
${(1/64)}^{0.75}$	0.87E-03	0.22E-03	0.91E-04	0.11E-04
(1 / 128)	0.71E-03	0.44E-03	0.58E-04	0.21E-04
O’Riordan et al., (1986)
1	0.11E+00	0.27E-01	0.69E-02	0.17E-02
${(1/16)}^{0.25}$	0.95E-01	0.23E-01	0.56E-02	0.13E-02
${(1/32)}^{0.5}$	0.78E-01	0.18E-01	0.42E-02	0.10E-02
${(1/64)}^{0.75}$	0.66E-01	0.16E-01	0.40E-02	0.10E-02
(1 / 128)	0.64E-01	0.17E-01	0.42E-02	0.13E-02
Lubuma et al., (2006)
1	0.51E-01	0.13E-01	0.32E-02	0.79E-03
${(1/16)}^{0.25}$	0.38E-01	0.96E-02	0.24E-02	0.60E-03
${(1/32)}^{0.5}$	0.25E-01	0.63E-02	0.16E-02	0.39E-03
${(1/64)}^{0.75}$	0.16E-01	0.43E-02	0.11E-02	0.27E-03
(1 / 128)	0.14E-01	0.79E-02	0.24E-02	0.62E-03

Any square integrable function y(x) defined on [0, 1] can be expressed in term of the Haar basis as follows:(3.4) $$\begin{array}{c}\hfill y(x)=c_1{h}_1(x)+c_2{h}_2(x)+\cdots =\sum _{i=1}^{\infty }{c}_i{h}_i(x),\end{array}$$(3.4)

where the Haar coefficients $c_i,i=1,2,\cdots$, are determined by(3.5) $$\begin{array}{c}\hfill c_i=⟨y,h_i⟩=2^j{\int }_0^{1}y(x)h_i(x)dx.\end{array}$$(3.5)

Table 3. Maximum absolute errors for different values of N and $\mathit{ϵ}$

$\mathit{ϵ}\downarrow$	$N=16$	$N=32$	$N=64$	$N=128$
Our method
1	1.1420E-06	2.8699E-07	7.1820E-08	1.7962E-08
1 / 5	7.2799E-05	1.8568E-05	4.6624E-06	1.1673E-06
$1/5^2$	1.0533E-03	4.0689E-04	1.1226E-04	2.8906E-05
$1/5^3$	7.0483E-03	1.3723E-04	1.2529E-05	5.8909E-06
$1/5^4$	3.6848E-04	1.4255E-04	4.9873E-05	1.2027E-05
$1/5^5$	1.4897E-05	5.9510E-06	2.3677E-06	9.2707E-07
$1/5^6$	5.9615E-05	2.3845E-05	9.5358E-06	3.8111E-06
Schatz et al. (1983)
1	2.2123E-04	1.9925E-04	5.2043E-05	2.7654E-05
1 / 5	3.8988E-03	1.1005E-03	5.8736E-04	2.8643E-05
$1/5^2$	3.8710E-02	1.7634E-03	6.8954E-04	1.2733E-04
$1/5^3$	5.9764E-03	5.9534E-04	2.8733E-04	7.8823E-05
$1/5^4$	4.7681E-05	1.1276E-05	7.8754E-06	2.9087E-06
$1/5^5$	2.7612E-03	3.8751E-05	1.7643E-05	4.8965E-06
$1/5^6$	7.7896E-06	4.8964E-06	3.6754E-07	1.9971E-07

Even though the series expansion of y(x) involves infinite terms, if y(x) is a piecewise constant or it may be approximated as a piecewise constant for each sub-interval, then y(x) can be terminated at finite terms. That means y(x) can be expressed as follows:(3.6) $$\begin{array}{c}\hfill y(x)=\sum _{i=1}^{2M}{c}_i{h}_i(x).\end{array}$$(3.6)

Equivalently, above relation can be written in the matrix form as follows:(3.7) $$\begin{array}{c}\hfill \mathbf{Y}={\mathbf{C}}_m^T{\mathbf{H}}_m,\end{array}$$(3.7)

where $\mathbf{Y}$ is the discrete form of the continuous function y(x) and ${\mathbf{C}}_m^T=[c_1,c_2,\cdots ,c_m]$ is the m-dimensional row vector. Moreover, ${\mathbf{H}}_m$ is the Haar wavelet matrix of order m and is defined by ${\mathbf{H}}_m={\left[{\mathbf{h}}_1,{\mathbf{h}}_2,\cdots ,{\mathbf{h}}_m\right]}^T$; that is,(3.8) $$\begin{array}{c}\hfill {\mathbf{H}}_m=\left(\begin{array}{c}{\mathbf{h}}_1\hfill \\ {\mathbf{h}}_2\hfill \\ ⋮\hfill \\ {\mathbf{h}}_m\hfill \end{array}\right)=\left(\begin{array}{cccc}{h}_{1,1}& h_{1,2}& \cdots & h_{1,m}\\ h_{2,1}& h_{2,2}& \cdots & h_{2,m}\\ ⋮& ⋮& ⋮& ⋮\\ h_{m,1}& h_{m,2}& \cdots & h_{m,m}\end{array}\right),\end{array}$$(3.8)

where ${\mathbf{h}}_1,{\mathbf{h}}_2,\cdots ,{\mathbf{h}}_m$ are the discrete form of the Haar wavelet basis. For Haar wavelet approximations, the following collocation points are considered:(3.9) $$\begin{array}{c}\hfill x_{\ell }=\frac{\ell -0.5}{m},\ell =1,2,\cdots ,m.\end{array}$$(3.9)

Table 4. Maximum absolute errors for different values of N and $\mathit{ϵ}$

$\mathit{ϵ}\downarrow$	$N=16$	$N=32$	$N=64$	$N=128$
1	4.2215E-06	1.0603E-06	2.6540E-07	6.6370E-08
1 / 5	7.3380E-05	1.8707E-05	4.6962E-06	1.1759E-06
$1/5^2$	1.0533E-03	4.0690E-04	1.1226E-04	2.8906E-05
$1/5^3$	7.0483E-04	1.3723E-04	1.2529E-05	5.8909E-06
$1/5^4$	3.6848E-05	1.4255E-04	4.9873E-05	1.2027E-05
$1/5^5$	5.4897E-06	1.9510E-06	6.3677E-07	1.2707E-07
$1/5^6$	5.9615E-06	2.3845E-06	9.5358E-07	3.8111E-07

For example, if $j=2\Rightarrow 2M=8$, so that the Haar matrix can be expressed as follows:$${\mathbf{H}}_8=\left(\begin{array}{cccccccc}\hfill 1& \hfill 1& \hfill 1& \hfill 1& \hfill 1& \hfill 1& \hfill 1& \hfill 1\\ \hfill 1& \hfill 1& \hfill 1& \hfill 1& \hfill -1& \hfill -1& \hfill -1& \hfill -1\\ \hfill 1& \hfill 1& \hfill -1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 1& \hfill -1& \hfill -1\\ \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1\end{array}\right).$$

At the collocation points as defined by (2.9), equation (2.6) becomes(3.10) $$\begin{array}{c}\hfill y(x_{\ell })=\sum _{i=1}^{2M}{c}_i{h}_i(x_{\ell }).\end{array}$$(3.10)

The Haar approximation $y_m$ of y is given by(3.11) $$\begin{array}{c}\hfill y_m(x)=\sum _{i=1}^N{c}_i{h}_i(x),N=2M=2^{j+1},j=0,1,\cdots ,J.\end{array}$$(3.11)

Therefore, the corresponding error at the mth level may be defined as follows:$$\Vert y(x)-y_m(x){\Vert }_2={∥y(x)-\sum _{i=1}^N{c}_i{h}_i(x)∥}_2={∥\sum _{i=2^{j+1}}^{\infty }{c}_i{h}_i(x)∥}_2.$$

3. Method of solution

With the aid of Haar operational matrices as defined in Section 2, we solve the following singularly perturbed reaction–diffusion problem of the form(4.1) $$\begin{array}{c}\hfill Ly(x)\equiv -\mathit{ϵ}{y}^{″}(x)+f(x)y(x)=g(x),y(0)={\mathit{\alpha }}_0,y(1)={\mathit{\alpha }}_1,\end{array}$$(4.1)

where f(x), g(x) are real-valued sufficiently smooth functions in [0, 1]. Let us assume that(4.2) $$\begin{array}{c}\hfill y^{″}(x)=\sum _{i=1}^N{c}_i{h}_i(x),\end{array}$$(4.2)

where $c_i$’s, $i=1,2,\cdots ,N$ are Haar coefficients to be determined. Integrating Equation (3.2) from 0 to x together with the given initial condition, we obtain(4.3) $$\begin{array}{c}\hfill y^{\prime }(x)=\sum _{i=1}^N{c}_i{P}_{i,1}(x)+y^{\prime }(0).\end{array}$$(4.3)

Figure 4. Comparison of numerical and exact solution at $N=32$ and $\mathit{ϵ}=1/5^6$.

Table 5. Numerical result of Example 4.5 at $\mathit{\epsilon }={10}^{-3}$ and $\mathit{\epsilon }={10}^{-4}$

	$\mathit{\epsilon }={10}^{-3}$			$\mathit{\epsilon }={10}^{-4}$
x	Our method	Kumar et al. (2007)	Exact sol.	Our method	Kumar et al. (2007)	Exact sol.
0.0	$-1.0000000$	$-1.0000000$	$-1.0000000$	$-1.0000000$	$-1.0000000$	$-1.0000000$
0.1	3.0995421	3.0995652	3.0995000	3.1004189	3.1004235	3.0995000
0.2	3.1995369	–	3.1995000	3.1995153	–	3.1995000
0.3	3.2995311	3.2995507	3.2995000	3.3002127	3.3002183	3.2995000
0.4	3.3995295	–	3.3995000	3.3995104	–	3.3995000
0.5	3.4995268	3.4995362	3.4995000	3.5000081	3.5000131	3.4995000
0.6	3.5995116	–	3.5995000	3.5995059	–	3.5995000
0.7	3.6995171	3.6995217	3.6995000	3.6998043	0.1899999	3.6995000
0.8	3.7995101	–	3.7995000	3.7995031	–	3.7995000
0.9	3.8995049	3.8995072	3.8995000	3.8996009	3.8996026	3.8995000
1.0	3.9995000	3.9995000	3.9995000	3.9995000	3.9995000	3.9995000

Figure 5. Comparison of numerical and exact solution at $\mathit{ϵ}={10}^{-3}$ and ${10}^{-4}$.

Again integrating Equation (3.3) with the initial condition, then we have(4.4) $$\begin{array}{c}\hfill y(x)=\sum _{i=1}^N{c}_i{P}_{i,2}(x)+x{y}^{\prime }(0)+y(0).\end{array}$$(4.4)

To calculate $y^{\prime }(0)$, we integrate Equation (3.3) between the limits 0 to 1 to get(4.5) $$\begin{array}{c}\hfill y^{\prime }(0)=y(1)-y(0)-\sum _{i=1}^N{c}_i{C}_{i,1}.\end{array}$$(4.5)

Hence, Equation (3.4) becomes(4.6) $$\begin{array}{c}\hfill y(x)=\sum _{i=1}^N{c}_i[P_{i,2}(x)-x{C}_{i,1}]+x[y(1)-y(0)]+y(0).\end{array}$$(4.6)

Table 6. Maximum absolute errors of Example 4.6 for different values of $\mathit{\epsilon }$ and N

$\mathit{\epsilon }\downarrow$	$N=16$		$N=32$		$N=64$		$N=128$		$N=256$
	HWCM	Natesan et al. (2003)	HWCM	Natesan et al. (2003)	HWCM	Natesan et al. (2003)	HWCM	Natesan et al. (2003)	HWCM	Natesan et al. (2003)
1.0e-00	0.0048	0.0079	0.0029	0.0038	0.0011	0.0019	0.0003	0.0009	0.0000	0.0005
1.0e-01	0.1288	0.1354	0.0604	0.0785	0.0379	0.0432	0.0113	0.0229	0.0047	0.0118
1.0e-02	0.1621	0.1753	0.1009	0.1156	0.0613	0.0786	0.0305	0.0487	0.0138	0.0293
1.0e-03	0.1619	0.1792	0.1013	0.1176	0.0621	0.0798	0.0311	0.0494	0.0141	0.0298
1.0e-04	0.1624	0.1796	0.1014	0.1177	0.0631	0.0800	0.0309	0.0495	0.0141	0.0298
1.0e-05	0.1624	0.1796	0.1016	0.1178	0.0631	0.0800	0.0311	0.0495	0.0139	0.0298
1.0e-06	0.1623	0.1796	0.1015	0.1178	0.0629	0.0800	0.0311	0.0495	0.0136	0.0298
1.0e-07	0.1622	0.1796	0.1015	0.1178	0.0632	0.0800	0.0311	0.0495	0.0136	0.0298
1.0e-08	0.1626	0.1796	0.1011	0.1178	0.0635	0.0800	0.0309	0.0495	0.0141	0.0298
1.0e-09	0.1623	0.1796	0.1015	0.1178	0.0635	0.0800	0.0309	0.0495	0.0141	0.0298

Substituting the values of $y^{″}(x)$ and y(x) in Equation (3.1) and the discretization is applied using the collocation points given by (2.9) resulting into a system of algebraic equations which contains unknowns vectors $c_i$’s. Solving this system of algebraic equations using the classical Newton’s method, we obtain the Haar wavelet coefficients $c_i$’s and then substituting these values in (3.4), we obtain the Haar wavelet collocation method for the numerical solution of singularly perturbed boundary value problem of the type (1.1).

4. Numerical experiments and discussion

In this section, we are going to study numerically the SPPs (3.1) with the known boundary condition. The main aim here is to show the accuracy and applicability of the present method, described in Section 3, for solving the SPPs. Performance of the proposed method is compared with the existing methods in literature (Khan et al., 2014; Kumar, Singh, & Mishra, 2007; Lubuma & Patidar, 2006; Natesan, Kumar, & Vigo-Aguiar, 2003; O’Riordan & Stynes, 1986; Rashidinia et al., 2007; Schatz & Wahlbin, lab26 ). The numerical results infer that the proposed method is very effective and superior in comparison with other existing methods. Numerical computations have been done with the software package MATLAB 7.0 and graphical outputs were generated by MAPLE 14 package.

Example 4.1

Consider the following singularly perturbed boundary value problem (Khan et al., 2014; Rashidinia et al., 2007):(5.1) $$\begin{array}{c}\hfill \left.\begin{array}{ccc}-\mathit{ϵ}{y}^{″}(x)+y(x)\hfill & =x,\hfill & x\in [0,1],\hfill \\ y(0)\hfill & =1,\hfill & y(1)=1+exp\left({\displaystyle \frac{-1}{\sqrt{\mathit{ϵ}}}}\right)\hfill \end{array}\right\}.\end{array}$$(5.1)

The exact solution of this problem is(5.2) $$\begin{array}{c}\hfill y(t)=t+exp\left(\frac{-t}{\sqrt{\mathit{ϵ}}}\right).\end{array}$$(5.2)

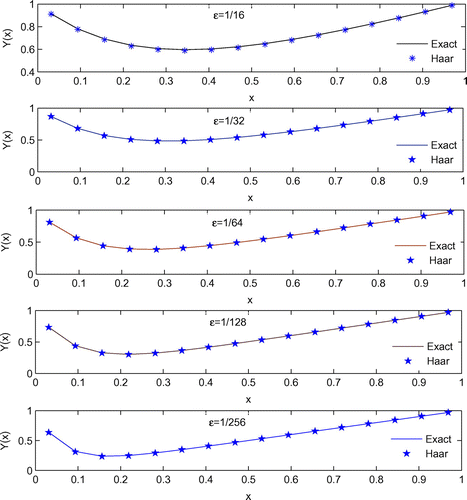
The obtained maximum absolute errors of (4.1) is presented in comparison with the existing methods and exact solution (4.2) in Table 1 for different values of $\mathit{ϵ}$ and N. From Table 1, it is clear that HWCM performs much better than existing methods (Khan et al., 2014; Rashidinia et al., 2007). Table 1 also shows improved convergence of HWCM, as with the increase in number of collocation points the maximum absolute errors decrease for the solution. The numerical result for $N=32$ and different values of $\mathit{ϵ}$ is shown in Figure 1.

Example 4.2

Let us consider the following singular perturbation problem (Lubuma et al., 2006; O’Riordan et al., 1986):(5.3) $$\begin{array}{c}\hfill \left.\begin{array}{cc}-\mathit{ϵ}{y}^{″}(x)+{\displaystyle \frac{4}{{(x+1)}^4}}[1+\sqrt{\mathit{ϵ}}(x+1)]y(x)=f(x),\hfill & x\in [0,1],\hfill \\ y(0)=2,\hfill & y(1)=-1,\hfill \end{array}\right\}\end{array}$$(5.3)

where$$\begin{array}{cc}\hfill f(x)& =-\frac{4}{{(x+1)}^4}\left[\left(1+\sqrt{\mathit{ϵ}}(x+1)+4{\mathit{\pi }}^2\mathit{ϵ}\right)cos\left(\frac{4\mathit{\pi }x}{x+1}\right)\right.\hfill \\ \hfill & \left.-2\mathit{\pi }\mathit{ϵ}(x+1)sin\left(\frac{4\mathit{\pi }x}{x+1}\right)+\frac{3(1+\sqrt{\mathit{ϵ}}(x+1))}{1-exp(-1/\sqrt{\mathit{ϵ}})}\right].\hfill \end{array}$$

The exact solution of the above problem is$$\begin{array}{c}\hfill y(x)=-cos\left(\frac{4\mathit{\pi }x}{x+1}\right)+\frac{3[exp(-2x/\sqrt{\mathit{ϵ}}(x+1))-exp(-1/\sqrt{\mathit{ϵ}})]}{1-exp(-1/\sqrt{\mathit{ϵ}})}.\end{array}$$

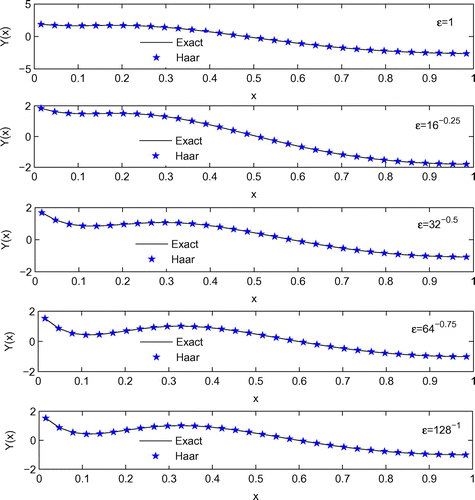
Table 2 gives the maximum absolute error for test Example 4.2. It is obvious that the error bound is inversely proportional to the level of resolution J of Haar wavelet. Hence, the accuracy in the proposed method (HWCM) improves as we increase the level of resolution J. The solution produced through HWCM for the singularly perturbed boundary value problem (4.3) is shown in Figure 2 for different values of $\mathit{ϵ}$ and $N=32$.

Example 4.3

We next consider the singularly perturbed problem (Schatz et al., 1983)(5.4) $$\begin{array}{c}\hfill \left.\begin{array}{ccc}-\mathit{ϵ}{y}^{″}(x)+y(x)\hfill & =(x-1)-xexp(-1/\mathit{ϵ}),\hfill & x\in [0,1],\hfill \\ \hfill & y(0)=0,\hfill & y(1)=0\hfill \end{array}\right\},\end{array}$$(5.4)

whose exact solution is given by$$y(x)=(x-1)-xexp(-1/\mathit{ϵ})+exp(-x/\mathit{ϵ}).$$

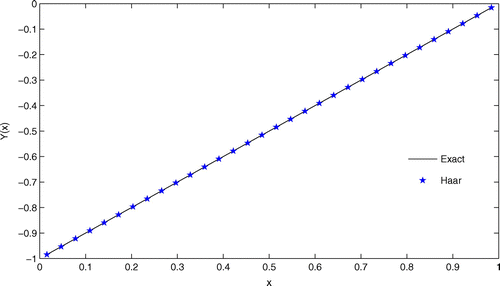
We solve this problem by HWCM method which developed in Section 2 and compare our numerical results with finite element method (Schatz et al., lab26). In this example, the computed maximum absolute errors are compared with the exact solution at specified points in reference (Schatz et al., lab26) and the results are shown in Table 3 and graphically shown in Figure 3. This table shows that our method is considerably accurate in comparison with method in (Schatz et al., 1983).

Example 4.4

Consider the following singular perturbed problem(5.5) $$\begin{array}{c}\hfill \left.\begin{array}{ccc}-{\mathit{ϵ}}^2{y}^{″}(x)+y(x)\hfill & =(-{\mathit{ϵ}}^2+1)e^x-x(e^1+e^{-1/\mathit{ϵ}})-2(1-x),\hfill & x\in [0,1],\hfill \\ \hfill & y(0)=0,\hfill & y(1)=0\hfill \end{array}\right\}.\end{array}$$(5.5)

The exact solution of the above problem is$$y(x)=e^{-x/\mathit{ϵ}}+e^x-x(e^1+e^{-1/\mathit{ϵ}})-2(1-x).$$

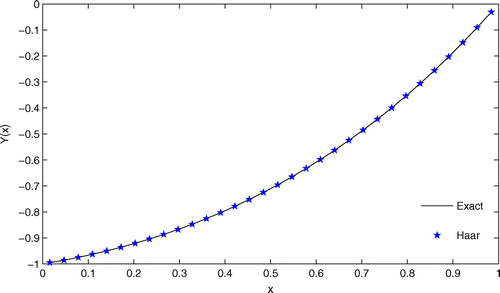
Next, we consider a nonlinear singular perturbation problem with left-end boundary layer. First, we convert the underlying problem as a sequence of linear singular perturbation problem using Newton’s quasi-linearization technique, i.e. replacing the nonlinear problem by a sequence of linear problems. Then, the outer solution (the solution of the given problem by putting $\mathit{\epsilon }=0$) is taken to be the initial approximation (Table 4 and graphically shown in Figure 4).

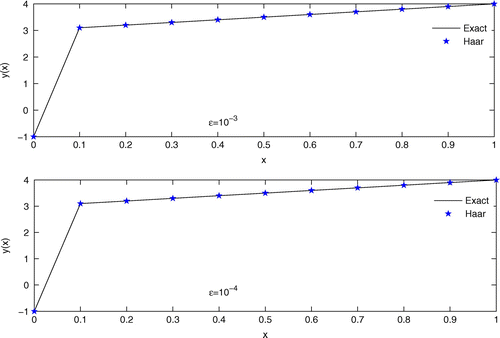
Example 4.5

We consider the following nonlinear singular perturbation problem (Kadalbajoo et al., 2010; Kumar, Singh, & Mishra, 2007)(5.6) $$\begin{array}{c}\hfill \mathit{\epsilon }{y}^{″}(x)+y(x)y^{\prime }(x)-y(x)=0,x\in [0,1]\end{array}$$(5.6)

with $y(0)=-1$ and $y(1)=3.9995$. The exact solution of the problem is(5.7) $$\begin{array}{c}\hfill y(x)=x+c_{1}tanh(c_1(x/\mathit{\epsilon }+c_2)/2),\end{array}$$(5.7)

where $c_1=2.9995$ and $c_2=(1/c_1){log}_e[(c_1-1)/(c_1+1)].$

For convenience, we convert the nonlinear Equation (4.6) into linear by taking the initial approximation from the problem $y(x)y^{\prime }(x)+y(x)=0$. For $x=0$, we assume that $y^{\prime }(x)=0$, and $y(x)=C$. Further, in order to satisfy the condition at $x=1$, we take $y(x)=x+2.9995$ so as a result, we obtain the linear version of (4.6) as follows:(5.8) $$\begin{array}{c}\hfill \mathit{\epsilon }{y}^{″}(x)-(x+2.9995)y^{\prime }(x)-(x+2.9995)=0,x\in [0,1]\end{array}$$(5.8)

with $y(0)=-1$ and $y(1)=3.9995$. The numerical results of Example 4.5 are presented in Table 5 and graphically shown in Figure 5 for $\mathit{\epsilon }={10}^{-3}$ and $\mathit{\epsilon }={10}^{-4}$.

Example 4.6

Finally, consider the following singularly perturbed turning point problem (Natesan et al., 2003):(5.9) $$\begin{array}{c}\hfill \mathit{\epsilon }{y}^{″}(x)-2(2x-1)y^{\prime }(x)-4y(x)=0,x\in [0,1]\end{array}$$(5.9)

with $y(0)=1$ and $y(1)=1$. The exact solution of the above problem is(5.10) $$\begin{array}{c}\hfill y(x)=e^{-2x(1-x)/\mathit{\epsilon }}.\end{array}$$(5.10)

Table 6 gives the maximum absolute error for test Example 4.6. It is obvious that the error bound is inversely proportional to the level of resolution J of Haar wavelet. Hence, the accuracy in the proposed method (HWCM) improves as we increase the level of resolution J. It further strengthens the claim that the proposed method gives excellent results even for very small $\mathit{ϵ}$.

5. Conclusion

The Haar wavelet collocation method is applied in order to find the numerical solution of one-dimensional singularly perturbed boundary value problems. The method is tested on several benchmark problems from the literature. The numerical results are compared with a few existing methods reported recently in the literature. The numerical evidence shows superiority of the new method in terms of fast convergence and better accuracy. The proposed method can safely and quickly be used for the solution of a wide range of similar problems.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Firdous A. Shah

Firdous A. Shah is a senior assistant professor in the Department of Mathematics at the University of Kashmir, India. His primary research interests include basic theory of wavelets and their applications in differential and integral equations, Economics and Finance, and Computer Networking. He has authored/co-authored over 60 research papers in international journals of high repute. He has recently co-authored a book on wavelets entitled Wavelet Transforms and Their Applications, Springer, New York, 2015. Rustam Abass received his MSc in Applied Mathematics from BGSB University Rajouri, India. His research interests are focused on different wavelet methods for the numerical treatment of integral and differential equations. Javid Iqbal received his MPhil and PhD degrees in Mathematics from Aligarh Muslim University, Aligarh, India. Currently, he is a senior assistant professor in the Department of Mathematical Sciences, BGSB University, Rajouri.

R. Abass

R. Abass received his MSc in Applied Mathematics from BGSB University Rajouri, India. His research interests are focused on different wavelet methods for the numerical treatment of integral and differential equations.

J. Iqbal

J. Iqbal received his MPhil and PhD degrees in Mathematics from Aligarh Muslim University, Aligarh, India. Currently, he is a senior assistant professor in the Department of Mathematical Sciences, BGSB University, Rajouri.