Approximate analytical solution with stability analysis of HIV/AIDS model

Abstract

Human Immunodeficiency Virus (HIV)/Acquired Immunodeficiency Syndrome (AIDS) is one of the major issues in various developing countries. In the present communication, a simple nonlinear deterministic mathematical model is proposed for HIV/AIDS infection in sex workers, which is based on Anderson and May’s model and obtained the approximate analytical solution by homotopy analysis method. For this model, the basic reproduction number R₀ is also calculated and its threshold properties are discussed. Moreover, the various numerical solutions are also discussed under general assumptions than the existing. The validity and applicability of the technique are discussed in the numerical results of the problem for different particular cases which are depicted through graphs. Further, the graphs of the proposed model are compared with the real life data of the HIV positive patients in Tamil Nadu.

Keywords:

• HIV/AIDS
• homotopy analysis method
• sex workers
• stability

Public Interest Statement

Over the last century, mathematics has been used to predict the spread of diseases, relating important public health questions to basic transmission parameters. To deal with the problems of HIV/AIDS among sex workers, epidemiologists can use the proposed deterministic model to obtain a numerical description of the disease tendency and to make forecasts about the disease. In most of the cases, it is difficult to solve nonlinear problems. HAM itself provides a convenient way to control and adjust the convergence region and rate of approximation series, when necessary. Thus, the approximate analytical solution of the proposed model for HIV/AIDS is obtained through this method.

1. Introduction

Acquired Immunodeficiency Syndrome (AIDS) is an infectious disease caused by a retrovirus called “Human Immunodeficiency Virus” (HIV). HIV can destroy various CD4 cells in the body such that the body can’t fight against the disease and thus the HIV infection progresses to AIDS. The life expectancy of an AIDS patient is 1–3 years (Jacquez, Simon, Koopman, Sattenspiel, & Perry, 1988). Granting to the UNAIDS report, about 35 million people were surviving with HIV globally, out of these 48 lakh cases are in Asia. In 1986, the first case of HIV infection as well as the first case of AIDS was reported in India (Lakhashe, Thakar, Godbole, Tripathy, & Paranjape, 2008). Nowadays, India bears the highest (49%) number of people in this continent, where 85% cases of HIV transmission occur through heterosexual contact with sex workers and their clients (Busenberg, Cooke, & Hsieh, 1995; Shah & Gupta, 2013; UNAIDS, 2009, 2014; Venkataramana & Sarada, 2001) (http://www.avert.org/history-hiv-aids-usa). Initially, the transmission rate of HIV/AIDS was comparatively slow, but over the last few years, it is a critical health problem for public in many countries (http://www.unaids.org/sites/default/files/media_asset/GARPR_2014_guidelines_en_pdf). HIV incidence varies from country to country and from region to region, depending on various risk factors. The risk of HIV is higher among sex workers. Sex workers include those female, male, and rogynous adults and young individuals who get money in exchange for sexual services, either repeatedly or periodically. Not only sex workers are at higher risk of HIV, but also those people who are unconscious about their HIV status can increase their risk of HIV transmission. In many countries, sex workers are extremely vulnerable to HIV due to numerous issues, including large numbers of sex partners, unsafe working conditions, and prevented to the negotiation of condom use (http://www.who.int/hiv/abouthiv/en/). At the present time, sex workers are a major issue in the modeling of HIV transmission. In the recent studies, occurrence of HIV/AIDS disease between female sex workers varies widely and it is more than 20 times higher than the HIV prevalence in the general population (Baral et al., 2012). According to the UNAIDS report, it has been calculated that the risk of HIV transmission from female-to-male sex workers (2.4%) is higher than the male-to-female sex workers (0.05%) (Boily et al., 2009).

Mathematical model plays a significant role in understanding the transmission dynamics of HIV/AIDS disease (Hethcote, 2000). At first, Anderson (1988) proposed a HIV transmission model that presents the progression from HIV infection to AIDS disease and the population is divided into classes of progressive infectious stages. Various mathematical models have been developed to monitor the epidemic of HIV/AIDS with the emphasis on the role of sex workers (Anderson & May, 1979, 1991; Kaur, Ghosh, & Bhatia, 2014). Busenberg et al. (1995) formulated a model for the recent rapid growth of the HIV/AIDS epidemic in Asia. They studied the spread of HIV/AIDS in the community, mainly due to the sexual interaction between a core group of female prostitutes and young unmarried males. Shah and Gupta (2013) studied a mathematical model for a community which holds the structure of two categories with different stages of sexual activity: one is the high activity group that includes commercial sex workers and their male customers and the other is a low activity group. Bhunu and Mushayabasa (2012) presented a mathematical model to assess the link between prostitution and HIV transmission. Kaur et al. (2014) developed a nonlinear mathematical model for studying the transmission dynamics of HIV/AIDS epidemic with emphasis on the role of female sex workers.

The aim of this paper is to discuss the stability analysis of the proposed model and also to find the approximate analytical solution of the given model using homotopy analysis method (HAM). First time, Liao (2004a, 2004b) proposed this method to find series solutions of various types of linear and nonlinear problem. This method is based on homotopy and a fundamental concept of topology, and it has a freedom in choosing initial approximations and auxiliary linear operators which often help to transfer the complicated nonlinear problem to its simpler form. HAM is applied to find approximate analytical solution of the problem and the numerical results of the problem for different particular cases are depicted graphically. Recently, HAM has been used to find the approximate analytical solution of SIR epidemic model, SIS epidemic model, and HIV infection model for CD4 cells (Awawdeh, Adawi, & Mustafa, 2009; Ghoreishi, Ismail, & Alomari, 2011; Sajid, Abbas, Ali, & Javed, 2013). It is an effective method to control the convergence of the series solution through ℏ-curve analysis. Here, the solution of above nonlinear system of equations is expressed in terms of the auxiliary parameter ℏ, which is then varied to determine its optimum value. Flow chart of the model is shown in Figure 1.

Figure 1. Flow chart of the model.

The rest of the manuscript is epitomized as follows: in Section 2, a nonlinear mathematical model is presented for HIV/AIDS disease among sex workers. Basic properties of the model and the computation of the basic reproduction number are discussed in Section 3 followed by the stability analysis of the model. In Section 4, description of the HAM is discussed and the numerical results are obtained for different values of parameters and further, convergence of the HAM series solution is analyzed and verified by taking real-life data of HIV infected in Tamil Nadu, in Section 5.

2. Model description

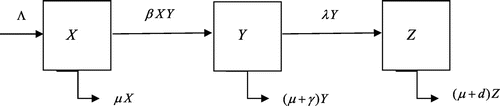
The differential equations for HIV/AIDS dynamics of sex workers are as follows:(1) $$X^{\prime }(t)=\mathrm{\Lambda }-\mathit{\beta }X(t)Y(t)-\mathit{\mu }X(t),$$(1)

(2) $$Y^{\prime }(t)=\mathit{\beta }X(t)Y(t)-(\mathit{\mu }+\mathit{\gamma }+\mathit{\lambda })Y(t),$$(2) (3) $$Z^{\prime }(t)=\mathit{\lambda }Y(t)-(d+\mathit{\mu })Z(t).$$(3)

With the initial conditions $X(0)=X_0,Y(0)=Y_0,$ and $Z(0)=Z_0$. Here, the total population of sex workers $N(t)=X(t)+Y(t)+Z(t)$ and the parameters $X(t),Y(t)\text{and}Z(t)$ denotes the susceptible, HIV-positive, and the AIDS-patients sex workers. The transfer diagram of the model is depicted through the graph in Figure 2.

Figure 2. Transfer diagram of the model.

3. Analysis of the model

3.1. Bounds of the solutions

Theorem 3.1

Let $\{\mathrm{\Omega }=(X,Y,Z):X(0)>0,Y(0)\ge 0,Z(0)\ge 0\}$. Then the solutions of Equations (1–3) is positive for all t > 0.

Thus, all the solutions of the system (1–3) with positive initial data will remain positive for t > 0, i.e. $X^{\prime }(t)\ge X(0)e^{-\mathit{\mu }t}\ge 0,Y^{\prime }(t)\ge Y(0)e^{-(\mathit{\lambda }+\mathit{\gamma }+\mathit{\mu })t}\ge 0$ and $Z^{\prime }(t)\ge Z(0)e^{-(d+\mathit{\mu })t}\ge 0.$

Theorem 3.2

For all time t > 0, the solutions of the system (1–3) are eventually confined in the compact subset $\mathrm{\Gamma }=\{(X,Y,Z)\in {\mathbb{R}}_{+}^3:N=(X+Y+Z)\le \frac{\mathrm{\Lambda }}{\mathit{\mu }},X\ge 0,Y\ge 0,Z\ge 0\}$.

Clearly, it has been proved that all the solutions of (1–3) which initiate in ${\mathbb{R}}_{+}^3$ confined in the region Γ, i.e. the solutions are bounded in the interval $[0,\infty )$, i.e. $\underset{t\to \infty }{lim}SupN(t)=\underset{t\to \infty }{lim}Sup(X+Y+Z)\le \frac{\mathrm{\Lambda }}{\mathit{\mu }}.$

3.2. Disease free equilibrium and endemic equilibrium

The disease free equilibrium (DFE) has been always feasible, as in this equilibrium the infection dies out from the population. The DFE and the endemic equilibrium of the system (1–3) is given by $E_0=(X^0,Y^0,Z^0)=\left(\frac{\mathit{\alpha }}{\mathit{\mu }},0,0\right)$ and $E^{\ast }=(X^{\ast },Y^{\ast },Z^{\ast }),$ respectively

where $X^{\ast }=\frac{(\mathit{\lambda }+\mathit{\mu }+\mathit{\gamma })}{\mathit{\beta }},Y^{\ast }=-\frac{(-\mathit{\alpha }\mathit{\beta }+\mathit{\mu }\mathit{\gamma }+\mathit{\mu }\mathit{\lambda }+{\mathit{\mu }}^2)}{\mathit{\beta }(\mathit{\lambda }+\mathit{\mu }+\mathit{\gamma })},Z^{\ast }=-\frac{\mathit{\lambda }(-\mathit{\alpha }\mathit{\beta }+\mathit{\mu }\mathit{\gamma }+\mathit{\mu }\mathit{\lambda }+{\mathit{\mu }}^2)}{\mathit{\beta }(d+\mathit{\mu })(\mathit{\lambda }+\mathit{\mu }+\mathit{\gamma })}$ with the constant natural mortality rate μ.

3.3. Basic reproduction number

To study the spread of HIV/AIDS disease, calculation of the basic reproduction number has been required. The basic reproduction number is the threshold quantity that determines whether an infectious disease will spread in a susceptible population or not. It is obtained by taking the largest eigenvalue (spectral radius) of the next generation matrix and mathematically written as $R_0=\mathit{\rho }(F{V}^{-1})$, where ρ is the spectral radius of the next generation matrix, F is the rate of appearance of new infections in the compartment Y and V is the transfer of individuals out of compartment Y by all other means.

By linearization approach, the associated matrix at DFE is obtained as$$F=\left[\begin{array}{cc}\frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }}& 0\\ 0& 0\end{array}\right]\text{and}V=\left[\begin{array}{cc}(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })& 0\\ -\mathit{\lambda }& (d+\mathit{\mu })\end{array}\right].$$

Therefore, $F{V}^{-1}=\left[\begin{array}{cc}\frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })}& 0\\ 0& 0\end{array}\right]$

and the spectral radius of the next generation matrix is$$R_0=\frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })}.$$

3.4. Local and global stability of disease-free equilibrium and endemic equilibrium

Lemma 3.4.1.

The DFE is locally asymptotically stable whenever $R_0<1$ and unstable otherwise.

Lemma 3.4.2.

The DFE is globally asymptotically stable in ${\mathbb{R}}_{+}^3$ for $R_0\le 1$ and unstable otherwise.

Proof

The maximum invariant set in $\{(X,Y,Z)\in \mathrm{\Gamma }:L^{\prime }\le 0\}$ is the singleton set {E₀}. Hence, it follows from the LaSalle’s principle that the DFE is globally asymptotically stable for $R_0\le 1$.

Lemma 3.4.3.

The endemic equilibrium is locally asymptotically stable for $R_0>1$ and unstable otherwise.

Lemma 3.4.4.

If $R_0>1,$ the endemic equilibrium E^* of the model (1–3) is globally asymptotically stable and unstable otherwise.

The whole proofs of the lemmas are elucidated in Appendix A.

4. Solutions by homotopy analysis method

To solve Equations (1–3) of HIV/AIDS model by HAM, the initial approximations are(4) $$X(0)=X_0,Y(0)=Y_0,Z(0)=Z_0,N(0)=N_0.$$(4)

The linear and nonlinear operators are defined as follows:$$L[{\mathit{\phi }}_1(t;q)]=\frac{d{\mathit{\phi }}_1(t;q)}{dt},$$$$L[{\mathit{\phi }}_2(t;q)]=\frac{d{\mathit{\phi }}_2(t;q)}{dt},$$$$L[{\mathit{\phi }}_3(t;q)]=\frac{d{\mathit{\phi }}_3(t;q)}{dt},$$$$N_1[{\mathit{\phi }}_1,{\mathit{\phi }}_2,{\mathit{\phi }}_3]=\frac{d{\mathit{\phi }}_1(t;q)}{dt}-\mathrm{\Lambda }+\mathit{\beta }(t){\mathit{\phi }}_1(t;q){\mathit{\phi }}_2(t;q)+\mathit{\mu }(t){\mathit{\phi }}_1(t;q),$$

$$N_2[{\mathit{\phi }}_1,{\mathit{\phi }}_2,{\mathit{\phi }}_3]=\frac{d{\mathit{\phi }}_2(t;q)}{dt}-\mathit{\beta }(t){\mathit{\phi }}_1(t;q){\mathit{\phi }}_2(t;q)+(\mathit{\mu }(t)+\mathit{\gamma }(t)+\mathit{\lambda }(t)){\mathit{\phi }}_2(t;q),$$

$$N_3[{\mathit{\phi }}_1,{\mathit{\phi }}_2,{\mathit{\phi }}_3]=\frac{d{\mathit{\phi }}_3(t;q)}{dt}-\mathit{\lambda }(t){\mathit{\phi }}_2(t;q)+(d(t)+\mathit{\mu }(t)){\mathit{\phi }}_3(t;q),$$

with the property that $L[c_i]=0$, where $c_i(i=1,2,3)$ is the integral constants. According to definitions (Liao 2004a, 2004b), the zeroth-order deformation equations are as follows:(5) $$(1-q)L[{\mathit{\phi }}_1(t;q)-X_0(t)]=ħq{N}_1[{\mathit{\phi }}_1(t;q),{\mathit{\phi }}_2(t;q),{\mathit{\phi }}_3(t;q)],$$(5) (6) $$(1-q)L[{\mathit{\phi }}_2(t;q)-Y_0(t)]=ħq{N}_2[{\mathit{\phi }}_1(t;q),{\mathit{\phi }}_2(t;q),{\mathit{\phi }}_3(t;q)],$$(6) (7) $$(1-q)L[{\mathit{\phi }}_3(t;q)-Z_0(t)]=ħq{N}_3[{\mathit{\phi }}_1(t;q),{\mathit{\phi }}_2(t;q),{\mathit{\phi }}_3(t;q)],$$(7)

whereas $q\in [0,1]$ be the embedding parameter and ℏ is the nonlinear auxiliary parameter. Obviously, when q = 0 and q = 1,$${\mathit{\phi }}_1(t;0)=X_0(t)\text{and}{\mathit{\phi }}_1(t;1)=X(t),$$$${\mathit{\phi }}_2(t;0)=Y_0(t)\text{and}{\mathit{\phi }}_2(t;1)=Y(t),$$$${\mathit{\phi }}_3(t;0)=Z_0(t)\text{and}{\mathit{\phi }}_3(t;1)=Z(t).$$

Therefore, as the embedding parameter q increases from zero to unity, ${\mathit{\phi }}_i(t;q):i=1,2,3,$ varies from the initial guess $X_0(t),Y_0(t),Z_0(t)$ to the exact solution $X(t),Y(t),Z(t)$, respectively. Now expanding ${\mathit{\phi }}_i(t;q):i=1,2,3$ in Taylor’s series with respect to q, we have$${\mathit{\phi }}_1(t;q)=X_0(t)+\sum _{m=1}^{\infty }{X}_m(t)q^m,$$$${\mathit{\phi }}_2(t;q)=Y_0(t)+\sum _{m=1}^{\infty }{Y}_m(t)q^m,$$$${\mathit{\phi }}_3(t;q)=Z_0(t)+\sum _{m=1}^{\infty }{Z}_m(t)q^m,$$

where$$X_m(t)=\frac{1}{m!}\frac{d^m{\mathit{\phi }}_1(t;q)}{d{q}^m}\text{at}q=0,$$$$Y_m(t)=\frac{1}{m!}\frac{d^m{\mathit{\phi }}_2(t;q)}{d{q}^m}\text{at}q=0,$$$$Z_m(t)=\frac{1}{m!}\frac{d^m{\mathit{\phi }}_3(t;q)}{d{q}^m}\text{at}q=0.$$

If the auxiliary linear operators, the initial guess and the auxiliary parameter ℏ are properly chosen, the above series is convergent at q = 1, then$$X(t)=X_0(t)+\sum _{m=1}^{\infty }{X}_m(t),Y(t)=Y_0(t)+\sum _{m=1}^{\infty }{Y}_m(t),Z(t)=Z_0(t)+\sum _{m=1}^{\infty }{Z}_m(t),$$

which must be one of the solutions of the original nonlinear equation. For further analysis, the vectors are defined as$$\overrightarrow{X_n}(t)=[X_0(t),X_1(t),\dots ,X_n(t)],$$

$$\overrightarrow{Y_n}(t)=[Y_0(t),Y_1(t),\dots ,Y_n(t)],$$

$$\overrightarrow{Z_n}(t)=[Z_0(t),Z_1(t),\dots ,Z_n(t)].$$

Differentiating Equations (5–7) “m” times with respect to q and dividing by m!, then the mth-order deformation equations are defined as follows:(8) $$L[X_m(t)-{\mathit{\chi }}_m{X}_{m-1}(t)]=ħN_1[X_{m-1}(t;q),Y_{m-1}(t;q),Z_{m-1}(t;q)],$$(8)

(9) $$L[Y_m(t)-{\mathit{\chi }}_m{Y}_{m-1}(t)]=ħN_2[X_{m-1}(t;q),Y_{m-1}(t;q),Z_{m-1}(t;q)],$$(9) (10) $$L[Z_m(t)-{\mathit{\chi }}_m{Z}_{m-1}(t)]=ħN_3[X_{m-1}(t;q),Y_{m-1}(t;q),Z_{m-1}(t;q)],$$(10)

where$${\mathit{\chi }}_m=\left\{\begin{array}{cc}0,\hfill & m\le 1\hfill \\ 1,\hfill & m>1\hfill \end{array}\right..$$

For $m\ge 1,$ the solutions of mth-order deformation Equations (8–10) becomes(11) $$X_m={\mathit{\chi }}_m{X}_{m-1}(t)+ħ\underset{0}{\overset{t}{\int }}{N}_1[X_{m-1}(\mathit{\xi };q),Y_{m-1}(\mathit{\xi };q),Z_{m-1}(\mathit{\xi };q)]d\mathit{\xi },$$(11) (12) $$Y_m={\mathit{\chi }}_m{Y}_{m-1}(t)+ħ\underset{0}{\overset{t}{\int }}{N}_2[X_{m-1}(\mathit{\xi };q),Y_{m-1}(\mathit{\xi };q),Z_{m-1}(\mathit{\xi };q)]d\mathit{\xi },$$(12) (13) $$Z_m={\mathit{\chi }}_m{Z}_{m-1}(t)+ħ\underset{0}{\overset{t}{\int }}{N}_3[X_{m-1}(\mathit{\xi };q),Y_{m-1}(\mathit{\xi };q),Z_{m-1}(\mathit{\xi };q)]d\mathit{\xi }.$$(13)

Therefore, for $m=1,2,\dots$, the solutions of Equations (11–13) becomes(14) $$X_1(t)=ħ(-\mathrm{\Lambda }+\mathit{\mu }{X}_0+\mathit{\beta }{X}_0{Y}_0)t,$$(14)

(15) $$Y_1(t)=ħ(-\mathit{\beta }{X}_0{Y}_0+(\mathit{\mu }+\mathit{\gamma }+\mathit{\lambda })Y_0)t,$$(15)

(16) $$Z_1(t)=ħ(-\mathit{\lambda }{Y}_0+(\mathit{\mu }+d)Z_0)t,$$(16) (17) $$X_2(t)=\left[ħ(1+ħ)(-\mathrm{\Lambda }+\mathit{\mu }{X}_0+\mathit{\beta }{X}_0{Y}_0)t+\frac{{ħ}^2}{2}\left(-{\mathit{\beta }}^2{X}_0^2{Y}_0+{\mathit{\beta }}^2{X}_0{Y}_0^2+\mathit{\beta }\mathit{\gamma }{X}_0{Y}_0+\mathit{\beta }\mathit{\gamma }{X}_0{Y}_0-\mathit{\beta }\mathrm{\Lambda }{Y}_0+3\mathit{\beta }\mathit{\mu }{X}_0{Y}_0-\mathrm{\Lambda }\mathit{\mu }+{\mathit{\mu }}^2{X}_0\right)t^2)\right],$$(17) (18) $$Y_2(t)=\left[ħ(1+ħ)(-\mathit{\beta }{X}_0{Y}_0+(\mathit{\mu }+\mathit{\gamma }+\mathit{\lambda })Y_0)t+\frac{{ħ}^2}{2}\left({\mathit{\beta }}^2{X}_0^2{Y}_0+\mathrm{\Lambda }\mathit{\beta }+{(\mathit{\mu }+\mathit{\gamma }+\mathit{\lambda })}^2-\mathit{\beta }{Y}_0-2(\mathit{\gamma }+\mathit{\lambda })-3\mathit{\mu }\right)t^2\right],$$(18) (19) $$Z_2(t)=\left[ħ(1+ħ)(-\mathit{\lambda }{Y}_0+(\mathit{\mu }+d)Z_0)t+\frac{{ħ}^2}{2}\left(d^2{Z}_0-d\mathit{\gamma }{Y}_0+\mathit{\beta }\mathit{\lambda }{X}_0{Y}_0-\mathit{\gamma }\mathit{\lambda }{Y}_0-{\mathit{\lambda }}^2{Y}_0-2d\mathit{\mu }{Z}_0-2\mathit{\mu }\mathit{\lambda }{Y}_0+{\mathit{\mu }}^2{Z}_0\right)\frac{t^2}{2}\right],$$(19)

and so on. Thus, the corresponding homotopy series solution is given by$$X(t)=\sum _{k=0}^{\infty }{X}_k(t),Y(t)=\sum _{k=0}^{\infty }{Y}_k(t),Z(t)=\sum _{k=0}^{\infty }{Z}_k(t),$$

which is convergent for any value of ℏ in convergence region.

5. Numerical results

HAM is applied to find the approximate analytical solution of the HIV/AIDS model and also to examine the effects of the auxiliary parameter on the convergence of the solution through ℏ-curve analysis. Numerical and graphical results are discussed to observe the effect of various values of parameters with respect to time, which are used in the above equations and plotted the graph using MATHEMATICA software.

Description and interpretation of the parameters used in the model are given in Table 1.

Table 1. Parameters and their interpretations

Symbol	Description	Values
Λ	Recruitment rate	120
β	Transmission rate	0.005
μ	Natural death rate	0.143
γ	Treatment rate	0.01
λ	HIV-infected who are developing full-blown AIDS class	0.36
d	Disease-related death rate	0.015

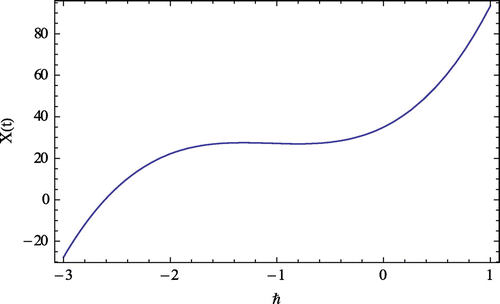
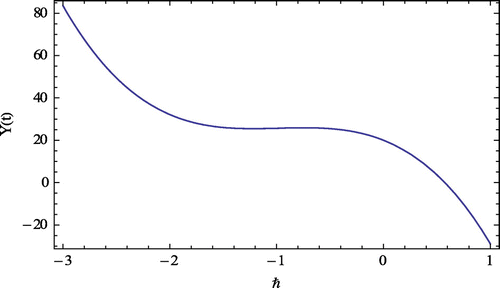
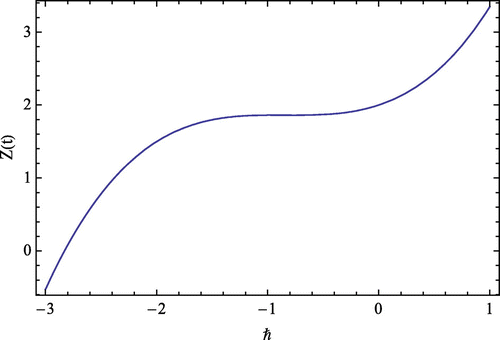
In Figures 3–5, the convergence region of the series solution for susceptible, HIV-positive, and AIDS-infected sex workers are shown, respectively, for various values of parameters at time t = 0.4 and converges to the exact solution for different values of ℏ. This shows that the validity of the region of convergence of the series solution for susceptible X(t), HIV positive Y(t) and AIDS-infected individuals Z(t) at ℏ = −1.4 to −0.6.

Figure 3. X(t) vs. ħ.

Figure 4. Y(t) vs. ħ.

Figure 5. Z(t) vs. ħ.

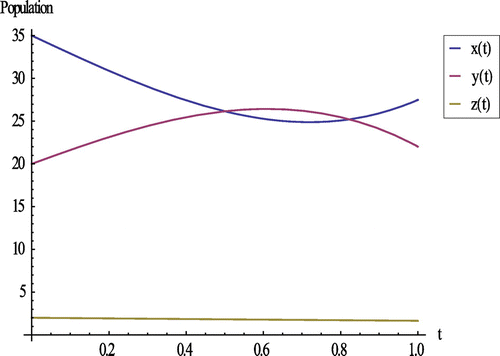
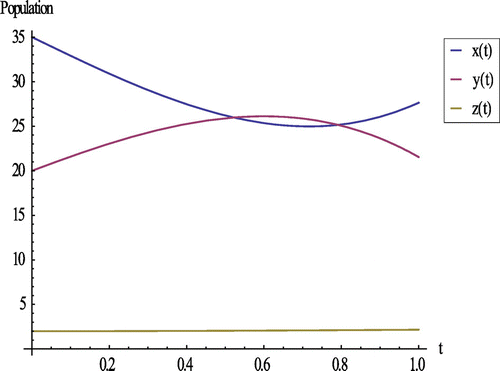
Figures 6 and 7 show the relation between susceptible, HIV-positive, and AIDS patients with respect to time at different values of treatment rate γ, i.e. γ = 0.03 and γ = 0.01, respectively.

Figure 6. Plot of population (susceptible, HIV-positive, and AIDS) vs. time “t.”

Figure 7. Plot of population (susceptible, HIV-positive and AIDS) vs. time “t.”

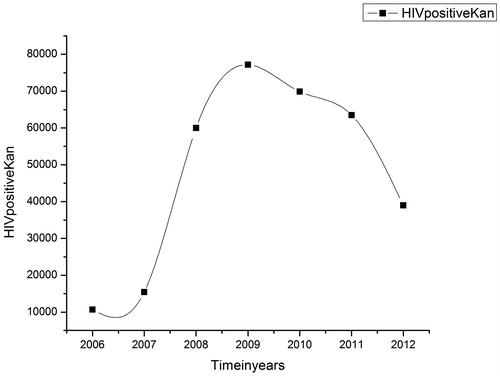
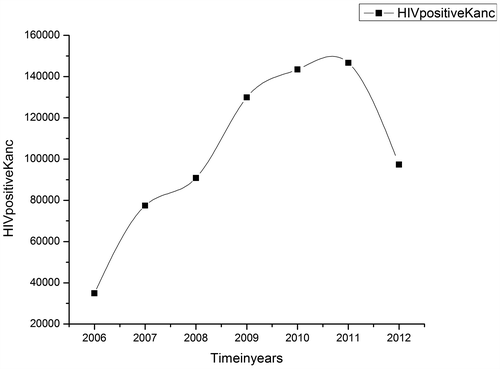
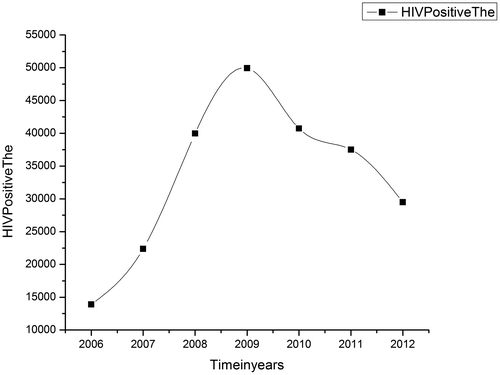
The National AIDS Control Programme (NACP) of NACO has a strong focus on epidemiological modeling of HIV/AIDS. According to NACO, the information about HIV is available in the monthly program reports, behavioral surveys, research studies, etc. for a number of districts. Here, in this communication, we study the survey reports of various districts of Tamil Nadu for HIV positive patients. The Tamil Nadu Government has formed “The Tamil Nadu State AIDS Control Society” to aware of the spread of HIV and takes care of the affected persons. Here, HIV-positive people’s data of some of the districts of Tamil Nadu have been taken from fact sheets (NAVO, 2014). Figures 8–10 represent the graphical representation of the data of HIV infected patients for seven consecutive years from 2006 to 2012.

Figure 8. HIV-positive in Kanyakumari district.

Figure 9. HIV-positive in Kanchipuram district.

Figure 10. HIV-positive in Nilgiri district.

The graphical representation of these data of Kanyakumari, Kanchipuram, and Nilgiris is in accordance with our model. And hence, it verifies the validity of the proposed model.

6. Conclusion and discussion

At present, sex workers are nucleus in the diffusion of sexually transmitted diseases in low income rural areas. Prevention and treatment of HIV in sex workers benefits both abandoned vulnerable group and the general population. The present paper provides the idea to concern about HIV/AIDS and explores the function of sex workers in its dissemination. In this study, the HAM is used to solve the nonlinear equations of the model. The analytical approximations to the result of the HIV/AIDS model are consistent and confirm the power and robustness of the HAM. This method provides a simple way to regulate and manage the convergence of the series solution by choosing proper values of auxiliary parameter. The difficulties and huge computational work avoid HAM that usually arises in parallel techniques like Homotopy Perturbation Method, Adomian Decomposition Method, Reduced Differential Transform Method, finite difference method, etc. Therefore, it is really a powerful and efficient method to resolve the complicated linear and nonlinear partial differential equations. The numerical illustration of the model is done and it is displayed by the graphs.

Further, the graphs are compared with the real-life data of the HIV-positive of Tamil Nadu, and it is concluded that the proposed model can justify the results of the real-life data.

Acknowledgments

The authors would like to thank the editors and reviewers for their valuable comments.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Pratibha Rani

Pratibha Rani has completed her MSc and MPhil in Mathematics from Banasthali University, Rajasthan. She is a full-time PhD scholar in Department of Mathematics, JUET, Guna. Her area of interest includes biomathematics, fuzzy information measures, and decision-making problems.

Divya Jain

Divya Jain is working as an assistant professor in Department of Mathematics, JUET, Guna. She has many research papers and attended several national and international conferences and seminars. Her area of interest includes Biomathematics, Fuzzy information measures, and fuzzy logic.

Vinod Prakash Saxena

Vinod Prakash Saxena is Ex. Vice Chancellor of Jiwaji University. He has organized several national and international conferences seminars, symposia, etc. on Mathematics and Engineering. Currently, he is working as an advisor in Sagar Group of Institutions, Bhopal. His area of interest includes Biomathematics and Finite element methods.

Appendix A.

Proof 3.4.1

Using linearization approach, the Jacobian matrix associated with the system (1–3) is given as$$M=\left[\begin{array}{ccc}-\mathit{\beta }Y& -\mathit{\beta }X& 0\\ \mathit{\beta }Y& \mathit{\beta }X-\mathit{\gamma }-\mathit{\lambda }-\mathit{\mu }& 0\\ 0& \mathit{\lambda }& -d-\mathit{\mu }\end{array}\right].$$

At the disease-free equilibrium, we have$$M(E_0)=\left[\begin{array}{ccc}0& -\frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }}& 0\\ 0& \frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }}-\mathit{\gamma }-\mathit{\lambda }-\mathit{\mu }& 0\\ 0& \mathit{\lambda }& -d-\mathit{\mu }\end{array}\right].$$

Therefore, the eigenvalues at the DFE are $-\mathit{\mu },\frac{-(-\mathrm{\Lambda }\mathit{\beta }+\mathit{\gamma }\mathit{\mu }+\mathit{\lambda }\mathit{\mu }+{\mathit{\mu }}^2)}{\mathit{\mu }}$ and $-d-\mathit{\mu }$. It can be seen that the eigenvalues of the system (1)–(3) at DFE are all negative and hence the DFE is stable. Since$$\frac{-(-\mathrm{\Lambda }\mathit{\beta }+\mathit{\gamma }\mathit{\mu }+\mathit{\lambda }\mathit{\mu }+{\mathit{\mu }}^2)}{\mathit{\mu }}<0,$$

$$\Rightarrow \mathrm{\Lambda }\mathit{\beta }-\mathit{\gamma }\mathit{\mu }-\mathit{\lambda }\mathit{\mu }-{\mathit{\mu }}^2<0,$$$$\Rightarrow \frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })}<1.$$

This result shows that the DFE is locally asymptotically stable for $R_0<1.$

Proof 3.4.2

To prove this, consider that the Lyapunov function $L(X,Y,Z):{\mathbb{R}}_{+}^3\to {\mathbb{R}}_{+}^3$ defined as(A) $$L(X(t),Y(t),Z(t))=\mathit{\phi }Y(t),\mathit{\phi }\ge 0.$$(A)

Differentiating (A) with respect to “t,” we have$$L^{\prime }(X(t),Y(t),Z(t))=\mathit{\phi }{Y}^{\prime }(t),$$$$L^{\prime }=\mathit{\phi }(\mathit{\beta }XY-\mathit{\gamma }Y-\mathit{\lambda }Y-\mathit{\mu }Y),$$$$L^{\prime }\le \mathit{\phi }\left(\frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }}-(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })Y\right),\text{since}X\le X_0=\frac{\mathrm{\Lambda }}{\mathit{\mu }},$$$$L^{\prime }\le \mathit{\phi }(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })\left(\frac{\mathrm{\Lambda }\mathit{\beta }}{\mathit{\mu }(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })}-1\right)Y,$$

which implies $L^{\prime }\le (R_0-1)Y\le 0$. Since L' = 0 only when Y = 0. Using Y = 0 in Equations (1–3) shows that $X\to \frac{\mathrm{\Lambda }}{\mathit{\beta }}$ and $Z\to 0$ as $t\to \infty$. Therefore, the maximum invariant set in $\{(X,Y,Z)\in \mathrm{\Gamma }:L^{\prime }\le 0\}$ is the singleton set {E₀}. Hence, it follows from the LaSalle’s principle that the DFE is globally asymptotically stable for $R_0\le 1$.

Proof 3.4.3

To prove the local stability of the endemic equilibrium, the Jacobian matrix associated with the system (1–3) is given by$$M^{\ast }=\left[\begin{array}{ccc}-\mathit{\beta }{X}^{\ast }-\mathit{\mu }& \mathit{\beta }{X}^{\ast }& 0\\ \mathit{\beta }{Y}^{\ast }& \mathit{\beta }{X}^{\ast }-(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })& 0\\ 0& \mathit{\lambda }& -d-\mathit{\mu }\end{array}\right].$$

At the endemic equilibrium, we have$$M^{\ast }(E_1)=\left[\begin{array}{ccc}-R_0& -\mathit{\gamma }-\mathit{\lambda }-\mathit{\mu }& 0\\ R_0-\mathit{\mu }& 0& 0\\ 0& \mathit{\lambda }& -d-\mathit{\mu }\end{array}\right].$$

Therefore, the eigenvalues are $-(d+\mathit{\mu }),$ $\frac{-R_0+\sqrt{R_0^2-4(R_0-\mathit{\mu })(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })}}{2}$ and $\frac{-R_0-\sqrt{R_0^2-4(R_0-\mathit{\mu })(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })}}{2}$. It can be seen that the eigenvalues of the system (1)-(3) at endemic equilibrium are all negative for $R_0>1$. using Routh–Hurwitz criteria, this shows that the endemic equilibrium is locally asymptotically stable for $R_0>1$.

Proof 3.4.4

To establish the global stability of the endemic equilibrium E^*, construct the following Lyapunov function:(B) $$V(X^{\ast },Y^{\ast },Z^{\ast })=\left(X-X^{\ast }-X^{\ast }log\frac{X}{X^{\ast }}\right)+\left(Y-Y^{\ast }-Y^{\ast }log\frac{Y}{Y^{\ast }}\right)+\left(Z-Z^{\ast }-Z^{\ast }log\frac{Z}{Z^{\ast }}\right).$$(B)

Differentiating (B), we have$$\frac{dV}{dt}=\left(\frac{X-X^{\ast }}{X}\right)\frac{dX}{dt}+\left(\frac{Y-Y^{\ast }}{Y}\right)\frac{dY}{dt}+\left(\frac{Z-Z^{\ast }}{Z}\right)\frac{dZ}{dt}.$$

This implies$$\frac{dV}{dt}=\left(\frac{X-X^{\ast }}{X}\right)(\mathrm{\Lambda }-\mathit{\beta }XY-\mathit{\mu }X)+\left(\frac{Y-Y^{\ast }}{Y}\right)$$$$(\mathit{\beta }XY-(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })Y)+\left(\frac{Z-Z^{\ast }}{Z}\right)(\mathit{\lambda }Y-(d+\mathit{\mu })Z),$$

it implies that(C) $$\frac{dV}{dt}=\left(\frac{X-X^{\ast }}{X}\right)(\mathrm{\Lambda }-\mathit{\beta }(X-X^{\ast })(Y-Y^{\ast })-\mathit{\mu }(X-X^{\ast }))+\left(\frac{Y-Y^{\ast }}{Y}\right)(\mathit{\beta }(Y-Y^{\ast })(Y-Y^{\ast })-(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })(Y-Y^{\ast }))+\left(\frac{Z-Z^{\ast }}{Z}\right)(\mathit{\lambda }(Y-Y^{\ast })-(d+\mathit{\mu })(Z-Z^{\ast })),\Rightarrow \frac{dV}{dt}=\mathrm{\Lambda }\left(\frac{X-X^{\ast }}{X}\right)-\mathit{\beta }\left(\frac{{(X-X^{\ast })}^2}{X}\right)(Y-Y^{\ast })-\mathit{\mu }\left(\frac{{(X-X^{\ast })}^2}{X}\right)+\mathit{\beta }(X-X^{\ast })\left(\frac{{(Y-Y^{\ast })}^2}{Y}\right)-(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu })\left(\frac{{(Y-Y^{\ast })}^2}{Y}\right)+\mathit{\lambda }(Y-Y^{\ast })\left(\frac{Z-Z^{\ast }}{Z}\right)-(d+\mathit{\mu })\left(\frac{{(Z-Z^{\ast })}^2}{Z}\right),\Rightarrow \frac{dV}{dt}=\mathrm{\Lambda }\left(\frac{X-X^{\ast }}{X}\right)-\left(\frac{{(X-X^{\ast })}^2}{X}\right)(\mathit{\beta }(Y-Y^{\ast })+\mathit{\mu })+\left(\frac{{(Y-Y^{\ast })}^2}{Y}\right)(\mathit{\beta }(X-X^{\ast })-(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu }))-(d+\mathit{\mu })\left(\frac{{(Z-Z^{\ast })}^2}{Z}\right)+\mathit{\lambda }\left(\frac{Z-Z^{\ast }}{Z}\right)(Y-Y^{\ast }),\Rightarrow \frac{dV}{dt}=\mathrm{\Lambda }-\frac{\mathrm{\Lambda }{X}^{\ast }}{X}-\mathit{\beta }Y\left(\frac{{(X-X^{\ast })}^2}{X}\right)+\left(\frac{{(X-X^{\ast })}^2}{X}\right)(\mathit{\beta }{Y}^{\ast }-\mathit{\mu })+\mathit{\beta }X\left(\frac{{(Y-Y^{\ast })}^2}{Y}\right)-(\mathit{\beta }{X}^{\ast }+(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu }))\left(\frac{{(Y-Y^{\ast })}^2}{Y}\right)-(d+\mathit{\mu })\left(\frac{{(Z-Z^{\ast })}^2}{Z}\right)+\mathit{\lambda }Y-\mathit{\lambda }{Y}^{\ast }-\frac{\mathit{\lambda }{Z}^{\ast }Y}{Z}+\frac{\mathit{\lambda }{Z}^{\ast }{Y}^{\ast }}{Z}.$$(C)

Rearranging the positive and negative terms in (C), we obtain(D) $$\frac{dV}{dt}=X-Y,$$(D)

where $X=\mathrm{\Lambda }+(\mathit{\beta }{Y}^{\ast }+\mathit{\mu })\left(\frac{{(X-X^{\ast })}^2}{X}\right)+\mathit{\beta }X\left(\frac{{(Y-Y^{\ast })}^2}{Y}\right)+\mathit{\lambda }Y+\frac{\mathit{\lambda }{Z}^{\ast }{Y}^{\ast }}{Z}$

and $Y=\frac{\mathrm{\Lambda }{X}^{\ast }}{X}+\mathit{\beta }Y\left(\frac{{(X-X^{\ast })}^2}{X}\right)+(\mathit{\beta }{X}^{\ast }+(\mathit{\gamma }+\mathit{\lambda }+\mathit{\mu }))$$$\left(\frac{{(Y-Y^{\ast })}^2}{Y}\right)+(d+\mathit{\mu })\left(\frac{{(Z-Z^{\ast })}^2}{Z}\right)+\mathit{\lambda }{Y}^{\ast }+\frac{\mathit{\lambda }{Z}^{\ast }Y}{Z}.$$

From (D), if X < Y, then $\frac{dV}{dt}$ will be negative definite, i.e. $\frac{dV}{dt}\le 0$. Also, $\frac{dV}{dt}=0$ if and only if $X=X^{\ast },Y=Y^{\ast }$ and $Z=Z^{\ast }$. Therefore, the largest compact invariant set in $\{(X^{\ast },Y^{\ast },Z^{\ast })\in \mathrm{\Gamma }:\frac{dV}{dt}=0\}$ is the singleton set {E^*}, where {E^*} is the endemic equilibrium. Hence, by LaSalle’s invariant principle, for $R_0>1,$ it implies that the endemic equilibrium is globally asymptotically stable in Γ.